The Effect of Temperature on Mechanical Resistance of the Native and Intermediate States of I27

Abstract

We investigated the effect of temperature on the mechanical unfolding of I27 from human cardiac titin, employing a custom-built temperature control device for single-molecule atomic force microscopy measurement. A sawtooth pattern was observed in the force curves where each force peak reports on the unfolding of an I27 domain. In early unfolding events, we observed a “hump-like” deviation due to the detachment of β-strand A from each I27 domain. The force at which the humps appear was ∼130 pN and showed no temperature dependence, at least in the temperature range of 2°C–30°C. The hump structure was successfully analyzed with a two-state worm-like chain model, and the Gibbs free energy difference of the detachment reaction was estimated to be 11.6 ± 0.58 kcal/mol and found to be temperature independent. By contrast, upon lowering the temperature, the mean unfolding force from the partly unfolded intermediate state was found to markedly increase and the unfolding force distribution to broaden significantly, suggesting that the distance (x_u) between the folded and transition states in the energy landscape along the pulling direction is decreased. These results suggest that the local structure of β-strand A are stabilized by topologically simple local hydrogen-bond network and that the temperature does not affect the detachment reaction thermodynamically and kinetically, whereas the interaction between the β-strands A′ and G, which is a critical region for its mechanical stability, is strongly dependent on the temperature.

INTRODUCTION

Many proteins are required to resist or respond to mechanical perturbation as part of their function. To understand how proteins achieve this diversity of response, it is necessary to measure the effects of mechanical extension and the resultant force on single proteins, which is the functional form of many proteins. Over the past decade single-molecule force techniques, particularly single-molecule force spectroscopy using atomic force microscopy (AFM), has allowed the mechanical properties of many proteins to be characterized. To perform this technique, a single protein molecule is tethered between the AFM cantilever and a substrate mounted on an AFM stage and stretched at a known pulling speed, incrementally loading force onto the protein. At a certain force (determined by the mechanical strength of the protein, the scaffold in which the protein is held, and the loading rate), the protein unfolds and the measured force rapidly decreases, providing the fingerprint that allows observation of the mechanical unfolding of an individual protein molecule. Since the force is applied to the tethered protein at specific points (the N- and C-termini in most cases), the reaction coordinate of the mechanical unfolding is well defined in contrast with chemical and thermal unfolding (see Best and Clarke (1) for review).

Single-molecule mechanical unfolding measurements using the AFM are typically performed under ambient conditions, and although much progress has been made in determining the generic features of proteins that endow mechanical strength (see Forman and Clarke (2), Sotomayor and Schulten (3), and Sulkowska and Cieplak (4) for review), there are relatively few studies on the effect of environmental factors such as chemical denaturant (5,6), solvent (7,8), pH (9), or temperature (10–13) on the mechanical stability of proteins. However, the stability of proteins is determined by a variety of intramolecular interactions whose relative importance can be modulated by the physicochemical properties of the environment. Consequently, a small change in the environment may significantly affect the energy landscape of (un)folding. To interpret the results of experiments performed in vitro in the context of biological function in vivo, it is thus necessary to understand how these environmental parameters affect the mechanical strength of a range of proteins with differing secondary structure, topology, and thermodynamic stability.

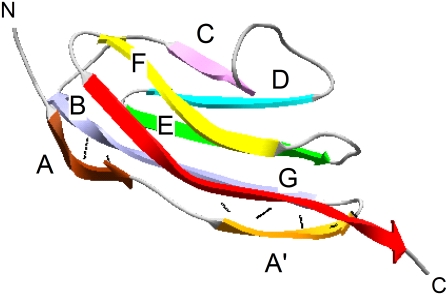
To date, the effect of temperature on the mechanical resistance of proteins is not well understood and has been investigated experimentally in detail on only spectrin (11) and ddFLN4 (12). Surprisingly, the effect of temperature on I27, a paradigm extensively studied by both experimental (14–18) and theoretical (19–21) approaches, has never been investigated. The I27 domain (or I91 using the nomenclature of Bang et al. (22)) of the distal region of the I-band segment of human cardiac titin is an 89 amino acid β-sandwich immunoglobulin (Ig) domain (Fig. 1). In titin, ∼300 similar Ig domains are arranged in tandem (interspersed with other domains) and are thought to play an important role as a molecular spring in muscle (23). Previous AFM experiments combined with steered molecular dynamics simulations showed that I27 unfolds by a three-state mechanism in which strand A first detaches from the rest of the protein, increasing the end-to-end length by ∼7 Å leading to a “hump” in the rising edge in the force-extension profiles of early unfolding events (15,24). This intermediate, which is more mechanically robust than native I27 when extended at rates accessible to the AFM, then unfolds by the simultaneous rupture of the hydrogen-bond network between strands A′ and G (18,25). However, at much slower pulling speeds than that used in typical AFM measurements, Williams et al. predicted that the native state unfolds directly to the unfolded state (17).

FIGURE 1.

Schematic representation of a single I27 domain (1TIT) (49). β-strands are depicted as colored ribbons. Black lines show a network of hydrogen bonds that link strand A to strand B and strand A′ to strand G. The figure was drawn using Swiss-PDB Viewer (50).

In this study, we investigated the influence of temperature on the mechanical resistance of I27 in detail using AFM equipped with a custom-built temperature control device. At typical AFM pulling speeds, the unfolding process from both the native and intermediate states are observed, allowing the effect of temperature to be investigated on these different species. We show that temperature does not affect the stability of local structure of the strand A, but weakened the interaction between the strand A′ and G significantly.

MATERIALS AND METHODS

Single-molecule force spectroscopy

The construction of (C47S, C63S I27)₅, its overexpression, and its purification were performed as described previously (16,26). All experiments were performed using a commercial AFM, MFP-1D (Asylum Research, Santa Barbara, CA). To control the temperature, a Peltier device was attached onto the AFM stage. Temperature was monitored using a thermocouple dipped in the sample buffer and located closely to the cantilever. To avoid unwanted contraction/expansion of the Peltier module by the fast change of electronic current through the Peltier module (27), no automatic feedback device (such as a proportional–integral–derivative controller) was used. Instead, we applied a constant current to the Peltier module. Slow temperature drift was observed, so the current output was finely adjusted manually every 30 min to bring the temperature back to the target value. In this way, temperature was controlled with a precision of 0.5°C. Using this device, the temperature of the sample chamber can be controlled from 0°C to 40°C.

The sample chamber of our AFM is not sealed, so these experiments were performed between 2°C and 30°C to minimize solvent evaporation, although other groups reported measurements at more than 50°C using other commercially available AFMs (10). Short cantilevers (BioLever A, Olympus Optical, Tokyo, Japan) with spring constants between 20 and 40 pN/nm were used. The spring constant of each cantilever was measured using the thermal noise method (28) under phosphate buffer saline at each temperature. Typically 20 μl of protein solution (0.05 mg/ml) was immobilized onto a template with a freshly stripped gold surface via the sulphydryl groups of two cysteine residues at the C-terminus of the polyprotein. After incubation for 5 min, the gold surface was rinsed with phosphate buffer saline to remove nonspecifically bound proteins.

Unfolding force distributions were obtained by measuring the “transition force” (see below) and the rupture force (reporting on the unfolding of the intermediate state) from many approach-retract cycles performed at the same retraction rate. The data were then binned and force-frequency histograms were constructed. To estimate experimental error, triplicate force distributions were accumulated for each retraction rate (50, 300, 1000, and 5000 nm/s) at each temperature (2°C, 10°C, 20°C, and 30°C) using a new cantilever for each data set.

Analysis of the hump region in force-extension curve

To analyze the hump seen in the force-extension curve of (C47S, C63S I27)₅, which reflects the partial unfolding reaction of strand A from the rest of the protein (15), we applied a two-state worm-like chain (WLC) model. A similar two-state model has previously been successfully applied to analyze the unfolding-refolding transition of the coiled-coil region of the myosin rod (29) and the force-induced conformational change of biopolymers (30,31). As for these other studies, it is assumed that each domain maintains a thermal equilibrium between the native state and the intermediate state during mechanical extension. The effect of an applied force (F) can be considered to lower the Gibbs free energy difference between the native state and the partly unfolded state. The effective Gibbs free energy difference under the force (ΔG_F) is modified as ΔG_F = ΔG₀ − FΔL_hump, where ΔG₀ is the Gibbs free energy difference under zero force and ΔL_hump is the increase in the contour length of a single I27 domain as a result of the partial unfolding. Therefore, the fraction of the partly unfolded domain under the force (γ(F)) is derived by the Gibbs equation as

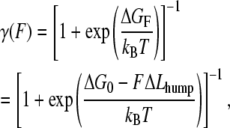(1)

where k_B is the Boltzmann constant and T is temperature. The total contour length (L′) of a polyprotein under the force F increases by nγ(F)ΔL_hump from the contour length at zero force (L₀) where n is the number of folded domains in equilibrium. Substituting the contour length in conventional WLC model, we obtain

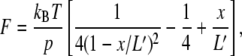(2)

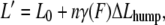where p is the persistent length and x is the extension. We defined F_t = ΔG₀/ΔL_hump (i.e., the force at which γ(F) = 1/2) as the transition force. We analyzed the peaks in which n ≥ 3 and used 6.6 Å as ΔL_hump (15) and 0.4 nm as p (16).

Transition-state analysis

In the analysis of unfolding force data, chemical kinetic theory was used to obtain the rate constant for unfolding at zero force (k_u) and the distance between the folded state and the unfolding transition state (x_u), as described previously (32). We analyzed the distributions of the unfolding forces measured at various pulling speeds. Briefly, the unfolding rate constant at force F is

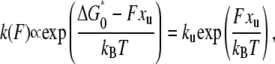(3)

where ΔG*₀ is the activation free energy at zero force. The rate constant is not measured directly but inferred from the distribution of unfolding force. The probability distribution for unfolding is

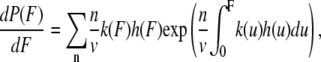(4)

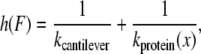(5)

where n is the unfolding event number, v is the pulling speed, h(F) is the compliance of the cantilever and protein, k_cantilever is the force constant of the cantilever, and k_protein(x) is that of protein concatamer, which is derived from the WLC model. To obtain x_u and k_u, the four force distributions measured at 50, 300, 1000, and 5000 nm/s were fitted simultaneously using a global nonlinear least-squares method with software, Igor Pro 5.05A (Wavemetrics, Lake Oswego, OR).

Estimation of energy landscape roughness

We estimated the roughness according to the method described by Nevo et al., in which the variation in x_u with temperature taken into account

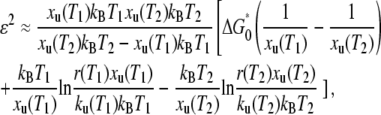(6)

where r(T₁) and r(T₂) are the loading rates (ΔF/Δt) that give rise to an identical unfolding force (F) at temperatures T₁ and T₂ (33). These values were calculated from the pulling speed v using the compliance of the system h(F) (Eq. 5) by r(T) = v/h(F).

RESULTS

Force-extension curve

Fig. 2 shows a typical force-extension profile for the mechanical unfolding of the I27 polymer used in this study (C47S, C63S I27)₅ at 2°C and 30°C. This variant has been studied extensively in both homo- and heteropolymeric forms (16,34) and has been shown to unfold in a three-state manner despite a decrease in its mechanical strength relative to previously studied variants (14–17). Consistent with these data, a characteristic sawtooth pattern was observed in which each force peak reflects the unfolding of an I27 domain. The difference in contour length (ΔL) between a folded and unfolded I27 domain (measured by fitting a WLC model to successive unfolding events) was found to be 28 ± 0.6 nm at 30°C, in accord with previous data (16,17). At 2°C, ΔL was found to be 29 ± 1.5 nm, showing the expected temperature independence of this parameter.

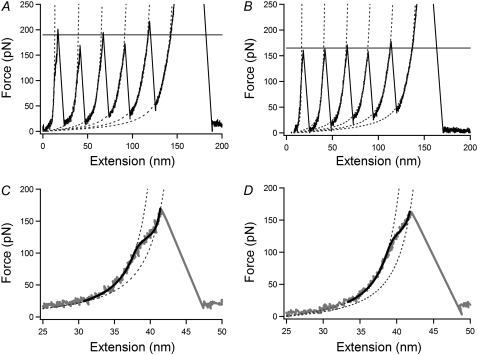
FIGURE 2.

Force-extension curve of (C47S, C63S I27)₅ at 2 (A and C) and 30°C (B and D) at an extension speed of 50 nm/s. (A and B) The characteristic sawtooth pattern in which there are five unfolding peaks. The dotted lines are fits using a conventional WLC model. The horizontal line represents the average of the five unfolding peak forces. (C and D) Enlargement of the second unfolding event in (A and B) showing the hump-like deviation. Dotted lines show a standard WLC fit to the force extension profile before and after detachment of strand A. The black line is a fit to the two-state WLC model.

Examination of the rising edge of the force-extension profiles of early unfolding events revealed a deviation from the expected WLC behavior for an unstructured polypeptide chain at ∼130 pN (Fig. 2, C and D). This hump reports on the conformational transition from the native to the intermediate state, which has been observed previously for I27 and is discussed above. The magnitude of the native to intermediate transition force was independent of the pulling speeds applied in this study (50–5000 nm/s; Fig. 3 E), implying that the reaction is a reversible process and is on a timescale much faster than the rate at which the proteins are extended. Interestingly, a similar result was reported for the unfolding of the coiled-coil domain of myosin (29) where the topologically simple coiled-coil allows fast refolding rates, rendering its mechanical unfolding reversible. The intermediate of I27 is highly native-like and surprisingly stable (ΔG_UN = 4.8 kcal/mol) (24) and seems to involve only the breakage of the local hydrogen-bond network between strands A and B. Topological simplicity and dissociation of a few localized hydrogen bonds may thus be crucial features of fast and reversible unfolding reactions and may provide a generic method by which structural proteins can resist small increases in force without undergoing catastrophic unfolding.

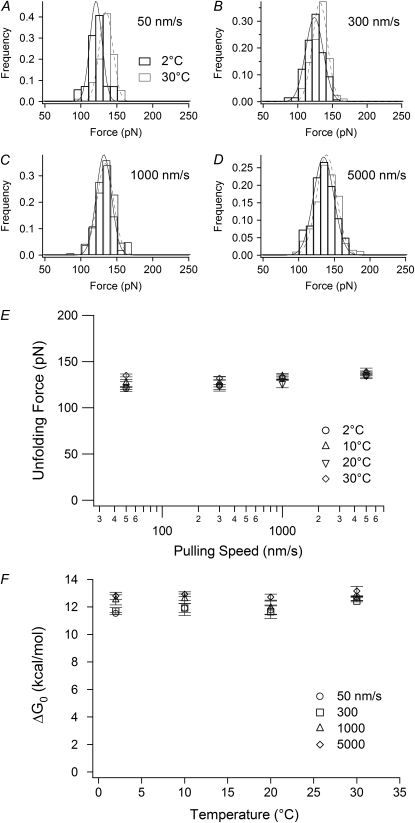
FIGURE 3.

The temperature and pulling speed dependence of the transition force. (A–D) Histograms of the transition force measured at 2°C and 30°C at pulling speeds of 50, 300, 1000, and 5000 nm/s, respectively. The solid lines are Gaussian fits. (E) Pulling speed dependence of the transition force at various temperatures. (F) The Gibbs energy difference between the native state and the intermediate state obtained from the two-state WLC analysis. Error bars represent ±SE of triplicate data sets.

To accurately quantify the transition force, the shape of the hump in the force-extension profile was fitted to a two-state WLC model (Materials and Methods, Eq. 2, Fig. 2, C and D). In the two-state WLC model, it is assumed that the transition rate between the native and intermediate states is at thermal equilibrium during pulling experiments and that under application of force the equilibrium shifts to favor the more extended intermediate state. We defined the transition force as the force at which the population of each state is identical. Our two-state WLC analysis provides the Gibbs energy difference between the native state and the intermediate state at zero force (ΔG₀) as a fitting parameter (see Materials and Methods). The value of ΔG₀ was estimated to be 13.2 kcal/mol with the force-extension profile shown in Fig. 2 C using ΔL_hump of 6.6 Å, which was similar to the mechanical work previously estimated from the area of the hump in the force-extension curve, 10.1 ± 0.63 kcal/mol (15). Meanwhile, Williams et al. estimated the value as 3.2 kcal/mol, assuming the distance between the native state and the intermediate state on the energy landscape to be 2.2 Å, which is the difference in x_u between wild-type (unfolding barrier between the intermediate and unfolded states) and V86A mutant (unfolding barrier between the native and unfolded states).

The transition force does not depend on temperature

The influence of temperature on the force at which the native state unfolded to the intermediate state (the transition force) and the stability difference between each state (ΔG₀) was investigated over a range of pulling speed (50–5000 nm/s) and temperature (2°C, 10°C, 20°C, and 30°C). Representative force distributions obtained at 2°C and 30°C for each speed are shown in Fig. 3, A–D, and summarized in Fig. 3 E and Table 1. Neither the transition force, the width of the force distribution, nor ΔG₀ showed either a temperature or pulling speed dependence (Fig. 3, E and F). The average ΔG₀ was found to be 11.6 ± 0.58 kcal/mol (∼20 k_BT).

TABLE 1.

Summary of mechanical unfolding data for I27

Temperature (°C)			Mode force (pN) at 50 nm/s	n	Mode force (pN) at 300 nm/s	n	Mode force (pN) at 1000 nm/s	n	Mode force (pN) at 5000 nm/s	n	ku (s−1)	xu (nm)
2	Take 1	Peak	190	72	216	124	229	83	280	87	0.0037	0.18
		Hump	123	28	126	39	131	29	140	28
	Take 2	Peak	182	54	214	42	239	56	273	83	0.0023	0.19
		Hump	120	26	125	13	136	18	128	22
	Take 3	Peak	188	60	206	118	231	124	275	112	0.0027	0.19
		Hump	120	21	121	43	128	52	138	29
10	Take 1	Peak	177	79	201	116	229	107	265	126	0.0017	0.21
		Hump	123	28	121	45	128	39	142	35
	Take 2	Peak	178	107	208	124	231	110	259	91	0.0011	0.22
		Hump	135	33	140	24	139	31	136	19
	Take 3	Peak	177	67	199	133	222	148	259	132	0.0024	0.22
		Hump	123	32	118	58	134	71	138	62
20	Take 1	Peak	169	46	186	82	206	62	247	48	0.0014	0.24
		Hump	127	13	132	39	131	28	138	27
	Take 2	Peak	167	61	198	45	212	101	245	114	0.0020	0.23
		Hump	130	23	128	23	130	41	137	48
	Take 3	Peak	161	105	192	159	216	115	253	101	0.0032	0.22
		Hump	112	13	113	29	117	32	132	37
30	Take 1	Peak	155	164	173	214	192	182	222	165	0.0017	0.27
		Hump	137	25	130	70	131	68	132	71
	Take 2	Peak	159	60	178	102	198	88	224	97	0.00095	0.28
		Hump	132	12	135	31	134	32	138	28
	Take 3	Peak	153	131	175	183	194	176	229	227	0.0016	0.27
		Hump	136	26	131	51	137	75	146	65

Unfolding from the intermediate state depends strongly on the temperature

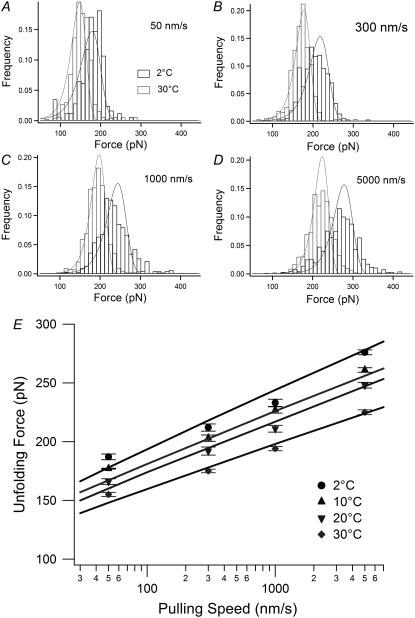
In contrast to the transition force, the unfolding force of the intermediate was found to be significantly dependent on temperature (Fig. 4 and Table 1). Upon lowering the temperature, the unfolding force showed a remarkable increase at all pulling speeds examined. For example, at a pulling speed of 300 nm/s, the mode unfolding force was 175 ± 1.5 pN (the mean ± SE of triplicate data sets) at 30°C but increased to 212 ± 3.1 pN at 2°C. Moreover, a decrease in temperature was found to significantly broaden the distribution of unfolding forces (Fig. 4, A–D), suggesting a temperature-induced change in the underlying unfolding energy landscape. To quantify these effects, we fitted the unfolding force distributions at each temperature to an analytical model based on Bell's equation (35) to obtain the parameters k_u (the unfolding rate constant at zero force) and x_u (the distance between the intermediate state and the transition state).

FIGURE 4.

The temperature and pulling speed dependence of the unfolding force. (A–D) The histograms of the unfolding force measured at 2°C and 30°C at pulling speeds of 50, 300, 1000, and 5000 nm/s, respectively. The solid lines are global fits with Eq. 4. (E) The pulling speed dependence of the unfolding force. The mode forces are plotted and error bars represent ±SE of triplicate data sets.

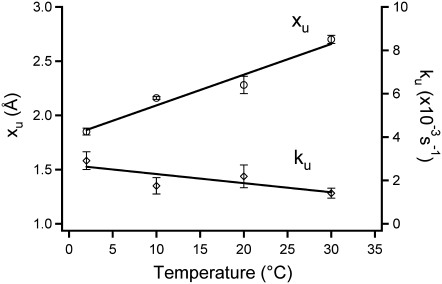
Fig. 5 shows the temperature dependence of these parameters and reveals that x_u increases significantly as temperature is increased (a 1.4-fold increase from 2°C (x_u = 1.9 Å) to 30°C (x_u= 2.7 Å)). On the other hand, k_u became slightly smaller upon increasing temperature. This might sound counterintuitive, but similar behavior has been reported for the Ig-like ddFLN4 domain (12). As k_u is related to the activation energy of the mechanical unfolding (ΔG*₀) by the Arrhenius equation (ΔG*₀ = k_BT ln(A/k_u), where A is the Arrhenius prefactor), it is possible to quantify the height of the unfolding barrier. The activation energy was found to increase slightly as temperature increased (ΔG*₀ = 20 and 23 k_BT at 2°C and 30°C, respectively, assuming A is 10⁷ s⁻¹(12)). An activation energy of 23 k_BT (14 kcal/mol) is slightly smaller than that of wild-type I27 estimated from experiment at room temperature (14) and simulation (20), ∼22 kcal/mol. This is because the mechanical strength of C47S, C63S I27 is slightly decreased relative to wild-type (16).

FIGURE 5.

The temperature dependence of the parameters which determine the energy landscape of the mechanical unfolding from the intermediate state to the unfolded state of I27 obtained from the transition-state analysis. These parameters are the distance between the intermediate state and the transition state (x_u, open circles) and the unfolding rate at zero force (k_u, open diamonds). The data represent mean ± SE of triplicate data sets.

Energy landscape of the mechanical unfolding

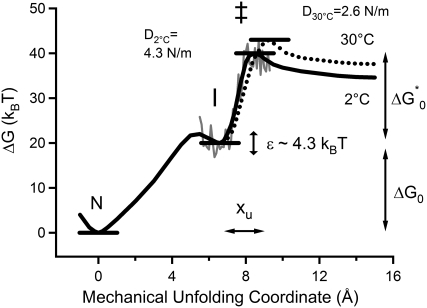
The parameters obtained from this analysis can be used to sketch a one-dimensional unfolding energy landscape for I27 at different temperatures (Fig. 6). Our analysis reveals that temperature has no effect on the Gibbs energy difference between the native and intermediate states but strongly affected the unfolding process from the intermediate to the unfolded state. Increasing temperature resulted in the remarkable increase of x_u and a slight increase of the activation energy. The observed decrease of unfolding force with increase of temperature was attributed to the increase of x_u.

FIGURE 6.

The energy landscape of the mechanical unfolding of I27 at 2°C (solid black line) and 30°C (dotted line). N, I, and ‡ represent the native state, the intermediate state, and the transition state of the intermediate state unfolding to the denatured state, respectively. The solid gray line represents roughness of the energy landscape estimated by the method of Nevo et al. (33). D_2°C and D_30°C are the spring constants of I27 (see Discussion).

Instead of temperature-softening effects, changes in mechanical strength can be interpreted in terms of the relative roughness of the landscape over which proteins traverse to unfold. The energy landscape of protein folding is thought not to be smooth but to have an intricate, rugged structure (36,37). Hyeon and Thirumalai described a method to extract the energy landscape roughness (ɛ) from single-molecule force spectroscopy data obtained at different temperatures (38).

Using this method (Materials and Methods, Eq. 6), the value of ɛ was estimated to be 4.3 k_BT (Fig. 6) both at 200 pN and 220 pN, which was consistent with ∼4–6 k_BT for the unfolding of soluble and membrane proteins (12,39), ∼5–8 k_BT for the dissociation of proteinaceous (33) and nonproteinaceous (40) ligands from proteins, and 4 k_BT in the force-induced conformational change of dextran (41).

DISCUSSION

In this study, single-molecule force spectroscopy was used to investigate the effects of temperature on the mechanical unfolding behavior of I27, the paradigm of the field. I27 unfolds in a three-state mechanism: at a force of ∼130 pN strand A detaches from the core of protein, extending the end-to-end length of I27 by ∼7 Å and causing a characteristic hump in the force-extension profile of I27. At a higher force (∼200 pN), this highly native-like intermediate unfolds in an all-or-none manner. Although the latter unfolding event is easy to quantify, the transition force of the initial unfolding event is more difficult to measure. Fitting the hump with a two-state WLC model has allowed the force at which the intermediate was populated to be quantified. This has, first, allowed the pulling speed dependence of transition to be measured and, second, the effects of temperature on this transition to be directly compared to that for the unfolding of the intermediate state for the first time to our knowledge.

The first transition force (native to intermediate state) is independent of temperature. The results showed that the Gibbs energy difference of the detachment reaction (ΔG₀) was also independent of temperature over the range examined here (2°C–30°C). The Gibbs energy is related to the enthalpy change (ΔH₀) and entropy change (ΔS₀) of a reaction by the Gibbs-Helmholz equation, ΔG₀ = ΔH₀ − TΔS₀. One possible explanation is that the reaction is mainly enthalpic (ΔH₀ ≫ TΔS₀) and temperature dependence of the enthalpy change of the reaction is negligible in this temperature range, similar to the force-induced conformational change of dextran (27). The other explanation is that the temperature-induced change of enthalpy is compensated by that of the entropic contribution, which is often found in biomolecule-related reactions (see Winzor and Jackson (42) for a review).

By contrast, the force at which the intermediate unfolded showed a significant dependence on the temperature. To interpret the temperature dependence of the unfolding forces, we performed a transition-state analysis based on the Bell model to obtain a basic description of the energy landscape of unfolding. Fitting force distributions obtained at the same speed but different temperatures to this model (Fig. 4) indicated that an increase in temperature perturbs the mechanical unfolding energy landscape by increasing the distance between the intermediate state and the transition state (x_u increased from 1.9 Å to 2.7 Å between 2°C and 30°C). The temperature softening of I27 (anti-Hammond behavior) can also be quantified in terms of changes in its “spring constant” (D) as a function of temperature. The protein spring constant, introduced by Schlierf and Rief, can be estimated assuming a parabolic function for the free energy, G(x) = 1/2 × Dx², analogically to the potential energy of Hooke's spring (12). The value of D was estimated roughly by substituting x as x_u and G(x_u) as ΔG*₀ in the above equation. The value of D for I27 reduces by half with increasing temperature (4.3 N/m at 2°C and 2.6 N/m at 30°C), indicating the nonnegligible temperature effect on the dynamics of the I27 domain.

What is the molecular basis of this temperature effect? Early studies by Fernandez, Schulten, and co-workers showed that the key event of the unfolding of the intermediate is the rupture of hydrogen bonds between A′ and G strands (15,19). Replacement of residues in the A′ strand with proline was found to increase x_u by 2.0–3.5 Å and to increase ΔG*₀ slightly relative to wild-type (25). As the effect of these mutations is similar to the effect of increasing temperature, it may imply that both perturbations cause the destabilization of the hydrogen bonds between A′ and G β-strands.

The influence of temperature on the mechanical unfolding of I27 has been investigated by simulation by two groups (21,43). In accord with our data, both studies found that the unfolding force decreased at higher temperatures. Each group, however, suggested slightly different molecular mechanisms. Pabón and Amzel suggested that the force does not directly break the interstrand hydrogen bonds between A′ and G strands; it destabilizes them to be replaced by hydrogen bonds to water molecules and temperature makes this process faster (43). By contrast, Cieplak et al. suggested that although most of the stress is carried through the bonds between A′ and G strands, other bonds contribute to the mechanical resistance indirectly by stabilizing the geometry of the A′ and G strands (21). In addition, experimental studies have also suggested the importance of the core region in stabilizing interactions between the A′ and G strands. Best et al. investigated the structure of the transition state for I27 unfolding by using Φ-value analysis and found that side-chain interactions between the A′ and G strands and interactions in the A′-B and the E-F loops contribute to the mechanical strength of I27 in addition to the hydrogen-bond network (44). Core mutations have also been found to modulate the mechanical strength of fibronectin type III domains (45) and are also thought to be important for the mechanical strength of protein L (32).

The effect of temperature on protein mechanical strength has been described previously for several proteins. Preiner et al. showed, using Jarzynski's equality, that the equilibrium free energy difference between the folded state and unfolded state of the membrane protein bacteriorhodopsin is temperature independent (46). Bullard et al. investigated mechanical unfolding/refolding of projectin, a titin-like protein in invertebrate muscles, and showed an increase in unfolding force at lower temperature (47). They also found that refolding becomes much slower at lower temperatures, suggesting the cooperative nature of the folding mechanism. Law et al. studied the first four N-terminal repeats of all α-helical erythroid βI spectrin (11). They noted a temperature-softening effect whereby unfolding forces decreased as the temperature approached the helix melting temperature. In addition, fewer simultaneous tandem repeat unfolding events were observed. This was thought to be due to the melting of the helical linker between each repeat which otherwise propagates the mechanical effects across adjacent repeats (11). Schlierf and Rief studied the fourth domain of filamin from Dictyostelium discoideum (ddFLN4), an Ig-like β-sandwich protein (12).

Similarly to I27, ddFLN4 unfolds by a three-state mechanism: the native state unfolds at a force of 63 pN, populating a partially unfolded intermediate state. However, by contrast to I27, the intermediate is highly unfolded (∼40 amino acids are removed) (48), which presumably disrupts the hydrophobic core of ddFLN4 that is intact in the intermediate of I27. In contrast to I27, significant temperature softening was observed for both unfolding events of ddFLN4: the x_u for the unfolding from the native state to the intermediate state at 37°C was 2.9-fold larger than that at 5°C, and x_u from the intermediate state to the unfolded state increased 1.7-fold. In this case it is thought that the rupture of hydrophobic interactions in the core is more important for reaching the transition state compared to I27 (12). Temperature softening was thus thought to change the position of the rate-limiting transition state by altering the relative importance of hydrophobic interactions and hydrogen bonding to the mechanical strength of ddFLN4. Comparison of the stiffness of each domain and how this varies with temperature also suggests that I27 is a less compliant domain. At lower temperature, the protein spring constants (D) for I27 and ddFLN4 are 4.3 N/m (2°C) and 1.72 N/m (5°C), respectively. These reduce by a factor of 2 (D_I27 = 2.6 N/m) and 7 (D_ddFLN4 = 0.25 N/m) on heating to 30°C and 37°C.

The difference in temperature effects between the native and intermediate states of I27 and the difference in magnitude between the temperature softening of the intermediate of I27 and ddFLN4 suggest that the temperature dependences of x_u may reflect the relative importance of hydrophobic interaction to hydrogen bonds in the formation of the transition state of each protein. The 1.4-fold temperature-induced increase of x_u observed for I27 taken together with the mutational data described above suggests that it is likely that not only the hydrogen bonds between A′ and G strands but also other bonds located in the vicinity of the A′ and G strands are related to the mechanical resistance of the molecule. In addition to these effects, an increase in temperature may increase protein dynamics local to these regions, some of which may facilitate the breakage of stabilizing interactions between the A′ and G strands.