Abstract
The high total concentration of macromolecules, often referred to as macromolecular crowding, is one of the characteristic features of living cells. Macromolecular crowding influences interactions between many types of macromolecules, with consequent effects on, among others, the rates of reactions occurring in the cell. Simulations to study the influence of crowding on macromolecular association rate were performed using a modified Brownian dynamics protocol. The calculated values of the time-dependent self-diffusion coefficients in different crowding conditions are in a very good agreement with those obtained by other authors. Simulations of the complex formation between the monoclonal antibody HyHEL-5 and its antigen hen egg lysozyme, both represented at atomic level detail, show that the calculated association rates strongly depend on the volume excluded by crowding. The rate obtained for the highest concentration of crowding particles is greater than twofold higher than the rate for proteins without crowding.
INTRODUCTION
The high total concentration of macromolecules is one of the characteristic features of living cells. Typically, proteins, nucleic acids and other macromolecules occupy ∼20–30% of the total volume of cytoplasm (1–3). Because no single macromolecular species is present at such high concentrations, but many different species taken together exclude a certain part of the volume, media such as cellular plasma are referred to as crowded, not concentrated (4,5).
Transport properties of macromolecules, such as diffusion coefficients, are significantly reduced by crowding. The excluded volume-induced change of time-dependent diffusion coefficients applies to molecules regardless of their size, but mobility of bigger molecules will be reduced more than that of smaller molecules (3). Macromolecular crowding has been observed to influence interactions between many types of macromolecules, with consequent effects on rate and equilibrium of reactions (6–8). The lowered diffusion decreases the rate of diffusion-controlled reactions, such as in some of the enzyme-substrate reactions. It has been theoretically predicted and experimentally proven that crowding can enhance reactions such as: self-association (6,9,10), association (4,11), polymerization (for example, in amyloid fibril formation (12)), and protein folding (6,10,13,14). In general, the presence of a crowding agent occupying a certain part of the volume shifts the equilibrium toward more compact, aggregate forms of macromolecules involved (3). The impact of crowding on rates of such reactions depends on the level of excluded volume, but also on sizes and shapes of crowding particles. The speeding influence can be explained by the so-called excluded volume effect. The effective concentration of reacting molecules is higher than their actual concentration due to volume excluded by crowding particles. From the thermodynamics point of view, the activity of solutes increases with excluded volume (4). The microscopic mechanism underlying the effect of crowding on the protein-protein association rates has not been addressed so far.
The above-mentioned experimental results obtained with different crowding agents led to very interesting results that are often very difficult to interpret quantitatively in terms of influence of volume exclusion on reaction rates in biological media. The main reason for this seems to be the problem with choosing proper crowding agents mimicking the cytoplasm properties (1). The crowding agent should have an adequate molecular weight range; should be soluble in water at high concentrations; should not aggregate; should consist of globular molecules; and should not interact with reacting molecules under test except for steric repulsion. None of the crowding agents that have been used so far actually fulfills all the conditions mentioned. This is why creating a theoretical model of macromolecular crowding, allowing for prediction of its influence on biochemical reactions, seems to be plausible. Several simulations regarding the influence of crowding on processes such as escape of a protein from GroEL chaperonin machinery (15), or protein folding and stability (16–19), have already been performed. In this work, we present a simple model allowing us to investigate the influence of crowding on protein-protein association rates from the microscopic point of view.
METHODS
Brownian dynamics
Brownian dynamics is the main computational method chosen for establishing the influence of crowded environment on association rates. It is a widely used technique for computations of biomolecular diffusional association rates (20–25). In this method, particles are subjected to random diffusional translational and rotational movements, mimicking effects of collisions with solvent molecules, which are not explicitly represented. The positions of molecules (Δr) at every time step (Δt) are computed according to the Ermak-McCammon equation (26),
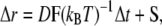 |
where D is the translational diffusion tensor (assumed here to be isotropic), F is the systematic interparticle force, kB is the Boltzmann constant, T is absolute temperature, and S is the random component of the displacement caused by collisions with solvent particles obeying the relationship
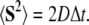 |
In the simulations, random displacement is taken from the Gaussian distribution. An analogical equation governs the rotational motion of each particle. The diffusion coefficient is obtained by means of Stokes-Einstein equations. In the case of translational motion, it is
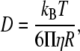 |
where η is the viscosity of the solvent and R is the Stokes radius of the macromolecule.
All simulations were performed in cubic boxes, while the classical Brownian dynamics is run in a spherical environment (for example see (22)). This was done due to the need to keep the number of particles in the system constant. To achieve this, periodic boundary conditions were applied, which is much more straightforward and computationally beneficial in the cube than in a sphere. Every simulation was started from random placement of molecules. Because of the cubical container, the calculation of the association rate had to be different from the classical Brownian dynamics. Here, the association rate depends on the number of occurrences of single association events in the simulation time. The association event is meant as mutual orientation of molecules taking part in the simulation, fulfilling simple geometrical criteria, namely—appropriately short distances between atoms known as interfacing the two proteins in the complex. Trajectories are run until the association takes place. In the macroscopic case, where one deals with a large number of reacting molecules, resulting in a large number of single associations, the rate is
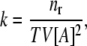 |
where nr is the number of single associations observed in the time T in conditions of volume V and concentration of the reactant [A]. If the concentration is treated as the number of molecules per volume, an expression appropriate for microscopic scale is obtained as
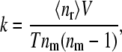 |
where 〈nr〉 is the average number of associations observed during the time T, and nm is simply the number of reactant molecules in the simulated environment. The “−1” term is a correction to macroscopic formula originating from the assumption that a single molecule cannot create a complex with itself. The temperature in all Brownian dynamics simulations was set to 298 K. All the molecules were represented as hard spheres except the last simulation, where full-atom representations of the reacting proteins were employed.
Simulations of the influence of macromolecular crowding on biomolecular association rates using Brownian dynamics are extremely time-consuming, especially in the case of the full-atom representation of the reactants. To obtain a certain level of statistical significance, every association has to occur many times. This is the main reason why far-reaching simplification in the simulated model of the crowding has been applied: the existence of any interactions except for hard steric repulsion was neglected. If a steric overlap between the molecules occurred during the simulation, the step of the dynamics was repeated. The number of steps that fail because of that depends on the longevity of the step. The timestep was set to 0.2 ps, which allows for keeping the number of repeated steps at a low level, namely <10%.
RESULTS
Spherical particle models
As the initial tasks, transport properties in the crowded media were calculated. The purpose of these simulations was only to check the performance of the software used. Next, the association rate of spherical particles in the presence of crowding was calculated.
Calculation of the time-dependent self-diffusion coefficients in different crowding conditions
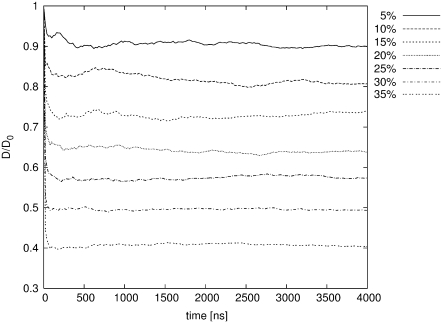
As a model of molecular species, for which the effective self-diffusion coefficients were calculated from the simulations, hard spheres of 18 Å radius were used. This size is considered the size of a typical small globular protein (27). Five-thousand such particles were placed in several cubic boxes of different size, giving excluded volumes ranging from 5 to 35%. Starting positions of all molecules were chosen randomly, the only limitation being that molecules could not overlap. Fig. 1 depicts molecules in 5 and 35% of excluded volume concentration. The diffusion coefficient (D) was calculated as
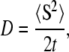 |
where 〈S2〉 is the mean of squared displacement vector in the time t. The results of these calculations are presented in Table 1 and Fig. 2. It is apparent that the observed diffusion coefficient strongly depends on excluded volume. In the case of 35% volume occupied by macromolecules, diffusion decreases more than twofold. This experiment was only a test for the system, a comparison with the previously obtained predictions. The results are very close to those obtained by Cichocki and Hinsen, who performed dynamics of hard spheres (28).
FIGURE 1.
Five-thousand spherical particles excluding 5% (a) and 35% (b) of the volume.
TABLE 1.
Dependence of observed self-diffusion coefficient (D) on percent of excluded volume; normalization factor D0 is the diffusion coefficient obtained for free spheres (without the crowding)
|
D/D0
|
||
|---|---|---|
| φ | Cichocki and Hinsen (28) | This work |
| 5.00% | 0.904 ± 0.6% | |
| 10.00% | 0.816 ± 2.3% | 0.817 ± 1.5% |
| 15.00% | 0.728 ± 0.9% | |
| 20.00% | 0.647 ± 1.7% | 0.641 ± 0.9% |
| 25.00% | 0.584 ± 0.9% | |
| 30.00% | 0.486 ± 1.2% | 0.496 ± 0.5% |
| 35.00% | 0.408 ± 0.7% | |
| 40.00% | 0.303 ± 1.4% | |
| 50.00% | 0.094 ± 1.4% | |
FIGURE 2.
Dependence of observed self-diffusion coefficient on the percentage of excluded volume.
Calculation of the association rate of two spherical particles in the presence of different crowding molecules
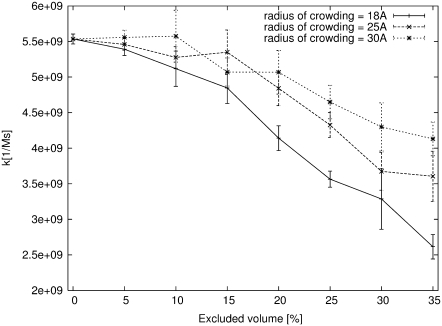
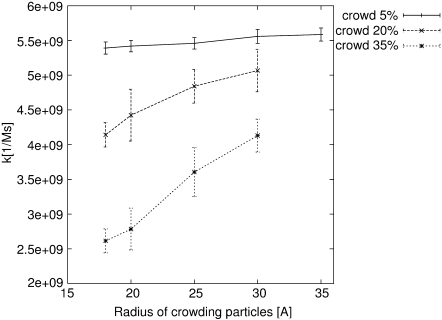
The association rates of spherical, centrosymmetrically active particles of 18 Å radius were calculated. In the simulations, two such particles were placed in a cubic box of volume 44444.44 nm3, giving 74.2 nM concentration. Reacting molecules shared the simulation box with crowding molecules. Hard spheres of the same radius (ranging in separate simulations from 18 to 35 Å) were used as the crowding molecules. For each of the crowding sphere radii, the simulations were repeated with excluded volumes ranging from 0 to 35%. Simulations were started with all molecules at random positions. The situation in which surfaces of reactants got closer than 2 Å to one another was considered as occurrence of the association. Then, molecules were randomly placed again and a new trajectory was started. Since the association rate is a macroscopic quantity, it was necessary to perform many repetitions of the whole procedure. Occurrence of the association can be considered as a rare event in the Poisson meaning, so its dependence on time can be described by a Poisson distribution. The standard error can then be simply estimated as the square root of the number of association events simulated. Results of these calculations are shown in Fig. 3, Fig. 4, and in Table 2. Without crowding, the molecules achieved a association rate of 5.53 × 109(±1.27%)[1/Ms], which is slightly less than the diffusion-limited association rate of hard spherical particles theoretically estimated by Smoluchowski (29)—∼7.80 × 109[1/Ms]. The association rate decreases in the presence of crowding: the greater the number of disturbing molecules in the solution, the higher the drop of association rate. The change of the rate depends not only on excluded volume, but on the size of crowding agents as well. The observed dependence of the rate on the size of crowding molecules can be understood when the mobility of molecules is taken into account. The bigger the molecule, the more slowly it diffuses, and hence, limits the diffusion of reactants less significantly.
FIGURE 3.
Dependence of association rate on excluded volume for crowding species of different size. The association rate is influenced much more strongly by the crowding agent composed of smaller molecules.
FIGURE 4.
Dependence of association rate on the size of crowding molecules. Every line depicts association rate change at a certain level of excluded volume (5, 20, and 35%). The only difference between points on the line is the size of crowding particles (sizes shown on vertical axis).
TABLE 2.
Dependence of the observed association rate (k) on the excluded volume (φ) and the size of the crowding molecules
|
k/109[1/Ms]
|
|||||
|---|---|---|---|---|---|
| φ | r = 18 Å | r = 20 Å | r = 25 Å | r = 30 Å | r = 35 Å |
| 5% | 5.39 ± 1.63% | 5.42 ± 1.52% | 5.46 ± 1.51% | 5.56 ± 1.80% | 5.59 ± 1.69% |
| 10% | 5.12 ± 4.84% | 5.30 ± 6.57% | 5.27 ± 2.85% | 5.57 ± 6.54% | |
| 15% | 4.84 ± 4.51% | 4.83 ± 2.45% | 5.35 ± 5.85% | 5.06 ± 3.92% | |
| 20% | 4.14 ± 4.21% | 4.44 ± 8.43% | 4.48 ± 5.02% | 5.05 ± 6.05% | |
| 25% | 3.56 ± 3.16% | 4.18 ± 5.88% | 4.32 ± 4.04% | 4.64 ± 5.10% | |
| 30% | 3.29 ± 12.94% | 3.32 ± 8.03% | 3.67 ± 7.23% | 4.30 ± 7.89% | |
| 35% | 2.61 ± 6.61% | 2.78 ± 10.82% | 3.61 ± 9.79% | 4.12 ± 5.76% | |
Calculation of the association rate of the hen egg lysozyme and the HyHEL-5 antibody in the presence of crowding
As in previous simulations, the crowding was represented as hard spheres of 18 Å radius, while the reacting proteins were represented by the atomic-detail models. The models were prepared as follows: The structure of the complex of monoclonal antibody HyHEL-5 and its antigen hen egg lysozyme (HEL) were downloaded from Protein Data Bank (3HFL entry). The 3HFL components were chosen as input proteins for the simulations, because association rates for those proteins are known (experimentally measured without presence of crowding agent (30)). The second, very important factor was very weak dependence of experimentally obtained association rate on the ionic strength of the solution. The measured association rate in 50 mM ionic strength (2.9 × 107[1/Ms]) was only twofold higher than in 500 mM conditions (1.5 × 107[1/Ms]) for the HyHEL-5 HEL pair. It has also been shown that changes in ionic strength weakly affect the rate of encounter complex formation (23,30). That was important, because electrostatic interactions between molecules were neglected in the simulations. This is, of course, great oversimplification in most cases; however, it was necessary for limiting the simulation time to acceptable limits.
The proteins were separated into two PDB files. Their translational and rotational diffusion coefficients were calculated by means of Hydropro software (31). Next, atoms accessible to the solvent were selected by means of an implementation of Shrake and Rupley algorithm (32) employing Fibonacci numbers for even distribution of points on the sphere surface. A probe sphere of 0.2-nm radius was used. The atoms that did not have any solvent-accessible surface were considered as buried and removed, giving models consisting of atomic shells. The latter step was taken to reduce computational complexity of the Brownian dynamics. Since inner atoms of the molecules could not take part in interaction with other macromolecules in the system, the outer atom shell was a sufficient representation of the protein. The association criteria were adapted from the atom contact criterion described by Gabdoulline and Wade (22). On the interface between the lysozyme and the antibody in the 3HFL PDB entry, pairs of atoms on both proteins that can create hydrogen bonds were selected. From those, 16 pairs of atoms with the distance not exceeding 3.20 Å were chosen as useful in defining criteria of the association. Those pairs are shown in Table 3.
TABLE 3.
Atoms in 3HFL PDB entry selected for definition of bound state of lysozyme (HEL) and its antibody (HyHEL-5)
| Lysozyme
|
Antibody
|
|||||
|---|---|---|---|---|---|---|
| Chain | Residue | Atom | Chain | Residue | Atom | Distance [Å] |
| Y | Gln-41 | NE2 | H | Gly-55 | O | 3.16 |
| Y | Gln-41 | O | H | Ser-56 | OG | 2.58 |
| Y | Thr-43 | OG1 | H | Thr-57 | O | 3.21 |
| Y | Thr-43 | OG1 | H | Asn-58 | ND2 | 2.6 |
| Y | Thr-43 | O | H | Asn-58 | ND2 | 2.8 |
| Y | Tyr-53 | OH | H | Trp-33 | NE1 | 3.07 |
| Y | Arg-45 | NH1 | H | Glu-50 | OE2 | 2.97 |
| Y | Arg-68 | NH1 | H | Glu-50 | OE1 | 3.3 |
| Y | Gly-67 | O | H | Tyr-97 | N | 3.01 |
| Y | Arg-45 | NH2 | L | Trp-91 | O | 2.95 |
| Y | Arg-45 | NH2 | L | Gly-92 | O | 3.11 |
| Y | Arg-45 | NE | L | Gly-92 | O | 3.05 |
| Y | Asn-44 | OD1 | L | Arg-93 | NH2 | 3.05 |
| Y | Asn-46 | OD1 | L | Arg-93 | NH2 | 3.01 |
| Y | Arg-45 | O | L | Arg-93 | NH2 | 3.2 |
| Y | Arg-45 | O | L | Arg-93 | NE | 2.49 |
During the simulation, distances between selected atom pairs were monitored. The creation of the diffusional encounter complex was defined as an event in which atoms for three of all possible selected pairs were closer than 3 Å+ distance in the bound state measured in the original PDB entry, with the restriction that a contact between two side chains is counted as one contact even if there are two or more contacts between atoms in those side chains. Using this model of proteins and definition of their association, several Brownian dynamics simulations were performed. The simulation process took much more time than in the case of simple spherical models of proteins for several reasons. First, due to complexity of simulated object (atoms), checking possible collisions between macromolecules required many more computations. The second, more important reason was that the interfaces require the proper mutual orientation for the association to occur. In other words, the association criteria for macromolecules are restrictive compared to reacting spheres. This is why the average time needed for the creation of a diffusional encounter complex was significantly longer than in simulations of centrosymmetrically active particles.
The models of antibody and lysozyme were placed in random positions and orientations in a cubic box with a 300 Å edge, giving ∼61.5 nM concentration of each protein species. In addition to the reacting molecules, different quantities of spherical particles of 18 Å radius were put into the simulation boxes, ranging from 0 to 30 percent of excluded volume (see Fig. 6, for example). Such systems underwent Brownian dynamics simulation in periodic boundary conditions at 298.14 K.
FIGURE 6.
Snapshot of the simulation of HEL and HyHEL5 in 20% excluded volume in periodic boundary conditions.
The timestep was 0.2 ps. To speed-up the computations, the Verlet neighbor lists or linked cells neighbor lists were used, depending on how many molecules were in the system. When the association criteria were satisfied, the proteins were given new random positions. In this manner the simulation was repeated many times from different starting positions, until statistical significance was achieved (standard deviation stabilized at the level allowing for certain distinction of results obtained for every excluded volume). The information about total simulated time and number of single associations for each system is shown in Table 4.
TABLE 4.
Time simulated for each crowding condition (T) and number of encounter complexes observed during the simulation (nr)
| φ | T[ms] | nr |
|---|---|---|
| 0% | 2329.41 | 4000 |
| 5% | 295.89 | 592 |
| 10% | 135.44 | 285 |
| 15% | 80.06 | 189 |
| 20% | 240.5 | 773 |
| 25% | 124.09 | 483 |
| 30% | 131.16 | 593 |
The association rate (k) was calculated as
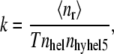 |
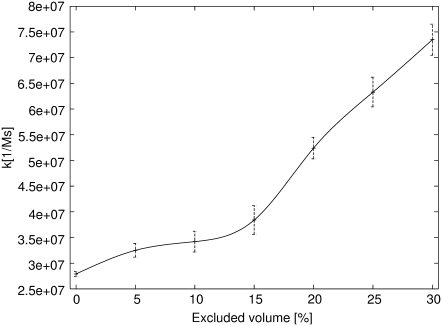
where 〈nr〉 is the average number of association events that occurred in the time T, and nhel and nhyhel5 represent the number or reacting molecules in the volume V. Results are presented in Fig. 5. Without crowding, the proteins create an encounter complex at the rate 2.79 × 107[1/Ms], while experimentally obtained association rate in 500 mM ionic strength was 1.5 × 107[1/Ms] and calculated rate was 4.0 × 107[1/Ms] (30). Calculated association rates strongly depend on the volume excluded by crowding. The rate obtained for the highest concentration of crowding particles is more than twofold higher than the rate for proteins without crowding.
FIGURE 5.
Dependence of association rate of HEL and HyHEL5 on the volume excluded by crowding particles.
Time profiles of HyHEL-5-HEL encounter complex formation
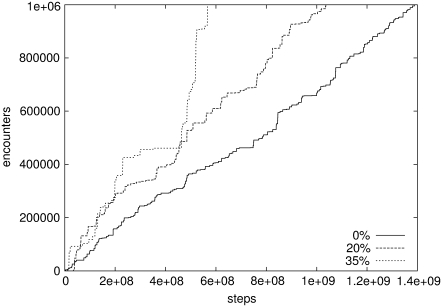
To observe the influence of crowding on dynamics of encounter complex formation, another set of simulations with the same protein models in crowded media were performed (see the snapshot in Fig. 6). Conditions of the simulations were the same as above. After the association criteria were fulfilled, the trajectories were not restarted from another random position. Instead, simulations were run until the encounter complex had been created for 1,000,000 steps. The count of the encounter complex formation in time during the simulation is shown in Fig. 7. These results will be discussed in the next section.
FIGURE 7.
Dependence of the number of steps in which HEL and HyHEL5 fulfilled the association criteria on the total number of steps in different crowding conditions. Every curve on this figure represents progress of only one, example trajectory.
DISCUSSION
Brownian dynamics simulations were performed to study the influence of crowding on diffusion coefficients and macromolecular association rate, and to find out whether the proposed simple model of crowding can mimic behavior of biological (or other experimentally investigated) crowded media.
The results of first computations—the drop in self-diffusion coefficient, and in the association rate, in the case of spherical models submerged in crowded solutions—can be intuitively understood. In the case of spherical molecules able to react by their whole surface, the only factor limiting the association rate is speed of the translational diffusion. Since the diffusion is lowered by crowding (33), the association rate is lower as well (see Table 1 and Table 2).
In contrast to these results, the influence of crowding in the next simulation (employing hen egg lysozyme and its antibody models) was exactly the opposite—the association rate increased with the crowd concentration (Fig. 5). It is known from experiments and previous theoretical predictions (6,9) that crowding can speed-up protein association. The increase of association rate due to exclusion of the volume in the case of HyHEL5-Hel simulations is in agreement with these observations. The key to the speedup of macromolecular associations occurring in crowded media seems to be the ratio of changes in translational and rotational diffusion compared with their values measured in uncrowded condition. Both rotational and translational diffusion of proteins are highly limited in solutions saturated with small molecules, such as glycerol (34), which increases viscosity. If, however, the media are occupied by large molecules, like PEG for example, the translational diffusion is highly affected by increased macroscopic viscosity, while macromolecules still can rotate almost freely. Thus, because of limited translational diffusion, when reactants get close to one another in crowded media, they have more time for assuming a proper mutual orientation allowing for the association than is had in diluted solutions. Large crowding particles create a cavity that does not allow fast dissociation of reactive proteins and does not disturb potential reactants in search for interactions by their binding interfaces (34).
In addition to the obtained association rate (Fig. 5), this phenomenon is well illustrated by the dynamics of encounter complex formation (Fig. 7). Horizontal fragments of curves reflect parts of simulations, in which orientations of proteins do not fall into association criteria. Vertical fragments correspond to situations in which molecules react. The resulting curve for the most crowded solution is the steepest one; molecules spend much more time in the reacting state, when the crowding is high. In addition, the stairs on the curve for crowded media are largest. It means that in the crowded media, it takes longer for molecules to get close to one another, but the time needed for getting proteins apart is much longer as well. Thus, the molecules have much more time to search for the proper orientation.
The model used was very simplified—it did not take electrostatic or hydrodynamic interactions into account. However, HyHEL5-Hel association does not strongly depend on electrostatics (23,30), and the chosen size of crowding molecules ensures very weak dependence of the rotational diffusion on excluded volume (34). Recently, computational studies employing simple spherical models have been conducted that took hydrodynamic interactions into account (35). The authors attempted to quantify the contributions coming from excluded volume and hydrodynamic interactions to the crowding effect. The results of this work suggest that neglecting hydrodynamic interactions leads to overestimation of the translational mobility. Because only spherical models have been used, the phenomenon of search for proper orientation between reacting molecules was beyond the scope of those simulations. The accelerating influence of crowding on association rates was not captured. Thus, the influence of hydrodynamic interactions on association of real proteins in crowded media has not been established.
Although very simple, the model presented in this work is still one of just a few quantitative approaches to the subject considering freely diffusing reacting macromolecules in crowded media, allowing for better understanding of nonspecific factors influencing association rates. Along with the growing computer power available, it will be possible to simulate more detailed representations of complex biological systems, such as cellular compartments, and also possible to grapple with many types of interacting molecules, that in turn may lead to better quantitative understanding of processes occurring in living cells. This can give clues about possible molecular causes of malfunctions (diseases), and suggest ways of dealing with them.
Editor: Ron Elber.
References
- 1.Ellis, J. R. 2001. Macromolecular crowding: obvious but underappreciated. Trends Biochem. Sci. 26:597–604. [DOI] [PubMed] [Google Scholar]
- 2.Ellis, J. R. 2001. Macromolecular crowding: an important but neglected aspect of the intracellular environment. Curr. Opin. Struct. Biol. 11:114–119. [DOI] [PubMed] [Google Scholar]
- 3.Zimmerman, S. B., and A. P. Minton. 1991. Estimation of macromolecule concentrations and excluded volume effects for the cytoplasm of Escherichia coli. J. Mol. Biol. 222:599–620. [DOI] [PubMed] [Google Scholar]
- 4.Minton, A. P. 2001. The Influence of macromolecular crowding and macromolecular confinement on biochemical reactions in physiological media. J. Biol. Chem. 276:10577–10580. [DOI] [PubMed] [Google Scholar]
- 5.Minton, A. P., and J. Wilf. 1981. Effect of macromolecular crowding upon the structure and function of an enzyme: glyceraldehyde-3-phosphate dehydrogenase. Biochemistry. 20:4821–4826. [DOI] [PubMed] [Google Scholar]
- 6.Rivas, G., J. A. Fernández, and A. P. Minton. 2001. Direct observation of the enhancement of noncooperative protein self-assembly by macromolecular crowding: indefinite linear self-association of bacterial cell division protein FtsZ. Proc. Natl. Acad. Sci. USA. 98:3150–3155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Wenner, J. R., and V. A. Bloomfield. 1999. Crowding effects on EcoRV kinetics and binding. Biophys. J. 77:3234–3241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Somalinga, B. R., and R. P. Roy. 2002. Volume exclusion effect as a driving force for reverse proteolysis. Implications for polypeptide assemblage in a macromolecular crowded milieu. J. Biol. Chem. 277:43253–43261. [DOI] [PubMed] [Google Scholar]
- 9.Rivas, G., J. A. Fernández, and A. P. Minton. 1999. Direct observation of the self-association of dilute proteins in the presence of inert macromolecules at high concentration via tracer sedimentation equilibrium: theory, experiment, and biological significance. Biochemistry. 38:9379–9388. [DOI] [PubMed] [Google Scholar]
- 10.Galan, A., B. Sot, O. Llorca, J. L. Carrascosa, J. M. Valpuesta, and A. Muga. 2001. Excluded volume effects on the refolding and assembly of an oligomeric protein. GroEL, a case study. J. Biol. Chem. 276:957–964. [DOI] [PubMed] [Google Scholar]
- 11.Murphy, L. D., and S. B. Zimmerman. 1995. Condensation and cohesion of λDNA in cell extracts and other media: implications for the structure and function of DNA in prokaryotes. Biophys. Chem. 57:71–92. [DOI] [PubMed] [Google Scholar]
- 12.Hatters, D. M., A. P. Minton, and G. J. Howlett. 2002. Macromolecular crowding accelerates amyloid formation by human apolipoprotein C–II. J. Biol. Chem. 277:7824–7830. [DOI] [PubMed] [Google Scholar]
- 13.Martin, J., and F. U. Hartl. 1997. The effect of macromolecular crowding on chaperonin-mediated protein folding. Proc. Natl. Acad. Sci. USA. 94:1107–1112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Tokuriki, N., M. Kinjo, S. Negi, M. Hoshino, Y. Goto, I. Urabe, and T. Yomo. 2004. Protein folding by the effects of macromolecular crowding. Protein Sci. 13:125–133. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Elcock, A. H. 2003. Atomic-level observation of macromolecular crowding effects: escape of a protein from the GroEL cage. Proc. Natl. Acad. Sci. USA. 100:2340–2344. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Stagg, L., S. Q. Zhang, M. S. Cheung, and P. Wittung-Stafshede. 2007. Molecular crowding enhances native structure and stability of α/β protein flavodoxin. Proc. Natl. Acad. Sci. USA. 104:18976–18981. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Cheung, M. S., and D. Thirumalai. 2007. Effects of crowding and confinement on the structures of the transition state ensemble in proteins. J. Phys. Chem. B. 111:8250–8257. [DOI] [PubMed] [Google Scholar]
- 18.Cheung, J. K., and T. M. Truskett. 2005. Coarse-grained strategy for modeling protein stability in concentrated solutions. Biophys. J. 89:2372–2384. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Cheung, M. S., D. Klimov, and D. Thirumalai. 2005. Molecular crowding enhances native state stability and refolding rates of globular proteins. Proc. Natl. Acad. Sci. USA. 102:4753–4758. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Gabdoulline, R. R., and R. C. Wade. 2002. Biomolecular diffusional association. Curr. Opin. Struct. Biol. 12:204–213. [DOI] [PubMed] [Google Scholar]
- 21.De Rienzo, F., R. R. Gabdoulline, M. C. Menziani, P. G. De Benedetti, and R. C. Wade. 2001. Electrostatic analysis and Brownian dynamics simulation of the association of plastocyanin and cytochrome f. Biophys. J. 81:3090–3104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Gabdoulline, R. R., and R. C. Wade. 1998. Brownian dynamics simulation of protein-protein diffusional encounter. Methods. 14:329–341. [DOI] [PubMed] [Google Scholar]
- 23.Gabdoulline, R. R., and R. C. Wade. 2001. Protein-protein association: investigation of factors influencing association rates by Brownian dynamics simulations. J. Mol. Biol. 306:1139–1155. [DOI] [PubMed] [Google Scholar]
- 24.Schreiber, G. 2002. Kinetic studies of protein-protein interactions. Curr. Opin. Struct. Biol. 12:41–47. [DOI] [PubMed] [Google Scholar]
- 25.Gabdoulline, R. R., and R. C. Wade. 1999. On the protein-protein diffusional encounter complex. J. Mol. Recognit. 12:226–234. [DOI] [PubMed] [Google Scholar]
- 26.Ermak, D. L., and J. A. McCammon. 1978. Brownian dynamics with hydrodynamic interactions. J. Chem. Phys. 69:1352–1360. [Google Scholar]
- 27.Northrup, S. H., and H. P. Erickson. 1992. Kinetics of protein-protein association explained by Brownian dynamics computer simulation. Proc. Natl. Acad. Sci. USA. 89:3338–3342. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Cichocki, B., and K. Hinsen. 1990. Dynamic computer simulation of concentrated hard sphere suspensions. Physica A. 166:473–491. [Google Scholar]
- 29.Smoluchowski, V. M. 1917. Mathematical theory of the kinetics of the coagulation of colloidal solutions. Z. Phys. Chem. 92:129–168. [Google Scholar]
- 30.Xavier, K. A., and R. C. Willson. 1998. Association and dissociation kinetics of anti-hen egg lysozyme monoclonal antibodies HyHEL-5 and HyHEL-10. Biophys. J. 74:2036–2045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.de la Torre, J. G. 2000. Calculation of hydrodynamic properties of globular proteins from their atomic-level structure. Biophys. J. 78:719–730. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Shrake, A., and J. A. Rupley. 1973. Environment and exposure to solvent of protein atoms. Lysozyme and insulin. J. Mol. Biol. 79:351–371. [DOI] [PubMed] [Google Scholar]
- 33.Elowitz, M. B., M. G. Surette, P. E. Wolf, J. B. Stock, and S. Leibler. 1999. Protein mobility in the cytoplasm of Escherichia coli. J. Bacteriol. 181:197–203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Kuttner, Y. Y., N. Kozer, E. Segal, G. Schreiber, and G. Haran. 2005. Separating the contribution of translational and rotational diffusion to protein association. J. Am. Chem. Soc. 127:15138–15144. [DOI] [PubMed] [Google Scholar]
- 35.Sun, J., and H. Weinstein. 2007. Toward realistic modeling of dynamic processes in cell signaling: quantification of macromolecular crowding effects. J. Chem. Phys. 127:155105. [DOI] [PubMed] [Google Scholar]