Gap Junction Coupling and Calcium Waves in the Pancreatic Islet

Abstract

The pancreatic islet is a highly coupled, multicellular system that exhibits complex spatiotemporal electrical activity in response to elevated glucose levels. The emergent properties of islets, which differ from those arising in isolated islet cells, are believed to arise in part by gap junctional coupling, but the mechanisms through which this coupling occurs are poorly understood. To uncover these mechanisms, we have used both high-speed imaging and theoretical modeling of the electrical activity in pancreatic islets under a reduction in the gap junction mediated electrical coupling. Utilizing islets from a gap junction protein connexin 36 knockout mouse model together with chemical inhibitors, we can modulate the electrical coupling in the islet in a precise manner and quantify this modulation by electrophysiology measurements. We find that after a reduction in electrical coupling, calcium waves are slowed as well as disrupted, and the number of cells showing synchronous calcium oscillations is reduced. This behavior can be reproduced by computational modeling of a heterogeneous population of β-cells with heterogeneous levels of electrical coupling. The resulting quantitative agreement between the data and analytical models of islet connectivity, using only a single free parameter, reveals the mechanistic underpinnings of the multicellular behavior of the islet.

INTRODUCTION

The pancreatic islet is a multicellular microorgan which consists mainly of β-cells (as well as a few α-cells, δ-cells, and other types of cells) that respond to elevated glucose levels by secreting insulin. At elevated glucose levels, a chain of metabolic and electrical events occurs that results in membrane depolarization and elevated intracellular free calcium concentration ([Ca²⁺]_i) (1,2). At glucose levels >∼7 mM, membrane potential (V_m) and [Ca²⁺]_i oscillations are observed and are synchronized across all β-cells in the islet (3). These oscillations result in pulsatile insulin release (4) with a sharp increase in glucose-stimulated [Ca²⁺]_i and insulin at ∼7 mM glucose. Isolated β-cells, however, show a much reduced dynamic range of insulin secretion (5) along with irregular oscillations in V_m and [Ca²⁺]_i and a heterogeneous glucose-stimulated response (6,7). These findings demonstrate that a high degree of communication occurs between β-cells within the islet to create synchronous oscillations in V_m, [Ca²⁺]_i, and insulin release, as well as the sharp glucose-stimulated response. Previously, we and others have shown that gap junction mediated electrical communication is critically important for maintaining proper electrical activity within the islet (8,9).

Despite these findings, details on how the heterogeneous β-cell population organizes into a single electrical synctium are not fully clear. Closer examination of the oscillations in [Ca²⁺]_i reveals that there is a small temporal offset in oscillations in different β-cells within the islet. Through time-lapse imaging, various groups have shown that these small temporal offsets appear to result from calcium waves propagating across the islet associated with the oscillatory increases in [Ca²⁺]_i (10,11). Furthermore it has been shown that partial inhibition of gap junction activity with chemical inhibitors disrupts [Ca²⁺]_i oscillations and calcium waves in the islet (11,12), although nonspecific effects of the gap junction inhibitor cannot be ruled out. Gap junction conductance has also been theoretically predicted to affect the calcium wave propagation (13,14). It is therefore of great interest to further study the spatiotemporal organization of islet electrical activity, characterized by oscillatory [Ca²⁺]_i and propagating calcium waves, and to understand how this behavior relates to the degree of gap junction coupling. To this end, we examined synchronized [Ca²⁺]_i oscillations and waves in the islet as a function of electrical coupling. We precisely modulated the gap junction coupling using both Cx-36 knockout mice and chemical inhibitors and quantified this modulation by electrophysiology measurements. By following how the calcium waves and oscillations are affected by graded changes in electrical coupling in the islet, we can assign a conceptually simple model that quantitatively describes how gap junction coupling coordinates the calcium oscillations across the β-cells of the islet. We then used this concept to generate a mathematical model of coupled β-cells, which reproduces the differences in measured [Ca²⁺]_i activity with the modulation of β-cell electrical coupling. The success of this quantitative model yields insight into the origin of the intercellular calcium waves and the emergent behaviors of this simple multicellular system.

EXPERIMENTAL METHODS

Islet isolation

Islets were isolated as described in Scharp et al. (15) and Stefan et al. (16) and maintained in Roswell Park Memorial Institute medium containing 10% fetal bovine serum, 11 mM glucose at 37°C under humidified 5% CO₂ for 24–48 h before imaging.

Imaging islets

Isolated islets were stained with 4 μM Fluo-4 AM (Invitrogen, Carlsbad, CA) in imaging medium (125 mM NaCl, 5.7 mM KCl, 2.5 CaCl₂, 1.2 mM MgCl₂, 10 mM HEPES, 2 mM glucose, 0.1% bovine serum albumin, pH = 7.4) at room temperature for 1–3 h before imaging. Islets were imaged in a polydimethylsiloxane (PDMS) microfluidic device, the fabrication of which has been previously described in Rocheleau et al. (8), which holds the islet stable for imaging and allows rapid reagent change, such as varying glucose stimulation or adding gap junction inhibitors. Fluo-4 fluorescence is imaged 15 min after a step increase in glucose from low (2 mM) to high (11 mM). High speed imaging is performed on an LSM5Live with a 20× 0.8 NA Fluar Objective (Zeiss, Jena, Germany) using a 488 nm diode laser for excitation and a 495 nm long-pass filter to detect fluorescence emission. The microfluidic device is held on the microscope stage in a humidified temperature-controlled chamber, maintained at 37°C. Images were acquired at a rate of 4–6 frames per second, with average powers at the sample being minimized to <200 μW/cm².

Electrophysiology measurements

Measurements of β-cell coupling conductance were performed using a strategy initially described in Mears et al. (17) and Sherman et al. (18) and further described in Gopel et al. (19). Isolated islets were continually perfused with an extracellular solution containing 115 mM NaCl, 5 mM KCl, 3 mM CaCl₂, 2 mM MgCl₂, 10 mM HEPES, 2 mM glucose, pH = 7.2. V_m and transmembrane current were monitored using the perforated patch method as described in Zhang et al. (7). Pipettes were filled with an intracellular solution of 11.8 mM NaCl, 28.4 mM K₂SO₄, 63.7 mM KCl, 1 mM MgCl₂, 20.8 mM HEPES, 0.5 mM EGTA, pH = 7.2, along with 0.1 mg/ml amphotericin B. After obtaining a GΩ seal on a patched peripheral β-cell, glucose levels were stepped from 2 to 11 mM. After transient effects died away, V_m was recorded in current clamp mode, then the coupling current was measured in voltage clamp mode at −65 mV. The coupling conductance (g_coup) was determined by the change in coupling current (ΔI_coup) normalized by the change in membrane potential (ΔV).

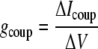(1)

Calculating [Ca²⁺]_i wave velocity and oscillation synchronization

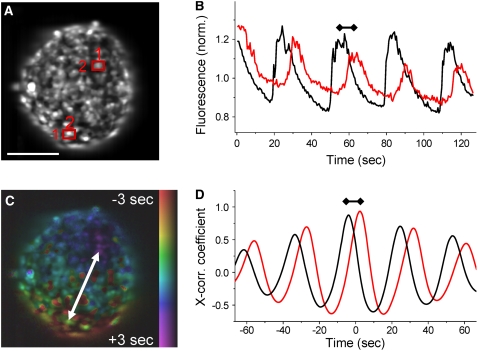
Calcium wave velocity was measured in a similar way to the method described in Skyggebjerg (20). After high-speed imaging of Fluo-4 fluorescence (intensity proportional to [Ca²⁺]_i), the time at which an increase in fluorescence intensity (increase in [Ca²⁺]_i) is observed is compared for all islet cells in the image. For each pixel in the image, a cross correlation is performed between the time course of fluorescence for that pixel and the time course of fluorescence averaged over the whole islet (Fig. 1). A phase map is constructed with each pixel value consisting of the time index of the maximum in the cross correlation coefficient. Thus, areas of the islet showing a low time index represent earlier increases in [Ca²⁺]_i compared to the islet average and thus indicate where the calcium wave originates. Conversely, areas of the islet showing a high time index represent later increases in [Ca²⁺]_i, indicating where the calcium wave terminates. Additionally, the peak value of the cross correlation coefficient is used to indicate the degree of correlation between [Ca²⁺]_i oscillations in an islet cell with [Ca²⁺]_i oscillations in the rest of the islet. If the cross correlation coefficient is <0.5 in a pixel, it is not considered to be synchronized with the rest of the oscillations in the islet.

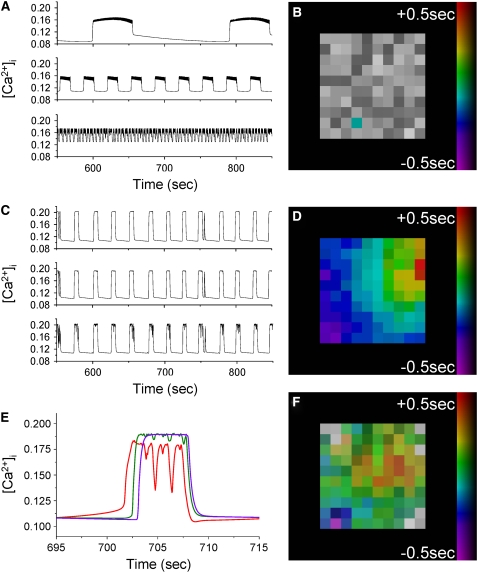
FIGURE 1.

Calcium wave velocity and islet [Ca²⁺]_i oscillation synchronization. (A) Fluorescence intensity image of a Fluo-4 stained islet in a microfluidic flow device. Scale bar represents 100 μm. (B) Time course of the Fluo-4 intensity in the-two-islet cells highlighted in A. Oscillations of cell 1 (black line) precede those of cell 2 (red line) by the propagation time of the calcium wave from cell 1 to cell 2 (indicated by dumbbell line). (C) False color scale phase map representing the propagation of the calcium wave across the islet from regions colored in red (early [Ca²⁺]_i increase) to regions colored in blue/purple (later [Ca²⁺]_i increase). (D) Example cross correlation trace of cell 1 and cell 2 with the whole islet oscillations. Difference in time between the peaks of the cross correlation represents the wave propagation time between the two cells, which is mapped in C. The peak cross correlation coefficients represent the degree of correlation with the average islet oscillations, which is high for both cells.

The information describing the calcium wave propagation and synchronization is represented as a false color hue-saturation-value image, where the hue (color) represents the time index of the oscillation, saturation (the amount of color) is set to 0 if the cross correlation coefficient falls below 0.5, and value (intensity) represents the mean fluorescence intensity. Thus the phase map shows the oscillation time (in false color) for all oscillations in the islet that are synchronized.

The wave velocity (v_[Ca]) is calculated in the direction of wave propagation, from areas of low time index to areas of high time index. The velocity is calculated by dividing the spatial separation of the wave start and end (Δr₁₂) with the difference in the oscillation time index between these two points (Δt₁₂), described by Eq. 1.

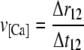(2)

The number of cells (N) that exhibit synchronous oscillations is determined by calculating the percentage area of the islet that shows a maximum cross correlation coefficient above 0.5. An intensity threshold is also applied to remove contributions from α-cells, since they show a large decrease in [Ca²⁺]_i, and therefore Fluo-4 intensity, upon elevated glucose levels (21).

Computational modeling

The previously published coupled phantom-burster model (22) was modified to include a more accurate description of K_ATP channel dynamics by accounting for metabolic factors such as ATP/ADP turnover (23). We further modified the model to account for β-cell heterogeneity, as well as heterogeneity in electrical coupling conductance. A brief description of the essential features of the model is included here, with further details available in Zimliki et al. (22), Bertram et al. (23), and Nunemaker (24).

The coupled phantom-burster model describes the electrical behavior of a population of β-cells with electrical coupling between neighboring β-cells. The following equation describes the membrane potential (V) of a single, uncoupled β-cell as a function of the various transmembrane currents (I_K, I_Ca, etc.):

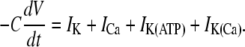(3)

Since we are modeling a series of coupled β-cells, the membrane potential in the ith β-cell surrounded by j adjacent β-cells is

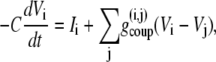(4)

where 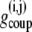is the coupling conductance between cells i and j. The islet is modeled as a 10 × 10 × 10 islet cube such that the index j represents coupling to six adjacent cells. In the presence of incomplete coupling, the index j has a probability of coupling to fewer than six cells. The total coupling conductance of a β-cell is the sum of 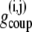over j, that is, the total coupling conductance from one β-cell to all surrounding β-cells.

The description of I_K(ATP) is modified from that in Zimliki et al. (22) by including the ADP/ATP dynamics described in Bertram et al. (23).

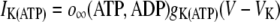(5)

(6)

where o_∞(ATP,ADP) represents the proportion of open K_ATP channels as a function of ATP/ADP levels, which is described in detail in Bertram et al. (23,25). The metabolic flux through citric-acid-cycle metabolism, which increases the cellular ATP/ADP ratio, is described by the parameter r and is an increasing function of glucose concentration. After a step increase in glucose stimulation from low (2 mM) to high (11 mM), generally only fast (tens of seconds) oscillations are observed in islets, which has been theoretically predicted and experimentally verified in Bertram et al. (23). We therefore do not include any terms to describe metabolic feedback onto phosphofructokinase activity that results in slow (∼5 min) oscillations in glycolysis, as described in Bertram et al. (23), and thus focus purely on electrical coupling of fast [Ca²⁺]_i oscillations.

We represent β-cell heterogeneity by randomly distributing a model parameter for each cell according to Gaussian distribution with mean μ and standard deviation σ. Values below zero were discarded. For electrical heterogeneity, we randomly distributed the calcium-sensitive potassium channel conductance (g_K(Ca)) value for each cell, as was performed in Zimliki et al. (22). For metabolic heterogeneity, we randomly distributed the metabolic flux (r) for each cell. Parameter distributions are adjusted to generate oscillations approximately equivalent to those experimentally observed. We also considered the case where there is heterogeneity in the gap junction conductance between β-cells, as was also modeled in Pedersen (14). The β-cell to β-cell coupling conductance values were randomly distributed according to a Gaussian distribution (again discarding negative values). The mean and standard deviation of the Gaussian were initially set such that the mean and standard deviation of total β-cell coupling conductance (sum of all coupling conductance from a single β-cell to surrounding β-cells) are equivalent to that which we experimentally observe with electrophysiology measurements. A list of all the parameters used in the model and their values is included in Table 1.

TABLE 1.

Values of the parameters used in the computational islet model

Symbol	Description	Value
gK	Delayed rectifier K+ channel conductance	3000 pS
Vn	Half-maximal activation of delayed rectifier K+ channel	−16 mV
sn	Activation range of delayed rectifier K+ channel	5.6 mV
τn	Activation time constant of delayed rectifier K+ channel	20 ms
gCa	Voltage-dependent Ca2+ channel conductance	1200 pS
Vm	Half-maximal activation of voltage-dependent Ca2+ channel	−20 mV
sm	Activation range of voltage-dependent Ca2+ channel	12 mV
gK(Ca)	Ca2+ sensitive K+ channel conductance	Distribution: mean = 453 pS; standard deviation = 255 pS
Kd	Ca2+ dissociation constant of K(Ca) channel	0.25 μM
nh	Hill coefficient of Ca2+ inhibition of K(Ca) channel	5
gK(ATP)	Nucleotide sensitive K+ channel conductance	8500 pS
K1,K2	Range of ADP, ATP effect on K(ATP) channel conductance	0.45, 0.012 mM
[A]	Total nucleotide concentration	1 mM
τa	Time constant of Ca2+-dependent ATP/ADP decrease	200,000 ms
r1	Concentration range of Ca2+ effect on mitochondria	0.35 mM
r	Mitochondrial ATP production rate	Distribution: mean = 1.3; standard deviation = 0.5
gcoup	Cell-cell gap junction coupling conductance	Variable distribution:
		mean = 0 pS; standard deviation = 0 pS (Fig. 5, A and B)
		mean = 95 pS; standard deviation = 70 pS (Fig. 5, C–E)
		mean = 40 pS; standard deviation = 28 pS (Fig. 5 F)
α	Current to flux conversion factor	2.25 × 10−6μM ms−1 fA−1
kPMCA	Rate constant of plasma membrane Ca2+ ATPase	0.1 ms−1
pER(leak)	Leak permeability constant in ER	4.0 × 105 ms−1
kSERCA	Rate constant of sarcoendoplasmic reticulum Ca2+ ATPase	0.2 ms−1
fcyt	Ratio of free to bound Ca2+ in cytosol and ER	0.01
Vcyt/VER	Ratio of cytosol volume to ER volume	50
VK	K+ Nernst potential	−75 mV
VCa	Ca2+ Nernst potential	25 mV
Cm	Membrane capacitance	5300 pF

ER, endoplasmic reticulum.

THEORY

We explored the use of two multicellular analytical models of intercellular connectivity in the islet: a percolation model and a continuous model. Both of these models can potentially be used to describe how properties of a coupled network alter the behavior of β-cells when gap junction coupling is reduced in the islet. The basic properties and predictions of these model types are described here and then considered in terms of the experimental data in the Results section, below.

Percolation theory

Percolation theory (26) is a mathematical theory that can often accurately describe the properties of a randomly coupled series of discrete units, such as the properties of a partially coupled resistor network (27). Two main properties of such a randomly coupled network are used in this study because they physically resemble the β-cell network in islets, which led us in turn to explore the use of percolation theory. First, the electrical conductance across the coupled resistor network is related to the number of unique paths that can traverse the network. As network connections are removed, the number of conducting paths decreases until, finally, only a single “critical” path exists. Second, the percolation probability is the proportion of the resistor connections that make up the path which traverses the coupled network. Both of these properties, the network conductance g and the percolation probability P, can be described according to a power law, depending on the proportion of resistor connections left in the network.

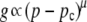(7)

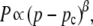(8)

where if q is the probability, a resistor connection is removed (or the proportion of connections removed) and p = 1 − q is the probability a resistor connection is not broken and thus remains (or the proportion of resistor connections remaining). The critical probability p_c is the probability at which no percolation can occur and is dependent on the lattice architecture and dimension, μ is the conductivity exponent, and β is the critical exponent, both of which are also dependent on the dimension of the network. Thus below the critical probability, g and P are equal to zero. For a three-dimensional cubic network with bond percolation, the values of these dimensional parameters are p_c = 0.2488, μ = 2, β = 0.4 (28).

Percolation (discrete) analytical model of islet connectivity

In vivo, islets are highly vascularized, and when they are isolated, the blood vessels remain within the islet, although these vessels will no longer be filled with blood. Thus, two β-cells that are seen in situ to be adjacent in an isolated islet may, in fact, be separated by a collapsed vessel, so they are not really neighbors, and we would not expect these cells to be coupled directly by gap junctions. Thus, some aspects of islet architecture lend themselves to description through a percolation model. In the percolation analytical model of islet connectivity, a reduction in coupling conductance is represented by the removal of a proportion of gap junction connections within the islet. Under this assumption, a 20% reduction in coupling conductance means that there is a 20% probability of β-cell to β-cell connections being broken (p = 0.8). This would then affect the wave velocity and degree of synchronization according to properties of the resistive network as described by percolation theory, Eqs. 7 and 8.

According to cable theory, the wave velocity is proportional to the square root of the conductance of the medium through which it propagates:

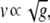(9)

where the medium is the discretely coupled β-cell network, with conductance (g) described in Eq. 7.

The percolation probability (P), described by Eq. 8, can be related to the proportion of the islet that is oscillating in synchrony: only those cells with connections that lie on the resistive network will oscillate synchronously with each other. Those cells with connections that lie outside the network are electrically isolated and therefore oscillate asynchronously. Thus, we can produce equations to describe two of the islet properties as a function of gap junctional coupling:

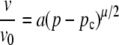(10)

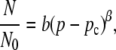(11)

where v is the wave velocity, v₀ is the wave velocity with full islet connectivity, N is the number of islet cells oscillating synchronously, N₀ is the number of islet cells oscillating synchronously with full islet connectivity, a and b are proportionality constants, and μ and β are parameters that specifically describe the properties of a percolating network as described above.

Ohmic (continuous) analytical model of islet connectivity

In the continuous analytical model of islet connectivity, a reduction in coupling conductance is represented as an equivalent reduction in the coupling conductance between every cell. For example, a 20% reduction in coupling conductance means that there would be a 20% reduction in the coupling conductance of each β-cell to β-cell connection. The resistor network is thus considered to be a continuous medium with a network conductance that is proportional to the individual β-cell coupling conductance (g α p). The whole network conductance will thus fall linearly with decreasing coupling conductance until there will be no network conductance when the coupling conductance is zero. This is in contrast to the percolation model where there is no overall network conductance even when a proportion of β-cells are still coupled. The degree of synchronization will remain constant with coupling conductance, until a value of the coupling conductance at which β-cells can no longer synchronize their oscillations. At this value (p₀), the oscillation synchronization will fall sharply to zero, and thus there will be no propagating calcium waves. We shall assume this coupling conductance to be p_c, as in the percolation model, but this value can also be considered as a free parameter. In the continuous analytical model, the mathematical description of islets parameters are

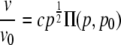(12)

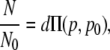(13)

where c and d are proportionality constants, Π(p,p₀) is a step function (Π = 0 when p < p₀, Π = 1 when p > p₀), and p₀ is initially assumed to be the same as that used in the percolation model, i.e., p₀ = 0.2488.

RESULTS

Measured wave velocities in isolated islets

Fluo-4 stained islets were loaded into a microfluidic device, and high-speed time-lapse images were recorded. Data of intracellular free calcium ([Ca²⁺]_i) at elevated glucose levels (∼11 mM) are displayed in Fig. 1 for a representative islet (Supplementary Material, Movie S1). Changes in Fluo-4 fluorescence showed that [Ca²⁺]_i follows near synchronous (phase-locked, i.e., the same frequency with a constant phase difference) bursting with a small temporal delay across the islet, as seen in Fig. 1, A and B, which is characteristic of calcium wave propagation. By calculating this temporal separation, the wave propagation can be displayed as a false color scale phase map. This allows the direction of wave propagation to be visualized, as seen in Fig. 1 C. Comparing Fig. 1, B and D, shows that the cross correlation algorithm accurately determines the temporal separation in [Ca²⁺]_i oscillations, which can then be used to calculate the calcium wave velocity.

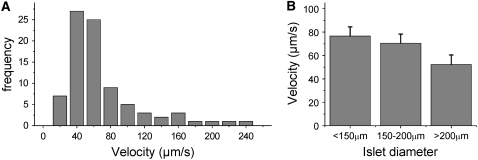
The mean calcium wave velocity was measured over a number of islets, in response to a constant level of glucose stimulation. A histogram of the calcium wave velocity after 11 ± 1 mM glucose stimulation can be seen in Fig. 2 A. The mean wave velocity across the islet was measured to be 69 ± 5 μm/s (mean ± SE n = 30 mice, 1–6 islets per mouse), although a broad asymmetric distribution of wave velocities ranging from ∼20 μm/s to >200 μm/s was observed. The measured distribution of wave velocities results in a tail of high velocity waves (fully synchronized oscillations), as was also observed by Aslandi and co-workers (10). There is a small decrease in wave velocity (v) with increased islet size (l), as shown in Fig. 2 B, which would be expected if the overall islet conductance (g) fell with islet size: v ≈ √g ≈ 1/√l. The variation in the measured wave velocity between islets is much greater than that seen in different sizes of islet (∼10-fold versus <2-fold, respectively). The mean wave velocity measured between 10 and 12 mM glucose stimulation did not vary significantly compared to the variation between islets at 11 mM glucose, indicating that the wide range in wave velocities is not due to small variations in glucose stimulation. Wave velocity (both direction and speed) was generally found to be constant within measurement uncertainty over 30 min measurement time, 15 min after elevated glucose stimulation (n = 3 mice). Over all islets studied, 81% ± 3% of the waves emerged and propagated in a consistent direction across the islet, with the remaining waves emerging in other regions of the islet.

FIGURE 2.

Summary of measured wave velocities. (A) Histogram of measured calcium wave velocities. The mean velocity is 69 ± 5 μm/s, which is many times faster than would be seen by simple diffusion of calcium across the islet. (B) The mean velocity calculated for different size ranges of islets studied. There is a trend for the wave velocity to decrease with increasing islet size, as expected if v ≈ √g ≈ 1/√l.

Gap junction blocking with chemical inhibitors slows calcium wave propagation

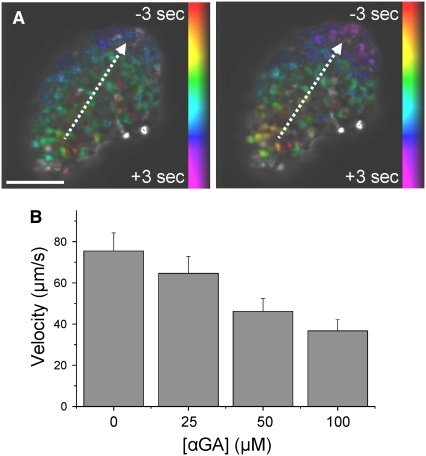
We next sought to test the effect of a reduction in gap junction activity on calcium wave propagation using chemical inhibitors. We utilized the gap junction inhibitor 18-α-glycerretnic acid (αGA), which has previously been used to show a disruption in coupled electrical activity, for example, in smooth muscle cells (29). After application of up to 50 μM αGA, regular [Ca²⁺]_i oscillations and propagating calcium waves were still observed. Fig. 3 A displays representative phase maps of the [Ca²⁺]_i wave propagation in an islet before and after the application of 50 μM αGA. A greater time delay is observed between the start and end of the calcium wave after application of the gap junction inhibitor. In this example, the wave propagation direction was maintained; however, in several cases a change in direction was observed after application of gap junction inhibitor.

FIGURE 3.

Chemical inhibitors of gap junction activity slow the calcium wave velocity. (A) Phase map of the calcium wave propagation across the islet before (left) and after (right) the application of 50 μM αGA. Dashed white lines indicated the direction of propagation from yellow/red regions to blue/purple regions. The phase difference of the oscillations increases after partial gap junction inhibition with αGA, representing a decrease in wave velocity. Scale bar represents 100 μm. (B) Decrease in the mean calcium wave velocity with increasing concentration of αGA. Error bars represent mean ± SE.

The decrease in wave velocity was measured for a number of concentrations of gap junction inhibitor. Fig. 3 B displays the mean calcium wave velocity upon treatment with increasing concentrations of αGA (n = 16 mice, 1–6 islets per mouse). Concentrations of 25 and 50 μM of αGA progressively decreased the calcium wave velocity, with a significant 32% ± 14% reduction observed at 50 μM αGA (P < 0.01, one-tailed t-test). At concentrations of 100 μM αGA, a reduction in the number of islet cells showing [Ca²⁺]_i oscillations was found (54% ± 12% of the islet, n = 5 mice, 1–3 islets per mouse). We observed similar decreases in wave velocity upon the application of 10–50 μM mefloquine, another gap junction inhibitor (30) (n = 3 mice, 1–3 islets per mouse, data not shown).

Gap junction knockout dramatically disrupts wave propagation

Chemical gap junction inhibitors are known to be weak and have many associated nonspecific effects, especially on calcium and potassium currents (29). We therefore utilized an alternative method for reducing gap junction activity through a genetic knockout of the gap junction forming connexin protein that couples β-cells. It has previously been shown that connexin 36 (Cx36) forms functional gap junctions that couple β-cells (9). We studied calcium oscillations and waves in islets harvested from mice with a knockout of one or both Cx36 alleles (Cx36+/−, Cx36−/−, respectively), which are described in Degen et al. (31). We would therefore expect that the islets from these mice represent ∼50% (+/−, heterozygous) and ∼0% (−/−, homozygous) of normal gap junction coupling.

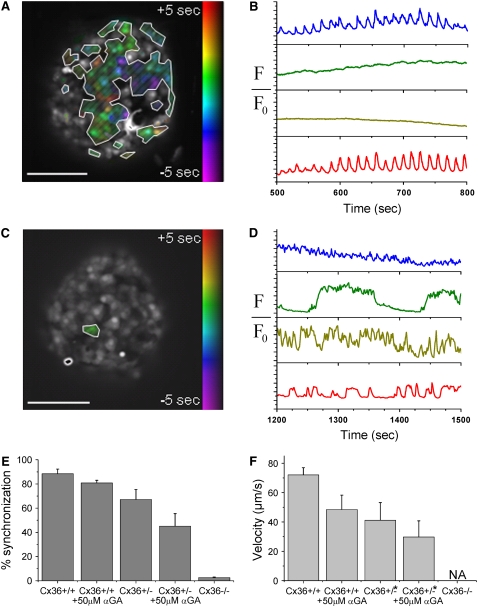
In islets from heterozygous Cx36+/− knockout mice, a reduction of the number of cells displaying synchronized, phase-locked oscillations was observed. Averaging over all Cx36+/− mice studied (n = 12), 67% ± 8% of the cells in the islet are synchronized, which is significantly less than that seen in wild-type (WT) mice. There was however a wide range in this average value between islets from different mice, ranging from 26.2% to 91.9% (mean over all islets from a single mouse, see Fig. S2 in Data S1). A wide range of calcium wave behavior was also observed in these islets. In islets from 7 out of 12 Cx36+/− mice studied, calcium wave propagation was still observed, similar to that seen in Figs. 1 and 3, although the wave velocity was reduced to 41 ± 12 μm/s: a 43% ± 17% (mean ± SE) reduction of the velocity compared to that seen in islets from WT control mice. In islets from the other 5 out of 12 Cx36+/− mice studied, the wave propagation was significantly disrupted.

Generally islets from mice in this second group exhibited both poor oscillation synchronization and disrupted wave propagation (see Fig. S2 in Data S1). Fig. 4, A and B, displays representative data of the [Ca²⁺]_i activity in islets of these mice (see Movie S2). Fig. 4 B displays representative oscillations at 11 mM glucose stimulation in different islet cells from a single islet. Only a proportion of the islet cells undergo synchronous, phase-locked oscillations in [Ca²⁺]_i, with the rest of the cells showing irregular or continual spiking [Ca²⁺]_i activity. Additionally, the mean oscillation period in islets from the Cx36+/− mice that have disrupted calcium wave propagation is 14.6 ± 0.4 s (mean ± SE), which is significantly less than the 21.2 ± 2.8 s (mean ± SE) seen in WT islets at 11 mM glucose (P < 0.01, one-tailed t-test), and the 19.4 ± 0.9 s (mean ± SE) seen in the Cx36+/− mice which still show calcium wave propagation (P < 0.001, one-tailed t-test).

FIGURE 4.

Genetic knockout of gap junctions disrupts wave propagation and islet oscillation synchronization. (A) Phase map of [Ca²⁺]_i oscillations in an islet of the heterozygous Cx36+/− knockout mouse used in B. No wave propagation is visible from examination of the individual phases of the β-cells; however, there are still synchronous phase-locked oscillations in a proportion of the islet cells as highlighted. (B) Representative oscillations of [Ca²⁺]_i in four cells of the Cx36+/− islet shown in A. Traces correspond to areas of the islet that are synchronized (blue, red) and unsynchronized (green, yellow). (C) Phase map of [Ca²⁺]_i oscillations in an islet of the heterozygous Cx36−/− knockout mouse used in D. Cells are not synchronized with the oscillations of any other cell. (D) Representative oscillations of [Ca²⁺]_i in four cells of the Cx36−/− islet shown in C. Oscillations are on a wide range of timescales from ∼1 s to ∼2 min. (E) Decrease in the proportion of cells in the islet that undergo synchronous oscillations. The decrease in islet synchronization is greater for the Cx36 gap junction knockout islets than the αGA treated islets. (F) The decrease in the wave velocity is greater for the Cx36 gap junction knockout islets (* when propagating calcium waves are still observed) than the αGA treated islets. Scale bars in A and C represent 100 μm.

The reduction in the oscillation synchronization is also shown as a representative phase map in Fig. 4 A. Only those cells that show synchronous, phase-locked oscillations are highlighted. Inspection of the phase map within the area of the islet that is synchronized shows no overall propagating calcium waves. Instead, there is an irregular distribution of cells that, although phase-locked, have a large temporal delay in their oscillation compared to other cells. The maximum temporal delay between phase-locked oscillations within a 100 μm area is 8.5 ± 2.9 s (mean ± SD), which is much greater than the temporal delay observed in oscillations that occurs due to wave propagation (on the order of 1 s). Upon the addition of 50 μM αGA to the Cx36+/− islets, the proportion of the islet that is synchronized is further reduced to 45% ± 10%. Where wave propagation is still seen, the velocity is further reduced on average by 28 ± 17%.

Islets from homozygous Cx36−/− knockout mice show a complete loss in synchronized [Ca²⁺]_i oscillations, as seen in Fig. 4, C and D (see Movie S3). Fig. 4 D displays representative oscillations at 11 mM glucose in different cells within a single islet. There is no evidence for any of the synchronous phase-locked oscillations or propagating waves that are observed in islets from WT and Cx36+/− mice. Additionally, [Ca²⁺]_i of cells within the same islet oscillate on a wide range of timescales from ∼1 s to several minutes, similar to what is typically seen in dispersed β-cells (7). No islet cell is synchronized with any other islet cell, as shown by the phase map in Fig. 4 C. This behavior is consistent over all islets from all homozygous Cx36−/− knockout mice studied (four mice, two to four islets per mouse). Thus upon Cx36 knockout, calcium waves are disrupted and islet synchrony is lost. Upon the addition of 50 μM αGA to the Cx36−/− islets, a small proportion of the cells (∼10%) showed either an increase in oscillation frequency or a loss in oscillations which could be due to nonspecific effects of the gap junction inhibitor.

Fig. 4 E summarizes the gap junctional dependence of the decrease in the proportion of islet cells that are synchronized. Compared with the small reduction in synchrony seen with the application of chemical inhibitors, a large reduction is seen with heterozygous and homozygous knockout of Cx36 gap junction forming protein that couples β-cells. Fig. 4 F summarizes the reduction in wave velocity seen in the heterozygous Cx36+/− mice. Of the Cx36+/− islets where wave propagation is still observed, a greater decrease in the wave velocity is seen compared to the velocity measured upon the application of gap junction inhibitors. This is further decreased with the combination of gap junction inhibitors and heterozygous Cx36 knockout.

Computer modeling of calcium oscillations and waves in coupled β-cells

We next sought to understand the mechanistic underpinnings of these behaviors by quantitative modeling of the islet β-cell electrical coupling. We simulated β-cell electrical and calcium activity using the coupled phantom-buster model (22) with heterogeneous electrical coupling. When no electrical coupling is present between neighboring β-cells, a wide range of oscillation timescales are produced, as displayed in Fig. 5 A. These oscillations range from continual spiking every 1 s to oscillations with a period of >200 s. This qualitatively matches what we observe from Cx36−/− islets in Fig. 4 D. There is no synchronization between these oscillations, as shown in the phase map in Fig. 5 B, again as seen in Cx36−/− islets.

FIGURE 5.

Computational modeling of coupled β-cell electrical activity. (A) A heterogeneous population of β-cells' [Ca²⁺]_i oscillations are seen when β-cells are not electrically coupled, similar to that seen in islets from Cx36−/− mice. (B) Phase map showing that in the absence of gap junction coupling, oscillations in individual cells are not synchronized. (C) Gap junction electrical coupling produces synchronized oscillations on an intermediate timescale to the oscillations produced in the uncoupled islet, as is also observed in islets from Cx36+/+ (WT) mice. (D) With gap junction coupling, calcium waves are observed associated with the oscillatory increases in [Ca²⁺]_i. The wave propagates from the top right to bottom left of the islet and crosses the 10 × 10 × 10 islet in ∼1 s. (E) A single [Ca²⁺]_i oscillation in D at the start (red), middle (green), and end (purple) of the wave showing the temporal offset of the oscillation at different points in the islet. (F) Reducing the mean coupling conductance by ∼50% disrupts wave propagation and reduces islet synchrony, as is also observed in islets from a proportion of the heterozygous Cx36+/− mice.

When adjacent β-cells are electrically coupled, with a mean conductance of 95 pS (within the range expected for WT mouse islets, e.g., Moreno et al. (32)), synchronized oscillations with an intermediate period of ∼20 s are observed as shown in Fig. 5 C. These oscillations are consistent with measurements made in islets from WT mice in Fig. 1. Analysis of the oscillation synchronization shows that they are synchronized across the islet, which is also seen in Fig. 1. Furthermore, the model produces propagating waves across the islet associated with oscillations of [Ca²⁺]_i, which is shown by the phase map in Fig. 5 D. A close-up of a single [Ca²⁺]_i oscillation is seen in Fig. 5 E for a cell at the start, middle, and end of the wave propagation. This shows the temporal separation in oscillations that produces these propagating waves. When both electrical and metabolic heterogeneity is included, as well as a broad heterogeneity in coupling conductance (mean of 95 pS, standard deviation of 70 pS), these waves propagate from the top right corner to the bottom left corner of the islet displayed in Fig. 5 D, with a temporal difference of >1 s, equivalent to a velocity of 80 μm/s assuming one β-cell is 10 μm in diameter.

Over a number of simulations, each with a different random number of seeds to represent different islets, wave velocities in the range of 70–150 μm/s are generated. Averaged over these modeled islets, 92% ± 6% of the waves traveled in a consistent direction, although each random number seed resulted in waves that initiate and terminate in different regions of the islet compared to that shown in Fig. 5 D. We note that waves are also produced when heterogeneity is either just electrical (varying g_KCa parameter) or just metabolic (varying r parameter), although the wave propagation velocity is ∼50% higher in each case (for an example, see Fig. S3 in Data S1). In the presence of a uniform coupling conductance (mean of 95 pS, standard deviation of 0 pS), an approximately twofold greater wave velocity is generated compared to that under heterogeneous coupling with the same mean conductance (not shown).

An ∼50% decrease in the mean coupling conductance results in the disruption of wave propagation. Fig. 5 F shows a phase map generated by the same model as in Fig. 5, C and D, but with a coupling conductance distribution with a mean of 40 pS and standard deviation of 28 pS (compared to a mean of 95 pS, standard deviation of 70 pS, which reproduces WT behavior). A reduction in the oscillation synchronization is seen at the surface of the islet, which is also seen in islets from Cx36+/− mice such as displayed in Fig. 4, A and B. In the case shown in Fig. 5 F, 92% of the model islet is oscillating synchronously, compared to 100% of the model islet that reproduces WT behavior (Fig. 5 C). Over a number of simulations with different random number seeds to represent different islets, between 87% and 100% of the islet is seen to oscillate synchronously.

If the mean coupling conductance is further reduced, a further reduction in the oscillation synchronization is observed. A coupling conductance distribution with a mean of 20 pS and standard deviation of 14 pS (∼25% WT conductance) results in 57% of the islet oscillating synchronously for the islet shown in Fig. 5, B, D, and F, and a variation between 35% and 92% of the islet oscillating synchronously over a number of modeled islets. This reduction in synchronization with a range of behavior also agrees with that seen in islets from different Cx36+/− mice, although the proportion of the islet with synchronous phase-locked oscillations upon ∼50% reduction in coupling conductance is higher than that experimentally observed. If the coupling conductance is reduced down to a mean of 10 pS and standard deviation of 8 pS, the oscillation synchronization over a number of islets varies between 0% and 7%.

Finally the oscillation characteristics of each cell in the islet model are compared in the presence and absence of electrical coupling (generated with the same random number seed). In the presence of electrical coupling, where the waves always originate in the same region of the islet, this area corresponds to cells in the uncoupled islet that are continually spiking (higher g_KCa) or exhibit an increased metabolic flux (higher r). This suggests that calcium waves can initiate in subregions of the islet where there is increased β-cell excitability (see Fig. S3 in Data S1).

Quantitative description of islet coupling and connectivity

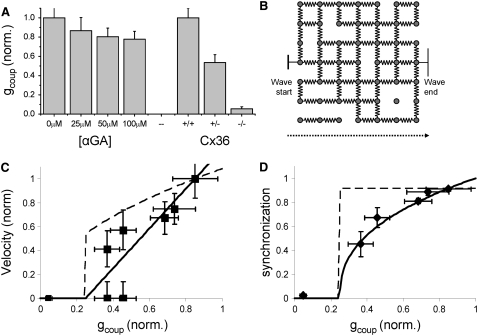
We have shown how the calcium wave velocity slows with the application of chemical inhibitors of gap junction activity. We have also shown how calcium waves slow or are dramatically disrupted upon a knockout of the gap junction forming protein Cx36. To quantitatively describe these wide variations in [Ca²⁺]_i activity, we utilized electrophysiological measurements to quantify the change in gap junction coupling after the application of αGA or the knockout of Cx36. The reduction in gap junction activity measured through a reduction in coupling conductance can be seen in Fig. 6 A. The application of αGA has only a minor effect on coupling conductance (up to 22% ± 8% reduction, mean ± SE), which shows no further increase above 50 μM αGA. The heterozygous knockout of Cx36 has a much greater effect on coupling conductance (46% ± 8% reduction, mean ± SE) and the homozygous knockout almost abolishes electrical coupling between islet β-cells (95% ± 2% reduction, mean ± SE). When these data are compared to the calcium wave data, as the calcium wave velocity progressively decreases, coupling conductance decreases until waves are partially disrupted at 50%–60% reduction in coupling conductance and fully disrupted at ∼95% reduction in coupling conductance.

FIGURE 6.

Dependence of [Ca²⁺]_i wave velocity and oscillation synchronization with gap junction conductance. (A) The measured decrease in coupling conductance (g_coup) for each treatment used to modify gap junction coupling. The decrease in coupling conductance in Cx36+/− (46%) is much more than that seen after αGA treatment (maximum 22%). (B) A two-dimensional schematic representation of the three-dimensional lattice resistor model used for the percolating model of islet β-cell electrical connectivity. Resistors represent electrical coupling between β-cells. Missing resistors represent missing connections due to vasculature or other endothelial cell types. Blockage or removal of gap junctions is represented by a reduction in the number of resistor connections. (C) Experimental data of calcium wave propagation, displaying the normalized change in wave velocity with the normalized mean coupling conductance in the islet. Solid line is theoretical and represents the percolating (discrete) model of islet connectivity; dashed line represents the ohmic (continuous) model of islet connectivity. The experimental data have better agreement with the percolation model than with the ohmic model. (D) Percolation model, ohmic model, and data of proportion of islet cells synchronized. The experimental data have good agreement with the percolation model and poor agreement with the ohmic model.

To functionally describe the decrease in wave velocity with reduced coupling conductance, we considered the islet as a lattice network of resistors connecting β-cells. The analytical models described in the Theory section can be used to describe the calcium wave propagating across such a lattice. A reduction in coupling conductance can be represented as a blocking of individual β-cell to β-cell connections (discrete/percolation model, schematically shown in Fig. 6 B), or a reduction in conductance of all β-cell to β-cell connections (continuous/ohmic model). The theoretical variation of the calcium wave velocity after a reduction in coupling conductance is shown in Fig. 6 C for both analytical models described by Eqs. 10 and 12 (discrete model: solid line, continuous model: dashed line). The theoretical variation of [Ca²⁺]_i oscillation synchronization with coupling conductance described by Eqs. 11 and 13 is shown in Fig. 6 D.

Fig. 6 C compares experimental data with the analytical models, relating gap junction coupling to the calcium wave speed, and Fig. 6 D compares experimental data with the analytical models of the proportion of islet cells exhibiting synchronized oscillations. In both models, only one free fitting parameter is used: the amount of β-cell connectivity in WT islets at elevated glucose levels. This value was optimally fit to 85% (±2%), that is, under normal gap junction coupling ∼15% of the neighboring β-cells are predicted to have no connectivity. This is in good agreement with dual cell electrophysiology measurements that show 15%–20% of neighboring β-cells are uncoupled (33) and is also in agreement with the proportion of vascular endothelial cells that exist in the islet, shown through immunofluorescence imaging (34). Experimental data in Fig. 6 C, relating gap junction coupling to the calcium wave speed, show a closer agreement with the percolation model than with the ohmic model (χ² = 1.01 for percolation model, χ² = 2.07 for ohmic model).

Experimental data in Fig. 6 D, relating gap junction coupling to the proportion of islet cells exhibiting synchronized oscillations, show good agreement with the percolation model and poor agreement with the ohmic model (χ² = 0.78 for percolation model, χ² = 8.90 for ohmic model). The data point corresponding to 100 μM αGA (not shown) strongly deviates from both analytical models, where fewer cells are observed to be oscillating (54%) than would be predicted (79%) from the percolating model of connectivity, but this effect is likely due to nonspecific effects of the inhibitor at this higher concentration. From measurements of [Ca²⁺]_i activity in islets of Cx36−/− mice after the application of αGA, we can judge that nonspecific effects resulting from up to 50 μM αGA will reduce the oscillation synchronization slightly, but not significantly compared to the effects of the partial gap junction inhibition.

DISCUSSION

We sought to quantify the role of gap junction connectivity in the synchronization and propagation of calcium oscillations and waves in pancreatic islets during glucose-stimulated insulin secretion. The use of high-speed optically sectioned imaging with the LSM5Live allows the velocity of these waves to be resolved with a high degree of accuracy. Our method of analysis allows direct visualization of wave propagation in the form of a phase map, which displays both the wave propagation direction and its speed across the islet. Additionally our analysis can show only those islet cells that exhibit calcium oscillations that are synchronized with those in the rest of the islet. By utilizing both a knockout of the gap junction forming protein and chemical inhibitors of gap junction coupling, we can be sure that the observed changes in [Ca²⁺]_i are not dominated by nonspecific effects of αGA (such as seen with 100 μM αGA) or compensatory factors of the Cx36 knockout. The use of islets from Cx36−/− mice also allows subtle nonspecific effects of chemical gap junction inhibitors on [Ca²⁺]_i dynamics to be analyzed in greater detail. This is a more robust approach to studying the effect of reduced gap junction coupling on the multicellular calcium dynamics in the islet. Through the measurement of gap junction coupling conductance for each treatment, we can quantitatively resolve the relationship between the measured intercellular calcium dynamics and electrical connectivity in the islet and make comparisons with analytical models of islet connectivity.

Although we measure a wide range of wave velocities, from ∼20 μm/s to >200 μm/s, these are all consistent with the waves arising due to the electrical propagation of action potentials. These velocities are in agreement with electrophysiological studies on islet cells that have seen temporal separation in oscillations in membrane potential in different islet cells (35). The calcium wave velocities we measure in the islet are much greater than those measured in airway epithelial cells or glioma cells (8–10 μm/s) (36,37). In airway epithelial cells the calcium waves are mediated by intercellular IP₃ diffusion via gap junctions. The velocities observed in those systems are consistent with the speed of diffusion of the second messenger molecule, and so it is highly unlikely that waves observed in the islet arise due to the diffusion of calcium or another second messenger between β-cells. In the time it takes the calcium wave to propagate across the islet (on average ∼2 s to cross ∼150 μm) calcium ions would diffuse in free space only ∼30 μm, and less in the presence of gap junction and/or intermediate extracellular signaling. These data therefore allow us to conclude that, likely, it is electrical coupling between β-cells via gap junction channels that leads to the synchronization of islet calcium oscillations. This therefore suggests that measuring changes in these oscillations upon a modulation in gap junction coupling can be used to gain insight into the fundamental mechanism of electrical coupling between β-cells in the islet.

Through computer modeling, we also showed how these calcium waves can arise in an islet consisting of an electrically coupled heterogeneous population of β-cells. This model shows that the islet does not require a pacemaker region which sets the oscillations of the rest of the β-cell. Instead, the origin of these waves is due to islet heterogeneity, as supported by the fact that isolated β-cells tend to show a large degree of heterogeneity in their metabolic and electrical response to high glucose (7,38). In the computer model of the islet, the calcium waves generally originate in subregions of higher excitability. This is consistent with published data showing that waves originate from regions of increased K_ATP channel inhibition (39) and thus suggests that the presence of a heterogeneity in β-cell excitability is sufficient to lead to consistently propagating calcium waves. The computer model of the islet also produces calcium waves with velocities equivalent to the range of velocities that we measure in intact islets of equivalent size of <150 μm in diameter. Generation of these wave velocities required the heterogeneous coupling conductance with a broad distribution (σ/μ ∼ 0.7).

This finding is also in agreement with a previous mathematical model of realistic wave velocities (14) and is consistent with our electrophysiology data, which exhibit a wide range of coupling conductance values. Furthermore, the ∼2 times greater wave velocity in the absence of this heterogeneity in coupling conductance is also consistent with the previously presented model (14). Aslandi and co-workers (13) initially simulated a wave velocity several times faster than the measured calcium waves. We do not, however, follow their reasoning that glucose is lower in the center of the islet (which was used to model lower velocity waves), since measurements of metabolic response through NAD(P)H imaging finds equal response throughout the islet only a few minutes after glucose stimulation (38). Further, our simulation of an ∼50% reduction in electrical coupling results in a reduction in oscillation synchronization which is in agreement with what is observed experimentally in islets of heterozygous Cx36+/− knockout mice. We can thus ascribe the wide range of wave velocities measured as well as the differences in Cx36+/− islet behavior to be due to the large amount of β-cell heterogeneity and coupling heterogeneity in the islet.

We should note, however, that we were still unable to model calcium waves with velocities in the 20–60 μm/s range, equivalent to the slower ∼40% of calcium waves that we measured. Furthermore the proportion of the islet that is synchronized upon an ∼50% reduction in coupling conductance is also modeled to be higher than what we experimentally measure. Interestingly, when the mean coupling conductance is reduced to 20 pS, the proportion of the islet showing synchronized oscillations is in closer agreement with what is experimentally observed in islets of Cx36+/− mice. Thus, setting the WT coupling conductance in the computer model of the islet to a distribution with a mean of 40 pS and a standard deviation of 28 pS gives more accurate [Ca²⁺]_i dynamics as gap junction coupling is reduced. Additionally, the reduction in oscillation synchronization with reduced mean coupling conductance agrees well with the percolation model if the mean WT coupling conductance is set to 40 pS. This is summarized in greater detail in Fig. S4 in Data S1. The fact that subphysiological gap junction coupling yields more accurate results suggests that in the coupled phantom-burster model, β-cells couple their electrical activity too readily.

The measured changes in [Ca²⁺]_i oscillations (wave velocity and synchronization) with a reduction in coupling conductance quantitatively agree with the analytical model that describes the islet as a lattice of randomly electrically coupled units (β-cells). Overall, considering both the wave velocity and proportion of the islet that shows synchronized oscillations, the experimental data showed a closer agreement with the discrete/percolation analytical model of connectivity. The percolation model also predicts the number of uncoupled β-cells in the islet to be in agreement with previously published data (33,34). We appreciate that an intermediate case between the two models of coupling is likely to be most accurate, representing heterogeneity in the β-cell to β-cell conductance. A wide range in heterogeneity is predicted by the coupled phantom-burster model (22) with heterogeneous electrical coupling, which successfully reproduces many aspects of the measured islet electrical dynamics. Nevertheless, the close agreement with the percolation model indicates that β-cells with weak or incomplete coupling dominate the spatiotemporal dynamics of the calcium oscillations. These analytical models can further be useful for predicting the islet connectivity from measurements of the spatiotemporal [Ca²⁺]_i dynamics. For example, we can make the prediction that ∼25% (p_c = 0.2488) of the WT coupling conductance will be insufficient to maintain any synchronization in the [Ca²⁺]_i oscillations. Thus under this level of gap junction disruption, we would expect to measure the same spatiotemporal electrical dynamics as would be seen in Cx36−/− islets. Appropriate genetic systems are under development to test this predication.

It is also of interest that in the absence of electrical coupling, we observed that calcium oscillations in individual β-cells of Cx36−/− islets occur on a wide range of timescales, representing very fast (approximately seconds), fast (∼10 s), and slow (approximately minutes) oscillations. This is in contrast to the fast oscillations that we focused on in this work. Many studies have been performed in analyzing the oscillation timescales in isolated β-cells and islets, e.g., Kinard et al. (6), Zhang et al. (7), and Pedersen (40). Since there is no electrical coupling between β-cells, islets of Cx36−/− mice are an ideal preparation for studies to contrast those carried out in dispersed β-cells. Cells within Cx36−/− islets still retain the cellular proximity and other architectural features which could be important for maintaining β-cell function.

From this study, we can draw some additional conclusions on the functional implications of gap junction coupling and calcium waves in islets in vivo. We have demonstrated through computer simulations that calcium waves in an islet can arise solely due to β-cell heterogeneity. We would therefore expect that calcium waves would also be present in islets in vivo to coordinate oscillations in [Ca²⁺]_i. We have quantitatively shown how gap junction coupling coordinates electrical oscillations at elevated glucose levels that would result in pulsatile insulin release, which has been shown to have a greater hypoglycemic effect compared to continuous levels of secretion (41). This predicts that a loss in coupling that approaches or exceeds the critical coupling conductance (∼25% WT conductance) would disrupt insulin pulsatility, as calcium waves could no longer propagate across the whole islet to coordinate calcium oscillations. A loss in insulin pulsatility is often seen in type II diabetics and obese individuals (42,43) and we speculate that this could result from the downregulation of gap junction forming connexin proteins, as well as the reduction in β-cell to β-cell proximity due to α-cell infiltration or β-cell degeneration in intermediate cells. These events are known to occur in hyperglycemic conditions (44,45), which are associated with the symptoms of type II diabetes. Furthermore, it has been observed that during pregnancy, an increase in gap junctional coupling is observed in islets, concomitant with increased islet size and enhanced insulin secretion (46,47). Since we saw a reduction in calcium wave velocity with islet size, we can speculate that the increased gap junction coupling is necessary to counteract the reduced calcium wave velocity to maintain proper coordination of [Ca²⁺]_i oscillations across the islet and thus maintain pulsatile insulin secretion.

To conclude, we have precisely measured the wave velocity and synchronization associated with [Ca²⁺]_i oscillations in the islet and can accurately predict these behaviors with a multicellular model framework. We have shown how the wave velocity and synchronization both decrease with a decreased gap junction connectivity in the islet and that the decrease can be quantitatively described by an analytical model of gap junction connectivity between β-cells in the islet. These results are also quantitatively reproduced in a heterogeneously coupled β-cell computational model. This has importance for describing the β-cell communication within the islet, as well as allowing the synchronized [Ca²⁺]_i oscillations and waves to be a precise measure of islet connectivity. The techniques we have used to introduce quantitative changes in the gap junction coupling and measure the impact of these changes on the whole islet electrical response provide a powerful approach that can be extended to study other aspects of the islet as well as to study the underlying properties of multicellular systems in general.

SUPPLEMENTARY MATERIAL

To view all of the supplemental files associated with this article, visit www.biophysj.org.