Bupivacaine Blocks N-Type Inactivating K_v Channels in the Open State: No Allosteric Effect on Inactivation Kinetics

Abstract

Local anesthetics bind to ion channels in a state-dependent manner. For noninactivating voltage-gated K channels the binding mainly occurs in the open state, while for voltage-gated inactivating Na channels it is assumed to occur mainly in inactivated states, leading to an allosterically caused increase in the inactivation probability, reflected in a negative shift of the steady-state inactivation curve, prolonged recovery from inactivation, and a frequency-dependent block. How local anesthetics bind to N-type inactivating K channels is less explored. In this study, we have compared bupivacaine effects on inactivating (Shaker and K_v3.4) and noninactivating (Shaker-IR and K_v3.2) channels, expressed in Xenopus oocytes. Bupivacaine was found to block these channels time-dependently without shifting the steady-state inactivation curve markedly, without a prolonged recovery from inactivation, and without a frequency-dependent block. An analysis, including computational testing of kinetic models, suggests binding to the channel mainly in the open state, with affinities close to those estimated for corresponding noninactivating channels (300 and 280 μM for Shaker and Shaker-IR, and 60 and 90 μM for K_v3.4 and K_v3.2). The similar magnitudes of K_d, as well as of blocking and unblocking rate constants for inactivating and noninactivating Shaker channels, most likely exclude allosteric interactions between the inactivation mechanism and the binding site. The relevance of these results for understanding the action of local anesthetics on Na channels is discussed.

INTRODUCTION

Local anesthetics are examples of pharmacological agents binding to ion channels in a state-dependent manner. The effects on voltage-gated Na (Na_v) channels have been summarized in the modulated-receptor hypothesis, first formulated by Hille (1) and Hondeghem and Katzung (2) in 1977. The main feature of this hypothesis is that the local anesthetic binds more tightly to inactivated channels than to resting or open ones, and that the tight binding to inactivated channels is accompanied by an allosterically induced increase in the propensity of the channel to inactivate; the inactivation gate is more likely to be shut when the local anesthetic is bound. This hypothesis has been extensively used to explain effects of various local anesthetics on Na_v channels of different origins—the negative voltage shifts of the steady-state inactivation curve, the slow recovery from inactivation, and the use-dependent block during repetitive pulsing (3–14). However, this version of the modulated hypothesis has not been unchallenged. Other forms, stressing open-state binding, have also been presented (15–20).

In this context, the action of local anesthetics on inactivating voltage-gated K (K_v), channels has been surprisingly little explored, considering the recent advances in understanding the molecular structure of these channels and their interaction with blocking molecules (21–28). An obvious experiment in this context would be to test the modulated receptor hypothesis developed for Na_v channels on inactivating K_v channels, the prediction being that introducing an inactivated state into a noninactivating channel increases the affinity for the local anesthetic.

In this investigation, we analyzed the effects of bupivacaine, an amino-amide type local anesthetic widely used for regional anesthesia, on the rapidly N-type inactivating wild-type Shaker and K_v3.4 channels (29,30). To explore possible interactions between the bupivacaine binding and the N-type inactivation process, we analyzed the bupivacaine effects on corresponding non-N-type-inactivating channels, a mutated Shaker isoform (Shaker-IR) and K_v3.2. The latter channel (K_v3.2) has previously been found to bind bupivacaine mainly in the open state (31,32).

The experiments on the inactivating channels showed that bupivacaine causes a time-dependent and relatively voltage-independent block, without shifting the steady-state inactivation curve markedly (slightly in negative direction) or prolonging the recovery from inactivation, and thus without causing use dependence. A kinetic modeling analysis showed that the block could best be explained by a scheme, assuming binding exclusively in the open state; no additional binding in closed or inactivated state is required. At first sight, the mechanisms of local anesthetic action on K_v channels seem to differ from those on Na_v channels. However, exploring the open-state binding model it can be shown that assuming a higher affinity, or alternatively faster gating kinetics, all the features described for the Na_v channel block can be simulated.

MATERIALS AND METHODS

Molecular biology

cRNA for the rK_v3.2, rK_v3.4, Shaker B (in the present study called Shaker) and Shaker H4 Δ6-46 (called Shaker-IR) were synthesized by using the plasmid pAS18 as template for SP6 polymerase (33). rK_v3.4 and Shaker inactivates rapidly while rK_v3.2 and Shaker-IR are lacking fast N-type inactivation. (For the molecular biology of Shaker B and Shaker H4, see (34,35).) The transcription reactions were performed using a commercial kit (mMessage mMachine, Ambion, Austin, TX) and T7 RNA polymerase. Oocytes of the South African clawed toad (Xenopus laevis) were used as expression system. The oocytes in stage V or VI were injected with the respective cRNA. The injected oocytes were maintained at 12°C until used for experiments. The electrophysiological experiments were performed days 3–5 after injection of cRNA.

Electrophysiology

The investigations were performed with a two-electrode voltage-clamp technique, modified to include a concentration-clamp technique (36) and with the two-electrode voltage-clamp technique (CA-1 amplifier, Dagan, Minneapolis, MN). The pipettes used were of borosilicate glass (Hilgenberg, Malsfeld, Germany) with a resistance of 0.5–1 MΩ when filled with 3 M KCl. Data acquisition and analysis were made with pCLAMP software (Axon Instruments, Foster City, CA). The holding potential was −80 mV (activation curves) or −100 mV (steady-state inactivation curves) and currents associated with steps as mentioned below.

To avoid a series resistance problem the critical measurements (midpoints) were performed at relatively low currents. The series resistance problem was estimated to be negligible in the experiments using the standard setup. In the concentration-clamp setup, only used for the K_v3 experiments, the volume resistance of the external solution between membrane and ground was estimated to be between 0.1 and 1 kΩ (36). A series resistance is predicted to increase the slope of the activation and inactivation curves, introducing an error that reduces the absolute value of the shift of activation curve and increases the shift of inactivation curve. Using the higher resistance value above (1 kΩ) the error introduced in the values given for the shifts of K_v3 curves can be calculated to be <1.5 mV. The relatively long settling time of the potential steps (partly due to the large membrane capacitance; (37)) clearly depended on the size of the current. The resulting error was negligible at currents at <5 μA, and consequently in the measurements at the used bupivacaine concentrations. It, however, affected the control currents at high potential steps. We therefore discarded the first 2 ms of these recordings in the quantitative analysis. The results are given as mean ± SE.

Solutions

The tissue culture solution used was a modified Barth's solution containing (in mM): NaCl 88, KCl 1, CaCl₂ 1.5, NaHCO₃ 2.4, MgSO₂ 0.8 and HEPES 5, supplemented with penicillin (100 IU/ml) and streptomycin (100 μg/ml). pH was adjusted to 7.4 by adding NaOH. The control Ringer solution used for the electrophysiological experiments on oocytes contained (in mM): NaCl 115, KCl 2, CaCl₂ 1.8, and HEPES 10. pH was adjusted to 7.2 by adding NaOH. The test solutions consisted of control solution with bupivacaine (Sigma Chemical, St. Louis, MO) added.

Analysis

The peak (for inactivating Shaker and K_v3.4 channels) or the steady-state currents (for noninactivating Shaker-IR and K_v3.2 channels), associated with steps to +60 mV from a holding potential of −80 mV, were fitted to

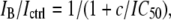(1)

where I_B/I_ctrl is the ratio between the current in test solution and in control solution, c is the bupivacaine concentration, and IC₅₀ is the concentration blocking 50% of the current. The K conductance of the membrane (G) was calculated as

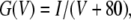(2)

where V is the membrane potential and I is the current. The steady-state inactivation curves for the fast inactivating channels in the oocyte experiments were calculated from measurements of the peak currents associated with holding potentials of −100 mV and a step to +20 mV (Shaker) or +60 mV (K_v3.4) after conditioning steps of 100 and 400 ms duration, respectively.

Computations

The kinetic schemes of the principal blocking mechanisms were extended versions of the following three-state scheme,

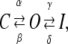(Scheme 0)

describing the kinetics of an N-type inactivating K channel. C, O, and I denote closed, open, and inactivated states, respectively; α, β, γ, and δ denote activation, deactivation, inactivation, and deinactivation rate constants, respectively. The activation and deactivation rate constants α and β were assumed to be voltage-dependent according to

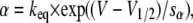(3)

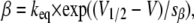(4)

where k_eq is the rate constant when V = V_1/2; V = V_1/2 when α = β; and s_α and s_β are constants determining the slope of the rate constant versus voltage curves. The parameter values used are listed in Table 1 and were chosen to yield a G(V) curve similar to that experimentally obtained with a midpoint at −20 mV and a slope close to 6 mV (e.g., (38)). The inactivation and deinactivation rate constants γ and δ are assumed to be voltage-independent (29,39), and are also listed in Table 1.

TABLE 1.

Parameter values used for calculation of kinetic models of Shaker and K_v3.4

	keq	V1/2	sα	sβ	γ	δ
	(ms−1)	(mV)			(ms−1)
Shaker	0.7	−20	50	7	0.5	0.03
Kv3.4	0.03	30	50	9	0.024	0.0007

The simple one-step activation (in Scheme 0) precludes a sigmoid time evolution of the open state at depolarization. However, computations with multistep-activation models gave similar results (see Supplementary Material, Fig. S1, Fig. S2, and Fig. S3), and we concluded that the one-step model was sufficient for the present purpose of exploring binding mechanisms. To calculate the behavior of a noninactivating Shaker channel mutant (Shaker-IR), we used a modified Scheme 0 with the inactivating state removed.

For the numerical analysis, the schemes were expressed as systems of parallel differential equations, according to the general formula

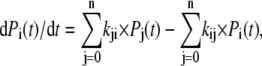(5)

where P_i is the probability that the channel is in state i; n is the number of conformational states; and k_ij is the transition rate from state i to state j. The differential equations were solved by a forward Euler integration method, using custom-developed software written in BASIC. A time-integration time step of 0.4–5 μs was found adequate to simulate the kinetic curves within the experimental parameter limits.

COMPUTATIONAL RESULTS

Block of noninactivating channels

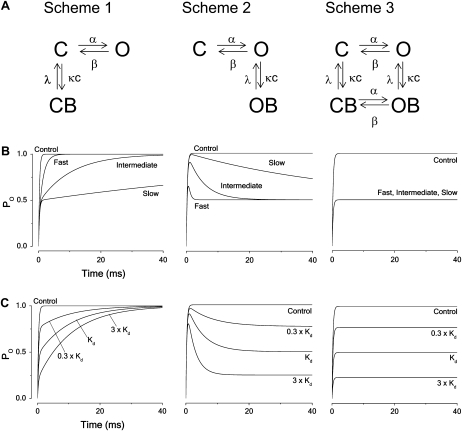
Fig. 1 A shows the kinetic schemes of three basic ways to block the two-state noninactivating channel model. The blocking and unblocking constants were assumed to be voltage-independent and are denoted κ and λ, yielding a dissociation constant K_d = λ/κ. Scheme 1 describes a closed-state binding mechanism, Scheme 2 an open-state, and Scheme 3 a state-independent (or all-state) binding mechanism. The effect of bupivacaine on noninactivating K_v1 and K_v3-type channels is explained by a Scheme 2 mechanism, while that on K_v2.1 is explained by a version of Scheme 3 (32). A version of Scheme 1 has been suggested to describe the action of 4-AP (4,40) and tetrahydroaminoacridine (41) on K_v channels. Fig. 1 B shows the time evolution of the open probability at +60 mV for the three principal blocking mechanisms for three levels of blocking rates; slow, intermediate, and fast (κ × c = λ = 0.01, 0.1 and 1 ms⁻¹, respectively), assuming the parameter values in Table 1 (Shaker). For Scheme 1 (closed-state binding), the slow block results in an almost 50% downscaled response, the fast block in a twofold slower activation rate but otherwise intact response, and the intermediately fast block in a more than twofold slower activation. For Scheme 2 (open-state binding), the slow block results in a slow induced inactivation, the intermediately fast block in a smaller peak amplitude and an intermediately fast induced inactivation, and the fast block an even smaller peak and faster inactivation. Increasing the rate of block further results in an apparent 50% downscaled response (although the activation seems faster). For Scheme 3 (all-state binding), all three block cases result in a 50% downscaled response.

FIGURE 1.

Principal blocking mechanisms of a noninactivating channel. (A) Kinetic schemes. C and O denote closed and open states of the unbound channel, CB and OB closed and open (but nonconducting) states of the local anesthetic bound channel; α, β, κ, and λ denote rate constants and c the local anesthetic concentration. (B) Computed time courses of the open probability for the different schemes. Calculated for K_d concentration from Eqs. 3–5, assuming V = +60 mV and using parameter values in Table 1 (Shaker) for fast, intermediate, and slow blocking rates (κ = λ = 1, 0.1, and 0.01 ms⁻¹, respectively). (C) Computed time courses of the open probability for the different schemes at concentrations 0.3 × K_d, K_d, and 3 × K_d, assuming intermediate blocking rates (κ = 0.1 and λ = 0.1 ms⁻¹).

Fig. 1 C shows the concentration dependence of the three types of block, assuming an intermediate blocking rate (κ × c = λ = 0.1 ms⁻¹). Increasing the concentration decreased the rate of the rising phase of the closed-state binding model (Scheme 1), increased the rate of the decaying phase of the open-state binding model (Scheme 2), and downscaled the open probability curve of the all-state binding model (Scheme 3) without affecting the time course.

Block of inactivating channels

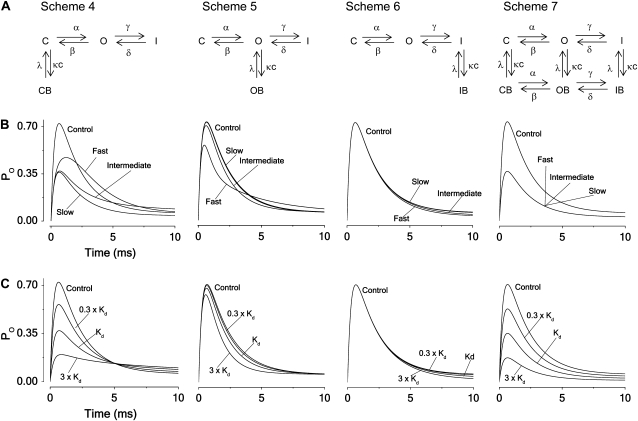
To explore the block of channels with fast (N-type) inactivation we used the schemes presented in Fig. 2 A. Fig. 2 B shows the time evolution of the open probability described by the four schemes at slow, intermediate, and fast block (κ × c = λ = 0.01, 0.1, and 1 ms⁻¹, respectively) and for the control situation (no block), assuming V = +60 mV and parameter values in Table 1 (Shaker). For Scheme 4 (closed-state binding), the slow block yields roughly a 50% downscaled response (as for Scheme 1), and the fast block a less decreased peak value and a slowed activation, causing the curve to cross the control curve. The intermediately fast block results in a more pronounced peak reduction and a slowed inactivation. For Scheme 5 (open-state binding), the slow and intermediate block only results in marginal alterations, while the fast block reduces the peak and slows down the latter part of the inactivation, causing the curve to cross the control curve. For Scheme 6 (inactivated-state binding), all three blocking cases have almost no effects, and for Scheme 7 (all-state binding), they all result in a 50% reduction. Combining Scheme 5 and Scheme 6, assuming equal blocking and unblocking rates for the open and inactivated state transitions, results in a hybrid scheme with properties that are very similar to those of Scheme 5 except for the important difference that no crossing-over effect is seen for the fast block (Fig. S4, A and B).

FIGURE 2.

Principal blocking mechanisms of an inactivating channel. (A) Kinetic schemes. Symbols as in Fig. 1. I denotes an inactivated state of the unbound channel and IB the inactivated state of the local anesthetic bound channel; γ and δ denote the inactivation rate constants and c the local anesthetic concentration. (B) Computed time courses of the current for the different block schemes. Calculated for K_d concentration from Eqs. 3–5, assuming V = +60 mV and using parameter values in Table 1 (Shaker) for fast, intermediate, and slow blocking rates (κ = λ = 1, 0.1, and 0.01 ms⁻¹). (C) Computed time courses of the open probability for the different schemes at concentrations 0.3 × K_d, K_d, and 3 × K_d, assuming intermediate blocking rates (κ = 0.1 and λ = 0.1 ms⁻¹).

The magnitude of a steady-state block of inactivating channels is in real voltage-clamp experiments difficult to estimate due to the small currents obtained. In such experiments, the reduction of the peak current is easier to determine, but difficult to relate to binding parameters.

Fig. 2 C demonstrates the varying concentration dependencies of the four types of block, assuming an intermediate rate of blocking (κ × c = λ = 0.1 ms⁻¹). Closed-state (Scheme 4) and all-state (Scheme 7) binding show clear effects on the peak amplitudes, while open-state (Scheme 5) binding shows smaller effects at this rate of block and inactivated-state (Scheme 6) none at all. Open-state (Scheme 5) binding shows an increased rate of decay with increased concentration, while closed-state (Scheme 4) binding shows the reverse. Inactivated-state (Scheme 6) binding shows relatively small effects, while all-state (Scheme 7) binding shows no effect at all. Analytical expressions of the concentration influence on the time constants for the decaying phases in Schemes 4–6 are derived in Appendix B.

Steady-state activation

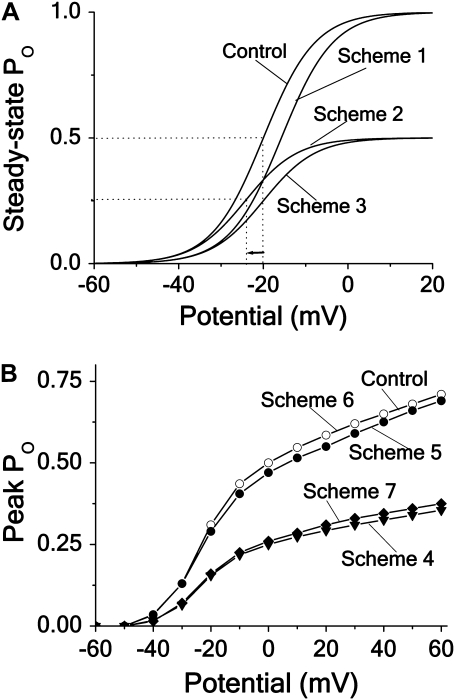
To obtain curves, reflecting the effect of the blocking agent on steady-state G(V) for the schemes assuming no fast inactivation, we calculated the steady-state open probabilities P_O(V) at control and K_d (i.e., c = λ/κ) concentration conditions, using the expressions of Appendix A. The results are shown in Fig. 3 A. Scheme 1 results in a +4.5 mV shift of G(V) with no reduction at positive voltages. Scheme 2 results in a 50% reduction of G(V) at positive voltages and in a shift of −4.5 mV. Scheme 3 results in a 50% reduction at all voltages.

FIGURE 3.

Effects of different block mechanisms on activation curves. Computed steady-state and peak open probability (P_O) plotted against potential for the different blocking schemes (see Figs. 1 and 2), assuming K_d concentration and intermediate blocking rate. (A) Noninactivating channels, Schemes 1–3 (see Appendix A). (B) Inactivating channels, Schemes 4–7.

Fig. 3 B shows corresponding curves for the schemes that include fast inactivation: We calculated peak P_O(V) curves assuming intermediately fast binding (κ × c = λ = 0.1 ms⁻¹). Open-state binding (Scheme 5) and inactivated-state binding (Scheme 6), as well as the hybrid scheme constructed from Scheme 5 and Scheme 6 (see Fig. S4), only marginally affect the peak values, while closed-state binding (Scheme 4) and binding in all states (Scheme 7) reduce the values, but without shifting the curve. In contrast to the distinct effects of different binding mechanisms on the activation curve of noninactivating channels (Fig. 3 A), the corresponding effects on the activation curve of inactivating channels are relatively uninformative.

Steady-state inactivation, recovery from inactivation, and frequency dependence

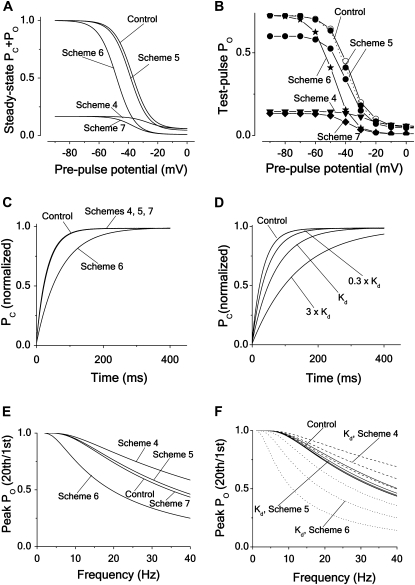
A more rewarding method to get information about the binding mechanisms in inactivating channels is to explore the steady-state inactivation curve for the different cases. A characteristic feature of many local anesthetics is to shift the inactivation curve in negative direction, traditionally interpreted as due to a Scheme 6 type binding (i.e., high-affinity binding to channels in inactivated state (1,42). It can easily be shown, however, that binding to the channel in the open state, as described by Scheme 5, also gives a shift in the same direction (but of a smaller magnitude). Fig. 4 A shows steady-state inactivation curves for Schemes 4–7 (see Appendix A for calculations). The parameter values used were the same as above except for the binding rate, which was κ × c = 0.5 ms⁻¹ (corresponding to a local anesthetic concentration of 5 × K_d). The calculations show that the different mechanisms shift (in both directions) and downscale the curves in different combinations. The curve for Scheme 4 (closed-state binding) is shifted +12 mV and downscaled sixfold, the curve for Scheme 5 (open-state binding) is shifted −2 mV without any size reduction, the curve for Scheme 6 (inactivated-state binding) is shifted −12 mV, also without any size reduction, and the curve for Scheme 7 (all-state binding) is downscaled sixfold with no shift.

FIGURE 4.

Effects of different block mechanisms on steady-state inactivation, recovery from inactivation and frequency dependence. Computations for Schemes 4–7, assuming intermediate blocking rates. Except for panel A, all calculations were made with Eqs. 3–5, using the parameter values for Shaker in Table 1. (A) Steady-state inactivation curves according to the expressions in Appendix A, assuming a blocker concentration of 5 × K_d. (B) Steady-state inactivation curves for the same cases as in A, but given as effect on the peak P_O, associated with a test step to +20 mV. (C) Recovery time course of P_C at −80 mV after a pulse step to +20 mV for the same cases as in A and B, but assuming a blocker concentration of K_d. (D) Recovery time course of P_C for Scheme 6 at three concentrations (0.3 × K_d, K_d, and 3 × K_d). Same protocol and parameter values as in C. The recovery for Schemes 4, 5, and 7 was not affected by the altered concentrations. (E) Peak P_O versus frequency curves, given as the ratio between peak P_O at the 20th and the 1st step of a pulse train, consisting of 10 ms pulses to +20 mV from a holding potential of −80 mV, plotted against frequency. (F) Peak P_O versus frequency curves at the concentrations 0.3 × K_d, K_d, and 3 × K_d. Same protocol and parameter values as in E. Control (thick continuous line), Scheme 4 (dashed lines, highest concentration at top); Scheme 5 (thin continuous lines, highest concentration at top) and Scheme 6 (dotted lines, lowest concentration at top).

However, experimental steady-state inactivation curves as a rule do not show real steady-state values, but are constructed from the peak-current values associated with a test pulse. To mimic experimental inactivation curves we therefore calculated the peak open probabilities at a test step after the conditioning steps. Fig. 4 B shows the results for Schemes 4–7. As seen, the open-state (Scheme 5) binding case deviates somewhat from the steady-state calculation in Fig. 4 A. However, when normalized (dashed line in Fig. 4 B), the inactivation curves become almost indistinguishable from the steady-state curves in Fig. 4 A, thus validating the use of the simple steady-state calculations when distinguishing binding mechanisms.

These results may seem to suggest that an open-state block (Scheme 5) only marginally shifts the inactivation curve. However, as will be shown in the Discussion, this only holds for the case assuming a relatively low binding affinity. Thus, a negative shift of the steady-state inactivation curve alone does not validate the conclusion that the underlying mechanism is of inactivated-state binding type (Scheme 6); to determine the underlying mechanism, the binding affinity of blocking agent has to be taken into account.

Another characteristic feature of many local anesthetics acting on Na_v channels is to slow down the rate of recovery from inactivation, causing use-dependent block. This is, as the negative shift of the steady-state inactivation curve, traditionally interpreted as due to a Scheme 6 type blocking (i.e., high-affinity binding to channels in inactivated state (42)). Fig. 4 C shows the time evolution of the recovery to state C after a pulse step to +20 mV at a K_d concentration for the four schemes at an intermediate blocking rate (κ × c = λ = 0.1 ms⁻¹). The calculations confirm a slowed recovery for the inactivated-state binding case (Scheme 6; half-time is more than doubled), while the recovery for the other schemes (Schemes 4, 5, and 7) is unaffected. The schemes also show distinctly different concentration dependencies of the recovery time, that of Scheme 6 being most dependent. Fig. 4 D demonstrates the recovery time course of Scheme 6 at different concentrations. The recovery time courses of the other schemes at the same three concentrations did not differ measurably from the control curve (not shown). However, as will be shown in the Discussion, these results also depend on the affinity of the substance.

As a consequence of a slowed recovery, many local anesthetics acting on Na_v channels also induce an increased block with increased stimulation frequency (i.e., a frequency-dependent or phasic block). Fig. 4 E shows the calculated frequency-dependent decrease of the peak open probability at +20 mV, measured as the open probability associated with the 20th pulse step divided by the probability associated with the first pulse step, at K_d concentration for the different blocking schemes. As expected from the results in Fig. 4 E, three of the schemes do not show any marked use-dependencies (exceeding that of the control curve). Somewhat unexpectedly, the curve of the closed-state binding case (Scheme 4) was shifted upwards. In contrast, and as expected, the curve of the inactivated-state binding scheme (Scheme 6) was clearly shifted downwards, demonstrating a marked use-dependence. Fig. 4 F shows how the concentration affects the use-dependence curves, confirming the concentration sensitivity order of Fig. 4 D, the Scheme 6 curve being most affected, the Scheme 4 curve less, the Scheme 5 curve even less, and the Scheme 7 curve not at all. Combining Schemes 5 and 6 into a hybrid scheme with both open- and inactivated-state binding shows similarities to Scheme 6 with regard to effects on the steady-state inactivation and recovery curves (see Fig. S4, C and D).

In conclusion, the kinetic analysis of the effects of different blocking mechanisms above highlights the need for a careful analysis when trying to understand the details of local anesthetic action. It demonstrates how one and the same binding model can lead to qualitatively different results depending on the rate of binding, but also how different models can lead to very similar results. Thus, a slow closed-state block of an inactivating channel (Scheme 4) has the same effect as an all-state block (Scheme 7) of all speeds. The crossing-over phenomenon is found for a fast closed-state block (Scheme 4) and for a fast open-state block (Scheme 5).

EXPERIMENTAL RESULTS

The effects of bupivacaine on inactivating Shaker channels suggest a fast open-state block

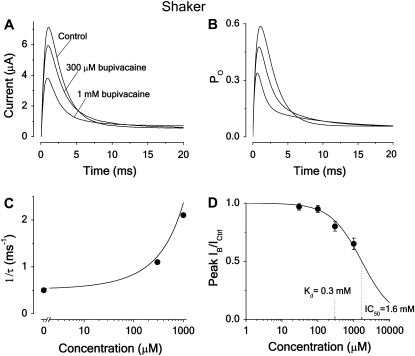
Fig. 5 A shows the effect of 300 μM and 1 mM bupivacaine on the time evolution of the current associated with a pulse step to +20 mV for inactivating Shaker K channels. The resulting decay displays an early fast phase and a late slow phase, leading to the bupivacaine curve crossing the control curve. A comparative analysis of the time course and the concentration dependence, using the calculations above (see Fig. 2), suggests that bupivacaine acts via a fast open-state block mechanism (Scheme 5). Fig. 5 B shows a calculated curve, based on Scheme 5, fitted to the experimental data in Fig. 5 A. The resulting binding rates are listed in Table 2. The K_d value, obtained from the estimated binding and unbinding rates (κ = 1.5 ms⁻¹ × mM⁻¹ and λ = 0.45 ms⁻¹) is 300 μM. (Note that the binding rates are relatively faster than those used for calculating the curves in Fig. 2 C, leading to larger amplitude effects in this calculation.)

FIGURE 5.

Effect of bupivacaine on time course of Shaker current. (A) Currents in 300 μM, 1 mM bupivacaine, and in control solution evoked from a voltage step to +20 mV. Holding potential was −80 mV. (B) Computed effect on an inactivating channel, based on Scheme 5 (open-state binding) and parameter values in Table 1. Resulting binding rates and dissociation constants are listed in Table 2. (C). Effect of bupivacaine concentration on the fast decay phase. Inverted time constants (1/τ), calculated as eigenvalues (r_i) from the matrix equation derived for Scheme 5 in Appendix B, using the values of Tables 1 and 2, and corresponding experimental values, estimated from the curves in A by fitting a sum of two exponentials to the decaying phase (between t = 2 and 10 ms), plotted against concentration. The eigenvalue expression used was r₂ = − 1/2 × (γ + δ + κ × c + λ + √((γ + δ + κ × c + λ)² – 4 × (δ × κ × c + γ × λ + δ × λ))). (D) Dose-response curve (Eq. 1) fitted to mean peak currents at +20 mV (n = 9). Resulting IC₅₀ = 1.6 mM.

TABLE 2.

Estimated activation and binding parameters and mean IC₅₀ for bupivacaine block of K_v channels

Channel type	α* (ms−1)	β* (ms−1)	κ (ms−1 mM−1)	λ (ms−1)	Kd (mM)	IC50 (n) (mM)	IC50/Kd
Inactivating channels
Shaker	1.0	0	1.5	0.45	0.30	1.6 ± 0.1 (9)	5.3
Kv3.4	0.2	0	0.1	0.006	0.06	1.2 ± 0.06 (10)	20
Noninactivating channels
Shaker-IR	0.42	0	1.2	0.34	0.28	0.24 ± 0.03 (5)	0.86
Kv1.1	0.23	0	0.5	0.10	0.20	0.24 ± 0.02 (4)	1.2
Kv1.2	0.27	0	1.2	0.22	0.18	0.21 ± 0.02 (12)	1.2
Kv1.5	0.15	0	0.8	0.10	0.12	0.13 ± 0.04 (6)	1.1
Kv3.1	0.16	0	0.5	0.06	0.12	0.13 ± 0.03 (4)	1.1
Kv3.2	0.17	0	0.5	0.04	0.09	0.11 ± 0.02 (5)	1.2

^*Value at V = +60 mV except for Shaker and Shaker-IR, where V = +20 mV. Values for K_v1.1, 1.2, 1.5, 3.1, and 3.2 from Nilsson et al. (32) included for a comparison.

The bupivacaine induced biphasic decay phase can be approximated by a sum of two exponential components, while the decay phase of the control case is approximately monoexponential. Fig. 5 C shows inverse time constants for the single (control) and the fast component (bupivacaine) of the decay phase of the experimental curves in Fig. 5 A, plotted against concentration. The values were obtained by fitting a monoexponential curve to the control curve, and by fitting sums of two exponentials to the bupivacaine curves. The continuous curve is the rate of the fast component (the largest eigenvalue = r₂) calculated from the expression derived for Scheme 5 in Appendix B, plotted against concentration. The corresponding inverse time constants of Scheme 4 are predicted to decrease with concentration (see Fig. 2 C and Appendix B).

Fig. 5 D shows a dose-response curve (Eq. 1) fitted to measurements of the peak current. The mean IC₅₀ is 1.6 ± 0.1 mM (n = 9; see Table 2), thus 5.3-fold higher than the K_d value, obtained from fitting Scheme 5 to the current time course (Fig. 5 B).

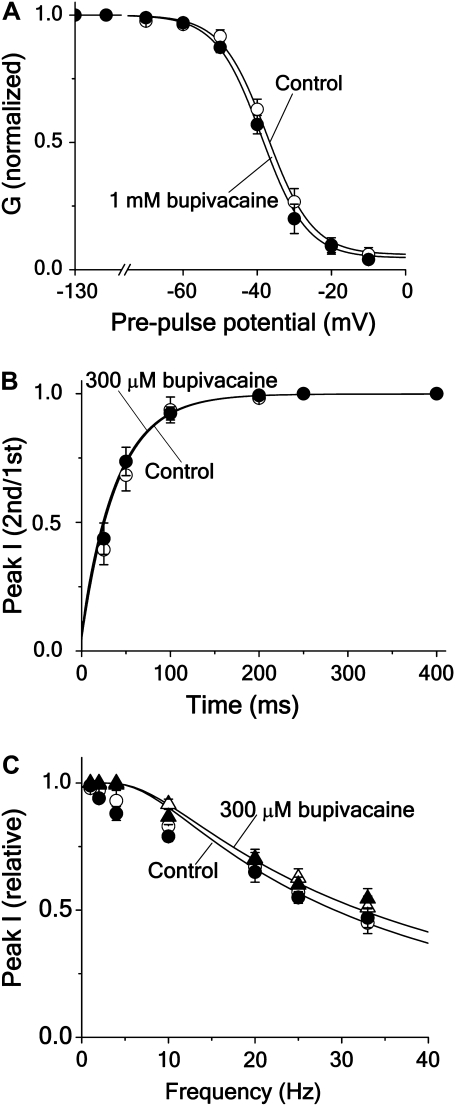
Fig. 6 A shows the effect of 1.0 mM bupivacaine (i.e., a concentration of 3.3 × K_d mM) on the steady-state inactivation curve, plotted as the normalized peak current evoked by a test pulse to +20 mV from different conditioning prepulses (−130 to −10 mV) of 100 ms. The relatively short conditioning pulse duration was used to avoid effects of the C-type inactivation. The curve is only marginally shifted (−3 ± 1 mV; n = 5) as expected from an open-state dependent block mechanism, but not for an inactivated-state dependent one (see curves for Scheme 5 and 6 in Fig. 4 B). The continuous lines show steady-state inactivation curves, calculated from the equation for Scheme 5 in Appendix A, using values in Tables 1 and 2.

FIGURE 6.

Effects of bupivacaine on steady-state inactivation, frequency dependence, and recovery of Shaker current. (A) Steady-state inactivation. Normalized peak current at a test pulse in 1.0 mM bupivacaine (•) and in control (○) solution. The currents were evoked by a 50 ms test pulse to +20 mV from a conditioning prepulse of 100 ms duration. Mean values from five oocytes. Continuous lines are calculations for Scheme 5 (see Appendix A), using activation and inactivation parameters in Table 1, and binding rates and dissociation constant in Table 2. (B). Recovery of current after a pulse step, given as the ratio between peak currents of the second and the first step in a two-step protocol in 300 μM bupivacaine (•) and in control (○) solution plotted against the interval between the pulses. The pulse protocol consisted of two 10 ms pulses to +20 mV from a holding potential of −80 mV with a varying interval. Mean values from three-to-five oocytes. Continuous lines are calculations for Scheme 5, using Eqs. 3–5 with activation and inactivation parameter values listed in Table 1, and with binding rates listed in Table 2. (C). The effect of frequency on the peak current in 300 μM bupivacaine (•) and in control (○) solution, given as the ratio between peak currents at the 20th and the first step of a pulse train consisting of 10 ms pulses to +20 mV from a holding potential of −80 mV, plotted against frequency. Also plotted is the ratio between the peak currents at the second and the first step in 300 μM bupivacaine (▴) and in control (▵) solution, to show effects without interference from the C-type inactivation. Mean values from three-to-five oocytes. Continuous lines are calculations for Scheme 5, using the same equations and parameter values as in panel B.

Fig. 6 B shows the result of applying a twin-pulse recovery protocol (two 10 ms pulses to +20 mV with a varying interpulse interval at −80 mV) to Shaker channels in control and 300 μM bupivacaine. The quotient between peak currents measured during the test (second) pulse and during the conditioning (first) pulse is plotted as a function of the recovery time. The current recovers equally fast in control and in bupivacaine in accordance with an open-state block mechanism (see curve for Scheme 5 in Fig. 4 C). The continuous lines show recovery curves for the control and the bupivacaine cases calculated for Scheme 5, using Eq. 5 and the same parameter values as in Fig. 6 A, except for the deinactivation rate (δ), which was slightly adjusted (from 0.03 to 0.024 ms⁻¹). Fig. 6 C shows the result of testing the frequency-dependence of bupivacaine on Shaker. The measurements were used in two ways; either 1), the quotient between peak currents associated with the second test pulse and currents associated with the first test pulse was plotted against frequency; or 2), the quotient between currents associated with the 20th pulse and currents associated with the first pulse. The first method was used to avoid effects of the C-type inactivation. As expected, considering the results of Fig. 6 A, 300 μM bupivacaine did not induce a frequency- or use-dependent block at any frequency within the range studied (2–33 Hz). Such a lack of extra reduction is predicted by an open-state dependent mechanism, but not by an inactivated-state dependent mechanism (see curves for Schemes 5 and 6 in Fig. 4 E). This conclusion was supported by the lack of effect of increasing the bupivacaine concentration to 1 mM (see Fig. 4 F). The continuous lines in Fig. 6 C are calculated for Scheme 5, using Eq. 5 and the parameter values used in Fig. 6 B. As seen, the fit between the values based on the second pulse current measurements (first method above) was better than that based on the 20th pulse current measurements (second method above), suggesting interference from the C-type inactivation in the latter case.

In conclusion, an open-state block of Scheme 5 type well explains the observed effects on bupivacaine on the inactivating Shaker channel. An inactivated-state binding of Scheme 6 type cannot explain the crossing-over phenomenon and a closed-state binding of Scheme 4 type cannot explain the slight negative shift of the steady state inactivation curve. Neither can Scheme 4 nor Scheme 6 explain the induction of an early fast and late slow inactivation time course by bupivacaine.

The effects of bupivacaine on noninactivating Shaker channels suggest no allosteric interaction between inactivation gate and binding site

A central point in the classical modulated receptor-hypothesis is that the inactivation gate allosterically interacts with the binding site for the blocking molecule, enhancing the binding affinity (1). To explore whether this hypothesis applies to the Shaker channel we used a Shaker channel where the inactivation gate was genetically deleted (Shaker-IR) and where the bupivacaine block can be studied in isolation, without any interference from the N-inactivation process.

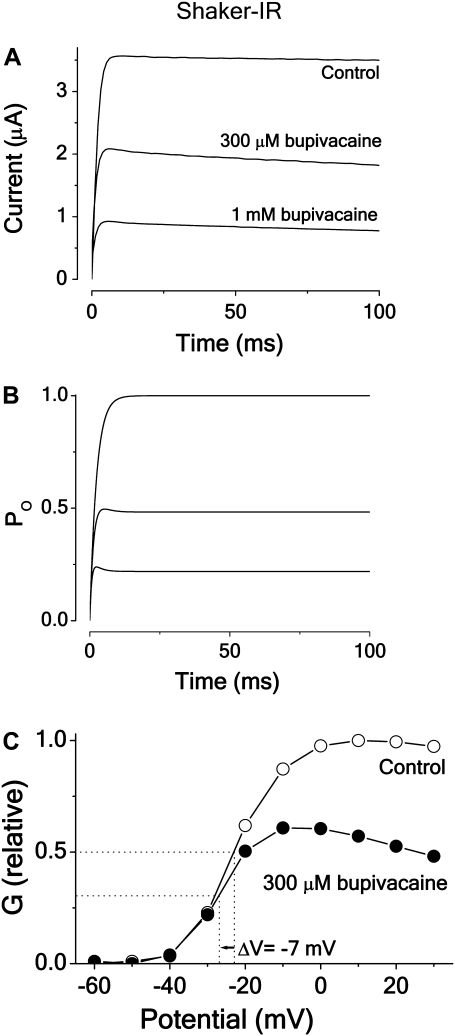
Fig. 7 A shows the action of 300 μM and 1 mM bupivacaine on the Shaker-IR channel current associated with a rectangular pulse to +20 mV. The main effect is a general concentration-dependent reduction. Analyzing the time courses over a wider voltage range and analyzing G(V) curves (see below), we conclude that the effect is explainable by a relatively fast open-state block mechanism (Scheme 2). Fig. 7 B shows the time courses of model currents corresponding to the currents in Fig. 7 A, calculated for Scheme 2, using activation values and binding rates listed in Table 2. Fig. 7 C shows the effects of 300 μM bupivacaine on the G(V) curve, demonstrating a shift in negative direction (−7 mV) and a general downscaling, combined with a slight voltage dependence at positive voltages. As seen from Fig. 3 A, the negative shift and the general downscaling is predicted by Scheme 2, but not by a closed-state binding scheme (Scheme 1), and only the downscaling by an all-state binding scheme (Scheme 3). Quantifying the predicted effect of 300 μM bupivacaine on the G(V) curve, using the equation for Scheme 2 in Appendix A, and activation parameter and binding values in Tables 1 and 2, we obtain a shift of −6 mV, reasonably close to the measured value of −7 mV.

FIGURE 7.

Effect of bupivacaine on current time course and G(V) curve of Shaker-IR. (A) Currents evoked from a voltage step to +20 mV from a holding potential of −80 mV in 300 μM and 1 mM bupivacaine (•) and in control (○) solution. (B) Computed time course of the open probability (P_O) of Scheme 2, using activation value and binding rates listed in Table 2. (C) Corresponding steady-state G(V) curves measured at t = 20 ms (Eq. 2). Same experiment as in panel A.

Plotting dose-response data (n = 5) for the steady-state measurements and fitting them to Eq. 1 yielded a mean IC₅₀ of 0.24 ± 0.03 mM. This is close to the K_d value for the open channel block of inactivation channels (0.30 mM), but clearly smaller than the IC₅₀ value for the inactivating channels (1.6 mM, see Table 2). In a previous investigation we have shown that the bupivacaine action on noninactivating K_v channels is well described by Scheme 2 (32). The K_d value, obtained from fitting Scheme 2 to the experimental Shaker-IR data (time courses and steady-state values) in Fig. 7 A and determination of the binding rates, was 0.28 mM (Table 2), suggesting that an IC₅₀ measurement reflects the binding affinity.

In conclusion, the results suggest that an open-state blocking mechanism of Scheme 2 and Scheme 5 types well explains the bupivacaine action on both the noninactivating and inactivating Shaker channels studied here. The close similarity between K_d values and between blocking and unblocking rate constants for the two channel types (Table 2) suggest that the inactivation gate does not allosterically interact with the binding site for bupivacaine.

The effects of bupivacaine on K_v3 channels suggest a general blocking mechanism for K_v channels

Can the open-state dependent blocking mechanism, suggested to explain the effects of bupivacaine on the two Shaker channels, be generalized to other types of K_v channels? Above, we have analyzed the binding of bupivacaine to a channel when the inactivation mechanism has been artificially removed. Since the packing patterns of membrane proteins are sensitive to mutations and are easily disrupted, we also wanted to test the effect on channels that have obtained or lost an inactivation gate by evolutionary processes rather than by lab-mediated procedures. We therefore chose to compare the effects of bupivacaine on the closely related K_v3.2 and K_v3.4 (100% identity between their S6 sequences), where K_v3.4 is inactivating and K_v3.2 is not. As mentioned, bupivacaine has been shown to block K_v3.2 by an open-state dependent mechanism of Scheme 2 type (32).

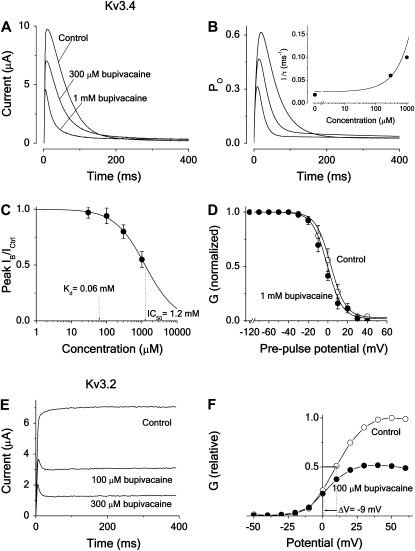
Fig. 8 summarizes some measurements and calculations of the bupivacaine action on K_v3.4 and K_v3.2 channels, showing that the conclusions from the Shaker experiments can be transferred to these two channels, suggesting that the bupivacaine effect on K_v channels may be explained by a common open-state blocking mechanism. Fig. 8 A shows the time evolution of the effect of 300 μM and 1 mM bupivacaine on the K_v3.4 current associated with a pulse to +60 mV. The shape of the bupivacaine-induced inactivation time course with a fast and slow phase, causing the curve to cross the control curve, suggests an open-state block mechanism of Scheme 5 type (compare to Fig. 2 B). Fig. 8 B shows the calculated time evolution of the open probability for Scheme 5, with parameters estimated from fitting the curve to the experimental data in Fig. 8 A (Table 1). The resulting K_d is 60 μM (Table 2).

FIGURE 8.

Effect of bupivacaine on inactivating and noninactivating K_v3-type channels. (A) Time course of K_v3.4 current at a voltage step to +60 mV from a holding potential of −80 mV in 300 μM and 1 mM bupivacaine, and in control solution. Note the crossing-over effect at 150 and 220 ms, respectively. (B) Computed time course of the open probability (Po) of Scheme 5, using activation and inactivation values listed in Table 1, and binding rates listed in Table 2. (Inset) Effect of bupivacaine concentration on the fast component of the decay phase. The continuous line shows the concentration dependence of inverted time constants (1/τ) of the fast component, calculated as largest eigenvalues from the matrix equation derived for Scheme 5 in Appendix B, using the values of Tables 1 and 2. Solid circles (•) show experimental values, estimated from the curves in panel A by fitting a sum of two exponentials to the decaying phase (between t = 20 and 40 and 200 ms). (C) Dose-response curve (Eq. 1) fitted to mean peak currents (•) at +60 mV (n = 10). Resulting IC₅₀ is 1.2 mM. (D) Steady-state inactivation curve of K_v3.4 in 1.0 mM bupivacaine (•) and in control (○) solution. Measured currents evoked by a 50 ms test pulse to +30 mV, from a conditioning prepulse of 400 ms duration, plotted versus potential (n = 5). Continuous lines are calculations for Scheme 5 (see Appendix A). (E) Time course of K_v3.2 current at a voltage step to +60 mV from a holding potential of −80 mV in 100 and 300 μM bupivacaine, and in control solution. (F) Steady-state G(V) curves (Eq. 2) for K_v3.2 in 100 μM bupivacaine (•) and in control (○) solution. Same experiment as in panel E.

In the inset, the bupivacaine effect on the fast component of the biphasic decay phase of the currents in Fig. 8 A is quantified. The rate (= inverse time constant) of the fast component, estimated by fitting a sum of two exponentials to the experimental curve, is plotted against concentration. Comparing these values with the rates predicted from the different schemes (Appendix B) shows that open-state binding (Scheme 5) best explains the data. The continuous line shows the rate of the fast component (the largest eigenvalue = r₂) calculated from the expression derived for Scheme 5, using parameter values in Tables 1 and 2. Corresponding rates for Scheme 4 are predicted to decrease with concentration (see Fig. 2 C and Appendix B).

Fig. 8 C shows a dose-response curve of first-order reversible reaction type (Eq. 1) fitted to experimental mean peak currents (n = 10), yielding an IC₅₀ of 1.2 ± 0.1 mM (Fig. 8 C and Table 2), thus 20-fold higher than corresponding K_d value.

Fig. 8 D shows the effect of 1.0 mM bupivacaine (17-fold higher concentration than the calculated K_d concentration in Fig. 8 B) on normalized steady-state inactivation curves of K_v3.4, measured as the effect on the current evoked by a test pulse (to +60) from different conditioning prepulses (from −120 to +40 mV) of 400 ms. The curve is shifted (measured as the shift of the curve midpoint, ΔV_1/2) −6 ± 2 mV (n = 5). Continuous lines are calculated steady-state inactivation curves (Appendix A). The resulting midpoint shift is −7 mV, thus well reproducing the experimental data.

Fig. 8 E shows the effect of 300 μM bupivacaine on the currents of the noninactivating K_v3.2 channel at +60 mV. The induced modifications, comprising a fast decay phase, suggest a relatively fast open-state block mechanism of Scheme 2 type (compare to Fig. 2 B). This is strongly supported by the finding of a bupivacaine-induced negative shift of the G(V) curve. Fig. 8 F shows the effect of 100 μM bupivacaine, displaying a shift of −9 mV and a downscaling. Both features are predicted by Scheme 2 (compare to Fig. 3 A), suggesting similar blocking mechanisms in the noninactivating K_v3.2 and Shaker-IR channels. Fitting Scheme 2 calculations to the experimental currents of Fig. 8 E yields a K_d of 90 μM (Table 2).

In summary, open-state block schemes (Scheme 2 for noninactivating channels and Scheme 5 for inactivating channels), well reproduce the experimental bupivacaine effects on inactivating and noninactivating Shaker and K_v3-type channels. Parameter values from the measurements and the fitting procedures are summarized in Tables 1 and 2, which also include data from noninactivating K_v channels of the previous study (32) to show the similar magnitudes of the parameters of related channels. The similar magnitudes of K_d as well as of blocking and unblocking rate constants for inactivating and noninactivating Shaker channels, suggest no allosteric interference of the inactivation mechanism with the binding site. The value of K_d for inactivating and noninactivating K_v3 channels was of similar magnitude, while those of the blocking and unblocking rate constants differed approximately fivefold, suggesting that for these channels the structure of the binding site or the entry/exit pathways differs somewhat, despite the sequence identity of the S6 segments, which form the wall of the internal vestibule, the presumed binding site of local anesthetics. Nevertheless, the main conclusion from both the Shaker and the K_v3 experiments is the same; the introduction of an inactivated state in a noninactivating channel does not seem to introduce a new high-affinity site.

DISCUSSION

Local anesthetics are one of the most widely used pharmaceuticals, having a worldwide application in regional anesthesia and pain therapy. The clinically relevant effects have traditionally been attributed to an action on Na_v channels. The increasing interest in the effects on K_v channels derives from two lines of insights. First, exploring the molecular details of K_v channel effects is today more rewarding than exploring Na_v channel effects due to a better understanding of the structural details of K_v channels. Second, it is today clear that direct action on K_v channels may be clinically relevant; several cases of pharmacologically induced long QT-syndrome have been attributed to direct effects on K_v channels (28,31,43–46). The reasons for exploring the molecular details of block are many—one, not always sufficiently appreciated, being the fact that the molecular mechanism of block determines the overall effect on neuronal firing patterns, while it is less discriminative in modulating the action potential. Different blocking mechanisms (state-dependent or state-independent binding), causing phenomenologically similar effects on the single spike level, may lead to totally different effects on the oscillatory pattern (increased or decreased firing frequencies) (47).

The dominant, traditional view on local anesthetic action on Na_v channels is the modulated-receptor hypothesis, assuming the strongest binding to channels in an inactivated state and an allosteric interaction between the inactivation machinery and the binding site (1,2). This view seems challenged by studies, suggesting a more important role for an open-state binding (15–18), or that the inactivation gate is unaffected by the binding process (19,20). Some recent studies suggest that the traditional view may have to be complemented; some local anesthetics seem unlikely to bind to inactivated channels unless the channels have opened first (48,49).

This investigation suggests that bupivacaine blocks the N-type inactivating K_v channels Shaker and K_v3.4 in a way that deviates from the traditional modulated-receptor hypothesis, developed for voltage-gated Na channels; it blocks by binding to channels exclusively in the open state (Scheme 5). This conclusion is based on several lines of evidence. The time evolution of the block showed crossing-over and a biphasic shape, excluding both closed-state (Scheme 4) and inactivated-state block (Scheme 6) (see Fig. 2 B). The small, but negative, shift of steady-state inactivation curves at K_d concentration excludes closed-state (predicts a positive shift) and inactivated-state block (predicts a much larger negative shift) (see Fig. 3 B). The approximately equal K_d values and equal blocking and unblocking rates for the inactivating and noninactivating Shaker channels suggest no or a very small allosteric interaction between the inactivation machinery and the binding site.

Relevance for the local anesthetic block of Na_v channels

The main difference between the presently observed blocking action of bupivacaine on inactivating K_v channels and the action of the most studied local anesthetics (lidocaine, etidocaine, and analogs) on Na_v channels is a lower affinity, reduced effect on recovery from inactivation, a smaller left shift of the steady-state inactivation curve, and a reduced effect on use-dependence.

The role of the open-state dependent binding for the block also seems to differ between the two channel families; while the present findings suggest a dominant role for open-state binding in K_v channels, most studies of local anesthetic action on Na_v channels suggest that the highest affinity is found in inactivated channels. However, the situation is not uncontroversial. From the relatively limited number of studies using the inactivation-removal paradigm, a rather complex picture emerges: both a dominating affinity for the inactivated state (3,4,8,50) and a dominating affinity for the open state (15–18) have been suggested.

The reasons for the different interpretations are many. Different local anesthetics have different binding affinities, varying experimental protocols highlight different parameters, and certain procedures (pharmacological inactivation-removal) may cause structural alterations of the channel proteins (see Figs. 1 B and 2 B for a clear variation in blocking action for different blocking rate constants; κ × c = λ = 0.01, 0.1 and 1 ms⁻¹, respectively). It may also be due to differences in the activation and deactivation rate constants of different channel subtypes.

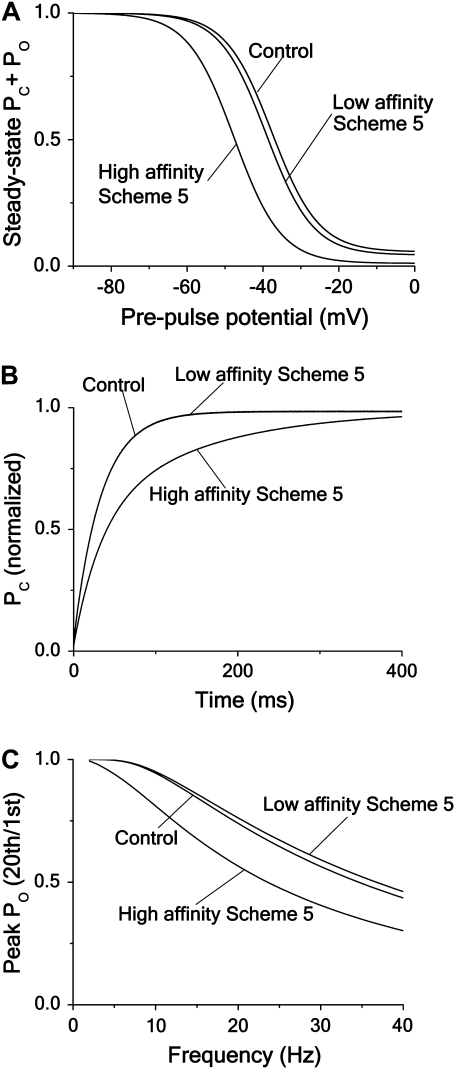
However, different blocking mechanisms can, under some circumstances, cause similar effects. Fig. 9 demonstrates how an open-state block can emulate an inactivated-state block. Increasing the affinity in the open-state block case (Scheme 5) shown in Fig. 2 (i.e., changing λ from λ = 0.1 ms⁻¹ to λ = 0.1/15 ms⁻¹), we obtain effects that resemble those of the inactivated-state block case at a lower affinity (Scheme 6 in Fig. 2). Thus a 15-fold increase of the affinity (due to a 15-fold decrease in the unblocking rate), used in the calculations for the schemes of Fig. 2, shifts the steady-state inactivation curve −10 mV (Fig. 9 A), prolongs the recovery half-time approximately twofold (Fig. 9 B), and induces a frequency-dependent block (Fig. 9 C), making these parameter curves resemble those of Scheme 6 in Fig. 2.

FIGURE 9.

Effect of increasing the affinity of an open-state blocker. Computations showing how a open-state block (Scheme 5) can mimic an inactivated-state block (Scheme 6). The same parameter values as for corresponding curves in Fig. 4 are used for demonstrating low-affinity block, while the high-affinity curves are computed with an unblocking rate of λ = 0.1/15 ms⁻¹. (A). Steady-state inactivation curves (same protocol as in Fig. 4 A). The shifts are −2 and −12 mV, respectively. (B) Time course of recovery from inactivation (same protocol as in Fig. 4 C). The half-time values are 22 ms and 44 ms, respectively. (C) Frequency dependence curve (same stimulation protocol as in Fig. 4 E).

Thus, a local anesthetic-induced left shift of the inactivation curve or a slowed inactivation-recovery rate does not, without further investigations, allow us to conclude that these effects are necessarily caused by an inactivated-state binding mechanism. Concerning the molecular action of local anesthetics on Na_v channels, we presumably have to await the crystallization of the channel before the details are understood.

SUPPLEMENTARY MATERIAL

To view all of the supplemental files associated with this article, visit www.biophysj.org.

APPENDIX A: EXPRESSIONS OF STEADY-STATE ACTIVATION AND INACTIVATION CURVES FOR THE KINETIC SCHEMES

To calculate the steady-state activation (P_O) and inactivation (P_C+P_O) curves for the kinetic schemes, describing the different blocking mechanisms, we used the following expressions, where P_O is the probability of being in the open state (O) and P_C is the probability of being in the closed state (C):

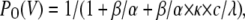(Scheme 1)

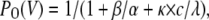(Scheme 2)

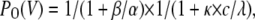(Scheme 3)

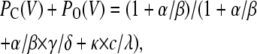(Scheme 4)

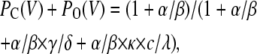(Scheme 5)

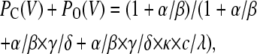(Scheme 6)

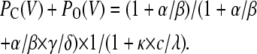(Scheme 7)

Values of activation and deactivation rate constants (α and β) were obtained from Eqs. 3 and 4 and parameter values in Table 1, values of inactivation and deinactivation rate constants (γ and δ) directly from Table 1, and values of blocking and unblocking rate constants (κ and λ) directly from Table 2.

APPENDIX B: CALCULATING THE CONCENTRATION-DEPENDENCE OF THE RATE OF BLOCK

To get analytical expressions for the concentration dependence of the blocking rates in the kinetic schemes of this investigation we derived analytical expressions for the eigenvalues of Eq. 5. This equation can be expressed in following matrix form,

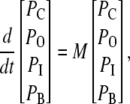where M is a matrix, formed by the rate constants of the kinetic schemes, and where P_C, P_O, P_I, and P_B (see Eq. 5) denote closed (C), open (O), inactivated (I) and blocked (B) states. Assuming that the blocked state is empty (P_B = 0) the matrix M has the following appearance:

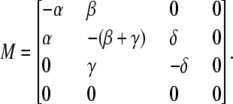To describe the kinetic schemes for the block of inactivating channels (Schemes 4–6) we add the following terms to the matrix elements (M_ij):

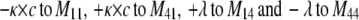(for Scheme 4)

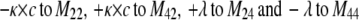(for Scheme 5)

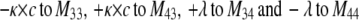(for Scheme 6).

The solution to the matrix equation above has the following general form,

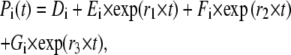where D_i denotes the steady-state value of P_i(t).

The eigenvalues r_i to the matrix above are given by the solutions to the quartic equation

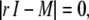where I is the identity matrix. One of the solutions is always zero, while the others are nontrivial and rather complex. However, by assuming β = 0, the system can be simplified and the solutions are

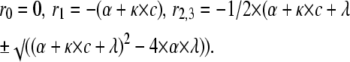(for Scheme 4)

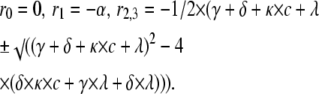(for Scheme 5)

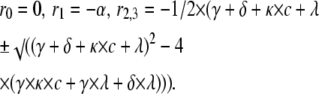(for Scheme 6)

The inverse eigenvalues form the time constants of the phases of the open probability time course. The expressions above were used to calculate the concentration-dependence of the fast decaying phase for the kinetic schemes in Figs. 5 and 8.