Structural Changes of Yellow Cameleon Domains Observed by Quantitative FRET Analysis and Polarized Fluorescence Correlation Spectroscopy

Abstract

Förster resonance energy transfer (FRET) is a widely used method for monitoring interactions between or within biological macromolecules conjugated with suitable donor-acceptor pairs. Donor fluorescence lifetimes in absence and presence of acceptor molecules are often measured for the observation of FRET. However, these lifetimes may originate from interacting and noninteracting molecules, which hampers quantitative interpretation of FRET data. We describe a methodology for the detection of FRET that monitors the rise time of acceptor fluorescence on donor excitation thereby detecting only those molecules undergoing FRET. The large advantage of this method, as compared to donor fluorescence quenching method used more commonly, is that the transfer rate of FRET can be determined accurately even in cases where the FRET efficiencies approach 100% yielding highly quenched donor fluorescence. Subsequently, the relative orientation between donor and acceptor chromophores is obtained from time-dependent fluorescence anisotropy measurements carried out under identical conditions of donor excitation and acceptor detection. The FRET based calcium sensor Yellow Cameleon 3.60 (YC3.60) was used because it changes its conformation on calcium binding, thereby increasing the FRET efficiency. After mapping distances and orientation angles between the FRET moieties in YC3.60, cartoon models of this FRET sensor with and without calcium could be created. Independent support for these representations came from experiments where the hydrodynamic properties of YC3.60 under ensemble and single-molecule conditions on selective excitation of the acceptor were determined. From rotational diffusion times as found by fluorescence correlation spectroscopy and consistently by fluorescence anisotropy decay analysis it could be concluded that the open structure (without calcium) is flexible as opposed to the rather rigid closed conformation. The combination of two independent methods gives consistent results and presents a rapid and specific methodology to analyze structural and dynamical changes in a protein on ligand binding.

INTRODUCTION

Förster resonance energy transfer (FRET) in aqueous solution is a photophysical process where the excited-state energy from a donor molecule is transferred nonradiatively to an acceptor molecule at close distance (<10 nm) via weak dipole-dipole coupling (1). Because FRET occurs between molecules in close proximity, it is used as a spectroscopic ruler to investigate interactions and conformational changes in biological macromolecules (2). A requirement for the occurrence of FRET is spectral overlap between the fluorescence emission spectrum of a donor molecule with the absorption spectrum of an acceptor molecule. The energy transfer efficiency is inversely proportional to the sixth power of the intermolecular distance (R). The critical or Förster radius (R₀) is the distance between donor and acceptor, at which the energy transfer efficiency is 50%. Because FRET is based on dipolar interactions, both distance and orientation between donor and acceptor transition dipoles are determining factors.

The development of biosensors based on FRET technology has provided information about a large variety of biochemical processes (3–8). For quantification of FRET, several methods are available, of which the one based on fluorescence lifetime measurements is the most straightforward method. The time that a molecule remains in the excited state, i.e., the fluorescence lifetime, gives information about the local environment of the chromophore and, in particular, the occurrence of FRET (9). Usually the fluorescence lifetime of the donor molecule is measured and reduction of this lifetime is an indicator for FRET. Donor fluorescence lifetime values often originate from two populations, namely interacting and noninteracting molecules. Therefore, the determined average lifetime does not reflect the real distance between the interacting molecules, because the lifetime (and thus distance) is too long.

We describe a methodology where the rise time of the acceptor fluorescence is followed on donor excitation for the observation of FRET. An advantage to using this approach is that only those molecules that are involved in energy transfer are monitored. Furthermore, time-dependent acceptor fluorescence anisotropy measurements on donor excitation provide information on the mutual dipolar orientation between FRET pairs. A Cameleon calcium sensor protein (YC3.60) was chosen as a model system to test this methodology. Cameleon sensors are fluorescent calcium indicators composed of genetically encoded protein constructs without any cofactors (5,10). The YC3.60 consists of a fusion of an enhanced cyan fluorescent protein (ECFP) (donor) and an enhanced yellow fluorescent protein derivative (Venus) moiety (acceptor) linked by calmodulin and a calmodulin binding peptide of myosin light chain kinase (M13). The binding of calcium ions to calmodulin makes calmodulin wrap around the M13 domain enhancing the FRET efficiency from ECFP to Venus, as the calmodulin changes its conformation from an extended calcium-free conformation to a more compact calcium-bound conformation. The dynamic range of the YC3.60 has been optimized by changing the position of the N-terminus via circular permutation of the Venus molecule (11). In this way, the relative orientation, position and distance between ECFP and Venus were modified resulting in the most sensitive Ca²⁺ sensor, YC3.60.

Support for these experiments came from polarized fluorescence correlation experiments when the Venus moiety of YC3.60 is excited and detected. The hydrodynamic parameters of YC3.60 in the presence and absence of calcium are clearly different, which must be ascribed to structural variations.

MATERIALS AND METHODS

Protein material and sample preparation

cDNA of YC3.60 was kindly provided by Dr. Atsitsu Miyawaki (RIKEN Brain Science Institute, Saitama, Japan). The full length sensor was cloned into the GST fusion vector (pGEX5x2 vector). The YC3.60 was isolated and purified as described previously (12). The purity of the YC3.60 protein was analyzed on SDS-PAGE and a single band of ∼75 kDa without degradation products was observed. A stoichiometry of 1:1 between ECFP and the Venus moiety was determined by size exclusion chromatography and absorption spectroscopy. The concentration of YC3.60 was determined with light absorption measurements at 514 nm using the Venus extinction coefficient ɛ = 92,200 M⁻¹ cm⁻¹. YC3.60 was diluted in 100 mM Hepes buffer at pH 7.9 containing either 50 μM EGTA alone or 50 μM EGTA and 100 μM Ca²⁺ to a final concentration of 100 nM (unless otherwise indicated) for time-resolved fluorescence experiments. The experiments were carried out in Hepes buffer pH 7.9. Ensemble fluorescence experiments were carried out in quartz cuvettes of 1.0 × 0.4 cm and at room temperature (22°C). The fluorescence intensity ratio between Venus (measured at 527 nm) and ECFP (measured at 475 nm) changes from 1.6 in the absence of Ca²⁺ to 8.3 in the presence of 100 μM Ca²⁺ similarly as reported previously (11).

Time-resolved polarized fluorescence experiments and data analysis

Time-resolved fluorescence measurements were carried out using a mode-locked continuous wave laser for excitation and time-correlated single photon counting (TCSPC) as detection technique as described previously (13). The samples were excited with plane polarized light pulses (0.2 ps FWHM) at an excitation frequency of 3.8 MHz and both parallel- and perpendicular-polarized fluorescence intensities were detected. At 400-nm excitation ECFP fluorescence was detected with a 480.5-nm interference filter (Schott, Mainz, Germany; half-bandwidth of 5.4 nm). The sensitized emission of Venus fluorescence was detected with an OG 530 cut-off filter (Schott) and 557.6-nm interference filter (Schott; half-bandwidth 5.9 nm). Some experiments were conducted at 420-nm excitation, but then Raman scattering turned out to be an interfering factor at 480.5-nm detection of the donor fluorescence. Another experiment was conducted using a much higher concentration of YC3.60 (500 nM as compared to the usual 100-nM YC3.60 concentration) to reduce the interference of Raman scatterering and background fluorescence on the quenched donor fluorescence decay. The dynamic instrumental response function of the setup (∼40 ps FWHM) was obtained at the ECFP or Venus emission wavelengths by using a solution of xanthione in ethanol as reference compound having an ultrashort fluorescence lifetime of 14 ps (14–16). The use of the reference convolution method (15,17) together with the current instrumentation enables determining fluorescence lifetimes with high accuracy and picosecond precision. A systematic study involving both simulations and experiments have shown that the standard error in determination of lifetimes can be in the order of one-tenth of the FWHM (16). With the setup used it was possible to accurately determine 7-ps fluorescence lifetimes and >10-ps correlation times (18–20). Two time scales were used in this study: 1 ps/channel and 5 ps/channel giving a time range of 4 ns and 20 ns for 4096 data points. Global analysis of the experimental data taken at short and long timescales using multi-exponential model functions was carried out as described previously (13,21) To obtain an optimal fit of the time-resolved fluorescence anisotropy data of YC3.60 an associative fitting protocol was used, in which short fluorescence lifetimes are grouped with short correlation times and longer fluorescence lifetimes with longer correlation times. Another experiment was conducted to observe the fluorescence anisotropy decay of YC3.60 when the Venus part is excited (492 nm) and monitored (557 nm).

Acceptor photobleaching experiments

The acceptor photobleaching (APB) experiments were carried out on microdroplets composed of YC3.60 ±Ca²⁺. Microdroplets of YC3.60 were prepared by mixing the protein solution with 1-octanol at a ratio of 1:9 v/v as described by Patterson et al. (22). Droplets of 50 μm in diameter were imaged using a confocal laser scanning microscope (LSM510; Carl Zeiss, Jena, Germany). The CFP moiety within YC3.60 was excited with the 458-nm argon laser line and the Venus with the 514-nm argon laser line, respectively. The fluorescence of CFP was detected using a bandpass filter of 470–500 nm and Venus fluorescence by a bandpass filter of 535–595 nm. FRET efficiencies were determined as described in Bastiaens et al. (23).

Polarized fluorescence correlation experiments and data analysis

Fluorescence correlation spectroscopy (FCS) was carried out with a home-built multiparameter fluorescence detection (MFD) setup based on an inverted confocal microscope (IX70, Olympus, Hamburg, Germany) using epi-illumination, as described earlier and summarized in the following references (24–26). The fluorescent molecules were excited by a linearly polarized argon-ion-laser (Innova Sabre, Coherent) at 496 nm in cw mode. The laser was focused into the sample by a NA = 1.2 water-immersion objective lens (UPLAPO 60x, Olympus). The fluorescence was collected by the same lens and separated from the excitation by a polychroic beamsplitter (488/636 PC; AHF, Tübingen, Germany). A confocal pinhole of 100 μm diameter and the slightly underfilled objective yielded a detection volume element of ∼1 μm diameter and 1.6 fl size, as determined by fluorescence correlation spectroscopy. The characteristic diffusion time of rhodamine 110 was 0.22 ms.

The applied mean irradiance in the focus was I₀/2 = 150 kW/cm² (27). The collected fluorescence light was separated first into its parallel and perpendicular components by a polarizing beamsplitter cube (VISHT11; Gsänger, Planegg, Germany), then divided again into two parts by 50% beamsplitters. Fluorescence bandpass filters (HQ533/46, AHF) blocked residual laser light and reduced Raman scattering from the solvent. The detectors used were single photon avalanche diodes (SPCM-AQR-14; PerkinElmer, Vaudreuil, Quebec, Canada). The single photon signal traces were recorded by two synchronized but otherwise independent TCSPC boards (SPC132; Becker and Hickl, Berlin, Germany). Each board monitored, via a router, one parallel and one perpendicularly polarized fluorescence channel. In this way by correlating traces from different boards, FCS curves down to picoseconds could be generated, not affected by the deadtime of detectors and electronics. Software-correlation was usually carried out in both directions (channel A → channel B, channel B → channel A). Both correlation curves were then averaged to reduce noise. In each presented experiment 7 × 10⁸ photons were recorded. Three different combinations of polarizations were computed: autocorrelation of the fluorescence polarized parallel to the excitation polarization (pp), perpendicular to the excitation (ss), and cross correlation of both polarizations (ps and sp).

The data was approximated by a multi-exponential model function in a global analysis (OriginPro 7.5; OriginLab Corporation, Northampton, MA). The range of data for the fit was limited to correlation times between t_c = 10⁻⁶ and 5 × 10⁻³ ms. At shorter times increased noise prohibits meaningful analysis. At longer times diffusion in and out of the focus becomes the dominating effect in the FCS. This term is distorted at high irradiances due to saturation and photobleaching, is prone to artifacts and requires sophisticated fitting models, which are beyond the scope of this study (28).

Modeling

Three-dimensional models of the open (−Ca²⁺) and closed (+Ca²⁺) conformation of YC3.60 were constructed. For the closed conformation the crystal structure files 2BBM.pdb (calmodulin wrapped around the light chain myosin kinase helix (M13)) and 1C4F.pdb (GFP) were used. For the open conformation the calmodulin part of 1XFU.pdb with M13 and 1C4F.pdb (GFP) were used. The different domains of the YC3.60 (CFP,CaM/M13, Venus) are connected by flexible linkers. These linkers provided flexibility to adapt the orientation within the YC3.60 for the open and closed conformations, which are based on the two different PDB-structures of the CaM/M13 unit. The lengths of the linkers were restricted to a maximal distance between the fluorescent moieties. The transition dipole moments in the molecular frame of the chromophore in GFP (29) and the relative angle between these vectors of the two chromophores within both fluorescent protein units were used to orient the individual parts of the YC3.60 molecule using the program PyMOL (http://www.pymol.org) (30). It is assumed that the absorption and emission dipole moments coincide in the molecular frame of the chromophore and that the transition dipoles have the same direction in the CFP and YFP chromophores as in the GFP chromophore. This assumption is more rigorous for the CFP chromophore than for the one of YFP, which is except for the π-stacking interaction with the phenolic group of Tyr²⁰³ identical to the GFP chromophore.

RESULTS

Time-resolved FRET spectroscopy

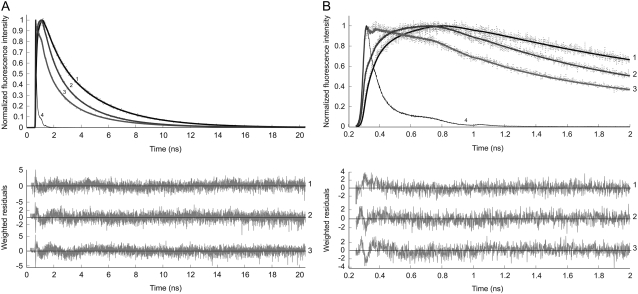
Time-resolved fluorescence experiments were conducted by monitoring donor fluorescence decay in which YC3.60 was excited at 400 nm (ECFP moiety) and the fluorescence of ECFP was detected at 480 nm. The fluorescence decay in the ECFP channel requires a three-component exponential model to obtain a satisfactory fit (Fig. 1). Analysis of the fluorescence decays resulted in fluorescence lifetimes of 0.67 ns (α₁ = 45%), 2.20 ns (α₂ = 36%), and 3.57 ns (α₃ = 19%) (Table 1) yielding an (amplitude-weighted) average fluorescence lifetime 〈τ〉 = 1.77 ns for the calcium-free YC3.60. In the presence of Ca²⁺ the fluorescence lifetimes were 0.28 ns (α₁ = 46%), 1.39 ns (α₂ = 34%), and 3.57 ns (α₃ = 20%) resulting in reduction of the average lifetime to 〈τ〉 = 1.31 ns (Table 1). The quenching of the ECFP fluorescence within the calcium sensor results in significantly shorter average lifetimes as compared to the unquenched average fluorescence lifetime of purified ECFP alone (Fig. 1 curve 1; 〈τ〉 = 2.71 ns).

FIGURE 1.

Normalized experimental (dotted line) and fitted (solid line) fluorescence decay curves of ECFP (curve 1), YC3.60 in absence of Ca²⁺ (curve 2), YC3.60 in presence of Ca²⁺ (curve 3) and the reference compound xanthione in ethanol (curve 4). The excitation wavelength was 400 nm and the detection wavelength of ECFP emission was 480 nm. In A the data are presented with a time scale of 5 ps/channel, whereas this is 1 ps/channel in B, in which only the first 2 ns are shown. The experimental data taken at both time scales are globally analyzed using a multiexponential model with amplitudes α_i and lifetimes τ_i as adjustable parameters for obtaining an optimal fit. In case of ECFP a bi-exponential decay model with lifetimes 0.97 ns and 3.57 ns was sufficient. The long 3.57-ns lifetime was fixed in the tri-exponential decay model of YC3.60 All recovered parameters (α, τ) are collected in Table 1 (case 1). Weighted residuals belonging to each fitted curve are presented in the bottom panels. Global χ² values are, respectively, for ECFP 1.11, for YC3.60 in absence of Ca²⁺ 1.14, and for YC3.60 in presence of Ca²⁺ 1.15.

TABLE 1.

Fluorescence decay and rise parameters of YC3.60 on excitation at 400 nm and detection at either donor or acceptor emission

Sample	Detection (nm)		α1 (%)	τ1 (ns)	α2 (%)	τ2 (ns)	α3 (%)	τ3 (ns)	α4 (%)	τ4 (ns)	〈τ〉 (ns)
ECFP	480		33	0.97 ± 0.06	67	3.57 ± 0.05					2.71
Case 1: all lifetimes and relative amplitudes are included in calculation of 〈τ〉*
YC3.60 −Ca2+	480		45	0.671 ± 0.008	36	2.20 ± 0.05	19	3.57 (fixed)			1.77
YC3.60 +Ca2+	480		46	0.280 ± 0.003	34	1.39 ± 0.01	20	3.57 (fixed)			1.31
Case 2: only FRET-active donor molecules contribute to 〈τ〉†
	Noninteracting CFP (20%)						Interacting CFP (80%)
YC3.60 −Ca2+	480	A	33	0.98 ± 0.02	67	3.59 ± 0.01	50	0.60 ± 0.01	50	2.2 ± 0.1	1.40
	480	B	36	1.04 ± 0.01	64	3.62 ± 0.01	48	0.500 ± 0.004	52	2.10 ± 0.01	1.33
	480	C	37	1.08 ± 0.01	63	3.65 ± 0.01	49	0.51 ± 0.01	51	2.25 ± 0.02	1.40
YC3.60 +Ca2+	480	A	33	0.98 ± 0.02	67	3.59 ± 0.01	60	0.269 ± 0.004	40	1.46 ± 0.01	0.69
	480	B	36	1.10 ± 0.02	64	3.40 ± 0.08	72	0.024 ± 0.007	28	0.28 ± 0.01	0.095
	480	C	36	1.04 ± 0.02	64	3.50 ± 0.01	67	0.024 ± 0.007	33	0.14 ± 0.02	0.063
Case 3: 〈τ〉 is calculated from average rise time of acceptor intensity‡
YC3.60 −Ca2+	557		−6	0.38 ± 0.06	−24	1.70 ± 0.3	70	3.10 (fixed)			1.40
YC3.60 +Ca2+	557		−26	0.056 ± 0.012	74	3.10 (fixed)					0.056

Standard errors of the fluorescence lifetimes are obtained from the fit.

^*Case 1. The sum of amplitudes has been normalized to 100%. The average fluorescence lifetime 〈τ〉 is the amplitude-weighted average lifetime.

^†Case 2. The parameters of interacting and noninteracting donor molecules were derived from the following 4-exponential model: 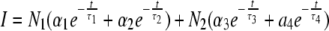in which N₁ = 20% and N₂ = 80%, and α₁ + α₂ = 1 (100%); α₃ + α₄ = 1 (100%). 〈τ〉 is obtained from the values of FRET-active ECFP. A: analysis of one experiment with 100 nM YC3.60; B: global analysis of 6 different experiments (100 nM YC3.60) linking common parameters; C: analysis of one experiment with 500 nM YC3.60.

^‡Case 3. A negative value of the amplitude α₁ indicates a rise of fluorescence intensity. The sum of the absolute values of the amplitudes has been normalized to 100%. YC3.60 −Ca²⁺: Rise time obtained from global analysis of 3 independent experiments using a 2-component fit model and presented as amplitude-weighted average rise time. C3.60 +Ca²⁺: Rise time values obtained using a 1-component fit model at one time scale (1 ps/channel).

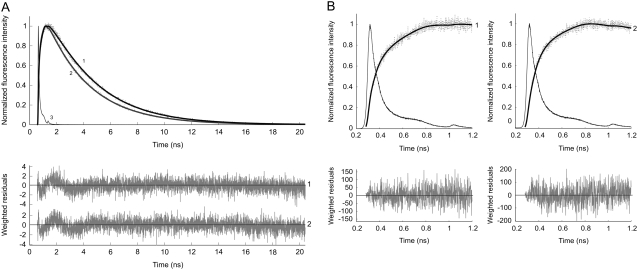
A correct method for the observation of FRET is to follow the time-dependent increase in fluorescence intensity of the acceptor, which is a direct consequence of energy transfer (21,31). The experiments were carried out by exciting the donor at 400 nm and detecting Venus at 557 nm (Fig. 2). The obtained data were analyzed using a multiple-component model with both positive and negative pre-exponential factors (Table 1). The short lifetime with negative amplitude reflects the energy transfer process, and the part of the decay with positive amplitude corresponds to the fluorescence of the acceptor. In the absence of Ca²⁺ an average fluorescence lifetime component (1.4 ns) with negative amplitude was found. On addition of Ca²⁺, a significant decrease of this short component (0.056 ns) was observed. A long fluorescence lifetime component (3.1 ns) of Venus with positive amplitude was found, independent of the presence of calcium.

FIGURE 2.

Normalized experimental (dotted line) and fitted (solid line) fluorescence rise and decay curves of the Venus acceptor, detected at 557 nm, in YC3.60 on donor excitation at 400 nm. In A the data are presented with a time scale of 5 ps/channel, whereas this is 1 ps/channel in B, in which only the first nanosecond is shown. Curve 1 is the fluorescence intensity trace of YC3.60 in the absence of Ca²⁺, whereas curve 2 is that of YC3.60 in the presence of Ca²⁺. Curve 3 represents the reference compound xanthione in ethanol. In B it can be observed that the rise time of curve 2 is shorter than that of curve 1, because curve 2 is already starting to decay. The experimental data taken at both time scales are globally analyzed using a bi-exponential rise (in case of calcium-free YC3.60) and mono-exponential decay model with amplitudes α_i and lifetimes τ_i as adjustable parameters for obtaining an optimal fit. The recovered parameters (α, τ) are collected in Table 1 (case 3). Weighted residuals are presented in the bottom panels. Global χ² values are, respectively, for YC3.60 in absence of Ca²⁺ 1.05, and for YC3.60 in presence of Ca²⁺ 1.05.

Time-resolved fluorescence anisotropy

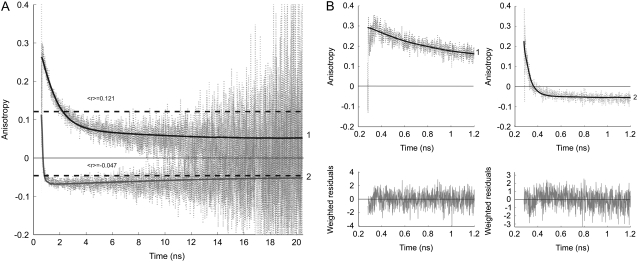
The time-dependent fluorescence anisotropy of the acceptor exhibits a peculiar pattern after donor excitation (Fig. 3). The fluorescence anisotropy shows an initial decay with a correlation time that is compatible to the rise time of the acceptor fluorescence. This correlation time becomes much shorter when calcium is present. In the latter case the anisotropy even becomes negative, followed by a slow increase to zero. The time-resolved fluorescence anisotropy curves were globally analyzed using an associative, two-component model yielding two correlation times (φ₁ and φ₂) and corresponding amplitudes (β₁ and β₂) (Table 2) (13,21). The long correlation time (φ₂) can be attributed to overall protein rotation (φ_prot). Its value was obtained after fitting the fluorescence anisotropy decay of YC3.60 on excitation and fluorescence detection of the Venus moiety (see below). The long correlation times were fixed during analysis. The short correlation time (φ₁), due to energy transfer, decreases from 1.29 ns (−Ca²⁺) to 0.056 ns (+Ca²⁺).

FIGURE 3.

Experimental (dotted line) and fitted (solid line) fluorescence anisotropy decays of the Venus acceptor, detected at 557 nm, in YC3.60 on donor excitation at 400 nm. Curve 1 is the time-dependent fluorescence anisotropy of YC3.60 in absence of Ca²⁺, whereas curve 2 is that of YC3.60 in presence of Ca²⁺. In A the data are presented with time scale of 5 ps/channel, whereas this is 1 ps/channel in B, in which only the first nanosecond is shown. The dashed horizontal lines in A represent steady-state anisotropy values belonging to curves 1 and 2. The steady-state anisotropy is obtained from 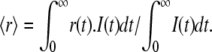I(t) is the total fluorescence decay (I(t) = I_‖(t) + 2I_⊥(t)) and r(t) is the time-dependent fluorescence anisotropy (r(t) = (I_‖(t) – I_⊥(t))/I(t)). An associative global analysis to a bi-exponential model was carried out to the polarized intensity components, in which the short correlation time is grouped with the short fluorescence lifetime and the long correlation time with the long fluorescence lifetime. The long correlation time was separately determined and fixed in the analysis (see Fig. 4 legend). The analyzed data yielded correlation times (φ_i) and amplitudes (β_i) that are collected in Table 2. Weighted residuals are presented at the bottom of B. Global χ² values are, respectively, for YC3.60 in absence of Ca²⁺ 1.11, and for YC3.60 in presence of Ca²⁺ 1.07.

TABLE 2.

Fluorescence anisotropy decay parameters of YC3.60 on excitation at 400 nm or 492 nm and emission detection at 557 nm

Sample	β1	φ1 (ns)	β2	φ2 (ns)
YC3.60 − Ca2+ (λex 400 nm)	0.19 (0.17–0.22)	1.29 (1.10–1.41)	0.08 (0.06 – 0.10)	31 (fixed)
YC3.60 + Ca2+ (λex 400 nm)	0.13 (0.12–0.23)	0.056 (0.047–0.069)	−0.060 (−0.063 to −0.057)	50 (fixed)
YC3.60 − Ca2+ (λex 492 nm)			0.368 (0.366–0.371)	31.2 (29.8–32.7)
YC3.60 − Ca2+ (λex 492 nm)	0.052 (0.043–0.063)	5.1 (3.4–6.8)	0.322 (0.310–0.332)	50 (fixed)
YC3.60 + Ca2+ (λex 492 nm)			0.360 (0.359–0.361)	50.4 (47.8–53.3)

Values in parentheses are the 67% confidence limits obtained from a rigorous error analysis. The recovered parameters in the first two entries (λ_ex 400 nm) were obtained by associative analysis of fluorescence anisotropy decays (taken at two time ranges), in which the short fluorescence lifetimes (Table 1, case 3) were grouped with the short correlation times (φ₁) and the long (fixed) fluorescence lifetimes with the long (fixed) correlation times (φ₂). The recovered parameters in the fourth entry (λ_ex 492 nm) were obtained after a bi-exponential decay analysis with the long correlation time (φ₂) fixed to 50 ns. In this case the fitted curve had the same quality criteria as for the mono-exponential model (see Fig. 4).

From the time-resolved fluorescence and fluorescence anisotropy results one can calculate the steady-state anisotropy 〈r〉. The calculated values are 〈r〉 = 0.121 (−Ca²⁺) and 〈r〉 = −0.047 (+Ca²⁺) (shown as dashed lines in Fig. 3 A). These values are in excellent agreement with experimental values reported previously (11).

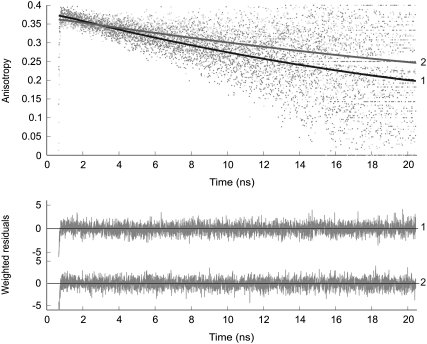
In Fig. 4 the experimental and fitted fluorescence anisotropies are presented for YC3.60 in the absence and presence of calcium. In these experiments the Venus moiety is selectively excited at 492 nm and its fluorescence detected at 557 nm. The fluorescence anisotropy decay is a single exponential in both cases. However, when calcium is absent the decay becomes significantly faster. The overall rotational correlation time changed on binding of calcium to calmodulin from 31 ns (−Ca²⁺) to 50 ns (+Ca²⁺).

FIGURE 4.

Experimental (dotted line) and fitted (solid line) fluorescence anisotropy decays of YC3.60 on excitation (492 nm) and detection (557 nm) of the Venus moiety in absence of Ca²⁺ (curve 1) and in presence of Ca²⁺ (curve 2). The decay model is a mono-exponential function yielding the anisotropy at time zero, r(0) = r₀, and rotational correlation time that are presented in Table 2. Weighted residuals are presented in the bottom panel. Global χ² values are, respectively, for YC3.60 in absence of Ca²⁺ 1.06, and for YC3.60 in presence of Ca²⁺ 1.09.

Acceptor photobleaching

It is desirable to obtain estimates of the FRET efficiency using another, independent method. Several APB experiments on droplets of YC3.60 were carried out using a confocal microscope. From results of APB analysis FRET efficiencies of 39 ± 4% in YC3.60 (−Ca²⁺) and 59 ± 14% in YC3.60 (+Ca²⁺) were obtained.

Fluorescence correlation spectroscopy

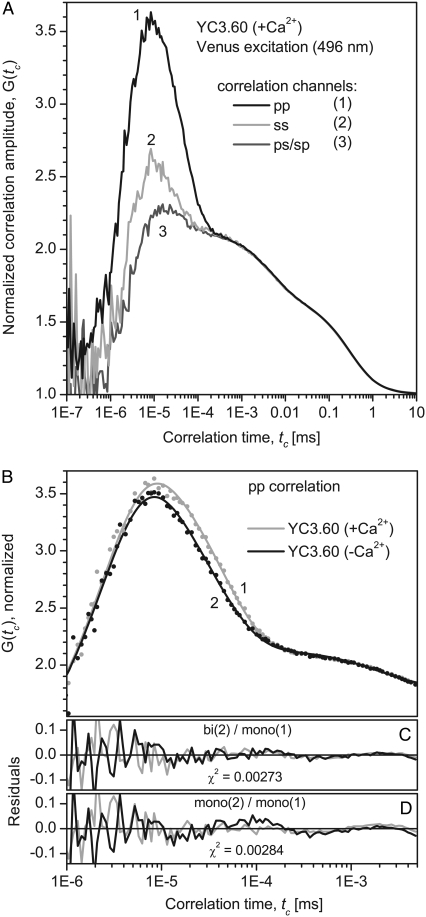
The FCS curves of YC3.60 on direct acceptor excitation showed a distinct polarization dependence in the range from t_c = 10⁻⁶ to 10⁻³ ms, as it is characteristic for rotational diffusion of (nearly) spherical molecules with transition dipole moments of absorption and emission oriented parallel to each other (Fig. 5 A). The observed relative amplitudes of the rotational terms (G_max − G_iso)/(G_iso − 1) of 1.2, 0.4, and 0.1 for pp, ss, and ps/sp crossed polarizations are consistent with the numbers predicted for spherical rotators of 1.78, 1.14, and 0.2, taking into account that the experimental values as directly read from the curves are strongly reduced by the overlap with the antibunching term (32–34). Theory predicts that correlation curves of even ideal spheres should exhibit two bunching terms for the rotational regime (t_rot and 0.3 t_rot). For autocorrelation of the fluorescence polarized parallel to the exciting laser light (pp, curve 1 in Fig. 5 A) the contribution of the second (shorter) time should be only 8% and is neglected in the following analysis.

FIGURE 5.

Experimental and fitted fluorescence correlation curves of YC3.60 after excitation and detection of the acceptor (λ_ex 496 nm, λ_det 510–556 nm). The curves are normalized at t_c = 1.2 μs. (A) Correlation curves for YC3.60 in presence of Ca²⁺. Three different combinations of polarizations are presented: autocorrelation of the fluorescence polarized parallel to the excitation polarization (pp, curve 1), perpendicular to the excitation (ss, curve 2), and cross correlation of both polarizations (ps and sp, curve 3). Only the polarization dependent part of the correlation curves can be assigned to rotational diffusion. The measurement time was 14 min. (B) pp-correlation curves of YC3.60 in presence of Ca²⁺ (curve 1) are compared to YC3.60 in absence of Ca²⁺ (curve 2). The rotational part of curve 1 (+Ca²⁺) can be reproduced well by a single exponential, whereas curve 2 (−Ca²⁺) shows significant deviations and exhibits a second decay time. Fit parameters are presented in Table 3. (C) Residuals for the global fit with: (YC3.60(+Ca²⁺): 3 exponentials, YC3.60(−Ca²⁺): 4 exp.). (D) For comparison residuals for the global fit with: YC3.60(±Ca²⁺): 3 exp; i.e., a single independent rotational correlation time for each of the two curves (fit not shown).

The parameters of the fluorescence correlation curve G(t_c) were derived from the following 4-exponential model, where t_c is the correlation time and t_i is the characteristic antibunching or bunching time.

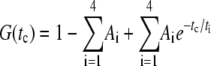(1)

A sum of 3–4 exponentials representing photon antibunching (t₁, mainly below 10⁻⁵ ms), rotational diffusion (t₂ and t₃, mainly between 10⁻⁵ and 10⁻⁴ ms) and photophysical triplet and/or protonation kinetics (t₄, mainly above 10⁻⁴ ms) was globally fitted to the pp-polarized correlation data obtained from YC3.60 in absence and in presence of Ca²⁺ (35). The only nonglobal parameters used corresponded to the rotational diffusion: one independent decay time for each curve and, in case of a biexponential decay, the relative amplitudes. Three fits have been carried out differing only in the modeling of the rotational diffusion: 1), one decay time for each curve; 2), two times for YC3.60 in absence, one time for YC3.60 in presence of Ca²⁺; and 3), two decay times for each curve. The results are summarized in Table 3.

TABLE 3.

Fluorescence correlation parameters of YC3.60 on excitation at 496 nm and emission detection at 510–556 nm

Sample	t1 (ns)	A2(rel.)	t2 (ns)	A3(rel.)	t3 (ns)	Fit No.
YC3.60 −Ca2+	2.56 ± 0.04 (global)	0 (fixed)	—	1 (fixed)	33.2 ± 1.1	1
YC3.60 +Ca2+					43.7 ± 1.5
YC3.60 −Ca2+	2.58 ± 0.04 (global)	0.30 ± 0.08	17.5 ± 4.3	0.70 ± 0.09	42.9 ± 1.6 (global)	2
YC3.60 +Ca2+		0 (fixed)	—	1 (fixed)
YC3.60 −Ca2+	2.68 ± 0.07 (global)	0.42 ± 0.08	15.0 ± 3.2 (global)	0.58 ± 0.08	50.4 ± 4.4 (global)	3
YC3.60 +Ca2+		0.22 ± 0.08		0.78 ± 0.07

Standard errors are obtained from the fit. A global fit was carried out in the data range from t_c =10⁻⁶ to 5 × 10⁻³ ms. The relative amplitudes A_i(rel) were determined from A_i(rel) = A_i/(A₂ + A₃). Values for t₄ for fit 1, 2, and 3 are 1.8 ± 0.5 μs, 2.2 ± 0.6 μs, and 2.9 ± 1.2 μs. χ² for fit 1, 2, and 3 is 0.00284, 0.00273, and 0.00267, respectively. Fit 2 is shown in Fig. 5 B, residuals in Fig. 5 C. Residuals of fit 1 are presented in Fig. 5 D.

The rise time at short times, t₁, is in all fits around 2.6 ns. This is consistent with the measured fluorescence lifetime for the Venus moiety of τ₂ = 3.2 ns and a high excitation rate k₀₁ (1/t₁ = 1/τ₂ + k₀₁) (24). The photophysics term (t₄ = 2–3 μs) was only taken into account in the fits because of a slight overlap with the tail of the rotational term and has otherwise no relevance for the topic of this study.

Fitting a single decay time to each of the correlation curves (fit 1) does not give a satisfactory result for YC3.60 in absence of Ca²⁺, as indicated by the residuals (Fig. 5 D) and by χ². The residuals indicate (Fig. 5 D) the necessity of a second bunching time in the regime of the rotational correlation especially for YC3.60 (−Ca²⁺). Adding this time improves the fit significantly (fit 2, Fig. 5 C). If there is also a second time allowed for YC3.60 in presence of Ca²⁺, only a small improvement of the fit is achieved (fit 3). The amplitude of the additional bunching term is relatively small and has a large statistical error. According to this analysis the rotational correlation of YC3.60 in absence of Ca²⁺ exhibits a biexponential decay with characteristic times of t₂ = 17.5 ± 4.3 ns and t₃ = 42.9 ± 1.6 ns. However, in presence of Ca²⁺ the contribution of this short rotation time vanishes or is at least strongly reduced.

DISCUSSION

Donor fluorescence decay in case of FRET

In time-resolved FRET studies, usually the fluorescence lifetime of the donor molecule is measured. Quenching of the donor fluorescence by an acceptor molecule leads to a shorter fluorescence lifetime of the donor. The experimental data of the donor fluorescence decay in YC3.60 was analyzed with three fluorescence lifetime components for an optimal fit. A complicating factor in the analysis is the already heterogeneous fluorescence decay of single ECFP molecules that needs to be analyzed with at least two components to obtain a satisfying fit (Table 1) (13,36–41). The origin of the two fluorescence lifetimes in ECFP has been attributed to the presence of two distinct chromophore conformations in the protein (42), which are in slow equilibrium (43) and exhibit similar spectra (44). The average donor lifetime of the YC3.60 decreased from 1.77 ns (−Ca²⁺) to 1.31 ns (+Ca²⁺) and the average donor fluorescence lifetime without acceptor was 2.71 ns (case 1: average donor fluorescence lifetime including all lifetime components). Close examination of Table 1, however, indicates that there are still, independent on calcium, long lifetime components >3 ns present in the donor fluorescence decay. These long lifetime components may originate from a population of YC3.60 molecules, in which no FRET occurs. For instance, when a certain population of the protonated form of the Venus is present, FRET is not observed because the overlap between absorption spectrum of the protonated acceptor and the donor fluorescence spectrum is strongly reduced. The pK_a of the Venus chromophore has been reported to be equal to 6.0 (45). This pK_a value may be different in the circular permutated variant of the Venus chromophore. The same observation has been made and discussed recently for CFP-YFP constructs in mammalian and fungal cells (40). Millington et al. (40) have proposed two models to explain the results. They have labeled their models 3tau and 4tau. The 3tau model comprises the simplest case: only one of the two ECFP conformations participates in FRET. The more complex (and more realistic) 4tau model assumes that both conformations participate in FRET. There are two complicating factors in the latter approach. One complication in the 4tau model is that there are two different critical transfer distances (R₀), because the fluorescence quantum yields of the two donors differ by a factor given by the ratio of the respective lifetimes (τ_D1/τ_D2). The other complication arises from the observation that the shorter, unquenched donor lifetime (τ_D1) becomes similar to the quenched donor lifetime τ_DA2 and cannot be distinguished any more. Although there are four lifetimes present, only three of them can be actually resolved in the decay analysis. We have analyzed the fluorescence decays of YC3.60 using the 4tau model with the following modifications. A global analysis was carried out on the fluorescence decay data of YC3.60 under high and low calcium conditions and of those of unquenched ECFP, in which a fixed amplitude ratio for the unquenched lifetimes was preserved. The other lifetime components then should represent the true donor lifetime values in case of FRET. These average lifetimes become shorter (1.4 ns, −Ca²⁺ to 0.69 ns, +Ca²⁺) when the long lifetime components are excluded in the average lifetimes (case 2A: average donor fluorescence lifetime from a FRET-active selection) (Table 1). Because the average donor fluorescence lifetime remains a factor of 10 longer than obtained from the acceptor rise time (see next paragraph), we decided to globally analyze all available experimental data taken at different days, from different YC3.60 preparations of the same concentration (100 nM) and with different excitation wavelengths (400, 420, and 440 nm). All common parameters were linked and potential contributions from Raman scattering and impurities from the background (taken from samples without protein and measured under identical conditions) were taken into account. The results of this extensive global analysis yielded parameters that are also collected in Table 1 (case 2B). The average fluorescence lifetime of the donor in the calcium-free form of YC3.60 remained unaltered. On the other hand, the average fluorescence lifetime of the donor in calcium-bound YC3.60 becomes distinctly shorter (0.095 ns). Therefore, we have to conclude that in cases of very large transfer efficiencies the donor fluorescence lifetime becomes so short, comparable to a very small intensity contribution, that its lifetime can be barely recovered in the presence of a dominant background fluorescence consisting of a nonquenched donor population and of Raman scattering and impurity fluorescence. In addition, the intrinsic heterogeneity of the ECFP fluorescence kinetics is a complicating factor in the decay analysis. To further support this conclusion we have analyzed experimental data of YC3.60 at relatively high protein concentration (500 nM) at which background contributions to the decay are expected to be minimal. Indeed, very good agreement between donor fluorescence lifetimes and rise times is obtained both in the absence and presence of calcium (case 2C).

Rise of acceptor fluorescence intensity in case of FRET

To recover a correct FRET efficiency a method is applied, in which the rise time of the acceptor fluorescence is detected on donor excitation (Fig. 2; parameters collected in Table 1). In this way one selectively observes the pure FRET process between donor and acceptor molecules, because the transfer rate constant (k_T) can be directly determined from the rise time of the acceptor fluorescence intensity, which is equivalent to the donor fluorescence lifetime in the presence of acceptor (τ_DA). The method of analysis of acceptor rise time has been described for single-tryptophan containing proteins transferring energy from tryptophan to a fluorescent acceptor (21,31). It was pointed out that this might be a useful approach in cases where the donor exhibits fluorescence lifetime heterogeneity as observed in the YC3.60. Although other research groups have made the same observations in case of energy transfer between two fluorescent proteins (4,39,40), this approach has not yet been assessed quantitatively. We will discuss the method in more detail in the next paragraph (case 3: average donor fluorescence lifetime from acceptor rise time). In Supplementary Material (Data S1) simulations are presented to investigate the resolvability of different rise times under certain conditions. The simulations were set up to mimic the experiment as closely as possible, for example by using convolution with an experimental impulse response function and two rise times corresponding to a biexponential donor fluorescence decay in the presence of acceptor. The main outcome of the simulations is that analysis of longer rise times (0.5–2 ns) with a two-component model yields a better fit quality than with a single-component model. In case of short rise times (50–200 ps) a model using two components has similar fit quality as that of a single-rise time model. Following the results of the simulations a global analysis was carried out on experimental fluorescence rise and decay traces of YC3.60 measured at both time resolutions (1 and 5 ps/channel) thereby linking common rise and decay parameters. For YC3.60 in the presence of calcium the data can be sufficiently analyzed using a mono-exponential model with one rise time of 0.056 ns and one decay time of 3.1 ns. In case of calcium-free YC3.60 a model with two rise times and one decay time yielded a much better fit than a one-component rise model. Because the longer rise time and the decay time exhibited a strong correlation, the decay time had to be fixed in the analysis to recover a reliable value of the longer rise time. All recovered parameters are collected in Table 1 (case 3).

Comparison of both methods: donor fluorescence decay and acceptor fluorescence rise

FRET efficiencies can be determined from E = 1 − τ_DA/τ_D, where τ_DA is the donor fluorescence lifetime in the presence of acceptor and τ_D that in the absence of acceptor. The rate constant of energy transfer (k_T) can be determined from k_T = 1/τ_DA − 1/τ_D. The transfer rate constant can be directly related to the distance through k_T = τ_D⁻¹(R₀/R)⁶. From the overlap integral between ECFP emission and enhanced yellow fluorescent protein absorption spectra, donor fluorescence quantum yield and, initially assuming an orientation factor κ² = 1, a critical distance R₀ = 4.90 nm was determined (46). Using the average lifetime values and τ_D = 2.71 ns, the FRET efficiency of YC3.60 changed on Ca²⁺ addition from 35% to 52% (case 1: all lifetime components and relative amplitudes are included in calculation of the average donor fluorescence lifetime). The FRET efficiencies become larger for case 2A (unquenched donor fluorescence lifetimes are excluded in the calculation of the average donor fluorescence lifetime), 48% (−Ca²⁺) and 75% (+Ca²⁺), respectively. The average rise times of case 3 (directly yielding the average donor fluorescence lifetime) show a transfer efficiency increase from 49% (−Ca²⁺) to 98% (+Ca²⁺). The slow average rise time in YC3.60 (−Ca²⁺) is in good agreement with the corresponding average donor fluorescence lifetime (cases 2A–C). The results of these experiments are therefore internally consistent. The fast rise time 0.056 ns for YC3.60 (+Ca²⁺) is much faster than the corresponding donor fluorescence lifetime (0.69 ns) obtained from analysis of a single experiment (case 2A), but in good agreement with the value of 0.095 ns obtained from global analysis of multiple experiments (case 2B) and in even better agreement with the 63-ps lifetime of the single experiment at relatively high YC3.60 concentration (case 2C). It should be noted that a single rise time is more straightforward to obtain than the average decay time of the donor fluorescence obtained after 4-exponential decay analysis with constrained conditions such as the presence of a certain percentage of nonquenched donor molecules and of impurity fluorescence. All these data are collected in Table 4. Transfer rate constants and distances between the ECFP and Venus moieties within YC3.60 are collected in Table 4 as well for all cases. A distance of 4.9 nm is the same as the critical transfer distance R₀ and can therefore accurately be determined, whereas a distance of 2.6 nm is so short that it corresponds to an energy transfer efficiency approaching 100%, making this distance less determined. The “corrected” FRET efficiencies are more realistic than the “raw” FRET efficiencies. FRET efficiencies and transfer rate constants determined from acceptor fluorescence rise times have the particular advantage that only the partners contributing to FRET are selected.

TABLE 4.

FRET parameters of YC3.60 on excitation at 400 nm and detection at donor or acceptor emissions

	τDA (ns)		Transfer efficiency (%)		kT (ns−1)		R (Å)
Analysis	−Ca2+	+Ca2+	−Ca2+	+Ca2+	−Ca2+	+Ca2+	−Ca2+	+Ca2+
Case 1	1.77	1.31	35	52	0.19	0.39	55	48
Case 2A	1.40	0.69	48	75	0.35	1.08	49	40
Case 2B	1.33	0.095	51	96	0.38	10.1	49	28
Case 2C	1.40	0.063	48	98	0.35	15.5	49	26
Case 3	1.35	0.056	49	98	0.37	17.5	49	26

τ_DA is the donor fluorescence lifetime in the presence of acceptor. The (FRET) transfer efficiency is determined from E = 1 − τ_DA/τ_D; τ_D is the fluorescence lifetime in the absence of acceptor and taken as 2.71 ns (see Table 1). The rate constant of energy transfer (k_T) is determined from k_T = 1/τ_DA − 1/τ_D. The distance R is obtained from k_T = τ_D⁻¹(R₀/R)⁶, in which the critical transfer distance R₀ = 49 Å. The three different cases are referred to in Table 1. Case 1 refers to inclusion of all fluorescence lifetimes in calculation of the average fluorescence lifetime τ_DA. Case 2 refers to inclusion of only fluorescence lifetimes involved in FRET in calculation of τ_DA. A: analysis of one experiment with 100 nM YC3.60; B: global analysis of 6 different experiments (100 nM YC3.60) linking common parameters; C: analysis of one experiment with 500 nM YC3.60. Case 3 is restricted to FRET parameters obtained from acceptor fluorescence rise times.

Acceptor photobleaching

APB experiments emphasize the emission properties of the donor before and after bleaching of the acceptor. It is therefore relevant to compare FRET efficiencies obtained from donor fluorescence lifetimes (Table 4: cases 1 and 2) and from APB. FRET efficiencies of 39% (−Ca²⁺) and 59% (+Ca²⁺) were found from APB experiments. These values are in good agreement with FRET efficiencies determined from lifetime data of case 1 (Table 4: 35% (−Ca²⁺) and 52% (+Ca²⁺)). The calculated donor lifetimes composed of 20% noninteracting CFP and 80% interacting CFP molecules (Table 4: case 2A) resulted in average fluorescence lifetimes of 1.67 ns (−Ca²⁺) and 1.10 ns (+Ca²⁺) yielding FRET efficiencies of 39% and 60%, respectively, which is in excellent agreement with those found by the APB method. An important conclusion is that the APB method is not able to resolve heterogeneity in the donor population. This conclusion is in sharp contrast with the method of determination of donor fluorescence lifetimes, in which two distinct populations of donor molecules can be distinguished: one fraction is involved in the FRET process whereas the other fraction is not.

Fluorescence anisotropy decay

With fluorescence anisotropy one measures the change in orientation of transition dipole moments. The time-resolved fluorescence anisotropy of YC3.60 in the absence of calcium shows an initial rapid decay followed by a much slower decay (Fig. 3, curve 1). In the case of the Ca²⁺-bound form of YC3.60 the first part of the decay is even more rapid and reaches a negative anisotropy value before it slowly rises to zero (Fig. 3, curve 2). The rapid decay is the characteristic time needed to change the transition dipole orientation of the initially photo-selected donor molecules to the transition dipole orientation of the acceptor molecules. However, one should realize that this energy transfer process occurs without radiation impeding to monitor the time-dependent initial depolarization of the acceptor. The early fluorescence signal in the acceptor channel is composed of two other sources, namely some remainder of ECFP emission (cross talk) and emission from Venus arising from direct excitation. The fluorescence carrier signal for observing the anisotropy change is therefore provided by fluorescence photons from ECFP and/or Venus that are not participating in the energy transfer process. A two-component analysis was used to fit the experimental time-resolved anisotropy data. The short correlation time arising from energy transfer changed from 1.29 ns (−Ca²⁺) to 0.056 ns (+Ca²⁺) (Table 2). These correlation times are in excellent agreement with the “transfer” times obtained from the rise of acceptor fluorescence leading essentially to the same rates and efficiencies of energy transfer. The long correlation time of YC3.60 was obtained by direct excitation and emission detection of the Venus part and fixed in the analysis (see Fig. 4). The pre-exponential factors (β) of the fluorescence anisotropy decay (Table 2) can be related to geometrical parameters describing the relative change in transition dipole moment orientations of ECFP and Venus in the YC3.60 complex. Because of experimental limitations the initial anisotropy is clearly smaller than the expected one r₀ ≅ 0.37 (13). One can then estimate the angle between the transition dipole moments of the chromophores in ECFP and Venus (θ_T) of YC3.60 from the amplitude β₂ connected to the rotation part of the anisotropy, as this amplitude can be more reliably estimated (see confidence limits of β₂ in Table 2) (47):

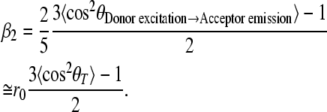(2)

No cross talk is assumed in Eq. 2. Taking r₀ ≅ 0.37 we determined an angle θ_T = 46° between the chromophores in YC3.60 in the absence of Ca²⁺. Binding of Ca²⁺ changed the angle to θ_T = 62°.

It is striking that the long rotational correlation times obtained from Venus excitation and detection are different for the two conformations of YC3.60: 50 ns for the calcium-bound and 31 ns for the calcium-free conformation. Because the rotational correlation time is for a given shape proportional to molecular mass and there is no mass change and only a small change in shape involved, this large change must have another origin. The reason for the much shorter correlation time must be sought in local flexibility of the Venus part in the calcium-free conformation, which can be considered as a more flexible structure (see also discussion of FCS measurements below). This type of flexibility measured by fluorescence anisotropy decay has been observed previously for GFP linked to a single-chain antibody (48). Hink et al (48) have discussed this observation by referring to simulations of the fluorescence anisotropy decay of two rigid proteins connected by a flexible hinge (49,50). An important outcome of these simulations is that the emission transition dipole of the Venus part can sample the flexibility of the hinge between two relatively rigid proteins, whereas the fluorescence anisotropy decay remains single exponential with a shorter correlation time. This is apparently the case for the calcium-free form of YC3.60. In contrast, the calcium-bound YC3.60 rotates as a rigid body with a 50-ns correlation time, which is in agreement with a protein complex of this size. To obtain an estimate of the correlation time characteristic for this flexibility we have reanalyzed the fluorescence anisotropy decay of calcium-free YC3.60 with a biexponential decay model in which the long correlation time was fixed to 50 ns and the shorter correlation time treated as a free adjustable parameter. The results of this analysis have been incorporated in Table 2. The fit quality was the same as for a single-component analysis, but a short correlation time of 5 ns shows up in agreement with the FCS rotational diffusion experiments described in the next section.

FCS experiments

The results from the FCS experiments are consistent with the anisotropy measurements by single-photon timing and support the idea of a flexible structure for YC3.60 in absence of Ca²⁺. Similar to the anisotropy decay data FCS also shows a significantly smaller mean rotational correlation time for this sample (t₃ = 33.2 ± 1.1 ns in fit 1) as compared to the calcium bound species (t₃ = 43.7 ± 1.5 ns in fit 1). This difference is much bigger than one would expect for rigid structures: a simulation of the rotational diffusion using HYDROPRO software (51) with PDB-data derived from the proposed structures (Fig. 6, next section) and assuming the recommended bead radius of 3.1 Å, which is a measure for solvation, yields mean correlation times of 50.7 ns (−Ca²⁺) and 46.4 ns (+Ca²⁺). If the bead radius is reduced to 2 Å, correlation times of 46.6 ns (−Ca²⁺) and 43.0 ns (+Ca²⁺) are obtained, which is very close to the experimentally observed values and supports the structural model in Fig. 6. Another outcome of the simulation is the small deviation of the five characteristic relaxation times from the mean for both structures of <9%. This justifies the assumption of a spherical shape and the treatment of the correlation data with an approximated model for spherical particles. The simulation predicts a slightly higher rotational correlation time for the open structure. The experimentally observed difference in the mean rotational correlation times with the closed structure exhibiting a longer time by 10–20 ns therefore cannot be attributed to a change in shape but rather to a conformational flexibility of protein structure in absence of calcium. Both TCSPC and FCS consistently found a characteristic relaxation time due to this conformational motion in the range of 5–15 ns.

FIGURE 6.

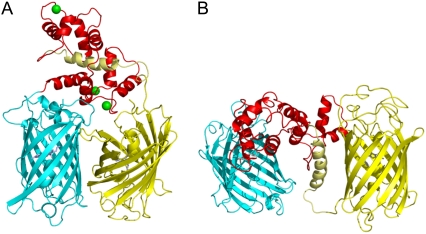
Cartoon representation of YC3.60 in the closed (A) and open (B) conformation. Calcium ions are shown as green balls in the closed conformation. The left, cyan barrel (ECFP) is connected at the N-terminus of the red calmodulin part (A, top; B, middle). The C terminus of the M13 peptide (gold) finally connects to the right, yellow barrel (Venus).

Cartoon representation of YC3.60 structures

To translate FRET-efficiency and hydrodynamic changes into structural changes it is highly desirable to build a molecular model of YC3.60 in both conformations for visualization purposes. Based on x-ray crystallography and fluorescence data we were able to design a realistic structural model of the two fluorescent protein moieties and the calmodulin-M13 complex of YC3.60 (±Ca²⁺) using the obtained distances and orientational angles (case 3). In the closed calcium-bound conformation a distance of 2.6 nm between the chromophores and a relative angle of 62° between the transition dipole moments were used for construction. For the structural model of the open conformation (−Ca²⁺), values of 4.9 nm and 46° were used. The short distance of 2.6 nm originates from the fact that the FRET efficiency approaches 95% resulting in the shortest possible distance. In the closed conformation (Fig. 6 A) the two fluorescent proteins are positioned adjacent to each other and the calmodulin is wrapped around the M13 peptide. In the open conformation the fluorescent proteins remain close to the calmodulin, but the M13 peptide is released from the calmodulin domain (Fig. 6 B).

The anisotropy experiments only yield the angle between the transition dipole moments of ECFP and Venus (θ_T), but not the angles θ_D and θ_A that the donor and acceptor transition moment make with the separation vector and that are also determining the orientation factor κ² (52). For that reason, the exact value of κ² cannot be evaluated. The exact spatial coordinates of the chromophores are necessary to determine the influence of κ² on this system. In Data S1 the dependence of κ² on the angles θ_D and θ_A (at fixed θ_T) is graphically presented. κ² can adopt any value up to a maximal value for κ² = 3. When the structural models were built, it could be noticed that slight structural changes induced by slightly rotating the fluorescent protein around a flexible linker while keeping the same average distance between ECFP and Venus, indeed gave rise to any value of the orientation factor. In Data S1 it is also shown that a fivefold change in orientation factor (from 0.5 to 2.5) only brings about a 1.3-fold increase in critical distance and thus actual distance indicating that the FRET process in YC3.60 is mainly distance dependent.

Finally, the correlation times recovered from anisotropy and FCS analysis are much slower than the characteristic times of the FRET process. Therefore the structural cartoons depicted in Fig. 6 must be considered as static models.

CONCLUSIONS

In this work we used the rise time of acceptor fluorescence on donor excitation to determine the rate of transfer from ECFP to Venus in the calcium sensor YC3.60. There are two advantages of this method as compared to measurements of the more conventional donor fluorescence lifetimes. The first advantage is that only FRET-active pairs are selected. The second advantage is that transfer rates can be accurately determined even in cases where FRET efficiencies are approaching 100% characterized by strongly quenched donor fluorescence intensities and ultrashort donor fluorescence lifetimes. From the transfer rate, the efficiency of transfer and the distance between both chromophores in YC3.60 can be determined. Because the transfer efficiency in the calcium-bound form of YC3.60 is approaching 100%, the distance between both fluorescent proteins must be so short that they must be nearly adjacent to each other. From the FRET parameters (distance, orientation) cartoon representations for calcium-free and calcium-bound conformations have been generated. The different structures have been compared with rotational diffusion properties of YC3.60 obtained with ensemble and single-molecule polarized fluorescence. There is excellent agreement between the hydrodynamic results of both methods. An important conclusion is that the rates of conformational fluctuations are smaller than the FRET rates implying a static regime of the FRET process. Summarizing, the described time-resolved polarized fluorescence methodology can be used as a rapid method for the observation of ligand-dependent changes in structure and dynamics of biological macromolecules.

SUPPLEMENTARY MATERIAL

To view all of the supplemental files associated with this article, visit www.biophysj.org.