Structural Refinement of Membrane Proteins by Restrained Molecular Dynamics and Solvent Accessibility Data

Abstract

We present an approach for incorporating solvent accessibility data from electron paramagnetic resonance experiments in the structural refinement of membrane proteins through restrained molecular dynamics simulations. The restraints have been parameterized from oxygen (ΠO₂) and nickel-ethylenediaminediacetic acid (ΠNiEdda) collision frequencies, as indicators of lipid or aqueous exposed spin-label sites. These are enforced through interactions between a pseudoatom representation of the covalently attached Nitroxide spin-label and virtual “solvent” particles corresponding to O₂ and NiEdda in the surrounding environment. Interactions were computed using an empirical potential function, where the parameters have been optimized to account for the different accessibilities of the spin-label pseudoatoms to the surrounding environment. This approach, “pseudoatom-driven solvent accessibility refinement”, was validated by refolding distorted conformations of the Streptomyces lividans potassium channel (KcsA), corresponding to a range of 2–30 Å root mean-square deviations away from the native structure. Molecular dynamics simulations based on up to 58 electron paramagnetic resonance restraints derived from spin-label mutants were able to converge toward the native structure within 1–3 Å root mean-square deviations with minimal computational cost. The use of energy-based ranking and structure similarity clustering as selection criteria helped in the convergence and identification of correctly folded structures from a large number of simulations. This approach can be applied to a variety of integral membrane protein systems, regardless of oligomeric state, and should be particularly useful in calculating conformational changes from a known reference crystal structure.

INTRODUCTION

The three-dimensional (3D) structure of proteins contains crucial information to understand their biological function. Despite their biological and pharmacological importance, relatively few high-resolution membrane protein structures are currently available, corresponding to <1% of the known 3D protein structures in the Protein Data Bank (1). This is due largely to well-known problems of protein expression, crystallization, and stability, which together hamper ongoing efforts toward high-resolution structure determination by x-ray crystallography or NMR spectroscopy. These are typically carried out in detergent micelles, which can alter their conformation to a variety of nonnative states (2–4). Furthermore, it is very difficult to determine membrane protein structures in more than one conformation, limiting efforts to establish the structural basis of functional mechanisms.

When conventional structure determinations are not possible, biophysical techniques such as solid-state NMR, electron paramagnetic resonance (EPR), and fluorescence spectroscopy can offer complementary structural information under physiological conditions and in a membrane environment (5–7). However, although these approaches provide a limited set of high resolution structural data, when combined with computational analysis they offer a viable alternative to the determination of detailed tertiary folds and conformational rearrangements of membrane proteins in the context of a lipid bilayer (8–11).

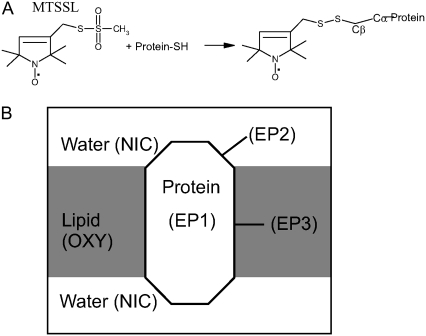
Site-directed spin-labeling (SDSL, Fig. 1) and EPR spectroscopy have shown to be versatile tools for the study of the structure and conformational dynamics in membrane protein (12,13–16). Typically, EPR-based structural information from spin-label proteins include i), direct estimation of nitroxide dynamics from line-shape analysis, ii), solvent accessibility of the labeled site through power saturation paramagnetic relaxation experiments, and iii), distances from dipolar coupling between nitroxide spins via spectral broadening (17–19). Analysis of these data can reveal secondary structural elements, membrane protein topology, and in some cases overall architecture (20–22). With some exceptions, however, the correlation between EPR information and protein structure relies heavily on qualitative interpretations of the data. This is due mostly to the intrinsic limitations of the technique (the effect of the spin-label “tether”) but also is the result of a dearth of quantitative structural descriptions of spin-label proteins (23,24) and the lack of a theoretical framework to use this structural information in structural refinement.

FIGURE 1.

Overview of SDSL and the three classes of spin-label pseudoatoms according to environment. (A) Methathiosulfonate spin-label (MTSSL) structure, the nitroxide attached to cysteine residue (Protein-SH) via disulfide linkage. (B) Simple representation of the pseudospin (EP1, EP2, and EP3) exposure to different environments in a membrane protein.

In contrast to NMR methods, where multiple constraints per residue are typically available, a key challenge in the use of EPR structural data is the structural interpretation of significantly fewer constraints in a computationally efficient and meaningful way. A number of semiquantitative molecular modeling approaches have been proposed that utilize SDSL/EPR data as restraints to model low-to-moderate resolution structure or conformational changes of membrane proteins (25–27), with recent advances that allow model building in the 1–2.6 Å resolution range (28). There are two general computational approaches when dealing with a limited data set: restraint-based structure generation and model evaluation. Conformational search algorithms such as molecular dynamics (MD), Monte Carlo, or purely geometric methods have been used to generate representative sets of global fold structures, which were subsequently evaluated based on experimentally derived energy or scoring functions. A fundamental aim of these approaches is to produce an ensemble of final conformations that are both energetically favorable and in agreement with experimental restraints.

Previously, we demonstrated the use of SDSL/EPR structure parameters such as spin-spin distances and spin-label solvent accessibility as restraints in calculating conformational changes in ion channels (29,30). These were based on the use of EPR-based constraints to drive defined rigid-body secondary structural elements in a Cartesian space. Using this approach (restraint-driven Cartesian transformations), we estimated conformational changes at the intracellular gate of KcsA by driving rigid-body transmembrane (TM) segment conformation to fit restraints derived from interspin distance changes (29,31). The method was subsequently modified with the addition of a hard-sphere solvent-accessible surface area calculation in the penalty function and applied to the intramembrane conformational changes in the Escherichia coli mechanosensitive channel of large conductance (MscL) in the open state (30). Since this approach is purely geometric, energy-based structure refinements were performed separately in the final step of the computation.

Although it has been relatively easy to rank and score structural models based on EPR data, it is much more difficult to drive structure refinement using this information, in particular, “soft” constraints like solvent accessibility. Here, we introduce an approach to refine membrane protein structures dynamically, using parameterized constraints derived from EPR solvent accessibility data. The method, pseudoatom-driven solvent accessibility refinement (PaDSAR) translates molecular oxygen (ΠO₂) and nickel-ethylenediaminediacetic acid (ΠNiEdda) collision frequencies into computationally tractable structural restraints, imposed in the form of an empirical potential function. As a test case, we have used the Streptomyces lividans potassium channel (KcsA) because of the availability of a high-resolution 3D structure and the experimental abundance of EPR data (32,33). In our hands, the method was able to refold a number of distorted KcsA structures back to the native conformation within a 3 Å or better root mean-square deviation (RMSD) and with high computational efficiency. Ongoing applications of this approach include structural analyses of the E. coli mechanosensitive channel of small conductance (MscS) on its closed conformation (34), the overall architecture of the membrane-embedded voltage sensing domain in KvAP (35).

METHODS

Generation of starting conformations

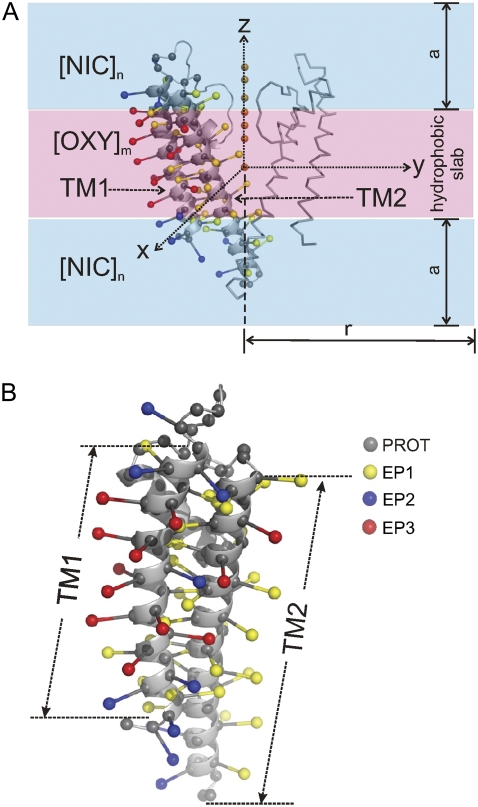
We used the 2-Å-resolution x-ray structure of the KcsA potassium channel (accession code: 1K4C (33)) to calibrate and test the method. KcsA is a homotetrameric protein and each subunit is composed of two transmembrane helices encompassing residues 22–51 (TM1) and 86–124 (TM2) (Fig. 2 A).

FIGURE 2.

System used for MD simulations and pseudoatom representations. (A) The KcsA x-ray structure (1k4c), an illustration of two subunits and a definition of restraining boundary for molecular oxygens (OXY) and Ni-EDDA complexes (NIC) for the simulations. Potassium ions are shown as orange spheres (B) the attachment of spin-label pseudoatom to protein backbone. The type of spin-labeled pseudoatom is color coded as EP1, yellow, EP2, blue, and EP3, red.

To develop and validate the methodology used here, a set of randomized starting conformations (or “decoys”) were generated by rigid-body movements of both TM segments. From the 1K4C crystal structure, the antibody FAB fragment and water molecules were removed; and to minimize the energetic contributions of the native side-chain conformations, these were rebuilt using SCWRL 3.0 (36)—a protein side-chain prediction program. All ionizable residues were assigned to their common charge, i.e., Glu⁻¹, Asp⁻¹, Lys⁺¹, and Arg⁺¹, except for E71 (37) and the truncated N-terminal S22 and the C-terminal H124. Protein topology and parameters were taken from the CHARMM 19 united-atom force field (38,39). Fourfold rotational symmetry was imposed using the IMAGE facility (38,39) to compute the final tetrameric assembly. Simulations in vacuum were performed by moving TM1 and TM2 helices from the reference KcsA crystal coordinates as rigid bodies as a way to generate different degrees of conformational deformation.

Residues 55–83 corresponding to the pore helix and the selectivity filter were kept fixed in their native conformation. The simulation protocol was repeated to obtain a wide range of randomly distorted conformations—after which energy minimization was subsequently performed. It should be noted that ∼90% of the decoy structures were obtained using this procedure. Additional decoys with larger distortions were made by a manual rotation to obtain a specific distortion of conformations, for instance, those by rotating either TM1 or TM2 along its helical axis or by a large degree of TMs movement (∼30 Å RMSD; see below). The generated structures were subsequently screened to eliminate those containing either steric clashes or bad covalent geometry. The final set of decoys consisted of distorted conformations or partially unfolded KcsA structures used for the next simulations of refolding with the solvent accessibility restraints.

Solvent accessibility as structural restraint

We developed a simple form of a molecular mechanical potential for the EPR-derived restraints based on the typical accessibility environments found in a spin-label membrane protein (Fig. 1 B). The nitroxide spin-label (denoted EP1, EP2, and EP3) can exist in three different environments: buried within the protein itself (EP1), exposed to the aqueous environment (EP2), or exposed to the membrane lipids (EP3). Surrounding the protein and spin-label pseudoatoms, we have included contrasting particles representing molecular oxygen (OXY) and NiEdda, a Ni-chelated complex collisional agent. The spin-label (at EP1, EP2, and EP3), contrasting particles (OXY, NIC), and membrane protein Cα particles (PROT) were virtually introduced in the system together with a complete atomistic representation of the protein during MD refinements.

Pseudoatom descriptions and assignment based on solvent accessibility

Nitroxide spin-labels and contrast agents were present in the system as pseudoatoms called “spin” and “environment”, respectively. Within the two categories, there are six different types of pseudoatoms used in the calculations. The first category is the pseudospin atoms including EP1, EP2, and EP3, classified according to the nitroxide moiety of the spin-label side chain. In the second category of pseudoatoms, PROT, OXY, and NIC represent amino acid residues O₂ and NiEdda, respectively, and serve as environmental probe particles with which the pseudospins interact. A description of the pseudoatom types is summarized in Table 1.

TABLE 1.

Pseudoatom descriptions

Name	Type	Descriptions
EP1*	Spin-label	Buried
EP2*	Spin-label	Water exposed
EP3*	Spin-label	Lipid exposed
PROT†	Environment	Amino acid residue
OXY	Environment	Molecular oxygen (O2)
NIC	Environment	NiEDDA complex

^*Nitroxide pseudoatom is covalently attached to the PROT of the labeled residue.

^†Residing at Cα and applying to all residues.

The approach requires the spin-label site to be assigned as EP1, EP2, or EP3 according to environmental collision frequency experimental data (ΠO₂ and ΠNiEdda). Thus, EP1 corresponds to sites with both low ΠO₂ and ΠNiEdda values. EP2 represents sites with high ΠNiEdda but low ΠO₂, whereas EP3 sites are defined by high ΠO₂ and low ΠNiEdda values. We assigned EP1 or EP2 or EP3 throughout KcsA TM1 and TM2 residues (Fig. 2 A) using available ΠO₂ and ΠNiEdda data from a total of 58 spin-label KcsA mutants (32). But for a few exceptions, all the assigned pseudospin types show excellent agreement with residue positions according to the x-ray structure (1K4C), suggesting that we have chosen a suitable model system for our study. Table 2 and the Supplementary Material (Data S1) summarize the environmental assignment of the 58 spin-label residues.

TABLE 2.

KcsA residues with the assignments of the pseudospin types

Residue number	Pseudospin
25, 26, 29, 30, 33, 36, 40, 44, 47, 48, 86, 87, 89, 91, 92, 95, 96, 97, 98, 99, 100, 101, 102, 103, 105, 106, 107, 108, 109, 110, 111, 113, 114, 115, 118, 119	EP1
23, 24, 27, 28, 39, 49, 50, 52, 117, 120	EP2
31, 32, 34, 35, 37, 38, 41, 42, 45, 46, 90, 94	EP3

Restraint energy

An empirical method to compute EPR restraint energy was employed in the form of a molecular mechanics (MM) potential function, which considered bond length, bond angle, improper torsion, and Lennard-Jones (LJ) potentials:

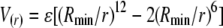in the force field parameters (though not the Coulombic term).

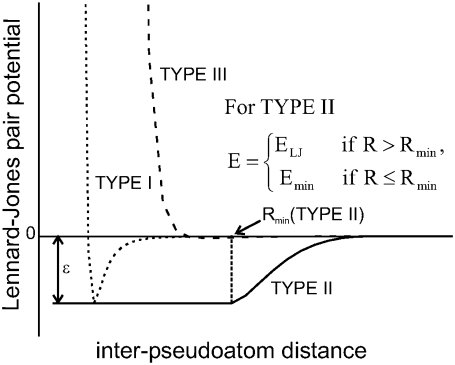
In the PaDSAR approach, nonbonding LJ interactions between the spin and environment particles represent the main driving force of the restraint. A total of nine possible interacting pairs, three spin-label classes versus three environment types (shown in Table 3), were introduced in the MD simulations for structure refinement. They were considered to be matching (EP1-PROT, EP2-NIC, and EP3-OXY) and mismatching (EP1-OXY, EP1-NIC, EP2-OXY, EP2-PROT, EP3-NIC, and EP3-PROT) pairs according to the pseudoatom descriptions defined above. Next, we applied a van der Waals “repulsion” to account for interactions of those virtual particles (Table 3) of which the nonbonding energy was described by three sets of LJ parameters, ɛ, and R_min (Fig. 3). The LJ types I and II were used for the matching pairs, and LJ type III applies to the mismatch between particle types, for instance, buried EP1-OXY or buried EP1-NIC pairs etc. (Table 4). This strategy provides a powerful restraint driving force so that a given spin-label (EP1 or EP2 or EP3) is repelled by the observed environmental mismatch unless it resides in the correct environment with a proper distance defined by their LJ potential function.

TABLE 3.

Repulsion of pseudospin with the environment pseudoatoms

	Repulsion
Nitroxide spin pseudoatom	PROT (protein)	NIC (water)	OXY (lipid)
EP1 (buried)	No	Yes	Yes
EP2 (water)	Yes	No	Yes
EP3 (lipid)	Yes	Yes	No

FIGURE 3.

LJ potential curves for the different pseudoatoms. Energy profiles for the three types of interactions are given as Type I, dotted line, Type II, solid line, and Type III, dashed line.

TABLE 4.

Force field parameters for the pseudoatoms

Bonds	kb (kcal mol−1 Å−2)	l0 (Å)
CA-EP1 (EP2, EP3)	100.0	6.00
Angles	kθ (kcal mol−1 rad−2)	θ0(degree)
N-CA-EP1 (EP2, EP3)	50.0	120.0
Improper torsions	kω (kcal mol−1 rad−2)	ω0(degree)
CA-X-X-EP1 (EP2, EP3)	55.0	0.0
van der Waals	ɛ (kcal mol−1)	Rmin(Å)
EP2-NIC, EP3-OXY	2.00 (attraction type I)*	2.00
EP1-PROT	2.00 (attraction type II)*	7.00†
EP1-OXY, EP1-NIC, EP2-OXY, EP2-PROT, EP3-NIC, EP3-PROT	0.05 (repulsion type III)*	6.00

^*See Fig. 3 for the potential curve.

^†Means overlap.

In particular, the LJ type II potential describing the EP1-PROT interaction is modified using a switching function (Fig. 3), given as

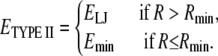(1)

We applied this function to the LJ type II potential and implemented it in CHARMM version c32a2, modified to allow the buried EP1 to overlap with PROT atoms without having an effect on the LJ energy. It should be noted that pseudoatoms see neither the protein atoms nor the pseudoatom of the same category. For instance, an EP1 does not see other EP1, protein, and EP2 and EP3 atoms, but interacts only with PROT, OXY, and NIC pseudoatoms. In other words, there are no interactions of the following pairs: protein-pseudoatoms, spin-spin, or environment-environment pseudoatoms. The LJ energy of the restraints is derived from the spin-environment interactions only.

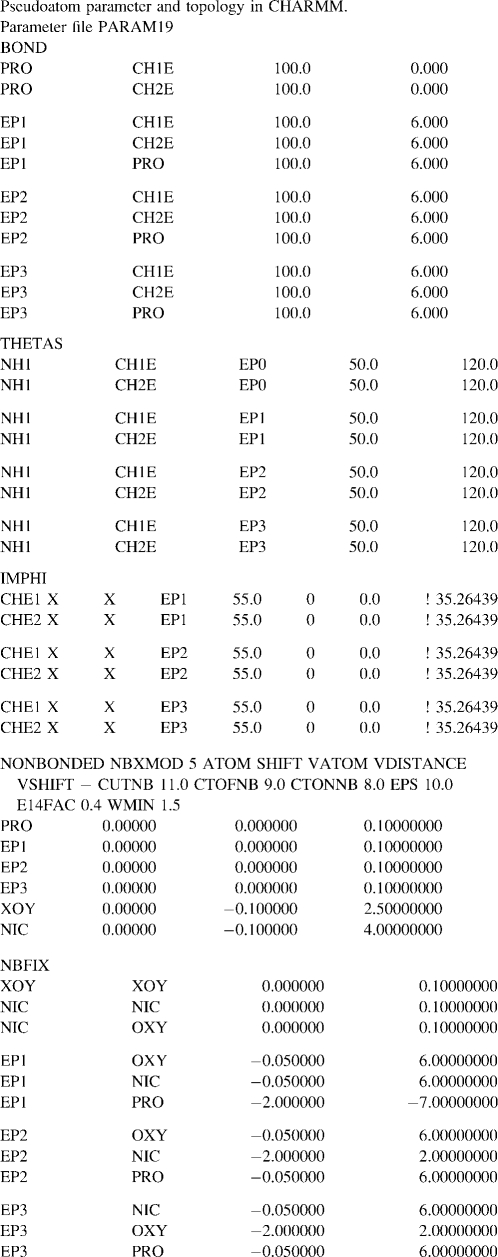
LJ parameters for the spin-environment interacting pairs were calibrated and optimized from MD simulations of the KcsA x-ray structure; 4 ns MD simulations were performed on the x-ray structure to test the effect of various LJ parameters of the EPR restraints on any structural deviations from the native conformation and contrasted with an MD run without the restraints as a control. The bonding and nonbonding parameters of the restraints were incorporated into the united-atom CHARMM19 force field parameters (39). The force field parameters of the restraints are shown in Table 4.

Pseudoatom patch and system construction

Each system consisted of a decoy protein onto which pseudoatoms were generated for the MD simulations with the EPR restraints. We used the CHARMM patch to construct a starting configuration of the system with the virtual particles by attaching the PROT, EP1, EP2, and EP3 on the backbone of the decoy structure and introduce OXY and NIC pseudoatoms as lipid and aqueous environments, respectively. The pseudospins (EP1, EP2, or EP3) were covalently attached to the Cα position (CA) of the assigned residue (Fig. 2 B). Their structural parameters including pseudobond length, pseudobond angle, and improper torsion angle were defined to allow a movement of CA-EP1 (or EP2 or EP3) reflecting the dynamics of a real spin-label (40,41). Our testing simulations suggested that a fairly stiff CA-EP bond (Table 4) was more compatible to native structures than a flexible bond. For the environmental contrast particles, PROT atoms were placed at the CA of each amino acid throughout the structure, whereas OXY and NIC coordinates were precalculated from an MD simulation. The OXY and NIC particles were subjected to distribution in the inner and outer membrane compartments, respectively. This was achieved through the miscellaneous mean field potential (MMFP) in CHARMM with restraint distance boundary (Fig. 4).

FIGURE 4.

Pseudoatom model system of the KcsA tetrameric assembly and contrast agents used in the simulations. The protein is shown in a cartoon representation, pseudoatoms EP1, EP2, and EP3 as ball and stick, and pseudoatoms NIC and OXY as van der Waals spheres.

Structure refinement

Each starting configuration consisted of a decoy monomer attached to 36 EP1, 10 EP2, 12 EP3, and 103 PROT atoms, plus 300 OXY and 300 NIC atoms. A fourfold rotational symmetry using the IMAGE facility was imposed throughout the simulations to provide a model of tetrameric channel. In all simulations, the pore helix and the selectivity filter residues were fixed due to the lack of experimental data coming from that region. Key to this decision is that the selectivity filter plays a critical role in K channel assembly and stability and that this region is not expected to undergo major structure changes (at least at the level of resolution afforded by the method) without affecting channel folding and stability. Furthermore, the backbone atoms in TM1 and TM2 residues were constrained by their secondary structure helices; so we have limited all calculations to α-helical regions of the channel.

An MMFP with a force constant of 1.0 was employed for OXY particles to partition in a hydrophobic slab of 24 Å thickness and for NIC particles to distribute in the aqueous phases on each side of the membrane (Fig. 2 A). NIC atoms move in the aqueous bath within 100 Å of the membrane interface. Additionally, both NIC and OXY were distributed in the cylinder-shape system with a radius r of 50 Å. The simulations were performed without periodic boundary conditions. The system was first relaxed by energy minimization to remove unfavorable steric contacts, and the pseudoatoms were free to move, whereas the positions of the decoy atoms were kept fixed. All positional restraints, except for those in residues 55–83, were removed during the MD simulations.

PaDSAR simulations were carried out using Langevin dynamics with a friction coefficient of 5 ps⁻¹ for all the atoms, except hydrogens. MD simulations were performed in a range of 300–600 K using the united-atom model PARAM19, and the dielectric constant was set to 1. The initial velocity of particles was assigned using the Gaussian distribution with a time step of 2 fs. The group-based method for the nonbond list was used with a distance cutoff of 16 Å of actual and image atom lists. The switching function of LJ and electrostatic potentials was applied for an interacting pair distance between 8 Å and 12 Å. We carried out 2 ns MD simulations for the decoy refinement and 4 ns simulations for testing the LJ parameters. The restraint energy and structure fluctuations were used to verify a convergence of the simulations, and we found that all the simulations converged within 1 ns MD runs.

Analysis and evaluation

We used energy and RMSD relative to the reference structure (1K4C) as the two selection criteria for selecting final structures. For each MD run with PaDSAR, structures of 250–500 snapshots were taken from the trajectory during the last 0.5–1 ns for analysis and evaluation. Unless otherwise specified, we used “RMSD to native” or “RMSD distortion” to denote a comparison between the obtained structure(s) and the x-ray KcsA structure. 〈 〉 indicates the trajectory-average quantity. For instance, 〈RMSD〉 is the trajectory-average RMSD. Each snapshot was used to compute the LJ interaction energy associated with EP1, EP2, and EP3 to identify structures with the correct fold. We found no significant difference between a representative structure selected from the K-mean cluster centroid and that chosen from the lowest interaction energy. Therefore, a representative PaDSAR structure of each run was selected and ranked based on the computed energy. The top 25 structures were chosen, and we measured their structural differences (RMSD). An in-house FORTRAN program for hierarchical clustering algorithm (42) was used to measure dissimilarities among selected structures.

RESULTS

As defined above, we have devised a strategy to parametrize EPR-based solvent accessibility data to drive the conformation of a preexisting membrane protein crystal structure. We tested and validated our approach by driving structurally distorted decoy structures back to its native conformation based on EPR environmental data (32) from the closed conformation of the potassium channel KcsA (33). A set of 100 decoys with varying degrees of distortion (between 2 and 30 Å RMSD) from the native closed conformation were generated for statistical analysis. In each case, MD simulations with and without EPR restraints were performed to evaluate the efficiency of the approach. The resulting structures from the simulations were validated based on a comparison of RMSD to the native structure.

Optimizing restraint parameters

Based on ΠO₂ and ΠNiEdda data (32), a total of 58 pseudospins were used in the calculations with the assignment of 36 EP1, 10 EP2, and 12 EP3 (Table 2) along TM1 and TM2 in the transmembrane regions KcsA in its closed conformation. Several MD runs of the x-ray KcsA structure were performed by varying LJ parameters, ɛ and R_min, of the pseudoatom interacting pairs. Because most of the experimental spin-label accessibility data were consistent with the x-ray KcsA structure, these restraints should satisfy or at least not severely violate the current conformation. Thus, RMSD is an ideal parameter for an initial validation of the results of each run to obtain an optimal well depth for the ɛ and R_min parameter set selected from the run giving the structure, on average, closest to the reference structure. Here, we have chosen the parameters from the run that gave the best fitting 〈RMSD〉, relative to the native KcsA conformation, of 1.18 ± 0.07 Å. The run that did not include the EPR restraints gave an ensemble of conformations with an RMSD distortion of 0.65 ± 0.10 Å. These changes of 0.53 Å RMSD are insignificant compared with the dynamics of the system.

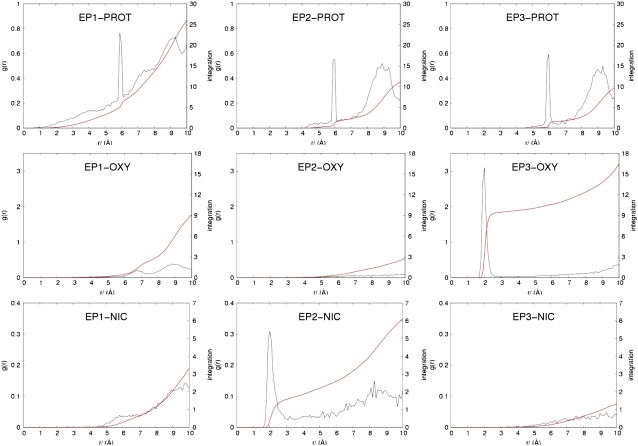
Plots of the radial distribution function, g(r), for the different interacting pairs (Fig. 5) were used to further refine the quality of the pair potential LJ parameters for all pseudoatoms. It is expected that the match pair particles defined with an attractive potential (EP1-PROT, EP2-NIC, and EP3-OXY) should get close to each other with respect to those mismatch pairs. A sharp peak at 6 Å for g(r) of EP1-PROT, EP2-PROT, and EP3-PROT corresponds to the distance from the pseudospin to its own residue, since PROT is located precisely at the Cα position (CA-EP1, EP2, or EP3 bond length 6 Å). PROT particles can get much closer to EP1 (r < 2 Å) than can EP2 and EP3 (the closest distances are ∼4 Å and ∼5 Å, respectively), and EP1 has a greater number of surrounding PROT particles, as indicated by the integration number (Fig. 5, red line). This LJ type II function allows EP1 to favor the buried spin type. Furthermore, the simulation showed the first strong peak at 2.0 Å for EP3-OXY and for EP2-NIC, suggesting that OXY particles provide favorable interactions with the lipid-exposure spin EP3 but not with EP1 and EP2. Finally, NIC particles get sufficiently close to give attractive interactions with the water-exposed spin EP2. This is a clear indication that the current set of the LJ functions and parameters adequately describes the pseudoatom features designed for this study. The force field parameters of pseudoatoms are summarized in Table 4. A series of trial parameter sets is provided as Supplementary Material (Data S1).

FIGURE 5.

Radial distribution function plots, g(r), and its integration (red line) of pseudoatom interacting pairs taken from the MD simulation of the SCWRL model.

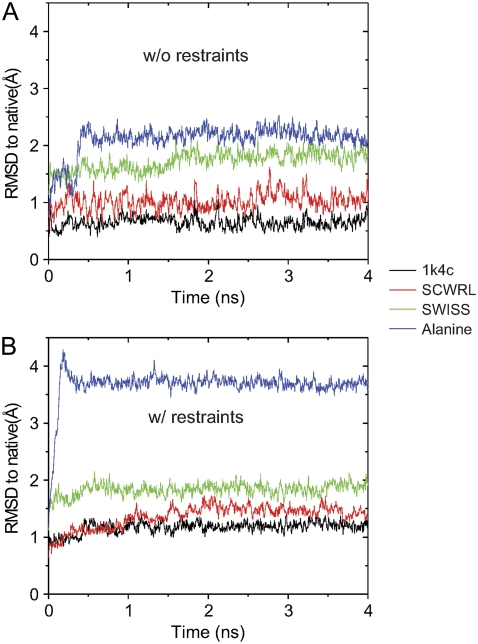
A major concern during the development of our method here was that the well-defined atomic positions of the x-ray structure may unduly bias the contributions of the EPR restraints in the refolding simulation (43). This influence might have a considerable impact on the selection of conformations close to the native structure. Therefore, we constructed a starting model having the x-ray backbone structure with rebuilt side-chain conformations as the basic template for decoy generation (see Methods). Simulations of the rebuilt side-chain model were performed to compare with that of the x-ray (1K4C), using SCWRL (36) and the Swiss-PdbViewer (44) to predict side-chain conformations; 4 ns MD runs were conducted starting with side-chain-rebuilt models, SCWRL, SWISS, and poly-Alanine and then compared with those from the x-ray model. It should be noted that these four models (1K4C, SCWRL, SWISS, and poly-Alanine) share the same context of the backbone x-ray conformation but differ in their side-chain torsions. In addition, the simulations were performed in the presence and absence of the EPR restraints.

MD results ranked according to 〈RMSD〉 (to native) were as follows: 1K4C < SCWRL < SWISS < Alanine (Fig. 6). The order appears to be the same for the simulations in the presence and absence of the restraints. From these results, 〈RMSD〉 ranges from 0.65 ± 0.10 Å to 2.19 ± 0.11 Å for the simulations with the absence of the EPR restraints and from 1.18 ± 0.07 Å to 3.70 ± 0.08 Å for the simulations with the EPR restraints (Table 5). As expected, the runs that include the EPR restraints had larger 〈RMSD〉to native values compared to those without the restraints. However, the increase in 〈RMSD〉 distortion is not dramatic, except for the poly-Alanine model (from 2.19 Å without restraints to 3.70 Å with restraints). These results indicate the importance of side-chain contributions and packing to maintain the structure close to the reference native conformation. The x-ray-based MD runs appear to have a minimal effect on conformation distortion because the side chains have been well defined. Consequently, we decided to use the SCWRL model as a base for generating all the decoy conformations to minimize the strong bias that side-chain packing may have in all refolding simulations.

FIGURE 6.

RMSD fluctuations from the MD simulations of the backbone-based x-ray structures: 1k4c (black), SCWRL (red), SWISS-PdbViewer (green), and Alanine (blue), (A) without and (B) with the restraints.

TABLE 5.

〈RMSD〉 results of the simulations

	〈RMSD〉 to the native (Å)
Model	With EPR restraints	Without EPR restraints
1K4C	1.18 ± 0.07	0.65 ± 0.10
SCWRL	1.48 ± 0.09	1.06 ± 0.15
SWISS	1.87 ± 0.09	1.82 ± 0.11
Alanine	3.70 ± 0.08	2.19 ± 0.11

Data with and without the restraints for the x-ray-based backbone models.

Structure refinement

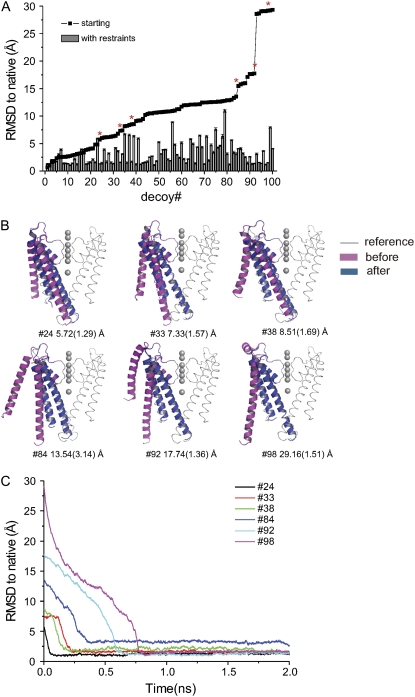
In the simulations here, each set of decoys contains 100 sampling conformations covering a broad range of randomly distorted structures, from 2 Å to 30 Å RMSD relative to the native KcsA structure. In our sets, there is an ∼20:20:50 relation for structures with RMSD ranges of 2–5 Å, 5–10 Å, and 10–20 Å, respectively. The remaining decoys, with very large RMSDs (∼30 Å) were manually generated from the native structure. An analysis of the resulting structural deviations after PaDSAR runs was performed on snapshot structures obtained from all 100 simulations. Fig. 7 shows the RMSD to native before (solid squares) and after (gray bars) PaDSAR simulations. From the RMSD plot, the majority of the refolding MD simulations successfully drove the starting distorted decoy toward the native conformation (Fig. 7 A). Indeed, most of the obtained PaDSAR structures converged to RMSD in a range of 1–4 Å, even those that have starting conformations with RMSD as large as 30 Å. Although convergence proceeds at different rates, depending on initial decoy RMSD, most convergences occurred within the first 1 ns simulation (Fig. 7 C).

FIGURE 7.

(A) 〈RMSD〉to native before (solid squares) and after (bar charts) the refolding simulation of 100 decoys. Red stars mark on decoys that their structures and RMSD profiles are shown in B and C, respectively. In B, red and blue ribbons are structures of decoy before and after the simulations, respectively. Decoy number and RMSD are also indicated. The Cα-trace with light gray is the reference. Potassium ions are shown as CPK (Corey, Pauling, and Koltun atom coloring) mode.

Structure selection criteria

After considering RMSD to native <3 Å as an acceptable cutoff for the identification of the correct folds, 54 out of the 100 MD runs produced PaDSAR structures that were in good agreement with the native KcsA structure. For the rest, 30 and 16 of the PaDSAR structures exhibited RMSD to native within 3–5 Å and larger than 5 Å, respectively. Among those PaDSAR structures with near-native KcsA conformation (RMSD < 3 Å), 80% had RMSDs to native conformations < 2 Å. In the case of unsuccessful refolding runs, the profiles of RMSDs to native conformations behave in a similar fashion as shown in Fig. 7 C. The RMSDs decrease at the beginning of the refolding simulation and then remain unchanged at the value larger than the cutoff (not shown). This suggested that some decoys were trapped by a local minimum of the potential energy surface and were unable to move to a configuration in which the restraints were fulfilled.

As a control, refolding simulations in the absence of the EPR restraints were performed. For a comparison, 50 decoys that adopt starting conformations with RMSDs to native conformations in a range of 2–17 Å were selected from the same decoy set used in the simulations with the restraints. It is clear that simulations including the restraints were on average more successful (Fig. 8 A) than those driven by the MD force field alone. The advantage of using the restraints is specially highlighted when the RMSD distortion of the decoys becomes larger (8–17 Å). In this range, MD runs without the restraints failed in the majority of cases (Fig. 8 B).

FIGURE 8.

〈RMSD〉 to native from MD simulations with and without the restraints. RMSDs of the starting decoy structures are also shown as solid squares. (B) Ribbons representation of some selected decoys (marked with stars in A, dark gray) shown after PaDSAR runs with EPR constraints (in gray) and without constraints (light gray).

Restraint energy as the primary selection

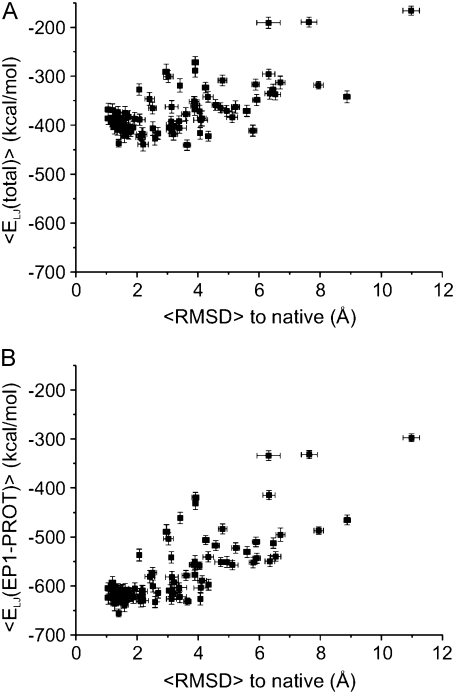
As shown in Fig. 7 A, the 100 refolding simulations produced a range of PaDSAR structures covering native and distorted fold representations. The individual configurations of the systems in the MD trajectories can be used to extract the energy from the EPR restraints associated with the PaDSAR-generated structures. The idea is to use energy information from the restraint as a criterion in the final structure selection. The LJ interaction energy in particular can be used as a structural indicator, as it is the most relevant parameter to determine the best fit between the calculation and the experiment data. It is, however, useful to quantify the correlation between restraint energy and correct fold structure.

This issue was evaluated by looking at the correlation between the LJ restraint energy components computed from MD snapshots and RMSDs to native from the resulting structures. Each snapshot of the system was taken from the trajectory and used to compute E_LJ(EP1), E_LJ(EP2), and E_LJ(EP3), the LJ energy associated with pseudoatom interactions. E_LJ(EP1) reflects interactions of EP1 with all the environment pseudoatoms (PROT, OXY, and NIC). The same analogy was applied to E_LJ(EP2) and E_LJ(EP3) to define interactions involving EP2 and EP3, respectively. Furthermore, E_LJ(total) was computed from the sum of each energy component. Energy and RMSD computations were carried out throughout the trajectory to obtain an average value. Fig. 9 A shows the E_LJ(total)-RMSD plot over the 100 runs. From this analysis, we found that both E_LJ(total) and E_LJ(EP1) give the best correlation with RMSD with respect to E_LJ(EP2) and E_LJ(EP3) (not shown). The E_LJ(total)-RMSD correlation is essentially similar in pattern to the E_LJ(EP1)-RMSD correlation, suggesting EP1 interactions provide the major contribution in the studied system.

FIGURE 9.

Structure discrimination based on the correlation between the LJ restraint energy components and RMSD to the native of the resulting structure. (A) 〈E_LJ(total)〉 versus 〈RMSD〉 and (B) 〈E_LJ(EP1-PROT)〉 versus 〈RMSD〉.

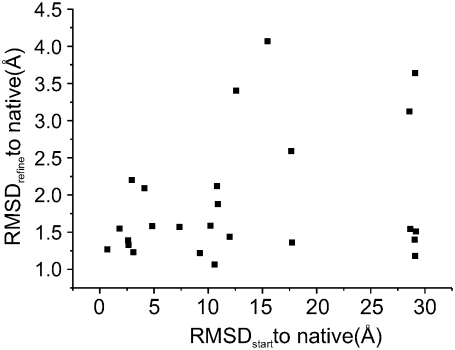
This is largely a result of the majority of EPR restraints being assigned to the buried EP1, in addition to the defined LJ type II potential function allowing its dense set of interactions with PROT atoms. This can be demonstrated from the E_LJ(EP1-PROT)-RMSD correlation. Fig. 9 B shows that the E_LJ (EP1-PROT)-RMSD plot is similar to the E_LJ(total)-RMSD but with a better correlation. Structures obtained from all the PaDSAR simulations were ranked from the lowest (most favorable) to the highest E_LJ(EP1-PROT) values, and the top 25 runs were selected. Fig. 10 shows a plot of RMSD to native computed from the structures before (RMSD_start) and after (RMSD_refine) the refolding simulation. As an illustration, the top 25 runs had the starting decoy conformations with RMSD in a range of 2–30 Å and produced PaDSAR structures with RMSD deceased to 1–4.5 Å after structure refinement. Applying a 3 Å cutoff for the RMSD distortion to the current set of PaDSAR structures showed that 20 out of 25 had the native-like conformation. The five remaining structures exhibit RMSD from 3 to 4.5 Å. The E_LJ(EP1-PROT) of these 25 selected PaDSAR structures is comparable to that calculated from the simulation of the x-ray structure. Thus, we concluded that correlation between the restraint energy and structural quality provides additional useful information for the initial screening of candidate structures from a large number of trial structures.

FIGURE 10.

Correlation between the restraint energy and structural quality provides additional useful information for the initial screening of candidate structures from a large number of trial structures. RMSD to native computed from the structures before (RMSDstart) and after (RMSDrefine) the refolding simulation. A 3 Å cutoff for the RMSD distortion to the current set of PaDSAR structures shows that 20 out of 25 had the native-like conformation.

Structure similarity as the secondary selection criterion

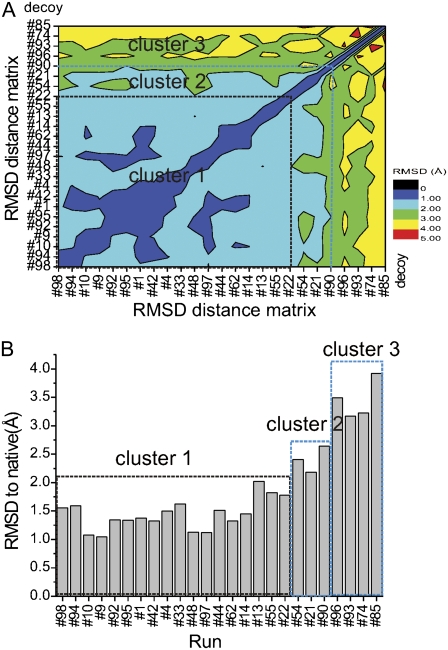
Because the above energy components are computed empirically, the analysis of the low energy alone may not be enough to produce robust selection criteria. A number of clustering algorithms designed to discriminate among a set of fold models have been successfully used in combination with the energy information for protein structure prediction (45,46). We further developed our discrimination criteria by computing pairwise RMSD within the 25 PaDSAR structures, giving rise to a 25 × 25 matrix of RMSD values. The RMSD matrix was then clustered based on a dissimilarity measure using hierarchical agglomerative clustering algorithm (42). In other words, we employed this method to rearrange RMSD values in the matrix from the lowest (lower left corner) to the highest (upper right corner) values as shown in Fig. 11 A. The smaller the RMSD, the lower the difference between the two compared structures. In the RMSD matrix, 25 PaDSAR structures were grouped into three clusters based on the RMSD range (Fig. 11 A). Eighteen out of the 25 PaDSAR structures belong to the cluster with the smallest RMSD range <2 Å (Fig. 11 B).

FIGURE 11.

(A) Pairwise RMSD contour plot of the 25 selected PaDSAR structures rearranged from the lowest (lower left corner) to the highest (upper right corner) RMSD values. A color legend bar indicates RMSD values. (B) RMSD to native versus the 25 PaDSAR structures. The 18 most similar structures are in the dashed square.

DISCUSSION

Analyses of structure-function relationships, particularly in the case of ion channels and membrane transport proteins, require the determinations and analyses of multiple conformational states, which are difficult to obtain with conventional structural methods. The use of solution NMR with isotope-enriched samples has been successful in a number of cases, though further development is still needed (47–49). Here, we have developed a restrained MD protocol, PaDSAR, to take advantage of probe/reporter group data based on EPR power saturation experiments to drive 3D structural conformation in proteins. An identical treatment is expected for similar types of data obtained through complementary techniques (50) and is complementary to very successful recent protocols to calculate folds based on sparse spin-labeling EPR distance data (28).

One advantage of the approach here is that the EPR accessibility data for each spin-label position holds local structure information that suggests a specific arrangement of the residue backbone with respect to its global fold and the solvent environments. The results demonstrate that novel restraints derived from a pseudoatom-based potential method associated with the experimental accessibility data and used as a “soft restraint” represent an effective approach for structural refinement or conformational modification in membrane proteins. The use of a single effective pseudoatom per residue to represent the relatively complex nitroxyde moiety is justified by the low-resolution character of the experimental EPR accessibility data. There is no loss of information, and the combined effect of multiple pseudoatom sites in the restrained MD allows the simulations to refold distorted structures back to the native conformation with ease and computational efficiency.

We have shown that an empirical method where an MD conformational search was guided by the protein force field and the restraints was efficient in computing structural assembly of transmembrane helical proteins. The main driving force of the EPR restraints incorporated in MD simulation is described by nonbonding LJ interactions. In this regard, the definition for the nonbonding term is key to maximize the importance of the restraints. In the bonding term, we used a fairly stiff bond between the pseudospin and the Cα backbone. Although this assumption may be only an approximation due to the conformational degree of freedom of the nitroxide side chain (40,41,51), the simulations with fairly rigid CA-EP1 (EP2 or EP3) bonds gave better results than those having flexible bonds.

The approach here is most useful in three key applications for membrane protein structural studies. First, it could be used to refine x-ray structures away from the conformation determined in detergent micelles or in a crystalline lattice to physiologically relevant states in a lipid bilayer. Second, the approach is useful in the case of refining 3D structures with low-resolution or with missing regions of the structure. Third, the method should perform equally well calculating conformational changes for systems for which state-dependent data sets exist.

There are some limitations to the approach and its implementation. One important problem is that the assignment of the spin type was done by relative comparison of accessibility data where ambiguous values were not considered in the calculations. Moreover, an incorrect pseudospin type could be easily assigned due to ambiguous values of solvent accessibility in some positions that cannot be identified as belonging to a specific environment. Unfortunately, at the moment there is no automated method to assign the pseudospin type. As a result, structure refinement needs to be repeated from time to time by changing the type of ambiguous assigned spins until an agreement between the experimental EPR data and the obtained structure is optimized. Other issues to consider include the fact that MD runs with a large number of decoy conformations are time consuming, whereas single MD runs can limit the conformational space to be sampled. Structure refinement was carried out under an assumption of known secondary structure elements. This makes the method less useful when refining the structure of an unstructured flexible region or when calculating structural rearrangements of TM segments associated with a change in secondary structure.

This approach can be further applied to other biophysical data that are derived based on accessibility experiments, for instance, cysteine or tryptophan accessibility scanning analysis. In calculating conformational changes, the method could be further developed to take into account relevant accessibility changes by applying different weights in the LJ parameters. Furthermore, conformational searches combined with scoring methods could be introduced before the MD run for a rapid screening of candidate structures. A recent application of the method has introduced an additional pseudoatom EP4 for the nitroxide spin at the water-lipid interface, as indicated by DOGS-NTA[Ni(II)] (the 1,2-dioleoyl-sn-glycero-3-[(N-(5-amino-1-carboxypentyl)imidodiacetic acid)succinyl] nickel(II)) (34). A strategy to improve the approach described above is in progress with an effort to predict the structural architecture of the nontransmembrane region of ion channels. These include the closed conformation and N-terminus of a mechanosensitive channel with small conductance (MscS) (34) and the voltage-sensing domain of the potassium KvAP channel in membrane (35).

CONCLUSION

We report the development of PaDSAR, a novel (to our knowledge) approach to modify the conformation of membrane proteins of known structure, using EPR-determined accessibility data as restraints in MD calculations. The novel restraint is based on different exposure of a spin-label to which O₂ or NiEdda molecules collide at a given frequency. We employed a pseudoatom method with empirical force field potentials to treat such collisions as a structural parameter. This study illustrated that structural refinement with the restraints combined with an energy-based screening and clustering method provides a promising tool in refolding a wide range of distorted conformations as much as 30 Å RMSD into the native-like KcsA conformation. Applications of PaDSAR to a number of membrane protein systems are underway in a variety of membrane protein systems.

SUPPLEMENTARY MATERIAL

To view all of the supplemental files associated with this article, visit www.biophysj.org.

APPENDIX