The Selectivity of K⁺ Ion Channels: Testing the Hypotheses

Abstract

How K⁺ channels are able to conduct certain cations yet not others remains an important but unresolved question. The recent elucidation of the structure of NaK, an ion channel that conducts both Na⁺ and K⁺ ions, offers an opportunity to test the various hypotheses that have been put forward to explain the selectivity of K⁺ ion channels. We test the snug-fit, field-strength, and over-coordination hypotheses by comparing their predictions to the results of classical molecular dynamics simulations of the K⁺ selective channel KcsA and the less selective channel NaK embedded in lipid bilayers. Our results are incompatible with the so-called strong variant of the snug-fit hypothesis but are consistent with the over-coordination hypothesis and neither confirm nor refute the field-strength hypothesis. We also find that the ions and waters in the NaK selectivity filter unexpectedly move to a new conformation in seven K⁺ simulations: the two K⁺ ions rapidly move from site S4 to S2 and from the cavity to S4. At the same time, the selectivity filter narrows around sites S1 and S2 and the carbonyl oxygen atoms rotate 20°−40° inwards toward the ion. These motions diminish the large structural differences between the crystallographic structures of the selectivity filters of NaK and KcsA and appear to allow the binding of ions to S2 of NaK at physiological temperature.

INTRODUCTION

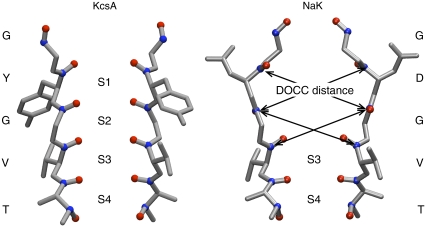
Ion channels play a key role in the membrane physiology of both excitable and nonexcitable cells. A key issue in understanding the relationship between ion channel structure and function is the mechanism whereby a given species of channel selects for certain ions, while allowing those ions to permeate at near-diffusion limited rates. For example, K⁺ channels are able to conduct K⁺ but not Na⁺ ions even though the Pauling radius of a K⁺ ion is only 0.4 Å larger than that of a Na⁺ ion. Fig. 1 shows how the conserved TVGYG signature sequence of KcsA, a K⁺ channel, forms a narrow constriction in the tetrameric pore called the selectivity filter and is responsible for determining which ions can permeate (1). The backbone carbonyl oxygen atoms of the TVGYG sequence point toward the center of the pore, forming four distinct ion-binding sites, labeled S1–S4. Each ion-binding site is composed of eight carbonyl oxygens from two adjacent amino acids (or four carbonyl oxygen atoms and four hydroxyl oxygen atoms from the side chain of Thr-75 in the case of S4).

FIGURE 1.

The selectivity filters of KcsA and NaK. Only two of the four monomers are shown and no hydrogens are drawn. The ion binding sites are labeled S1–S4 and the carbonyl and hydroxyl oxygen atoms that define these sites are drawn as red spheres. The backbone carbonyl carbon atoms are drawn as blue spheres and several distances between diagonally opposite carbonyl carbons (DOCC) are drawn on the NaK structure using black arrows.

Three main hypotheses have been suggested to explain how K⁺ channels select for K⁺ over Na⁺ ions. The first is the “snug-fit hypothesis” (2,3). It is sometimes not clear from the literature precisely how this hypothesis is defined and therefore we shall arbitrarily distinguish between strong and weak variants solely to cope with this lack of clarity. The strong variant states that K⁺ channels maintain a rigid scaffold in which the cation sits and that this is optimized for K⁺ but not Na⁺, ions. The weak variant states that a K⁺ channel merely needs, for example, to “conform more favorably to an ion of a particular size” (4) and is therefore an example of an induced-fit model. The strong variant has been criticized on the basis that the atoms of the selectivity filter fluctuate in position by significantly >0.4 Å at physiological temperature (5), a conclusion supported by crystallographic B-factors (6), experimental structures at low concentrations of K⁺ ions (1), and computer simulations (7–10).

Noskov et al. (5) proposed what may be called the carbonyl-repulsion mechanism: this is the idea that, as the coordinating ligands crowd around smaller ions, they electrostatically repel one another and this leads to selectivity. This mechanism suggests that altering the number and/or the chemistry of the ligands coordinating the bound ions will change the selectivity of a K⁺ ion channel; for example, increasing both the number and dipole of a ligand will increase the repulsion between individual ligands (although the attraction between the ligands and the bound ion is also altered and this must be taken into account). Their key result was that switching-off the interactions between the carbonyl groups in S2 of KcsA removed selectivity according to free energy calculations. This is consistent with the repulsion between the carbonyl groups driving selectivity but does not prove that it is the type, rather than the number, of ligands that is the dominating factor. Noskov et al. (5) emphasized that it is the chemistry of the ligands, specifically their field strength, which leads to selectivity. This is what we shall call the “field-strength hypothesis” and draws on earlier work by Eisenman (11).

What may be called the “over-coordination hypothesis” is the third argument, and was recently proposed independently by several groups (12–15). This hypothesis asserts that each cation is coordinated by more ligands than it would experience in bulk water. Altering the number of ligands, not their field strength, therefore is the dominant explanation of selectivity in K⁺ ion channels. The structure of the protein is considered as either applying a topological-constraint (e.g., forces) to the ligands (12) or maintaining the bidentate nature of the ligands (13,14). Consequently, the ligands have an intermediate degree of flexibility; i.e., they are neither liquidlike nor rigid.

All three hypotheses can be reconciled with the known crystallographic structures of KcsA (1) and other related K⁺ channels. The determination of the structure of the NaK ion channel (16) has reinvigorated the debate since NaK conducts both Na⁺ and K⁺ ions. The structure of its selectivity filter is similar but not identical to that of KcsA (Fig. 1): the selectivity filter of NaK is wider toward the top and no ions were observed to bind at S1 and S2. Free energy calculations have shown that the different sites in both channels exhibit varying degrees of selectivity (17–19). Each hypothesis must therefore explain not only the variation in selectivity between the ion-binding sites S1–S4 but also the selectivity of KcsA for K⁺ over Na⁺ ions and the lack of selectivity of NaK for either K⁺ or Na⁺ ions. Comparing NaK and KcsA therefore provides an opportunity to rigorously test these hypotheses. We note that a degree of confusion has arisen because these three hypotheses are not mutually exclusive; the field-strength and over-coordination hypotheses place different emphases on aspects of the carbonyl-repulsion mechanism. These hypotheses are also variants of the weak snug-fit hypothesis but with the important differences that they explicitly explain how selectivity is produced and they make predictions that can be tested.

Although selectivity is, we assume, primarily determined by the thermodynamics, it is instructive to try to relate changes in the energetics to changes in the structures of the K⁺ channels. This would give us an intuitive understanding of selectivity and is, of course, easiest when the structural (or dynamical) differences are comparatively large. For example, the strong variant of the snug-fit model is described geometrically (2) and therefore it is simple to relate the structure to the energetics. The field-strength and over-coordination hypotheses are much more subtle and therefore will require careful analysis to be distinguished.

In this article, we shall answer two questions:

1. What conformations do the selectivity filters adopt at physiological (∼300 K) temperature compared to the low (∼100 K) temperatures of an x-ray diffraction study?

2. Can our observations support or refute any of these hypotheses?

The first question has a significant bearing on the second since, as we have alluded to, each hypothesis may be characterized by how flexible it requires the selectivity filter to be: the strong variant of the snug-fit hypothesis requires a rigid selectivity filter and the over-coordination hypothesis requires an intermediate degree of flexibility. It is not clear how flexible the field-strength hypothesis requires the selectivity filter to be. Although Noskov et al. (5) state that the behavior of the ligands is liquidlike, implying a high degree of flexibility, their toy model prevents the coordinating ligands from moving too far away from the ion by the application of a flat-bottomed harmonic potential and therefore there is a degree of structural rigidity. Examining the flexibility of the selectivity filters will therefore provide an indirect test of the different hypotheses. Since the field-strength and over-coordination hypotheses state that different aspects of the carbonyl repulsion mechanism dominate, support for one hypothesis will naturally reduce the likelihood that the other hypothesis is correct. We shall investigate the number of coordinating ligands around the bound ions to test the over-coordination hypothesis. It is difficult to test directly the field-strength hypothesis, but it has been predicted that selectivity is lost by the addition of water molecules to the shell of coordinating ligands (19): we shall therefore also examine the type of coordinating ligands.

With the exception of the modeling of the selectivity filter performed by Asthagiri et al. (20) and the free energy calculations carried out by Noskov et al. (5), all the existing studies used relatively simple models to propose and test the different hypotheses. This was partly to maintain physical clarity and partly out of necessity so that ab initio or polarizable descriptions could be used. In contrast, we have chosen to simulate the behavior of tetrameric KcsA and NaK ion channels embedded in two-component (7:3 POPE/POPG) lipid bilayers solvated by explicit water using classical molecular dynamics. This will permit us to determine whether it is possible using these hypotheses to detect the differences in selectivities known to be exhibited by the different ion binding sites. In an attempt to ensure that the conclusions we draw are robust we have used two different force fields, repeated all simulations several times, and examined the effect of changing the initial conditions.

MATERIALS AND METHODS

The experimental structures of KcsA (1K4C, resolution 2.0 Å (1)) and NaK (2AHZ, resolution 2.8 Å (16)) from the Protein Data Bank were used as initial conformations for our simulations. MODELLER (21) was used to model in the M0 helix of KcsA using the experimental NaK structure as a template resulting in a helix at a slight angle to the bilayer. The side chain of Glu-71 in the KcsA structure was protonated. One (or two for NaK) additional waters were placed in each monomer to mediate interactions between the P helix and the selectivity filter. The calcium ion found at the extracellular entrance to the selectivity filter in the structure of NaK was retained. A K⁺ ion and 17 or 39 waters were also placed in the cavity of the KcsA and NaK structures, respectively. Waters were placed at S1 and S3 in the KcsA model with K⁺ ions additionally placed at S2 and S4. Since the experimental structure of NaK indicated that only S3 and S4 exist (16), a single K⁺ ion was placed at S4 with waters at S1, S2, and S3.

A bilayer that contained POPG was used since anionic lipids are required for KcsA activity (22). The resulting homotetramers were then inserted into a mixed bilayer containing POPE/POPG in the ratio 7:3. This was done by first manually moving the protein using VMD (23) to align the positions of basic and aromatic amphipathic residues so that they could interact with the phosphate groups of the lipids. This ensured that the M0 helices were located at the interface of the bilayer. The M0 helices maintained their initial orientations in all simulations. Any lipid that was within 3.5 Å of the protein was then deleted. Both bilayers initially contained 512 lipids and after deletion, 425–435 lipids remained. The resulting complexes were then solvated and counterions added to neutralize the electrostatic charge. To assess and minimize the error introduced into our calculations by our choice of force field we repeated our simulations using both the CHARMM27 (24) and GROMOS43a1 (25) force fields. The CHARMM and GROMOS systems contained ∼114,000 and 80,000 atoms, respectively. The GROMOS force field requires fewer atoms to describe the system since it uses a unified-atom approach and only explicitly includes hydrogens that can participate in hydrogen bonds. Simulations of these systems were run using the NAMD2.5 (26) and GROMACS3.3 (27) programs, respectively.

The energy of the system was first minimized for up to 1000 steps. A Berendsen barostat (28) was then applied anisotropically to maintain the pressure of the system at 101 kPa with a compressibility of 4.5 × 10⁻⁵ bar⁻¹ and a relaxation time of either 1 ps (GROMACS) or 0.2 ps (NAMD). Maintaining a constant pressure has the additional benefit of rapidly squeezing the bilayer around the ion channel thereby ensuring that no water enters the bilayer during the initial relaxation. The temperature was progressively warmed from 100 K to 310 K in 20 K increments with 50 ps of molecular dynamics run at each step. During this warming, a restraining force of 2.4 kcal mol⁻¹ Å⁻² was applied to the headgroups of the lipids in the z direction only. No restraints were applied to maintain a constant area per lipid headgroup. A further 100 ps of molecular dynamics was run at 310 K, after which all restraints were removed and 20 ns of production molecular dynamics simulation were run. The temperature was maintained at 310 K using either a Langevin (NAMD) or Berendsen (GROMACS) thermostat. The Berendsen thermostat (28) was applied separately to the protein, ions, water, and lipids using a relaxation time of 0.1 ps and the Langevin damping coefficient was 1.0 ps⁻¹. Electrostatic forces were calculated using the particle mesh Ewald method (29) and van der Waals forces were cut-off at 12 Å with a switching distance of 10 Å. In all NAMD simulations, SHAKE (30) and SETTLE (31) were applied to constrain the lengths of all bonds that involve a hydrogen. In all GROMACS simulations, the lengths of all bonds were constrained using LINCS (32). This allowed an integration timestep of 2 fs to be used. All coordinates were written to disk every 1–10 ps.

In total 0.4 μs of simulation were run, 140 ns using NAMD/CHARMM27 and 260 ns using GROMACS/GROMOS43a1. Each ion channel was simulated four times for 20 ns with K⁺ ions bound; twice using CHARMM27 and twice using GROMOS43a1. Four additional simulations of each channel with Na⁺ ions in the selectivity filter were run; for half of these the simulations were repeated from the start with Na⁺ instead of K⁺ ions in the filter, whereas for the other half the ions were substituted by Na⁺ in the structure after 10 ns and a further 10 ns was run. Finally, the sensitivity to initial conditions was tested by repeating one of the 20 ns K⁺ bound GROMACS simulations using either a simple POPC bilayer or removing the M0 helix (or both). This makes a total of 22 simulations. All the simulations have been deposited in the Potassium Channel Database (KDB, http://sbcb.bioch.ox.ac.uk/kdb/) (33). This database is free to access and holds movies and the results of, e.g., root mean-square deviation, root mean-square fluctuation, and protein-lipid contact analyses. The aim of this database is make available data and analysis that historically would not have been included in articles and would have been difficult to obtain.

The simulated structures of both ion channels were stable as indicated by the low C_α root mean-square deviation (RMSD) values (data not shown) for either the whole tetramer or individual monomers (both 2–3 Å). Analysis of the number of protein-lipid contacts (data not shown) and the number of protein-lipid hydrogen bonds (data not shown) indicated that both proteins integrated within the first 5 ns into the lipid bilayer. Where appropriate, correlation times were estimated by applying the method of statistical inefficiency to the metric under consideration (34). The results of these analyses indicated that 500 ps was a suitably conservative estimate for the motion of the selectivity filter. The data were then binned and the statistical error calculated in the usual way.

To study the selectivity of a K⁺ channel we shall compare the behavior of K⁺ and Na⁺ ions bound to the same sites in the selectivity filter. Since there are no restraining potentials applied during the simulations the ions and waters in the selectivity filter are free to move. When this occurs we cannot investigate selectivity since it is no longer possible to, for example, count the number of coordinating ligands for a specified site for both ions. This was a problem when Na⁺ was simulated bound to S2 and S4 of KcsA using the GROMOS force field. Two additional simulations were run, but in all but one case the Na⁺ ion did not remain bound at S2.

RESULTS

We shall first study the dynamics of the selectivity filters of KcsA and NaK before investigating the number and type of ligands coordinating each bound ion. Finally we shall briefly examine the hydrogen bonding between the selectivity filter and the remainder of the protein; this has been suggested to play an important role in the selectivity of K⁺ channels (13).

To explore the conformational changes of the selectivity filters of KcsA and NaK at physiological temperature, we shall use four different metrics. First, we will analyze the average and distributions of the distances between diagonally opposed backbone carbonyl carbons (DOCC) in the selectivity filter before studying the rotation of these carbonyl groups in the plane of the bilayer. Finally we shall compute the radially symmetric width of the pore and the RMSD of the backbone filter atoms. We shall present results from the four K⁺ bound simulations for each ion channel, but where it is impractical to display this quantity of data, we shall describe the results in the text. Note that, to exclude any transient effects caused by either the integration of the protein into the lipid bilayer or the mutation of the bound ions from K⁺ to Na⁺, all calculations used only the final five nanoseconds.

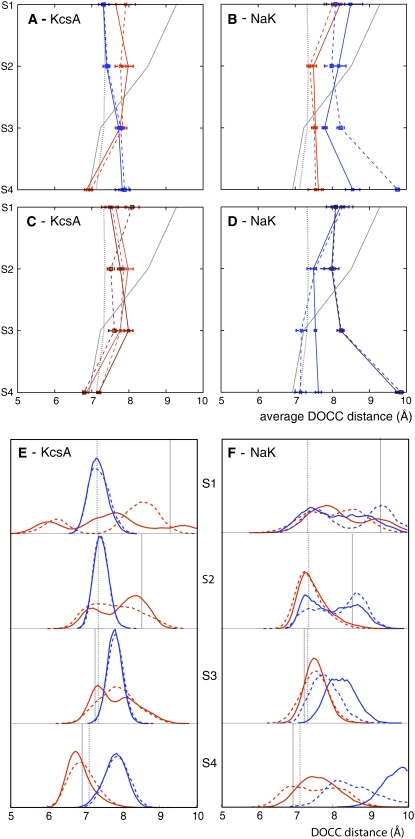
The diagonal distances between the backbone carbonyl carbon atoms belonging to adjacent amino acid residues opposite one another in the tetramer (DOCC as defined in Fig. 1) were measured. The average values for each site for the four K⁺ bound CHARMM and GROMOS simulations of KcsA and NaK are drawn in Fig. 2, A–D. If we compare the average DOCC distance between the two experimental structures we can clearly see that NaK is wider than KcsA at S1 and S2. The average DOCC distances for the sites of KcsA are the same or up to 1 Å greater than measured in the experimental structure; this is independent of the force field used or the initial conditions. This indicates a slight widening of the selectivity filter of KcsA at physiological temperature when ions are simultaneously bound at S2 and S4. The average DOCC distances for S3 and S4 of NaK are also greater than the same distance measured from the experimental structure. Sites S1 and S2 do not exist in the experimental structure of NaK at cryogenic temperature (16), however, we note that the average DOCC distances for S1 and S2 are significantly less than in the experimental structure; we shall discuss this more later. We interpret this as a simultaneous narrowing and widening at the top and bottom, respectively, of the NaK selectivity filter at physiological temperature.

FIGURE 2.

The average DOCC distances of KcsA and NaK for the four K⁺ bound simulations (A and B) and the four K⁺ bound simulations (C and D) that start from different initial conditions. The distributions that contribute to the averages in panels A and B are shown in E and F, respectively. The distances for the two CHARMM27 and two GROMOS43a1 simulations in panels A, B, E, and F are drawn in blue and red, respectively, while the distances for the different initial conditions in C and D are drawn in different shades of blue and red. The DOCC distances for the crystal structures of KcsA and NaK are drawn as dotted and solid gray lines, respectively, and any error bars were calculated by dividing the data into 10 blocks of 500 ps as described in Materials and Methods.

It is likely that these averages hide a significant level of variation and so we shall now examine the distribution of DOCC distances (Fig. 2, E and F). We observe that the DOCC distance varies significantly at physiological temperature, confirming the dynamic behavior of the selectivity filter even when K⁺ ions are bound. We hypothesize that the magnitude of this flexibility is affected by the state of the filter and other events, notably “carbonyl flips.” These occur when one or more backbone carbonyl groups rotates away from the pore axis. As we shall see shortly, a carbonyl oxygen belonging to one of the Val-76 residues has flipped in one of the GROMOS simulations of KcsA thereby contributing to the bimodal distributions seen here. We note that the DOCC distributions for the different force fields can be significantly different even when the averages are similar. This effect may reflect both the difficulties in sampling adequately and the differences between the force fields. We note that the first effect is probably dominating since DOCC distance distributions from GROMOS simulations starting from different initial conditions have also not fully converged with one another (data not shown).

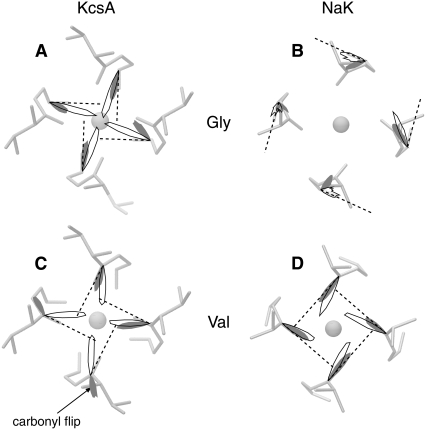
Having examined in some detail the width of the selectivity filters of KcsA and NaK we shall now investigate what angles the backbone carbonyl bonds make in the plane of the bilayer (i.e., perpendicular to the axis of the pore) at physiological temperature (Fig. 3). We have chosen to focus on S2 since this is the site in KcsA that is thought to be most selective for K⁺ ions (17–19) and S2 was not observed in NaK (16). It can clearly be seen that all the carbonyl groups twist slightly toward the axis of the channel for both KcsA and NaK independent of the force field used. The total rotation is ∼20°−40° for both KcsA and NaK. The distribution of angles observed is, in general, small. One exception is the carbonyl flip seen on Val-76 of KcsA when simulated with GROMOS. This carbonyl remains flipped for the remainder of the simulation.

FIGURE 3.

The polar distributions of the angles made in the plane of the lipid bilayer by the backbone carbonyl bonds from residues Val-76 (A and B) and Gly-77 (C and D), which form S2 of the selectivity filter. For clarity, only two of the 4 K⁺ bound simulations are depicted; the results for the remaining two simulations, which are similar, can be found in Fig. S1 in Data S1. The dashed lines indicate the angles found in the crystallographic structures. The angular distributions from the CHARMM27 and GROMOS43a1 simulations are drawn with solid lines or in shaded representation, respectively. The magnitude of each curve represents the probability of that angle occurring and therefore the areas sum to unity. Note that the dynamic angular distributions have been superimposed on the static crystallographic structure.

Since the backbone carbonyl bonds for these two residues in the crystallographic structure of NaK are roughly orthogonal to the channel axis, this magnitude of rotation does not lead to the carbonyl oxygen atoms pointing directly at the axis of the channel, as in KcsA. At the same time the K⁺ ion at S4 of NaK moves up to S2 and the K⁺ ion in the cavity moves into S4. This occurs in all seven simulations of NaK (see Supplementary Material, Fig. S2 in Data S1). This is a surprising result since no ions are bound at S2 in the x-ray structure of NaK. There is no external force applied to the channel, for example a transmembrane potential difference, that could be responsible for the motion of these ions. The movement of the ions and the conformational changes in the selectivity filter must therefore be a result of forces applied by the protein and the other ions and waters. We shall comment on this more later.

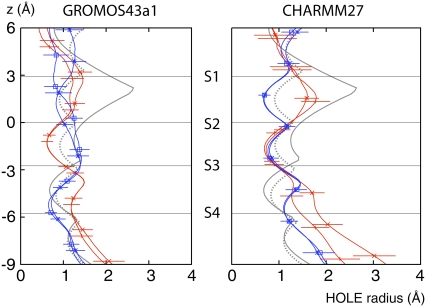
The net result of these rotations and movements is that the pores, as measured by HOLE (35), are on average more similar to one another (Fig. 4). The pore of NaK is noticeably narrower at S2, although this is less pronounced when CHARMM27 is used, while the pore of KcsA is similar to its experimental structure. The pore profiles have a wide range of widths and there is significant overlap between the pore profiles from both ion channels. This further illustrates the conformational change that has occurred around S2 in NaK. The width of the pore can be as low as 0.5 Å between the ion binding sites, i.e., in the plane of the carbonyl oxygens. This leads to the scalloped shape of the HOLE profile and represents a kinetic barrier that prevents, in most cases, ions moving between different binding sites over the course of our simulations.

FIGURE 4.

The radius of the selectivity filter, as measured by HOLE (35) for the last 5 ns of the four K⁺ bound GROMOS and CHARMM simulations. The dotted and solid gray lines are the HOLE pore profiles for the x-ray crystal structures of KcsA and NaK, respectively. The HOLE profiles of the KcsA and NaK simulations are drawn with blue and red lines, respectively. To indicate the dynamic variation in the HOLE profiles, the standard deviation is drawn. For clarity, this is done only occasionally, and only for one set of the results. The centers of mass of the ion binding sites, as measured from the experimental structures, are plotted as horizontal gray lines.

Analysis of the selectivity filter RMSDs supports these conclusions. Note that Table 1 and Table S1 in Data S1 contain RMSD values comparing the crystallographic and simulation structures for both ion channels. For clarity the data are divided into six sets; the first three refer to the tetramer and the last three refer to individual monomers. If we first consider the RMSD values for the selectivity filter tetramer we see that the lowest values, and therefore the most similar sets of structures, arise when simulations of the same ion channel using different force fields are compared (marked 1 in Table 1). The next lowest set of RMSD values occur when the ensemble of structures from a simulation is compared to its corresponding experimental structure (marked 2). The largest RMSD values arise when any pair of selectivity filters from different proteins are compared (marked 3). These results indicate that the structure of the whole selectivity filter at physiological temperature is most similar to its respective crystallographic structure.

TABLE 1.

Selectivity filter RMSDs

		KcsA			NaK
		1K4C	GROMOS	CHARMM	2AHZ	GROMOS	CHARMM
KcsA	1K4C	—	1.83 ± 0.042	1.72 ± 0.032	4.263	4.27 ± 0.073	4.43 ± 0.073
	GROMOS	1.67 ± 0.066	—	1.35 ± 0.071	4.44 ± 0.073	4.17 ± 0.103	4.31 ± 0.103
	CHARMM	1.64 ± 0.016	1.09 ± 0.104	—	4.43 ± 0.053	4.19 ± 0.103	4.31 ± 0.093
NaK	2AHZ	1.486	1.93 ± 0.056	1.94 ± 0.016	—	1.91 ± 0.052	1.98 ± 0.052
	GROMOS	1.84 ± 0.026	1.33 ± 0.095	1.17 ± 0.075	1.74 ± 0.096	—	1.47 ± 0.121
	CHARMM	1.84 ± 0.036	1.30 ± 0.105	1.08 ± 0.065	1.72 ± 0.036	0.96 ± 0.104	—

The RMSD values in Ångstroms between the selectivity filters of the K⁺ bound KcsA and NaK simulations and the crystallographic structures. Conformations of the selectivity filter from the simulations were fitted onto a variety of experimental structures and other simulations and the backbone RMSD (including the C_β atoms, if present) was calculated. This was done both for the set of four monomers that make up the selectivity filter and for each monomer separately. The values for the whole tetramer and the individual monomers of the ion channels are shown above and below the diagonal, respectively. Superscript numbers 1–6 are referred to and explained in the main body of the text. Each monomer was assumed to contribute one independent measurement of the RMSD and the errors were then calculated in the usual way. For clarity, only two of the four K⁺ bound simulations are compared; the results for the remaining two, which are similar, can be found in Fig. S1 in Data S1.

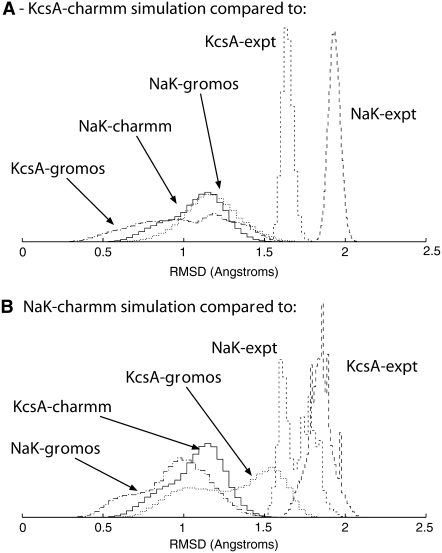
The picture is different when we separately analyze the individual monomers that make up the selectivity filters. The lowest RMSD values again occur when we compare simulations of the same protein using different force fields (marked 4). However, we find that these values are often indistinguishable from the RMSD values when monomers of KcsA and NaK are compared (using any force-field combination, marked 5). All these RMSD values are significantly less than the RMSD value for any comparison involving an experimental structure (marked 6). These trends are the same if we extend our RMSD definition to exclude C_β atoms (data not shown). The distributions of RMSD values for two representative CHARMM simulations are drawn in Fig. 5: this more clearly shows the overlap as measured by RMSD between the ensembles of selectivity filter monomer structures generated by the simulations of NaK and KcsA.

FIGURE 5.

The distributions of the selectivity filter monomer RMSDs for two representative CHARMM27 simulations. Panel A compares structures from one of the two KcsA CHARMM27 simulations with either individual x-ray crystallographic structures or a set of structures drawn from other representative simulations and panel B makes a similar comparison for NaK.

Our observations indicate that, at physiological temperature, while the ensembles of conformations of the selectivity filter monomers of KcsA and NaK overlap, the ensembles of conformations of the whole selectivity filter (i.e., the tetramer) do not overlap. This implies that the convergence in the pore widths is primarily due to conformational changes in the individual monomers and not to the distances between the monomers changing.

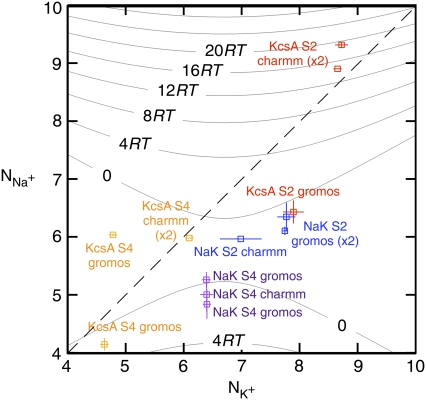
We shall now investigate the number and type of coordinating ligands around each bound ion (Table 2). The over-coordination hypothesis asserts that altering the number of coordinating ligands produces selectivity. To test this hypothesis we plot in Fig. 6 the average number of ligands around each Na⁺ ion () against the average number of ligands around each K⁺ ion (). We find that for 10 of the 13 datapoints, 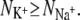As discussed in Materials and Methods, the ions in the selectivity filter are free to move. In several simulations, one of the bound ions moved to an adjacent site, suggesting that it is not stable in the original site. This also prevents any measurement of the number of ligands around the ion when bound to the original site. For example, sodium ions appear to be unstable in S2 when KcsA is simulated using the GROMOS force field. This is especially a problem since the difference in the GROMOS and CHARMM datapoints is large and we would like to determine whether this is due to differences between the force fields, incomplete sampling, or is an anomaly. Despite running repeat simulations, we were only able to measure a single GROMOS datapoint, and therefore our confidence in this datapoint is diminished. There is also a large difference in the measured values of 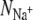for S4 of KcsA when simulated using the GROMOS force field. This indicates that for these simulations the average number of ligands have not converged. Finally, the number of ligands around each bound ion is, in most cases, broadly similar to what is expected when the ion is solvated in water (12). The exception to this is S2 of KcsA, which over-coordinates both K⁺ and Na⁺ ions when simulated using the CHARMM force field. The free energies of these states are therefore likely to be higher, but, as shown by Varma and Rempe (13), if the K⁺ ion experiences only a slight increase in free energy upon entering the selectivity filter whereas the Na⁺ ion experiences a large increase in free energy then this ensures that the channel is both selective and can conduct K⁺ ions at near diffusion-limited rates.

TABLE 2.

The average number of coordinating ligands around S2 and S4

			Total		Carbonyl		Water
			K+	Na+	K+	Na+	K+	Na+
S2	KcsA	GROMOS	7.9 ± 0.2	6.5 ± 0.2	6.1 ± 0.3	4.5 ± 0.2	1.8 ± 0.1	2.0 ± 0.1
		CHARMM	8.7 ± 0.1	8.9 ± 0.1	8.0 ± 0.1	8.0 ± 0.1	0.7 ± 0.1	0.9 ± 0.1
	NaK	GROMOS	7.8 ± 0.2	6.4 ± 0.2	7.0 ± 0.4	5.4 ± 0.2	0.8 ± 0.2	1.0 ± 0.1
		CHARMM	7.0 ± 0.4	6.0 ± 0.1	5.5 ± 0.2	4.0 ± 0.0	1.5 ± 0.5	2.0 ± 0.1
S4	KcsA	GROMOS	4.6 ± 0.1	4.2 ± 0.1	3.9 ± 0.1	1.5 ± 0.3	0.8 ± 0.1	2.6 ± 0.3
		CHARMM	6.1 ± 0.1	6.0 ± 0.1	4.0 ± 0.1	4.0 ± 0.1	2.1 ± 0.1	2.0 ± 0.1
	NaK	GROMOS	6.4 ± 0.1	5.0 ± 0.3	3.8 ± 0.1	3.2 ± 0.3	2.6 ± 0.2	1.8 ± 0.3
		CHARMM	6.4 ± 0.1	5.3 ± 0.1	2.0 ± 0.1	0.6 ± 0.2	4.5 ± 0.1	4.7 ± 0.2

A ligand is defined as any oxygen atom within 3.5 Å of the relevant ion bound at either S2 or S4. For clarity, only two of the four K⁺ bound simulations are compared; the results for the remaining two, which are similar, can be found in Table S2 in Data S1.

FIGURE 6.

The average number of ligands around a K⁺ ion (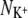) plotted against the number of ligands around a Na⁺ ion (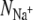) in the same ion binding site. Note that there are two data points almost coincident for KcsA S4 using the CHARMM force field. Points that do not lie on the dashed gray line therefore have different coordination numbers for each bound ion. A ligand is defined as any oxygen atom within 3.5 Å of the bound ion. Superimposed on these data are the selectivity free energy contours from Fig. 5 of the Supplementary Information from Bostick and Brooks III (12). These contours, drawn as gray lines, were derived using a nonpolarizable classical force field. The average number of ligands around ions at sites S2 and S4 are colored red and orange for KcsA and blue and purple for NaK, respectively. The discrete nature of the data made estimating a correlation time difficult and so the errors were conservatively produced by dividing each simulation into only three blocks.

Bostick and Brooks III (12) calculated the selectivity free energy as a function of 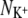and 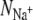through a population analysis of hydrated cations. Overlaying our results on their selectivity free energy contours thus gives us a means of testing the over-coordination hypothesis since, if it is true, the resulting predicted selectivity of our four ion binding sites should agree with previous experiments and calculations. The free energy contours were calculated using OPLS, another classical nonpolarizable force field. Despite the use of different force fields we expect free energy contours calculated using CHARMM or GROMOS to be similar since, as shown by Bostick and Brooks III (12), there are few differences in the region applicable to K⁺ channels between free energy contours calculated with either AMOEBA, a classical polarizable force field, or OPLS. The results indicate that S4 of KcsA and S2 and S4 of NaK are either not selective or are selective toward Na⁺ ions by up 2RT (1.2 kcal/mol). S2 of KcsA is predicted to be either selective for K⁺ ions by up to 20RT (12.3 kcal/mol) or not selective, depending on the force field used. Examining the radial distribution functions of the bound ions shows that for most simulations there is a minimum at 3.5 Å, indicating that this is a sensible choice for the cutoff. This does not hold for all the simulations and therefore the results are moderately sensitive to the value of the distance within which oxygen atoms are considered ligands. Assuming the free energy contours do not change significantly, increasing this distance from 3.5 Å to 4.0 Å separates the S2 GROMOS datapoints for KcsA and NaK and indicates that S2 of KcsA is selective for K⁺ ions by ∼4RT (2.5 kcal/mol) and S2 of NaK is either not selective or marginally selective for K⁺ ions (Fig. S3 in Data S1). The studies of Varma and Rempe (13) and Thomas et al. (14) support these conclusions. Their calculations indicate that eightfold coordination yields selectivities of ∼10.7 kcal/mol (17RT) and, depending on the partial charges of the carbonyl ligands, 5–10 kcal/mol (8.3–16.7RT), respectively. Our analysis assumes that the number of coordinating ligands is constant whereas we observe each simulation sampling from a range of coordination states. We do not expect this assumption to significantly change our results since the regions where the number of coordinating ligands varies significantly are also those regions where the predicted selectivity free energy is less sensitive to the number of coordinating ligands.

Noskov and Roux (19) asserted that any loss of selectivity is primarily due to a change in the field strength of the coordinating ligand, especially the introduction of water. Computational free energy studies (17–19) have shown that S2 of KcsA is more selective than S4 and therefore we would expect the number of waters coordinating ions bound in S2 to be greater in NaK than KcsA. We find that the number of waters coordinating an ion at S2 is indeed greater in NaK compared to KcsA when the CHARMM force field is used; however, the opposite trend is observed when the GROMOS force field is used. Simulations using either force field indicate that the number of waters coordinating an ion at S4 is greater for NaK than KcsA. These waters come from the cavity immediately beneath the selectivity filter (see Materials and Methods).

The number of waters that surround an ion in solution is a balance between the interactions of the waters and the ion and of the waters themselves. Varma and Rempe (13) suggested that selective K⁺ channels, such as KcsA, are able to over-coordinate ions using carbonyl ligands because there are no proximal hydrogen bond donors that could interact with the carbonyl oxygens. There are therefore no interactions equivalent to those between coordinating and bulk waters. This effect, along with a degree of structural rigidity, led them to characterize the selectivity filter as a quasiliquid environment. The mechanism predicts that selectivity can be indirectly disrupted by the introduction of hydrogen bond donors into the vicinity of the selectivity filter. Unfortunately, we cannot test this prediction since neither KcsA nor NaK have any viable hydrogen bond donors within 5 Å of carbonyl oxygens in the selectivity filter in their respective x-ray crystallographic structures (Fig. S4 in Data S1). This cannot be the only mechanism to reduce or abolish selectivity in a K⁺ channel since the selectivity across the ion binding sites varies and NaK is overall not selective for K⁺ or Na⁺ ions. Increasing the flexibility (13) or reducing the degree of topological-constraint (12) is suggested to diminish the selectivity of different ion binding sites. This can be done by reducing the number of hydrogen bonds formed between the selectivity filter and the remainder of the protein.

The number of hydrogen bonds formed between the selectivity filter and the remainder of the protein is similar for both the KcsA (15.1 ± 1.4) and NaK (18.2 ± 1.9) simulations and therefore this does not appear to support the hypothesis (Table S3 in Data S1). It is reasonable to assume, however, that hydrogen bonds made directly with the amide groups on the backbone of the selectivity filter will increase the stiffness of the selectivity filter more than hydrogen bonds made with the side chains of amino acids of the selectivity filter. Indeed we find that in the simulations the majority of hydrogen bonds made between the selectivity filter of NaK and the remainder of the protein involve the side chain of Asp-78 (11.8 ± 1.6). These results are tentative but suggest that mutations that reduce not only the number, but also the moment or torque of stabilizing hydrogen bonds, will reduce the selectivity of a K⁺ ion channel.

Computer simulation has suggested that the carbonyl flips we observe are part of a process that inactivates the channel (36). Carbonyl flips have also been observed by experiment (37) and in other computer simulations (38,39). These flips remain in place for the remainder of the simulation and therefore the period of a carbonyl flip is much longer than 20 ns; indeed, Bernèche and Roux (36) estimate that this state has a lifetime of approximately milliseconds. No hydrogen bonds are formed between these flipped carbonyl groups and the remainder of the protein and therefore these flips do not represent the states that disrupt the quasiliquid environment. Interestingly, free energy calculations have shown that these flipped states are less selective for K⁺ ions, which is consistent with the over-coordination hypothesis (36).

DISCUSSION

We have examined the behavior of the selectivity filters of two ion channels, KcsA and NaK, using classical molecular dynamics. We found that the selectivity filters of KcsA and NaK are more similar to one another at physiological temperature. Specifically we found that the backbone of the selectivity filter of KcsA is slightly wider in the simulations than in the x-ray structure, whereas the backbone of the selectivity filter of NaK is wider at the base and narrower at the top. Simultaneously, the carbonyl groups of S2 twist such that they point more toward the axis of the channel. The net result of these motions is that the ensembles of the conformations of the selectivity filter monomers are more similar to one another than they are to their respective crystal structures. Consequently there is significant overlap between the distributions of pore radius profiles for both ion channels.

This behavior clearly rules out the strong snug-fit hypothesis since this degree of flexibility is incompatible with the requirement that the selectivity filter be rigid. Our observations, however, are compatible with the weak snug-fit hypothesis although, as its name suggests, this hypothesis does not make any detailed predictions about the mechanism of selectivity and is therefore not very satisfactory. Our simulations estimate that S2 of KcsA is either not selective for K⁺ ions or is selective by up to 12.3 kcal/mol while S2 and S4 of NaK and S4 of KcsA are either not selective or select for Na⁺ by up to 1.2 kcal/mol. These results are in broad agreement with previous experimental (40) and computational free energy studies (17–19). Our results are therefore consistent with, but do not prove, the over-coordination hypothesis.

In agreement with the study by Noskov and Roux (19) we find that there are more waters coordinating ions in S2 of NaK than KcsA when the CHARMM force field is used but we observe the opposite trend with the GROMOS force field. Our direct test of the field-strength hypothesis was therefore inconclusive. Given the agreement between our simulations and the over-coordination hypothesis, however, this suggests that the lack of selectivity seen in NaK is not primarily due to an increase in the hydration number immediately around the bound ions but instead results from a reduced number of coordinating ligands, especially around Na⁺ ions. It also indicates that it is the over-coordination not the field-strength hypothesis that explains the selectivity of K⁺ ion channels.

The x-ray crystal structure of NaK suggests that sites S1 and S2 do not exist in NaK (16), yet in all seven of our K⁺ bound NaK simulations, a K⁺ ion that was originally bound to S4 moved up the filter to S2 and the cavity K⁺ ion binds to S4. This was accompanied by a narrowing of the filter and the rotation of the carbonyl oxygen atoms discussed earlier. This observation is robust since altering both the force field and the initial conditions did not change the result. The presence of S2 in NaK is relevant to the current debate about the origin of K⁺ channel selectivity since it is assumed that the differences observed in the x-ray crystal structures persist at physiological temperatures. If our observations are correct then the mechanism that leads to selectivity is subtle. There is limited experimental evidence that the selectivity filter of NaK is flexible: a recent structural article noted a correlation between the lack of a bound Ca²⁺ ion and more sparse electron density in the selectivity filter (41). This could indicate that when calcium is not bound the selectivity filter is more flexible. Our simulations of NaK included a bound calcium ion and in all cases it dissociates during the simulation, although not before the conformational change in the filter has occurred (Fig. S2 in Data S1).

Overall, the partial convergence of the structures of the monomers of the selectivity filters of NaK and KcsA indicates that at physiological temperatures the regions of the free energy landscapes accessible to the monomers of both selectivity filters are similar. The free energy minima into which each structure settles as the protein in its crystal environment is cooled (42) must therefore be different if we are to explain why the structures determined at cryogenic temperatures using x-ray crystallography are not the same. The selectivity filter is a loop and is stabilized laterally by interactions with permeant species and the hydrogen bonds formed with the remainder of the protein. Differences in the strength and number of these interactions could therefore lead to the selectivity filters adopting different structures at cryogenic temperatures. We note that a small reduction in the stability of the selectivity filter could lead to a large effect if it also destabilized a bound ion causing it to leave the selectivity filter. This is feasible since all these motions occur more quickly than the time taken to flash-freeze a protein crystal (42). Although the selectivity filters of both KcsA and NaK were observed to form similar numbers of hydrogen bonds in our simulations, comparatively few of these involved the backbone of the selectivity filter of NaK. These, we assume, stabilize the selectivity filter more than hydrogen bonds made by the side chains and therefore this accounts for the observed differences between the experimental structures of KcsA and NaK.

Compared to KcsA, there is little experimental physiological data on NaK. For example, the only evidence of the selectivity of NaK currently comes from ⁸⁶Rb flux experiments (16) in addition to a computational free energy study (19). We note that the recent application of isothermal titration calorimetry to calculate the binding free energy of different cations to KcsA potentially provides a direct way to validate theoretical free energy calculations (43). Applying this technique to NaK would be useful as it would provide a more quantitative analysis of the selectivity. We also note that the dynamic behavior of the selectivity filter we observe may provide support for the expansion of the selectivity filter necessary for Brownian dynamics models (44).

The selectivity of K⁺ channels is a good example of a biological phenomenon that critically depends on the dynamics of the proteins involved and their interactions with ligands (here the permeant ions). Classical molecular dynamics has proved a useful tool in studying selectivity; however, care must be taken to ensure that the results can be meaningfully interpreted. To validate our results we repeated simulations, altered the initial conditions, and changed the force field used. For phenomena as subtle as selectivity, this type of scrupulous approach is necessary and goes beyond the usual concerns about sampling, which as recent studies as shown, remains a difficulty for membrane proteins (45). Even with these precautions there remain a number of shortcomings in our study: Bucher et al. (46) showed that there is a significant transfer of charge from the backbone atoms to the bound cations. We have assumed throughout that the interaction between the bound ions and the selectivity filter is well described using the classical approximation: this lack of polarization is a potential source of error. In common with all previous studies, we have used the closed structure of KcsA and have therefore implicitly assumed that the selectivity filter does not change conformation when the channel opens. We anticipate open-state structures of KcsA to be published shortly (47) and if the selectivity filter adopts a different conformation this assumption will need investigating in further studies. The lack of any potential difference across the membrane is a further shortcoming. Despite these qualifications, classical molecular dynamics remains a useful approach in the study of the selectivity of potassium ion channels.

SUPPLEMENTARY MATERIAL

To view all of the supplemental files associated with this article, visit www.biophysj.org.