Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 2008 Aug 1;95(11):5021–5029. doi: 10.1529/biophysj.108.133579

Free-Energy Profiles of Membrane Insertion of the M2 Transmembrane Peptide from Influenza A Virus

In-Chul Yeh *, Mark A Olson †, Michael S Lee *,†,‡, Anders Wallqvist *
PMCID: PMC2586585  PMID: 18676651

Abstract

The insertion of the M2 transmembrane peptide from influenza A virus into a membrane has been studied with molecular-dynamics simulations. This system is modeled by an atomically detailed peptide interacting with a continuum representation of a membrane bilayer in aqueous solution. We performed replica-exchange molecular-dynamics simulations with umbrella-sampling techniques to characterize the probability distribution and conformation preference of the peptide in the solution, at the membrane interface, and in the membrane. The minimum in the calculated free-energy surface of peptide insertion corresponds to a fully inserted, helical peptide spanning the membrane. The free-energy profile also shows that there is a significant barrier for the peptide to enter into this minimum in a nonhelical conformation. The sequence of the peptide is such that hydrophilic amino acid residues at the ends of the otherwise primarily hydrophobic peptide create a trapped, U-shaped conformation with the hydrophilic residues associated with the aqueous phase and the hydrophobic residues embedded in the membrane. Analysis of the free energy shows that the barrier to insertion is largely enthalpic in nature, whereas the membrane-spanning global minimum is favored by entropy.

INTRODUCTION

The membrane insertion of proteins or peptides plays important roles in the mechanisms of viral infections, toxin actions, and antimicrobial defense (1–3). The proper understanding of the mechanism of membrane insertion of peptides and proteins forms the basis for developing therapeutic interventions against bacterial and viral diseases (4,5). Since typically the biologically active membrane-protein or peptide functions only in the membrane environment, it is critical to have an understanding of the membrane-bound structure. However, despite significant advances in experimental techniques, only a limited number of membrane-protein structures have been experimentally determined (6). The same experimental bottlenecks exist for small, membrane-bound peptides. In addition, these peptides may also undergo large conformational changes as part of the natural membrane-insertion process. The structure and dynamics of membrane-bound peptides have been partly investigated experimentally by studying the insertion process of carefully designed small synthetic peptides (7,8). For these types of studies, atomic-detailed molecular dynamics (MD) simulation techniques represent a valuable complementary methodology to investigate membrane-insertion of peptides (7). Thus, computer simulations of membrane insertion of peptides have been performed based on various models of membranes and proteins ranging from full all-atom to coarse-grained models with different levels of complexities (9–14).

There are two conflicting views on the mechanism of the membrane insertion of peptides. One view is that the peptide folds from an unstructured solvent state to a helix at the membrane interface before the insertion. This avoids the high energetic cost of desolvating the hydrogen bonds of the peptide backbone in solution before the peptide associates with the hydrophobic membrane (8). The other view holds that the peptide will fold into a helix once inside the membrane. This view is based on the results of a replica-exchange MD (REMD) simulation (15) of a WALP16 synthetic model peptide with explicit solvent and lipid-bilayer molecules, where interface folding was not observed (11). This mode of insertion and intramembrane folding was accompanied by a large increase in the system entropy, which compensated for the desolvation penalty (11). The membrane-insertion mechanism of the individual peptide may be dependent on its amino acid sequence composition. However, it is not sufficient to predict the preferred membrane-insertion mechanism of the individual peptide with the sequence data alone. A more extensive study with a diverse set of model peptides is needed to reach a general conclusion on the mechanism of the membrane-insertion process.

The M2 protein from influenza A virus is an essential component of the viral envelope and forms a four-helix bundle that exhibits a highly selective, pH-regulated, proton ion-channel activity. The influenza A virus enters the infected cell by endocytosis, and the interior of the virion must be acidified while it is contained in the endosome as a prerequisite for uncoating (release of genetic material to the cytoplasm) (16). The proton channel formed by the M2 proteins provides this acidification function and is a potential therapeutic target (16). The M2 transmembrane peptide (M2-TMP) is a truncated, synthetic peptide consisting of 25 amino acids spanning the transmembrane domain of the original 97-amino-acid M2 protein. The sequence of the M2-TMP is modeled as SSDPLVVAASIIGILHLILWILDRL (17). This sequence is effectively hydrophobic but contains hydrophilic anchoring residues aspartate (D) and arginine (R) at the ends. Although the truncated C- or N-terminal regions of the full-length M2 protein undoubtedly play important roles in the viral life cycle, an ion channel activity was demonstrated with the truncated M2-TMP (16,17). Recently, Stouffer et al. (18) determined the high-resolution structure of the M2-TMP in the presence of an amantadine-like inhibitors with x-ray crystallography. In a companion article, Schnell and Chou (19) used NMR techniques to determine the channel structure of a slightly differently truncated version of the M2 protein. Both structural assemblies share general structural features of the M2 channel, such as a four-helix bundle state. However, they also show significant differences in structural details related to the amantadine inhibition mechanism. Further structural studies need to be carried out to resolve these differences. Additionally, the M2-TMP four-helix bundle has been studied by explicit atomistic MD simulations with carefully chosen initial starting configurations to address issues regarding structure and dynamics of the bundle in the membrane (20–22). These studies did not address the stability of the four-helix bundle in the membrane interface. In contrast, Bu et al. (23) used an implicit solvent/membrane models to determine the optimal aggregation number of helices in the membrane. Even though the M2-TMP tetramer is more relevant to the biological function of the proton channel, the M2-TMP monomer in the membrane environment has been studied experimentally (24) and computationally (12–14,25) to understand its structure and dynamics in the absence of multimeric interactions. In these computational studies, the M2-TMP was either preinserted into the membrane (12,25) or its backbone was fixed to the helical configuration (13,14). However, missing from these studies is the complete picture of the structural and energetic changes undergone by the M2-TMP upon penetrating the membrane from an aqueous solution.

Here, we report an extensive MD simulation study of the insertion of the M2-TMP into a membrane. Different initial conditions, replica exchange (15), and biased sampling techniques with peptide position restraints (umbrella sampling) have been used to ensure sampling of sufficient conformations. This is done to avoid trapping the system in local minima and to ensure that enough conformations of the M2-TMP are sampled at all locations across the membrane interface. Im and Brooks (9) contemplated the use of REMD simulations combined with umbrella sampling to obtain membrane-insertion free-energy peptide profiles. Recently, MD simulations employing an extensive two-dimensional (2D) biased-sampling technique with explicit solvent/membrane representation were performed to study the thermodynamic stability of a charged arginine in a transmembrane helix (26,27). Similarly, the distribution of individual amino acids in explicit solvent and lipid bilayer was studied using umbrella sampling techniques (28,29). We find that it is essential to include both biased and REMD samplings to obtain a reliable description of the membrane-insertion process for the case of the M2-TMP. Indeed, all simulations except those that employed the REMD simulation combined with the umbrella sampling displayed deficiencies in the sampling of the peptide conformation of the M2-TMP. To gain an understanding of the mechanism of membrane insertion of the peptide, we calculated the potential of mean force (PMF) (30), or the Helmholtz free energy, of the peptide insertion. We find that, at the global free-energy minimum, the M2-TMP is a fully inserted helix with a tilt angle with respect to the membrane normal closely matched to the experimentally measured value. In addition, we find that there is a significant free-energy barrier for the nonhelical peptide to insert into a membrane from the aqueous phase commensurate with the traditional view of peptide insertion. The constructed free-energy surface also reveals an entropic barrier for the transfer from the aqueous solution to the fully formed helix spanning the membrane.

MATERIALS AND METHODS

MD simulations were performed with the CHARMM MD simulation program version c31b2 (31). We used the all-atom CHARMM 22 force field with CMAP modification for proteins (32,33). The membrane and the water solvent were represented by an implicit membrane/solvent model implemented in the “Generalized Born with a simple SWitching” (GBSW) module of CHARMM (25). The implicit membrane model has been successfully applied to study membrane insertions of various model peptides (9). The membrane thickness of 25 Å, a membrane smoothing length of 5 Å, and the surface tension coefficient of 0.04 kcal/(mol Å2) were used to represent the dimyristoylphosphatidylcholine (DMPC) membrane unless specified otherwise (9,25). The DMPC was chosen because it is typically used in experimental studies of the M2-TMP system (34).

Initial structures of the M2-TMP for simulations were taken from either a fully extended conformation or an ideal α-helix structure as determined by solid-state nuclear magnetic resonance (NMR) techniques (34). These starting structures were optimized by energy minimization with a distance-dependent dielectric constant of ɛ = 4r that included 50 steps of initial steepest-descent minimization followed by minimization with the implicit membrane model over 200 steps. During the minimization, Cα/Cβ atoms of all residues were restrained to their initial positions with a force constant of 0.5 kcal/mol, except for the last 100 steps. The resulting minimized conformations were used as starting structures of the subsequent MD simulations.

A time step of 2 fs was used in the MD simulations. Langevin dynamics with a friction coefficient of 5.0 ps−1 was used for the temperature control (9). Covalent bonds between the heavy atoms and hydrogens were constrained by the SHAKE algorithm (35). Distances used for the onset of a switching function for nonbonded interaction, the cutoff for nonbonded interactions, and the cutoff for nonbonded list generation were 20, 22, and 25 Å, respectively. Coordinates were saved at every 1 ps for further analysis. We performed REMD simulations (15) by running the CHARMM MD simulation program with the Multiscale Modeling Tools for Structural Biology (36). Temperatures used for REMD simulations were 32 temperatures exponentially spaced over the range from 300 to 800 K unless specified otherwise. The exchange of the conformations in neighboring temperatures was attempted at every 500 time steps (1 ps) according to the Metropolis criterion.

In simulations with the peptide-position biasing, the Z-component of the center-of-mass position of the peptide with respect to the membrane center was restrained by the harmonic potential with a force constant of 2 kcal/(mol Å2) using the GEO command in the Miscellaneous Mean Field Potential module in CHARMM. The Z-axis is defined as an axis oriented parallel to the membrane normal with the membrane center as its origin, so that the membrane with the thickness of 25 Å used in our study is bound by two planes at Z = ±12.5 Å. The applied force constant was found to give overlapping histograms of the peptide Z-positions for all neighboring Z-position biased systems. The weighted histogram analysis method (WHAM) (37) described by Gallicchio et al. (38) was used to remove biases due to temperatures or peptide positions and obtain PMF or free-energy profiles of membrane insertion of the peptide. The statistical uncertainties in the WHAM analysis were also estimated by the procedure outlined in Gallicchio et al. (38). We calculated the PMF as 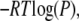Inline graphic where P is a probability distribution as a function of the root mean-square distance (RMSD), the Z position of the peptide, or the tilt angle at temperature T obtained from the WHAM analysis, and R is the ideal gas constant in units of kcal/mol/K. The RMSD between two structures is defined as the square root of the minimum average square distance between respective backbone atoms of the two structures with respect to all rigid body rotations and translations (39). The RMSD was calculated with respect to the α-helix structure determined by solid-state NMR techniques (34) unless specified otherwise. The tilt angle was defined as an angle between the long axis of the peptide, as determined from the inertia tensor, and the membrane normal.

The durations of the simulations performed in this study were as follows: The REMD simulation of the M2-TMP in aqueous solution lasted 5 ns. REMD simulations of the fully extended M2-TMP preinserted in the membrane and placed outside the membrane lasted 30 and 40 ns, respectively. We performed 81 5-ns MD simulations of the M2-TMP using a helical starting configuration with its center-of-mass Z-position restrained at locations ranging from Z = 0 Å to 40 Å in 0.5-Å increment. For the 31 systems restrained between Z = 0 Å and 15 Å, we performed additional 4-ns REMD simulations. This was done to enhance sampling of the barrier regions of the free energy.

The temperature ranges used for unrestrained REMD simulations of a fully extended M2-TMP in the presence of the membrane were from 300 to 500 K when it was preinserted, and from 300 to 800 K when it was placed outside the membrane. The average acceptance ratios for the replica exchange during the last 10 ns of production runs were 77% and 57% for the narrower and wider temperature ranges, respectively. The numbers of round trips of replicas from the lowest temperature to the highest and back were 138 with the average round-trip time of 3.4 ns for the 30-ns REMD run with the preinserted M2-TMP, and 32 with the average round-trip time of 9.1 ns for the 40-ns REMD run of the M2-TMP started outside the membrane. All replicas were not distributed equally among the temperatures. However, every replica visited each temperature at least 23 times with the preinserted M2-TMP, and all the temperatures except for the lowest two were visited at least three times by every replica when the M2-TMP was placed outside the membrane.

RESULTS

We present our results in the following order: We first report on the solution structure of the M2-TMP using REMD simulations. This is followed by the results of REMD simulations to characterize the M2-TMP in the presence of a membrane. We then report on the calculation of the free-energy surface of the M2-TMP across the membrane interface using extensive REMD simulations combined with biased sampling techniques.

M2-TMP in aqueous solution

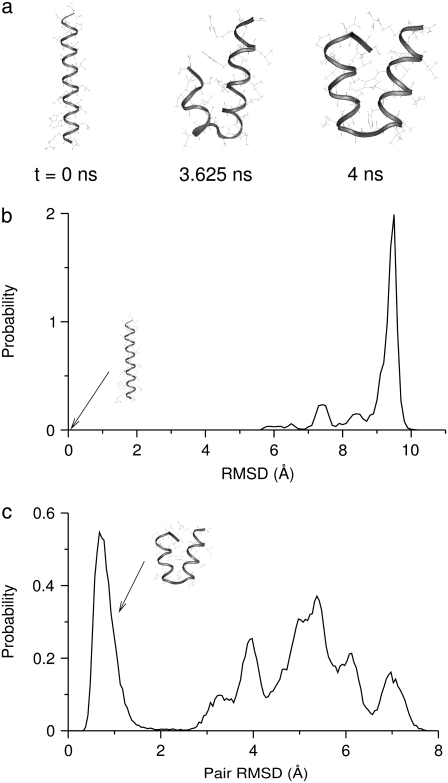
To understand the structural preferences of the M2-TMP in aqueous solution, we performed an REMD simulation of the peptide in the absence of a membrane. The water solvent was described implicitly with the GBSW model. This simulation was started from the helical conformation shown in Fig. 1 a and lasted 4 ns. The distribution of RMSD of structures at the room temperature of 300 K with respect to the initial helical conformation is shown in Fig. 1 b. This was calculated by performing the WHAM analysis on the data from the last 2 ns of the simulation. Snapshots and the RMSD distribution of the M2-TMP at room temperature shown in Fig. 1, a and b, indicate that the initial helical structure of the M2-TMP decays rapidly and is not present in any measurable quantity in the solution phase. To examine the structures of the M2-TMP in aqueous solution in more detail, we calculated the distribution of all pairwise RMSD between 400 structures randomly selected from the last 2 ns of the 300 K trajectory. This distribution is shown in Fig. 1 c, and its lack of uniformity is indicative of the presence of diverse solution structures. In particular, the distribution has an isolated peak at a pairwise RMSD of 0.7 Å, indicating that there may be a set of dominant structures. Indeed, it was found that 199 of the randomly selected 400 structures belong to a set of structures within a pairwise RMSD of 2 Å. This set includes the last configuration shown in Fig. 1 a. In this set of structures, the helicity is broken in the middle of the peptide sequence. The structure of the M2-TMP at 3.625 ns in Fig. 1 a shows a disruption of the helicity at a slightly different location of the peptide chain and belongs to the second-largest cluster with 38 structures whose pairwise RMSD are within 2 Å. However, there is a significant population of structures (163 out of 400) that are not part of these two main conformational groups, which indicates a diverse set of peptide conformations in solution. This is consistent with the experimental observations that many α-helical membrane peptides can exist in a variety of semi- or unstructured forms in aqueous solutions (40,41).

FIGURE 1.

FIGURE 1

Open in a new tab

(a) Snapshots of the M2 transmembrane peptide (M2-TMP) (sequence: SSDPLVVAASIIGILHLILWILDRL) from the REMD simulations in the implicit solvent at 300 K. The initial [time (t) = 0 ns] helical conformation corresponds to the experimentally determined structure. (b) The RMSD distribution of the M2-TMP in aqueous solution without the membrane obtained from the WHAM analysis on the last 2 ns of trajectories from the REMD simulation. The RMSDs are calculated with respect to the initial helical conformation. (c) The distribution of pairwise RMSD of 400 structures randomly selected from the last 2 ns of the 300-K trajectory. This distribution was calculated by forming all possible pairs between the 400 structures and calculating the RMSD for each pair. Almost half of the structures (199 out of 400) belonged to a cluster in which all members were within an RMSD of 2 Å from each other. This set includes the last configuration of the M2-TMP at 4 ns shown in a. The second-largest cluster (38 members) contains the configuration of the M2-TMP at 3.625 ns, shown in a.

M2-TMP in the presence of a membrane

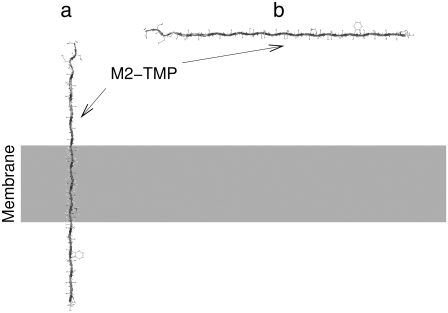
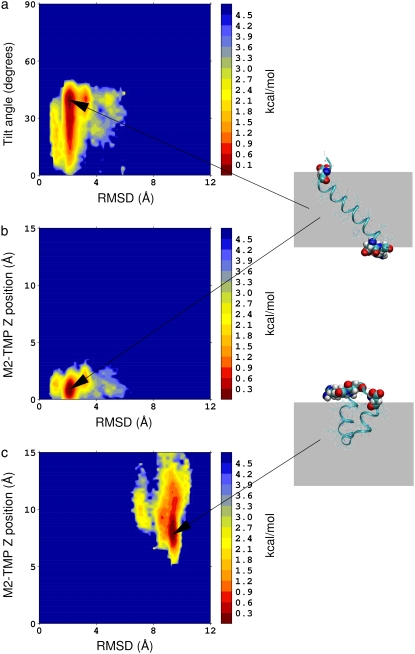
We performed MD simulations of the M2-TMP in the presence of a membrane with different initial conditions. However, we determined that simple applications of MD simulations at constant temperatures are not adequate to properly and efficiently sample intramembrane folding or membrane insertion of the M2-TMP. Therefore, we performed two REMD simulations starting from the fully extended peptide conformation: one preinserted perpendicularly into a membrane, and the other placed parallel outside the membrane as shown in Fig. 2, a and b, respectively. In the REMD simulation of the preinserted M2-TMP, we employed 32 temperatures ranging from 300 to 500 K and a membrane smoothing length of 0.6 Å. The temperature range and the membrane smoothing length were chosen to match those used in a previous REMD simulation by Im et al. (25) of the preinserted M2-TMP. Ulmschneider et al. (12) performed a replica-exchange Monte Carlo simulation of the same system, but with a different implicit membrane model. Our simulation lasted 30 ns, and the last 10 ns of the simulation were used for the analysis. It is important to note that extensive equilibrations are required in REMD simulations to avoid simulation artifacts (42). The PMF surface was constructed as a function of tilt angle and the RMSD from the helical structure. This is shown in Fig. 3 a. Similarly, the PMF surface was also calculated as a function of the Z-distance of peptide from the membrane center and the RMSD from the helical structure, as shown in Fig. 3 b. The most probable tilt angle in the PMF surface in Fig. 3 a is consistent with the experimentally observed value of 38° ± 3° in the DMPC membrane (34). It corresponds to the tilt angle needed to localize the charged groups of the helix to the membrane interface. The tilt angle is also in agreement with the 35° ± 2° observed in the recently determined crystal structure of the M2-TMP four-helix bundle (18). The PMF surfaces in Fig. 3, a and b, and examination of the configurations of the M2-TMP at the lowest temperature show that REMD simulations of the preinserted peptide converged to those of membrane-spanning helical conformation (RMSD = 0 Å), consistent with results of previous replica-exchange simulations (12,25).

FIGURE 2.

FIGURE 2

Open in a new tab

Two different starting configurations of the fully extended M2-TMP. (a) The M2-TMP is preinserted perpendicularly into the membrane. (b) The M2-TMP is initially placed outside but parallel to the membrane surface.

FIGURE 3.

FIGURE 3

Open in a new tab

PMF surfaces at 300 K calculated from the conformations generated by REMD simulations of the M2-TMP. (a) PMF surface as a function of the RMSD and tilt angle of the M2-TMP initially preinserted into the membrane. (b) PMF surface as a function of the RMSD and Z-position of M2-TMP initially preinserted into the membrane. A membrane-spanning configuration of the peptide is shown in atomic detail at right. The hydrophilic residues are drawn with atomic van der Waals spheres and are shown located at both sides of the membrane. (c) PMF surface as a function of the RMSD and Z-position of the M2-TMP initially placed outside of the membrane at a distance of 45 Å away from the membrane center. The minimum of the PMF is set to 0 by normalizing the probability distribution with the maximum probability. Here, a representative, trapped peptide conformation is shown with the hydrophilic residues at both ends of the peptide at the interface and the hydrophobic middle residues solvated in the membrane core.

In an attempt to simulate spontaneous membrane insertion of the M2-TMP from the aqueous solution, we also performed an REMD simulation of the M2-TMP initially placed 45 Å away from the center and parallel to the membrane in an initially fully extended peptide conformation, as shown in Fig. 2 b. In this REMD simulation, we employed 32 temperatures ranging from 300 to 800 K and a membrane smoothing length of 5.0 Å. The same set of parameters was used in REMD simulations of membrane insertions of other peptides with the same implicit membrane model (9). The simulation lasted 40 ns, and configurations from the last 10 ns were used for the analysis. We calculated a PMF surface as a function of the Z-position of the peptide and RMSD with respect to the helical conformation using the WHAM analysis. The PMF surface along with the last configuration of the M2-TMP at the temperature of 300 K is shown in Fig. 3 c. In this case, however, structures generated by the REMD simulation did not contain structures that were fully inserted into the membrane (Z = 0 Å), as seen by the lack of any conformations in the lower part of the PMF surface in Fig. 3 c. Instead, the REMD simulation generates bent conformations where the middle section of the peptide is inserted into membrane while the two end groups remain near the interface outside the membrane core, as shown by the van der Waals spheres at right in Fig. 3 c. This trapped conformation of the M2-TMP resembles the final solution structure shown Fig. 1 a with an RMSD of 3.5 Å. Both structures share a common motif of a U-shaped conformation even though the details of the structures differ. However, U-shaped conformations of the M2-TMP in the membrane interface and the solution are thought to have different origins. The U-shaped conformation of M2-TMP in the solution may arise from the interresidue hydrophobic interactions. The U-shaped conformation at the membrane interface is mainly due to the partitioning of hydrophilic end groups and hydrophobic groups between aqueous and membrane environments, respectively. According to hydrophobicity scales developed by Wimley and White (43) and more recently by Hessa et al. (44,45), both N- and C-terminal ends of the M2-TMP contain strongly hydrophilic residues Asp and Arg, whereas the middle section of the M2-TMP includes hydrophobic residues, e.g., Leu, Val, Ile, and Trp. Although these strong hydrophilic amino acid residues may play important roles in anchoring this peptide in specific position and tilt angle, they also appear to present a significant barrier to the full membrane insertion of this peptide in the current implicit membrane model. We also did not observe a spontaneous peptide insertion in an REMD simulation with the different smoothing parameter of 0.6 Å (results not shown). Our observations on the lack of spontaneous insertion are thus not strongly parameter dependent. A remaining question is whether we can identify the global conformation minimum from these two different peptide conformations shown in Fig. 3. The results up to this point suggest that a simple application of REMD simulation with temperature perturbation is not sufficient to overcome the problem of initial condition dependency and determine the global minimum structure of the peptide.

Free-energy REMD simulations with peptide-position biasing

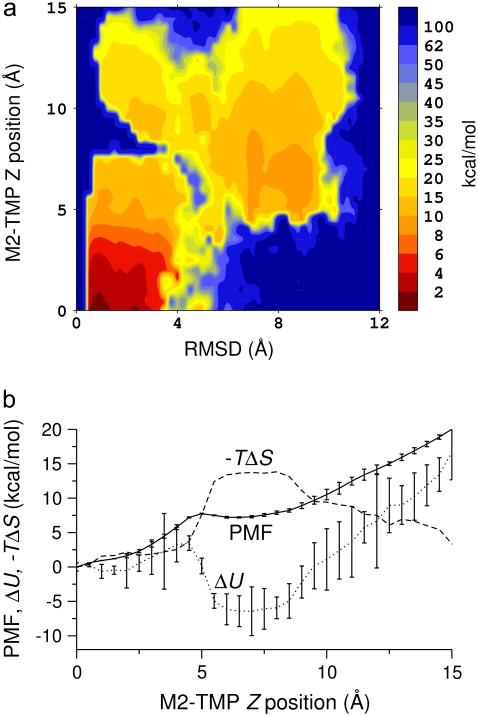
To avoid trapping the M2-TMP in local minima of the free-energy surface and to sample peptide conformations at a wider range of points across the membrane/water interface, we performed MD simulations of the M2-TMP with its center-of-mass Z-position restrained at multiple locations across the membrane interface. These simulations were started from the helical conformation based on the NMR experimental structure. The peptide was initially oriented parallel to the membrane interface. The center-of-mass Z-position of the peptide was restrained at 81 points across the membrane interface in intervals of 0.5 Å starting at the center of the membrane (Z = 0 Å) and ending at Z = 40 Å. Only the upper half of Z-positions (Z ≥ 0 Å) was considered because the peptide-membrane interaction is expected to be symmetric with respect to the membrane center. These MD simulations with peptide position restraints lasted 5 ns. Analysis of these MD simulations revealed a lack of sampling of peptide conformations characterized by the dependency on initial conditions. Therefore, to ensure proper samplings of peptide conformations of the M2-TMP across the membrane interface, we performed additional 4-ns REMD simulations starting from each of the restrained M2-TMP/membrane systems after 5-ns MD simulations. REMD simulations were not extended to points past Z = 15 Å since peptide conformations beyond this distance are not relevant to the membrane-insertion process. It is to be noted that conformations of the M2-TMP in the limit of large Z were sampled by the REMD simulation of the M2-TMP in aqueous solution as described above. The last 1 ns of REMD simulation trajectory was used for the analysis. We removed the biasing imposed by the Z-position restraints and calculated PMF surfaces as a function of Z-positions and RMSD with the WHAM analysis. The calculated free-energy surface in Fig. 4 a shows the relative free-energy change of each conformation with respect to the distance from the membrane center and the RMSD from the experimental helical conformation. At near Z = 15 Å, structures with large RMSD values are dominant, in agreement with the solution structure shown in Fig. 1 b. However, near the interface at Z = 10 Å, small and large RMSD values coexist with similar free energies. This surface shows that the global minimum conformation of the peptide is that of a fully inserted helix, as indicated by the favorable free-energy region at small RMSD near the membrane center. However, the free-energy surface also shows that there is a significant barrier, exceeding 90 kcal/mol, for the M2-TMP to fully insert into a membrane in a nonhelical peptide conformation. Indeed, the surface indicates that conformations starting outside the membrane are funneled into a secondary minimum corresponding to a set of nonhelical conformations trapped outside the membrane core (Z ∼7 Å, RMSD ∼9 Å). The PMF surface in Fig. 4 a also indicates that there are considerable kinetic barriers between the two conformations, i.e., the U-shaped-trapped and membrane-spanning conformations. For example, a structural transformation of the peptide from a nonhelical conformation to a near helical conformation at a peptide center-of-mass position of Z ∼7 Å followed by membrane insertion is associated with a free-energy barrier on the order of 50 kcal/mol. Fig. 4 a also indicates that there are narrow, lower-energy paths between the two conformations with a free-energy barrier on the order of 10 kcal/mol. However, these paths require specific peptide conformations at specific Z positions, and their significance may need to be checked with further simulations. Since there is no clear “path” in this energy surface between the two regions in the surface, the preceding REMD simulations were never able to switch between the conformations. The probability of traversing the barrier in a regular MD simulation without the biased potential is thus negligible, and traditional non-free-energy simulations will always show a strong dependence on the initial conformations.

FIGURE 4.

FIGURE 4

Open in a new tab

PMF at 300 K of the M2-TMP calculated from REMD simulations combined with the center-of-mass Z-positional restraints. The peptide center-of-mass Z-position is restrained at various locations extending from the center of the membrane to the point where Z = 15 Å at 0.5-Å intervals. The final PMF surface is pieced together from restrained simulations by the WHAM analysis. (a) PMF surface as a function of the M2-TMP's Z-position and RMSD with respect to the experimental helical conformation. The overall global minimum is seen as the dark red area in the lower left-hand corner and corresponds to a helical conformation spanning the membrane with the appropriate experimental tilt angle. (b) 1D energy profiles obtained by averaging the 2D probability distributions over all RSMD values. The PMF profile as a function of the Z-position of the M2-TMP clearly shows the overall hydrophobic attraction of the solvated peptide to the membrane, but it also shows a barrier to full penetration into the membrane core. The averaged potential energy (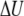Inline graphic) profile shows that the partially inserted trapped peptide is stabilized by the enthalpic component outside the membrane core, and that these states are more energetically favorable than a fully inserted peptide at Z = 0 Å. The entropic contribution (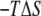Inline graphic) to the free-energy surface was calculated from the difference between the PMF and the ensemble average potential energy (PMF 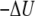Inline graphic). This graph clearly shows that the trapped states outside the membrane core are disfavored whereas the fully inserted peptide (which is experimentally observed) is favored. The statistical uncertainties in the PMF and the average potential energy profiles are twice the standard deviation estimated by the WHAM error analysis.

To look at the overall changes in energies, we constructed PMF profiles in only the Z-direction from the one-dimensional (1D) probability distribution of the peptide Z-position obtained by averaging the unbiased 2D probability distribution for all values of the RMSD coordinate. The free-energy profile along the Z axis with the estimated error from the WHAM analysis in Fig. 4 b clearly identifies a global minimum at Z = 0 Å and displays a shallow local minimum at around Z = 7 Å. This local minimum is reflective of the M2-TMP trapped outside the membrane core in a nonhelical conformation where the hydrophobic middle part of the peptide and the charged residues at the ends are attracted to the membrane core and the water phase, respectively. As the M2-TMP is further pushed in, the repulsion increases due to the loss of water solvation of the charged residues, and an effective free-energy barrier separating the global and local minima is created. This barrier is centered at around Z = 5 Å. The magnitude of the barriers in the 2D free-energy profile in Fig. 4 a appears more pronounced because of the detailed structural breakdown provided in the 2D profile. Once the peptide overcomes this barrier, it readily finds the global minimum at the membrane center where the hydrophobic middle and the charged residues at each end occupy the membrane core and the hydrophilic solvent, respectively. The potential energy profile along the Z-axis in Fig. 4 b shows that the overall minimum of the potential energy is located at around Z = 7 Å instead of at the membrane center, suggesting that the trapped configuration is energetically favorable. The fact that the fully inserted M2-TMP is at the global minimum is due to entropic components in the free energy. This is illustrated in Fig. 4 b, where we show the difference between the PMF and the internal energy, i.e., the entropic contribution (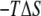Inline graphic) to the free energy. It is to be noted that this estimate of the entropic contribution does not include the contribution from the nonpolar solvation energy in the implicit solvent/membrane model. The U-shaped trapped conformation of the M2-TMP is favored by enthalpy but disfavored by entropy, whereas the membrane spanning helical conformation is actually disfavored by enthalpy but favored by entropy. The favorable entropic contribution to the free energy was also observed in a simulation study of the WALP16 peptide using an atomically explicit membrane model (11).

DISCUSSION

In this study, we performed extensive MD simulations of the M2-TMP at various positions across the membrane interface to study the membrane-insertion process of an atomically detailed peptide. The aqueous solution and the bilayer membrane itself were treated in the continuum approximation using a generalized Born model. To enhance samplings of peptide conformational states beyond those trapped in local minima, we performed REMD simulations with and without peptide positional restraints. REMD simulations without peptide positional restraints were able to find the experimental helical conformation of the M2-TMP when it was preinserted, but failed to show a spontaneous membrane insertion when the peptide was initially placed outside the membrane. Only by performing REMD simulations combined with peptide positional restraints were we able to identify the fully inserted M2-TMP helix as the global minimum state in the free-energy surface, which is in agreement with the experimental results. These findings underscore the importance and difficulties of sampling enough conformational states to obtain a meaningful and statistically significant free-energy surface from MD simulations.

There have been conflicting notions regarding the mechanism of peptide membrane insertion. The central question is whether the α-helix formation precedes the peptide insertion into a membrane or not. In the broadly accepted model (8), protein folding at the interface always precedes membrane insertion of proteins. However, a recent REMD simulation study (11) of membrane insertion of the WALP16 peptide using explicit solvent/lipids indicates that the interfacial folding is not required for bilayer insertion. The current result from the M2-TMP using an implicit membrane model suggests that the peptide would have difficulty penetrating the membrane in a nonhelical conformation due to a large free-energy barrier. It is possible that peptides, such as the M2-TMP, that have strongly hydrophilic groups follow different membrane-insertion mechanisms than the WALP16 peptide. It is also possible that detailed interactions of the peptide with explicit lipid headgroups and water molecules may be important in the initial stages of the peptide insertion to escape any trapped conformational state in local minima. In recent simulation studies of a charged arginine side chain in a transmembrane helix using an explicit atom representation of the lipid membrane and waters, it was shown that the charged side chain is significantly stabilized by favorable interactions with water molecules and lipid headgroups (26,27). It is suggested that the depolarization effects are overestimated in implicit membrane models that do not account for the flexibility of the membrane interface, and hence the effective barriers to hydrophilic peptide penetration are overestimated in such models (26,27,46). In the explicit atom simulations, the fluctuations of motions of lipids and water can create vacancies that can facilitate the membrane insertion of the peptide. However, performing fully atomistic simulations and employing extensive sampling techniques still remain a significant challenge. The implicit membrane model in conjunction with good sampling techniques can still provide insights into the peptide membrane-insertion process by capturing the gross physical features of the system. Improvements of the implicit membrane model with varying local dielectric coefficients across the membrane interface (47) could be used to further improve the implicit representation. Possible alternatives to either the costly explicit-membrane model or simplistic implicit membrane representations are various coarse-grained membrane models (48–52). Fine-tuning of the implicit membrane model with the results from simulations with explicit membrane/water would be highly desirable (28). The formation of multimeric complexes may also play an important role by facilitating self-solvation of hydrophilic peptide groups in the hydrophobic membrane environment. Further experimental and computational studies with a diverse set of peptides may be needed to arrive at any definitive conclusion on the mechanisms of membrane insertion of peptides. The results from this study of the membrane-insertion mechanism demonstrate that careful analysis of the simulations with proper samplings of conformational states is needed to obtain meaningful information from the simulations.

Acknowledgments

We thank Drs. E. Gallicchio and R. M. Levy for making their software code for the WHAM error analysis available to us.

Funding support for this work came from the Department of Defense High Performance Computing (HPC) Modernization Program Office under the HPC Software Applications Institute Initiative, the U.S. Army Medical Research and Materiel Command, and the Defense Threat Reduction Agency (grant 4.10011_07_RD_B to M.A.O.). Computational time was provided by the U.S. Army Research Laboratory Major Shared Resource Center and the Maui High Performance Computing Center.

The opinions or assertions contained herein are the private views of the authors and are not to be construed as official or as reflecting the views of the U.S. Army or of the U.S. Department of Defense. This article has been approved for public release with unlimited distribution.

Editor: Klaus Schulten.

References

  • 1.Poranen, M. M., R. Daugelavicius, and D. H. Bamford. 2002. Common principles in viral entry. Annu. Rev. Microbiol. 56:521–538. [DOI] [PubMed] [Google Scholar]
  • 2.Sandvig, K., and B. van Deurs. 2002. Membrane traffic exploited by protein toxins. Annu. Rev. Cell Dev. Biol. 18:1–24. [DOI] [PubMed] [Google Scholar]
  • 3.Yeaman, M. R., and N. Y. Yount. 2003. Mechanisms of antimicrobial peptide action and resistance. Pharmacol. Rev. 55:27–55. [DOI] [PubMed] [Google Scholar]
  • 4.Andreev, O. A., A. D. Dupuy, M. Segala, S. Sandugu, D. A. Serra, C. O. Chichester, D. M. Engelman, and Y. K. Reshetnyak. 2007. Mechanism and uses of a membrane peptide that targets tumors and other acidic tissues in vivo. Proc. Natl. Acad. Sci. USA. 104:7893–7898. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 5.Rusconi, S., A. Scozzafava, A. Mastrolorenzo, and C. T. Supuran. 2007. An update in the development of HIV entry inhibitors. Curr. Top. Med. Chem. 7:1273–1289. [DOI] [PubMed] [Google Scholar]
  • 6.White, S. H. 2004. The progress of membrane protein structure determination. Protein Sci. 13:1948–1949. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 7.Killian, J. A., and T. K. M. Nyholm. 2006. Peptides in lipid bilayers: the power of simple models. Curr. Opin. Struct. Biol. 16:473–479. [DOI] [PubMed] [Google Scholar]
  • 8.White, S. H., and W. C. Wimley. 1999. Membrane protein folding and stability: physical principles. Annu. Rev. Biophys. Biomol. Struct. 28:319–365. [DOI] [PubMed] [Google Scholar]
  • 9.Im, W., and C. L. Brooks. 2005. Interfacial folding and membrane insertion of designed peptides studied by molecular dynamics simulations. Proc. Natl. Acad. Sci. USA. 102:6771–6776. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 10.Lopez, C. F., S. O. Nielsen, G. Srinivas, W. F. DeGrado, and M. L. Klein. 2006. Probing membrane insertion activity of antimicrobial polymers via coarse-grain molecular dynamics. J. Chem. Theory Comput. 2:649–655. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 11.Nymeyer, H., T. B. Woolf, and A. E. García. 2005. Folding is not required for bilayer insertion: replica exchange simulations of an α-helical peptide with an explicit lipid bilayer. Proteins. 59:783–790. [DOI] [PubMed] [Google Scholar]
  • 12.Ulmschneider, J. P., M. B. Ulmschneider, and A. Di Nola. 2007. Monte Carlo folding of trans-membrane helical peptides in an implicit generalized Born membrane. Proteins. 69:297–308. [DOI] [PubMed] [Google Scholar]
  • 13.Ulmschneider, M. B., M. S. P. Sansom, and A. Di Nola. 2006. Evaluating tilt angles of membrane-associated helices: comparison of computational and NMR techniques. Biophys. J. 90:1650–1660. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 14.Ulmschneider, M. B., J. P. Ulmschneider, M. S. P. Sansom, and A. Di Nola. 2007. A generalized Born implicit-membrane representation compared to experimental insertion free energies. Biophys. J. 92:2338–2349. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 15.Sugita, Y., and Y. Okamoto. 1999. Replica-exchange molecular dynamics method for protein folding. Chem. Phys. Lett. 314:141–151. [Google Scholar]
  • 16.Pinto, L. H., and R. A. Lamb. 2006. The M2 proton channels of influenza A and B viruses. J. Biol. Chem. 281:8997–9000. [DOI] [PubMed] [Google Scholar]
  • 17.Duff, K. C., and R. H. Ashley. 1992. The transmembrane domain of influenza-A M2 protein forms amantadine-sensitive proton channels in planar lipid bilayers. Virology. 190:485–489. [DOI] [PubMed] [Google Scholar]
  • 18.Stouffer, A. L., R. Acharya, D. Salom, A. S. Levine, L. Di Costanzo, C. S. Soto, V. Tereshko, V. Nanda, S. Stayrook, and W. F. DeGrado. 2008. Structural basis for the function and inhibition of an influenza virus proton channel. Nature. 451:596–599. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 19.Schnell, J. R., and J. J. Chou. 2008. Structure and mechanism of the M2 proton channel of influenza A virus. Nature. 451:591–595. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 20.Zhong, Q. F., T. Husslein, P. B. Moore, D. M. Newns, P. Pattnaik, and M. L. Klein. 1998. The M2 channel of influenza A virus: a molecular dynamics study. FEBS Lett. 434:265–271. [DOI] [PubMed] [Google Scholar]
  • 21.Schweighofer, K. J., and A. Pohorille. 2000. Computer simulation of ion channel gating: the M-2 channel of influenza A virus in a lipid bilayer. Biophys. J. 78:150–163. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 22.Smondyrev, A. M., and G. A. Voth. 2002. Molecular dynamics simulation of proton transport through the influenza A virus M2 channel. Biophys. J. 83:1987–1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 23.Bu, L. T., W. Im, and L. I. Charles. 2007. Membrane assembly of simple helix homo-oligomers studied via molecular dynamics simulations. Biophys. J. 92:854–863. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 24.Kovacs, F. A., J. K. Denny, Z. Song, J. R. Quine, and T. A. Cross. 2000. Helix tilt of the M2 transmembrane peptide from influenza A virus: an intrinsic property. J. Mol. Biol. 295:117–125. [DOI] [PubMed] [Google Scholar]
  • 25.Im, W., M. Feig, and C. L. Brooks. 2003. An implicit membrane generalized Born theory for the study of structure stability and interactions of membrane proteins. Biophys. J. 85:2900–2918. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 26.Dorairaj, S., and T. W. Allen. 2007. On the thermodynamic stability of a charged arginine side chain in a transmembrane helix. Proc. Natl. Acad. Sci. USA. 104:4943–4948. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 27.Allen, T. W. 2007. Modeling charged protein side chains in lipid membranes. J. Gen. Physiol. 130:237–240. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 28.MacCallum, J. L., W. F. D. Bennett, and D. P. Tieleman. 2008. Distribution of amino acids in a lipid bilayer from computer simulations. Biophys. J. 94:3393–3404. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 29.MacCallum, J. L., W. F. D. Bennett, and D. P. Tieleman. 2007. Partitioning of amino acid side chains into lipid bilayers: results from computer simulations and comparison to experiment. J. Gen. Physiol. 129:371–377. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 30.Roux, B. 1995. The calculation of the potential of mean force using computer-simulations. Comput. Phys. Commun. 91:275–282. [Google Scholar]
  • 31.Brooks, B. R., R. E. Bruccoleri, B. D. Olafson, D. J. States, S. Swaminathan, and M. Karplus. 1983. CHARMM: a program for macromolecular energy, minimization and dynamics calculations. J. Comput. Chem. 4:187–217. [Google Scholar]
  • 32.MacKerell, A. D. 1997. Influence of magnesium ions on duplex DNA structural, dynamic, and solvation properties. J. Phys. Chem. B. 101:646–650. [Google Scholar]
  • 33.MacKerell, A. D., D. Bashford, M. Bellott, R. L. Dunbrack, J. D. Evanseck, M. J. Field, S. Fischer, J. Gao, H. Guo, S. Ha, D. Joseph-McCarthy, L. Kuchnir, K. Kuczera, F. T. K. Lau, C. Mattos, S. Michnick, T. Ngo, D. T. Nguyen, B. Prodhom, W. E. Reiher, B. Roux, M. Schlenkrich, J. C. Smith, R. Stote, J. Straub, M. Watanabe, J. Wiórkiewicz-Kuczera, D. Yin, and M. Karplus. 1998. All-atom empirical potential for molecular modeling and dynamics studies of proteins. J. Phys. Chem. B. 102:3586–3616. [DOI] [PubMed] [Google Scholar]
  • 34.Wang, J. F., S. Kim, F. Kovacs, and T. A. Cross. 2001. Structure of the transmembrane region of the M2 protein H channel. Protein Sci. 10:2241–2250. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 35.Ryckaert, J. P., G. Ciccotti, and H. J. C. Berendsen. 1977. Numerical integration of the cartesian equations of motion of a system with constraints: molecular dynamics of n-alkanes. J. Comput. Phys. 23:327–341. [Google Scholar]
  • 36.Feig, M., J. Karanicolas, and C. L. Brooks. 2004. MMTSB Tool Set: enhanced sampling and multiscale modeling methods for applications in structural biology. J. Mol. Graph. Model. 22:377–395. [DOI] [PubMed] [Google Scholar]
  • 37.Kumar, S., D. Bouzida, R. H. Swendsen, P. A. Kollman, and J. M. Rosenberg. 1992. The weighted histogram analysis method for free-energy calculations on biomolecules. I. the method. J. Comput. Chem. 13:1011–1021. [Google Scholar]
  • 38.Gallicchio, E., M. Andrec, A. K. Felts, and R. M. Levy. 2005. Temperature weighted histogram analysis method, replica exchange, and transition paths. J. Phys. Chem. B. 109:6722–6731. [DOI] [PubMed] [Google Scholar]
  • 39.Hummer, G., A. E. García, and S. Garde. 2000. Conformational diffusion and helix formation kinetics. Phys. Rev. Lett. 85:2637–2640. [DOI] [PubMed] [Google Scholar]
  • 40.Concannon, S. P., T. D. Crowe, J. J. Abercrombie, C. M. Molina, P. Hou, D. K. Sukumaran, P. A. Raj, and K. P. Leung. 2003. Susceptibility of oral bacteria to an antimicrobial decapeptide. J. Med. Microbiol. 52:1083–1093. [DOI] [PubMed] [Google Scholar]
  • 41.Heise, H., S. Luca, B. L. de Groot, H. Grubmueller, and M. Baldus. 2005. Probing conformational disorder in neurotensin by two-dimensional solid-state NMR and comparison to molecular dynamics simulations. Biophys. J. 89:2113–2120. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 42.Yeh, I.-C., M. S. Lee, and M. A. Olson. 2008. Calculation of protein heat capacity from replica-exchange molecular dynamics simulations with different implicit solvent models. J. Phys. Chem. B. In press. [DOI] [PubMed]
  • 43.Wimley, W. C., and S. H. White. 1996. Experimentally determined hydrophobicity scale for proteins at membrane interfaces. Nat. Struct. Biol. 3:842–848. [DOI] [PubMed] [Google Scholar]
  • 44.Hessa, T., H. Kim, K. Bihlmaier, C. Lundin, J. Boekel, H. Andersson, I. Nilsson, S. H. White, and G. von Heijne. 2005. Recognition of transmembrane helices by the endoplasmic reticulum translocon. Nature. 433:377–381. [DOI] [PubMed] [Google Scholar]
  • 45.Hessa, T., N. M. Meindl-Beinker, A. Bernsel, H. Kim, Y. Sato, M. Lerch-Bader, I. Nilsson, S. H. White, and G. von Heijne. 2007. Molecular code for transmembrane-helix recognition by the Sec61 translocon. Nature. 450:1026–1030. [DOI] [PubMed] [Google Scholar]
  • 46.Grabe, M., H. Lecar, Y. N. Jan, and L. Y. Jan. 2004. A quantitative assessment of models for voltage-dependent gating of ion channels. Proc. Natl. Acad. Sci. USA. 101:17640–17645. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 47.Tanizaki, S., and M. Feig. 2005. A generalized Born formalism for heterogeneous dielectric environments: application to the implicit modeling of biological membranes. J. Chem. Phys. 122:124706. [DOI] [PubMed] [Google Scholar]
  • 48.Goetz, R., and R. Lipowsky. 1998. Computer simulations of bilayer membranes: self-assembly and interfacial tension. J. Chem. Phys. 108:7397–7409. [Google Scholar]
  • 49.Izvekov, S., and G. A. Voth. 2005. A multiscale coarse-graining method for biomolecular systems. J. Phys. Chem. B. 109:2469–2473. [DOI] [PubMed] [Google Scholar]
  • 50.Marrink, S. J., A. H. de Vries, and A. E. Mark. 2004. Coarse grained model for semiquantitative lipid simulations. J. Phys. Chem. B. 108:750–760. [Google Scholar]
  • 51.Shelley, J. C., M. Y. Shelley, R. C. Reeder, S. Bandyopadhyay, and M. L. Klein. 2001. A coarse grain model for phospholipid simulations. J. Phys. Chem. B. 105:4464–4470. [Google Scholar]
  • 52.Shih, A. Y., A. Arkhipov, P. L. Freddolino, and K. Schulten. 2006. Coarse grained protein-lipid model with application to lipoprotein particles. J. Phys. Chem. B. 110:3674–3684. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES