Light Transmission in the Human Cornea as a Function of Position across the Ocular Surface: Theoretical and Experimental Aspects

Abstract

This article investigates the theoretical basis for differences in visible light transmission through the human cornea as a function of distance from the center. Experimentally, transmission decreases approximately linearly up to 3 mm from the central axis, then quadratically beyond this. It is known that collagen fibril number density and collagen fibril radii change from the central region to the corneal periphery. We modeled, using the direct-summation-of-scattered-fields method, the effects these ultrastructural changes would be expected to have on light transmission, accounting for the increase in corneal thickness from center to edge. Fibril positions for the modeling were obtained from electron micrographs of human cornea. Theoretically, transmission remains fairly constant across the central cornea; then, as the fibril diameter increases, the predicted scattering increases. Interfibrillar spacing changes alter the refractive index ratio between matrix and fibril; this was modeled in our theoretical deductions. Fibril number density had a minimal effect on light propagation. Our theoretical deductions were in broad agreement with our experimental data. It is concluded that the reduced transparency in the peripheral stroma is primarily caused by changes in fibril radius and an increase in refractive index ratio between the fibril and the interfibrillar substance.

INTRODUCTION

The transparent cornea at the front of the eye is the primary refractive component in the terrestrial visual system. It combines its interesting optical properties with great tensile strength and thus must have a structure that allows strength and transparency to be achieved simultaneously. From the front surface to the back surface, it can be divided into several layers. The thickest layer is the stroma, composed in the main of type I hybrid collagen fibrils. These fibrils are arranged in layers known as lamellae in which they run parallel to each other and to the corneal surface (Fig. 1). There are some 240 lamellae within the central human cornea (1–3). Although lamellae are arranged at all rotational angles throughout the depth of the cornea, there would seem to be preferential orientations (4,5) in which a larger proportion of fibrils lie in the inferior-superior and medial-lateral directions. The collagen fibrils are surrounded by an interstitial matrix of proteoglycans. These molecules are not thought to play a role in light scattering due to their small dimensions compared to the wavelength of light (6). The collagen fibrils in the central cornea possess a highly uniform diameter (∼32 nm in the human) and have a center-to-center interfibrillar spacing of ∼62 nm (7).

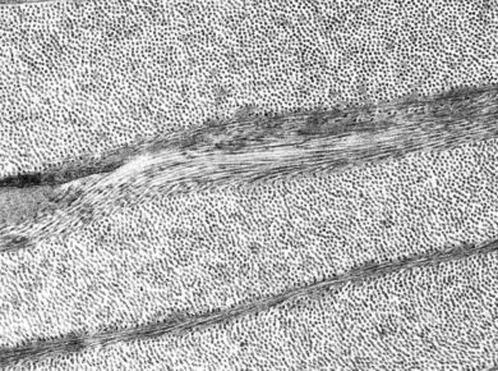
FIGURE 1.

Transmission electron micrograph of human cornea (courtesy of R. D. Young).

The corneal stroma also contains fibroblastic cells known as keratocytes. The density, volume, and size estimates of the keratocytes suggest that light traveling through the human cornea has to pass through up to 100 layers of these cells (8) Although these have the potential to affect light propagation (9), it has been suggested that, under normal circumstances, intracellular crystallin proteins act to match the overall refractive index of keratocytes to that of the stromal matrix. This delicate balance renders the cell cytoplasm transparent, with only the nuclei contributing to specular scatter (10). In an attempt to model scattering from keratocytes using classical theory, Hahn et al. (11) concluded that small changes in the refractive index of keratocytes probably underlie the development of corneal haze when the cornea is injured.

Maurice (2) was one of the first to attempt a solution of the problem of why a tissue containing light-scattering collagen fibrils is transparent. He proposed that the corneal collagen fibrils were arranged in a hexagonal lattice, and that the scattered fields from the fibrils would interfere destructively in all directions except that of the incident beam. When edematous, however, the fibrils would be perturbed from the perfect lattice and laterally scattered light would not be removed from the beam (2,12).

Subsequent electron microscopy studies have, however, indicated that the fibrils are not arranged in a perfect lattice. X-ray diffraction techniques have in fact suggested a liquid-like paracrystalline arrangement with some form of local order (13,14). Several mathematical formulations of corneal transparency have thus attempted to prove that the paracrystalline form seen in electron micrographs and implied by x-ray diffraction can give rise to transparency (6,15,16).

Despite the number of models proposed to explain corneal transparency, all the currently recognized paradigms accept that the crucial parameters affecting corneal transparency are:

1. Number density of collagen fibrils.

2. Collagen fibril diameter.

3. Refractive index differential between the interfibrillar or ground substance and the fibrils.

4. Stromal thickness.

5. Spatial ordering of the fibrillar array.

The effects of each of these parameters on light propagation through the cornea, and more comprehensive discussions of corneal transparency and light scattering by biological systems, can be found in the literature (17–20). It has been shown that several of the listed parameters do not stay constant across the cornea in relation to translational position from the central cornea to the limbus, the region where the cornea adjoins the white sclera. Both interfibrillar spacing and fibril diameter are found to show variation approaching the limbus (21,22), and the cornea thickens in the same region. To date, light scattering from the peripheral cornea has been neglected, despite the contribution of this region to peripheral vision. The current study, therefore, is designed to model the observed change in corneal transparency from the center to the limbus.

Measurement of corneal transparency

There are a small number of studies in the literature of the transmission spectrum of the cornea, whether it is being investigated as a tissue in isolation or in association with the other optically transparent tissues and fluids within the ocular sphere. Although adaptations of conventional spectrophotometry are most commonly used, it is possible to make estimations of transparency based on backscattered light in the confocal microscope (23–25). Optical coherence tomography can also be used to calculate backscattered light but these measurements may not be valid outside the central region (26). A blue-green argon laser has shown the human cornea to be 94% transparent when it is in vivo in an enucleated eye (27,28); however, these studies, although useful, utilized a detector mounted within the anterior chamber and as such may not be accurate because of a large contribution from scattered light.

Physiologically hydrated corneas absorb significantly in the ultraviolet and infrared because the aromatic amino acids of proteins absorb strongly at ∼300 nm (29) in the ultraviolet; the hydrated component of the cornea cause extensive infrared absorbance (30). Within the visible region of the spectrum there is generally no absorption, and scattering is minimal; specifically the relationship between optical propagation and wavelength is inverse-cubic (6,31). This wavelength dependence is thought to be indicative of a short-range ordering model of fibril distributions within the stroma. Long-range order models, which are based on hexagonal lattices (16), produce a fifth power inverse-wavelength dependence. By contrast, the wavelength dependencies of swollen corneas are found to differ, considerably in the case of severely edematous corneas, which have inverse-square wavelength dependence (31). It is also of note that recent transmission measurements on bovine cornea have shown that the inverse-cubic relation may not hold in the long wavelength region of the visible spectrum (32).

Calculation of corneal transparency

To evaluate the transmitted flux through a system of scattering cylinders embedded within a material of different refractive index it is necessary to know how the electric field scattered in every direction from each cylinder interferes with that scattered from its neighbors. These interference effects depend on the path lengths between each point. In a perfect lattice, these parameters are known exactly. In a quasi-ordered system such as the corneal stroma, it is necessary to turn to an alternative mathematical device to make the problem tractable.

The direct-summation-of-fields theory allows for the direct evaluation of the scattered electric field from each fibril with information on fibril positions obtained from electron micrographs (33). Assuming the cornea is structurally isotropic throughout, the result is extrapolated throughout the stroma. The interested reader is directed to the original article for a full mathematical discussion although it is of note that the model does not account for the cellular contribution to light scattering. Additionally, the cornea is modeled as a single lamella. This assumption is valid for calculating the total scattering cross section for unpolarized light (34).

This investigation utilizes the direct-summation-of-scattered-fields method of predicting corneal transparency (33) to model how the transparency of the cornea is expected to change in the peripheral regions of the stroma, with reference to the structural parameters obtained by synchrotron x-ray diffraction (21). Although a small decrease in transmission in the peripheral limbal regions was expected because of the increase in stromal thickness, the measured decrease in light propagation was greater than could be explained by thickness changes alone.

METHODS

Experimental samples

The project was approved by the NHS Research Ethics Committee and was carried out in accordance with the tenets of the Declaration of Helsinki. Human corneas with an intact scleral rim were obtained from the UK Transplant Service Bristol Eye Bank. These corneas were not suitable for transplant due to low endothelial cell count, and consent for their use in research projects had been given.

Sample preparation

All corneas were debrided of their endothelium and epithelium using laboratory razor blades and blotting paper. They were then equilibrated to physiological hydration using 20 kDa polyethylene glycol. The method is outlined in detail elsewhere (32,35,36). In brief, the corneas were dialyzed against 5 mM HEPES buffer, pH 7.4 containing 0.154 M sodium chloride, and polyethylene glycol (2.8% w/v). At the conclusion of transmission measurements, a 6 mm button was trephined from the central portion of each cornea. After weighing, they were heated at 60°C for a minimum period of 48 h before reweighing. Corneal hydration was determined from the wet and dry weights (Hydration = wet weight of tissue-dry weight of tissue/dry weight of tissue).

Transparency measurement

The method used to determine transmitted intensity in the visible region has been described previously (37). A model No. SP8-100 double-beam spectrophotometer (Pye-Unicam, Cambridge, UK) with detector half-angle acceptance of 3° and beam size adjusted to 1 × 1 mm was used to determine the transmitted light intensity through a corneal preparation clamped within custom-built sample chambers. Experimental specimen cells, with Perspex windows in the optical path, were constructed in the form of two half-chambers between which the cornea could be clamped and pressurized. The half-chambers were filled with silicon oil (cat. No. 200/5cS, Dow Corning, Midland, MI). Baseline readings were made from cells filled only with silicon oil and were recorded before each corneal measurement. Measurements from corneas were then expressed as a ratio of the transmission recorded to the baseline reading. The cell position in the beam path could be adjusted laterally by the aid of a Vernier scale and intensity measurements were thus recorded at 1-mm intervals radiating outwards from the apparent geometric center of the sample cells. If the optical center was found not to coincide with the geometric center, the results were laterally shifted. In this work, position 0 is the center; negative displacements are to the left of the central point and positive to the right when viewed relative to the incident beam direction. The sample cell was placed within the spectrophotometer such that the beam was perpendicular to the cell window at all times.

Theoretical calculations of transparency

An in-house computer program (20,38) based on a direct-summation-of-scattered-fields method (33) was used. The model required input files containing fibril coordinates and fibril radii. These were derived from extant electron micrographs of human corneal stroma, using a method outlined elsewhere (39). Here, we used the micrographs to obtain relative spatial positions of the fibrils; diffraction data free of shrinkage effects were used to obtain interfibrillar spacing and radius.

Knowledge is also required of how thickness and refractive indices change across the corneal surface. It is well understood that the cornea increases its thickness from ∼550 μm in the center to some 800 μm in the peripheral region. For the purposes of this work, more detailed mapping of corneal thicknesses was required. Optical coherence tomography data from the literature was used for this work (40). In our transmission measurements, since the incident light beam was not perpendicular to the corneal surface in the peripheral regions, a correction was applied to the thickness data to account for the exaggerated tissue thickness that the beam would traverse (here termed the optical thickness). This correction was achieved by a simple geometric model of two circles, with one of smaller radius enclosed within a larger one, thus supplying a basic model of the cornea (41). The equations of the circles were set such that a correct perpendicular thickness was achieved in the central and peripheral regions. It was then straightforward to determine a correction from perpendicular to optical thickness. The eccentricity of the cornea is not known accurately, but taking a value 0.42 (42) would lead to a maximum 10% underestimation of corneal thickness, which would have a negligible effect on transmission calculations using the summation-of-scattered-fields-method (20). The spherical approximation is therefore sufficient for our purposes, and the values appear to be consistent with measurements obtained from images of cornea and anterior segment obtained by OCT (40).

Variations in fibril diameters and interfibrillar spacing will lead to changes in the fibril volume fractions and therefore, changes in the refractive indices of the hydrated interfibrillar matrix. The refractive index of the interfibrillar matrix cannot be measured directly, but in principle, can be calculated from knowledge of the refractive index of the stroma as a whole (43). Using an Abbe refractometer, we attempted to measure corneal refractive index as a function of position but were unable to do so because of the relatively small size of the human cornea compared to the illuminating beam in the refractometer. Therefore, with the data of Boote et al. (21) and application of Gladstone and Dale's Law (43), appropriate refractive indices from the central cornea to the limbus were calculated as follows.

The first step was to measure the disorder parameter for the packing of collagen fibrils in the stroma. The volume associated with each fibril (V_s) is related to the center-to-center fibril spacing (i), thus

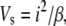(1)

where the constant of proportionality or disorder parameter (β), in the case of a crystallike arrangement of fibrils with Bragg scattering planes, relates the separation of the Bragg planes (d_B) to the center-to-center spacing, i:

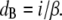(2)

Worthington (14) has derived the relationship among β, i, and the fibril number density, ρ:

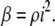(3)

Here, we have replaced his notation with our own, so β is 1/α and ρ is σ in his notation. The quantities i and ρ were determined from fibril radial distribution functions (6,44) obtained from three electron micrographs, two taken from the literature (45,46) and the third from Fig. 1 in the this article. An average value of β was then calculated as 1.06, which may be compared with Worthington's factor of 1.12 for liquidlike fibril arrangements.

Equations 1 and 2 indicate that 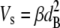and this can be combined with our measured value of the disorder parameter to give the volume fraction of hydrated collagen fibrils f_f,

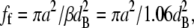(4)

where a is the fibril radius. The volume fraction of hydrated fibrils in the stroma f_f, the volume fraction of dry collagen molecules in a fibril f_m, and the volume fraction of dry fibrillar matter in the stroma f_c are related; thus,

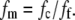(5)

Using f_c and f_f data in Leonard and Meek (43) for the average of 40 species, f_m is calculated to be 0.39. If the hydration state of the fibril remains constant as a function of position in the cornea (47), then f_m is constant, as this is dependent on molecular spacing within the collagen fibril (see Eq. 14 in (43)).

With known values for f_f and f_m for the central cornea, we can now turn our attention to formulating how the refractive indices will change away from the central axis. This can be simplified somewhat by assuming that the dry volume of extrafibrillar component remains constant, as does the hydration state of the collagen fibril. Changes in the fibril diameter are taken into account by changes in the fibril volume fraction f_f, so those changes will not need to be considered separately.

The total solvent or hydration fraction of the cornea (H) is given simply by (48)

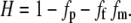(6)

Here, f_p is the volume fraction of dry nonfibrillar material in the stroma. By Eq. 5, the final term is simply f_c, the volume fraction of dry fibrillar material in the stroma. In the central cornea we can set H = 0.78, which corresponds to a physiological hydration of 3.2 (48). The other parameters are then known, and in the central cornea, we thus obtain f_p = 0.11.

Applying Gladstone and Dale's Law (20) to the central cornea, the total stromal refractive index n_S is given by

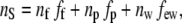(7)

where n_f is the refractive index of hydrated collagen, 1.416 (20); n_w is the refractive index of water, 1.333; n_p is the refractive index of the dry ground substance; and f_ew is the volume fraction of extrafibrillar water, which is given by 1 − f_p − f_f. The value of n_S is 1.375 (20). Using these formulae, a value of 1.501 is obtained for n_p.

If the volume of extrafibrillar material remains constant but the volume associated with each fibril (V_s) increases, then the volume fractions of the components change. This has no effect on the refractive index of the hydrated fibril but will affect the ground substance and total stromal refractive indices (see Eqs. 5 and 8 of (43)). The value of f_p will decrease and f_ew will therefore increase. This can be represented mathematically by

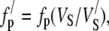(8)

where dashed quantities indicate states modified from that which exists in the central cornea. The value of V_s may be derived from the interfibrillar spacing using Eq. 1. The change in f_p is thus calculated as a function of position across the cornea. It is therefore fairly straightforward to calculate how the refractive index of the hydrated ground substance, n_g, changes, using Eqs. 4 and 8 together with Eq. 3 of Leonard and Meek (43):

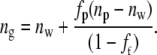(9)

The other experimental and mathematically derived ultrastructural parameters are illustrated in Table 1. The quantity m is the ratio between the refractive index of the fibril and that of the ground substance.

TABLE 1.

Ultrastructural parameters used for modeling stromal transmission

Position (mm)	Bragg spacing, db (nm)	Fibril diameter (nm)	ff	fp	few	ng	m
0	53.4	33.0	0.283	0.110	0.608	1.3585	1.042
1	54.1	33.0	0.276	0.107	0.618	1.3576	1.043
2	55.2	33.0	0.265	0.103	0.632	1.3563	1.044
3	57.0	33.0	0.249	0.096	0.655	1.3544	1.045
4	57.9	34.0	0.256	0.093	0.651	1.3539	1.046
5	62.7	35.5	0.238	0.080	0.683	1.3504	1.049

RESULTS

Measurement of corneal transparency

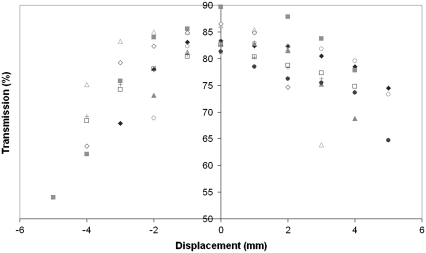
Fig. 2 shows the variation in transmission for 10 human corneas as a function of position in an arbitrary meridian across the surface. For ease of presentation, data for only one wavelength is presented (500 nm).

FIGURE 2.

Translational transparency for human corneas (n = 10) near physiological hydration at 500 nm.

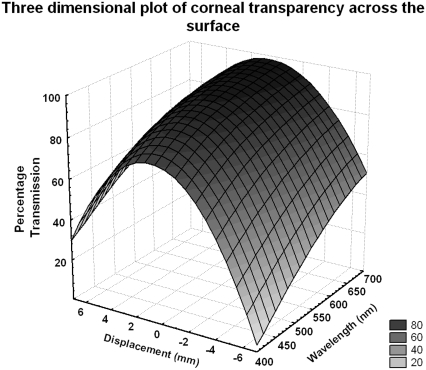
Fig. 3 shows, for a given cornea, a three-dimensional plot of position and wavelength versus intensity. It is quite noticeable that although the transmission decreases away from the center of the cornea, the wavelength dependence remains constant even at the far periphery.

FIGURE 3.

Representative three-dimensional plot of translational transparency versus wavelength across a meridian of the human cornea at physiological hydration (this cornea is represented in Fig. 2 by gray square points).

The data presented in Figs. 2 and 3 shows that transparency decreased at a gradual rate for ∼2–3 mm either side of the optical center point. Beyond this limit, the decrease in transparency became more rapid. It was also found that some corneas with inadequate scleral rim were displaced slightly within the sample chamber, causing the optical center to shift in relation to the geometric center of the cell. This is apparent in the results presented in Fig. 2 where there appears to be a degree of anisotropy between any two given meridians.

Since the exact orientations in which corneas were placed in the holder were unknown, the average of the two displacements either side of the optical center, shown in Fig. 4, was compared. Due to small variances in collagenous mass between samples, not all corneas achieved the same hydration end-point. The average end hydration was 3.3 ± 0.2. The actual range of hydrations extended from 3.0 to 3.8. The transmission properties of the cornea are relatively insensitive to hydration changes until the thickness increases beyond ∼25% of its normal value (31). Since hydration has a linear relationship to corneal thickness (49) we can calculate that our upper hydration of H = 3.8 is within this tolerance limit. To compare our results, the ensemble of transmission values for each cornea was normalized to a central corneal thickness of 550 μm, equivalent to a hydration of 3.2 according to the methods of Farrell and McCally (17) and Farrell et al. (31).

FIGURE 4.

Transparency at 500 nm as a function of radial distance from the optical center of the cornea (n = 10 for positions 0–4 mm, n = 3 for 5 mm, error bars are standard deviation, and fit line is a quadratic function).

From Fig. 4, we can see that the transmission observed off central axis decreases approximately linearly up to 3 mm, with a more rapid rate of change beyond this point.

Modeling transmission in the human cornea

Corneal transmission was computed using average ultrastructural parameters derived from the study of Boote et al. (21), by further averaging both raster scan directions, from center to 5 mm displacement. Stromal thicknesses were corrected to actual optical depth traversed by a beam incident on and parallel to the central optical axis, and the refractive indices calculated in Table 1 were used. Relative fibril positions were measured from several micrographs and the predictions made were based on an image from our laboratory (Fig. 1), and two published images (45,46) of a normal human cornea. The average fibril spacing (determined by the radial distribution function) and fibril radius in the micrographs were set to the parameters in Table 1 with the aid of a simple scaling algorithm.

It is of note from Table 2 that corneal transmission remains relatively constant across the central, prepupillary cornea, covering some 3 mm from the optical center. Beyond this point, as the fibril diameter starts to increase approaching the limbal region, the scattering increases. It has been shown previously that changes in organization between anterior and posterior collagen fibrils affect the transmission predicted by the direct sum method, and recognized that these may in themselves be artifacts of the hydration at which the samples were held before fixation (50). However, using the average of the three transparency predictions for physiologically hydrated corneas, the decrease in transmission from optical center to the limbal region was calculated to be 9.7 ± 1.2%.

TABLE 2.

Theoretical and experimental transmission values compared at 500 nm

		Theoretical transmission				Experimental average transmission (error ± SD)
Position (mm)	Optical depth (μm)	Fig. 1	Muller et al.	Komai and Ushiki	Average (error ± SD)
0	550	89.6	87.1	89.1	88.6 ± 1.3	87.1 ± 2.0
1	590	88.9	86.0	88.5	87.8 ± 1.6	85.7 ± 2.1
2	605	88.7	85.6	88.3	87.5 ± 1.7	84.8 ± 2.9
3	645	86.7	84.1	87.7	86.1 ± 1.9	82.0 ± 3.1
4	760	84.5	81.0	84.1	83.2 ± 1.9	78.7 ± 4.5
5	800	79.5	76.1	81.0	78.9 ± 2.5	72.9 ± 5.9

DISCUSSION

From both experimental and theoretical standpoints our findings indicate that there is a reduction in absolute transmitted intensity through human corneas as a function of distance from the optical center. It was therefore of interest to determine the cause of this decrease and how it relates to ultrastructural observations. Corneal thickness is known to increase at the periphery, and although this will increase transmitted intensity losses, we have previously shown that in bovine corneas this is incompatible with the observed data, even after correction for nonnormal incidence (37). Two main possibilities are suggested:

1. Increased specular scattering.

2. Ultrastructural changes.

Although it is known that the keratocyte density increases toward the peripheral and limbal zones (51) in the normal cornea, the excess contribution that these cells would make to specular scattering is unknown, but considered to be small.

In analyzing the relationship between ultrastructural changes and transmission, the transparency of the stroma can be explained by reference to (33)

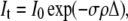(10)

where I_t and I₀ are the transmitted and incident intensity, respectively, σ is the total scattering cross section per fibril, ρ is the number density of fibrils, and Δ is the optical path length, or the actual thickness of stroma traversed by an incident beam. It is easiest to investigate the effects of ultrastructural parameters by reference to Eq. 10 and to the differential scattering cross section per unit length for an individual fibril formulated as in the equation below (33),

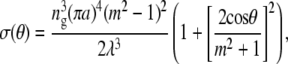(11)

where symbols have their usual meanings and λ and θ represent the photon wavelength and the scattering angle, respectively.

When the interfibrillar spacing is increased, it of course follows that the fibril number density ρ decreases. Mathematically, this is evidenced by the equation relating density to interplanar separation, which may be derived from Eqs. 2 and 3 above:

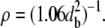(12)

By using Eq. 12 on the ultrastructural data presented in Table 1, it can be shown that fibril number density decreases by ∼27% from the center to the far periphery. Using Eq. 10, it can be shown that the lower fibril number density is sufficient in the peripheral regions to mathematically cancel out much of the effect that the increase in corneal thickness has on light propagation through the stroma.

X-ray diffraction data has suggested that fibril radii increase by a modest amount (21) and it is mathematically straightforward to show the impact that this may have on visible light propagation with the aid of Eq. 11. In doing so, it is noted from Eq. 11 that fibril radius is expressed by a fourth-power term. Assuming a 1-nm diameter increase, the fourth-power radial dependence term in Eq. 11 will cause a 22% increase in the differential scattering cross section per length. The increase in fibril radius thus has a great effect on light propagation through the stroma, and under numerical analysis seems to be the source of the quadratic decrease in transmission as a function of position seen in the peripheral regions.

There is one additional factor that must be accounted for in this formulation, and this is the relative refractive index between the hydrated fibrils and the interfibrillar matrix. In this article, a simplified model was developed which assumed that volumetrically the amount of extrafibrillar material remains constant as the unit cell dimensions expand.

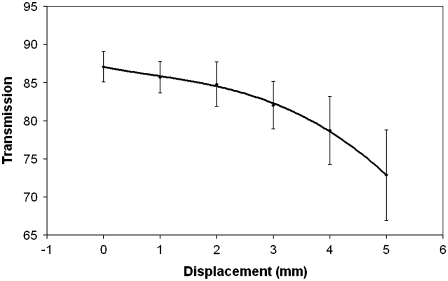
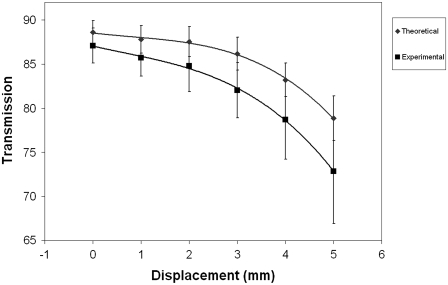
It was found experimentally that the transmitted intensity showed only a gradual decrease across the central, prepupillary zone, which is some 3 mm in diameter. This was consistent with our theoretical deductions, and by reference to Tables 1 and 2, it can be seen that the experimental and predicted transmitted light fractions are similar. Outside the central zone, as the fibril radii start to increase, scatter increases. Experimentally, an average decrease of ∼14% in light propagation is observed going from the central optical axis to a displacement of 5 mm at the periphery. The 9.7% change predicted by theory is consistent with the standard deviations of the experimental results, as illustrated in Fig. 5.

FIGURE 5.

Theoretical deduction compared with experimental measurement of corneal transparency across the corneal surface at 500 nm. Error is ±SD; fit lines are quadratic functions.

Although the theoretical and experimental analyses here are comparable, they do not coincide exactly. There are a number of explanations for this. First, it is necessary to apply the caveat that we can compute the transparency only for a small segment of one cornea assuming that the spatial ordering is homogeneous throughout the whole path length; we have, however, attempted to account for this by analyzing more than one micrograph from several sources. It must also be noted that theoretical computation is from average parameters; there is some, albeit quite small, variance in structural parameters between different individual corneas. We have previously commented on a possible anisotropy of light propagation between any two given meridians of a stroma radiating outwards from the optical center (37). Since, in the experiments described, we are unable to place human corneas with a known orientation in the holder, this anisotropy leads to a large standard deviation in our results.

Our simplified model of corneal refractive indices assumes that the amount of proteoglycan and other interfibrillar proteins in the cornea is constant and not a function of position. However, it is known that proteoglycan concentration is reduced by 24% peripherally compared to the center (22). If we account for this in our model by altering the value of f_p, the decrease in transmission from center to 5 mm would be 12%, and closer to our observed experimental decrease. Unfortunately, because it is difficult to relate Borcherding's experimental zones (22) to the equatorial scans performed in this work, further correction of our theoretical deductions are prohibited. However, this may explain some of the remaining difference between theoretical and experimental values.

It was pointed out earlier that keratocyte cell density increases in the periphery. The human corneas used in this study were likely to contain some dead keratocyte cells, which essentially form voids in the stroma, which in turn act as Mie scattering points; this could therefore further contribute to the divergence between experiment and theory.

It is obvious that nonnormal incidence effects will occur on the collagen fibrils in the periphery, especially in certain lamellar orientations. The effects this will cause are unclear; adjustment of the direct-summation-of-scattered-field's model is beyond the scope of this work. It must be remembered that the algorithms used to predict transparency (33) are, in effect, utilizing two-dimensional projections of the fibril distribution and thus the angle of incidence is a parameter, which is not implicit. Nonnormal incidence effects are difficult to avoid even in the central region under normal incidence due to undulations in the lamella (52), and in any spectrometry investigation on the corneal stroma, these effects will also occur due to the size of the beam. An examination of the scattering theory for an infinitely long dielectric cylinder (53) shows us that, in oblique incidence, additional components are generated which are dependent on the incident angle. It is crucial to understand that nonnormal incidence angles will only be large for a small number of lamellar orientations even in the far peripheral regions. The total intensity signal of a dielectric cylinder at nonnormal incidence as a function of scattering angle is known (54). Specifically, it is known that as the angle of incidence deviates from the perpendicular, the scattered intensity as a function of angle becomes smoother and the distribution of scattered light resembles that from a cylinder of smaller radius (if the total signal from 0° to 180° is analyzed). The scattering in the forward direction, however, would appear to be largely unaffected, with high angle components having the greatest degree of perturbation from the form at normal incidence. It would seem that if nonnormal incidence effects were significant, the x-ray diffraction method for deriving fibril radii would be unusable on the peripheral cornea; however, the determinations by this method (21) are known to be consistent with those obtained from electron microscopy (22).

In conclusion, we have investigated how corneal transparency changes away from the central axis and shown that the observed decrease is much greater than would be expected if the transmission decreased purely as a function of thickness. Using the direct-summation-of-scattered-field's method, we have also shown that the decrease in the peripheral regions is explained by reference to the increase in fibril diameter and the scaling of refractive indices caused by the increase in interfibrillar spacing. A better fit between experiment and theory is obtained when the proteoglycan concentration changes in the peripheral regions are accounted for.