A musculoskeletal model of the upper extremity for use in the development of neuroprosthetic systems

Abstract

Upper extremity neuroprostheses use functional electrical stimulation (FES) to restore arm motor function to individuals with cervical level spinal cord injury. For the design and testing of these systems, a biomechanical model of the shoulder and elbow has been developed, to be used as a substitute for the human arm. It can be used to design and evaluate specific implementations of FES systems, as well as FES controllers. The model can be customized to simulate a variety of pathological conditions. For example, by adjusting the maximum force the muscles can produce, the model can be used to simulate an individual with tetraplegia and to explore the effects of FES of different muscle sets. The model comprises six bones, five joints, nine degrees of freedom, and 29 shoulder and arm muscles. It was developed using commercial, graphics-based modeling and simulation packages that are easily accessible to other researchers and can be readily interfaced to other analysis packages. It can be used for both forward-dynamic (inputs: muscle activation and external load; outputs:motions) and inverse-dynamic (inputs: motions and external load; outputs: muscle activation) simulations. Our model was verified by comparing the model-calculated muscle activations to electromyographic signals recorded from shoulder and arm muscles of five subjects. As an example of its application to neuroprosthesis design, the model was used to demonstrate the importance of rotator cuff muscle stimulation when aiming to restore humeral elevation. It is concluded that this model is a useful tool in the development and implementation of upper extremity neuroprosthetic systems.

1. Introduction

Neuroprosthetic systems restore function after spinal cord injury (SCI) using a combination of functional electrical stimulation (FES) and reconstructive surgeries such as tendon transfers (Keith and Lacey, 1991). An FES system consists of a controller that outputs the muscle excitations needed for a particular task and electrodes that deliver the stimulation to the appropriate paralyzed muscles. Upper extremity neuroprostheses to date have focused on restoring hand function in individuals with mid to low cervical level injuries (C5–C8), using open loop controllers that are tuned and tested using trial and error (Keith et al. 1988, Kilgore et al. 1989). However, purely experimental methods are inefficient in cases of high cervical level injuries (C1–C4), where almost all voluntary muscle function below the neck is lost. In these cases, there are a large number of shoulder and elbow muscles that must be controlled by the neuroprostheses, many of which generate moments about two or more degrees of freedom. For example, the biceps muscle originates on the scapula and inserts on the radius, which means it crosses the glenohumeral, humero-ulnar, and radio-ulnar joints. As a result, the task of determining which muscles to stimulate and developing appropriate control schemes becomes more complicated. Trial and error techniques would require extensive testing of all possible muscle combinations, a time-consuming process for both the researcher and the FES participant. The use of a musculoskeletal model can facilitate the design and testing of the system, minimizing the inconvenience to the subjects.

There have been a number of computer models of the shoulder developed in the last few decades, and most of them are strictly inverse. The first models were two-dimensional, restricted to single-motion patterns, and did not include all the shoulder muscles (DeLuca and Forrest 1973, Dul 1987). There are very few three-dimensional models, mostly because of the complexity of the shoulder mechanism. The “Swedish” shoulder model was developed by Karlsson and Peterson, based on morphological measurements by Hogfors et al (Karlsson and Peterson 1992, Hogfors et al. 1987). The “Delft” model, by van der Helm, is based on morphological data from Veeger et al (van der Helm 1994, Veeger et al. 1991, 1997). The “Newcastle” shoulder model, described by Charlton and Johnson, is based on data from Johnson et al., van der Helm and Veeger (Charlton and Johnson 2000). The only forward model developed to date, by van der Helm and Chadwick, is still under development and has very slow simulation speed (van der Helm and Chadwick 2002).

In this study, a new model of the shoulder and elbow was developed that can be used for both inverse and forward dynamic simulations, thus providing a complete description of the upper extremity. Verification of the model was achieved in an inverse dynamic manner, by correlating the EMG activity in different muscles during arm movements performed by able-bodied individuals, to the activation patterns predicted by inverse dynamic simulations using the model. Finally, an example of the model use in neuroprosthesis design is presented. The model was adjusted to simulate a C3 SCI individual, and the effect of two different sets of stimulated muscles in the performance of a humeral abduction movement was investigated.

2. Methods

2.1 Model Construction

The muscle and joint parameters for the model were obtained from cadaver studies by Klein-Breteler et al (1999). These parameters include the position of joint centers, inertial parameters for body segments, the number of elements representing each muscle, and the optimal fiber length, origin and insertion, tendon slack length, physiological cross-sectional area and pennation angle of every element.

The software used to create the model was SIMM (Musculographics, Inc.), a graphics-based system developed especially for musculoskeletal modeling. The model consists of six bones (sternum, clavicle, scapula, humerus, ulna and radius) and five joints (sterno-clavicular, acromio-clavicular, glenohumeral, humero-ulnar and radio-ulnar). The three joints at the shoulder are ball joints, with three degrees of freedom each, while the elbow and forearm joints are one-degree-of-freedom, single-axis joints. The model includes the so-called scapulothoracic gliding plane (van der Helm 1994), which means that the medial border of the scapula is constrained to maintain contact with the thorax.

The muscles are represented by one or more elements, depending on their size and the width of their attachment site (Table 1). The model includes 29 muscles, with a total of 138 elements. If the muscle wraps over a bone surface, a “wrap object” is used to represent that surface such that the muscle path is not allowed to pass through the bone.

Table 1.

The muscles included in the model, and the number of elements that represent each one.

Muscle	Number of elements	Muscle	Number of elements
Trapezius, scapular part (mid and lower)	11	Biceps, long head	1
Trapezius, clavivular part (upper)	2	Biceps, short head	2
Levator scapulae	2	Triceps, long head	4
Pectoralis minor	4	Triceps, medial head	5
Rhomboid	5	Triceps, lateral head	5
Serratus anterior	12	Latissimus dorsi	6
Deltoid, scapular part (post and mid)	11	Pectoralis major, thoracic part	6
Deltoid, clavicular part (anterior)	4	Pectoralis major, clavicular part	2
Coracobrachialis	3	Brachialis	7
Infraspinatus	6	Brachioradialis	3
Teres minor	3	Pronator teres	2
Teres major	4	Supinator	5
Supraspinatus	4	Pronator quadratus	3
Subscapularis	11	Anconeus	5

In order to run dynamic simulations, two additional software packages were used. The first package was SD/FAST (Parametric Technology Corp), which uses parameter files created by SIMM to compute the equations of motion of the modeled system. The second package, the Dynamics Pipeline (Musculographics, Inc.), connects SIMM to SD/FAST in order to perform forward and inverse dynamic simulations. In the case of forward dynamic simulations, the model inputs are muscle activations and possible external loads, and the output is the resulting movement. In the case of inverse dynamic simulations, the desired movement and possible external loads are the inputs, and the required muscle activations are the outputs.

In the second case, since there are more muscles than degrees of freedom in the musculoskeletal system, a non-linear constrained optimization routine, CFSQP (AEM Design) is used in order to solve the load-sharing problem (Tsirakos et al, 1997). Three types of constraints are included: first, for every degree of freedom, the muscle forces are constrained to produce the torques required by the input movement. Second, the muscle forces acting on the glenohumeral joint are constrained to pull the humerus towards the glenoid cavity, thus ensuring the joint stability. And third, the muscle forces acting on the scapula are constrained to keep the scapula pressed against the thorax, in accordance with the scapulothoracic gliding plane, described earlier. The objective function currently used was proposed by Praagman et al (2006) to minimize energy consumption:

$$\text{min}{\displaystyle \sum E_m={\displaystyle \sum (E_f+E_a)={\displaystyle \sum m\left\{c_1\frac{F_m}{\mathit{\text{PCSA}}}+c_2{\left(\frac{F_m}{F_{\text{max}}}\right)}^2\right\}}}}$$

where E_f and E_a are the muscle energy consumption due to the detachment of cross bridges and re-uptake of calcium respectively, m is the muscle mass, F_m is the muscle force, PCSA is the physiological cross-sectional area, F_max is the maximum muscle force, and c₁ and c₂ are two constants chosen to achieve equal contributions from the linear and nonlinear terms at 50% activation (Praagman et all, 2006).

2.2 Experimental setup

Five able-bodied subjects participated in the study after giving informed consent. The subjects were asked to perform a set of movements with their right arm, while their arm position and the EMG signals of selected arm muscles were recorded. Figure 1 shows the experimental setup.

Figure 1.

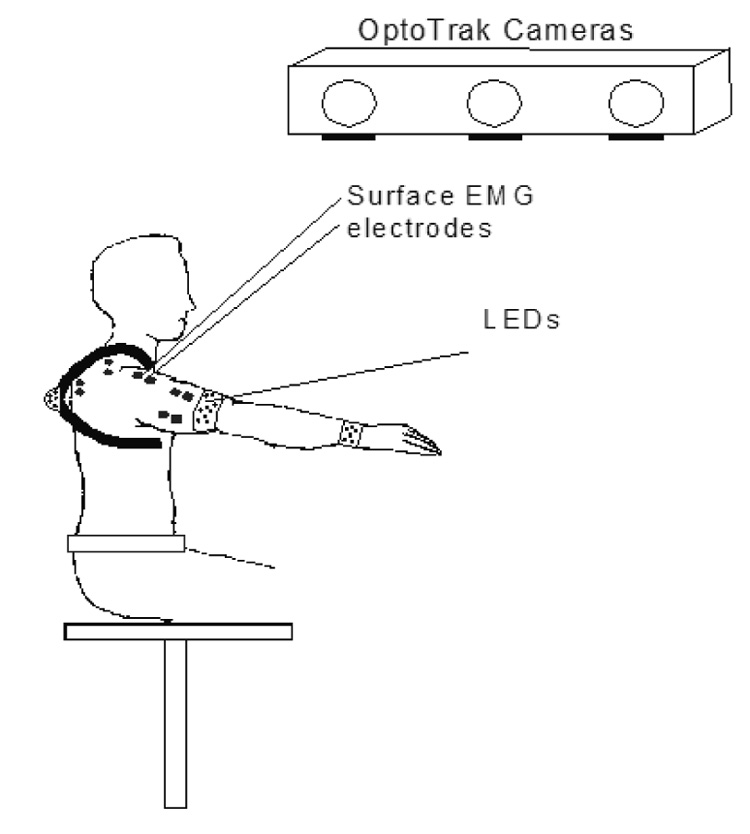
Experimental Setup. Sets of LED were fixed over the thorax, humerus and forearm of the subjects, and the three-dimensional position of these segments was recorded using three cameras. The positions of the clavicle and scapula were estimated using a regression model based on the scapulohumeral rhythm. Surface and percutaneous electrodes measured the EMG signals from selected shoulder and arm muscles.

The arm movements were recorded using an Optotrak system (Northern Digital Inc.) that consists of three cameras capable of recording the 3D positions of light emitting diodes (LED) located within the workspace. Sets of LED were fixed over the thorax, humerus and forearm of the subjects to locate the three-dimensional position of these segments. The locations of the scapula and clavicle are difficult to track dynamically using markers fixed to the skin, because they show large displacements with respect to the skin. However, there is a well-defined relation between scapular and humeral motion, which is that during a normal arm elevation movement, about one-third is due to scapulothoracic motion, and two-thirds is due to glenohumeral rotation (De Groot and Brand, 2001). Moreover, because of the closed chain between the thorax, clavicle and scapula created by the sternoclavicular and acromioclavicular joints, and the scapulothoracic gliding plane, the orientations of the clavicle and scapula are related. Based on these relations, a three-dimensional regression model was built, using the positions of scapular, clavicular, and humeral bony landmarks recorded in a series of static trials covering the workspace. The bony landmarks were chosen according to van der Helm, 1997, and the recorded positions consisted of five levels of humeral elevation between 0° and 120°, evenly distributed in that range, in the coronal (i.e. elevation to the side), scapular (45° from coronal) and sagittal planes (to the front), with the elbow fully extended. During the dynamic trials, the regression model was used along with the orientation of the humerus to determine the dynamic orientation of the scapula and the clavicle.

EMG data were recorded in the first three subjects using surface electrodes on six muscles. In order to evaluate the model predictions for more muscles, including ones too deep to be easily accessible by surface electrodes, the last two subjects had surface electrodes placed on eight muscles, and fine wire percutaneous electrodes placed on three muscles: infraspinatus, supraspinatus and pronator teres. The list of muscles for each subject is shown in table 2. All EMG signals were rectified, low pass filtered at a cutoff frequency of 4 Hz, and normalized by their values during maximum voluntary contractions.

Table 2.

Electrodes used to measure EMG signals for correlation to model-predicted activations. In the first three subjects, only surface electrodes were used, placed on six muscles. In the last two subjects, eight surface and three fine wire percutaneous electrodes were used.

subjects	S1 and S2	S3	S4 and S5
surface	biceps	biceps	biceps
electrodes	triceps	triceps	triceps
	anterior deltoid	anterior deltoid	anterior deltoid
	middle deltoid
	posterior deltoid	posterior deltoid	posterior deltoid
	upper trapezius	upper trapezius	upper trapezius
		pectoralis major	pectoralis major
			latissimus dorsi
			serratus anterior
percutaneous			infraspinatus
electrodes			supraspinatus
			pronator teres

The same movements were performed by all subjects. They were relatively slow (joint velocities around 30 degrees/second), in order to simulate the expected performance of a person with an FES system. They consisted of a set of planar movements: shoulder abduction/adduction in the coronal, scapular, and sagittal planes, horizontal flexion/extension, internal/external rotation, elbow flexion/extension and forearm pronation/supination, reaching movements to three different heights: knee level, shoulder level, and above shoulder level, and two movements simulating activities of daily living (ADL): eating, and combing the hair. Data were recorded at 30Hz.

2.3 Model evaluation

The model predictions were evaluated based on the shape and timing of the signals and not the actual amplitude, because EMG amplitude depends on the properties and locations of the electrodes used and therefore is not a reliable measure of muscle activation. For this reason, the model was evaluated by cross-correlation of the model-predicted activations and the EMG signals from the selected muscles.

In order to avoid correlating signals with very low amplitudes but (in the case of EMG) with noisy baseline activity, muscles with EMG values that did not rise above a specified threshold for the duration of a given trial were excluded from the correlation calculations for that trial. The threshold was defined as one standard deviation above the baseline, as described in Hodges and Bui 1996. For these cases, a different measure was used to summarize the ability of the model to predict the lack of activity in a given muscle: the false positive rate. That is, the number of trials in which muscle activity was predicted by the model but none was measured using EMG was expressed as a percentage of the total number of trials where no activity was measured using EMG.

2.4 Application to C3 SCI with and without FES

A spinal cord injury at the C3 level causes paralysis of almost all upper extremity muscles, with the possible exception of the levator scapulae and upper trapezius (Kirsch et al, 2001). To simulate a subject with C3 SCI, all other muscles were set to have zero active force, and in addition, the maximum force for the levator scapulae and upper trapezius was set to 50% of able-bodied maximum force to simulate the effects of possible muscle denervation and partial paralysis (within the range of 20–60% measured by Kobetic and Marsolais, 1994).

Two sets of muscle candidates for FES were evaluated: the first included the serratus anterior and deltoids, and the second included the serratus anterior, deltoids and three rotator cuff muscles (supraspinatus, infraspinatus and subscapularis). To simulate FES, the maximum forces of these sets of muscles were set to 50% of the corresponding able-bodied maximum muscle forces. This reduction simulates possible muscle denervation, disuse atrophy, and limited spatial muscle activation due to electrode placement.

The task used to evaluate the effect of FES was abduction of the arm in the coronal plane from 0 to 100 degrees of elevation, with the elbow fully extended. Inverse dynamic simulations were performed by the model under four conditions: (1) able-bodied, (2) C3 SCI, (3) C3 SCI with FES of muscle set 1, and (4) C3 SCI with FES of muscle set 2. The maximum humeral elevation for each case was determined either by the successful completion of the movement (i.e. the model reached 100 degrees of elevation), or by the highest elevation achieved before the simulation failed. In the case of failure, the model specified which constraint was violated: the muscle forces were either insufficient for the required joint torques, they caused instability of the glenohumeral joint, or they were unable to keep the scapula pressed against the thorax.

3. Results

Figure 2 demonstrates the evaluation procedure, using as an example, the middle deltoid of subject 2 during a humeral abduction movement. It shows the raw EMG data (part A), the processed EMG data (part B), the corresponding model-predicted middle deltoid activation (part C), and a comparison of the processed EMG and model-predicted activation (part D). In part D, it is shown that the timing of the measured EMG and the model-predicted activation are quite similar. Also note that in part D, the magnitudes of the signals are not the same, but this is not taken into account since the model verification is based on timing, not amplitude. The cross-correlation in this case was 0.850.

Figure 2.

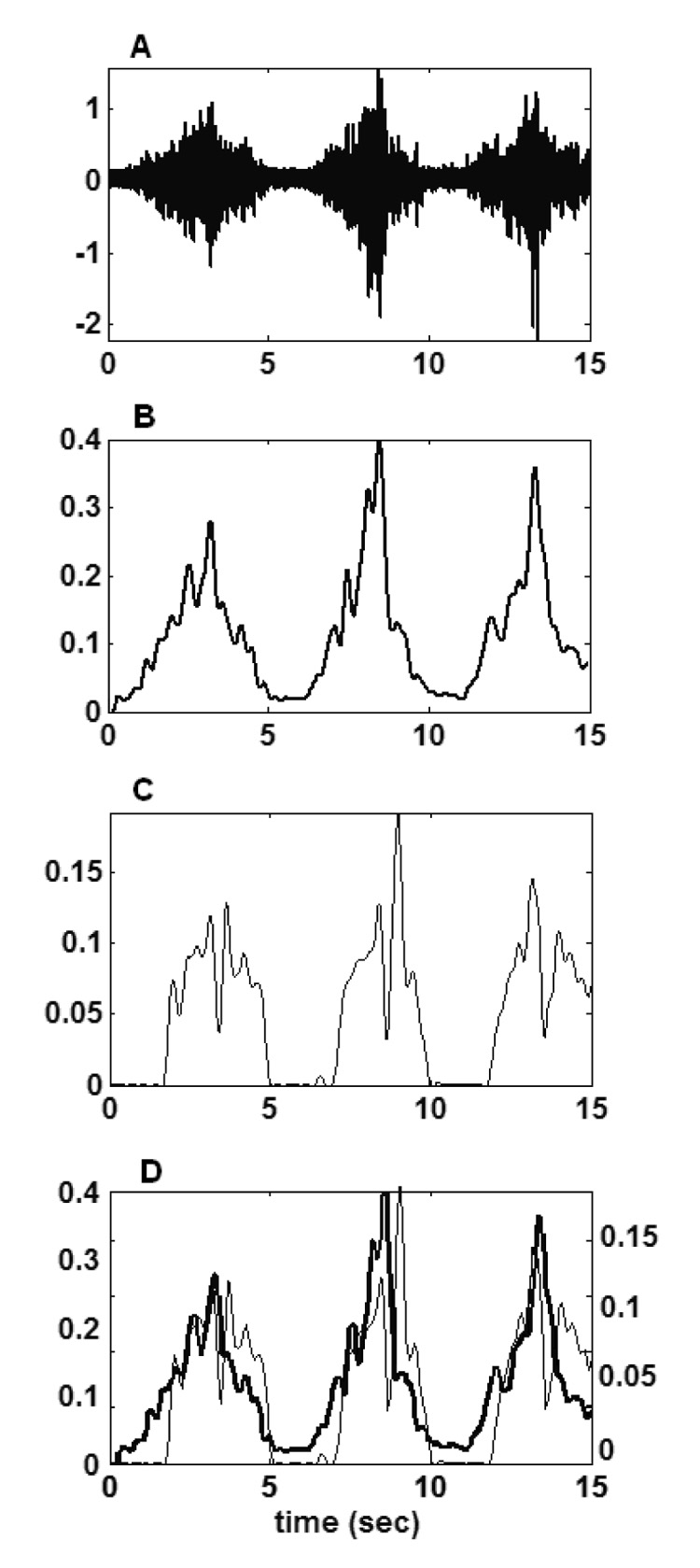
EMG recording, processing, and comparison to model-predicted activations. For example, the EMG and model-predicted activations of middle deltoid muscle during a repeated humeral abduction movement are illustrated. Raw EMG (A), processed (rectified, low pass filtered at 4Hz and normalized) EMG (B), model-predicted activation (C), processed EMG (black line) and model-predicted activation (grey line) (D). For part D, the vertical axis for the EMG is on the left, and for the activation is on the right.

Figure 3 shows an example of a typical correlation between EMG and model-predicted activation. This is also a humeral abduction movement, and the muscles shown are the serratus anterior (A), supraspinatus (B) and infraspinatus (C). These plots show that the model-predicted activation peaks generally match the EMG peaks. The similarity of shape is reflected in the cross-correlation values, which in this case were 0.610, 0.650 and 0.625 respectively.

Figure 3.

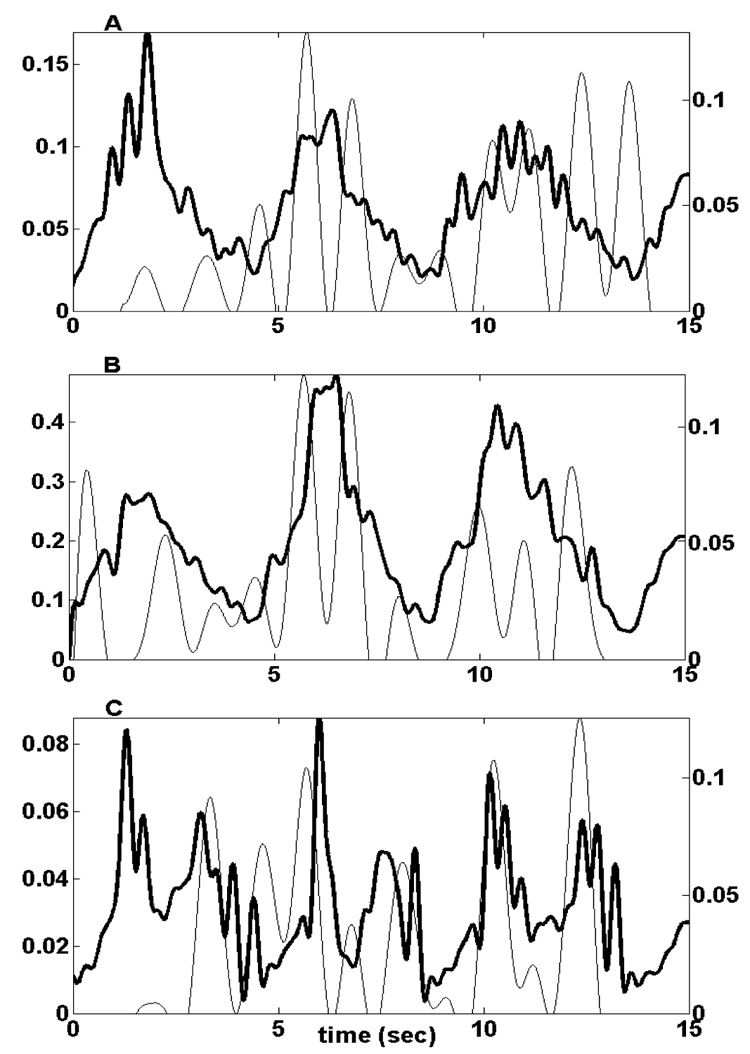
Serratus anterior (A), supraspinatus (B), and infraspinatus (C) signals during a repeated humeral elevation movement. For all muscles, the processed EMG signal is the black line, and the model-predicted activation is the grey line. The vertical axes for the EMG signals are on the left, and for the model-predicted activations are on the right.

Figure 4 shows a situation where the correlation between EMG signals and model predictions is less accurate, for the biceps (A) and triceps (B) during a repeated elbow flexion/extension movement. In this figure, the amplitudes were not scaled, to highlight the model-predicted inactivity of the triceps, which does not agree with the active EMG measurement. The cross-correlation values for the biceps and triceps were 0.391 and 0.290 respectively.

Figure 4.

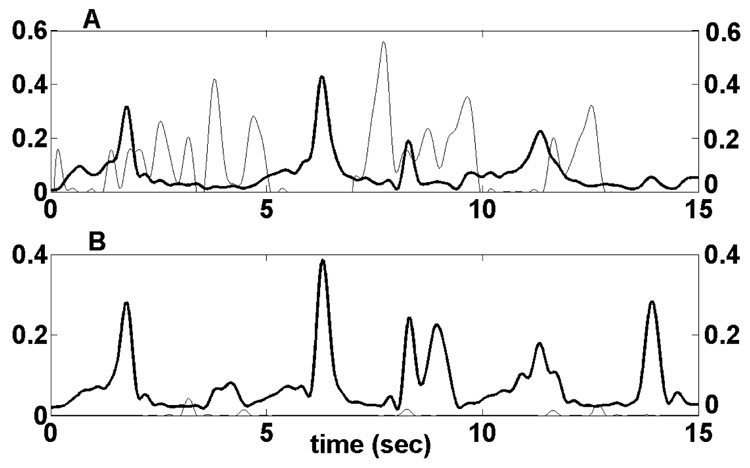
Biceps (A) and triceps (B) signals during a repeated elbow flexion/extension movement. The processed EMG signal is the black line, and the model-predicted activation is the grey line. Co-contraction of the biceps and triceps is recorded in the EMG signals, but is not predicted by the model.

Figure 5 shows the cross-correlation values between activations and EMG signals for the measured muscles of each of the five subjects, averaged across all tasks. Averaged across subjects, the cross-correlation ranged from 0.282 for the triceps to 0.726 for the middle deltoid. The overall mean correlation was 0.455. In most subjects, the three heads of the deltoid had the best predictions, and the biceps and triceps had the worst. For the last two subjects that had more EMG electrodes, the prediction was poor for the latissimus dorsi, but generally good for the muscles that stabilize the scapula and the humerus: serratus anterior, supraspinatus and infraspinatus.

Figure 5.

Cross-correlation between EMG and model-predicted muscle activations, averaged across tasks. Every row corresponds to one muscle, and every column to one subject. The vertical scale of every plot ranges from 0 to 1.

The false positive rate is presented in Table 3. The lowest value was 23.3% for the triceps, while the highest was 80% for the middle deltoid, but it should be noted that this was calculated from only five trials, since the middle deltoid showed above-threshold EMG activity in all but five trials. Overall, no muscle activation was systematically overestimated by the model.

Table 3.

False positive rate. The first column is the number of trials in which muscle activity was predicted by the model but none was measured using EMG. The second column is the total number of trials where no activity was measured using EMG. The third column is the false positive rate, defined as the ratio of the first two columns.

	EMG off act. on	Total EMG off	False positive rate (%)
anterior deltoid	5	13	38.5
middle deltoid	4	5	80.0
posterior deltoid	20	33	60.6
biceps	7	25	28.0
triceps	10	43	23.3
upper trapezius	14	30	46.7
pectoralis major	17	48	35.4
latissimus dorsi	9	34	26.5
serratus anterior	6	15	40.0
supraspinatus	4	14	28.6
infraspinatus	11	41	26.8
pronator teres	8	25	32.0
Total	115	326	35.3

Figure 6 shows the results of inverse dynamic simulations performed by the model adjusted to represent an able-bodied subject, a C3 SCI individual without FES, and a C3 SCI individual with FES of two different muscle sets. The maximum humeral elevation possible by the able-bodied simulation was 100 degrees. Without FES, the model failed immediately (i.e., zero elevation) due to the extended paralysis at this level of injury. Simulation of FES of the serratus anterior and deltoids produced humeral elevation of 12 degrees. For higher elevations, the model failed because glenohumeral stability was not maintained. Addition of the rotator cuff muscles to the simulation increased the maximum elevation to 81 degrees (i.e., almost to the able-bodied range).

Figure 6.

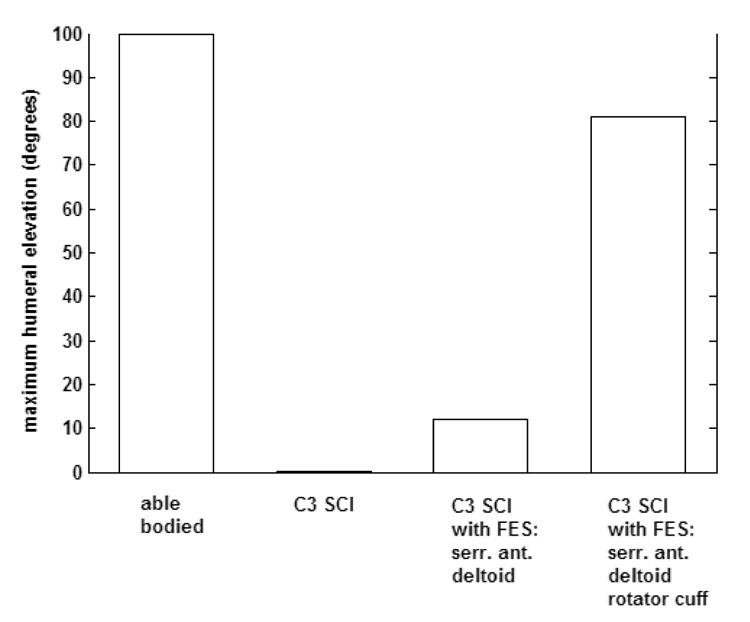
Maximum humeral elevation achieved in four cases: (a) able-bodied (b) C3 SCI (c) C3 SCI with FES of serratus anterior and deltoids (d) C3 SCI with FES of serratus anterior, deltoids, infraspinatus, supraspinatus and subscapularis.

4. Discussion

A dynamic model of the upper extremity has been described. It was developed using a set of commercially available software packages, with a user-friendly, graphical interface. It can be used both for forward and inverse dynamic simulations. For the three heads of the deltoid, which are primary arm movers, the model predicts activations that correspond to the timing of the measured EMGs quite accurately. The same can be said for the serratus anterior and the rotator cuff muscles (infraspinatus and supraspinatus), whose role is to stabilize the scapula and the glenohumeral joint respectively. Our model can therefore accurately predict the functions of key muscles of the upper extremity, making it a valuable tool for exploratory simulations aiming to provide insight into the performance of the real arm under various conditions. Specifically, this model can be a useful tool for the design and testing of upper extremity neuroprosthetic systems.

Validation of musculoskeletal models is generally difficult to achieve. Thorough validation is not practical because the muscle excitation patterns that are the model inputs are not directly measurable in the actual musculoskeletal system. For his model of the upper extremity, van der Helm compared the predicted muscle forces with electromyographical (EMG) recordings (van der Helm 1994). The problem with this approach is that it did not take into account the dependency of the EMG amplitude on muscle length. van der Helm concluded that EMG amplitude cannot be used to validate musculoskeletal models, and he pointed out that in this case, only verification, and not strict validation of the model is possible. Instead of EMG, Praagman et al. (2003) suggested the use of local oxygen consumption in a muscle, measured by near infrared spectroscopy (NIRS). However, the dynamic properties cannot be evaluated with this method since NIRS cannot be used for dynamic measurements. In other studies, evaluation of the model is performed by comparing predicted forces with measurements from the literature. This method cannot give quantitative conclusions, since the modeling parameters are different among the studies, but it can result in a qualitative agreement (Karlsson and Peterson 1992, Charlton and Johnson, 2000).

In this study, the performance of the model was verified by comparing the shape over time of the calculated muscle activations to the corresponding EMG recordings. Figure 3 shows that the best correlation is achieved for the three heads of the deltoid, while for muscles like the biceps and triceps, the agreement is not good. One reason for this might be co-contraction of the biceps and triceps during the low velocity movements examined, something that would not be predicted by the model using the selected energy-related cost function for load sharing. Figure 4 shows an example of this. The EMG signals for the biceps and triceps reveal significant co-contraction during flexion, as opposed to the model that does not predict any triceps activity, most likely because in this task, extension can be achieved entirely through gravity. Since the nervous system probably uses different strategies for different conditions, a cost function that takes into account the stiffness of the arm could work better for this movement. However, an FES system does not aim to replace the nervous system, so the choice of cost function, even if not a perfect model of an intact nervous system, can still lead to muscle activation patterns that, applied by the FES system, will produce the desired movement.

In some cases, disagreement between EMG and model-predicted activation can probably be attributed to EMG measurement errors. The latissimus dorsi has a small cross-correlation value (0.310, averaged across subjects) and it would not be expected to be active unless the subject pushes down or adducts against resistance (Jenkins 2002). Since neither of these actions were included in the task set, it is likely that the surface electrodes detected EMG signals from neighboring muscles such as the serratus anterior. In fact, a cross-correlation analysis of the signals from latissimus dorsi and serratus anterior produces an average value of 0.886. This could be due to poorly placed electrodes, or (more likely) to inter-muscle crosstalk, a common problem when surface electromyography is used (Solomonow et al 1994).

Another possible reason for disagreement between EMG and model-predicted activation could be that the cadaver-based model parameters do not correspond well to the participants of this study. Parameters like the maximum muscle force cannot be directly measured in individual subjects. However, it is unlikely that such differences will significantly impact the effectiveness of model-based simulations in reaching general conclusions about the configuration of potential FES systems. In the example of humeral abduction presented above, the model predicted that including rotator cuff muscles in the stimulation set can greatly improve the restored function. Even though the exact level of improvement may be different depending on the specific person’s remaining function and possible denervation, the model results can be used as a guideline for choosing the most effective muscle set for FES.

In conclusion, we believe that the model presented here can significantly facilitate the design of neuroprosthetic systems, by replacing the current trial-and-error methods that would be impractical in the case of high level injuries with a simulation system that can explore the mechanical considerations associated with different movements and different stimulated muscle sets. The model was successfully verified using EMG as a measure of muscle activation and is now ready for use in aiding the development of advanced FES systems for restoring arm and shoulder movements.