Integrating VBM into the General Linear Model with Voxelwise Anatomical Covariates

Abstract

A current limitation for imaging of brain function is the potential confound of anatomical differences or registration error, which may manifest via apparent functional “activation” for between-subject analyses. With respect to functional activations, underlying tissue mismatches can be regarded as a nuisance variable. We propose adding the probability of gray matter at a given voxel as a covariate (nuisance variable) in the analysis of voxelwise multisubject functional data using standard statistical techniques. A method is presented to assess the extent to which a functional activation can reliably be explained by underlying anatomical differences, and simultaneously, to assess the component of the functional activation which cannot be attributed to anatomical difference and thus is likely due to functional difference alone. Extension of the method to other intermodal imaging applications is discussed. Two exemplary data sets, one PET and one fMRI, are used to demonstrate the implementation and utility of this method, which apportions the relative contributions of anatomy and function for an apparent functional activation. The examples show two distinct types of results. First, a so-called functional activation may actually be caused by a systematic anatomical difference which, when modeled, diminishes the functional effect. In the second result type, including the anatomical differences in the model can account for a large component of otherwise unmodeled variance, yielding an increase in the functional effect cluster size and/or magnitude. In either case, ignoring the readily available structural information can lead to misinterpretation of functional results.

I. Introduction

The goal of an increasing number of functional imaging studies is to examine how in vivo metabolism or physiology is related to a parameter of interest such as group difference (e.g. normal vs. diseased) or a subject-specific measure (e.g. age). Early efforts typically employed a Region-of-Interest (ROI) drawn directly on the functional image for each subject. Use of a coregistered high-resolution anatomic image (e.g. MRI) for each subject increased the accuracy but still required time-consuming drawing of individual ROIs. By registering images from every subject to a single reference frame, a single ROI for each structure of interest could be used, vastly speeding up the process. A far reaching consequence of a common reference frame was the development of an automated voxelwise approach to data analysis (e.g. [Friston, 1995]), where each voxel is treated as an atomic ROI. The voxelwise approach has become the de facto standard for functional brain analysis and forms the basis for most popular neuroimaging software tools..

I.A. Functional Data Analysis Steps

Typical data processing for a multi-subject functional study employs the following steps:

1. Process individual subjects’ functional data to yield images which can be compared across subjects. For PET this typically involves voxelwise normalization to whole-brain tracer concentration, or for quantitative results, calculating voxelwise rate constants. For fMRI an initial fixed-effects General Linear Model (GLM) analysis is performed for each scan to yield one or more functional contrast maps for each subject, with associated variance maps.

2. Coregister each subject′s functional data to their anatomical image, usually a high-resolution MRI image. For fMRI data, a coplanar T1 image may be preferable for registration.

3. Coregister each subject′s MRI image to a single target image (template) in the desired spatial coordinate system. Most workers employ the Talairach coordinate system [Talairach & Tournoux, 1988] or a similar one such as the MNI system [Evans et al., 1993].

4. Cumulate the transforms and register the functional data into the anatomical template space.

The precise data processing steps are unimportant for the implementation of voxelwise covariates, but are presented as a basis for the following discussion.

Coregistration accuracy is an important limiting factor for the validity of multi-subject functional image analysis. Inaccurate registration can lead to either false activations if there is a systematic difference in registration of a particular structure across a parameter of interest (e.g. between groups), or can yield a loss of sensitivity if a functional region from several individuals is scattered about its true location in the reference space. The impetus for this paper was to explore the former problem of false activations which are attributable more to anatomical than true functional differences, but it became evident that the latter problem of decreased sensitivity was at least equally as important. In this discussion, measurements obtained from PET and fMRI display similar characteristics with regard to false activations: both modalities depend on a change in concentration of a tracer molecule for their effect (e.g. radiolabeled glucose for PET, oxygenated hemoglobin for fMRI-BOLD). This discussion assumes a typical registration algorithm which preserves the concentration measurements, as opposed to preserving the total amount of tracer.

I.B. Functional Activation Sources

Statistically significant effects observed in a multi-subject study can arise from underlying differences in anatomical structure or from misregisration, as well as from actual metabolic and physiological differences. In this paper, the term “activation” refers to a cluster of voxels which emerge as significantly distinctive, whether the result is true or not. The term “metabolic difference” refers to an actual underlying physiological effect, whether or not this effect is noticed by the analysis software.

Functional activations can result from systematic differences in the following circumstances:

1. Difference in a specific metabolic process which influences measured signal. Such a metabolic difference is the only true activation in this discussion.

2. Difference in tissue composition within a supposedly homogenous structure.

3. Misregistration of a structure to the target template.

4. Partial volume effect (PVE), a special case of spatial blurring.

Item (1) above could be considered a generalization of item (2), but whereas the former is due to an altered metabolic rate constant, the latter addresses the possibility of a different or altered metabolic process due to different tissue type. Examples include a tumor, or white-matter myelenation defects. This distinction is made because, while there is a bona fide functional difference, it is not due to an altered physiological rate constant in comparable tissue. Misregistration (item 3) typically occurs when nearby structures have stronger features which exhibit a greater influence on the registration algorithm. The resulting comparison is invalid to the extent that the underlying tissue is not comparable. A structure that is small in relation to the spatial resolution can lead to item (4), PVE [Hoffman et al., 1979; Muller-Gartner et al., 1992], yielding an inaccurate measurement within the structure boundaries. False activations can result when differences in size or shape of an anatomical structure lead to differences in measured signal .

I.C. Voxel-Based Morphometry (VBM)

Voxel-Based Morphometry (VBM) [Ashburner & Friston, 2000; Good et al., 2001] can be used to explore regional anatomical differences much as similar functional approaches examine physiological differences. Typically, data are compared across scans by converting each anatomic image to a Gray-Matter Probability (GMP) map which is coregistered into a common template space. A GLM is then used to determine voxels with statistically significant differences in gray matter composition. VBM is commonly used to search for possible differences in anatomic structure between groups. Differences found in VBM are due to a subset of the reasons for an apparent functional activation, namely:

1. Differences in the tissue component of a structure (e.g. more WM in the thalamus);

2. Misregistration, i.e. underlying differences in structure shape not removed by the coregistration process.

The overlap of causes for functional and VBM activation can lead to ambiguity in data interpretation.

VBM depends crucially on the coregistration process. If the coregistration is gravely inaccurate, few structures will align properly, leading to a large error term and consequent low probability of finding differences. Conversely, if the registration is perfect, then (by definition) all of the structures will align perfectly, leaving no discernible differences. Thus, VBM depends on a registration algorithm which is good, but not too good; using an affine (∼12 parameter) or slightly better registration seems to be a popular choice. Since VBM is easy to use, it is widely used, but there is ongoing discussion as to its validity in specific applications [Bookstein, 2001; Ashburner & Friston, 2001; Davatzikos, 2004; Duran et al., 2006; Kennedy et al., 2006].

I.D. Anatomical Confounds to Functional Activations

Systematic differences in size or location of a structure do not necessarily lead to spurious functional activations; if the registration algorithm performs correctly, the functional signal will accurately reside in the corresponding template location. However, although there can be several interpretations for statistically significant VBM findings, a VBM signal can invalidate overlapping functional activations. Stated differently, any apparent difference in signal not attributable to a metabolic process is not a true functional activation. Such a difference can still be interesting, but the source of the activation must be properly interpreted. In the analysis scheme outlined above (section I.A), inaccuracies in registering the MRI data to the template propagate directly to the functional data, so it is appropriate to use VBM to highlight poor local registration which might influence the results of functional image analysis.

Recent work [Momenan et al., 2004] points out that VBM can be used to highlight suspect regions, and introduces a confidence interval to help evaluate whether significant activations are more likely due to functional or structural differences. This approach stops short of incorporating the VBM results as a correction into the functional analysis. Mehta et al. [2006] proposed a voxelwise correlation using T1-weighted MRI images; this approach attempts to integrate information from all tissue types, but without segmentation or some other type of scaling it suffers from a lack of comparability of signal values across subjects. Casanova et al. [2006] presented a voxel-wise covariate method similar to the approach described in this work, combining functional and anatomic results via the software “Biological Parametric Mapping Toolbox”, which interfaces with the commonly used SPM5 analysis software (http://www.fil.ion.ucl.ac.uk/spm).

Differences in underlying tissue should be regarded as a source of error in analyzing functional data, and as such can be formally incorporated into a GLM analysis. By treating the tissue type as a continuous variable, the effect of varying tissue type can be modeled explicitly and, if desired, its contribution to functional activations can be removed. There are several possibilities for the interaction of tissue type with functional activations:

1. In anatomically homogenous areas (i.e. similar GMP across subjects), tissue type will have no effect, and functional activations will be unaffected by modeling of the tissue type.

2. If the region is homogenous with respect to the anatomic data but misaligned (e.g. the medial portion of a subject′s amygdala appears in the lateral portion of the template amygdala), the underlying structural/functional mismatch may not be accounted for. However, nearby regions showing a significant VBM activation can indicate that closer inspection in this region is warranted.

3. If the region is anatomically inhomogeneous across subjects and this variation is orthogonal to other parameters of interest (e.g. group membership) the variance term for the VBM results will be large. Including such data in the model as a covariate will tend to decrease the overall error, yielding higher functional t-values in such regions.

4. If the region is anatomically inhomogeneous across subjects and the variation is correlated to modeled parameters, an apparent functional activation is likely due to underlying tissue differences. In such cases, the variance apportioned to the parameter of interest as well as the associated statistical values will be appropriately reduced by inclusion of VBM covariates.

In the approach presented by Momenan et al., significant VBM clusters are used to flag regions with functional activations which should be examined more closely. The confidence interval these authors introduce provides some guidance about the validity of a functional activation. However, this approach only applies to entire clusters, and does not address the extent to which a functional activation colocated with a VBM activation is due to functional or anatomical differences, especially if the VBM signal fails to reach statistical significance. In other words, must a functional activation always be rejected if there is an overlapping VBM activation, or can the anatomical differences be taken into account to see if the functional effect is still strong enough to stand on its own?

By incorporating the VBM results directly into the GLM, the contribution of anatomical effects to a functional activation can be accounted for. This not only provides a convenient and objective approach to removing spurious functional activations, but also enables remaining functional effects to be properly evaluated. Furthermore, by including a known source of potential variance in the model, the overall error term may decrease, leading to a possible increase in functional t-statistic values.

II. Overview of the Method

II. A. Statistical Model

The standard model for an across-subjects regression analysis is:

$$Y_{\mathrm{j}}={{\mathrm{z}}^{\prime }}_{\mathrm{j}}\gamma +{\eta }_{\mathrm{j}}$$ Eq. 1

• Y_j is the observed functional value for the j^th subject.

• z′_j is the vector of regressor variables for the j^th subject.

• γ is a vector of parameters (1 coefficient for each regressor variable) that varies from voxel to voxel.

• η_j is a normally distributed error term with a mean of zero and a variance of S² _j and varies across voxels.

In traditional multi-subject voxelwise analyses an identical random effects model is applied to each voxel independently. A correction for multiple comparisons is then performed to obtain a global threshold for statistical significance. For independent data points (voxels), the multiple comparison correction is simply a Bonferroni correction, but becomes more complex if the data are correlated. This discussion initially presents a framework for independent voxels, and later considers how a voxelwise covariate affects the estimation of voxel correlation.

To incorporate anatomical variance into the GLM, an additional regressor is concatenated to the matrix of regressor variables, i.e. [z′_j | x’_j]. Notationally, square brackets “[]” are used to represent matrices (vectors), and a vertical line “|” represents concatenation of two matrices. The model is typically estimated using standard maximum likelihood estimation (MLE) at each voxel. A model adapted for random effects analysis [e.g. Pinheiro and Bates, 2000] covarying for anatomy can be formulated as:

$$Y^{\ast }{}_{\mathrm{j}}=[{{\mathrm{z}}^{\prime }}_{\mathrm{j}}\mid {{\mathrm{x}}^{\prime }}_{\mathrm{j}}]\gamma +\eta ^{\ast }{}_{\mathrm{j}}$$ Eq. 2

• Y*_j is the observed functional value for the j^th subject, given both voxelwise and non-voxelwise covariates.

• x’_j is the probability that the voxel is gray matter for the j^th subject.

• η*_j is the corresponding error term.

• Other variables as defined in Eq. 1.

Extending this technique using hierarchical multiple regression techniques [Cohen et al., 2003] permits investigation of the unique contribution of functional differences beyond the voxelwise VBM covariate. The variance explained in the functional data by the GMP only (the reduced model) is compared to the variance explained by gray matter probability and the regressor vectors of interest (the full model). Using the above definitions for x’_j and γ,

$$Y^{\#}{}_{\mathrm{j}}=\left[{{\mathrm{x}}^{\prime }}_{\mathrm{j}}\right]\gamma +\eta ^{\#}{}_{\mathrm{j}}$$ Eq. 3

• Y^#_j is the observed functional value for the j^th subject given only voxelwise covariates (e.g. VBM results)..

• η^#_j is the corresponding error term.

The expected value resulting from each of these models (Eqs. 1-3) can be estimated by subtracting the error component, which is generally different for each model:

$${\mathrm{E}}_{\mathrm{j}}={\mathrm{Y}}_{\mathrm{j}}-{\eta }_{\mathrm{j}}$$ Eq. 4

The proportion of total variance explained by the model, R², can be described as:

$${\mathrm{R}}^{\ast 2}=1-({\mathrm{E}}^{\ast 2}∕{\mathrm{Y}}^2)$$ Eq. 5

$${\mathrm{R}}^{\#2}=1-({\mathrm{E}}^{\#2}∕{\mathrm{Y}}^2)$$ Eq. 6

• where

• Y is the observed voxelwise data

• E* is the estimated data given the both voxelwise and non-voxelwise covariates (full model).

• E^# is the estimated data given only voxelwise covariates (reduced model).

The change in R² is defined as the difference in the proportion of variance explained between full and reduced models, and its significance can be tested using an F-statistic. This change, ΔR², and its corresponding F statistic can be described as:

$$\Delta {\mathrm{R}}^2={\mathrm{R}}^{\ast 2}-{\mathrm{R}}^{\#2}$$ Eq. 7

$${\mathrm{F}}_{\text{change}}=(\Delta {\mathrm{R}}^2∕\mathrm{m})∕(\left({\mathrm{R}}^{\ast 2}\right)∕(\mathrm{n}-\mathrm{m}-\mathrm{k}-1)$$ Eq. 8

• where

• n is the number of subjects.

• m is the number of voxelwise covariates.

• k is the number of non-voxelwise covariates.

This test goes beyond having a voxelwise covariate, and directly investigates the unique contribution of the non-voxelwise covariates (i.e. covariates of interest) in explaining the functional data. It is worth noting that this approach is different from more sophisticated hierarchical linear models [Bryk & Raudenbush, 1992; Goldstein, 1995; Neter et al., 1996], in which multiple nested factors can be modeled. The current examples do not employ nested factors, although the technique is in principle extensible to hierarchical models with nested factors. The current approach is also somewhat different from “backward” or “step-down” procedures [Neter et al., 1996; Rao and Toutenburg, 1999], in that such stepwise procedures often include or exclude predictor variables on the basis of their unique contribution to explained variance, and are frequently used to optimize model selection. In the present neuroimaging examples, the inclusion of voxelwise covariates was determined by theoretical considerations, so the models (full and reduced) have distinct roles.

Effect of a voxelwise covariate on the statistical threshold estimate

Since a large number of voxels are considered, a correction for multiple comparisons must be performed to obtain an acceptable statistical threshold. An important issue is how a covariate which varies from one voxel to the next might affect the estimate of a statistical threshold. Individual voxels for most imaging modalities are usually correlated to some extent with neighboring voxels, so an estimation of this effect must be obtained. A straightforward Bonferroni correction is usually too conservative, so Worsley et al. [1996] and Kiebel et al. [1999] developed a framework for estimating the effective number of independent resolution elements, or “resels”, contributing to an image. Their work is based on estimating the smoothness of the image from the voxelwise residuals of the model fit by modeling the noise estimate (residual) as a convolution of a Gaussian kernel with white noise. In this way the noise is correlated and multiple correction can proceed based on random field theory.

Using the method of Kiebel et al. [1999] as embodied in popular analysis software such as SPM5, the voxelwise residuals throughout the image contribute to the smoothness estimate, so a voxelwise covariate will implicitly be properly incorporated into the calculation of the statistical threshold for a large volume such as the whole brain. Furthermore, some neuroimaging software (e.g. “fmristat” [Worsley et al., 2002]) currently includes covariates for each slice, which has little or no effect on the estimation of the significance threshold. The underlying assumption of a constant error variance across voxels (homoscedasticity) becomes more valid as sources of variance are included in the model. If the statistical threshold is calculated based on the distribution of the data set using e.g. a permutation test (see [Nichols & Holmes, 2001]), the use of voxelwise covariates will not affect the accuracy of the threshold estimate.

II.B. Implementation

The voxelwise covariate method was implemented by modifying the program “multistat” contained in Worsley’s “fmristat” Matlab-based analysis package. The modified computer program is available (with permission from Dr. Worsely) by contacting the author of this paper. It is planned that the voxelwise covariate approach will be included as a feature of the NiPy neuroimaging software (http://neuroimaging.scipy.org/), an anticipated vehicle for a Python version of fmristat.

All computation was performed using a standard linux-based desktop computer. The GMP for each subject is read from a previously created file (details further on) and a covariate vector across subjects is created at each voxel. Since this occurs in the innermost loop of the computer algorithm, an additional computational burden is incurred. For example, the second level analyses required 104 (fMRI) or 29 (PET) seconds for the standard analysis, but took 566 (fMRI) or 766 (PET) seconds when voxelwise covariates were included. The additional computational burden scales roughly with the number of voxels within each plane, but other factors (e.g. a non-local disk used for PET data analysis) are also important. Nevertheless, since the voxelwise covariates are incorporated at the second level of analysis, the computational burden relative to analyzing the fMRI time series is relatively small.

In the current implementation, no explicit effort was made to detect inestimable voxels beyond the error checking inherent in the fmristat code, which checks if the standard deviation of the contrast is infinite. The covariates are folded into the model prior to this check.

II.C. Exemplar Data Sets

Two previously existing multisubject data sets were selected to demonstrate the generality of this method: (i) FDG PET in rhesus monkeys with two separate scans (activation and control conditions); and (ii) a human fMRI event-related task. The studies from which these data were drawn and associated preprocessing steps have been described in detail elsewhere [Fox et al., 2005; Kalin et al., 2005; Oakes et al., 2005; Johnstone et al., 2006]. For both data sets, a similar approach was used to prepare the anatomical and functional data. A summary pertinent to the current work follows.

Anatomical Data

Whole brain anatomical MRI data were acquired for all of the rhesus monkeys using a GE Signa 3.0 Tesla scanner (General Electric Medical Systems, Milwaukee, WI) with a standard quadrature birdcage headcoil using an axial 3D T1-weighted inversion-recovery fast gradient echo sequence (TR=9.4ms, TE 2.1ms, FOV=14cm, flip angle=10°, NEX=2, matrix=512×512, voxel size=0.2734mm, 248 slices, slice thickness=1mm, slice gap=-.05mm, prep time=600, bandwidth=15.63, freq=256, phase=224). Before undergoing MRI acquisition, the monkeys were anesthetized with ketamine (15 mg/kg) intramuscularly and monitored throughout the scan.

Human anatomical images were acquired on a GE Signa 3.0 Tesla scanner with a quadrature head coil, and consisted of a high resolution 3D T1-weighted inversion recovery fast gradient echo image (T1 highres: inversion time = 600 msec, 256×256 in-plane resolution, 240mm FOV, 124×1.1mm axial slices), and a T1-weighted spin echo coplanar image with the same slice position and orientation as the functional images (T1 coplanar: 256×256 in-plane resolution, 240mm FOV, 30×4mm sagittal slices with a 1mm gap), and T2-weighted fast spin echo image (256×256 in-plane resolution, 240 mm FOV, 81× 2 mm sagittal slices). Human data were acquired initially for 40 subjects, although 8 subjects were rejected due to incomplete or suboptimal fMRI data, and a further 7 were rejected due to poor tissue segmentation, yielding 25 subjects in this study. Subjects were drawn from the population at large and are representative of “control” subjects, and were balanced across gender (F = 11, M=14) and age (18-50 yrs, approximately ⅓ of each gender in each of the ranges 18-29, 30-39, 40-50).

PET Data

Rhesus monkeys were injected with 7mCi of [¹⁸F]-FDG and placed singly in a testing room, with a human “intruder” in the room looking near the monkey but avoiding eye contact. After 30 minutes the monkeys were anesthetized, transported to the PET scanner (Concorde microPET-P4), and PET images of the brain were acquired from 50-80 minutes post-injection. For this example, two groups of monkeys were compared: those who, in previous testing, exhibited a low level of anxiety-associated “freezing” behavior (n=12) vs. those who exhibited a high amount of freezing behavior (n=11). The globally normalized, coregistered data for these two groups of subjects were compared using a one-tailed t-test. All rhesus data (PET and anatomical) were registered to a template that approximates the atlas proposed by Paxinos et al. [1999], which has the anterior and posterior commisures in the same axial and sagittal plane. PET data were smoothed using a 4.0mm FWHM Gaussian filter. A mask was created for the PET data using manually drawn whole-brain regions (ROIs) for each subject based on T1-weighted MRI images. Functional data voxels outside of this mask were set to 0.

fMRI Data

fMRI data were acquired from 25 normal human subjects on a 3-Tesla GE SIGNA 3.0 Tesla MRI scanner with a quadrature head coil using a gradient echo EPI sequence. Subjects responded to angry and happy facial expressions, while concurrently listening to either emotionally congruent or discrepant vocal expressions, a task previously used to examine the crossmodal processing of fear expressions [Dolan et al., 2001]. Half of the participants were instructed to decide the mood of the pictured face on the basis of the facial expression (′respond to face′ group), while the other half were instructed to base their decision on the vocal expression (′respond to voice′ group). Spatial smoothing employed a 5.0mm FWHM Gaussian filter. A liberal brain mask was created from each subject’s T1 MRI image using BET [Smith, 2002] with voxels outside of the brain set to 0. Results are presented from the conditions in which the facial and vocal expressions were congruent (happy face with happy voice, angry face with angry voice) compared to those which were discrepant (happy/angry, angry/happy). Individual subject data were modeled using a GLM with FSL (http://www.fmrib.ox.ac.uk/fsl/). Gender (male versus female) was included as a predictor of interest in the second-level (multisubject) GLM analysis..

Gray-Matter Probability (GMP) Maps

T1-weighted MRI images were roughly registered to a MRI T1 weighted template using a rigid-body (6-parameter) transform to obtain a uniform orientation. An initial binary mask of each subject’s brain was created from T1 weighted MRI images using BET and then carefully refined manually for each subject. Whole brain masks were checked by 3 researchers to ensure a high degree of accuracy and intersubject consistency. Functional data were registered to each individual′s MRI T1-weighted high-resolution anatomic image using a 6-parameter fit. The anatomic images were then registered to an appropriate anatomic template (rhesus or human) using AIR [Woods et al., 1998] with a 5^th order nonlinear transformation (for rhesus), or FLIRT [Jenkinson & Smith, 2001] with a 12-parameter fit (for humans), and the transforms were cumulated and applied to bring the functional images into the template space. The MRI images were segmented into 3 (rhesus) or 4 (human) tissue classes: cerebral spinal fluid (CSF), gray matter (GM). white matter (WM), and “other” using FAST (rhesus) [Zhang et al., 2001] or MFAST (human). Visual inspection was performed after each step, and 7 human subjects (of 32) were rejected due to poor segmentation.

The Gray-Matter Probability (GMP) maps were masked (i.e. voxels outside of the brain set to 0), then smoothed with a Gaussian kernel (rhesus:4mm, humans:7mm) to yield images with approximately the same smoothness as the corresponding functional data, in order to minimize partial volume effects. The smoothness of the contrast image maps was estimated using the AFNI program “3dFWHM” (http://afni.nimh.nih.gov/afni/) [Cox 1996] to verify that the paired modality’s data were similar in this regard. Average smoothnesses (mm FWHM) were: rhesus PET:4.80; rhesus GMP:6.27; human fMRI and GMP:9-10. Prior to groupwise analysis, the GMP images were zero-meaned, i.e. the mean GMP map calculated across subjects was subtracted from each subject’s GMP map. The resulting voxel-wise GMP covariates (x’_j from Eq. 2) are the primary focus of this work.

III. Results

PET results

The original between-group functional analysis yielded several significant clusters; two clusters, in prefrontal cortex and putamen, are shown in Fig. 1b. The smaller cluster at the top is in Area 13 (orbito-frontal lobe) while the larger lower cluster is in the putamen. The corresponding analysis of between-group GM differences also yielded several clusters (Fig. 1a), with one of particular interest since it overlaps a functional activation cluster. Simply excluding this functional cluster from further consideration risks making two mistakes: i) there still may be a significant contribution due to actual differences in metabolism that would be ignored; and ii) since the GM activation cluster is drawn from a continuous 3D map, it is possible that anatomical differences contribute to the functional result beyond the statistically significant GM-difference cluster, so ignoring sub-significant anatomical differences may lead to the acceptance of false functional activations.

Figure 1.

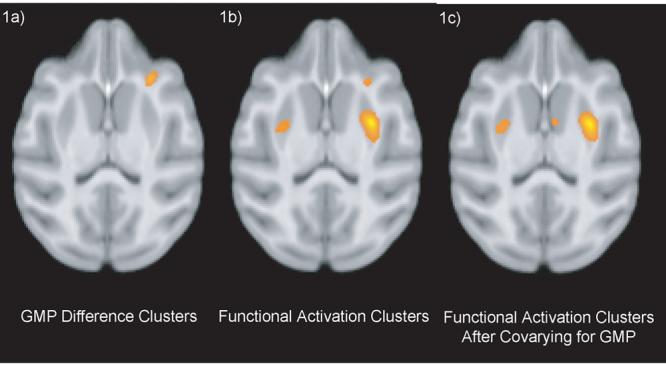
Rhesus FDG-PET activation results. 1a) cluster showing VBM result for between-group difference in GMP. 1b) results for a standard GLM between-group comparison of FDG metabolism. 1c) Functional activation from Fig. 1b, but including gray matter probability as a voxelwise covariate (as in Eq. 2). All results are thresholded at p<0.005 uncorrected.

The original functional activations (Fig. 1b) were included in two different models to account for anatomical differences that could affect the interpretation of functional results. The first model uses Eq. 2, and Fig. 1c demonstrates the functional activation remaining after removing the voxelwise GM-probability covariate. The second model performs a hierarchical linear regression to calculate ΔR² (Eqs. 3-7) and its significance via the F_change (Eq. 8), and can be used to determine the fraction of the effect that is attributable only to the functional data (image data not shown). The resulting maps have a nearly identical spatial pattern but a somewhat different interpretation. A summary of each cluster’s maximum voxel is shown in Table 1.

Table 1.

Summary of rhesus FDG-PET data for two exemplary significant clusters. The coordinates (x, y, z) are in mm relative to the posterior edge of the anterior commisure (AC). The maximal value from the standard functional analysis is indicated by “Standard GLM t-test” for each cluster. At each cluster maximum, the corresponding VBM results (“GMP t-test”) were extracted, as were the t-test value for the analysis using voxelwise VBM results as a covariate as in Eq. 2 (“GLM with voxelwise GMP covariates”) and the associated F-change as in Eq. 8 (“F-change”).

	putamen	area 13
coordinates (mm from AC)	13.8, -0.6, 6.3	12.5, 11.9, 5.0
GMP t-test	-1.00	-3.06
Standard GLM t-test	-4.45	-3.20
GLM with voxelwise GMP covariates	-4.35	-1.93
F-change	5.89	1.26

In both models, the functional activation in prefrontal cortical Area 13 is removed and can be attributed primarily to differences in underlying anatomy. However, the functional activation in the putamen, which demonstrates little influence due to anatomical differences, remains as a significant cluster.

fMRI results

Results from the fMRI data are used to illustrate three different effects of incorporating voxelwise GMP values as covariates:

1. A functional activation remains unaffected since there is only a small GMP effect.

2. An increase in magnitude and size of functional effect cluster due to better modeling of anatomically-related variance.

3. A functional activation is removed (fails to remain significant) due to colocalization with VBM activation.

These effects are listed in the order of the number of occurrences observed in this fMRI data set, i.e. most of the significant activation clusters were unaffected, many of the clusters increased in size and/or magnitude, and a few of the clusters were removed.

Figure 2 shows three examples of affected clusters from various locations. The t-values under the crosshairs are listed in Table 2. GLM results are displayed with a lower threshold of t=1.9, set slightly below the statistical threshold of 2.05 (p<0.05) to illustrate the effect of voxelwise covariates on marginally subthreshold data.

Figure 2.

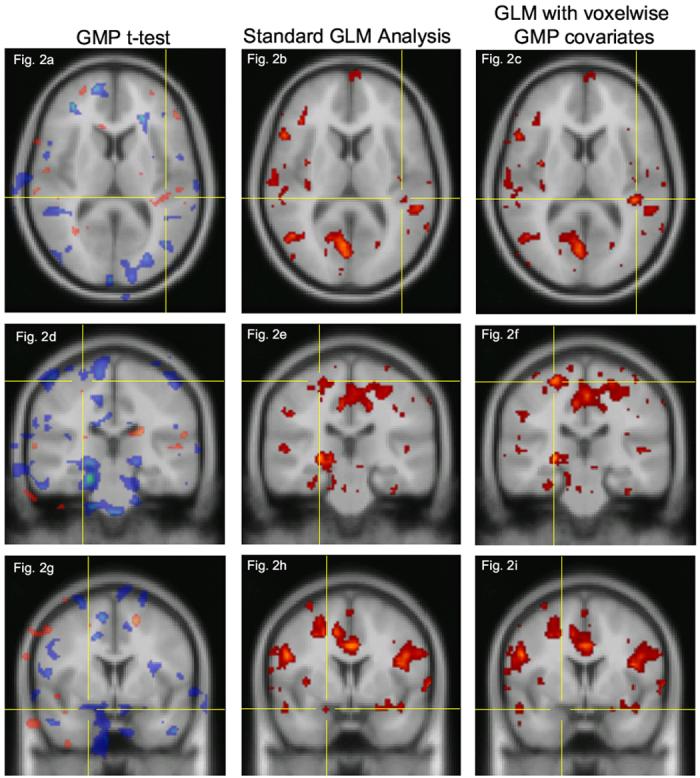
Human fMRI activation results at three locations. Left column: t-statistic map for GMP differences between groups showing a 2-tailed t-test. Negative t-values are shown in blue, positive values in red. Center column: Standard GLM analysis. Right column: GLM analysis with voxelwise Gray Matter Probability (GMP) covariates included in the model. Color scale is the same for both functional SPMs (center and right columns), which have a lower threshold of t=1.9, set slightly below the statistical threshold of t=2.05 (p<0.05). Top row and middle row: the functional cluster designated by the crosshairs increased in both size and magnitude with GMP voxelwise covariates. Bottom row: the cluster designated by the crosshairs drops below the significance level when GMP voxelwise covariates are included in the model. Note how in all three rows, most of the clusters are unchanged. See text for description of data and analysis.

Table 2.

Summary of human fMRI data for three exemplary clusters. The t-values were obtained from the pixels at the center of the crosshairs in each of the images from Fig. 2. Labeling in first column follows same scheme as in Table 1. Statistical significance (p<0.05) is achieved for t=2.05.

	Figs. 2a-c	Figs. 2d-f	Figs. 2g-i
coordinates (mm from AC)	42, -32, 10	-26, -26, 62	-22, 2, -18
GMP t-test	2.21	-1.32	-1.23
Standard GLM t-test	1.93	2.21	2.40
GLM with voxelwise GMP covariates	4.07	3.91	1.87
F-change	16.54	15.25	3.52

The outstanding feature of this comparison is that most of the activation clusters remain unchanged, indicating that the proposed method is fairly selective. The top two rows show clusters (designated by crosshairs) which grew larger in both magnitude and size when voxelwise GMP covariates were 20 included in the model, presumably due to improved modeling of sources of variance. In particular, the cluster emphasized in the top row was small and just at the threshold for statistical significance with the standard GLM analysis, but became quite significant when GMP covariates were included in the model. The bottom row shows a cluster which drops below the significance level when GMP covariates were included, indicating that the original activation is driven substantially by an underlying anatomical difference between subject groups rather than solely by a true metabolic difference.

IV. Discussion

Activation clusters are drawn from a continuous 3D map of t-values, but they are typically examined only when they reach an acceptable level of statistical significance. Thus, although a functional activation can appear free of anatomical contamination when examining thresholded VBM maps, there may still be a major component attributable to sub-significant anatomical differences. It is crucial to account for this contribution throughout the entire brain volume, and not just on a case-by-case basis for only the significant functional and VBM clusters. Furthermore, the voxelwise variation of tissue class can be expected to account for an important proportion of variance, so including it as a covariate in the model can lead to an increase in functional t-statistic values in multiple regions.

There are two major limitations to this approach: (i) the sensitivity of VBM to non-normality in the error term of the model, and (ii) the accuracy and intersubject consistency of the segmentation. Neither of these limitations are specific to this approach, but rather are derived from well-known limitations in the constituent methodologies. The VBM method can be sensitive to non-normality in the error term due to e.g. an unbalanced design or minimal spatial smoothing [Salmond et al., 2002], leading to an increase in false-positive results. When VBM is integrated into the analysis of functional data, any false positives will reduce the significance of cospatial functional results. In both data sets (humans and rhesus), the segmentation algorithm had difficulty in consistently assigning deep GM structures (striatum, amygdala) to the GM segment, so the GMP covariates had little effect on these regions. Poor image quality (e.g. poor GM/WM contrast, large inhomogeneity artifacts) can adversely affect segmentation. It is important to inspect the individual and group segment maps, since regions that are inaccurately or inconsistently segmented will not receive the appropriate correction. Poor segmentation examples might require focused attempts with automated or manual segmentation tools, or for extreme cases, exclusion from analysis. As image acquisition methods and segmentation algorithms improve, the quality of the segmentation will become less of an issue in the implementation of this technique. In the two data sets presented here, incorrectly segmented regions seem to have little effect on the original GLM activation estimates; the hoped-for correction based on GMP does not occur, but in these regions the estimate is at least no worse than if the correction had not been attempted.

VBM results can be fairly sensitive to the size of the smoothing kernel used to smooth the tissue segment images. The criteria used in this work was to match the smoothness of the GMP data to that of the corresponding functional data. Note that “smoothness” is not necessarily the same as “voxel size”, but rather refers to the spatial extent and magnitude of autocorrelation across the image. GMP data which are undersmoothed, due e.g. to poor signal:noise ratio and/or small voxel size, can add undesirable noise to subsequent processing steps. If the GMP data are much smoother than the functional data, a partial volume effect will result, most likely resulting in reduced sensitivity of the GMP correction. By matching the smoothness of the two modalities, the noise properties become similar and also the partial volume effect is minimized, yielding more consistent results across subjects.

The usual assumption is that anatomical differences are always more important than functional differences, i.e. any functional difference in a region of anatomical difference is suspect. However, one could also create an R²-term for the effect of function alone and estimate the residual or sole effect of function and subtract this from the dual effect of function and anatomy to find out the unique contribution of anatomy. The F_change metric (Eq. 8) can be used to examine the effect of including voxelwise covariates and whether the full model is needed (e.g. [Clogg et al., 1992]), or an optimization technique such as a “backward” or “stepdown” approach [Neter et al., 1996; Rao and Toutenburg, 1999] could be employed to determine the benefit of including voxelwise covariates. However, an unresolved issue is how this information should be used. Reducing the voxelwise F_change metric to a single global descriptor might lead to neglecting local regions in need of correction, while on the other hand an unbiased approach would be needed to apply the method to only a subset of activation clusters.

Intriguingly, the use of voxelwise GMP covariates is a specific instance of a technique which can be generalized to compare any multimodal image data. For instance, functional data such as fMRI and PET could be combined to determine where overlapping as well as unique activations are found in each modality. Another application would be to use MRI perfusion to see how baseline metabolism is associated with subsequent fMRI activation results, a question that might be of paramount importance in clinical studies of groups expected to show underlying baseline differences. Recent work by Casanova et al. [2006] facilitates the interchange of anatomical and functional image data between the primary and secondary data source using voxelwise covariates, encouraging the inspection of data from several viewpoints. Furthermore, the approach is not limited to using a single covariate. By combining multiple voxelwise covariates, seemingly disparate data sources can be integrated into a single comprehensive analysis. For instance, EEG, fMRI and PET have quite different temporal scales and neurological interpretations; most previous multimodal analyses have been limited to colocalization of significant effects, but by casting these data as voxelwise covariates the unique aspects of each data set could be more fully explored. The data presented here represent two specific implementations of a method that can easily be generalized to include a broad spectrum of data.

V. Conclusion

Type I error, incorrectly rejecting the null hypothesis, can result when an apparent functional activation is actually due to an underlying difference in tissue type. Type II error, failing to reject a false null hypothesis, can result if there are unmodeled sources of variance in the data. The proposed method of including voxelwise tissue information as a covariate in a GLM analysis of functional data can reduce both Type I and Type II error rates. The major limitation on the accuracy of this method is the validity of the covariates, in this case the GMP maps, requiring critical evaluation of the gray matter segmentation step. Nevertheless, given the ease and popularity of performing VBM analysis, the inclusion of gray matter probability maps as a voxelwise covariate in functional data analysis should become a routine aid for data interpretation.