A Model of Interdomain Mobility in a Multi-Domain Protein

Abstract

Domain mobility plays essential role in the biological function of multidomain systems. The characteristic times of domain motions fall into the interval from nano- to milliseconds, amenable to NMR studies. Proper analysis of NMR relaxation data for these systems in solution has to account for interdomain motions, in addition to the overall tumbling and local intradomain dynamics. Here we propose a model of interdomain mobility in a multi-domain protein, which considers domain reorientations as exchange/interconversion between two distinct conformational states of the molecule, combined with fully anisotropic overall tumbling. Analysis of ¹⁵N-relaxation data for Lys48-linked di-ubiquitin at pH4.5 and 6.8 showed that this model adequately fits the experimental data and allows characterization of both structural and motional properties of di-ubiquitin, thus providing information about the relative orientation of ubiquitin domains in both interconverting states. The analysis revealed that the two domains reorient on a time scale of 9–30 ns, with the amplitudes sufficient for allowing a protein ligand access to the binding sites sequestered at the interface in the closed conformation. The analysis of possible mechanism controlling the equilibrium between the interconverting states in di-ubiquitin points toward protonation of His68, which results in three different charged states of the molecule, with zero, +e, and +2e net charge. Only two of the three states are noticeably populated at pH4.5 or 6.8, which assures applicability of the two-state model to di-ubiquitin at these conditions. We also compare our model with the “extended model-free” approach and discuss possible future developments of the model.

Introduction

Many proteins in the cell have modular architecture, i.e. they are composed of several well-folded regions (domains). Relative orientation of the domains and interdomain dynamics often play key regulatory role in functional regulation and molecular recognition events in these systems ^1–3. NMR is a powerful tool for studying molecular motions, and recent developments based on spin-relaxation and residual dipolar coupling measurements offer a unique possibility to characterize the conformation and dynamics of multi-domain proteins. Despite significant progress in the determination of interdomain orientation by these methods ^4–9, the process of interdomain motion is largely unexplored.

Reorientational motion detected in NMR experiment in solution results from a combination of the overall tumbling and inter- and intradomain dynamics. Deconvolution and separate characterization of these motions from experimental data is non-trivial. A full analysis, accounting for coupling between various modes of motion in a protein, is extremely complex and could involve a many-body stochastic treatment of rotational motions, e.g. like that of Freed and co-workers ^10,11. Recent approaches ^12–18 based on mode-coupling ideas have been focused on the effect of the overall tumbling on intradomain dynamics. Adequate treatment of multidomain systems, however, requires account for the effect of domain motion on the shape/overall tumbling of the molecule and vice versa, and is currently not available.

The only quantitative treatment of interdomain motions in a protein thus far was the analysis of domain dynamics in Ca²⁺-ligated calmodulin by Tjandra and co-authors ^19,20, based on a variant of the so-called “extended model-free” approach ²¹. In this model, the overall tumbling and interdomain dynamics are considered independent from each other, and the latter is characterized by an order parameter that measures the angular amplitude of domain motions. The structure of calmodulin in the Ca²⁺-ligated form is characterized by the absence of a definitive interdomain conformation, thus the “extended model-free” or “wobbling-in-a-cone” models ^19,20,22 considering a continuum of available interdomain orientatons seem adequate for that protein. While acceptable in describing domain dynamics in calmodulin, these models have limited applicability when the distribution of domain orientations is asymmetric or discontinuous, like in the case of Lys48-linked di-ubiquitin (Ub₂) considered here. Indeed, NMR data²³ clearly indicate that in solution Ub₂ is in fast dynamic equilibrium between a “closed” conformation with a well-defined Ub/Ub interface and one of more “open” conformations with no direct contact between Ub domains. Models that could adequately represent this situation are currently missing.

Here we present a more structurally detailed than the “model-free” yet still simple model that describes interdomain dynamics in a dual-domain system as interconversion (exchange²⁴) between two distinct conformational states (ITS) of the molecule. The two-state-exchange paradigm is often used as the simplest model of a system undergoing transitions between distinct states. With regard to NMR applications to protein dynamics, exchange or random jump models were applied to fast internal rotations in a molecular label ²⁵ and in amino acid side chains ²⁶. Inspired by these papers, we applied similar ideas to describe reorientational dynamics of protein domains. We show that analysis of ¹⁵N relaxation data for Lys48-linked di-ubiquitin based on the ITS model allows determination of both the motional characteristics and the structure of the molecule in the two interconverting states. A preliminary analysis of Ub₂’s dynamics has been published elsewhere ²⁷, here we focus on theoretical aspects of the model, its justification, and further development.

Theory

NMR relaxation measurements directly probe the spectral density function (e.g. ref.28), J(ω), which is a cosine Fourier transform of the time-dependent angular autocorrelation function C(t) describing reorientational motion of an internuclear vector under the observation (throughout this paper we focus on ¹⁵N relaxation, hence the ¹⁵N-¹H-bond motion):

$$J(\omega )=2{\displaystyle \underset{0}{\overset{\infty }{\int }}\text{cos}(\omega t)\text{}C(t)dt}$$ (1)

where

$$C(t)={\langle D_{q,0}^{(2)*}({\mathrm{\Omega }}_{L\to I}^0)D_{q,0}^{(2)}({\mathrm{\Omega }}_{L\to I}^t)\rangle }_{L\to I}.$$ (2)

Here $D_{m,n}^{(2)}\left(\mathrm{\Omega }\right)$ is an element of the Wigner rotation matrix ²⁹ (Supporting Information), the asterisk means complex conjugation, and Ω_L→I = {α_L→I, β_L→I, γ_L→I} denotes a set of three Euler angles (0 ≤ α_L→I ≤ 2π, 0 ≤ β_L→I ≤ π , and 0 ≤ γ _L→I ≤ 2π) which specify the orientation of a unit vector µ in the direction of a given NH vector with respect to the laboratory coordinate frame (L), aligned with the static magnetic field ${\overrightarrow{B}}_o$ (see Fig.1 ). Note that, strictly speaking, only two Euler angles are required to define the orientation of a vector, i.e. the value of the angle γ_L→I is arbitrary. However, for consistency with the other definitions of coordinate frames (see below), we define an “instantaneous” coordinate frame (I) with its z-axis along the instantaneous direction of the NH bond, and the x,y-axes defined such that, for simplicity, γ_L→I = 0.

Figure 1.

Schematic representation of the various reference frames introduced here and the rotational transformations between them.

Note that the general expression for the correlation function in the right-hand side of Eq. 2 explicitly contains the index q. However, in the case of protein tumbling in isotropic solutions considered in this work, the correlation functions (Eq.2) for different values of q are all equal – this is a consequence of the orientational (ensemble) averaging in the isotropic medium²⁸. Thus the correlation function C(t) and the corresponding spectral density J(ω) both are independent of the actual value of q.

The angular brackets 〈…〉_L→I in Eq. 2 denote an equilibrium ensemble-averaging with respect to all possible initial, ${\mathrm{\Omega }}_{L\to I}^0$, and final, ${\mathrm{\Omega }}_{L\to I}^t$, orientations of µ, separated by the time interval t:

$$\begin{array}{l}{\langle D_{q,0}^{(2)*}({\mathrm{\Omega }}_{L\to I}^0)D_{q,0}^{(2)}({\mathrm{\Omega }}_{L\to I}^t)\rangle }_{L\to I}=\\ \hfill ={\displaystyle \iint D_{q,0}^{(2)*}({\mathrm{\Omega }}_{L\to I}^0)D_{q,0}^{(2)}({\mathrm{\Omega }}_{L\to I}^t)P_{eq}^{LI}({\mathrm{\Omega }}_{L\to I}^0)P^{LI}({\mathrm{\Omega }}_{L\to I}^0|{\mathrm{\Omega }}_{L\to I}^t,t)d{\mathrm{\Omega }}_{L\to I}^{0}d{\mathrm{\Omega }}_{L\to I}^t}\end{array}$$ (3)

where $P_{eq}^{LI}({\mathrm{\Omega }}_{L\to I}^0)d{\mathrm{\Omega }}_{L\to I}^0$ is the equilibrium probability to have the initial orientation of µ in the angular interval $({\mathrm{\Omega }}_{L\to I}^0,{\mathrm{\Omega }}_{L\to I}^0+d{\mathrm{\Omega }}_{L\to I}^0)\text{and}{P}^{LI}\left({\mathrm{\Omega }}_{L\to I}^0|{\mathrm{\Omega }}_{L\to I}^t,t\right)d{\mathrm{\Omega }}_{L\to I}^t$ is the conditional probability that at the time moment t the orientation of µ is within the interval $({\mathrm{\Omega }}_{L\to I}^t,{\mathrm{\Omega }}_{L\to I}^t+d{\mathrm{\Omega }}_{L\to I}^t)$ provided that the initial orientation (at t=0) was $({\mathrm{\Omega }}_{L\to I}^0)$.

Thus the problem of describing protein dynamics is reduced to the determination of the probability density functions, $P_{eq}^{LI}({\mathrm{\Omega }}_{L\to I}^0)\text{and}{\text{P}}^{LI}({\mathrm{\Omega }}_{L\to I}^0|{\mathrm{\Omega }}_{L\to I}^t,t)$, which enter Eq. 3. In principle, these functions could be obtained from the corresponding stochastic dynamics equation (for example, a Fokker-Planck or Smoluchowski equation) that should account for all interactions, both within a protein and with the solvent. However, the complexity of proteins as molecular systems possessing a variety of motions with different amplitudes and time scales makes such ab initio theoretical description impossible. This leads to the necessity of developing a model that would account for the motions of interest.

The model

In this paper we consider motions relevant to spin relaxation in a NH group in protein backbone, and therefore consider only orientational dynamics leading to a change in orientation of a given NH-bond vector. To simplify the problem, we consider three dynamic modes:

1. the overall tumbling of the protein as a whole;

2. the interdomain-mobility mode, that is the reorientation of one domain with respect to the other; and

3. the local dynamics mode, which includes a wobbling-type motion of a given NH bond about its average orientation with respect to a coordinate frame associated with each individual domain.

To separate and analyze the contributions from these dynamics modes to the NMR-observed picture of the NH-bond motion, we consider the orientation of the NH vector with respect to the static magnetic field ${\overrightarrow{B}}_o$ as a set of subsequent rotations: from the laboratory frame L to the protein reference frame (P) which describes rotation of a protein as a whole (e.g. the principal axes frame of the rotational diffusion tensor), then to the coordinate frame (D) for each individual domain (e.g. PDB coordinate frame), then to the residue-specific frame (R) associated with the average (over the time interval longer than the correlation time of the local motion) orientation of a given NH-vector within each individual domain, and, finally, to the instant frame (I) attached to the NH-vector (Fig. 1). These rotations are characterized by the four sets of Euler angles: angles: Ω_L→P, Ω_P→D, Ω_D→R, and Ω_R→I, respectively.

Using properties of Wigner rotation matrices (see Supporting Information) Eq. 2 can then be rewritten in the following form

$$\begin{array}{l}C(t)={\displaystyle \sum _{m=-2}^2{\displaystyle \sum _{n=-2}^2{\displaystyle \sum _{k=-2}^2{\displaystyle \sum _{l=-2}^2{\displaystyle \sum _{s=-2}^2{\displaystyle \sum _{h=-2}^2\langle D_{q,m}^{(2)*}({\Omega }_{L\to P}^0)D_{q,n}^{(2)}({\Omega }_{L\to P}^t)D_{m,k}^{(2)*}({\Omega }_{P\to D}^0)D_{n,l}^{(2)}({\Omega }_{P\to D}^t)}}}}}}\\ \hfill {\times D_{k,s}^{(2)*}({\Omega }_{D\to R}^0)D_{l.h}^{(2)}({\Omega }_{D\to R}^t)D_{s,0}^{(2)*}({\Omega }_{R\to I}^0)D_{h,0}^{(2)}({\Omega }_{R\to I}^t)\rangle }_{L\to I}\end{array}$$ (4)

The model considered here rests on two assumptions:

Postulate I

All three dynamics modes: the overall, interdomain, and local, are statistically independent from each other. This allows factorization of each term in Eq. 2 into a product of separate correlation functions corresponding to these modes (see below).

Postulate II

On a time scale slower than the characteristic time of local NH-bond (wobbling) motion the tertiary structure of each domain holds constant, therefore the Euler angles Ω_D→R that describe the averaged orientation of a NH bond with respect to the domain’s reference frame are time-independent.

The usual justification for an assumption like Postulate I is the large separation of the characteristic time scales of the motions. Indeed, the experimentally observed correlation time for local (internal) dynamics in proteins (τ_local) is typically in the 1–100 ps range (e.g. ³⁰), whereas the overall tumbling time (τ_overall) is of the order of several nanoseconds and longer (~8 ns for Ub₂ ²³). Thus the statistical independence of these two modes of motion seems a reasonable approximation and is typically assumed, as e.g. in the model-free approach ^31,32, although the effect of their coupling on local motion has recently been included in data analysis ^14–18.

The situation with interdomain motion is more complex, and one can envision several scenarios. The characteristic time scale of the interdomain dynamics (τ_interdomain) could either fall in-between (i.e. the hierarchy of the time scales is formulated as τ_overall >> τ_interdomain >> τ_local) or could significantly exceed the overall tumbling time, τ_interdomain>> τ_overall >> τ_local. Moreover, the difference between the time scales of the overall and interdomain motions could be less pronounced, as e.g. in the case of calmodulin ¹⁹, where τ_interdomain ≈ 3 ns compared to τ_overall ≈ 9 ns. If domain reorientation involves tumbling within some energy well, rather than crossing of substantial energy barriers, one might expect that the ratio of τ_interdomain and τ_overall should reflect the ratio of the rotational friction coefficients (in solution) for the domain and for the whole protein molecule.

Rigorous mathematical treatment of such a system is further complicated by the fact that domain motion can alter the shape of the molecule, hence the assumption of time-independent rotational diffusion tensor might not be valid in the general case. Unlike the restricted local (intradomain) backbone dynamics that are not expected to affect the rotational diffusion, the interdomain dynamics and the overall tumbling could have mutual effect. Adequate treatment of this phenomenon is currently not available. This problem, however, does not exist in a hypothetical case of spherical-shape domains, when their only motion involves rotations around the (fixed) centers of mass of each individual domain, because these rotations will not change the overall shape or the diffusion tensor of the molecule. Our analysis of data (below) suggests that, to a good approximation, Ub₂ falls into this category.

The hierarchy of time scales could also imply causality, in that the properties of slower time-scale dynamics are determined by motion on faster time-scales. In contrast, Postulate I assumes no causality between the dynamic modes under consideration, which are therefore completely decoupled from each other (see also below).

Under these assumptions the correlation function Eq. 4 simplifies:

$$\begin{array}{l}C(t)={\displaystyle \sum _{m=-2}^2{\displaystyle \sum _{n=-2}^2{\displaystyle \sum _{k=-2}^2{\displaystyle \sum _{l=-2}^2{\displaystyle \sum _{s=-2}^2{\displaystyle \sum _{h=-2}^2\langle D_{q,m}^{(2)*}}}}}}}\left({\mathrm{\Omega }}_{L\to P}^0\right)D_{q,n}^{(2)}{\left({\mathrm{\Omega }}_{L\to P}^t\right)\rangle }_{L\to P}·\langle D_{m,k}^{(2)*}\left({\mathrm{\Omega }}_{P\to D}^0\right)D_{n,l}^{(2)}{\left({\mathrm{\Omega }}_{P\to D}^t\right)\rangle }_{P\to D}\times \\ \hfill D_{k,s}^{(2)*}\left({\mathrm{\Omega }}_{D\to R}\right)·D_{l,h}^{(2)}\left({\mathrm{\Omega }}_{D\to R}\right)·\langle D_{s,0}^{(2)*}\left({\mathrm{\Omega }}_{R\to I}^0\right)D_{h,0}^{(2)}{\left({\mathrm{\Omega }}_{R\to I}^t\right)\rangle }_{R\to I}=\hfill \\ \hfill ={\displaystyle \sum _{m=-2}^2{\displaystyle \sum _{n=-2}^2{\displaystyle \sum _{k=-2}^2{\displaystyle \sum _{l=-2}^2{\displaystyle \sum _{s=-2}^2{\displaystyle \sum _{h=-2}^2{C}_{qm,qn}^{LP}\left(t\right)·C_{mk,nl}^{PD}\left(t\right)·D_{k,s}^{\left(2\right)*}\left({\mathrm{\Omega }}_{D\to R}\right)·D_{l,h}^{\left(2\right)}\left({\mathrm{\Omega }}_{D\to R}\right)·C_{s0,h0}^{RI}\left(t\right)}}}}}}\hfill \end{array}$$ (5)

This equation implies that each dynamic mode can be described by its own correlation function:

$$\text{overall}\text{tumbling}:C_{qm,qn}^{LP}\left(t\right)=\langle D_{q,m}^{(2)*}({\mathrm{\Omega }}_{L\to P}^0)D_{q,n}^{(2)}{({\mathrm{\Omega }}_{L\to P}^t)\rangle }_{L\to P};$$ (6a)

$$\text{interdomain}\text{mobility}:C_{mk,nl}^{PD}\left(t\right)=\langle D_{q,m}^{(2)*}({\mathrm{\Omega }}_{P\to D}^0)D_{n,l}^{(2)}{({\mathrm{\Omega }}_{P\to D}^t)\rangle }_{P\to D};$$ (6b)

$$\text{local}\text{motion}:C_{s0,h0}^{RI}\left(t\right)=\langle D_{s,0}^{(2)*}({\mathrm{\Omega }}_{R\to I}^0)D_{h,0}^{(2)}{({\mathrm{\Omega }}_{R\to I}^t)\rangle }_{R\to I}.$$ (6c)

Each of these correlation functions has its own pair of probability density functions (cf. Eq. 3), $P_{eq}^{LP}({\mathrm{\Omega }}_{L\to P}^0)\text{and}{\text{P}}^{LP}({\mathrm{\Omega }}_{L\to P}^0|{\mathrm{\Omega }}_{L\to P}^t,t)$ for overall tumbling, $P_{eq}^{PD}({\mathrm{\Omega }}_{P\to D}^0)\text{and}{\text{P}}^{PD}({\mathrm{\Omega }}_{P\to D}^0|{\mathrm{\Omega }}_{P\to D}^t,t)$ for interdomain mobility, and and $P_{eq}^{RI}({\mathrm{\Omega }}_{R\to I}^0)\text{and}{P}^{RI}({\mathrm{\Omega }}_{R\to I}^0|{\mathrm{\Omega }}_{R\to I}^t,t)$ for local motion; and every pair of probability densities is assumed to be independent from the others. Thus, in the framework of this model the description of NMR-relevant dynamics in a multidomain protein reduces to the problem of deriving the corresponding equilibrium and conditional probability densities. These functions are considered here for each of the dynamics modes specified above.

The overall tumbling mode

For the overall tumbling we used the model of rotational diffusion of a fuly anisotropic rigid body ^33,34. Following the derivation by Favro ³³, we write

$$C_{qm,qn}^{LP}\left(t\right)=\langle D_{q,m}^{(2)*}({\mathrm{\Omega }}_{L\to P}^0)D_{q,n}^{(2)}{({\mathrm{\Omega }}_{L\to P}^t)\rangle }_{L\to P}=\frac{1}{5}{\displaystyle \sum _{r=-2}^2{e}^{-E_{r}t}{a}_{r,m}^{*}{a}_{r,n}}$$ (7)

where a_r,_m are decomposition coefficients and E_r are the corresponding rate constants which depend solely on the principal values {D_x, D_y, D_z} of the rotational diffusion tensor D (see Supporting Information).

Note that the representation in Eq. 7 assumes a diagonal form of the diffusion tensor, which implies that protein reference frame P is the principal axes frame (PAF) of the diffusion tensor. Another point worth mentioning here is that Eq. 7 implies that the principal values of the diffusion tensor remain constant; this follows from Postulate I, in that the characteristics of the overall tumbling are considered independent of the other dynamics modes in a protein. This approximation might not hold for those proteins where interdomain mobility could alter the overall diffusion tensor.

The domain mobility mode

The simplest model of domain mobility considered here involves interconversion between two states (ITS) of the protein, states A and B, characterized by distinct orientations of each domain with respect to the protein’s global coordinate frame P. These orientations are given for each domain by two sets of Euler angles, $({\mathrm{\Omega }}_{P\to D}^A)$ and $({\mathrm{\Omega }}_{P\to D}^B)$, and the transitions from A to B and backwards are characterized by the rate constants k_AB and k_BA, respectively. We also assume here that the domain structure and intradomain (backbone) dynamics are the same in both states (see Postulate II).

In this case the continuous probability density functions, that determine the statistical averaging of the correlation function, Eq. 6b, have to be replaced with discrete occupation and transition probabilities:

$$\begin{array}{l}{C}_{mk,nl}^{PD}\left(t\right)=\langle D_{m,k}^{(2)*}({\mathrm{\Omega }}_{P\to D}^0)D_{n,l}^{(2)}{({\mathrm{\Omega }}_{P\to D}^t)\rangle }_{P\to D}=\\ \hfill ={\displaystyle \sum _{{\mathrm{\Omega }}_{P\to D}^0,{\mathrm{\Omega }}_{P\to D}^t={\mathrm{\Omega }}_{P\to D}^A,{\mathrm{\Omega }}_{P\to D}^B}{p}_{eq}\left({\mathrm{\Omega }}_{P\to D}^0\right)p\left({\mathrm{\Omega }}_{P\to D}^0|{\mathrm{\Omega }}_{P\to D}^t,t\right)D_{m,k}^{(2)*}({\mathrm{\Omega }}_{P\to D}^0)D_{n,l}^{(2)}({\mathrm{\Omega }}_{P\to D}^t)}\end{array}$$ (8)

where the conditional probabilities

$$\begin{array}{c}p\left({\mathrm{\Omega }}_{P\to D}^A|{\mathrm{\Omega }}_{P\to D}^A,t\right)=p_A+p_B\text{exp}\left\{-t/{\tau }_{ITS}\right\}\\ \hfill p\left({\mathrm{\Omega }}_{P\to D}^A|{\mathrm{\Omega }}_{P\to D}^B,t\right)=p_B\left(1-\text{exp}\left\{-t/{\tau }_{ITS}\right\}\right)\hfill \\ \hfill p\left({\mathrm{\Omega }}_{P\to D}^B|{\mathrm{\Omega }}_{P\to D}^A,t\right)=p_A\left(1-\text{exp}\left\{-t/{\tau }_{ITS}\right\}\right)\hfill \\ \hfill p\left({\mathrm{\Omega }}_{P\to D}^B|{\mathrm{\Omega }}_{P\to D}^B,t\right)=p_B+p_A\text{exp}\left\{-t/{\tau }_{ITS}\right\}\hfill \end{array}$$ (9)

are given by the solutions to the corresponding kinetic equations (Supporting Information), and the occupation probabilities

$$\begin{array}{c}{p}_A\equiv p_{eq}\left({\mathrm{\Omega }}_{P\to D}^A\right)=\frac{k_{BA}}{k_{AB}+k_{BA}}\\ \hfill p_B\equiv p_{eq}\left({\mathrm{\Omega }}_{P\to D}^B\right)=\frac{k_{AB}}{k_{AB}+k_{BA}}\hfill \end{array}$$ (10)

are normalized, p_A + p_B = 1, and satisfy the condition of detailed balance, p_A/k_BA = p_B/k_AB, where k_AB and k_BA are the forward and backward transition rates, respectively. The characteristic correlation time for this interconversion mode, τ_ITS = 1/(k_AB+k_BA), is the reciprocal of the interconversion rate, K = k_AB+k_BA.

Combining Eq. 8–Eq. 10, the correlation function describing the interdomain mobility mode can be recast in a “model-free”-like form (cf. Eq(12)):

$$C_{mk,nl}^{PD}\left(t\right)=\langle D_{m,k}^{(2)*}({\mathrm{\Omega }}_{P\to D}^0)D_{n,l}^{(2)}{({\mathrm{\Omega }}_{P\to D}^t)\rangle }_{P\to D}=S_{mk,nl}^2+\left(Q_{mk,nl}-S_{mk,nl}^2\right)\text{exp}\left(-t/{\tau }_{ITS}\right)$$ (11a)

where matrix

$$Q_{mk,nl}=p_A{D}_{m,k}^{(2)*}({\mathrm{\Omega }}_{P\to D}^A)D_{n,l}^{(2)}({\mathrm{\Omega }}_{P\to D}^A)+p_B{D}_{m,k}^{(2)*}({\mathrm{\Omega }}_{P\to D}^B)D_{n,l}^{(2)}({\mathrm{\Omega }}_{P\to D}^B)$$ (11b)

replaces the unity matrix and

$$S_{mk,nl}^2=\left[p_A{D}_{m,k}^{(2)*}({\mathrm{\Omega }}_{P\to D}^A)+p_B{D}_{m,k}^{(2)*}({\mathrm{\Omega }}_{P\to D}^B)\right]\left[p_A{D}_{n,l}^{(2)}({\mathrm{\Omega }}_{P\to D}^A)+p_B{D}_{n,l}^{(2)}({\mathrm{\Omega }}_{P\to D}^B)\right]$$ (11c)

is a matrix analog of the (scalar) squared order parameter.

The local mobility mode

Detailed description of the correlation function of local mobility, Eq. 6c, requires proper selection of the model of motion (not known a priori) for a given group of atoms (for a review see e.g. ref. 35). This problem can be circumvented by using the so-called “model-free” approach ^31,32 that assumes a simple form for the correlation function:

$$C_{s0,h0}^{RI}\left(t\right)={\langle D_{s,0}^{(2)*}\left({\mathrm{\Omega }}_{R\to I}^0\right)D_{h,0}^{(2)}\left({\mathrm{\Omega }}_{R\to I}^t\right)\rangle }_{R\to I}={\delta }_{s,0}{\delta }_{h,0}\left[S^2+\left(1-S^2\right)\text{exp}\left\{-t/{\tau }_{loc}\right\}\right]$$ (12)

where δ_a,b is the Kronecker delta, τ_loc is the correlation time for local motion, and S is the generalized order parameter: $S=\langle D_{0,0}^{(2)*}({\mathrm{\Omega }}_{R\to I}^0)\rangle =\langle D_{0,0}^{(2)}({\mathrm{\Omega }}_{R\to I}^t)\rangle =\langle \frac{1}{2}\left(3{\text{cos}}^2{\beta }_{R\to I}-1\right)\rangle ,$ where the equilibrium ensemble averaging 〈…〉 = ∫ …P_eq (Ω) sin β dβ is performed with respect to the Euler angle β. The order parameter is a model-independent measure of the degree of spatial restriction for the local motion: S = 0 when this motion uniformly samples all possible directions in the three-dimensional space, while S = 1 in the case of completely restricted local motion.

The “model-free” form, Eq.12, is just one of the possible models for the correlation function of local motion; examples of explicit mechanical models can be found in refs. ^25,26,35,36. It is worth mentioning here that the analysis below is focused on structurally well-defined regions in the protein, where the amplitudes of local backbone dynamics are restricted. In this case the results presented in this paper do not directly depend on the particular form of the correlation function for the local dynamics mode.

Methods

Representation of relaxation data

The analysis of ¹⁵N relaxation data here is based on the approach developed in ⁵ which, instead of dealing with actual NMR relaxation rates, is focused on their ratio

$$\rho =\frac{R_1\text{'}}{2R_2\text{'}-R_1\text{'}}\cong \frac{3J\left({\omega }_N\right)}{4J\left(0\right)}$$ (13)

where R₁ and R₂ are the ¹⁵N longitudinal and transverse relaxation rates, respectively, and the primes indicate that the measured rates were modified to subtract the contributions from high-frequency components of the spectral density (see e.g. 37):

$$\begin{array}{l}{R}_1\text{'}=R_1-6.246P_{HF}\cong 3\left(d^2+c^2\right)J\left({\omega }_N\right)\\ R_2\text{'}=R_2-5.3944P_{HF}\cong 0.5\left(d^2+c^2\right)\left[4J\left(0\right)+3J\left({\omega }_N\right)\right]\end{array}$$ (14)

where $P_{HF}=d^{2}J\left(0.87{\omega }_H\right)\cong -\frac{{\gamma }_N}{{\gamma }_H}\frac{R_1}{5}\left(1-NOE\right).$ Here γH and γN are the gyromagnetic ratios for ¹H and ¹⁵N, respectively, ω_N is the Larmor frequency of ¹⁵N, and d and c represent the strengths of the ¹H-¹⁵N dipolar coupling and of the ¹⁵N chemical shift anisotropy (CSA) (c = − ω_N ·CSA/3). As shown in refs.^5,38 the ratio ρ, Eq. 13, is independent, to the first approximation, of the site-specific values of the ¹⁵N CSA and the NH-distance. Moreover, for well-ordered regions in a protein, where the local backbone mobility is restricted (S² ≥ 0.8) and fast (τ_loc << τ_overall), J(0) and J( ω_N) both scale approximately as S², so the order parameters in the numerator and denominator of Eq. 13 cancel out, thus rendering the ratio ρ independent of the characteristics of local motion³⁸, to a good approximation³⁹.

The spectral density J( ω) for the ITS model (which takes into consideration all the dynamic modes discussed above) can be obtained as analytical Fourier transform of Eq. 5, combining Eq. 7, Eq. 11, and 12. However, because for the well-defined structural regions, considered here, the ratio ρ is insensitive to the local backbone dynamics, in the subsequent analysis we set the order parameter of local backbone motion in Eq.12 to S = 1. This essentially eliminates the contributions from local motion to the resulting spectral density function, and hence to ρ. Thus in the following analysis we replace the spectral density J(ω) in Eq.13 with its reduced form (designated here as J_ρ(ω)):

$$\begin{array}{l}{J}_{\rho }\left(\omega \right)=\frac{2}{5}{\displaystyle \sum _{m=-2}^2{\displaystyle \sum _{n=-2}^2{\displaystyle \sum _{k=-2}^2{\displaystyle \sum _{l=-2}^2{\displaystyle \sum _{r=-2}^2{a}_{r,m}^{*}{a}_{r,n}{D}_{k,0}^{(2)*}({\mathrm{\Omega }}_{D\to R})D_{l,0}^{(2)}({\mathrm{\Omega }}_{D\to R})\times }}}}}\\ \times \left\{\frac{E_r}{E_r^2+{\omega }^2}{S}_{mk,nl}^2+\frac{E_r+{\left({\tau }_{ITS}\right)}^{-1}}{{\left[E_r+{\left({\tau }_{ITS}\right)}^{-1}\right]}^2+{\omega }^2}\left(Q_{mk,nl}-S_{mk,nl}^2\right)\right\}\end{array}$$ (15)

which was obtained directly from Eq.5 as described above; an explicit expression for this spectral density can be found in our earlier paper ⁴⁰. The applicability of this treatment to Ub₂ is supported by the observation ⁶ that the backbone dynamics in the core of each Ub domain in Ub₂ are restricted and fast and the corresponding order parameters are essentially identical to those in monomeric Ub.

After this paper was submitted, we have learned that a similar, “model-free” like functional form of the spectral density in Eq.15 was recently derived by Bernatowicz et al.⁴¹ for an anisotropically tumbling molecule with the intramolecular dynamics modeled using a two-site exchange. Although our paper and that of Bernatowicz et al. both consider essentially the same physical picture of random exchange superimposed by a fully anisotropic overall tumbling, it is instructive to discuss differences between the specific models utilized here and in ref. 41. In that paper, the orientations of each individual spin pair (as, e.g., N-H group in our case) in the exchanging states are not correlated with the other pairs, and the quantities analogous to our matrices $S_{mk,nl}^2$ andQ_mk,nl (Eqs.11) are simply scalars (see Eqs. 20–22 in ref. 41). This simplifies the equations, but inevitably limits the structural information available from these parameters. The treatment applied here (see also refs. ²⁷, ref 40) is conceptually different in that we consider random exchange between orientations of the whole domain, thus the P→D transformation is applied to all spin pairs within each domain, while the local intradomain dynamics are neglected. Moreover, the use of stepwise transformations between the corresponding reference frames (Fig.1), allowed us to isolate the dependence of J(ω) on domain orientation, which is one of the principal results of our paper. The dependence of $S_{mk,nl}^2$ and Q_mk,nl on the indices k, l links J(ω) to NH-bond orientations within a given domain, which thus allowed us to determine the orientation of each domain in both interconverting states (see below); this would not be possible if $S_{mk,nl}^2$ and Q_mk,nl were scalars.

Fitting procedure and parameters

All parameters in the ITS model can be separated into two types: global parameters that describe motion of the whole protein and domain parameters that are specific for every domain. Thus, the principal values D_x, D_y, and D_z of the diffusion tensor and the transition rates k_AB and k_BA are the same for all NH vectors in the protein, as they describe reorientation of the whole protein and correlated changes in the mutual orientation of the domains. The sets of Euler angles $({\mathrm{\Omega }}_{P\to D}^A)$ and $({\mathrm{\Omega }}_{P\to D}^B)$ which specify orientation of the domain’s coordinate frame (D) with respect to the global protein coordinate frame are domain-specific, i.e. apply only to a subset of NH vectors belonging to a particular domain. The Euler angles Ω_D→R that are also present in Eq. 15 and specify the averaged orientation of each NH bond within the domain, are defined by the three-dimensional structure (e.g. PDB coordinates) of each domain and therefore are fixed throughout the analysis. Thus, when considering a protein system of n domains that simultaneously change their mutual orientation between two distinct conformations of the whole protein, the ITS model will require 5 global parameters (D_x, D_y, D_z, k_AB and k_BA) and 6n domain-specific parameters (6 Euler angles, $({\mathrm{\Omega }}_{P\to D}^B)$ and ${\mathrm{\Omega }}_{P\to D}^A$, for each domain). Thus, the total number of ITS parameters is N_p=17 in the case of Ub₂.

The parameters of the ITS model were obtained by minimizing the following target function:

$${\chi }^2={{\displaystyle \sum _{j=1}^N\left[\frac{{\rho }_j^{\mathit{\text{exp}}}-{\rho }_j^{\mathit{\text{calc}}}\left(F\right)}{{\sigma }_j}\right]}}^2$$ (16)

where for each of the N residues included in the sum, ${\rho }_j^{\mathit{\text{exp}}}$ is the value of ρ derived directly from the experimental data according to the first equality in Eq. 13 and ${\rho }_j^{\mathit{\text{calc}}}$ is obtained by substituting into the second equality in Eq. 13 the value of J_ρ(ω) calculated from Eq. 15 for the current values of the N_p fitting parameters F = {X₁,X₂, …X _Np}. Here σ_j is the experimental uncertainty in ${\rho }_j^{\mathit{\text{exp}}}$ extimated as ${\sigma }_j={\rho }_j^{\text{exp}}{\left[{\left(\delta R_{1j}\text{'}\right)}^2{\left(\frac{1}{R_{1j}\text{'}}+\frac{1}{2R_{2j}\text{'}-R_{1j}\text{'}}\right)}^2+{\left(\delta R_{2j}\text{'}\right)}^2{\left(\frac{2}{2R_{2j}\text{'}-R_{1j}\text{'}}\right)}^2\right]}^{\frac{1}{2}}$, where δR_1j' and δR_2j' are the experimental uncertainties in the relaxation rates R_1j' and R_2j', respectively, for residue j.

The minimization of the target function, Eq. 16, was performed using in-house Matlab program based on the simplex algorithm. Multiple runs with different starting conditions were performed to assure that the resulting set of fitting parameters is the global minimizer. The confidence intervals for the fitting parameters were obtained using the method of constant- χ² boundaries and the bootstrap method⁴². The latter method, becoming increasingly popular for confidence interval estimations in complex systems, is based on the idea of using the original experimental data set to generate a number of synthetic data sets in which a certain fraction of the original data points (1/e≈37%) is replaced by randomly chosen duplicates of the remaining data. Thus, these synthetic data sets should have the same statistical properties as the original one. At least 200 sets of synthetic data were generated in each case. These synthetic data were analyzed in the same way as the original data, and the confidence intervals reported here were obtained from the resulting distributions of the values of fitting parameters.

Degeneracy of interdomain orientation

As indicated above, the Euler angles ${\mathrm{\Omega }}_{P\to D}^A$ and ${\mathrm{\Omega }}_{P\to D}^B$ define the orientation of a given domain with respect to the global protein frame. However, determining the interdomain orientation from these angles requires caution, because of the degeneracy of the problem, which stems from the fact that the diffusion tensor has no directionality, i.e. it is not sensitive to the inversion of one or more of its principal axes (two axes if the right- or left-handedness has to be preserved). This results in a four-fold degeneracy (e.g. ⁴) of the eigenvectors of the diffusion tensor (assuming they form a right-handed system), such that if one set of the vectors is known, the other three can be obtained by rotations specified by the Euler angles { π,0,0}, {0,π,0}, and {0,π,π}.

Applied to domain orientation procedure, this means that a given set of Euler angles $({\mathrm{\Omega }}_{P\to D}^A$ or ${\mathrm{\Omega }}_{P\to D}^B$, obtained from the fit) determines four different domain orientations which, however, have equivalent spin-relaxation properties. Thus, the fitted values of two sets of Euler angles ${\mathrm{\Omega }}_{P\to D}^A$ and ${\mathrm{\Omega }}_{P\to D}^B$ for one domain and sets of similar angles for another domain could belong to different branches of solution. However, a pair of ${\mathrm{\Omega }}_{P\to D}^A$ and ${\mathrm{\Omega }}_{P\to D}^B$ for a given protein domain should belong to the same solution branch, because the correlation function of the interdomain dynamics, Eq. 11, is independent of the overall diffusion and, therefore, has no such degeneracy. Which of all possible (degenerate) domain orientations is selected should be based on additional information, for example, chemical linkage, chemical shift perturbation mapping, spin-labeling data or other considerations ⁶. When the branches of solution for all domains are chosen, the appropriate angles ${\mathrm{\Omega }}_{P\to D}^A$ should be used to orient the domain’s coordinate frame with respect to the PAF of the overall diffusion tensor and to obtain the conformation for the state with the occupation probability p_A. The sets of ${\mathrm{\Omega }}_{P\to D}^B$ should be used in the same way to get the conformation with occupation probability p_B.

Results and Discussion

Analysis of ¹⁵N relaxation data for di-ubiquitin

To illustrate the ITS model, we apply it here to interdomain dynamics in Lys48-linked Ub₂. The ¹⁵N relaxation data, R₁, R₂, and steady-state {¹H}-¹⁵N NOE were collected at 14.1 Tesla and 24°C in segmentally ¹⁵N-labeled Ub₂ at pH 4.5 and 6.8. Details of the measurements are reported elsewhere ²³. The ratio of relaxation rates (ρ^exp, Eq.13) for the two Ub units in Ub₂ is shown in Fig.2. Throughout this paper, the Ub unit that carries the free C-terminus is defined as the proximal Ub domain. The other Ub unit in Ub₂ is defined as the distal domain. Thus, the two Ub molecules in Ub₂ are linked via an isopeptide bond between the C-terminal Gly76 of the distal Ub and Lys48 of the proximal Ub.

Figure 2.

Comparison between the experimental data and the various fitting models. Symbols represent ρ^exp, the ratio of relaxation rates for the experimental data included in the fit. Lines represent the values of ρ^calc for all amides in Ub back-calculated for all three approaches to data analysis considered here: the ITS model (red), the IDT model, where anisotropic diffusion was applied separately to each domain (IDT) (blue), and are for the SID model that corresponds to domain dynamics being turned off (green). The horizontal bars on the top indicate the location of the secondary structure elements (black for the β-strands; magenta for the helices).

The ratio of relaxation rates (ρ^exp, Eq.13) for the two Ub units in Ub₂ is shown in Fig.2. The observed average value of ρ^exp~7·10⁻² corresponds to the overall correlation time of ~8.5 ns, i.e. twice that for monomeric Ub, which indicates that to a good approximation the two domains tumble as a single molecular entity rather than completely independent “beads on a flexible string”. However, differences in the levels of ρ^exp between the two Ub units evident from this Figure indicate that Ub₂ still possesses some degree of interdomain mobility, which has differential effect on the relaxation data measured for the two domains. Note that the backbone dynamics in the two Ub units are essentially identical (and similar to those in monomeric Ub)⁶; this excludes the possibility that the observed differences in ρ^exp between the two Ubs could be caused by differences in their local intradomain motions. Ignoring interdomain dynamics in Ub₂ results in a striking discrepancy between the characteristics of the diffusion tensor of Ub₂ reported by the two domains²⁷ (see also below).

The chemical shifts and residual dipolar couplings indicate that the tertiary structure of both Ub domains in Ub₂ is essentially the same as in monomeric Ub ^6,23. Therefore the solution structure of monomeric Ub (PDB code 1D3Z ⁴³) is used here as the structure model for each Ub unit in Ub₂. Because the structural deviations within the ensemble of 10 NMR structures are small, the first conformer from 1D3Z was used here as a representative model of Ub structure.

Altogether, 71 and 91 residues from both domains were included in the analysis of relaxation data at pH 6.8 and 4.5, respectively. At pH 6.8 these comprise 36 backbone amides from the proximal Ub (residues 2–6, 11–17, 21, 28, 32–34, 36, 39–45, 49, 50, 57–59, 61, 64–67, 69) and 35 from the distal Ub (2–4, 13–18, 26–30, 32–36, 40–43, 45, 48–50, 54, 57, 59, 65–69). The corresponding numbers for pH 4.5 were 43 residues from the proximal Ub (2, 3, 5–7, 13–18, 20–22, 26–30, 32, 34–36, 39–44, 50, 52, 54–58, 61–67) and 48 from the distal Ub (2–5, 13, 14, 16–18, 20–22, 26–36, 39, 40, 42–50, 54, 55, 57–68). These amides belong to well-defined structural regions in Ub. Residues in the flexible regions and those amides showing conformational exchange ⁶ were excluded from the analysis, along with those amides that could not be reliably quantified due to signal overlap in the spectra.

Models for data treatment

Based on the chemical shift perturbations observed in Ub₂ upon pH titration, it has been suggested that Ub₂ is in dynamic equilibrium between two states, corresponding to the closed and open conformations ²³. Lowering the pH from 7.5 to 4.5 results in a transition from a predominantly closed to the predominantly open conformation of Ub₂. The observation of a single set of signals in the ¹H-¹⁵N HSQC spectra in a broad pH range (from 4.5 up to 8.0), indicates that the interconversion is fast on the NMR chemical shift time scale. The estimated relative population of the closed conformation at pH6.8 is ≥0.85. This makes Ub₂ an appropriate molecular system for testing the ITS model of domain motion. The fitting parameters included (see Methods) the principal values D_x, D_y, D_z of the diffusion tensor, the rates of interconversion, k_AB and k_BA, all of which were considered global parameters, and two sets of Euler angles, ${\mathrm{\Omega }}_{P\to D}^A$ and ${\mathrm{\Omega }}_{P\to D}^B$, per domain, altogether 17 adjustable parameters. The results of the fit are presented in Table 1. In order to validate these results, we used two additional data treatment procedures described below, as controls.

Table 1.

Parameters of the ITS model for Lys48-linked Ub₂ derived from ¹⁵N relaxation data measured at pH 6.8 $({\chi }_{\text{min}}^2/\left(N-N_p\right)\approx 1.7)\text{and}\text{pH}4.5({\chi }_{\text{min}}^2/\left(N-N_p\right)\approx 16.8).$

	pH 6.8		pH 4.5
Dxa	1.53 (0.32)		1.61 (0.13)
Dya	1.73 (0.06)		1.71 (0.06)
Dza	2.20 (0.08)		2.20 (0.06)
τITS b	9.3 (4.8)		31.9 (9.8)
pA c	0.90 (0.06)		0.82 (0.06)
	Proximal	Distal	Proximal	Distal
αA d	218 (35)	91 (28)	147 (30)	213 (24)
β A d	109 (11)	58 (7)	112 (16)	80 (8)
γ A d	140 (4)	321 (19)	322 (8)	350 (12)
αB d	203 (38)	156 (33)	191 (25)	151 (29)
βB d	110 (9)	96 (38)	122 (14)	51 (20)
γB d	72 (8)	356 (33)	45 (13)	328 (23)

Numbers in the parentheses represent estimated uncertainties in the parameters.

^aPrincipal components, D_x, D_y, and D_z, of the overall diffusion tensor, in 10⁷ s⁻¹ (ordered as D_x ≤ D_y ≤ D_z).

^bCharacteristic time constant for the interconversion between the two states, τ_ITS=1/K, in 10⁻⁹ s.

^cOccupation probability for the more populated state (this state is called state A); the occupation probability for state B is p_B =1- p_A.

^dThe Euler angles, in degrees, specify for the states A and B (indicated by the superscripts) the orientation of the PDB frame for each Ub domain with respect to the PAF of the overall diffusion tensor. Protein atom coordinates in this study were from the solution structure of monomeric Ub (PDB entry 1D3Z ⁴³, model 1). The use of these coordinates for the individual domains in Ub₂ has been validated by RDC measurements ⁶. The original Ub coordinates were rotated by {90°, 90°, 180°} to avoid having β ~ 0 or 180° when the angles α and γ cannot be accurately separated.

The same relaxation data were analyzed earlier ²³ applying fully anisotropic rotational diffusion model to each Ub domain separately. In that treatment, the interdomain mobility was not explicitly taken into account, i.e. the effects of the overall and interdomain dynamics were not separated from each other. Instead, both these motions contributed to the resulting effective diffusion tensor. Thus it is instructional to compare the results of that approach (henceforth called the “individual-domain treatment”, IDT) with those from the ITS model. For this purpose we repeated the analysis of ref.23, using the same list of residues as for the ITS model. The IDT requires six fitting parameters per domain: the principal values of the effective diffusion tensor and three Euler angles, altogether 12 adjustable parameters for Ub₂. The results of the analysis are presented in Table 2.

Table 2.

Values of the fitting parameters for the IDT model applied to Lys48-linked Ub₂. The residuals of fit per degree of freedom, ${\chi }_{\text{min}}^2/\left(N-N_p\right),$ were 1.9 and 16.3, for the ¹⁵N relaxation data measured at pH 6.8 and pH 4.5, respectively.

	pH 6.8		pH 4.5
	Proximal	Distal	Proximal	Distal
Dxa	1.68 (0.09)	1.73 (0.10)	1.78 (0.04)	1.69 (0.08)
Dya	2.06 (0.06)	1.86 (0.06)	2.00 (0.05)	1.77 (0.06)
Dza	2.30 (0.09)	2.69 (0.13)	2.15 (0.05)	2.50 (0.12)
τov b	8.28	7.96	8.44	8.39
αd→D c	89 (8)	127 (28)	114 (13)	139 (27)
βd→D c	145 (13)	126 (4)	66 (13)	112 (4)
γ d→D c	139 (9)	134 (6)	148 (9)	145 (4)

Numbers in the parentheses represent estimated uncertainties in the parameters.

^aPrincipal components, D_x, D_y, and D_z, of the overall diffusion tensor, in 10⁷ s⁻¹ (ordered as D_x ≤ D_y ≤ D_z).

^bApparent overall correlation time, τ _ov, in 10⁻⁹ s.

^cEuler angles, in degrees, determine orientation of the PDB coordinate frame for each Ub domain with respect to the PAF of the overall diffusion tensor. Note that here we rotate the reference frame, whereas the coordinate vectors instead are being rotated in the ROTDIF program ⁵⁰ used in ref 6; both methods use the so-called “y-convention” for the reference frame rotations (Supporting Information). Therefore the rotation matrices for the same transformation here and in ROTDIF are transposed to each other.

As one can see from Fig. 2, the overall levels of ρ are different for the two domains. Not surprisingly, when analyzed separately, the two Ub domains yield slightly different effective diffusion tensors, likely reflecting the contributions from domain dynamics, as discussed above. As also shown above, the ITS model also nicely fits the experimental data – in this case both domains are analyzed together. Therefore, in another control fit, the interdomain mobility was turned off by setting 1/k_BA=0, which resulted in a single fixed orientation per domain, hence a single Ub₂ conformation. In this case, termed suppressed interdomain dynamics (SID) here, the interconversion is completely suppressed by pushing the equilibrium entirely towards one of the two interconverting states (in this case A). This fit served as a test of whether an alternative treatment that involves simultaneous analysis of both domains but no interdomain dynamics could fit the data. It is worth noting that, in contrast to the IDT, the SID model implies a single overall diffusion tensor for both protein domains. Thus, the analysis includes 9 adjustable parameters: D_x, D_y, D_z as global parameters and a set of three Euler angles Ω_P→D for each domain. The results of this analysis are presented in Table 3.

Table 3.

Values of the fitting parameters for suppressed interdomain dynamics (SID) model for relaxation data measured at pH 6.8 $({\chi }_{\text{min}}^2/\left(N-N_p\right)=5.5)$ and pH 4.5 $({\chi }_{\text{min}}^2/\left(N-N_p\right)=33.1)$.

	pH 6.8		pH 4.5
Dxa	1.81 (0.03)		1.78 (0.02)
Dya	2.01 (0.03)		1.92 (0.02)
Dza	2.43 (0.03)		2.27 (0.02)
τovb	8.00		8.38
	Proximal	Distal	Proximal	Distal
αd→ D c	231 (17)	9 (8)	111 (10)	172 (10)
βd→D c	16 (5)	51 (3)	71 (3)	113 (4)
γd→D c	152 (14)	347 (8)	151 (3)	177 (6)

Numbers in the parentheses represent estimated uncertainties in the parameters.

^aPrincipal components, D_x, D_y, and D_z, of the overall diffusion tensor, in 10⁷ s⁻¹ (ordered as D_x ≤ D_y ≤ D_z).

^bApparent overall correlation time, τ_ov, in 10⁻⁹ s.

^cEuler angles, in degrees, specify the orientation of the PDB coordinate frame for each Ub domain with respect to the PAF of the overall diffusion tensor.

The quality of fit

Because all these models use different number of fitting parameters, we first compare the residuals of fit per degree of freedom, χ²/(N-N_p) as an objective criterion of the quality of data fit to each model. The data (Table 1– Table 3) suggest that at both pH values, the worst agreement between the model and the experiment was for the SID treatment. The two other models, ITS and IDT, have approximately the same values of χ²/(N-N_p) and both exhibit a remarkably better agreement with the experimental data (see Fig. 2). Also the correlation between the experimental and back-calculated values of ρ (Fig. 3) indicates that the suppressed interdomain dynamics model is the least adequate for Ub₂. The Pearson’s correlation coefficient ⁴² for both IDT and ITS was 0.95 (pH6.8) and 0.94 (pH4.5), while turning off the interdomain dynamics reduced it to 0.84 and 0.86 at these pH. These results indicate that the ITS model is a significant improvement, and thus support the necessity of including interdomain dynamics into Ub₂ data analysis.

Figure 3.

The agreement between experimentally measured (ρ^exp) and back-calculated (ρ^calc) values of the ratio of relaxation rates, Eq.13, for the ITS, IDT, and SID models. The top and bottom rows correspond to pH6.8 and 4.5, respectively. The lines are guides-for-eye representing the case of absolute agreement. The values of the Pearson’s correlation coefficient r are indicated.

The interdomain orientations in Ub₂

The reconstruction of interdomain orientation in the IDT is based on the idea of aligning the axes of the diffusion tensor of Ub₂ experienced by the two Ub domains, as detailed in ⁶. The domain alignment in the ITS model is relatively straightforward, because the Euler angles Ω_P→D determine the orientation of each domain with respect to the common, global coordinate frame (P). It should be emphasized that only the relative orientation of the domains not their position with respect to each other is available from the Euler angles. Therefore, the domains are positioned here somewhat arbitrarily in the three-dimensional space. In addition, one should bear in mind the issue of orientational degeneracy discussed above. Thus, additional information is necessary in order to pinpoint the proper conformation. One such piece of information is the chemical link between the two Ub domains, which requires that the C-terminus of the distal Ub is located close to Lys48 of the proximal Ub. In addition, chemical shift perturbations observed in Ub₂ at pH6.8 ²³ indicate a close contact between the β-sheets of the two Ub units. Fig. 4 depicts the conformations of Ub₂ derived using these considerations for all three fitting models.

Figure 4.

Conformations of Lys48-linked Ub₂ obtained from the analyses using various models considered here. The left panels correspond to pH6.8, the right panels to pH4.5. In all structures, the proximal domain is colored green, the distal is blue. The principal axes of the overall diffusion tensor are shown as cyan rods. Panels a through d show two distinct conformations of Ub₂ obtained using the ITS model; the red rods represent the rotation axes for each domain (Supporting Information). Panels e and f depict the Ub₂ conformations obtained for anisotropic diffusion model applied to each domain separately (IDT). Panels g and h represent Ub₂ conformations obtained by the simultaneous analysis of both domains assuming that the interdomain dynamics are turned off (SID model). The location of the hydrophobic patch residues Leu8, Ile44, Val70 on each Ub domain is represented by spheres (C_β atoms, colored gold), the side chain of Lys48 of the proximal domain is shown in stick representation, colored orange. All molecular drawings here were made using MolMol ⁴⁹.

As expected, the ITS model yields two different (interconverting) conformations of Ub₂ for both pH6.8 and 4.5 data sets (see Figs. 4A and B). For these structures, the transition between the two orientations of each domain (states A and B), derived from the Euler angles ${\mathrm{\Omega }}_{P\to D}^A$ and ${\mathrm{\Omega }}_{P\to D}^B$, can be represented as a rotation about some fixed axis (Supporting Information). It is remarkable that, while the actual Ub₂ conformations are significantly different between the two pH values, the spatial orientation of the rotation axes, as well as the rotation angles are quite similar for both pH. Note that the rotation axes for both domains go through the Ub-Ub linker region, consistent with the expectation that the linker acts as a hinge in the interdomain motion in Ub₂.

The Ub₂ conformations obtained for the IDT model, applied separately to proximal and distal domains, are shown in Figs. 4e and 4f. These conformations are virtually identical to the ones reported in ²³, where it has been proposed that they correspond to the “closed” (Fig. 4e, pH 6.8) and “open” (Fig. 4f, pH 4.5) conformations of Ub₂. There is a remarkable similarity between these conformations from the IDT analysis and the most populated conformations for the ITS model: the closed conformation is similar to that in state A at pH6.8 (p_A = 0.90) and the open conformation resembles that in state A at pH4.5 (p_A = 0.82). In contrast, the conformations obtained from the SID treatment are ambiguous: the conformation at pH 4.5 (Fig. 4h) looks similar to the open conformation whereas that at pH 6.8 (Fig. 4g) is different from all others.

pH dependence of the Ub₂ conformations

As mentioned earlier, NMR data ²³ indicate the disappearance of a defined Ub/Ub interface as pH is titrated from 7.5 to 4.5. The Ub/Ub interface is stabilized by a balance between the hydrophobic effect pushing the two domains together and their electrostatic repulsion caused by positively charged side chains surrounding the hydrophobic patches on both Ub domains. Lowering the pH from 7.5 to 4.5 is expected to cause the protonation of His68 (pKa = 5.5 ⁴⁴) adjacent to the hydrophobic patch on both Ub units.

The accompanying increase in the Coulomb repulsion between the two domains is perhaps the reason that the closed state (Fig. 4a) becomes energetically unfavorable at low pH. From the ratio of the occupation probabilities of states A and B, the difference in their Gibbs free energies is ΔG = G_A–G_B ≈ −5.5 kJ/mol (pH6.8) and −3.8 kJ/mol (pH4.5), where the lower-energy state (state A) corresponds to the closed conformation at pH 6.8 (Fig. 4a) and the open one at pH 4.5, shown in Fig.4d.

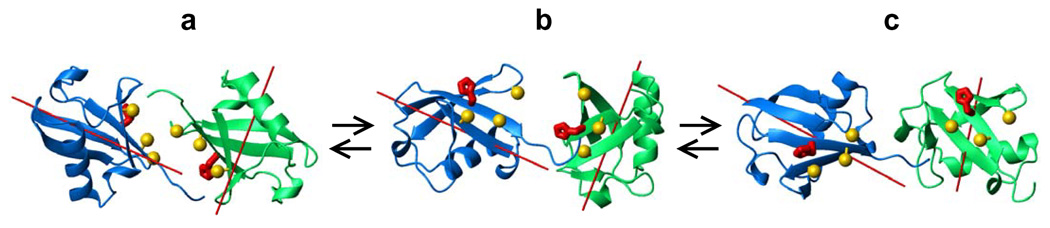
The picture of interconverting Ub₂ conformations obtained here (Fig.4a–d) appears more complex than a simple, seemingly intuitive model in which the limiting states, open and closed, would be the same at both pH values and only their relative population would change with pH. In this regard it is worth noting a striking similarity between the Ub₂ conformations in the weakly populated state B for different pH (Figs.4b and c). While further studies are necessary to understand these results in detail, there is a simple scheme that can explain the relations between Ub₂ conformations obtained here for different pH. The observed three conformational states of Ub₂: the closed (Fig.4a), the open (Fig.4d), and the intermediate one (Figs. 4b,c), can be explained when taking into account that the stable conformations of Ub₂ are determined by the balance between the hydrophobic effect (favoring the interdomain interface) and electrostatic repulsion between the two Ub units. For simplicity, consider that in the pH range from 4.5 to 6.8, the only residue in Ub that is expected to undergo a significant change in the charge state of its side chain is His68. Located in the middle of the hydrophobic patch on Ub (Fig.5), His68 side chains from both Ub domains face each other in the closed conformation. With the distance of approximately 8.3Å between protonatable nitrogens of the two imidazole rings in the crystal structure of Ub₂, one could expect a strong electrostatic repulsion between Ub domains in the case when both rings are protonated (at low pH). Depending on its protonation state, His68 on each Ub unit could have a charge of either zero or +e (for simplicity, we are not considering states with partial charges here). Therefore, Ub₂ can be in one of the three possible states:

1. The state of zero net charge, Q=0, (the histidines on both domains of Ub₂ are neutral) – this state corresponds to the closed state in Fig 4a, because the hydrophobic effect is predominant.

2. The state with the intermediate net charge, Q=+e, when only one of the two histidines is protonated. In this state the electrostatic repulsion (between His68 on one Ub and the positively charged side chains surrounding the hydrophobic patch on the other Ub unit) is stronger than in the neutral state. This could drive Ub₂ into the intermediate conformation (Fig.4b,c), in which a new balance is reached between the hydrophobic effect and the electrostatic repulsion.

3. The state of maximal net charge, Q=+2e, when both histidines are protonated – here the electrostatic repulsion is the strongest and could drive Ub₂ into an open conformation (Fig.4d), thus keeping the His-containing hydrophobic patches on the two Ub units apart from each other.

Figure 5.

Available conformational states of Lys48-linked Ub₂ in solution: (a) closed, (b) intermediate, and (c) open. The spheres (colored gold) indicate the location of the hydrophobic patch residues Leu8, Ile44, Val70 on each Ub unit; the side chains of the histidines (His68) are shown in stick representation, colored red. The distal Ub is colored blue; the proximal Ub is green. The experimental and predicted occupation probabilities for these conformations are shown in Table 4.

Given the pKa value of His68 in Ub₂ is 5.5 ⁴⁴, the fraction of protonated histidines at pH6.8 is 0.048, such that the fractions of the Ub₂ chains in the closed (I), intermediate (II), and open (III) states are p_I^pH6.8=0.907, p_II^pH6.8=0.091, and p_III^pH6.8=0.002, respectively. A reverse situation is expected at pH 4.5, where each histidine side chain carries a positive charge of +e with the probability of 0.909, and the fraction numbers for the three states are p_I^pH4.5=0.008, p_II^pH4.5=0.165, and p_III^pH4.5=0.826, respectively. These numbers suggest that only two out of the three possible charge states/conformations of Ub₂ are significantly populated and, therefore, can be experimentally detected at the pH values considered here: states I and II at pH6.8 and states II and III at pH4.5. The occupation probabilities for these states are in excellent agreement with the p_A and p_B values obtained from our relaxation data analysis at both pH values (Table 4). This then supports the applicability of the two-state model at the pH values considered here. Obviously, a more sophisticated, three-state model might be necessary at intermediate pH values, where the occupation probabilities of all three states could be comparable. Further refinement of this model of the charged states of Ub₂ could involve consideration of the partial charges on all titratable side chains (especially Glu and Asp at pH4.5), which is beyond the scope of this study. Relaxation studies at intermediate pH values also might be required to provide further details on the Ub₂ conformations.

Table 4.

Occupation probabilities of various conformational states of Lys48-linked Ub₂ at the two pH values used in this study. The experimental values are from the ITS model (numbers in the parentheses indicate experimental uncertainties), the predicted values are based on the populations of the possible charged states of His68 (see text).

pH	Source	Closed conformation	Intermediate conformation	Open conformation
		(Fig.5a)	(Fig.5b)	(Fig.5c)
6.8	Experiment	0.90 (0.06)	0.10 (0.06)	--
	Prediction	0.909	0.091	0.002
4.5	Experiment	--	0.18 (0.06)	0.82 (0.06)
	Prediction	0.909	0.165	0.826

A posteriori validation of the ITS model for Ub₂

The critical assumption (Postulate I) in the ITS model is that the interdomain and overall motions are statistically independent from each other. As discussed above, because the interdomain dynamics happen on the time scale comparable with the overall tumbling, this assumption needs validation. Statistical independence of these motions implies that domain reorientations do not affect the shape/diffusion tensor of the molecule. Indeed, the overall diffusion tensors of Ub₂ at pH 6.8 (predominantly closed conformation) and pH 4.5 (predominantly open conformation) are essentially identical (Table 1), thus posteriori supporting the validity of this assumption. To further test this assumption, we compared the derived Ub₂ structures (Figs. 4a–d) for the interconverting states at a given pH. As reported earlier²⁷, hydrodynamic calculations based on the Ub₂ structures yielded very similar principal values of the overall rotational diffusion tensor for the states A and B. In addition, the Ub₂’s radius of gyration, another parameter sensitive to the shape of the molecule⁴⁵, is identical for both interconverting states at a given pH (Supporting Information). Thus the likely reason the analysis based on Postulate I works well in the case of Ub₂ is that the overall diffusion tensors of the various conformational states of this molecule are quite similar.

The derived structures are also in good agreement with other available experimental data. In particular, the “closed” state (Fig. 4a) is consistent with the chemical shift perturbations observed in the hydrophobic patch residues at pH6.8 ²³, when this conformation is predominant. This conformation also agrees both with the crystal structure of Ub₂ ⁴⁶ and with solution Ub₂ structure⁴⁷ obtained based on the chemical shift perturbations and residual dipolar couplings. It is worth emphasizing that no information about chemical shift perturbations was included in the calculation of the structures shown in Fig.4. The “open” conformation (Fig.4d), predominant at pH4.5, is also in agreement with the NMR data, as no direct interdomain contacts were observed at this pH. Note also that the Ub₂ structures at pH6.8 agree well with the paramagnetic spin-labeling data ²⁷.

Interestingly, the Ub₂ conformations in the less populated states (Figs.4b,c) are very similar to each other. The interdomain orientation in these conformations is also very similar to Ub₂ structure in the complex with UBA2 domain ⁴⁸: they superimpose with the backbone RMSD of 1.7Å. This observation has functional significance because it suggests that the partly open conformation (Figs.4b,c) represents some intermediate, binding-competent conformation of Ub₂ and thus indicates that the amplitudes of interdomain motions at pH6.8 are sufficient for allowing ligands as big as UBA domain access to the hydrophobic patches on Ub units.

Comparison with the extended mode-free approach

It is instructional to discuss the relationship between the ITS model and the “extended model-free” approach to domain mobility, the only other model for domain mobility currently available. Proposed as a model for domain dynamics in calmodulin ^19,22, this approach treats the effect of domain motions using the “extended model-free” form ²¹ for the correlation function of local motion, originally developed to account for “fast” and “slow” backbone dynamics in a protein:

$$C_{s0,h0}^{RI}\left(t\right)\cong {\delta }_{s,0}{\delta }_{h,0}\left\{S_f^2\left[S_s^2+\left(1-S_s^2\right)\text{exp}\left(-t/{\tau }_s\right)\right]+\left(1-S_f^2\right)\text{exp}\left(-t/{\tau }_f\right)\right\}.$$ (17)

The original ²¹ interpretation of dynamic parameters entering Eq. 17 is such that the order parameters, S_s and S_f, as well as the correlation times, τ_s and τ_f, represent the “slow” and “fast” ( τ_s >> τ_f) modes of local motion of a particular NH bond. The extension of this model to domain dynamics in calmodulin ^19,22 treats only S _f and τ _f as local parameters representing the mobility of a NH bond, while the other pair of parameters, S _s and τ _s , is attributed to domain’s mobility. Note that in this case, as well as in the original “extended model-free” model, the fast and slow motions, i.e. the local and domain mobility modes, are assumed decoupled from each other and from the overall tumbling.

Following the notations of Eq. 4,Eq. 5, the total correlation function corresponding to the “extended model-free” treatment of ^19,22 in the case of fully anisotropic overall tumbling can then we written as follows:

$$\begin{array}{l}C(t)={\displaystyle \sum _{m=-2}^2{\displaystyle \sum _{n=-2}^2{\displaystyle \sum _{k=-2}^2{\displaystyle \sum _{l=-2}^2{\displaystyle \sum _{s=-2}^2{\displaystyle \sum _{h=-2}^2{C}_{qm,qn}^{LP}\left(t\right)·D_{m,k}^{(2)*}\left({\mathrm{\Omega }}_{P\to D}\right)D_{n,l}^{(2)}\left({\mathrm{\Omega }}_{P\to D}\right)\times }}}}}}\hfill \\ \hfill \times D_{k,s}^{(2)*}\left({\mathrm{\Omega }}_{D\to R}\right)D_{l,h}^{(2)}\left({\mathrm{\Omega }}_{D\to R}\right)·C_{s0,h0}^{RI}\left(t\right)\cong \\ \cong \frac{1}{5}{\displaystyle \sum _{m=-2}^2{\displaystyle \sum _{n=-2}^2{\displaystyle \sum _{r=-2}^2{e}^{-E_{r}t}{a}_{r,m}^{*}{a}_{r,n}{D}_{m,0}^{\left(2\right)*}({\mathrm{\Omega }}_{P\to R})D_{n,0}^{(2)}({\mathrm{\Omega }}_{P\to R})\times }}}\hfill \\ \hfill \times \left\{S_f^2+\left[S_s^2+\left(1-S_s^2\right)\text{exp}\left(-t/{\tau }_s\right)\right]+\left(1-S_f^2\right)\text{exp}\left(-t/{\tau }_f\right)\right\}\end{array}$$ (18)

In the spirit of ^19,22, here we introduced the Euler angles Ω_P→R that define the (time-averaged) orientation of the residue-specific frame R with respect to the PAF of the diffusion tensor and thus replace two consecutive transformations, P→D and D → R. Note that Ω_P→R (as well as Ω_P→D) are now time-independent, because domain motion is already included in $C_{s0,h0}^{RI}\left(t\right)$, Eq. 17.

Our ITS model for domain reorientations, Eq. 11, provides a more detailed structural picture while preserving a mono-exponential, “model-free”-like form of C(t). Indeed, the “extended model-free” approach provides information about time scales of domain reorientation and the related order parameters (i.e. amplitudes of motions) only. In contrast, the ITS parameters, $S_{mk,nl}^2$ and Q_mk,nl (Eq.11), bear dependency on domain orientations, ${\mathrm{\Omega }}_{P\to D}^A$ and ${\mathrm{\Omega }}_{P\to D}^B$. Thus, the ITS treatment yields the times scales of domain reorientations and particular domain arrangements in different conformations -- not only amplitude of motion -- together with the occupation probabilities for each state. This provides structural “snapshots” of the system in different conformations, unavailable from the “extended model-free” approach. It should be pointed out that in the case of the Ub₂ molecule characterized by preferred domain orientations, the “extended model-free” model is inadequate. Indeed, in this approach (Eq.18) domain dynamics are characterized by a scalar order parameter (corresponding to a continuum of available interdomain orientations), while tensorial quantities, $S_{mk,nl}^2$ and Q_mk,nl, are required even for a simple two-site exchange model, Eq.11.

To have a quantitative comparison with the “extended model-free” treatment, we also analyzed our relaxation data using Eq.18. The results of this analysis (Supporting Table 1) show that for Ub₂ this approach leads to a markedly worse description of experimental data than the one provided by the ITS model. Thus, this analysis resulted in a 2-fold increase (compared to the ITS model) in the residuals of fit per degree of freedom at both pH values and in a worse correlation between the experimental and back-calculated data: Pearson’s r was 0.89 at pH 6.8 and 0.86 at pH 4.5, compared to 0.95 and 0.94, respectively, for the ITS model. Moreover, in contrast to the ITS analysis, the “extended model-free” treatment produced physically unreasonable values of the fitting parameters. Here the overall tumbling time of Ub₂ was 17 ns (pH 6.8) and 11 ns (pH 4.5) and the squared order parameters (S_s²) associated with the interdomain mobility were 0.02 for the distal and 0.3 for the proximal domain at pH 6.8 and 0.2 and 0.56, respectively, at pH 4.5.

Conclusions

In this paper, we present a framework for building a motional model for a multi-domain protein that takes into account interdomain dynamics, together with other motional modes, including the overall tumbling and local intradomain dynamics. Our approach is based on the assumption of statistical independence of the various dynamic modes. Specifically, we developed a model of motion in a dual-domain protein that treats interdomain dynamics as an exchange, or interconversion, between two conformational states of the protein. We demonstrate that this model provides a reasonable first-order approximation to experimentally observed dynamics in Lys48-linked di-ubiquitin at both neutral and acidic pH. The analysis of NMR data using this model revealed many unknown details of domain mobility in di-ubiquitin, including structural information about the interconverting conformations of the molecule and the rates and energies associated with this process. The assumption of statistical independence between the overall motion and domain dynamics is a strong one and can be inadequate in the case when domain motion alters the overall shape of the molecule (hence its overall diffusion tensor). In the case of di-ubiquitin this assumption is justified by the close-to-spherical shape of ubiquitin monomers. Thus, domain reorientations in di-ubiquitin do not significantly alter the overall shape of the molecule and its overall rotational diffusion tensor. The similarity of the diffusion constants for various conformational states of di-ubiquitin is the likely reason the analysis works well for this system. Note that the assumption of statistical independence of the overall and interdomain motions is a separate one from the ability to accurately and independently extract their characteristics from experimental data. In fact, the characteristic time of the interdomain mobility in di-ubiquitin happens to be comparable to that for the overall tumbling, which necessarily limits the precision of the derived rates of interconversion.

The analysis of Ub₂ data presented in this paper shows that in this particular system the characteristic time of the interdomain motion (τ_ITS) is comparable to the overall tumbling time: τ_ITS ~τ_overall. It is worth pointing out that the model of domain motion described here requires no a priori assumption regarding the relationship between τ_overall and τ_ITS. Thus, for example, the above equations also describe the situation when domain motion is significantly slower than the overall tumbling (τ_ITS >> τ_overall), yet faster than the spin relaxation. In this case it can be shown that the relevant spectral density (e.g. Eq. 15) becomes independent of τ_ITS and is a weighted average of the spectral densities describing overall tumbling in the individual conformational states of the molecule, in full agreement with the expectation that the measured relaxation rate be an average of the corresponding relaxation rates for these states.

The particular treatment of domain dynamics utilized here can be improved in many ways. While the two-state model is sufficient for Ub₂ at the pH conditions used here (see Table 4 and the discussion above), a three-state model might be required at the intermediate pH values. Moreover, the application of our model to other protein systems might also require considering exchange between more than two states. The extension of the ITS model to n>2 is relatively straightforward and will require modification of the corresponding equations, Eqs.8–9, for$C_{mk,nl}^{PD}\left(t\right)$ and for conditional probabilities (see e.g. 25). Other modifications, beyond the simple n-site exchange model, might be required to describe domain dynamics in other multi-domain systems. These could include random domain rotations (diffusion) about a fixed axis, analogous to the model applied by D. Wallach ²⁵ to describe the effect of internal rotations in a molecular label attached to a macromolecule. Furthermore, when domain’s diffusion is limited to some angular interval, it might be necessary to consider restricted rotational diffusion about a fixed axis. Such a model was originally introduced for the description of restricted internal rotations in the side chains by R. J. Wittebort and A. Szabo ²⁶. The correlation functions for the interdomain mobility mode corresponding to these two cases of domain’s axial diffusion can be found in Supporting Information. However, further conceptual development of the approach presented here is necessary in order to take into account possible coupling between domain motion and the overall tumbling.

Supplementary Material

si20061226_012. Supporting Information Available.

A table with the results of the “extended model-free” analysis of the Ub₂ data; a table with the predicted values of the radius of gyration for Ub₂ conformations; the procedure of defining the axis of rotation between two orientations of a molecule, and a summary of the relevant information on Wigner rotation matrices and Euler rotations, probabilities and correlation functions for anisotropic rotational diffusion, the conditional probabilities for the two-site exchange model, and the correlation functions of domain dynamics mode for axial diffusion models.