A multi-compartment vascular model for inferring arteriole dilation and cerebral metabolic changes during functional activation

Abstract

Functional hemodynamic responses, measured by methods such as fMRI or optical imaging, are the composite, downstream results of underlying variations in cerebral oxygen consumption and the dilation of arteriole vessels, which follow from changes in neuronal activity. The separation of metabolic and vascular effects is an actively growing area of interest, motivated by increasing evidence of the role of neural-metabolic-vascular coupling in health and disease. However, this coupling cannot be easily or directly observed in vivo. Vascular modeling plays an important role by relating these underlying physiological responses to the hemodynamic variables measured with non-invasive imaging. In this paper, we describe a multi-compartment model of the cerebral vascular and oxygen transport dynamics associated with stimulus driven neuronal activation. The unique formulation of this model allows both the estimation of the dynamic arteriole dilation and metabolic processes associated with the functional response to stimuli, and also enables us to infer details of the structural and baseline properties of the vascular anatomy, such as baseline oxygen consumption, blood flow, and resting hemoglobin concentrations. We apply this model to multimodal optical spectroscopic and laser speckle imaging of the rat somato-sensory cortex during nine conditions of whisker stimulation. We estimate baseline blood flows to be 94(±15) mL/100g/min and baseline oxygen consumption to be 6.7(±1.3) mL O₂/100g/min. We calculate parametric, linear increases in the arteriole dilation (R²=0.96) and CMRO₂ (R²=0.87) responses over the nine conditions. We find that our model more accurately describes these observed oxygenation changes when compared to a single compartment model.

Introduction

Measurements of the functional changes in hemodynamic variables, such as blood volume, flow, or hemoglobin oxygenation, have led to important advances in modern neuroscience and have contributed to our current understanding of the functional anatomy of the brain [reviewed by (Nair 2005)]. One of the primary reasons for these advances has been the development and refinement of optical and functional MR imaging methods over the last several decades. The hemodynamic response can now be readily measured by a number of such techniques and is a compilation of the competing effects of increased metabolic demand for oxygen to support glycolysis and the increased supply of oxygen offered by the elevated regional perfusion of blood via the dilation of feeding arterioles [reviewed by (Buxton et al. 2004; Mintun et al. 2001)]. In the activated brain, increased oxygen consumption is typically met with an overcompensating increase in regional blood flow. This results in an overall decrease in oxygen extraction from the blood vessels and a net increase in the oxygen content of the activated brain region. Hemodynamic measurements, such as the BOLD (blood oxygen level dependent) signal in functional MRI or optical imaging, measure these composite changes and are less revealing than direct measures of neuronal or metabolic function (Nair 2005). In addition, the relationships between hemodynamic measurements and the vascular and metabolic changes are dependent on the baseline state and are thus sensitive to fluctuations in baseline blood flow and oxygen saturation (Nair 2005). This limits the reproducibility of hemodynamic measurements (Aguirre et al. 1998) and the use of functional imaging in clinical diagnosis (Brooks 2000; Nair 2005). Thus, the utility of functional hemodynamic imaging could be improved if it provided a more reliable measure of metabolic function.

The introduction of vascular descriptions, such as the Balloon (Buxton and Frank 1997; Buxton et al. 1998) and Windkessel models (Mandeville et al. 1999a; Mandeville et al. 1999b) have helped to shed light on the metabolic and neuronal functions of the brain by providing interpretation of the hemodynamic parameters measured by fMRI or optical methods. Such vascular modeling has been instrumental in progressing the understanding of the relationships between blood flow, volume, and oxygenation responses and their relationships to neuronal activation [reviewed in (Buxton et al. 2004; Zheng et al. 2005)]. By separating and identifying the individual contributions of arteriole dilation and oxygen consumption to the measured hemodynamic response, these models help to elucidate the differences between the effects of vascular “plumbing” and the cerebral metabolic rate of oxygen consumption (CMRO₂). Such insights could eventually lead to the use of functional imaging tools in clinical applications, since distinguishing these differences could enable quantitative interpretation of hemodynamic signals for the neurosciences and potentially make longitudinal and cross-subject studies more fruitful (Nair 2005). As other groups have noted in results from animal models, insight into the underpinnings of the neural-vascular response might have a significant impact in diagnosis and treatment of conditions such as stroke or Alzheimer's disease (Girouard and Iadecola 2006).

In recent years, the development of invasive optical imaging experiments in animal models have allowed us to examine hemodynamic changes at a higher temporal and spatial resolution than has been previously possible with fMRI methods or in human models (Devor et al. 2005; Dunn et al. 2005; Sheth et al. 2005; Vanzetta et al. 2005; Zheng et al. 2005). These types of experiments have been invaluable in exploring the assumptions of vascular models. With this more comprehensive information, a discrepancy has been noted between experimental results and the assumptions of the earlier, vascular models based on single-compartment, vascular changes (Zheng et al. 2005). In particular, Zheng et al noted that observed deoxy-hemoglobin changes measured by optical imaging spectroscopy were inconsistent with the predictions of a single-compartment model (Zheng et al. 2005). In order to reconcile these differences, multi-compartment models of the vascular network have been recently described (Kocsis et al. 2006; Zheng et al. 2005), which model the hemodynamic changes in all three vascular compartments, i.e. arteriole, capillary, and venial compartments.

In this paper, we present a multiple compartment model of the vascular and oxygen transport changes, in order to model the composite hemodynamic response. In this model description, we introduce several improvements that extend from previously described single-(Buxton et al. 2004; Buxton et al. 1998; Mandeville et al. 1999b) and three-compartment models (Kocsis et al. 2006; Zheng et al. 2005). In particular, we introduce a capillary compliance model motivated by experimental observations of microvascular (or parenchymal) volume changes indicative of increased capillary perfusion (Vanzetta et al. 2005). In addition, we extend the description of oxygen transport used by Zheng et al (Zheng et al. 2005) in order to model oxygen extracted from the arteriole and venial compartments and to allow potential changes in the oxygen tension within the extra-vascular parenchyma tissue. The role of oxygen transport from the arterioles and venials has been motivated by recent experimental results (Berwick et al. 2004; Vovenko 1999) and theoretical descriptions (Herman et al. 2006; Kocsis et al. 2006).

A further defining characteristic of this work, which significantly distinguishes it from previous models, is that our model allows the estimation of absolute baseline properties from measurements of relative, functional changes in hemodynamic parameters. While this model is formulated using normalized parameters, we are able to estimate baseline values by exploiting the complement of the percent and absolute (i.e. micro-molar) functional changes measured between multimodality methods, such as optical spectroscopy and laser speckle imaging. This allows us to determine the absolute scale of these parameters and infer baseline hemoglobin concentration, blood volume, and blood flow in physiologically relevant units. In addition, the baseline oxygen saturation of each compartment is estimated as a state variable in the model. This allows us to estimate the absolute baseline oxygen delivery and baseline CMRO₂. The ability of the model to predict baseline conditions is a significant development over previous models, where baseline conditions are typically assumed (i.e. (Buxton et al. 2004; Zheng et al. 2005)). Calculation of baseline conditions helps to accurately quantify the hemodynamic changes being modeled and allows comparison of CMRO₂ and blood volume values to previously published literature.

Theory

General description of multi-compartment model

In comparison to previous models, our multi-compartment model is built using an inductive or bottom-up approach (Riera et al. 2005), schematically illustrated in figure 1. Model error is minimized by the simultaneous comparison of the model predictions to experimental measurements in order to estimate CMRO₂ and arteriole dilation, which are hidden state variables. We incorporate the underlying biophysical principles for each method (i.e. observation models), which give rise to such multimodality measurements. This allows us to fuse multimodality information from differing measurement sources to directly infer the physiological states giving rise to such contrast. This provides a direct estimate of the vascular and metabolic changes with information contributed from the measurements of blood flow, volume, and oxygenation and combined within a pseudo-Bayesian statistical framework. The model provides a more robust estimation of the state variables by accounting for the differing sources of noise and measurement errors associated with individual instruments. This bottom-up framework offers several advantages and introduces an extendable structure for future work as demonstrated by Riera et al. (Riera et al. 2005).

Figure 1. Schematic to the model framework.

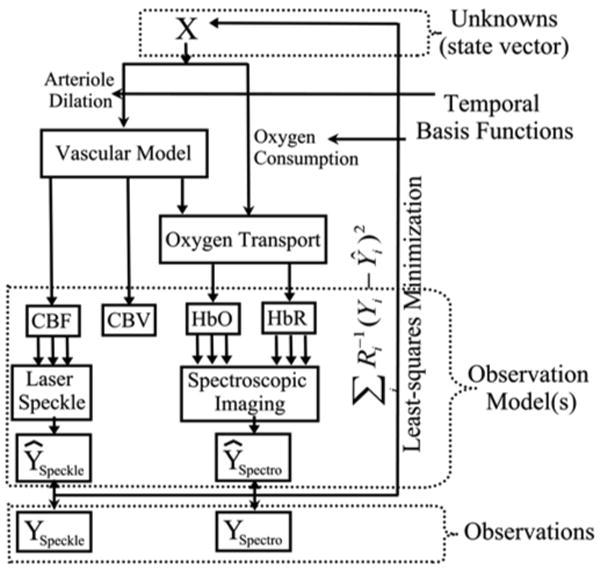
The proposed multi-compartment model is based on a bottom-up approach to state estimation. A state vector of unknowns (X) is passed through a set of differential equations describing the vascular and oxygen transport components of the hemodynamic response. These outputs predict changes in blood flow, volume and oxygenation. These predictions are inputs into observation models, which describe measurement process for each measurement modality and are based on the biophysical principles governing each method. Multiple observation models create predictions of multimodality data, which are minimized to the experimental data using a pseudo-Bayesian fusion model, in the form of a weighted least-squares cost function.

Vascular model

The vascular component of the model is described by a set of physical relationships that depict three connected compliant, vascular compartments (namely the arteriolar, capillary, and venial compartments) and a constant volume compartment to model the pial venous structure. The model of vascular changes described in this work is an extension of several previously proposed vascular models (reviewed in (Buxton et al. 2004; Zheng et al. 2005)). These models are built around the relationships between blood flow and volume changes originally proposed in the Balloon model (Buxton and Frank 1997; Buxton et al. 1998) and later extended to include an empirical description of vascular compliance in the Windkessel model (Mandeville et al. 1999a; Mandeville et al. 1999b).

The vascular compartments can be represented by an analogous bridge circuit of resistors and capacitors (electrical) elements as depicted in figure 2 (Mandeville et al. 1999b). Changes in blood flow and volume are driven by the active dilation of the arterioles, which decreases the input vascular resistance of the system. The pressure gradient between compartments (equivalent to electrical potential or voltage) drives the flow of blood (analogous to electrical current) between compartments. As the pressure increases, the vascular compartment expands causing blood volume to increase. The increase in blood volume in a compartment is equivalent to the build-up of charge on a non-linear capacitor, whose capacitance decreases as the compartment expands against the pressure of the surrounding brain, leading to a saturating blood volume expansion. Finally, the heart and systemic circulation create a constant pressure drop across the entire system and are modeled as a single constant DC voltage source across the entire system.

Figure 2. Schematic of the Windkessel vascular model.

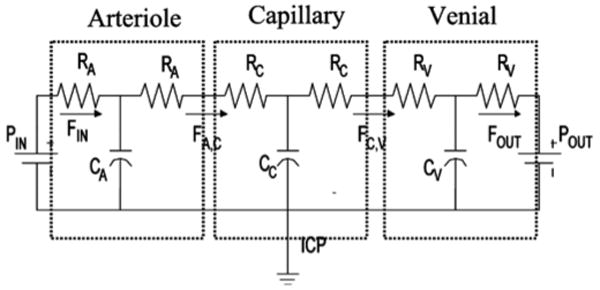
The Windkessel vascular model can be described based an analogy to the electrical shown here. Cerebral blood volume is equivalent to electrical charge. The flow of charge (i.e. current) models blood flow changes and is proportional to the blood pressure drop across compartments and inversely proportional to vascular resistance. Non-linear capacitor elements model the vascular compliance of each compartment.

The correspondence of this model with an electrical circuit readily allows the derivation of the differential equations to govern the physical flow and volume changes based on Kirchoff's relationships and summarized by the following physical principles.

1. The flow between each compartment is calculated using the Ohm's law analogy (V=I·R), where I, V and R are analogous to the blood flow, blood pressure and vascular resistance, respectively. The pressure (P) drop across vascular compartments (n → n+1) is the product of the flow (F) from the n^th into the (n+1)^th compartment and the vascular resistance (R) between the compartments,

   $$P_n(t)-P_{n+1}(t)=F_{n,n+1}(t)\cdot \left[R_n(t)+R_{n+1}(t)\right].$$ (1)
   This leads to the set of differential equations that describe the differential volume changes in each compartment based on flow mismatch,

   $$\frac{\partial V_n}{\partial t}=F_{n-1,n}(t)-F_{n,n+1}(t)$$ (1i)

   $$\frac{\partial V_n}{\partial t}=\frac{P_{n-1}(t)-P_n(t)}{R_{n-1}(t)+R_n(t)}-\frac{P_n(t)-P_{n+1}(t)}{R_n(t)+R_{n+1}(t)}.$$ (1ii)
2. In this model, the capillary and venial compartments are compliant. The capacitance (C_n) describes the variable vascular compliance and hence the limit for volume changes in these compartments. In the electrical circuit analogy, charge build-up on these capacitors models blood volume changes. However, in the vascular network, capacitance is a non-linear function of the pressure (P_n) between the vascular compartment and the intra-cranial pressure (ICP) and varies according to an inverse power law relation of Windkessel volume reserve (Mandeville et al. 1999b)

   $$C_n(t)=A_n\cdot {\left[P_n(t)\right]}^{\left(1/{\beta }_n\right)-1}n\in \left\{\text{Capillary},\text{Venial}\right\}.$$ (2)
   In this model, β_n is the Windkessel vascular reserve of the n^th compartment. We assume the vascular reserve to have the same value for both the capillary and venous compartments. A_n is a scaling constant, which is determined by the initial conditions,

   $$A_n=V_n(0)/{\left(F_{n-1,n}(0)\cdot \left(R_{n-1}(0)+R_n(0)\right)\right)}^{1/\beta }.$$ (3)
   Combining equations 1-4, the flow in the capillary and venous compartments is a function of the pressure, volume and the resistance of the compartments and is described by

   $$F_{n-1,n}=\frac{P_{n-1}-V_n{(t)}^{\beta }/A^{\beta }}{R_{n-1}(t)+R_n(t)}$$ (4i)

   $$F_{n,n+1}=\frac{V_n{(t)}^{\alpha +\beta }}{A^{\beta }\cdot V_n{(0)}^{\alpha }\cdot \left(R_n(0)+R_{n+1}(0)\right)},$$ (4ii)

   where α = 2 and represents laminar flow in the compartments (Boas et al. 2003).

3. Volume expansion of the arterioles is the result of the active dilation of these vessels. The changes in arterial volume (ΔV_A) are determined by the change in the diameter of the compartment (ΔD_A).

   $$\frac{V_A(t)}{V_A(0)}={\left(\frac{D_A(t)}{D_A(0)}\right)}^2$$ (5)
4. The arterial resistance (R_A) is proportional to the vessel's length (ℓ_A) and inversely proportional to the fourth power of its diameter (D_A) according to Poiseuille's Law (Washburn 1921). η is the viscosity of blood and is removed with normalization.

   $$R_A(t)=\frac{128\cdot \eta }{\pi }\cdot \frac{{\ell }_A}{D_A{(t)}^4}$$ (6)

In order to calculate the blood flow and volume changes for each of the vascular compartments, we use a differential temporal update sequentially applied to the arteriole, capillary and finally venial compartment. This update is driven by changes in the arteriolar resistance, which is an input to the system and is described variables estimated within the state vector. The value of the hydrostatic pressure of the subsequent compartment (i.e. capillary) at the previous time instance, and the vascular resistance and inflow to the current (i.e. arteriole) compartment at the current time instance are used to calculate the differential update in the system (including vascular resistance, capacitance, and out-flow from arterioles). This differential change is used to update the set of physiological changes (blood flow and volume) for the arteriole compartment at the current instance. Following the update of the arteriole compartment, the same procedure is used to update the capillary and the venial compartments. The fourth compartment representing the pial veins is assumed to have constant blood volume, defined by the flow and mean transit time through this vascular segment (τ_pial). The inclusion of a pial compartment was motivated by experimental observations of the role of these structures in measuring hemodynamic changes (Nielsen et al. 2000; Watanabe et al. 1994). The transit time through the pial compartment is determined by an additional parameter in the state model.

The differential equations (defined by equations 1-5) can be formulated with variables of flow and resistance represented as unit-normalized quantities. Thus, the model naturally estimates relative changes in the hemodynamic parameters. Although the laser speckle measurement of blood flow is a relative change, the spectroscopic measurements of hemoglobin concentration changes are absolute (i.e. micro-molar). Thus, an additional state parameter, baseline total-hemoglobin (HbT_o), is used to scale the fractional changes in volume predicted by the model to the absolute concentration changes measured by optical imaging. At baseline, the relationship between the Windkessel volume and the incoming blood flow is given by the vascular transit time (V_W(0) = F_in(0) · τ), where the Windkessel volume is equal to the sum of the volumes of the three vascular compartments (arteriole, capillary and venial). We assume initial volume fractions of 25%, 15%, and 60% for the arteriole, capillary and venial compartments (Duong and Kim 2000; Zheng et al. 2005). The sum of the initial total resistance in the three compartments is set at unity. The value for baseline arteriole resistance (Ra(0)) is estimated by the state vector and the remaining resistance is equally distributed between the capillary and venous compartments, which is in agreement with the model assumption described in Boas et al (Boas et al. 2003).

Arteriole Dilation

The arteriolar dilation variations that drive the flow and volume changes in the vascular network are defined in the state vector (X) and are estimated as part of the minimization of the model error with the hemodymanic measurements. We use a temporal Gaussian function to describe the response of arteriolar resistance during cerebral activation, which is in agreement with the methods described in Boas et al (Boas et al. 2003),

$$R_A(t)=R_A(0)\cdot \left(1-\frac{\Delta R_A}{\sqrt{{\sigma }_R^2\cdot \pi }}\cdot exp\left(\frac{-{(t-{\tau }_{\text{peak}})}^2}{{\sigma }_R^2}\right)\right)$$ (7)

This function is defined by the baseline resistance (R_A(0)), the functional percent change in resistance (ΔR_A), the time-to-peak (τ_peak), and the temporal width (σ_R) of the response. These four unknown parameters are estimated in the model fitting procedure as part of the state vector. The temporal basis function reduces the degrees of freedom of the arteriolar resistance subset of state variables instead of estimating the full dynamic variation and is similar to the use of temporal basis functions in the generalized linear model (Friston et al. 2005). As a future extension, this model could be improved with the inclusion of an explicit model of the release of vaso-reactive signaling molecules in response to measured neuronal stimulation (Friston et al. 2005; Riera et al. 2005).

Oxygen Transport Model

In addition to vascular changes, increased neuronal activity results in a localized increase in the mitochondrial function (Mintun et al. 2001). This increase results in elevated oxygen consumption, which increases the extraction of oxygen from the vascular network, while increased blood flow competes to lower the oxygen extraction fraction. The second element of our model, describes the process of oxygen extraction from the vascular compartments. We introduce a model of the oxygen transport dynamics between the arteriole, capillary, and venial compartments and the extra-vascular parenchyma tissue, which considers the differing permeability of these vessels. The oxygen extraction from all three compartments is based on recent experimental observations of these effects in animal models (Berwick et al. 2004; Tsai et al. 2003; Vovenko 1999). The system is built on the principle of oxygen diffusion caused by the gradient of oxygen content between the arteriole, capillary, and venial compartments and the extra-vascular tissue (c_nO₂ where n ∈ {arteriole, capillary, venial, and tissue}) (Herman et al. 2006; Zheng et al. 2002). The vessels of the pial veins are assumed to negligibly contribute to oxygen delivery to the tissue and are only affected by the wash-out effects of increased flow.

The oxygen content is the amount of oxygen carried within the blood and is the sum of the oxygen bound to hemoglobin and oxygen dissolved in the blood plasma (Habler and Messmer 1997).

$$c_n{O}_2(t)={\alpha }_p\cdot p_n{O}_2(t)+H_n\cdot \text{Hct}\cdot S_n{O}_2(t)$$ (1)

The Hüfner number (H_n) is the amount of oxygen bound per gram of hemoglobin (H_n=1.39 ml O₂/gm Hb(Habler and Messmer 1997)). Hemotrocrit (Hct) is assumed to be 16 gm Hb/dL of blood (Habler and Messmer 1997). Finally, α_p is the solubility of oxygen in blood plasma (α_p = 0.0039 ml O₂/mmHg/dL (Habler and Messmer 1997; Herman et al. 2006)). In the extra-vascular tissue, oxygen solubility is greater than in the plasma (α_t = 0.0118 ml O₂/mmHg/dL (Herman et al. 2006)). Tissue oxygen content depends only on oxygen partial pressure (i.e. c_tO₂(t) = α_t · p_tO₂(t)). Under normal physiological conditions, the amount of plasma-dissolved oxygen in the blood offers a negligible contribution (∼2-3%). However, including plasma oxygen allows this model to be generic enough to be used to model hyperoxic or hyperbaric conditions in future work.

To define oxygen transport between the vascular segments and the surrounding tissue, we derive a system of differential equations dependent on (i) the flow changes described by the vascular component of the model and (ii) changes in mitochondrial metabolism, which result in changes in oxygen consumption in the extra-vascular tissue compartment (Herman et al. 2006; Zheng et al. 2002).

The changes in the oxygenation of each vascular compartment are functions of the amount of oxygen flowing into and out of the compartment and are governed by the vascular flow and the oxygen extracted from the compartment by the surrounding extra-vascular tissue. Oxygen extraction is driven by the differences in the oxygen content between the vascular compartments and the surrounding tissue (Zheng et al. 2005; Zheng et al. 2002),

$$\frac{\partial c_N{O}_2(t)}{\partial t}=-K_N\cdot \left[c_N{O}_2(t)-c_T{O}_2(t)\right]$$ (1)

where n ∈ {Arteriole,Capillary,Venial}

In equation 9, K_N is the intrinsic rate constant for this process and can be defined from the baseline relationships between SO₂, blood flow, and the pO₂ levels of the compartment and extra-vascular tissue. In this model, we include the effect of oxygen diffusion across both the arteriole and venial walls, which has been suggested by experiential findings (Berwick et al. 2004; Vovenko 1999).

In order to derive the equations for oxygen transport, we assume that all compartments obey the principles of mass balance of the amount of O₂ (N_O2). I.e.

$$\frac{\partial N_{O2}}{\partial t}={\left(\frac{\partial N_{O2}}{\partial t}\right)}_{\text{Flow in}}-{\left(\frac{\partial N_{O2}}{\partial t}\right)}_{\text{Flow out}}-{\left(\frac{\partial N_{O2}}{\partial t}\right)}_{\text{Extracted}}$$ (1)

Using the relationship between the amount of oxygen carried in each compartment and the oxygen concentration (N_O2(t)=c_nO₂(t)·V_n(t)), we arrive at a set of differential equations for the delivery of oxygen into each the vascular compartments,

$$\frac{\partial N_{O2}}{\partial t}=F_{\text{In}}(t)\cdot c_{\text{In}}{O}_2(t)-F_{\text{out}}(t)\cdot c_{\text{out}}{O}_2(t)-K\cdot \left[\frac{1}{2}\left(c_{\text{In}}{O}_2(t)+c_{\text{Out}}{O}_2(t)\right)-c_T{O}_2(t)\right]\cdot V_n(t)$$ (1)

The mean oxygen content of a vascular segment has been defined as the average of the concentration (content) of either end (i.e. $c_n{O}_2(t)=\frac{1}{2}\left(c_{\text{In}}{O}_2(t)+c_{\text{Out}}{O}_2(t)\right)$). In the extra-vascular compartment, the change in the amount of oxygen is the difference between oxygen delivered to the tissue and oxygen consumed,

$$\frac{\partial N_{\text{tissue}}(t)}{\partial t}=\sum _n{K}_n\cdot \left(\frac{1}{2}\left(c_{\text{in}}{O}_2(t)-c_{\text{out}}{O}_2(t)\right)-c_t{O}_2(t)\right)-{\text{CMRO}}_2(t)$$ (1)

The system of equations described by 3 and 1 can be readily solved using a discrete temporal update. From the baseline conditions, which dictate that baseline oxygen content in each compartment and the tissue is at steady-state, the baseline CMRO₂ (unit normalized) and rate constants (K_n) can be calculated.

After solving for the temporal dynamics of oxygen content in each compartment, the oxygen saturation of hemoglobin and the partial pressure of oxygen dissolved in the plasma can be recovered with the non-linear inversion of equation 1. The saturation of hemoglobin is a function of the oxygen content and is related to the partial pressure of oxygen by the hemoglobin dissociation curve described using Kelman's equation (Severinghaus 1979).

CMRO₂

Similar to the arteriole dilation, we use a modified version of the gamma function as a basis function describe the temporal response of CMRO₂

$${\text{CMRO}}_2(t)={\text{CMRO}}_2(0)\cdot \left(1+\frac{\Delta {\text{CMRO}}_2\cdot {(t-{\tau }_{\text{onset}})}^2}{N}\cdot exp\left(\frac{-{(t-{\tau }_{\text{onset}})}^2}{{\sigma }_{{\text{CMRO}}_2}^2}\right)\right),$$ (1)

where CMRO₂(0) represents the baseline CMRO₂ in the mitochondria and ΔCMRO₂ represents the maximum percent change in CMRO₂ from its baseline value. τ_peak is the time to maximum change in CMRO₂ and σ_C is the temporal width of the response and N is the proper normalizing factor. In future work, this CMRO₂ function may be defined from an impulse response function and measured neuronal spiking (Friston et al. 2005). The bottom-up framework of this model allows the incorporation of direct neuronal measurements from electro-encephalography or magneto-encephalography for the inference of neuronal, metabolic, and hemodynamic functions as recently demonstrated by Riera et al (Riera et al. 2005).

Measurement Models

As part of the bottom-up framework of this model, the final component of this system is a model of the observation process depicted in figure 1. We use module measurement model functions to describe the biophysics by which the auxiliary states (HbO₂, HbR, CBV, and CBF) are measured by one or more imaging modalities. Separating the measurement model from the rest of the system, allows us to readily extend this work to multimodality imaging measurements (Riera et al. 2005). In this work, we focus on the analysis of region-of-interest averages from laser speckle and optical spectroscopy. The measurement models are assumed to have uniform sensitivity to each compartment and these measurements represent the sum or the average of the contributions from all the vascular compartments

(n ∈ {Arteriole,Capillary,Venial, Pial Vein}),

$$Y_{\text{Spectral},\text{HbX}}(t)=\sum _n\Delta {\text{HbX}}_n(t),$$ (1i)

$$Y_{\text{Speckle}}(t)=\sum _n{\text{CBF}}_n(t)/\sum _n{\text{CBF}}_o.$$ (3ii)

The framework of this model allows the incorporation of true measurement sensitivity profiles, such as those obtained from the consideration of the optical photon transport process or fMRI measurement models. This could be extended to the fusion of multimodality data into image reconstructions of hemodynamic and metabolic changes and will be explored in future work.

Materials and Methods

Experimental Methods

Animal preparation

The MGH Subcommittee on Research Animal Care approved all experimental procedures. Male Sprague-Dawley rats (250-350g, n = 7) were anesthetized with 2% halothane and prepared as previously described in Dunn et al (Dunn et al. 2005). The skull over the somato-sensory cortex was thinned until transparent (approximately 100μm) and covered with a glass coverslip for imaging. Following surgery, anesthetic was switched to a 50mg/kg bolus of α-choralose followed by continuous infusion at 40mg/kg/hr.

Stimulation Protocol

A whisker deflection stimulus was used for stimulus as described in Devor et al (Devor et al. 2003). The stimulus consisted of a single whisker deflection of varying amplitude (from 1 to 9) and 20ms duration. The angular velocity increased from 203°/s (vertical displacement of 240μm- condition 1) to 969°/s (vertical displacement of 1200μm- condition 9), with equal amplitude increments. Stimuli were presented using a rapid, randomized event-related paradigm.

Description of optical spectroscopy system and analysis

Multi-wavelength spectroscopic imaging of total hemoglobin concentration and oxygenation were preformed using the instrument and methods described in Dunn et al. (Dunn et al. 2003). Briefly, the cortex was illuminated by a filtered mercury xenon arc lamp (10-nm bandpass filters centered at wavelengths of 560, 570, 580, 590, 600, and 610nm). Images were acquired onto a cooled 12-bit CCD camera at an effective frame rate of 18Hz. The modified Beer-Lambert law was used to convert these spectral images into images of oxy- and deoxy-hemoglobin concentration changes. Differential path-length factors that accounted for the different optical path-lengths of each wavelength were used as described in Kohl et al (Kohl et al. 2000).

Description of laser speckle system and analysis

Blood flow was imaged using laser speckle contrast by the method and instrument described in Dunn et al (Dunn et al. 2003; Dunn et al. 2005). Images of CBF changes were determined by calculating the changes in the speckle contrast in a series of laser speckle images. The speckle contrast is defined as the ratio of the standard deviation to the mean pixel intensities, <I²>/<I> within a localized region of the image (Briers 2001). Each raw speckle image was converted to a speckle contrast image using a sliding window of 7×7. Speckle contrast images were averaged across trials and the averaged set was converted to relative blood flow (1 + ΔCBF/CBF_o) by converting each speckle contrast value to an intensity autocorrelation decay time (Briers 2001) and dividing by baseline (Dunn et al. 2005).

Determination of hemodynamic response

Both laser speckle and spectroscopic results were deconvolved using the stimulus presentation timing to determine the blood flow and hemoglobin responses. Colocalized regions-of-interest were manually selected and averaged for each experimental run of all rats. The group average of the seven rats was calculated after normalizing to the amplitude of the 9th condition. The measurement error was computed from the variance of the data compared to the average of the seven rats.

Model parameters and initial conditions

In order to estimate the states describing the CMRO₂ and arteriole dilation functions, we use a non-linear, Levenberg-Marquardt algorithm implemented in Matlab (Marquardt 1963). We used a differential time step of 2 ms for the update of the vascular and oxygen transport models. Smaller time steps were also tested to verify that the time-step did not affect the results. To integrate the multimodality measurements, we used a weighted least-squares cost function, with the weights given by the inverse of the measurement variances for each modality as depicted in figure 1. These weights are estimated from the variance in the estimate of the hemodynamic responses across the seven rats.

In table 4, we summarize the variables, which are estimated in this minimization process. The physiological range of values for each of the parameters was used to impose a constraint on the upper and lower range of fitting values. The fitting routine was iterated until a defined convergence criterion was met (10^-6 times the variance of the measurement error). Each of the nine stimulus conditions was fit independently and the process took approximately 120 minutes per condition (Pentium(R) 4; 3.0 GHz). We verified that the final estimate was independent of the choice of the initial guess for each state and the same initial guess was used for each of the nine conditions.

Table 4. State estimates.

In this table, we present the model estimates from the nine stimulus conditions for the fourteen state variables discussed in table 3. For the structural parameters, the mean of the nine conditions is shown. None of the changes in these parameters significantly varied with stimulus condition (discussed in the text). In the last column, we show the values estimated jointly from all nine conditions. The asterisks (*) indicate parameters, that varied significantly (p<0.05) with stimulus condition. The amplitude and time-to-peak of arteriole dilation both increased significantly with stimulus condition for the nine independent fits. CMRO₂ estimated in the independent fits trended to increase, but this was not significant due to variance of the estimates. In contrast, CMRO₂ significantly increased in the estimates obtained by joint-fits to all nine conditions (shown in figure 5).

		Variable	Stimulus Condition									Mean	Fit Together
			1	2	3	4	5	6	7	8	9
Dynamic	Arteriole dilation temporal basis	ΔRA	0.94	1.05	1.41	1.72	1.69	1.84	2.57	2.65	3.00	*	--
		τpeak	3.00	3.11	2.96	3.12	3.11	3.03	3.32	3.26	3.22	*	--
		σA	2.38	1.97	1.35	1.15	1.48	1.32	1.55	1.56	1.36		--
	CMRO2 temporal basis	ΔCMRO2	0.53	0.24	0.34	0.35	0.22	0.27	1.28	0.36	0.28		--
		τpeak	1.49	1.86	1.68	1.49	1.71	1.91	1.32	1.37	1.27		--
		σc	1.77	1.15	1.11	1.72	1.61	1.54	2.12	1.84	1.08		--
Structural		RA(0)	0.73	0.77	0.74	0.73	0.76	0.77	0.66	0.68	0.76	0.73	0.79
	Windkessel parameters	β	1.32	1.33	2.27	2.79	1.21	1.14	2.94	1.52	1.19	1.75	1.45
		τ	0.79	0.68	0.65	1.31	0.70	0.66	0.75	0.62	0.61	0.75	0.60
		τpial	1.27	0.77	0.75	1.09	0.59	0.71	1.40	0.80	0.63	0.89	0.96
		[HbT]o	113.8	118.7	114.3	133.4	112.9	110.7	133.4	92.4	87.7	113.04	102.5
		SaO2	0.940	0.940	0.950	0.972	0.947	0.943	0.973	0.939	0.938	0.95	0.938
		ScO2	0.709	0.704	0.731	0.749	0.740	0.712	0.732	0.730	0.747	0.73	0.694
		SvO2	0.635	0.631	0.656	0.687	0.667	0.635	0.655	0.656	0.673	0.66	0.616

In order to estimate the confidence-bounds for each of the states, we performed a Markov Chain Monte Carlo sampling of the state-space (Carter and Kohn 1996). We used the change in χ² (Chi-Squared) value at each sample step to approximate “energy cost” for determining the probability of the acceptance of each step using the equation,

$$P(k|\left\{j<k\right\})=\left[\begin{array}{cc}1\hfill & \hfill \text{if}\Delta {\chi }^2\le 1\\ e^{-\Delta {\chi }^2}\hfill & \hfill \text{else}\end{array}\right],$$ (1)

where k defines the index current iteration and {j<k} is the set of all previous steps. The density of samplings approximates the n^th-dimensional probability density function where n is the number of degrees-of-freedom in the state-vector. This defines the confidence bounds on each of the state estimates.

Single-compartment Windkessel Model

In addition to fitting experimental data with our proposed multi-compartment vascular model, we compare our results to the previously published, single-compartment version of the Windkessel model (Boas et al. 2003; Mandeville et al. 1999b) using a similar fitting procedure to our multi-compartment model. A single compartment simplification of the current model was constructed from a dilating arteriole and a single compliant (Windkessel) compartment (Mandeville et al. 1999b). In our construction of the single-compartment model, we follow the same model framework as used in our multi-compartment model and diagramed in figure 1. We used temporal basis functions to describe the arteriole dilation and CMRO₂ time-courses while performing a non-linear minimization to estimate the unknown states. This inductive modeling approach is similar to fitting of arteriole dilation described in Boas et al (Boas et al. 2003), but represents a significant deviation from the deductive approaches used in most other similar model descriptions. This allows us to infer arteriole dilation and CMRO₂ from the joint set of measurements within the same pseudo-Bayesian framework used in the multiple compartment model and to make direct comparisons of the results obtained in both cases.

The single-compartment model had eleven degrees-of-freedom (refer to table 3), where the pial transit time was eliminated and the capillary and venial oxygen saturations were reduced to a single compartment. The bounded ranges for all parameters were the same as the multi-compartment model, which is in agreement with previous literature (Boas et al. 2003). The baseline vascular fractions were assumed to be 20% and 80% for the arteriole and Windkessel compartments (Boas et al. 2003).

Table 3. State variables.

A total of fourteen independent states are fit to each data set in this model. The dynamic changes in arteriole dilation and CMRO₂ are modeled by several amplitude and timing parameters, which describe the temporal basis functions used in the model (described in the text). In addition, several static parameters describing components of the model are also fit. In the joint-fitting of multiple conditions, these static variables are estimated globally across all conditions, while independent estimates are obtained for each of the dynamic variables. Physiological ranges were used to bound the estimates of each of these parameters. *Oxygen saturations were estimated as a change from the previous compartment to avoid discontinuities in the model fitting routine.

		Symbol	Description	Physiological Range	Citation
Dynamic	Arteriole dilation temporal basis	ΔRA	Change arterial resistance	[0-10] %	--
		τpeak	Time to maximum resistance change	[0-6] s	--
		σA	Width of temporal resistance change	[0-6] s	--
	CMRO2 temporal basis	ΔCMRO2	Relative change CMRO2	[0-10] %	--
		τonset	Time to onset of CMRO2 change	[0-6] s	--
		σc	Width of temporal CMRO2 change	[0-6] s	--
Structural		RA(0)	Initial arterial resistance	[0.20-0.90] AU	(Mandeville et al 1998b; Boas et al 2003
	Windkessel parameters	β	Windkessel vascular reserve	[1-5] AU	(Mandeville et al 1998b; Boas et al 2003; Zheng et al 2005)
		τ	Vascular transit time	[0.5-4] s	(Mandeville et al 1998b; Zheng et al 2002; Boas et al 2003)
		τpial	Pial venous transit time	[0-4] s	--
		[HbT]o	Total baseline blood volume	[40-140] uM	(Zheng et al 2005; Boas et al 2003)
		SaO2	Baseline arteriole saturation	[95-100] %	(Herman et al 2006)
		ScO2	Baseline capillary saturation	[60-90] % *
		SvO2	Baseline venial saturation	[55-89] % *

Calculating baseline parameters

A unique feature of this model is that the concentration of baseline total hemoglobin is fit from the scale between the percent-change predictions of the model and the micro-molar measured changes in hemoglobin concentrations of the spectroscopic optical data. This value sets the scale for the entire model. This allows the value of baseline blood flow to be calculated from the equation,

$${\text{CBF}}_o={\text{HbT}}_o/(\tau \cdot \text{Hct}),$$ (1)

The vascular transit time (τ) is estimated as part of the model. Hct is the hematocrit value, assumed to be 16gm Hb/dL (Habler and Messmer 1997). Note that if the hematocrit is unknown, we can still estimate hemoglobin flow [gm Hb/sec].

Oxygen delivery is the product of the incoming flow of blood and oxygen content of the blood (defined in equation 1). The oxygenation of incoming blood was assumed to be 100mmHg (Herman et al. 2006), which equates to an oxygen saturation of 98.7% (Severinghaus 1979). Similarly, at baseline steady-state, CMRO₂ is the product of blood flow and the oxygen extraction fraction across the compartments (OE = s_inO₂-s_outO₂). Oxygen extraction is a fit in this model and determined by the baseline oxygen saturation of each compartment.

Results

Multi-compartment estimates

Using the multi-compartment model to fit the region-of-interest averaged response of the seven rats, we are able to estimate the unknown state parameters listed in table 3. We initially fit the response curves from each of the nine conditions independently. The state estimates for each of these nine stimulus amplitudes are provided in table 4 and the model fits to the experimental data are shown in figure 4 for (representative) conditions 3, 6, and 9. The resulting multi-compartment fits modeled nearly all the variance of the response for all hemodynamic parameters and yielded highly significant R-squared fits to each of the nine conditions, as summarized in table 5. The partial R-square values (adjusted for the model degrees-of-freedom) were calculated from the variance of the individual hemodynamic measurements (HbO₂, HbR, total-HB, and/or CBF) using the model results. This allows us to examine the goodness-of-fit for each of the multimodal observations. This calculation demonstrated nearly equally distributed variances across each of these measurements and showed that the model equally incorporated each of the measured components.

Figure 4. Parametric estimates in CMRO₂ and arteriole dilation changes.

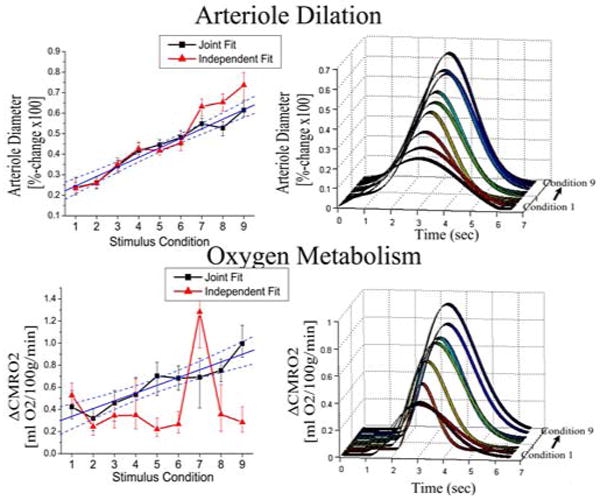
The multi-compartment model estimated parametric increases in both arteriole dilation and CMRO₂ changes over the nine stimulus amplitudes. In the plots on the left, we show the parametric changes in the diameter of the arteriole vessels (expressed as a percent change) and CMRO₂ (expressed in mL O₂/100g/min as described in the text). The temporal basis functions estimated from the model fits to the nine conditions (fit jointly) are shown in the figures on the right, where the stimulus lasted from 1.5 to 6 seconds. The results of both the independent (red lines-triangle) and joint (black lines-square) model fits of the nine conditions were consistent. However, the joint-estimates had lower variance than the independent fits for both estimates. The changes in both CMRO₂ and arteriole diameter were linear with the stimulus condition (R² = 0.87 and 0.96 respectively). The blue lines show the linear fit to the estimates from the joint fitting, with 95% confidence bounds.

Table 5. Single- and multi-compartment model fits to experimental data.

In this table, we show the R-squared values (goodness-of-fit) for the model fits to the nine-stimulus conditions. Both the fits using the single- and multi-compartment models are shown. These R-squared values have been adjusted for the degrees-of-freedom in each model. For each condition, we calculated the partial R-squared value for the flow, volume and oxy-/deoxy-hemoglobin measurements (Devore 1995). This value indicates the explained model variance considering only that component of the measurements. The total R-squared indicates the fraction of the total variance accounted for by all measurements. The multi-compartment model significantly improved the fits to the data (p<8×10^-5) [Z-transform/T-test; described in text]. The most notable improvements were observed in the modeling of deoxy-hemoglobin (p<8×10^-6).

	Stimulus Condition
	1	2	3	4	5	6	7	8	9
Multi-compartment
R2adj - HbO2	0.94	0.98	0.97	0.90	0.99	0.98	0.98	0.99	0.99
HbR	0.81	0.98	0.98	0.95	0.96	0.98	0.97	0.99	0.98
HbT	0.94	0.96	0.93	0.87	0.99	0.97	0.98	0.99	0.99
CBF	0.92	0.73	0.86	0.92	0.99	0.96	0.98	0.92	0.97
Total	0.91	0.95	0.95	0.89	0.98	0.98	0.98	0.98	0.99
Single-compartment
R2adj - HbO2	0.94	0.96	0.93	0.85	0.98	0.97	0.95	0.98	0.98
HbR	0.62	0.81	0.66	0.68	0.81	0.79	0.76	0.81	0.74
HbT	0.94	0.95	0.90	0.87	0.98	0.95	0.97	0.98	0.98
CBF	0.93	0.63	0.85	0.92	0.97	0.93	0.98	0.88	0.95
Total	0.89	0.88	0.87	0.87	0.95	0.93	0.94	0.95	0.95

The state parameters estimated by this model consist of both structural and functional properties of the system. The parameters characterizing the functional response (CMRO₂ and arteriole dilation) are expected to differ between the stimulus conditions, whereas, the structural estimates are expected to be conserved. To test this hypothesis, we grouped the results of conditions 1-3, 4-6, and 7-9 and performed a one-way ANOVA test between groups. As expected, the estimates of the functional states varied significantly (p<0.05) across the three groups, as indicated with an asterisk in table 4. We found that magnitude and time-to-peak of the estimated arteriole dilation and CMRO₂ responses increased with stimulus condition. These estimates are shown in figure 4. In contrast to the functional parameters, the estimate for the structural parameters did not vary significantly across the three groups. For these parameters, the mean of the nine conditions is shown in table 4. The Windkessel vascular reserve (β) was estimated in the range of 1.1–2.9 (mean 1.8) for the nine conditions. Similarly, the estimate of the vascular transit time (τ) was also conserved across the three groups of conditions with a range of 0.61-1.31sec (mean 0.70sec). In addition, we estimated baseline total-hemoglobin to be 88-133μM (mean 113μM).

Joint estimates using all stimulus conditions

After fitting the nine stimulus conditions independently and noting the expected constancy of the structural parameters, we concatenated the state-vectors such that the model independently estimated the arteriole dilation and CMRO₂ functions for each condition, but used common estimates for the structural and static variables. This allowed us to get a better estimate of the arteriole dilation and CMRO₂ responses by reducing the degrees-of-freedom of the model and simultaneously incorporating data from all nine conditions. The structural parameters from this fit were consistent with the average values obtained from the independent fits (see table 4).

The arteriole dilation and CMRO₂ changes estimated by using all nine conditions are shown in figure 4. The variance in these estimates was reduced as compared to the results obtained by independently fitting each condition. The solid lines shown in figure 4, demonstrate the linear fits through the estimates from the simultaneous fitting of all nine conditions. The arteriole dilation response increased linearly with stimulus amplitude (R² = 0.96). Similarly, the CMRO₂ change increased linearly with stimulus amplitude (R² = 0.87).

Model uniqueness

To examine the uniqueness of the model fits, we examined the results using Markov chain Monte Carlo simulations to estimate the variance in each of the estimates. This approach allows us to examine underlying connections between the estimates of the individual states. In figure 5, we show the correlation of the error in the state estimates for the joint-fitting of all nine conditions. In such an image, a high degree of correlation would indicate inter-dependence between two (or more) state-variables. Instead, we observe low correlation between most of these individual state estimates, which indicates that these states were fairly independently estimated. A positive correlation was observed between the estimates of the Windkessel vascular reserve (β) and transit time (τ) (R² = 0.32). In addition, we noted a slight negative correlation between the baseline SO₂ for the three compartments and fractional change in CMRO₂ (R² = 0.07, 0.13, 0.05; S_aO₂, S_cO₂, S_vO₂). A similar negative correlation was observed between the error in the estimate of the Windkessel vascular reserve and transit time and SO₂. This result is not surprising since baseline SO₂ and transit time determine baseline CMRO₂. We further examined the state estimates of the Windkessel vascular reserve (β), transit time (τ), and baseline total hemoglobin ([HbT_o]). In figure 5b, we show the cross-section through the probability distribution clouds along these degrees-of-freedom. Contour lines are shown at the 99%, 95%, and 90% boundaries. In these plots, correlation between these variables would manifest as alignment along the diagonals of the plots. The correlation between vascular reserve and transit time had the largest such correlation. The histograms for the projection along the axis of each degree-of-freedom yield the confidence bounds for each of the states.

Figure 5. Markov Chain Monte Carlo Results.

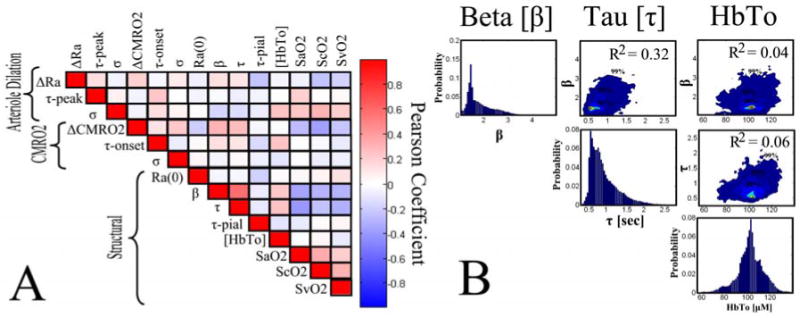
We used Markov Chain Monte Carlo techniques to examine the variance in the estimates of each state fit by the model and the independence of these estimate (Carter and Kohn 1996). In subplot A, we show a correlation matrix formed from the pair-wise correlation of the errors in the state variables. High correlation indicates interdependence between two variables, which could indicate cross-talk between these parameters in the model. In subplot B, we show probability densities for three of the structural parameters (β, τ, and [HbT_o]). The histograms (diagonal element sub-plots) show the probability densities projected through all other degrees-of-freedom and indicate the error in the estimate (i.e. width of peak). The contour plots are created by the cross-section of this probability density along the two degrees-of-freedom in the plot (i.e. the correlation between β and [HbT_o]- top right image). These cross-sections indicate the interdependence of these two variables by showing the correlation between them. Contour lines are indicated at the 99%, 95%, and 90% boundaries.

To further investigate the behavior of the model, we examined the dependence of our final state estimates on the initial guess of the minimization routine. Although the Levenberg-Marquardt algorithm was chosen for its robustness to initial seed (Marquardt 1963), it is important to verify this in our experimental fits. We used a Monte Carlo sampling of the initial guess value for several of the stimulus condition data sets and found that the final fits were independent of this seed (data not shown).

Comparison to the single compartment Windkessel model

To further examine the validity of the proposed multiple compartment model, we compared our results to those from the previously described single-compartment Windkessel models (Boas et al. 2003; Mandeville et al. 1999b). We found that the single-compartment Windkessel model fits to the experimental data (shown in figure 6) demonstrated shortcomings of this model for estimating the oxygenation component of the hemodynamic response. This result is in agreement with the similar findings by Zheng et al, of a multi-compartment model (Zheng et al. 2005). The degree-of-freedom adjusted R-squared and partial R-squared values for both the multi-compartment and single Windkessel-compartment model fits are shown in table 5. We found that both models were able to reproduce the blood flow and volume changes as well as oxy-hemoglobin changes in the measured data. Using a Z-transform, we performed a paired T-test of these fits (Devore 1995). We found that the single Windkessel-compartment model had significantly worse agreement for the deoxy-hemoglobin (p<8×10^-6) and oxy-hemoglobin (p<2×10^-4) time-courses. The blood flow and volume estimates were also significantly better in the multi-compartment model by this test (p<6×10^-3 and p<2×10^-3). The overall model fit to all observations was also significantly better for the multi-compartment model (p<8×10^-5).

Figure 6. Single-compartment model fit to the experimental data.

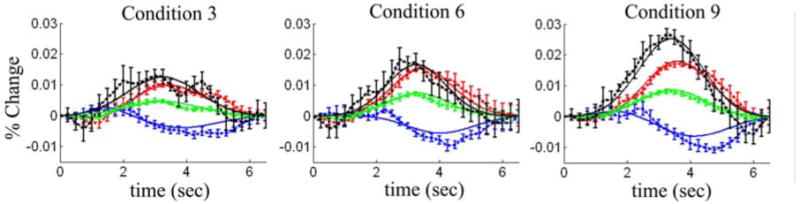
The experimental data (dots) was fit using the single-compartment model (lines). Here we show representative results from the model fits to stimulus conditions 3, 6, and 9. Each condition was fit independently to generate these plots. The R-squared values for these fits are shown in table 5. Blood flow, volume, oxy- and deoxy-hemoglobin changes are shown in black, green, red, and blue respectively. The error bars represented standard errors estimated from the seven rats used in this experiment.

The estimates of arteriole dilation and CMRO₂ are shown in figure 7. We found that the estimates of CMRO₂ are significantly higher for the single compartment, than the multiple compartment model. This is in agreement with findings reported previously (Zheng et al. 2005) Additionally, the errors in the estimates were higher in the single compartment model fits.

Figure 7. Comparison of CMRO₂ and Arteriole dilation changes from single- and multi-compartment models.

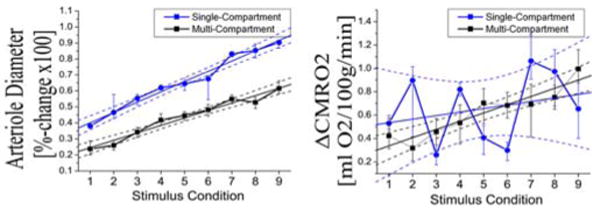
In these two plots, we show the parametric changes in arteriole diameter [left] and CMRO₂ [right] estimated by the single-compartment (blue line circle) and multi-compartment (black line-square) models. Both estimates are from the joint-fitting of the nine conditions. In both models, arteriole diameter changes were linear with stimulus amplitude (R² = 0.98 [single] and R² =0.96 [multi]). The single-compartment estimates were significantly greater than the multi-compartment estimates (p<2×10^-6)[paired T-test]. CMRO₂ changes estimated with the multi-compartment model were linear (R²=0.87) with stimulus condition. The single-compartment estimates were more variable (R²=0.08). Due to this variance, the difference in the two model estimates was not significantly.

Estimated baseline properties

Our model allows the estimation of the vascular transit time, baseline oxygenations, and the absolute baseline hemoglobin concentration. These can be used to estimate baseline blood flow and oxygen consumption from the initial relationship between the initial Windkessel volume and incoming blood flow (V_w(0) = F_in(0) · τ). At baseline, we can assume steady-state conditions, in which case, relative CMRO₂ can be calculated directly from the baseline blood flow and oxygen extraction fraction (OEF) (i.e. rCMRO₂(0) = F_in(0) · OEF). The estimates of these baseline properties are shown in table 6. From the mean of the nine stimulus conditions, we estimate baseline blood flow to be 94 +/-15 mL/100g/min using an assumed hematocrit of 16 g/dL (Habler and Messmer 1997). From the oxygen carrying capacity of oxy-hemoglobin (H_n = 1.39 mL O₂/g Hb (Habler and Messmer 1997)), we calculated baseline oxygen delivery to be 20.0+/-3.1 mL O₂/100g/min. Our model estimated a baseline oxygen extraction fraction of 0.33 +/-0.02 based on the model fit values of the oxygen saturation in the three compartments. From these values, the baseline CMRO₂ is estimated at 6.7 +/-1.3 mL O₂/100g/min. These baseline values were consistent for the nine independent fits and the joint-estimates (shown in table 6). None of these estimated baseline values showed any significant cross-talk with stimulus condition (one-way ANOVA).

Table 6. Estimates of baseline properties.

Baseline blood flow and oxygen consumption are estimated from the model parameters as described in the text. The values for baseline blood flow, oxygen delivery, and CMRO₂ were calculated from the model fits to the nine-stimulus conditions. The 75% confidence bounds of these estimates were calculated from the propagation of error in the individual state estimates (estimated from the Markov Chain Monte Carlo procedure detailed in the text). The baseline values of CMRO₂ estimated with the model are consistent with values from the literature.

	Stimulus Condition									Mean	Fit Together		Literature
	1	2	3	4	5	6	7	8	9
Baseline Flow	87	105	107	61	98	101	107	89	87	94 (15)	104(12)	mL/100g/min	70 (Herman et al 2006) 56 (Minun et al 2001)
Baseline O2 delivery	18.6	22.4	22.8	13.1	20.9	21.5	22.9	19.1	18.6	20.0 (3.1)	22.1(2.6)	mL/100g/min
Baseline OEF	0.35	0.36	0.33	0.30	0.32	0.35	0.33	0.33	0.31	0.33 (0.02)	0.37(0.01)	[AU]
Baseline CMRO2	6.6	8.0	7.6	4.0	6.7	7.6	7.6	6.4	5.9	6.7 (1.3)	8.2(0.8)	mL/100g/min	5.6 (Heman et al 2006)

Flow-volume and Flow-consumption ratios

From the functional responses, we found that the ratio of maximum flow to maximum volume changes was 2.84 [range 2.83-2.85]. This estimate was extremely well conserved between the nine conditions. However, this value tended to increase with stimulus condition (R²=0.78). This trend tested significant in the grouped ANOVA test (p<0.006).

We also found that the ratio of maximum flow to maximum CMRO₂ change was 2.5 +/- 0.3. This also did not vary significantly with stimulus condition (one-way ANOVA). The estimates of these values were more conserved in the joint fitting results.

Compartmentalized changes in hemodynamics

In figure 8, we show the predicted hemodynamic changes in each of the vascular compartments for stimulus condition 9. The time courses of blood flow and oxy-, deoxy-, and total-hemoglobin changes are shown for the three vascular compartments and the modeled observation (i.e. the sum or mean of the three compartment changes shown in equation 15). The neighboring plots show the time-course of the initial response from 0-2 (3) seconds post stimulus. We found similar dynamic behavior with the model fits to the other eight experimental conditions. We did not note any differences between the independent and the joint estimates for the nine conditions.

Figure 8. Compartmental hemodynamic changes.

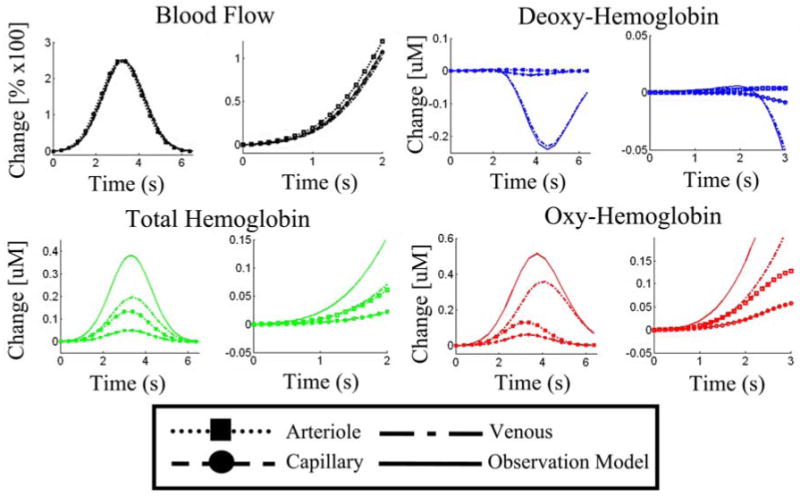
Vascular changes were modeled in the arteriole, capillary, and venous compartments. The time-courses plotted here from the ninth stimulus condition, show the representative changes in these three compartments. The solid lines, show the predicted observation model for either laser speckle imaging (blood flow) or spectroscopic imaging. The figures to the right of each plot show an enlargement of the initial onset times [0-2(3) seconds].

Discussion

We have demonstrated that the model proposed in this work was able to reproduce the majority of the measured hemodynamic responses, as noted by the large R-squared values for the model fits to each condition shown in table 5.

In the model fits to the parametric whisker stimulus, our estimates of the change in CMRO₂ and arteriole dilation increased linearly with stimulus amplitude (R²=0.87 and 0.96 respectively). Because of the framework of the model, we were able to estimate these changes independently for the nine conditions or by jointly estimating these changes using the complete parametric data and assuming common values for baseline properties for the nine conditions. We found consistent estimates with both of these approaches, while the variance in the estimates decreased for the joint estimation as expected.

Using Monte Carlo methods, we found that the state estimates were robust to the starting position of the minimization routine. The model consistently estimated the state variables representing structural and baseline properties. Since we do not expect these values to vary between the nine stimuli conditions, the finding that the model estimated values independent of the stimulus condition is further supporting evidence of the utility of the model to infer details of the vascular anatomy.

Multi- versus single-compartment models

Although simpler, single-compartment models have been previously demonstrated to model fMRI data (Buxton et al. 2004; Buxton et al. 1998; Mandeville et al. 1999b), we found that the higher temporal resolution and spectroscopic information of optical imaging requires a more detailed model. In agreement with previous work (Zheng et al. 2005), we found that the multi-compartment model performed better than the single-compartment formulation, even after the additional degrees-of-freedom for the more complicated model were accounted for (p<8×10^-5). Comparison of this previously published single compartment model and our multiple-compartment Windkessel model revealed that both models accurately reproduced the relationship between flow and volume, as indicated by the goodness-of-fit of blood flow and volume measurements by both models (refer table 5). The difference in these two models was significant in our fitting procedure, but was not significant if only blood flow and volume were fit. This finding is consistent with the previous report, which found that both a single and three-compartment model could nearly equally model flow and volume changes (Zheng et al. 2005). The estimates of arteriole dilation were significantly higher in the single-compartment model (p<2×10^-6). Both models predicted a linear relationship with stimulus condition (R²=0.98 [single] and R²=0.96 [multi]).

In contrast, we found that the multi-compartment model performed significantly better at modeling oxy- and deoxy-hemoglobin measurements, as well as the overall data set. We report that the single-compartment model had significantly lower R-squared values for all nine conditions of model fits to oxy- and deoxy-hemoglobin data than the multi-compartment model. The discrepancy between measured and predicted oxygenation changes affected the estimates of CMRO₂ changes with the single-compartment model. We found that the CMRO₂ changes predicted by the multi-compartment model were significantly better correlated with stimulus condition than those of the single-compartment model (R²=0.08 [single] and R² = 0.87 [multi]). Due to the large variance in the estimate of CMRO₂ changes in the single-compartment model, the difference in the two estimates was not statistically different (paired T-test).

Compartmentalized changes in hemodynamics

The predicted response curves for each of the vascular compartments, shown in figure 7, are in qualitative agreement with previously published experimental findings (Vanzetta et al. 2005). We found that the largest magnitude of blood volume changes originated from the venous compartment. However, the arteriole compartment had the largest fractional volume changes. Blood volume changes in the arterioles initiated and peaked slightly before the volume changes in the capillaries or venials.

In the blood flow response, we found that the magnitude of the change in all three compartments was nearly identical. The blood flow response was slightly lagged from the arteriole to venous compartments. This result is consistent with statements made by Zheng et al (Zheng et al. 2005). In addition, we found that the majority of the contrast of oxy- and deoxy-hemoglobin changes arose from the venous structures. These large changes are the result of the large wash-out effects in this compartment, which has the lowest initial SO₂. From the model, we estimated venous oxygen saturation to be around 62-66%. This low saturation allows large changes in the blood oxygenation of the venous compartment in response to the same magnitude of increased blood flow and similar volume changes as the other compartments. In comparison, the oxygen saturation of the arteriole compartment (95%) is very close to that of the feeding (artery) blood (98.7%). Thus in the arteriole compartment, changes in oxy- and deoxy-hemoglobin arise from blood volume changes with little direct influence of increased flow. In all nine conditions, we observed larger and more latent oxy-hemoglobin changes then total-hemoglobin. This result can only be explained by the direct contribution of blood flow changes, which wash-out the baseline deoxy-hemoglobin concentration.

Determination of baseline properties

A key feature of our model is the bottom-up methodology that allows us to recover baseline blood volume and oxygenation properties of the tissue from the measured hemodynamic responses. This is possible because the range of hemodynamic responses allowed by the model is constrained by the baseline state. The estimates of the baseline oxygen delivery (20.0 mL O₂/100g/min) and CMRO₂ (6.7 mL O₂/100g/min) calculated with this model are consistent with the physiological ranges reported in previous literature (Habler and Messmer 1997; Mintun et al. 2001; Ostergaard et al. 1998) (Herman et al. 2006). Our estimates of blood flow are slightly higher than those found in literature. This could result from an incorrect assumption for hematocrit, which affects the absolute magnitude of the blood flow response.

Conclusions

We conclude that the proposed multiple compartment model makes three significant contributions: (i) The multi-compartment model shows significant improvements in the modeling of measured oxy- and deoxy-hemoglobin changes. (ii) Our model allows the estimation of baseline hemodynamic and metabolic parameters from the time-courses of dynamic hemodynamic measurements (iii) The bottom-up framework of this model allows for inclusion of multimodality data in a Bayesian model, which improves the accuracy of the estimated states and compensates for uneven measurement noise across modalities. This framework can be readily extended to the analysis of human functional neuroimaging measurements.

Figure 3. Multi-compartment model fit to the experimental data.

The experimental data (dots) was fit using the multi-compartment model (lines). Here we show representative results from the model fits to stimulus conditions 3, 6, and 9. The error bars show standard error estimated from the seven rats used in this experiment. Each condition was fit independently to generate these plots. The R-squared values for these fits are shown in table 5. Blood flow (black) was measured by laser speckle imaging (Dunn et al. 2003). Blood volume changes (green) and oxy- and deoxy-hemoglobin changes (red/blue) were measured by optical spectroscopy (Dunn et al. 2003).

Table 1. Variables used in vascular model.

In this table is shown the modeling parameters and symbols used in the vascular component of this model.

Description	Symbol	Comments	Value	Citation
Resistance	Rn(t)	Resistance of nth compartment	Modeled-Dynamic
	Rtotal	Total vascular resistance	1 [AU]
Capacitance	Cn(t)	Capacitance of nth compartment	Modeled-Dynamic
Flow	Fn,m(t)	Flow from compartment n --> m	Modeled-Dynamic
	Fin(t)	Flow into system	Modeled-Dynamic
	Fout(t)	Flow out of system	Modeled-Dynamic
Pressure	Pn(t)	Pressure of nth compartment	Modeled-Dynamic
	Pin	Mean arterial blood pressure	1 [AU]
	Pout	Mean venous blood pressure	0 [AU]
Volume Fraction	ΦA	Baseline Arterial Volume fraction	25%	(Duong and Kim 2000 Zheng et al 2005)
	ΦC	Baseline Capillary Volume fraction	15%
	ΦV	Baseline Venous Volume fraction	60%
Windkessel Model	β	Windkessel vascular reserve	Modeled-Static
	τ	Windkessel (vascular) transit time	Modeled-Static

Table 2. Variables used in oxygen transport model.

In this table is shown the modeling parameters and symbols used to model oxygen transport in this work.

Description	Symbol	Comments	Value	Citation
Partial Pressure O2	pnO2(t)	Partial pressure of O2 in vascular segments	Modeled-Dynamic
	pinO2	Mean incoming pO2	100 mmHg	(Herman et al 2006)
	ptissueO2	Mean Tissue pO2	16 mmHg
Oxygen Saturation	Sn02(t)	Baseline	Modeled-Static
		{Art, Cap Vein, Tissue}	Modeled-Dynamic
Oxygen Content	Cn02(t)	Baseline	Modeled-Static
		{Art, Cap Vein, Tissue}	Modeled-Dynamic
Diffusivity Rate Constant	Kn	Oxygen permeability rate constant	Modeled-Static
Cerebral Metabolism	CMRO2(t)	Metabolism temporal basis function	Modeled-Static