A method to estimate the spatial extent of activation in thalamic deep brain stimulation

Abstract

Objective

The goal of this study was to develop, evaluate, and apply a method to quantify the unknown spatial extent of activation in deep brain stimulation (DBS) of the ventral intermedius nucleus (Vim) of the thalamus.

Methods

The amplitude-distance relationship and the threshold amplitudes to elicit clinical responses were combined to estimate the unknown amplitude-distance constant and the distance between the electrode and the border between the Vim and the ventrocaudal nucleus (Vc) of the thalamus. We tested the sensitivity of the method to errors in the input parameters, and subsequently, applied the method to estimate the amplitude-distance constant from clinically-measured threshold amplitudes.

Results

The method enabled estimation of the amplitude-distance constant with a median squared error of 0.07–0.23 V/mm² and provided an estimate of the distance between the electrode and the Vc/Vim border with a median squared error of 0.01–0.04 mm. Application of the method to clinically-measured threshold amplitudes to elicit paresthesias estimated the amplitude-distance constant to be 0.22 V/mm².

Conclusions

The method enabled robust quantification of the spatial extent of activation in thalamic DBS and predicted that stimulation amplitudes of 1–3.5 V would produce a mean effective radius of activation of 2.0–3.9 mm.

Significance

Knowing the spatial extent of activation may improve methods of electrode placement and stimulation parameter selection in DBS.

I. Introduction

Deep brain stimulation (DBS) requires selective and controlled effects on populations of neurons, but the distance over which DBS activates neurons is unknown. The unknown spatial extent of activation complicates surgical placement of electrodes and post-operative programming of the active contacts and stimulation parameters (Kuncel and Grill, 2004). The distance over which neurons are activated is dependent on the orientation of the electrode and the neurons, the electrical properties of the tissue including inhomogeneity and anisotropy, the electrode geometry, and the stimulation parameters (Ranck, 1975). Due to the large number of factors that contribute to determining the spread of excitation, it has been suggested that the spatial extent of activation should be approximated for each experimental situation (Stoney et al., 1968; Bagshaw and Evans, 1976). The objective of this study was to develop and evaluate a method to estimate empirically the spatial extent of activation for thalamic DBS.

The threshold amplitude required to activate a neuron increases as the distance between the neuron and the electrode increases. The relationship between the threshold amplitude, Vth, and the distance between the neuron and the electrode relative to the location of minimum threshold, r, can be described by equation 1.

$$Vth(r)=v+k{r}^2$$ (1)

The offset, v, determines the minimum threshold at the closest relative distance of the electrode to the neuron (i.e., r=0), and the amplitude-distance constant, k, determines the increase in threshold as the relative distance between the electrode and the neuron changes (Stoney et al., 1968). To determine the spatial extent of activation, it is first necessary to estimate the amplitude-distance constant. Estimates of the amplitude-distance constant in the central nervous system range from 0.1 to 4 V/mm² (for a resistance of 1 kΩ) (Stoney et al., 1968; Shinoda et al., 1976; Marcus et al., 1979; Hentall et al., 1984; Yeomans et al., 1986). In this study we combined experimental measurements of the response to DBS through individual electrode contacts and the amplitude-distance relationship to estimate the amplitude-distance constant for thalamic DBS.

II. Methods

The goal of this study was to design and evaluate a method that uses the amplitude-distance relationship (1) and a reproducible response to stimulation to estimate the amplitude-distance constant in DBS of the ventral intermedius nucleus (Vim) of the thalamus. The method includes a mathematical model of the amplitude-distance relationship for each of the four contacts of the DBS electrode where the distance between the contacts and the border between the ventrocaudal nucleus (Vc) of the thalamus and the Vim are expressed as a function of the ring and arc angles as defined for the Leksell stereotactic frame. Thresholds to evoke reproducible side effects, described as paresthesias, were measured with monopolar stimulation and were assumed to be due to spread of activation to the Vc. We evaluated the sensitivity of this method to errors in the inputs, and subsequently used the method to estimate the amplitude-distance constant in thalamic DBS.

A. Method to estimate spatial extent of activation

The amplitude-distance relationship (1) was combined with experimental measurements of threshold voltages to estimate the unknowns (k and y′₀) using optimization. The threshold amplitude for each contact, c can be expressed as:

$$Vt{h}_c({y^{\prime }}_c)=v+k{y^{\prime }}_c^2$$ (2)

where k is the unknown amplitude-distance constant and y′_c is the unknown distance between contact c and the border between the Vim and the Vc nuclei of the thalamus. The offset, v, is equivalent to the threshold for activation if the electrode contact was positioned within the Vc (i.e., y′_c ≤ 0), and was set equal to 0.1 V, the smallest stimulation voltage available in the implanted pulse generator. The value of the offset, v, depends on the pulse width. In this study, pulse width was set at 90 µs, and according to the strength-duration relationship, decreasing the pulse width from 90 to 60 µs would increase the value of the offset, while increasing pulse width would decrease the offset. For each contact (c = 0, 1, 2, 3), the distance to the Vc/Vim border can be expressed as (see Appendix A):

$$y_c^{\prime }=\left(-x_0\text{sin}\mathrm{\Psi }+y_0\text{cos}\mathrm{\Psi }-cd\text{sin}\mathrm{\Phi }\text{sin}\mathrm{\Psi }+cd\text{sin}\theta \text{cos}\mathrm{\Psi }\right).$$ (3)

The coordinates x₀ and y₀ represent the location of contact 0 before accounting for the oblique posterolateral slope (Ψ) of the Vc/Vim border (Hirai et al., 1989), d is the center-to-center separation between contacts (d = 3 mm for Model 3387, Medtronic Inc., Minneapolis, MN), and the geometric angles, θ and Φ, are the differences between 90° and the stereotactic ring and arc angles, respectively, as defined for the Leksell stereotactic frame. The Leksell frame was placed such that the y-axis was parallel to, and the z- and x-axes were perpendicular to, the anterior-posterior axis of the head, and therefore the AC/PC line, and we assumed that the the Vc/Vim border is parallel to the z-axis (dorsal-ventral) in the Leksell frame (See Discussion and Appendix A).

We estimated the unknown parameters, k and y′_c, by minimizing the objective function:

$$f={\displaystyle \sum _{c=0}^3{(Vt{h}_c-Vt{h^{*}}_c)}^2}$$ (4)

Vth_c is the clinically-measured threshold amplitude to elicit side effects for contact c in monopolar configuration, and Vth^*_c is the model-estimated threshold amplitude expressed as a function (2) of the unknowns, k and y′_c. The unknown parameters were varied to minimize the objective function using a simplex direct search minimization (fminsearch(), MATLAB, The Mathworks, Inc., Natick, MA). A range of initial conditions was tested for the unknown parameters, and the parameter estimates were independent of the initial conditions for initial values of y′_c and k ranging from 1–2 mm and 0.1–4 V/mm², respectively.

B. Model-Based Evaluation of the Method

Before the method was applied to clinically-measured threshold amplitudes, the sensitivity of the model-estimated unknowns (k and y′₀) to errors in the inputs was evaluated. For this sensitivity analysis, we simulated patient datasets by generating Vth with known values of θ, Φ, Ψ, k, and y′₀. Values used to generate datasets were selected randomly from a uniform distribution with a range from 0.1 to 4 V/mm² for k and from −2 to 4 mm for y′₀. The angles, θ and Φ, were selected to represent angles used clinically, and the angle Ψ was estimated from histological data (Hirai et al., 1989). To evaluate the sensitivity of the method to errors in the inputs, errors were first added to each input (Vth, θ, Φ, and Ψ), individually. Subsequently, errors were added simultaneously to all inputs (Table 1). Errors in the geometric angles were normally distributed around the mean angles determined from clinical records (θ and Φ) and histological data (Ψ) to account for variability in frame placement and anatomy across subjects. The estimated and actual values of k an y′₀ were compared to determine the accuracy of the estimated parameters in the presence of measurement errors.

Table 1.

Errors added to the model inputs to evaluate the accuracy of the method. The inputs include a vector of clinically-determined threshold amplitudes for each contact (Vth),the angle of the posterolateral slope of the Vc/Vim border (Ψ), the medial-lateral electrode angle (Φ), and the anterior-posterior electrode angle (θ). Random errors were added to each input, and the distributions from which errors were selected are listed.

Input	Error distribution
Vth	Uniform (−0.5 to 0.5 V)
Ψ	Normal (µ = 0°, σ = 2, 4°)
Φ	Normal (µ = 0°, σ = 2, 4°)
θ	Normal (µ = 0°, σ = 2, 4°)

C. Experimental Measurement of Threshold Amplitudes

The thresholds to evoke paresthesias by Vim thalamic DBS were measured in 8 subjects (9 thalami) with essential tremor. Subjects were an average 29 ± 10 months (mean ± standard deviation, range 11–43 months) post-implant at the time of the study, and the average subject age was 65 ± 21 years (range 27–80 years). Subjects had quadripolar macroelectrodes (Model 3387, Medtronic Inc., Minneapolis, MN) implanted in the Vim. One subject had bilateral stimulation, and each side was tested during different sessions with the stimulator for the side not being evaluated turned off. The study protocol was approved by the Cleveland Clinic Foundation institutional review board, and written informed consent was obtained from all subjects.

The objective was to determine the threshold stimulation amplitude to elicit side effects, which were described as paresthesias, for each contact in monopolar configuration, with the active contact set as the cathode and the implanted pulse generator as the anode. Stimulation pulse width and frequency of stimulation were set at 90 µs and 160 Hz, respectively, and these were not varied during the experiment. The experiment was conducted in 2 phases to minimize patient discomfort due to strong side effects. During the first phase, a voltage limit was defined for each contact by increasing voltage until the side effect approached a level that the subject found uncomfortable. Voltages that fell above these limits were eliminated from the second phase. In the second phase, combinations of contact and voltage were tested in a random order. In 5 thalami, we tested each combination of contact and voltage twice to assess the repeatability of the response. For these thalami, phase 2 was repeated after re-randomizing the order of combinations of contact and voltage. SE was rated by the subject on a scale from 0 (no side effect) to 10 (strong side effect) and was recorded at an average of 32 (range: 19 to 42) combinations of active contact and voltage in a single 2- to 4-hour session.

D. Application of the Method to Human Experimental Data

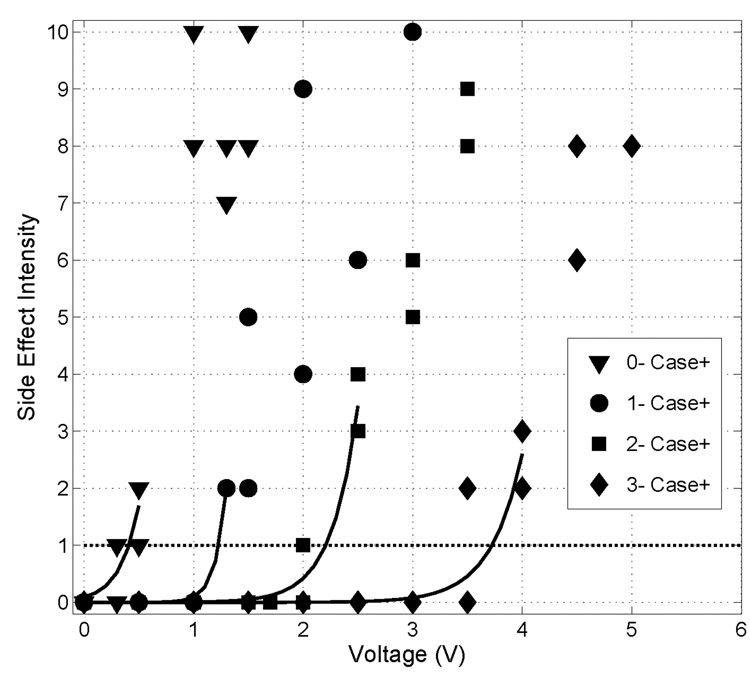
For each thalamus, we used interpolation to estimate the threshold amplitude to elicit the lowest non-zero SE, 0.5 or 1, for each contact (i.e., the threshold amplitude at which activation spread into the Vc from the Vim) (Fig. 4). The SE data for each contact were fit with an exponential equation of the form SE=ae^bV, where a and b were parameters fit to the data, and V was the stimulation voltage. Since our objective was to estimate threshold, we used data straddling the threshold voltage, and data from stronger SEs were not included in the curve fits because there was more variability within subjects at high SEs. If a voltage elicited a SE rated as a 0.5 or 1, then the SEs at that voltage, the SEs at voltage one increment higher, and the SEs at all lower voltages were included in the curve fit. If the subject did not rate a 0.5 or 1 for a particular contact, the SEs at the lowest voltage that elicited a non-zero rating and the SEs at all lower voltages were included in the curve fit. For thalami in which phase 2 was repeated, both repetitions of data were included in the curve fits. The resulting curve fits were used to interpolate the threshold voltages required to generate a SE rating of 0.5 or 1, depending on the lowest rating the subject used, for each contact. The threshold amplitudes, along with the clinically-recorded Leksell stereotactic ring and arc angles were input into the model, and we estimated the values of k and y′₀ for each thalamus.

Figure 4.

Side effect intensity (SE) as a function of stimulation voltage for each contact in monopolar configuration for subject 2L. Phase 2 was repeated in this subject, and data points for both repetitions are shown. The minimum SE rated was a 1, and the threshold voltages (Vth = [0.43 1.23 2.20 3.73]) were found by determining the voltage at which the exponential curve fits crossed SE = 1.

III. Results

We developed a method to estimate the spatial extent of activation by thalamic DBS by combining the amplitude-distance relationship and experimental measurements of the response to DBS. The sensitivity of the model-estimates to errors in the inputs was evaluated using model-generated data, and the method was subsequently applied to the clinically-measured threshold amplitudes to provide an estimate of the unknown amplitude-distance constant and the distance between the contacts and the Vc/Vim border.

A. Model-Based Evaluation of the Method

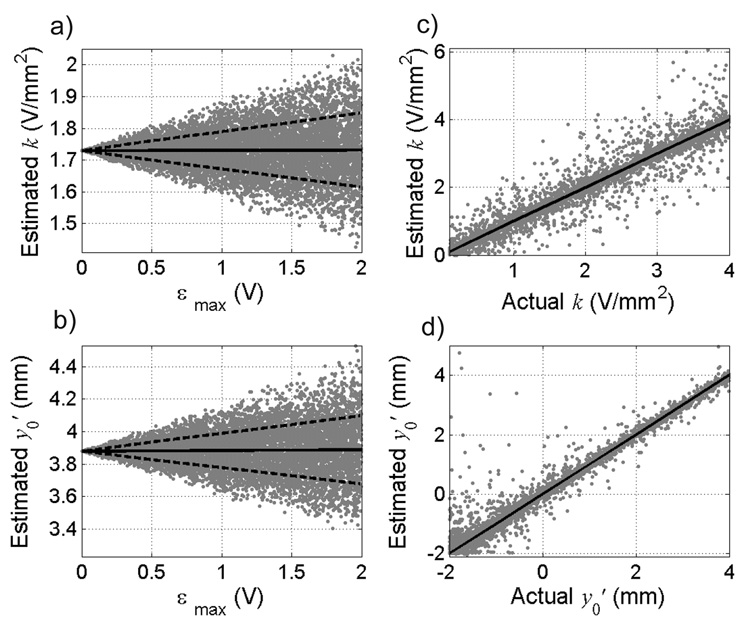
The sensitivity of the model-estimated parameters (k, y′₀) to error added to each input (Vth, θ, Φ, and Ψ) individually was assessed. First, voltage error was added to each element of Vth, which was generated with known k, y′₀, θ, Φ, and Ψ. The error was selected randomly from a uniform distribution ranging from −ε_max to ε_max, where ε_max, the maximum voltage error, ranged from 0–2 V. Figures 1a and 1b show the estimates of the parameters as a function of the maximum voltage error (ε_max) added to Vth. With increased ε_max, the mean estimate of k did not change (slope = 0.0005, p = 0.57) and increased only slightly for y′₀ (slope = 0.0047, p = 0.03), but the spread (variance) of the estimates increased for both parameters. For an ε_max of 0.5 V, there was a strong linear correlation (R² = 0.98, slope = 1.0) between the estimated k and the actual k (Fig. 1c), and the spread of the estimates about the mean was constant across all values of k. Similarly, there was a strong linear correlation (R² = 0.98, slope = 0.99) between the estimated y′₀ and the actual y′₀ (Fig. 1d), and the spread of the estimates around the mean decreased as the value of y′₀ increased.

Figure 1.

Effect of error in threshold amplitudes (Vth) on estimates of the amplitude-distance constant, k and the distance from contact 0 to the Vc/Vim border, y′₀. Estimates of a) k and b) y′₀ as a function of the maximum voltage error (ε_max) added to the threshold voltages for 10,000 trials. Threshold amplitudes were generated with a randomly selected k = 1.73 V/mm² and y′₀ = 3.88 mm. Angles θ, Φ, and Ψ were set at 25°, 5°, and 30°, respectively. Solid lines represent means and dashed lines represent ±1standard deviation. Estimates of c) k and d) y′₀ for a range of actual k and y′₀ values, with ε_max set at ± 0.5 V. Solid line represents unity slope. Fifteen outliers (estimates of y′₀ exceeding 5 mm) are not shown for clarity, and all occurred for actual y′₀ less than 0 mm.

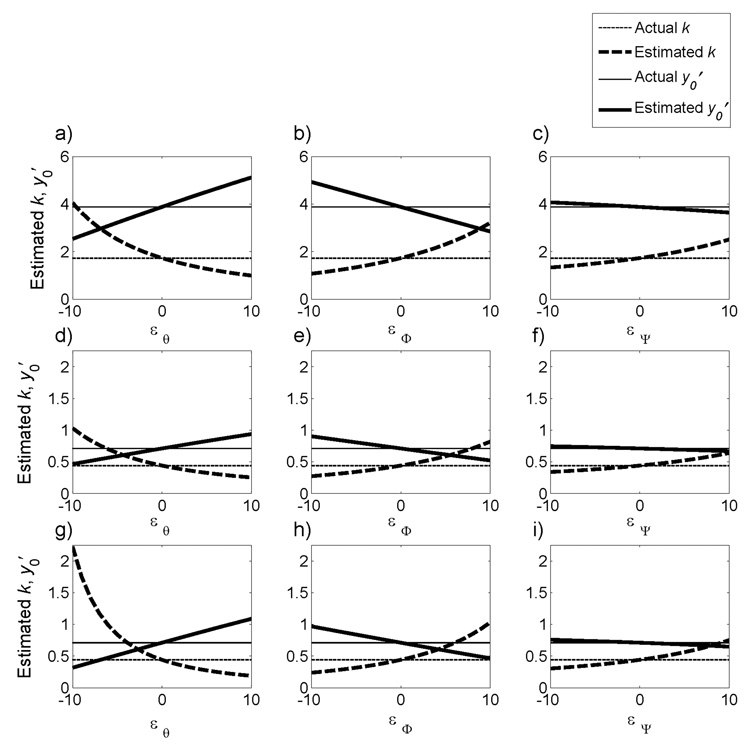
Next, the sensitivity of the estimated parameters to errors in the geometric angles θ, Φ, and Ψ was evaluated. As the error in any angle increased, the estimate of y′₀ changed linearly. An error of ±10° in θ, Φ, or Ψ resulted in respective errors of 35% (Fig. 2a, d), 28% (Fig. 2b, e), or 7% (Fig. 2c, f) in the estimate of y′₀. The estimate of k changed nonlinearly as the error in any angle increased. An error of −10° in θ resulted in 134% error in the estimate of k, and an error of 10° resulted in a 43% error (Fig. 2a, d). An error of −10° in Φ resulted in 39% error in the estimate of k, while an error of 10° resulted in an 86% error (Fig. 2b, e). Finally, an error of −10° in Ψ resulted in 23% error in the estimate of k, and an error of 10° resulted in a 45% error (Fig. 2c, f). Percentage errors in the estimates of k and y′₀ for ±10° errors in the angles were consistent for all values of k and y′₀.

Figure 2.

Influence of errors (ε) in the geometric angles θ, Φ, or Ψ on the model estimates of k and y′₀. Threshold voltages were generated with randomly selected k and y′₀, indicated by the horizontal lines. a–c) k = 1.73 V/mm² and y′₀ = 3.88 mm. d–h) k = 0.44 V/mm² and y′₀ = 0.71 mm. θ, Φ, and Ψ were set at 25°, 5°, and 30°, respectively, in all cases except in g) θ was set at 15°, in h) Φ was set to 15°, and in i) Ψ was set to 40°.

The sensitivity of the estimated parameters, k and y′₀, to errors in the stereotactic frame angles was dependent on the actual angles used to generate the Vth data. The estimates of k and y′₀ were more sensitive to errors added to small values of θ than to large values of θ. For example, 10° of error added to θ = 25° resulted in 35% error in the estimate of y′₀ and 43–134% error in the estimate of k (Fig. 2a, d), while 10° of error added to θ = 15° resulted in 55% error in the estimate of y′₀ and 57–405% error in the estimate of k (Fig. 2g). Conversely, model-estimated parameters were more sensitive to errors added to large values of Φ and Ψ than to small values of Φ and Ψ. For example, 10° of error added to Φ = 5° resulted in 28% error in the estimate of y′₀ and 39–86% error in the estimate of k (Fig. 2b, e), while 10° of error added to Φ = 15° resulted in 37% error in the estimate of y′₀ and 45–135% error in the estimate of k (Fig. 2h). Similarly, 10° of error added to Ψ = 30° resulted in 7% error in the estimate of y′₀ and 23–45% error in the estimate of k (Fig. 2c, f), while 10° of error added to Ψ = 40° resulted in 8% error in the estimate of y′₀ and 32–70% error in the estimate of k (Fig. 2i).

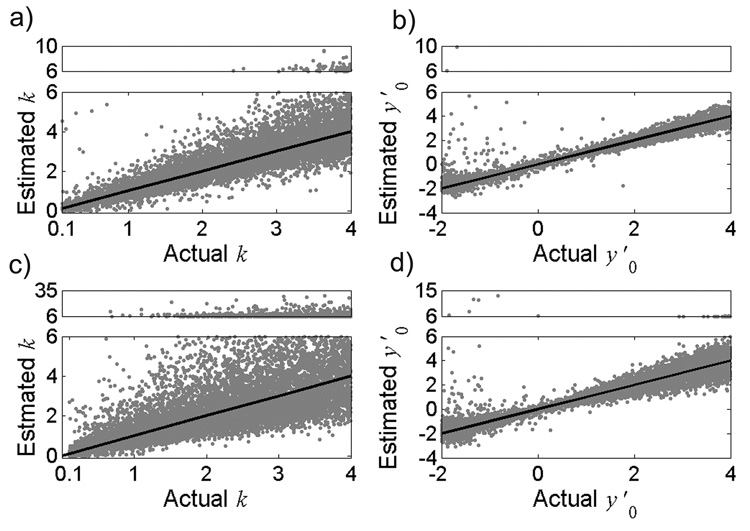
To determine the sensitivity of the method to all errors (error in clinically-measured threshold amplitudes (Vth), as well as errors in the angles θ, Φ, and Ψ), we generated 10,000 simulated datasets, added error to each dataset according to the distributions shown in Table 1, and estimated the parameters, k and y′₀. The estimated parameters as a function of their actual values are shown in Figure 3. The results indicate that in the presence of the expected experimental errors, the method provided robust estimates of k and y′₀. The estimates of k were not normally distributed around the actual value (Fig. 3 a,c), and the median square error of the estimate increased as the standard deviation of the error distribution on angles θ, Φ, and Ψ increased from σ=2° (Median SE = 0.07) (Fig. 3a) to σ=4° (Median SE = 0.23) (Fig. 3c). Similarly, for values of y′₀ less than 0, the estimates were not normally distributed around the actual value (Fig. 3b,d), and the median square error of the estimate increased as the standard deviation of the error distribution of θ and Φ increased from σ=2° (Median SE = 0.01) (Fig. 3b) to σ=4° (Median SE = 0.04) (Fig. 3d).

Figure 3.

Model sensitivity to errors in Vth and geometric angles θ, Φ, and Ψ (Table 1). Model estimates (n=10,000) of a) k and b) y′₀ as a function of the actual parameter values for σ = 2°. Model-estimates of c) k and d) y′₀ as a function of the actual parameter values for σ = 4°. Solid lines represent unity slope. Note that estimates greater than 6 are shown in the upper box of each plot, where the y-axis scale is condensed. Nine outliers of the estimated y′₀ are not shown in b) and 6 outliers are not shown in d) for clarity.

B. Thresholds to Evoke Paresthesias with Thalamic DBS

The intensity of side effects resulting from Vim thalamic DBS was measured at an average of 32 combinations of stimulation voltage and active contact for each thalamus. Side effects were elicited in all thalami, and were described as paresthesias in the contralateral hand, arm, and/or face. Subjects rated the intensity of side effects on a scale from 0 (no side effects) to 10 (strong side effects). For each contact, the intensity of side effects increased as voltage was increased (Fig. 4). The side effects were repeatable; there was a strong correlation between the ratings across the two repetitions of phase 2 (Average slope = 0.9, R² = 0.7, n = 5). In 6 of 9 thalami, the stimulation amplitude required to elicit a side effect increased with contact number, with contact 0 requiring an average of 1.6 ± 0.9 V (n = 6), contact 1 requiring 2.6 ± 1.2 V (n = 6), contact 2 requiring 4.0 ± 1.4 (n = 5), and contact 3 requiring the highest amplitude (6.1 ± 1.7 V, n = 6). In the remaining three thalami there was a non-monotonic dependence of threshold voltage on contact number.

C. Estimation of k and y′₀ from Clinical Data

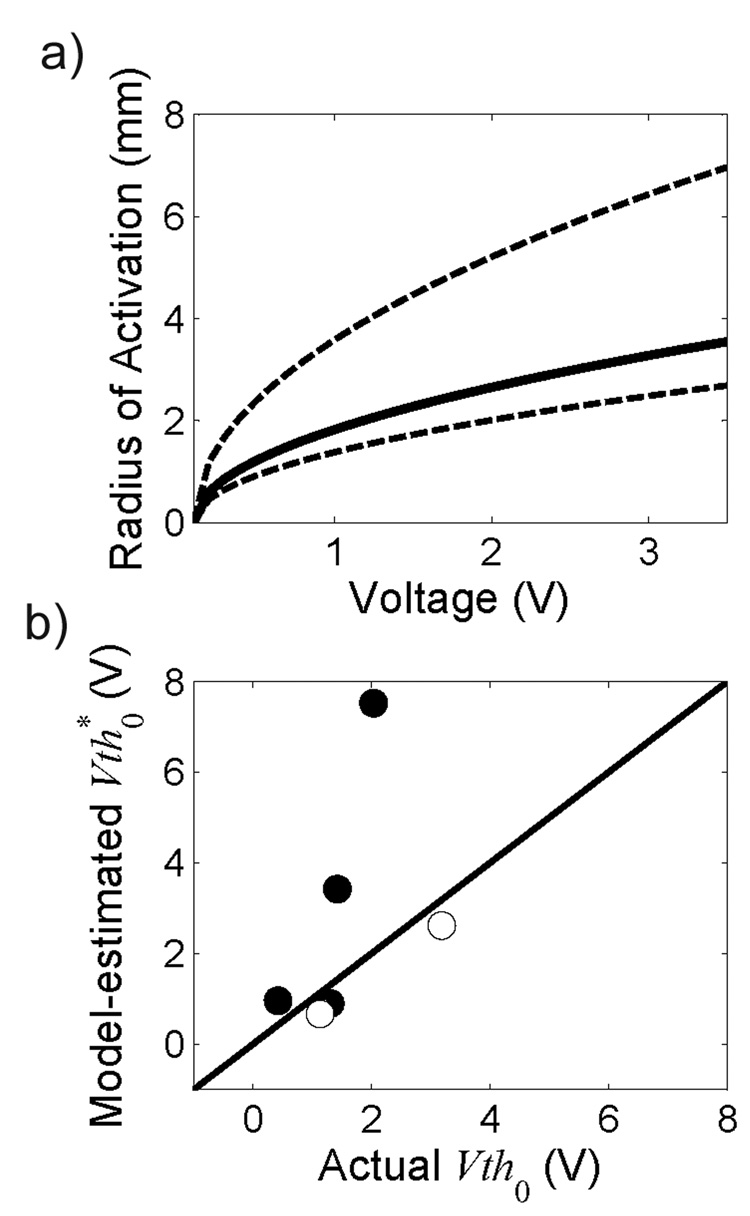
The clinically-measured threshold amplitudes to elicit side effects by thalamic DBS and the geometric angles θ and Φ, calculated from the stereotactic ring and arc angles, were entered into the model, and the unknown parameters were estimated for 6 thalami (Table 2). In three thalami (1, 4, and 8R), the stimulation amplitude required to elicit a side effect did not increase monotonically with contact number, and these thalami were not included as the estimated values of k and y′₀ were dependent on the initial conditions used in the optimization. The median estimate of the amplitude-distance constant was 0.31 V/mm² (n = 6 thalami). The estimates of k and y′₀ were most sensitive to errors in θ for small values of θ (Fig. 2g), and for θ = 20°, an error of 10° in θ resulted in up to 200% error in the estimate of k and 45% error in y′₀. Therefore, 2 thalami in which θ was less than 20° were excluded from the calculation of k, resulting in an average amplitude-distance constant of 0.22 ± 0.17 V/mm². Common clinical stimulation amplitudes in DBS range from 1.0–3.5 V (Rizzone et al., 2001; Moro et al., 2002; Volkmann et al., 2002; O'Suilleabhain et al., 2003), and the estimated k predicts an increase in the mean effective radius of activation from 2.0 mm at 1 V to 3.9 mm at 3.5 V (Fig. 5a).

Table 2.

Geometric angles, estimated amplitude-distance constant, k, and distance, y′₀ between contact 0 and the Vc/Vim border for 6 thalami in which the threshold amplitude increased monotonically with contact number. θ and Φ were calculated from the stereotactic ring and arc angles, respectively. Two thalami were excluded (gray) from calculation of parameter estimates due to the strong sensitivity of the parameter estimates when θ was less than 20°. In three thalami, the threshold amplitude did not increase monotonically with contact number, and the estimates of k and y′₀ are listed as NA (not available) for these thalami.

Subject	Side	θ	Φ	Estimated k (V/mm2)	Estimated y0' (mm)
1	L	32	5	NA	NA
2	L	24	6.5	0.22	1.3
3	L	25	6	0.11	3.29
4	L	29	2	NA	NA
5	L	24.8	−3.2	0.09	5.1
6	R	16.7	13.1	0.4	2.8
7	L	25	4	0.46	1.21
8	L	10	0	1.55	0.8
8	R	9.5	17.3	NA	NA

Figure 5.

a) Effective radius of activation as a function of stimulation voltage predicted using the mean threshold-distance constant k = 0.22 V/mm². Dashed lines represent ±1 standard deviation around the mean (solid line). b) Model-estimated threshold amplitudes for contact 0, calculated as Vth^*₀ = v + ky′₀ ² (where v = 0.1 V and k = 0.22 V/mm²) as a function of the actual threshold voltage required to elicit a side effect with contact 0. Black circles represent 4 thalami with θ > 20°, and white circles represent 2 thalami with θ < 20°. Solid line is unity slope.

The estimates of distance between contact 0 and the Vc/Vim border, y′₀, ranged from 1.3 to 5.1 mm. There was a weak linear correlation (R²=0.19, slope = 1.21, n=6) between the actual threshold voltages and the predicted threshold voltages for contact 0, calculated using k=0.22 V/mm² and the model-estimated y′₀ (Fig. 5b).

IV. Discussion

The goal of this study was to develop a method to estimate empirically the amplitude-distance constant to determine the spatial extent of activation for Vim thalamic DBS. The spread of stimulation in Vim thalamic DBS is presently unknown, and determining the spatial extent of activation will allow correlations to be established between the volume of tissue activated and the clinical response. These correlations will help to refine further the anatomical target and determine the optimal electrode geometry or stimulation parameters.

We developed a method incorporating the amplitude-distance relationship (1) to estimate the unknown amplitude-distance constant, k, and the distances between the contacts and the Vc/Vim border, y′. In contrast to refractory interaction methods to estimate k (Yeomans et al., 1986), which require precisely timed pulses to be delivered to two different electrodes, our method used measurements of clinical response thresholds. Thus, this method can be used with the existing implanted pulse generator, which cannot deliver independent pulses to two different electrodes.

A. Estimates of k and y′₀ from Clinical Data

Application of the method to clinically-measured threshold amplitudes provided an average amplitude-distance constant of 0.22 V/mm². The amplitude-distance constant has not been determined previously for thalamic DBS, but it was estimated to be 0.1–4 V/mm² (assuming a load resistance of 1,000 Ω) from studies in a variety of experimental settings (Ranck, 1975). The value of the amplitude-distance constant depends on many factors including the stimulation pulse width (Grill and Mortimer, 1996). The pulse width used in this study, 90 µs, is representative of pulse widths used clinically, and increasing the value of pulse width would increase the spatial extent of activation and decrease the value of the amplitude-distance constant.

This method also provided an estimate of the distance from the active contact to the Vc/Vim border. Post-operative electrode localization provides insight for programming and contact selection. Present methods of localization include fluoroscopy, stereotactic radiograophy, CT, and MRI. MRI and CT provide better resolution of deep brain structures, but require complicated imaging and reconstruction techniques (Rezai et al., 2006). Further, distortion of images due to artifacts complicates post-operative localization, and estimates of errors range from 1–3 mm (Zonenshayn et al., 2000; Saint-Cyr et al., 2002). The thalamic nuclei (i.e., Vc, Vim) cannot be differentiated from surrounding structures on MR images (Schlaier et al., 2005), and therefore it is not possible to see the Vc/Vim border, further complicating post operative identification of electrode location. The method presented here provides an estimate of the electrode location relative to the Vc/Vim border with a median error of less than 1 mm (Fig. 3b, d).

Intraoperative electrode localization may be a useful application of this method. Present methods of electrode placement target a location anterior to the Vc/Vim border, and this method could be used to estimate the distance between the active contact and the Vc/Vim border. The experiment design used to determine threshold amplitudes in this study included testing an average of 32 contact/voltage combinations, many of which were not needed to determine the threshold amplitudes. Intraoperative use of this method would require a much shorter time to determine the threshold amplitudes, and an experimental design which only tests for low SE would greatly reduce the number of test combinations and the experiment time.

B. Limitations of the Method

The estimated parameters, k and y′₀, were sensitive to errors in the inputs, including the clinically-measured threshold voltages (Vth), the geometric angles, θ and Φ, calculated from the Leksell frame stereotactic ring and arc angles, and the angle, Ψ, of the posterolateral slope of the Vc/Vim border. The error in the estimates of k and y′₀ increased as the size of error in the threshold voltage increased. Sources of error in the clinically-measured threshold voltages include the size of voltage interval tested and subject uncertainty (subjective rating of paresthesias intensity). Errors in Vth could be minimized through repetition of measurements and/or through use of a smaller voltage increment. Current DBS systems allow voltage to be varied by 0.1 V increments, and while smaller voltage errors would increase the accuracy of the estimates of k and y′₀, they would also prolong the length of the experiment. We used experimental voltage increments of 0.5 V as a compromise between error and time to conduct the experiment. The model-based results (Fig. 1, Fig 3) indicate that this voltage increment still enabled robust estimates of k and y′₀.

Errors in the angles θ and Φ also translated into errors in the estimated parameters. We assumed that the z-axis of the Leksell frame was parallel to the vertical plane of the Vc/Vim border so that a θ and Φ of zero were parallel to the z-axis of the Lesksell frame. Errors in θ and Φ occur when the Leksell frame is placed on the head in such a way that the z-axis is not parallel to the Vc/Vim border. Other sources of error in θ and Φ include inaccuracies of the arc placement system (Maciunas et al., 1994) and bending of the canula or electrode during surgical placement. The error in the model-estimated parameters increased as the error increased in each angle, and the estimates were most sensitive to errors in θ. Parameter estimates were more sensitive to errors in θ when θ was small than when θ was large, and more sensitive to errors in Φ when Φ was large than when Φ was small. Thalami tested had θ ranging from 9.5 to 32°, and those with θ less than 20° were excluded from the final estimation of k due to the large sensitivity of the estimates to error in θ at small values of θ.

The Leksell frame’s coordinate system is aligned with the patient coordinate system, in which the y-axis (anterior-posterior) is the AC-PC line and the z-axis (dorsal-ventral) is perpendicular to the AC-PC line. From the Schaltenbrand-Wahren stereotactic atlas (Schaltenbrand and Wahren, 1977), the Vc/Vim border is 5–10° off the dorsal-ventral axis perpendicular to the AC-PC line in the saggital plane. Variations in anatomy and frame placement result in an unknown net error in the angle between the Vc/Vim border and the z-axis. We therefore assumed that the Vc/Vim border was parallel with the z-axis of the frame, and a slant in the Vc/Vim border would result in an error in θ. Using thalami in which the electrode is implanted with a large θ will minimize the error due to misalignment between the z-axis of the Leksell frame and the Vc/Vim border.

The accuracy of the estimates decreased as θ decreased, or as the ring angle increased. Values of θ range from 0–50° (ring angles 40–90°) and depend on the surgical technique used to implant the electrode. One technique is to insert the electrode parallel to the Vc/Vim border to maximize the number of contacts in Vim. An electrode that is parallel to the Vc/Vim interface has a small θ, and the estimated parameters will be more sensitive to errors in θ. Another technique is to insert the electrode at a steeper angle (larger θ) that traverses the Vc/Vim border and facilitates electrophysiological mapping (Gross et al., 2006). If the electrode is implanted with a large θ, the estimated parameters will be less sensitive to errors in θ. Ring angles of 45–60° (θ = 30–45°) are most common (Gross et al., 2006). Due to the sensitivity of the parameter estimate to errors in small values of θ, it is recommended that θ < 20° (or ring angle >70°) be an exclusion criterion in patient selection to minimize the error in the estimated parameters.

Estimates of k and y′₀ decreased in accuracy as the difference between the actual value of the offset, v, and the selected value of 0.1 V increased. An error of 0.1 V in the value of the offset resulted in an error up to 2 mm in the estimate of y′₀ and up to .075 V/mms in the estimate of k. The model estimates were more sensitive to error for smaller values of k and y′₀, and the model did not converge when k = 0.1 V/mm² and contact 0 was more than 1 mm posterior to the Vc/Vim border.

This method predicts the average effective amplitude-distance constant, k, and implicit is a uniform radial spread of current from the active contact. However, patterns of activation are influenced by the inhomogeneous and anisotropic electrical properties of the tissue resulting in non-spherical volumes of activation (Butson et al., 2007). These effects are not captured in our method.

This method did not work for thalami in which the threshold amplitudes did not increase monotonically with the contact number. In 3 of 9 thalami tested, the threshold voltages increased non-monotonically with contact number. Application of the method to these datasets resulted in non-unique parameter estimates, dependent on the initial conditions used in the optimization. These non-monotonic responses may be caused by anatomical variations in the Vc/Vim border or error in the threshold amplitudes due to the voltage increment used. For the other thalami, 10 randomly selected initial conditions, from within the defined space, were tested and the parameter estimates were independent of the initial condition. Therefore, it is unlikely that the estimates of k and y′₀ represent local minima in the optimization.

Mathematical Abbreviations

Vth

4-element vector of clinically-measured threshold amplitudes to elicit paresthesias (V)

Vth_c

Clinically-measured threshold amplitude for contact c -, case + (V)

Vth^*

4-element vector of model-estimated threshold amplitudes (V)

Vth^*_c

Model-estimated threshold amplitude for contact c-, case + (V)

y′

4-element vector of distances between each contact and the Vc/Vim border (mm)

y′_c

Distance between contact c and the Vc/Vim border (mm)

k

Amplitude-distance constant (V/mm²)

x₀

x-coordinate of contact 0 (mm)

y₀

y-coordinate of contact 0 (mm)

v

offset (V)

c

Contact number (0,1,2, or 3)

d

Center-to-center contact distance on deep brain stimulation electrode (mm)

Ψ

posterolateral angle of rotation of the Vc/Vim border around z-axis

θ

anterior-posterior electrode angle = 90° - stereotactic ring angle^†

Φ

medial-lateral electrode angle = stereotactic arc angle^† - 90° (left brain) or 90° - stereotactic arc angle^† (right brain)

APPENDIX A: Stereotactic angles and electrode position

We developed a method to solve for the amplitude-distance constant, k and the distance, y′_c, from each contact, c to the border between the ventral caudal (Vc) and ventral intermediate (Vim) nuclei of the thalamus, in thalamic DBS. In this method, we use a mathematical model of the amplitude-distance relationship for each of the four contacts of the DBS electrode to solve for the unknown parameters. The derivation of the mathematical model is given below.

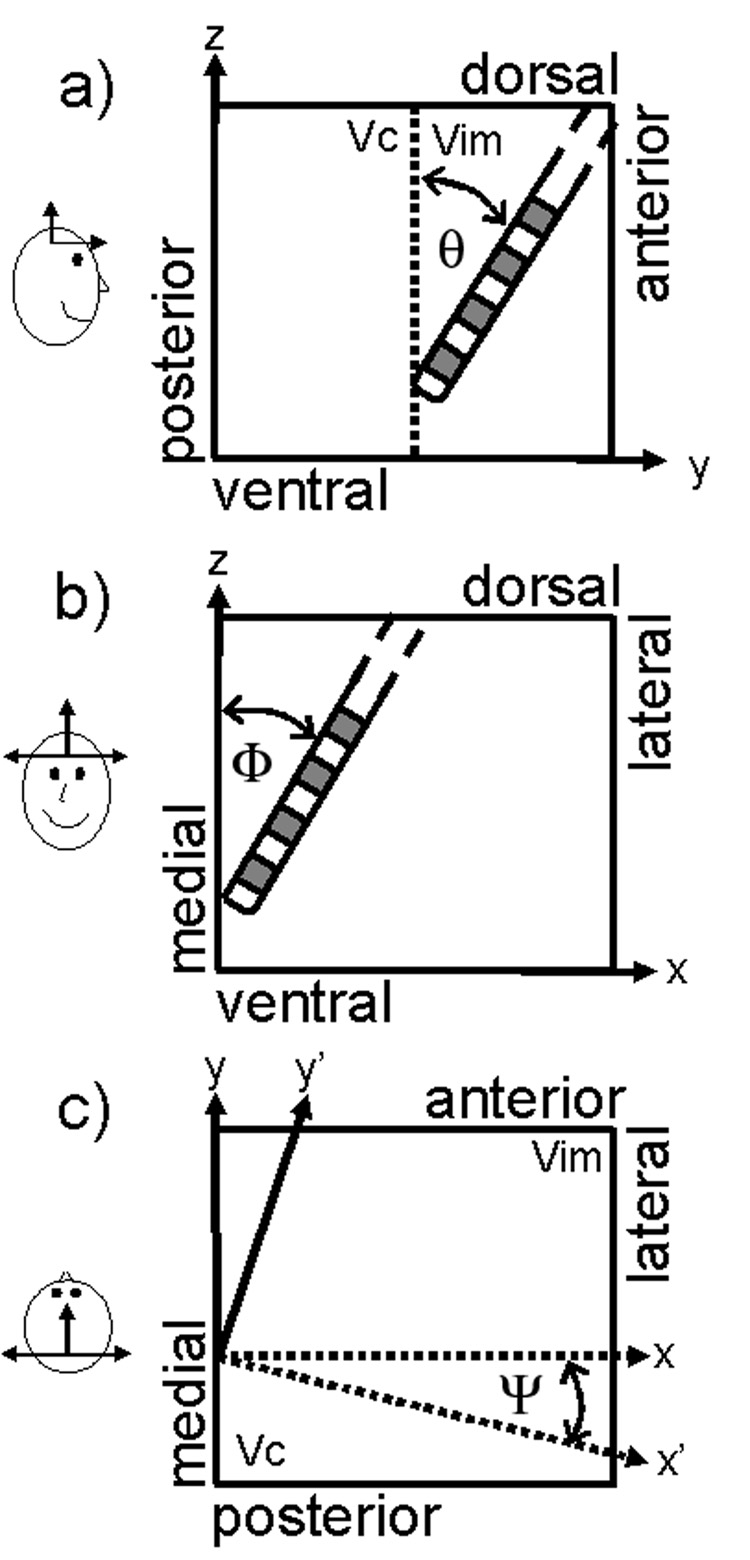
The Vc is posterior and adjacent to the cerebellar-receiving Vim. The Vc receives inputs from the medial lemniscal and spintothalamic sensory afferents (Hassler, 1982), and stimulation of the Vc elicits paresthesias (Lenz et al., 1993). The distances, y′ between each of the four contacts and the Vc/Vim border can be expressed as a function of several angles. The angles of interest are the anterior-posterior electrode angle, θ (Fig. A1a), the medial-lateral electrode angle, Φ (Fig. A1b), and the oblique posteroventral slope of the Vc/Vim border, Ψ (Fig. A1c). The angles θ and Φ were determined from the stereotactic ring and arc angles which were recorded from surgical notes. The ring angle is 90° if the electrode is parallel with the stereotactic z-axis and 0° if it is perpendicular to the z-axis, and parallel to the y-axis. The angle θ was calculated as 90° minus the ring angle. The arc angle is 90° if the electrode is parallel with the stereotactic z-axis, 0° if the electrode is perpendicular to the z-axis, parallel to x-axis and in the right side of the brain, and 180° if the electrode is perpendicular to the z-axis, parallel to the x-axis, and on the left side of the brain. The angle Φ was calculated as the arc angle minus 90° for an electrode in the left brain and 90° minus the arc angle for an electrode implanted in the right brain. The Vim is wedge shaped, resulting in an oblique posterolateral slope in the Vc/Vim border. The angle Ψ is the angle between the Vc/Vim border interface and the medial-lateral axis. We estimated this angle to be 30° from histological data (Hirai et al., 1989).

Figure A1.

Angles that define the position of the DBS electrode contacts relative to the Vc/Vim border. a) θ is the anterior-posterior angle of the electrode calculated from the stereotactic frame ring angle. b) Φ is the medial-lateral angle of the electrode calculated from the stereotactic frame arc angle. c) Ψ is the posterolateral angle of the Vc/Vim interface, approximated from histological data (Hirai et al., 1989).

We are interested in the distance between the contacts on the DBS electrode and the Vc/Vim border, which is represented by the x-z plane. The Cartesian coordinates of each contact, (x_c, y_c) can be expressed as a function of the angles θ and Φ, the center-to-center contact distance, d, and the coordinates of contact 0 (x₀, y₀) and represented in matrix form, where x_c and y_c are vectors with 4 columns, 1 for each contact.

$$\left(\begin{array}{c}{\mathbf{x}}_{\mathrm{c}}\\ {\mathbf{y}}_{\mathrm{c}}\end{array}\right)=\left(\begin{array}{c}{x}_0+cd\text{sin}\mathrm{\Phi }\\ y_0+cd\text{sin}\theta \end{array}\right)$$ (A2.1)

The Vim is wedge-shaped with its base oriented laterally. The dorsoventral height and mediolateral width are both 8–9 mm. The rostrocaudal thickness varies from 3–3.5 laterally to 1.5–2 mm medially (Hirai et al., 1989). To account for the oblique posterolateral slope of the Vc/Vim border, we rotated the coordinate system by Ψ degrees about the z-axis. The rotation matrix for a 2-dimensional clockwise rotation about the z-axis:

$${\mathbf{R}}_z=\left(\begin{array}{cc}\text{cos}\mathrm{\Psi }& \text{sin}\mathrm{\Psi }\\ -\text{sin}\mathrm{\Psi }& \text{cos}\mathrm{\Psi }\end{array}\right)$$ (A2.2)

The coordinates of the contacts are rotated about the z-axis by multiplying the coordinates (x_c, y_c) by the rotation matrix, R_z.

$$\left(\begin{array}{c}{\mathbf{x}}_{\mathrm{c}}\text{'}\\ {\mathbf{y}}_{\mathrm{c}}\text{'}\end{array}\right)={\mathbf{R}}_z\left(\begin{array}{c}{\mathbf{x}}_{\mathrm{c}}\\ {\mathbf{y}}_{\mathrm{c}}\end{array}\right)$$ (A2.3)

$$\left(\begin{array}{c}{\mathbf{x}}_{\mathrm{c}}\text{'}\\ {\mathbf{y}}_{\mathrm{c}}\text{'}\end{array}\right)=\left(\begin{array}{c}{x}_0\text{cos}\mathrm{\Psi }+y_0\text{sin}\mathrm{\Psi }+cd\text{sin}\mathrm{\Phi }\text{cos}\mathrm{\Psi }+cd\text{sin}\theta \text{sin}\mathrm{\Psi }\\ -x_0\text{sin}\mathrm{\Psi }+y_0\text{cos}\mathrm{\Psi }-cd\text{sin}\mathrm{\Phi }\text{sin}\mathrm{\Psi }+cd\text{sin}\theta \text{cos}\mathrm{\Psi }\end{array}\right)$$ (A2.4)

We are interested in the distance from each contact to the Vc/Vim border, y_c’.

$$({\mathbf{y}}_{\mathrm{c}}\text{'})=(-x_0\text{sin}\mathrm{\Psi }+y_0\text{cos}\mathrm{\Psi }-cd\text{sin}\mathrm{\Phi }\text{sin}\mathrm{\Psi }+cd\text{sin}\theta \text{cos}\mathrm{\Psi })$$ (A2.5)

The first two terms of this equation are equal to the distance, y′₀ between contact 0 and the Vc/Vim border.