Reproducibility of Tumor Blood Flow Quantification with ¹⁵O-Water PET

Abstract

Noninvasive methods for quantifying tumor blood flow (TBF) have a potentially important role in the field of drug development. ¹⁵O-water PET has been used in several studies aimed at monitoring response to novel treatments. Assessing the significance of changes in TBF requires knowledge of the reproducibility of the technique. This article quantifies the reproducibility of the ¹⁵O-water technique for TBF applications.

Methods

A total of 43 pairs of replicate ¹⁵O-water studies were performed on 23 different patients with cancer. TBF was estimated using a standard, single-compartment model, and the replicate data were used to assess the reproducibility of the method.

Results

The magnitude of the differences between replicate flow measurements was found to be proportional to their means. TBF was measured with a within-subject coefficient of variation of 13.4% and a repeatability of 37.1%. The volume of distribution was measured with a within-subject coefficient of variation of 8.6% and a repeatability of 24.0%.

Conclusion

¹⁵O-water PET can be used to measure TBF with a reproducibility that is consistent with other applications of the technique. The short half-life of the isotope permits multiple replicate studies to be performed during the same imaging session, allowing the reproducibility of the average flow estimate to be adapted to the required task. ¹⁵O-water PET is a powerful and robust tool for TBF quantification.

Methodology for quantifying characteristics of tumor vascular physiology is currently of great interest in the field of anticancer drug development because these data can potentially be used to assess the effectiveness of vascular disrupting or antiangiogenic agents. Successful clinical outcome is obviously the measure of any new drug, but clinical response criteria often develop slowly, making trials of new drugs time-consuming and expensive. In addition, the effect of a new drug with promising therapeutic potential may be dominated by confounding factors that result in a poor clinical response. Surrogate markers of clinical response may help overcome these difficulties if they can provide early evidence of the effectiveness of a new compound. Evidence for lack of effectiveness is, of course, also important as it allows unsuccessful drugs to be eliminated at an early stage. Noninvasive imaging has the potential to provide evidence of drug effectiveness, and CT has been widely used in clinical trials to assess changes in tumor size. For drugs that target tumor vasculature or angiogenesis, it may be more appropriate to measure quantitative indices that reflect vascular physiology, as opposed to anatomic size. Changes in parameters such as tumor blood flow (TBF) or blood volume are expected to precede anatomic changes, and these characteristics can be quantified with increasing sophistication using modern imaging modalities.

CT, MRI, and PET have been used to assess tumor vasculature, although ultrasound and optical technologies also play a role. The literature on blood flow quantification with ¹⁵O-water PET is extensive, but most applications have been confined to neurology and cardiology. Recent interest in oncology has seen the method extended to tumors throughout the body. Early TBF studies used the ¹⁵O steady-state method to investigate brain tumors (1–3) and also breast cancer (4). The method involved inhalation of ¹⁵O-carbon dioxide, which was converted to ¹⁵O-water in the lungs by carbonic anhydrase. The steady-state method assumed a fixed value for the volume of distribution of water that tended to bias flow estimation. This method has now been superseded by a dynamic method that is used in conjunction with a single-compartment model to measure both blood flow and volume of distribution. Several studies have used both steady-state and dynamic methods (5–7), and the advantage of the dynamic approach has been confirmed (7). ¹⁵O-carbon dioxide gas has been used with dynamic acquisition protocols to measure flow in breast (8) and intra-abdominal cancers (9), although intravenous injection of ¹⁵O-water is now the preferred method of administration. Most recent reports have adopted similar protocols involving intravenous ¹⁵O-water injection, dynamic acquisition, and single-compartment kinetic analysis (10–29). Some of these studies (10–15) used the autoradiographic method to estimate TBF, although this method assumes a fixed value for the volume of distribution. Nonlinear regression with a single-compartment model has been used to estimate both flow and volume of distribution (16–29) and has been the approach most widely adopted in recent studies. The need for an arterial input function has meant that many of these studies have concentrated on tumors located close to large blood vessels, allowing the determination of image-derived input data (10,16,18,20–25,28). Other centers have reported the use of arterial blood sampling for TBF studies (12– 15,17,19,26,27,29).

Assessing the usefulness of TBF estimation is the subject of ongoing research and is expected to be highly dependent on the reproducibility of the measurement. Although assessing the significance of TBF changes after treatment requires knowledge of the reproducibility of the measurement, only limited reproducibility data have been published. For PET and the dynamic ¹⁵O-carbon dioxide method, 2 publications address reproducibility (8,9), although both involve only 5 patients. For the dynamic ¹⁵O-water method that has been more commonly used in recent studies, the data are even more limited (18,24). Reproducibility of PET blood flow measurements has been reported previously for the brain and heart, but these data may not be applicable to tumors because tumors typically are smaller and are more difficult to locate in the ¹⁵O-water images. The present study aims to specifically address this need for reproducibility data by performing a series of test–retest TBF measurements using the dynamic ¹⁵O-water method.

Materials and Methods

Patient Population

A total of 23 patients with cancer were studied under a research protocol that had been approved by the appropriate Institutional Review Board. The mean age (±SD) of the study participants at the time of scanning was 62 ± 16 y. Patients had a variety of cancers, including renal cell (n = 14), kidney (n = 3), colon (n = 1), sarcoma (n = 2), mesothelioma (n = 1), bladder (n = 1), and esophageal (n = 1) cancer. All patients were known from previously acquired CT and MRI to have lesions greater than 2 cm in diameter, located in the chest or abdomen such that both the tumor and the heart (used for noninvasive determination of the arterial input function) could be imaged simultaneously by the PET scanner. Five patients were studied on 1 occasion, 16 patients were studied on 2 occasions, and 2 patients were studied on 3 occasions, resulting in a total of 43 imaging sessions. The first imaging session was a baseline scan, and the subsequent sessions, when performed, took place after treatment. The details of the treatment and its effect on the patient's disease are not considered in the present article.

PET Acquisition

At each of the 43 imaging sessions, 2 identical ¹⁵O-water studies were performed followed by an additional ¹⁸F-FDG study. Patients were encouraged to remain motionless throughout the scanning period; the 3 image series were, therefore, approximately aligned. The patients were positioned such that both the tumor and the heart were within the field of view of the scanner and could be imaged simultaneously without bed translation. The two ¹⁵O-water studies were started 15 min after each other, and there was no intervention between data acquisitions. For each ¹⁵O-water study, approximately 1,850 MBq were administered as an intravenous injection. Injection was performed manually and consisted of a bolus over approximately 10 s. A total of 370 MBq of ¹⁸F-FDG were administered in a similar fashion. The effective dose equivalent corresponding to 3,700 MBq of ¹⁵O-water and 370 MBq of ¹⁸F-FDG is approximately 13 mSv. A total of 25 imaging sessions were performed on an Advance PET scanner (GE Healthcare) (30), and 18 imaging sessions were performed on a Discovery RX PET/CT scanner (GE Healthcare) (31). Both scanners have an axial field of view of 15 cm and were operated in septa-extended, 2-dimensional mode. The study protocol was compatible with both scanners, although some relevant differences between the 2 tomographs are shown in Table 1.

Table 1.

Differences Between Advance and Discovery RX PET Scanners

Parameter	Advance	Discovery RX
Detector material	Bismuth germanate	Lutetium yttrium orthosilicate
Detector size (mm)
Tangential	4.0	4.2
Axial	8.1	6.3
Detector thickness (mm)	30	30
Detectors per block	6 (tangential) × 6 (axial)	9 (tangential) × 6 (axial)
Blocks (axial direction)	3	4
Detector rings (axial direction)	18	24
Image slices	35	47
Slice thickness (mm)	4.25	3.27
Crystals per ring	672	630
Detectors in whole gantry	12,096	15,120
Septa (mm)
Length	120	54
Thickness	1	0.8
Discriminator (keV)
Lower level	300	425
Upper level	650	650
Coincidence timing window (ns)	12.5	6.5
Attenuation correction	68Ge pin source	64-slice CT
Randoms correction	Delayed channel	Singles

Both ¹⁵O-water and ¹⁸F-FDG protocols involved dynamic data acquisition that began at the time of tracer injection. The ¹⁵O-water studies each lasted 5 min, and the ¹⁸F-FDG study lasted 60 min. The frame times were as follows: 12 × 10, 3 × 20, and 2 × 60 s for the ¹⁵O-water study and 6 × 10, 3 × 20, 2 × 90, 2 × 150, 2 × 300, and 4 × 600 s for the ¹⁸F-FDG study. Before the first tracer injection, transmission data were acquired for attenuation correction. On the Advance, this consisted of a 10-min ⁶⁸Ge transmission scan that was segmented according to the manufacturer's standard protocol. On the Discovery RX, CT data were acquired (140 kVp, 200 mAs), and a standard algorithm (32) was used to transform these data to the attenuation coefficients appropriate for 511-keV annihilation radiation. Emission data were corrected for dead-time losses, scatter, and randoms. On the Advance, the randoms correction was based on online subtraction of delayed events. On the Discovery RX, the randoms correction was based on detector singles rates. Image reconstruction used the ordered-subsets expectation maximization algorithm (33) with 2 iterations, 21 subsets, and a gaussian postreconstruction smoothing filter of 5.1 mm in full width at half maximum.

Image Analysis

TBF was quantified by placing regions of interest (ROIs) in the dynamic images and determining time–activity data. As expected, tumor identification was difficult in the ¹⁵O-water images, so tumor ROIs were defined in the last frame of the dynamic ¹⁸F-FDG data. These ROIs were then applied to the ¹⁵O-water data (Fig. 1) under the assumption that the patient did not move between studies. Circular ROIs (diameter, 15 mm) were manually positioned in 3 consecutive slices over the most metabolically active part of the tumor. This choice of ROI represented a compromise between the wish to reduce noise with an extended volume of interest and not greatly increase partial-volume error with too large an ROI. This fixed ROI size has been used in other studies of TBF (23,24,28) and helped standardize our analysis. Alternative ROI schemes involving 3-dimensional threshold techniques, although highly appropriate for this task, were not used as we wanted to use a simple scheme that could be readily reproduced at other centers. ROIs were also defined in the left atrium or left ventricular cavity for noninvasive estimation of the arterial input function. These ROIs were also 15-mm-diameter circles and were manually positioned in 3 adjacent slices using an early frame of the dynamic ¹⁵O-water data that clearly showed the blood pool. Additional ROIs were defined in the myocardium as a tool to evaluate the accuracy of our method. Manually drawn, irregularly shaped ROIs were defined using a combination of the early- and late-phase ¹⁵O-water images to identify the myocardium. The ROIs were placed in 3 adjacent (transaxial) slices and included the septum, anterior wall, and lateral wall of the left ventricle.

Figure 1.

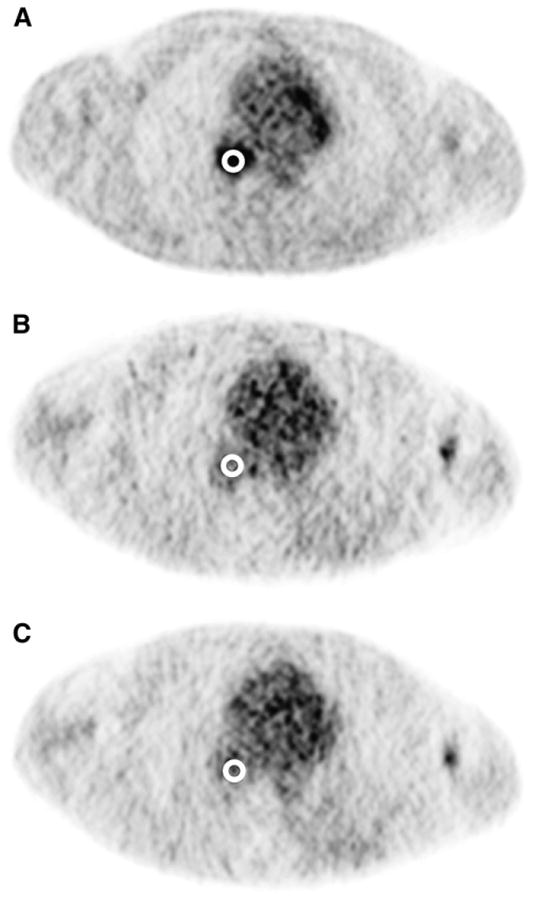
Circular ROIs (diameter, 15 mm) were manually placed over the most metabolically active part of tumor, as seen in last frame of dynamic ¹⁸F-FDG images (A). ROIs were defined in 3 adjacent image slices (not shown). This volume of interest was subsequently applied to 2 ¹⁵O-water image series (B and C) under assumption that patient did not move between ¹⁵O-water and ¹⁸F-FDG studies.

Kinetic Model

¹⁵O-water is a chemically inert, freely diffusible tracer, and its behavior in tissue can be described by a single-compartment model (34). The rate of change of the tracer concentration in tissue as a function of time can be expressed as:

$${\text{dC}(\text{t})/\text{dt}=\text{k}}_1{\times \text{C}}_{\text{a}}(\text{t})-{\text{k}}_2\times \text{C}(\text{t}),$$ Eq. 1

where C(t) is the tracer concentration in tissue at time t, and C_a(t) is the tracer concentration in arterial blood at time t. k₁ is the rate constant for the transport of tracer from plasma to tissue. In this article, we make no correction for the unknown partial-volume effect, and we interpret k₁ as TBF per gram of perfused tissue. k₂ is the rate constant for transport of tracer from tissue back to blood and can be considered to be flow divided by the volume of distribution for water V_d. V_d is defined as the ratio of the water concentration in tissue to that in blood at equilibrium and is unknown for the different tumors in our patient group. To compensate for the contamination of the PET tissue data by arterial blood from vessels nearby or within the volume of interest, a spillover term, V_a, was added to the model. An additional delay term, Δt, was also added to account for the time difference between the measurement of the input function in the left atrium and its arrival at the tumor. Solving Equation 1 and adding these 2 additional terms resulted in the following equation:

$$\begin{array}{ll}{\text{C}}_{\text{i}}(\text{t})=\hfill & (1-{\text{V}}_{\text{a}}{)\times \text{k}}_1{\times [\text{C}}_{\text{a}}(\text{t}-\Delta \text{t})\otimes \text{exp}(-{\text{k}}_2\times \text{t})]\hfill \\ \hfill & +{\text{V}}_{\text{a}}\times {\text{C}}_{\text{a}}(\text{t}-\Delta \text{t}),\hfill \end{array}$$ Eq. 2

where C_i(t) is the tissue activity concentration measured from the PET image, and ⊗ denotes convolution. Note that V_a (the fraction of the arterial blood concentration that appears in the tissue) is assumed to be proportional only to the arterial activity concentration, although in certain regions venous blood may dominate and this assumption will be in error. The unknown parameters in the model—k₁, k₂, V_a, and Δt—were determined by least-squares estimation using commercially available software (PMOD Technologies) (35). In keeping with most previous applications of the technique, TBF was obtained from k₁, whereas myocardial blood flow (MBF) was obtained from k₂ under the assumption of a fixed value for V_d of 0.91 mL/g (MBF = k₂ × V_d) (36).

Statistical Analysis

The primary dataset for statistical analysis consisted of 43 pairs of replicate TBF data (86 TBF studies in total). The reproducibility of k₁ (TBF), k₂, and V_d was individually calculated according to the method of Bland and Altman (37), which is summarized as follows: The absolute differences between repeated measurements were plotted as function of their mean, and Kendall τ was used to identify any proportionality that may be present. Failure to identify and account for a relationship between the difference and the mean will bias the estimate of reproducibility (38). In the event of a relationship being found, the data were log transformed and the analysis repeated. Log transformation is effective at removing unwanted proportionality of this sort and also allows the results to be related back to the original measurements. After log transformation, the Shapiro-Wilk test was used to confirm that the difference data were normally distributed and the within-subject SD (wSD) was calculated (Table 2). Although this SD was determined on the log scale, it can be readily related to the original units because of the properties of log transformation. The inverse log of wSD is not an SD in the original units but a quantity relative to the mean. In fact, taking the inverse log of wSD and subtracting 1 produces the SD as a proportion of the mean in the units of the original measurement. This is the within-subject coefficient of variation (wCV). The product of wCV × 2.77 has been referred to as the repeatability (37). The difference between 2 measurements for the same subject is expected to be less than the repeatability for 95% of pairs of observations. All statistical tests were performed using SPSS (version 15.0; SPSS Inc.) for Windows (Microsoft).

Table 2.

Statistical Parameters Used to Quantify Reproducibility

Abbreviation	Parameter	Calculation
dsd	SD of the difference	$\sqrt{\frac{\sum {\text{d}}^{\text{2}}}{\text{n}}},$ where d is the difference data and n is the number of pairs
wSD	Within-subject SD	$\frac{\text{dsd}}{\sqrt{\text{2}}}$
wCV	Within-subject coefficient of variation (%)	For data in original units: $\frac{\text{wSD}}{\overline{\text{X}}}\times 100$, where X̄ is the mean.
		For log-transformed data: (antilog(wSD)−1)×100
	Repeatability (expressed as a percentage of the mean)	$1.96\times \sqrt{2}\times \text{wCV}$

Results

Figure 2 shows example tumor time–activity data from paired ¹⁵O-water studies performed on the same patient. The curve produced by fitting the data to the kinetic model is also shown, along with the corresponding parameter estimates for this particular patient. Table 3 shows descriptive statistics for k₁, k₂, V_a, and V_d (k₁/k₂) for all studies (n = 86). No statistically significant difference (P > 0.3) between injection 1 and injection 2 for any of the parameters was demonstrated. The mean, median, and SD of k₁ (which approximates TBF within the limitations of the partial-volume effect) for all 86 studies were 1.01, 0.53, and 1.18 mL/min/g, respectively.

Figure 2.

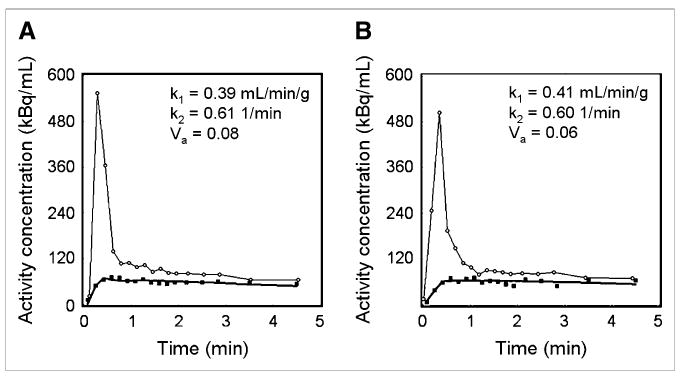
Example time–activity curves for replicate ¹⁵O-water studies performed on same patient. Data for first (A) and second (B) administrations are shown. Circles represent (image-derived) input function and squares denote tumor data. Solid line near tumor data is model fit that produced parameter estimates shown in each figure.

Table 3.

Descriptive Statistics for Kinetic Parameters Derived from All Patient Studies

	Injection 1			Injection 2
Parameter	Mean	Median	SD	Mean	Median	SD
k1 (mL/min/g)	1.03	0.52	1.28	0.99	0.65	1.09
k2 (1/min)	1.58	1.00	1.79	1.52	1.01	1.60
Va (dimensionless)	0.13	0.08	0.13	0.12	0.08	0.14
Vd (mL/g)	0.66	0.67	0.22	0.67	0.68	0.22

Figure 3A shows k₁ data for the repeated acquisitions performed on each patient. Figure 3B shows the absolute magnitude of the difference between the 2 repeated k₁ measurements as a function of their mean. It can be seen that the magnitude of the difference data was proportional to their mean (Kendall τ = 0.57, P < 0.01), and log transformation was required. Figure 3C shows a Bland–Altman plot after log transformation of the data. Kendall τ confirmed (τ = 0.01, P = 0.91) that log transformation was effective at eliminating the relationship between the magnitude of the difference data and their mean. The mean value of the difference data was 0.003, and the SD of the difference (dsd) was 0.178 on the log scale. The Shapiro-Wilk test confirmed that these data were consistent with the normal distribution (W statistic = 0.96, P = 0.21). Ninety-five percent confidence intervals (CIs) (1.96 × dsd) are shown in Figure 3C as dashed lines above and below the mean. In the units of the original measurement, this corresponded to a wCV of 13.4% and a repeatability of 37.1% for k₁ (TBF). In Figures 3A–3C, solid symbols represent data acquired on the Advance PET scanner, and open symbols represent data acquired on the Discovery RX PET/CT scanner. The repeatability for k₁ data acquired on the Advance and Discovery RX scanners was 38.1% and 35.6%, respectively.

Figure 3.

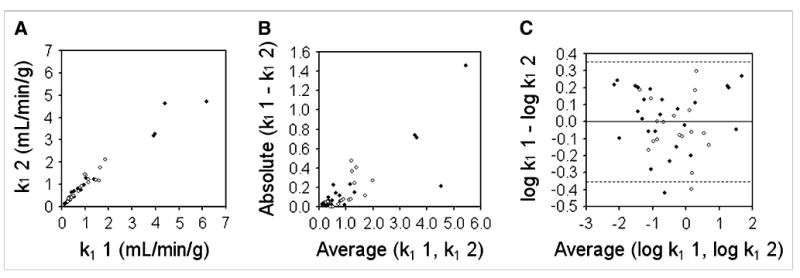
Bland–Altman analysis of reproducibility of k₁ for tumors (TBF). (A) Replicate measures of k₁ are plotted against each other. Solid symbols represent data acquired on Advance scanner; open symbols represent data acquired on Discovery RX scanner. (B) Absolute difference between replicate k₁ measurements are plotted as function of their mean and show clear proportionality. (C) After log transformation, dsd for k₁ was calculated as 0.178. Dashed lines denote 95% CIs on either side of mean (1.96 × dsd).

Figure 4 shows k₂ data, analyzed in a way similar to how the k₁ data shown in Figure 3 were analyzed. As in Figure 3, solid symbols represent data acquired on the Advance PET scanner, and open symbols represent data acquired on the Discovery RX PET/CT scanner. Kendall τ (τ = 0.41, P < 0.01) confirmed that the magnitude of the k₂ difference data was proportional to their mean (Fig. 4B). After log transformation (Fig. 4C), this proportionality was eliminated (Kendall τ = −0.05, P = 0.61). The mean value of the difference data was 0.038, and the dsd was 0.259 on the log scale. The Shapiro-Wilk test (W statistic = 0.97, P = 0.33) confirmed that these data were consistent with the normal distribution, and 95% CIs are shown in Figure 4C. In the units of the original measurement, this corresponded to a wCV of 20.1% and a repeatability of 55.8% for k₂ (efflux rate constant). The repeatability for k₂ data acquired on the Advance and Discovery RX scanners were 65.8% and 39.1%, respectively.

Figure 4.

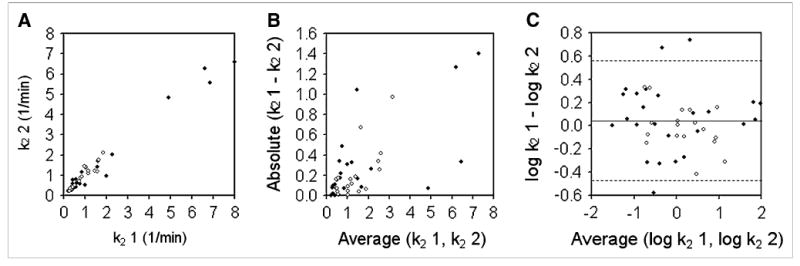
Bland-Altman analysis of reproducibility of k₂ for tumors (efflux rate constant). (A) Replicate measures of k₂ are plotted against each other. Solid symbols represent data acquired on Advance scanner; open symbols represent data acquired on Discovery RX scanner. (B) Absolute differences between replicate k₂ measurements are plotted as function of their mean and show clear proportionality. (C) After log transformation, dsd for k₂ was calculated as 0.259. Dashed lines denote 95% CIs on either side of mean (1.96 × dsd).

Figure 5 shows V_d data, analyzed in a way similar to how the k₁ and k₂ data above were analyzed. In this case Kendall τ (τ = 0.14, P = 0.18) did not indicate that the V_d difference data were proportional to their mean (Fig. 5B), so the data were not log transformed. The mean value of the difference data was −0.013 mL/g, and the dsd was 0.082 mL/g. The Shapiro-Wilk test (W statistic = 0.99, P = 0.92) confirmed that these data were consistent with the normal distribution, and 95% CIs are shown in Figure 5C. This corresponded to a wCV of 8.6% and a repeatability of 24.0% for V_d. The repeatability for V_d data acquired on the Advance and Discovery RX scanners was 27.5% and 18.0%, respectively.

Figure 5.

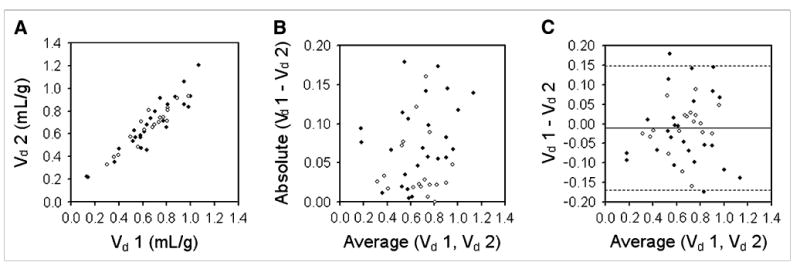
Bland–Altman analysis of reproducibility of V_d for tumors. (A) Replicate measures of V_d are plotted against each other. Solid symbols represent data acquired on Advance scanner; open symbols represent data acquired on Discovery RX scanner. (B) Absolute differences between replicate V_d measurements are plotted as function of their mean and show no clear proportionality. (C) dsd for V_d was calculated as 0.082 mL/g. Dashed lines denote 95% CIs on either side of mean (1.96 × dsd).

Further support for our technique was provided by analyzing flow to the myocardium. All TBF studies included the heart in the field of view, and MBF was determined using the same ¹⁵O-water image data. The average whole-myocardium resting blood flow for all patients was 1.08 ± 0.30 mL/min/g. The subgroups of patients who were studied on the 2 different scanners had mean myocardial flow values that were not significantly different (Student t test, P = 0.19): 1.11 ± 0.36 mL/min/g on the Advance and 1.03 ± 0.20 mL/min/g on the Discovery RX.

Discussion

In this study, we measured the repeatability of TBF estimation to be 37.1%. The difference between 2 flow measurements on the same subject would, therefore, be expected to be less than 37.1% for 95% of pairs of observations. In other words, changes in TBF measurements of up to 37.1% could be accounted for by measurement error and should not imply any treatment effect. One of the advantages of ¹⁵O-water is that its short physical half-life makes it practical to acquire multiple studies during the same scanning session. In this article, we have used replicate studies to quantify reproducibility, but in general these replicates would be averaged to reduce variability. On the basis of our finding that the coefficient of variation for a single TBF measurement was 13.4%, and assuming that the errors combine in quadrature, the coefficient of variation for the average of 2 repeated measurements would be 9.5%, with a repeatability of 26.3%. A response-monitoring protocol that involved averaging 2 replicate flow measurements at each imaging session would therefore expect measurement variability to account for differences between the before and after flow estimates of up to 26.3% for 95% of observations. Further improvements in reproducibility can be obtained by increasing the number of repeated measurements at each imaging session. Despite increasing the number of ¹⁵O-water administrations, the total radiation dose associated with such paradigms can be maintained within an acceptable range by the use of 3-dimensional data acquisition. For modern scanners with good timing and energy resolution, 3-dimensional acquisition has the potential to reduce the administered activity for each study while maintaining the statistical quality of the data.

The replicate data acquired under this protocol were not strictly representative of the situation encountered in a clinical response-monitoring study. In the present study, we based our estimate of reproducibility on images acquired one after another during the same imaging session. The patients were instructed not to move, and we were able to use the same attenuation correction data and the same tumor ROIs for each of the 2 images. In a typical response-monitoring study involving multiple imaging sessions on different days, the patient would inevitably lie in slightly different positions. Separate attenuation correction data would have to be acquired, and tumor ROIs would have to be repositioned. These additional factors will increase the variability between measurements, and the data presented in the current article are likely to underestimate the reproducibility that should be expected in practice. Our data, therefore, represent a surrogate measure of reproducibility. We justify the use of this surrogate by the additional burden that would be placed on patient volunteers if we were to have required them to get off the bed between paired ¹⁵O-water studies. Such a protocol, although more realistic, would have required an additional transmission scan (either CT or ⁶⁸Ge) for attenuation correction and consequently increased radiation dose to the patient. Although the dose from a ⁶⁸Ge transmission scan is relatively low, these images contain little anatomic information and would likely require an additional ¹⁸F-FDG study for ROI placement.

Kaufmann et al. (39) report the reproducibility of MBF measurements with ¹⁵O-water PET. Under resting conditions, which are approximately the same flow range as the tumors encountered in the present study, they report a repeatability of 18% for the global myocardium. For the septal, anterior, lateral, and inferior walls, the repeatability was 42%, 46%, 38%, and 22%, respectively. The average of these 4 smaller regions is 37% and is similar to the repeatability encountered in the present study of TBF (37.1%). These data lend support to our findings and suggest that the small size of the ROI required for tumor studies may account for the higher variability, compared with previous flow studies of other organs such as the whole myocardium.

In addition to the reproducibility of TBF derived from k₁, we also present data for k₂. The efflux rate constant k₂ also contains flow information and has been used to measure TBF in response-monitoring studies (25). Deriving flow from k₂ has the significant advantage that it is independent of the partial-volume effect. It does, however, require an assumed value for V_d in the tumor that may vary with treatment and, as we have shown in the present study, k₂ is more variable than k₁.

Measurement of MBF was not the main aim of the present study, but it was performed as a quality assurance tool. Mean blood flow for the whole myocardium was found to be 1.08 ± 0.30 mL/min/g. Although slightly higher than some reports for the healthy resting heart, these data are consistent with data for the age range encountered in the present patient population. Uren et al. (40) report data on the effect of age on myocardial perfusion in asymptomatic volunteers using ¹⁵O-water PET. An average resting MBF of 1.12 ± 0.26 mL/min/g (nonweighted average of the data in Table 2 in Uren et al. (40)) was reported for normal volunteers in the age range 40–79 y and is similar to the average observed in our patient population. Finally, the data presented in this article provide an estimate of the reproducibility that can be expected with the current acquisition and processing protocol. Alternative protocols may result in a reproducibility that is potentially somewhat different and should be measured as an important part of future response-monitoring studies.

Conclusion

¹⁵O-water PET can be used to measure TBF with a reproducibility that is consistent with other applications of the technique. The short half-life of the isotope permits multiple replicate studies to be performed during the same imaging session, allowing the reproducibility of the average flow estimate to be adapted to the required task. ¹⁵O-water PET is a powerful and robust tool for TBF quantification.