Summary
Triple resonance E.COSY-based techniques were used to measure intra-residue and sequential HN-Hα residual dipolar couplings (RDCs) for the third IgG-binding domain of protein G (GB3), aligned in Pf1 medium. Measurements closely correlate with values predicted on the basis of an NMR structure, previously determined on the basis of a large number of one-bond backbone RDCs measured in five alignment media. However, in particular the sequential HN-Hα RDCs are smaller than predicted for a static structure, suggesting a degree of motion for these internuclear vectors that exceeds that of the backbone amide N-H vectors. Of all experimentally determined GB3 structures available, the best correlation between experimental 1H-1H couplings is observed for a GB3 ensemble, previously derived to generate a realistic picture of the conformational space sampled by GB3. However, for both NMR and X-ray-derived structures the 1H-1H couplings are found to be systematically smaller by ca 10% than expected on the basis of alignment tensors derived from 15N-1H amide RDCs, assuming librationally corrected N-H bond lengths of 1.041 Ǻ.
Keywords: 1H-1H dipolar coupling, backbone dynamics, GB3, residual dipolar coupling, RDC
Introduction
15N relaxation experiments, routinely used to study protein backbone dynamics, capture motions on time scales shorter than the rotational correlation time of the system in question, which is typically in the nanosecond range (Lipari and Szabo, 1982). A variety of more recent, rotating frame experiments add motions slower than ca 104 s-1 to this accessible range, although in most cases the amplitude of such motions remains difficult to evaluate (Ishima and Torchia, 2000; Mulder et al., 2001; Palmer et al., 2001; Eisenmesser et al., 2005). Residual dipolar couplings (RDCs), usually measured in an anisotropic environment, most commonly a liquid crystalline suspension or a compressed hydrogel (Tjandra and Bax, 1997; Clore et al., 1998b; Hansen et al., 1998a; Sass et al., 2000; Tycko et al., 2000), report on time-averaged internuclear vector orientations but also carry information on their motions, integrated over the entire range of time scales faster than ca 100 s-1 (Meiler et al., 2001; Tolman et al., 2001; Peti et al., 2002; Tolman and Ruan, 2006; Zhang et al., 2006). Provided RDCs can be measured under five linearly independent alignment orientations, their values provide information not only on the amplitude of motions, but also on their asymmetry and the direction of this asymmetry (Tolman, 2002; Tolman and Ruan, 2006).
The presence of 1H-1H RDCs in weakly aligned proteins was first demonstrated by the presence of COSY cross peaks between protons far apart in the ubiquitin sequence (Tjandra and Bax, 1997), and similarly for DNA by TOCSY cross peaks between protons attached to different bases (Hansen et al., 1998b). The potential of 1H-1H RDCs for structural studies of oligosaccharides (Bolon and Prestegard, 1998; Tian et al., 1999), DNA (Wu et al., 2003), and proteins (Cai et al., 1999; Pellecchia et al., 2000; Tian et al., 2000; Tjandra et al., 2000) also has been well documented. Peti and Griesinger assessed relative magnitudes of order parameters of H-H and H-N bonds by comparing RDCs (Peti and Griesinger, 2000). The 1H-1H RDCs, which they obtained from a 3D NOESY-based exclusive-correlation type experiment (Griesinger et al., 1986; Peti and Griesinger, 2000), suggest that they are subject to significantly stronger rescaling as a result of internal motion than H-N RDCs.
Here, we use E.COSY type experiments (Griesinger et al., 1985; Montelione and Wagner, 1989; Wang and Bax, 1996) for measurements of intraresidue and sequential DHNHα RDCs in GB3. The precisely measured RDCs, corrected for the effect of passive spin flips together with an NMR structure calculated on the basis of a very extensive set of RDCs, measured in five alignment media (Ulmer et al., 2003), allows re-evaluation of the impact of motions on backbone DHNHα RDCs.
Ensembles of structures that are constrained to yield a simultaneous fit to both the structural (NOE, J coupling, and RDCs) and dynamical (15N relaxation rates) data have been shown to yield improved cross validation statistics when compared with a single static structure (Lindorff-Larsen et al., 2005). A variation on this approach has previously been used by Clore and Schwieters (2006) to derive an ensemble representation of GB3, and we therefore also evaluate whether this ensemble yields a better prediction of the DHNHα RDCs than any single static representation.
Theoretical Section
Residual dipolar couplings in presence of motions
Assuming the absence of correlation between internal motion and molecular alignment, a residual dipolar coupling between nuclei i and j is described by (Prestegard et al., 2000):
| (1) |
The angular brackets denote time averages, Y2q are the second rank spherical harmonics, γi is the gyromagnetic ratio of nucleus i, rij is the distance between nuclei i and j, μ0 is the permeability of free space, and h denotes Planck’s constant. The term Y2q(ζ(t), ξ(t)) describes the time dependence of the magnetic field orientation in molecular frame, and can be recast as an alignment tensor (Bax et al., 2001). The first term in angular brackets describes the angular and radial fluctuations of the bond vector ij within the molecular frame. A transformation into the principal axis system of the bond vector can be carried out using the Wigner rotation matrix elements and yields (Prestegard et al., 2000):
| (2) |
where (θij,av, ϕij,av) define the averaged internuclear orientation, and ψ is the principal direction of the internal motion anisotropy. The Σq<Y2q(ζ(t), ξ(t))> term can be transformed into a diagonal matrix, with order parameters as their elements, where
| (3a) |
| (3b) |
Eq 3a is commonly referred to as the axially symmetric (axial) component of the alignment tensor, and the ratio of the right hand sides of eq 3b and 3a as the rhombicity (Clore et al., 1998a). Motion of the internuclear vector relative to the molecular frame involves both angular and radial fluctuations, and the term describing this motion in eq 2 can be rewritten as
| (3c) |
| (3d) |
The symbol rijeff absorbs the radial motion and eqs 3c and 3d reduce to the standard order parameters only if the time dependence of rij is not correlated with that of Y20. Additionally assuming axially symmetric internal motion of the bond vector about the mean orientation, eq 2 can be written in the commonly used form (Tjandra and Bax, 1997):
| (4) |
Tensor fits assuming a rigid structure
The molecular alignment tensor is commonly derived by fitting a set of RDCs to an a priori known set of . If the fit assumes the structure to be rigid, motion actually present is absorbed into an “effective” alignment tensor and eq 1 can be rewritten as
| (5) |
As can be seen from the complexity of eq 2, physical interpretation of eq 5 is difficult because each element of the effective alignment tensor is impacted to a different extent by the orientation and amplitude of the fluctuation of each internuclear vector. However, if internal motion is assumed to be axially symmetric, eq 4 shows that all elements describing the effective alignment tensor are scaled in a uniform manner by real coefficients, and therefore the tensor elements obtained from fits to a data set are scaled by a factor that reflects an “average” over all vectors
| (6) |
where aa = xx, yy, zz, and the curled brackets describe a single value obtained from a singular value decomposition (SVD) fit of an RDC set to their corresponding ij vectors.
Predicting an RDC set B using a tensor obtained from set A
For a protein of known structure, a molecular alignment tensor can be obtained by fitting eq 5 to a set of RDCs, A, consisting of couplings DAij, usually carried out by SVD (Losonczi et al., 1999). If only one alignment medium is used, it is not straightforward to rigorously extract dynamics as well as structural information from RDCs, and a static structure is commonly assumed. As described above, motional effects of set A then are absorbed into the effective alignment tensor . A second set of RDCs, DBkl, now can be predicted using eq 5 and the effective tensor obtained from set A. However, because set B may be subject to different types of motion, in particular when sets A and B comprise different types of interactions, the prediction may under- or overestimate the true values. This effect can be quantified by calculating a linear regression through pairs of experimental and predicted kl internuclear RDCs, (DBexpkl, DBpredkl), yielding a slope referred to as .
Assuming axially symmetric internal motion, the expression for the slope simplifies considerably:
| (7a) |
This can be further simplified if the bond lengths are not correlated with the orientation:
| (7b) |
and this result can therefore be conveniently used to evaluate relative amplitudes of internal motions of different types of internuclear vectors, while ensuring that the alignment tensor used for the two sets of dipolar couplings is the same.
Longitudinal flips of passive spins
Spin flips of passive spins, coupled to a spin of interest, result in different relaxation rates of the in-phase and anti-phase coherences. The time dependence of the spin states |α> and |β> of spin I, coupled to spin S, impacts the evolution of the transverse magnetization of I-spin doublet components:
| (8) |
where RtransI is the transverse autorelaxation rate of spin I, and R1S is the longitudinal relaxation rate of spin S as observed in a selective inversion recovery experiment (Hu et al., 2006). In a spin state-selective experiment, one doublet component can be selected while the other is being suppressed. However, the two components cross relax when R1S is non-zero and integration of eq 8 then shows an increase in the intensity of the unselected component and an attenuation of the selected component, with a time dependence given by
| (9.1) |
| (9.2) |
where selected = α, unselected = β, or vice versa. As a consequence, the two components that are ideally suppressed in an E.COSY pattern (Griesinger et al., 1985) become observable. If these weaker components overlap the selected components, the apparent positions of the selected components and thereby the measured couplings are affected. When the passive spin S is 1H, its relaxation is dominated by homonuclear dipolar couplings and their J(0) spectral density terms (Wang and Bax, 1996). If S is15N, R1S will be considerably smaller, but long transfer delays (e.g. NOE mixing) increase the impact of this term (Peti and Griesinger, 2000), also resulting in an underestimation of the true (D + J) coupling value if the effect is not accounted for. Although experiments have been proposed to mitigate this effect (Rexroth et al., 1995; Vogeli et al., 2007), due to extensive homonuclear 1H-1H dephasing these schemes are less suitable for measuring couplings in the aligned state. On the other hand, if R1S is known, the impact of the spurious component on the measured E.COSY splitting is easily simulated (Wang and Bax, 1996), and the result can be used to correct the experimental data. This approach is used in the present study.
As a second consequence of the finite lifetime of the passive spin, S, the apparent (D + J)ISapp coupling between spins I and S measured from the splitting on spin I is given by (Harbison, 1993):
| (10) |
Eq 10 can be used to calculate the impact of the passive spin relaxation during data acquisition, and thereby to apply a second correction to the measured apparent (D+J) coupling.
Experimental Section
Sample expression and purification
Escherichia coli BL21 (DE3*) cells transformed with a pET-11 vector containing the GB3 gene were grown in M9 minimal media, containing 15NH4Cl and uniformly 13C-enriched glucose. Protein expression was induced by 0.2 mM IPTG. This culture was centrifuged and resuspended in 20 ml PBS. The cells were lysed at 80 °C and centrifuged again. The supernatant was loaded to a Superdex 75 HiLoad 26/60 (Amersham Biosciences) column, equilibrated with NMR buffer (50 mM sodium phosphate buffer, 50 mM NaCl, and 0.05% w/v NaN3 at pH 7.0). The 13C,15N-enriched NMR sample contained 400 μl of a 2.3 mM protein solution (95%/5% H2O/D2O). For measurement of RDCs, the sample was titrated with Pf1 phage (http://www.asla-biotech.com) until the solvent quadrupolar 2H splitting reached 9.5 Hz (Hansen et al., 1998a).
NMR spectroscopy
All NMR experiments were carried out at 296 K on a Bruker DMX600 spectrometer, equipped with a three-axes gradient triple resonance probe, or on a Bruker DRX600 spectrometer, equipped with a z-axis gradient cryogenic probe.
The 3D HNCA[HA]-E.COSY experiments for measurement of 3(J+D)HNHα (Wang and Bax, 1996) were recorded with 32(t1) × 38(t2) × 400(t3) complex points, t1max = 19.2 ms, t2max = 12.9 ms, t3max = 51.4 ms, an interscan delay of 1.0 s and 8 scans per FID. The time domain data were apodized with a squared, 90°-shifted sine bell function in the direct dimension and with regular 90°-shifted sine bell functions in both of the indirect dimensions, and zero-filled to 128 × 256 × 2048 complex points. The 1HN selective sinc-shaped pulses used by (Wang and Bax, 1996) were replaced by selective 90° EBURP and 180° 1HN ReBURP pulses (Geen and Freeman, 1991).
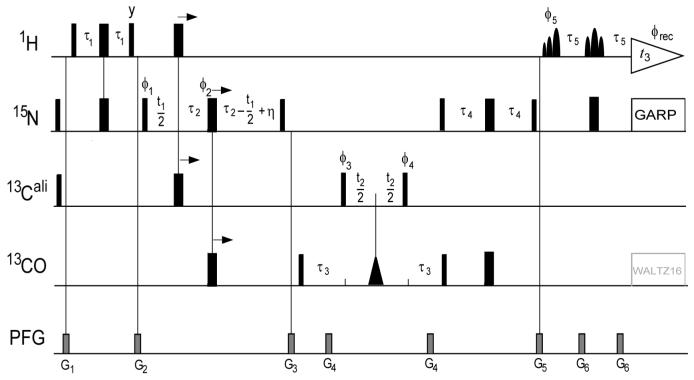
The 3D HN(CO)CA[HA]-E.COSY experiment for measurement of 4(J+D)HNHα (Figure 1) is very similar to the HNCA[HA]-E.COSY experiments for measurement of 3(J+D)HNHα (Wang and Bax, 1996) but includes the two additional INEPT steps transferring magnetization from 15N(i) to 13Cα(i-1) via 13C’(i-1) and back (Vuister and Bax, 1994). As in the HNCA[HA]-E.COSY experiment, the 1HN selective pulses in the final reverse INEPT of the HNCA[HA]-E.COSY experiment are of the 90° EBURP and 180° ReBURP type (Geen and Freeman, 1991), thereby avoiding 1Hα excitation which is advantageous in terms of preserving the spin state of Hα. More details are given in the figure caption of Figure 1. The experiments were recorded with 32(t1) × 38(t2) × 400(t3) complex points, t1max = 19.2 ms, t2max = 12.9 ms, t3max = 51.4 ms, an interscan delay of 1.0 s and 8 scans per FID. The time domain data were apodized with a squared, 90°-shifted sine bell function in the direct dimension and with regular 90°-shifted sine bell functions in both the indirect dimensions, and zero-filled to 128 × 256 × 2048 complex points.
Figure 1.
Pulse sequence of the 3D HN(CO)CA[HA]-E.COSY experiment for measurement of sequential DHαHN couplings. The radio-frequency pulses on 1H, 15N, 13Cα and 13C’ are applied at 4.7, 120, 56 and 174 ppm, respectively. Narrow and wide bars indicate non-selective 90° and 180° pulses. The triangular shape represents a 13C’-selective 180°-Gaussian pulse of duration p1 = 150 μs; the shaped 1HN-selective EBURP and ReBURP pulses (Geen and Freeman, 1991) have durations p2 = 1.0 ms and p3 = 1.5 ms and are applied at 10.2 ppm and 9.9 ppm, respectively, on a 600 MHz instrument. The duration of the shaped pulses needs to be adjusted inversely with the strength of the static magnetic field. 15N-decoupling is achieved with WALTZ16 (Shaka et al., 1983) at a RF field strength γB1 = 1.1 kHz, and optional 13C’-decoupling is also achieved with WALTZ16 (γB1 = 600 Hz). Unless indicated otherwise, all radio-frequency pulses are applied with phase x. The phase cycle is: ϕ1 = x; ϕ2 = {x, y,-x,-y}; ϕ3 = x; ϕ4 = {x, x,-x,-x}; ϕ5 = {x, x, x, x,-x,-x,-x,-x}; ϕrec = {x,-x,-x, x,-x, x, x,-x}. The delays have the following values: τ1 = 1/(4JHN) = 2.6 ms, τ2 = 1/(4JNC’) = 13.5 ms, τ3 = 6.5 ms = 0.7 × 1/(2JCαC’), τ4 = 11 ms < 1/(4JNC) and η is the length of the 13Cα 180° pulse. Pulsed field gradients (PFG) are applied along the z-axis with duration/strength of: G1, 0.5 ms / 12 G/cm; G2, 2 ms / 18 G/cm; G3, 1.5 ms / -10 G/cm; G4, 0.7 ms / -18 G/cm; G5, 1 ms / 15 G/cm; G6, 0.2 ms / 18 G/cm. Quadrature detection in the 15N (t1) and 13C(t2) dimension is achieved by the States-TPPI method, applied to the phases ϕ1 and ϕ3, respectively.
A 2D HACA(CO)NH experiment was used for measurement of longitudinal relaxation rates of Cαz and 2CαzHαz. The decay of 2CαzHαz, observed after the Hα→Cα INEPT, and the decay of Cαz after a refocused Hα-Cα INEPT transfer, was sampled at τ = 0, 100, 200, and 300 ms (Figure S1 in Supporting Information).
All spectra were processed and analyzed using the software package NMRPipe (Delaglio et al., 1995). Peak positions were determined by parabolic interpolation.
Results and discussion
Under weak alignment, resolution in the 1H-dimension of multidimensional NMR spectra is adversely affected by the presence of large numbers of unresolvable 1H-1H residual dipolar couplings, superimposed on the regular 1H-1H J-multiplet patterns. Quantitative measurement of 1H-1H RDCs tends to be more challenging than for one-bond 1H-13C or 1H-15N couplings, not only because of this decreased resolution, but also because of their typically smaller size associated with the larger internuclear distance, which is only partially offset by both spins having a high magnetogyric ratio. Of the various approaches available, E.COSY experiments (Griesinger et al., 1985; Griesinger et al., 1986) appear best suited for measurement of RDCs because they do not require the coupling of interest to be resolvable, and when carried out in a heteronuclear fashion (Montelione and Wagner, 1989; Biamonti et al., 1994) they also yield the sign of the 1H-1H coupling relative to that of a (larger) one-bond 1JNH or 1JCH interaction. We recorded two separate E.COSY experiments: HNCA[HA] for intraresidue 1HN-1Hα couplings and HN(CO)CA[HA] for measurement of sequential 1Hα-1HN interactions. Accurate 3JHNHα couplings for the isotropic sample were available from a recent set of multiple quantum experiments, and fit the Karplus equation with a root-mean-square difference (rmsd) of less than 0.4 Hz. Four-bond isotropic 4JHαHN couplings are known to be vanishingly small (Vuister and Bax, 1994) and therefore were assumed to be zero. Hence, E.COSY experiments were carried out only for the aligned sample.
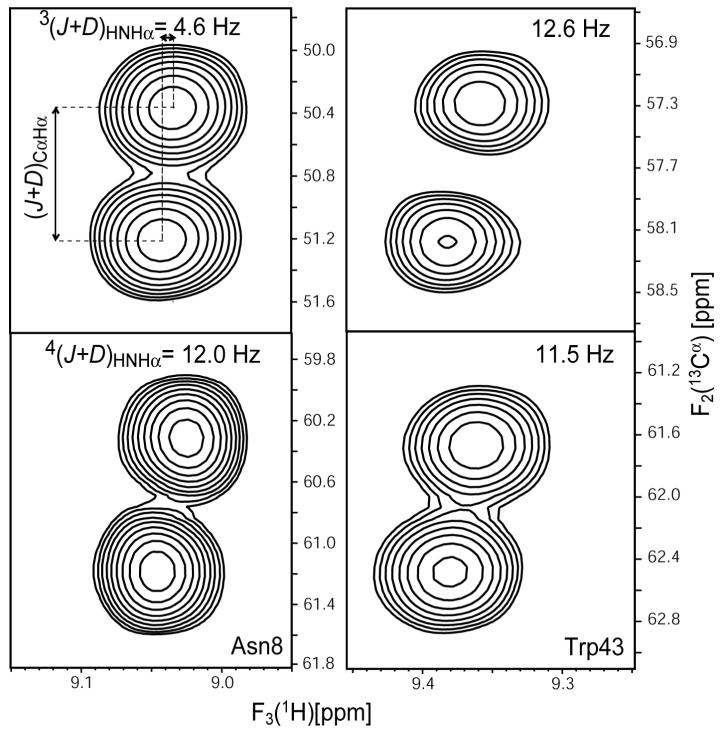
Figure 2 shows small regions of cross sections through the 3D HNCA[HA] and HN(CO)CA[HA] E.COSY spectra, exhibiting the 1JCαHα + 1DCαHα displacement in the 13C dimension, and the JHαHN + DHαHN splitting in the HN dimension. The acquisition time in the 13C dimension, and hence the resolution, was adjusted to be sufficient for resolving the two 13Cα-{1Hα}doublet components, but no effort was made to optimize the measurement for 1JCαHα + 1DCαHα couplings as these values are known at high accuracy from prior experiments (Ulmer et al., 2003). Due to the presence of multiple unresolved 1H-1H couplings, line widths in the 1HN dimension are relatively large (ca 25-45 Hz; Fig.2) but the pairwise rmsd of measured JHαHN + DHαHN splittings in a duplicate set of experiments was only 1.4 Hz for both intraresidue and sequential couplings, indicating random errors of 0.7 Hz in the averaged values.
Figure 2.
Small regions of (F2,F3) cross sections through the HNCA[HA] (top, intraresidue) and HN(CO)CA[HA] (bottom, sequential) E.COSY spectra of GB3 taken at the 15N frequencies of Asn8 (left) and Trp43 (right). Multiplets exhibit the 1JCαHα + 1DCαHα splitting in the 13C dimension, and the JHαHN + DHNHα displacement in the HN dimension.
Correction for the effect of 1Hα spin flips
As pointed out in the Theoretical Section, a change in 1Hα spin state between 13Cα evolution and 1HN detection gives rise to weak additional but frequently unresolved components in the 1HN-13Cα multiplet structure (Wang and Bax, 1996). The impact of these 1Hα spin flips on the measured JHαHN + DHαHN splitting is a function of the 1Hα spin-flip rate, the 1HN line width, and the 1Hα-1HN coupling, and is most easily evaluated by simulating the E.COSY multiplets (Wang and Bax, 1996). To accomplish this, the 1Hα R1Hα were measured from the difference in the relaxation rates of Cαz and 2CαzHαz (Peng and Wagner, 1992) (Supporting Information Table S1). These measured rates were found to be in fair agreement with rates simulated on the basis of the NMR structure (PDB entry 2OED), assuming isotropic rotational diffusion with a rotational correlation time of 3.4 ns (Hall and Fushman, 2003), and including all protons within a 5-Ǻ radius from 1Hα (Supporting Information Table S1). The Pearson’s correlation coefficient between the experimental and calculated sets of R1(1Hα) values equals 0.82 (Figure S2 in Supporting Information), and for all final evaluations the experimental values were used to correct the observed splittings because they resulted in slightly better fits between RDCs and structure than did the calculated R1(1Hα) values.
The effect of 1Hα spin flips during the period between the end of 13Cα evolution and the start of 1HN acquisition on the E.COSY cross peak multiplet was simulated using the program MATLAB and eq 9, assuming a uniform 1HN line width of 35 Hz. As seen in Figure 3, the effect of 1Hα spin flips on the splittings can be considerably larger than the random measurement error, and always attenuates the total splitting measured. For intraresidue interactions, this can lead to an increase or decrease of the magnitude of the resulting RDC, depending on whether the RDC is smaller in magnitude and of opposite sign to 3JHNHα or not. For sequential Hα-HN RDCs, the effect of 1Hα spin flips always reduces the magnitude of the RDC, by an amount roughly proportional to its size. In the following analysis, Lorentzian peak shapes were assumed, although internal RDCs may render the shapes partially Gaussian. As can be seen from Figure 3, corrections derived for Lorentzian shapes are slightly smaller than for Gaussian shapes and therefore may be considered a lower limit.
Figure 3.
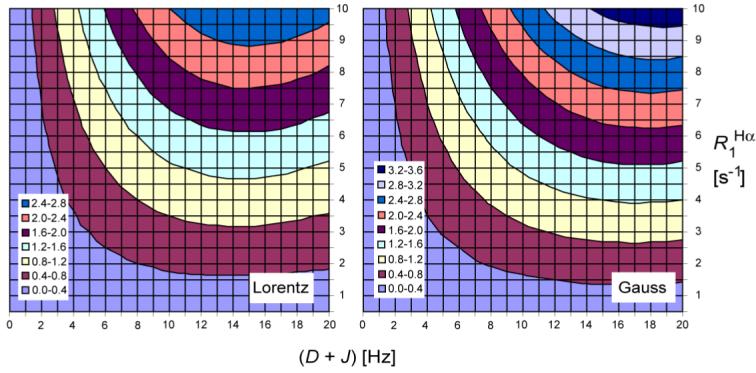
Correction in Hz to be applied to the (D + J) value as measured from the E.COSY spectra, as a function of (D + J) and R1Hα. Opposite sign corrections of the same magnitude are required for interactions where (D + J) < 0. Corrections were derived using peak picking on multiplets simulated using eq 9, assuming HN Lorentzian (left) or Gaussian (right) line shapes with line width at half height of 35 Hz, and Hα spin flips occurring between the end of the Cα evolution period and the start of direct detection (28.8 ms).
The frequencies of the 1HN-{1Hα} doublet components in F3 are affected by 1Hα spin flips during the detection period, t3 (Harbison, 1993). The impact of 1Hα spin flips during t3 is readily accounted for by eq 10 and tends to be somewhat smaller than the effect of 1Hα spin flips taking place between the end of 13Cα evolution and the start of t3. Supporting Information Table S1 reports both the measured “raw” splittings, the isotropic 3JHNHα value, and the corrected RDC values. Note that the isotropic 3JHNHα couplings were measured in the indirect dimension of a multiple quantum experiment, designed to minimize the effect of the finite life time of the passive spins (Rexroth et al., 1995; Vogeli et al., 2007), and therefore did not require any such corrections. Unfortunately, for weakly aligned proteins, such multiple quantum schemes are adversely affected by the extensive dephasing resulting from the multitude of homonuclear 1H-1H couplings. Therefore, such experiments were not used to measure RDCs.
Comparison of 1H-1H RDCs with values expected for static structure
The 13C’-13Cα and 13C’-15N one-bond RDCs for ubiquitin and GB3 were found to be in excellent agreement with those calculated based upon their respective X-ray structures (Ottiger and Bax, 1998; Ulmer et al., 2003). Considering that the impact of zero-point librations on these two types of RDCs is negligible, and that the corresponding interatomic distances are quite uniform and known at high accuracy (Engh and Huber, 1991) these couplings have previously been used to define the molecular alignment tensor. When subsequently evaluating the 1DHN and 1DCαHα couplings, these were found to be ca 6% smaller than anticipated for the standard bond lengths, rNH = 1.02 Ǻ and rCH = 1.09 Ǻ (Ottiger and Bax, 1998), in perfect agreement with predictions for the effect of zero point librations (Case, 1999). Therefore, librationally-corrected bond lengths of rNH = 1.041 Ǻ and rCH = 1.117 Ǻ are commonly used when deriving the molecular alignment tensor from 1DHN and 1DCH RDCs. This procedure is followed here too, and using 1DHN couplings the alignment tensor was determined by fitting these data either to the original X-ray structure (PDB entry 1IGD (Derrick and Wigley, 1994), with protons added by MOLMOL (Koradi et al., 1996)) or to the NMR-refined structure (PDB entry 2OED)(Ulmer et al., 2003), yielding better fits for the NMR structure (Table 1). In the following analysis, coordinates from the NMR structure are used. Using these alignment tensors and structures, values for the 1H-1H RDCs are readily calculated using eq 4. When deriving the molecular alignment tensor from an SVD fit to N-H or Cα-Hα RDCs, the tensor magnitude scales with the inverse cubed of the bond length, rNH-3 or rCH-3. However, whereas for one-bond couplings a change in the effective bond lengths simply scales the predicted RDC, for DHH a change in N-H and/or Cα-Hα bond length also alters the orientation of the interproton vector. Rather than using the librationally corrected effective bond lengths, which artificially lengthen the internuclear N-H and Cα-Hα distances, we therefore use the standard rNH = 1.02 Ǻ and rCH = 1.09 Ǻ bond lengths obtained from neutron scattering for defining the 1H positions when deriving the interproton vectors, even while using rNH = 1.041 Ǻ for deriving the alignment tensor. Subsequently, we will also evaluate the impact of the NH bond lengths on the correlation between observed and predicted DHH RDCs.
Table 1.
Comparison of measured HN-Ha RDCs and values predicted from an alignment tensor obtained from 1H-15N RDCs
| Coupling type | # res | structure | rmsdd [Hz] | rmsd /range | r | slopee |
|---|---|---|---|---|---|---|
| intra DHNHα | 41a | 2OED | 1.32 | 0.057 | 0.981 | 1.01±0.03 |
| 1IGD | 1.39 | 0.060 | 0.978 | 0.99±0.04 | ||
| DIDCb | 1.22 | 0.053 | 0.984 | 0.99±0.03 | ||
| Ensemblec | 1.45 | 0.062 | 0.980 | 1.06±0.04 | ||
| sequential DHNHα | 46a | 2OED | 2.04 | 0.047 | 0.978 | 1.10±0.03 |
| 1IGD | 3.11 | 0.072 | 0.943 | 1.02±0.05 | ||
| DIDCb | 1.86 | 0.043 | 0.982 | 1.13±0.03 | ||
| Ensemblec | 1.28 | 0.030 | 0.991 | 1.11±0.02 |
Dynamic residues 12, 40, 41 are excluded.
For the 2OED structure with the N-H and Cα-Hα vectors replaced by those derived from iterative DIDC analysis of six GB3 mutants, all aligned in Pf1 medium (Yao et al., 2008).
160-member ensemble from(Clore and Schwieters, 2006).
rmsd relative to the regression line.
The slope of the correlation between predicted (y axis) and observed RDCs.
Although both the intraresidue and sequential 1HN-1Hα RDCs correlate well with values expected for a static structure (Figure 4), in both cases the pairwise rmsd exceeds the lower limit of the experimental uncertainty (estimated from reproducibility of the measurement, see above) by more than two-fold (Table 1). In particular, a best fit results in the scaling of observed DHH values by factors of ca 0.99 and 0.91 for the intraresidue and sequential HN-Hα couplings, respectively, indicating that these couplings are scaled down relative to backbone 13C’-13Cα and 13C’-15N one-bond interactions, presumably as a result of internal motion. For the intraresidue DHNHα RDCs, this scaling is less pronounced than the 6% previously noted for the 1DHN and 1DCH RDCs (Ottiger and Bax, 1998). On the other hand, a slightly more pronounced scaling is observed for sequential DHαHN interactions, suggesting more dynamic averaging for this interaction than for the one-bond N-H and Cα-Hα RDCs. Residues for which the prediction overestimates the magnitude of the observed RDC value are mostly located in strand β4 (residues 50-56). This observation is consistent with slightly elevated motions in edge strand β4 relative to core of the protein (Yao et al., 2008). On the other hand, our 1H-1H couplings do not systematically differ from predictions for the other edge strand, β2, which has also been assigned above average amplitude backbone motions (Hall and Fushman, 2003; Bouvignies et al., 2005; Yao et al., 2008).
Figure 4.
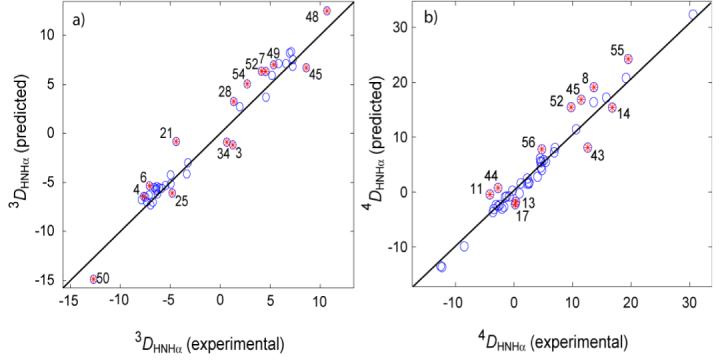
Correlation plots showing predicted versus experimental RDCs for (a) 3DHNHα and (b)4DHαHN for 2OED. The effective alignment tensor is obtained from the 1DHN RDCs and used for the prediction of all RDCs (rNHeff is 1.041 Ǻ). Table 1 presents statistics regarding the observed correlations. Highly flexible residues 12, 40 and 41 are excluded. Symbols embossed with red asterisks correspond to residues that fall more than one standard deviation from a linear regression best fit. Residue labeling corresponds to the residue on which HN resides.
Comparison of 1H-1H RDCs with values expected for a dynamic ensemble
The use of eqs 4, 6 and 7 is based on the assumption of axially symmetric motion of the internuclear vectors, leading to a simple scaling of the internuclear dipolar coupling. True internal motions in many cases will be far more complex, and may include significant asymmetry. Only if RDCs can be measured in five linearly independent alignment orientations does it become possible to extract the amplitude and asymmetry of internal motion in a model free manner (Tolman, 2002; Tolman and Ruan, 2006; Yao et al., 2008). However, it is interesting to note that NMR structures also can be generated in an ensemble representation that reflects the dynamic behavior of the protein (Lindorff-Larsen et al., 2005; Clore and Schwieters, 2006). A problem in calculating an ensemble of conformers that simultaneously satisfy the experimental NMR restraints has been that the number of NMR observables is insufficient to uniquely define the coordinates when the number of members of the ensemble is greater than one. Incorporation of generalized order parameter restraints derived from relaxation data (Lindorff-Larsen et al., 2005; Clore and Schwieters, 2006), possibly in combination with crystallographically derived temperature factors (Clore and Schwieters, 2006), can mitigate this problem but at the same time limits the amplitude of motions that may be taking place on a time scale much slower than the molecular tumbling. Nevertheless, ensemble structures previously derived by Clore and Schwieters for GB3 yielded not only modest improvements in RDC cross validation statistics (Clore and Schwieters, 2006), they also provided an even better fit to 3JHNHα couplings recently measured for this protein (rmsd = 0.36 Hz) than did the static NMR structure (rmsd = 0.42 Hz) (Vogeli et al., 2007). Below, we therefore also evaluate how well our newly measured DHH couplings agree with this ensemble presentation.
Clore and Schwieters used RDCs from five media, 15N-relaxation derived order parameters, and crystallographic B factors to generate twenty 8-member ensembles of structures. In order to obtain a statistically better sampling of the conformational space accessible to GB3, all 160 members of these 20 ensembles are considered simultaneously in the analysis presented below. Eq 1 provides a straightforward avenue to predict RDCs for an ensemble of structures. First, spherical harmonics for the various internuclear interactions are calculated for the ensemble by averaging the values from all 160 conformers. Ensemble-averaged values for the bond vector rhombicities vary considerably from residue to residue, but mostly are quite small: 0.028 (1DHN), 0.007 (3DHNHα), 0.015 (4DHNHα) and 0.010 (1DCαHα). Note that these small values for the rhombicities do not necessarily exclude considerable asymmetry of the internal motions because, following the definition of eqs 3c and 3d, the accessible range of rhombicity falls between zero and 1-S3dzz,int(i,j). Eq 1 is then used to fit the alignment tensor simultaneously to all 15N-1H vectors, using the averages of the corresponding spherical harmonics from 160 conformers. As expected, with dynamic averaging of the bond vector orientations, slightly larger alignment is observed than when fitting with a single, static structure (Supporting Information Tables S2 and S4). Figure 5 shows the agreement between the observed 1H-1H RDCs and values predicted for the 160-member ensemble. In particular for the sequential Hαi-HNi+1 RDCs, a significantly better correlation between observed and predicted couplings is observed for this ensemble (Figure 5b) than for either the static X-ray (PDB entry 1IGD) or NMR structure (PDB entry 2OED), where the rmsd between observed and predicted couplings drops from 2.04 to 1.28 Hz. Remarkably, the difference in the slopes of the two regression lines that relate the predicted to the measured couplings for intraresidue and sequential HN-Hα interactions drops from 0.09 to 0.05, and then falls within the experimental uncertainties of these slopes. Note, however, that for both intraresidue and sequential RDCs, predicted values remain larger than observed values. Therefore, even though the 1H-1H RDC data provide strong evidence that the ensemble representation provides a better description of the protein in solution, the 1H-1H RDC data either point to the presence of some additional motion, beyond what is seen in the ensemble, or to a remaining small systematic error that attenuates the measured 1H-1H RDCs.
Figure 5.
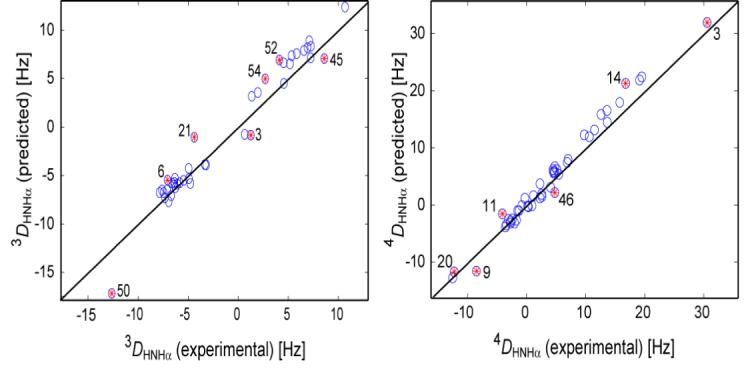
Correlation plots showing predicted versus experimental RDCs for (a) 3DHNHα and (b) 4DHαHN, for a 160 conformer ensemble (Clore and Schwieters, 2006). The effective alignment tensor is obtained from the 1DHN RDCs and used for the prediction of all other RDCs (rNHeff is 1.041 Ǻ). Table 1 presents statistics regarding the observed correlations. Symbols embossed with red asterisks correspond to RDCs that differ by more than 1.5 standard deviations from a linear regression best fit. Residue labeling for 4DHαHN corresponds to the residue on which HN resides.
N-H and Cα-Hα bond lengths from DHH couplings
The orientation of 1HN-1Hα vectors is directly impacted by the N-H and Cα-Hα bond lengths. DHNHα couplings therefore provide an opportunity to evaluate which bond lengths are in best agreement with the observed RDCs, i.e., which bond lengths yield H-H vectors that correlate best with the RDCs. When systematically stepping the N-H and Cα-Hα bond lengths through a reasonable range, plus or minus a few percent of the commonly used equilibrium bond lengths, changes in 1H-1H vector orientations are very small, at most a few degrees. Therefore, in order to improve the statistics, we assume that for both N-H and Cα-Hα equilibrium bond lengths are uniform throughout the protein. As discussed above, variations in dynamics along the backbone also impact the measured 1H-1H couplings in a non-uniform manner, adversely affecting the correlation between structure and RDCs. However, considering the above results, the 160-member ensemble at least partially accounts for the effect of internal dynamics, and we therefore use this ensemble to evaluate which N-H and Cα-Hα bond lengths agree best with the RDCs.
Figure 6 shows two-dimensional contour plots, as a function of rNH and rCαHα, of the rmsd between observed 1H-1H RDCs and those predicted by the ensemble. If only sequential couplings in β-sheet are considered, contours run mostly parallel to the diagonal (Fig. 6). The reason for this correlation between rNH and rCαHα is that the Cα-Hα and N-H vectors in sequential β-sheet positions are approximately parallel, and an equal lengthening of both bonds has little impact on the 1HN-1Hα vector. Also, because these sequential interactions correspond to short interproton distances, the impact of varying rNH and rCαHα on DHNHα tends to be larger than for residues in helices, for example. When considering the 46 sequential DHNHα RDCs, a minimum is observed that includes the canonical rNH = 1.02 Ǻ and rCαHα = 1.09 Ǻ values, but as can be seen this minimum is quite shallow, and the observed χ2 is statistically compatible with a rather broad range of values: rNH = 1.00-1.11 Ǻ and rCαHα = 1.04-1.14 Ǻ.
Figure 6.
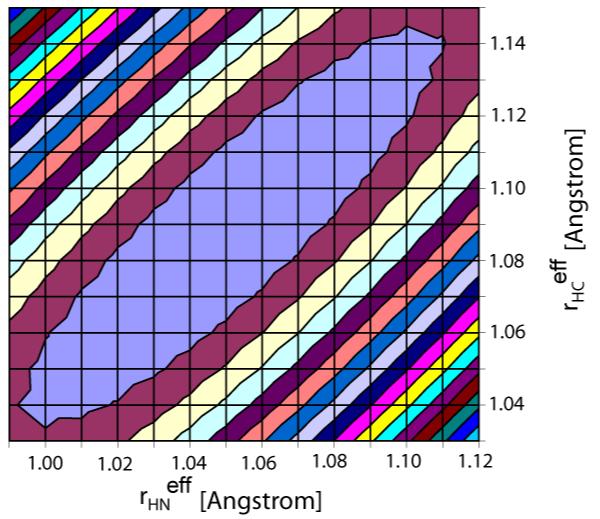
RMSD between experimental and predicted sequential DHNHα couplings in GB3 versus rHN and rCαHα bond lengths for the 160-conformer ensemble. Equidistant lines are drawn in steps of 0.03 Hz above the minimal rmsd of 1.16 Hz (at rHN = 1.05 Ǻ and rCαHα = 1.09 Ǻ). The blue ellipse covers bond length pairs with an rmsd which is not statistically significantly larger than the minimal rmsd (<1.19 Hz).
Concluding Remarks
The E.COSY experiments used in our study yielded quantitative measurement of both intraresidue and sequential DHNHα couplings. Corrections were made for the finite lifetime of the passive spin (1Hα) in these experiments, and such corrections were found to be larger than the random measurement error. In principle, such corrections are also required in the analogous experiments by Peti and Griesinger (Peti and Griesinger, 2000), but there it is the lifetime of the 15N spin which gives rise to the analogous spurious multiplet components. Considering that 15N longitudinal relaxation rates tend to be considerably longer than selective 1Hα relaxation rates, their experiment is intrinsically less sensitive to such passive spin flips. However, this favorable 15N relaxation dependence may be offset by the longer (NOE mixing) time that separates evolution in the indirect and direct dimensions. It therefore remains ambiguous why in their measurements a larger reduction (22% for HN-Hα) for backbone 1H-1H couplings was observed than in our study. For GB3, the DHNHα couplings are 1±4% (intraresidual) and 9±3% (sequential) smaller than what is expected on the basis of a single static structure with librationally averaged 1.041-Ǻ N-H bond lengths. Using standard rNH = 1.02 Ǻ and the same alignment tensor, the observed 1DNH RDCs therefore are ∼6% smaller than those predicted for such a structure, whereas backbone 1DCαC’ and DC’N couplings would correlate to predicted RDCs with a slope of one. Therefore, the intraresidue DHNHα RDCs, which are attenuated by about 1±4% relative to what is predicted for the static structure, point to motions that are indistinguishable in amplitude from those of the Cα-C’ and C’-N bonds.
The sequential DHNHα RDCs are 9±3% smaller than expected for a single static structure, suggesting larger fluctuations in the orientation of these vectors relative to those of the C-C and C-N bonds in the peptide backbone. In this respect it is interesting to note that these couplings agree considerably better with the ensemble structure of Clore and Schwieters (2006), where the rmsd between observed and predicted DHNHα RDCs drops from 2.04 Hz for a static structure to 1.28 Hz for the ensemble. The ensemble representation also accounts for one half of the stronger rescaling observed for sequential RDCs compared to intraresidue interactions. On the other hand, a molecular dynamics trajectory does not provide any indication of systematically lower order parameters for sequential Hα-HN interactions compared to intraresidue HN-Hα vectors (Supplementary Material). Conceivably, the motions that cause a slight lowering in the sequential Hα-HN interactions take place on a time scale longer than the 5-ns duration of the dynamics trajectory. Alternatively, it cannot be completely excluded that small systematic errors in either type of DHNHα measurement are at the origin of the difference in the average order parameters.
In principle, our measurement of DHNHα couplings presents a unique opportunity to evaluate N-H and C-H bond lengths without being significantly affected by high frequency librations about their average orientations. Although such librations may scale the magnitude of the 1H-1H RDC, albeit by a smaller factor than for the shorter one-bond N-H and C-H RDCs, they do not result in a systematic change in orientation of the 1H-1H vectors relative to the alignment frame. Librations therefore cause small perturbations to the correlations shown in Figures 4 and 5, equivalent to adding structural noise (Zweckstetter and Bax, 2002). Unfortunately, the scatter in the correlations of Figures 4 and 5 is so large that changing the N-H and Cα-Hα bond lengths does not lead to a statistically significant increase in χ2 until these bond lengths fall well outside the canonical range.
Supplementary Material
Acknowledgment
We thank Drs. Lisa Parsons for help in sample preparation, and Dennis A. Torchia and G. Marius Clore for helpful discussions. Financial support was obtained from the Swiss National Science Foundation grant to B.V. This work was supported by the Intramural Research Program of the NIDDK, NIH, and by the Intramural AIDS-Targeted Antiviral Program of the Office of the Director, NIH.
Footnotes
Supporting Information Available: One figure showing typical decays of Cαz and 2CαzHαz; one figure showing the correlation between calculated and experimental R Hα1 relaxation rates; one figure showing order parameters derived from a 5.6-ns molecular dynamics trajectory; one table listing experimental RDCs, 1Hα longitudinal relaxation rates, “raw” (J+D) couplings and J couplings, two tables listing order parameters obtained for 2OED and the 160-conformer ensemble when independently fitting each coupling type, two tables listing scalar products between the respective tensors and their relative norms.
References
- Bax A, Kontaxis G, Tjandra N. Dipolar couplings in macromolecular structure determination. Meth Enzymol. 2001;339:127–174. doi: 10.1016/s0076-6879(01)39313-8. [DOI] [PubMed] [Google Scholar]
- Biamonti C, Rios CB, Lyons BA, Montelione GT. Multidimensional NMR experiments and analysis techniques for determining homo- and heteronuclear scalar coupling constants in proteins and nucleic acids. Advances in Biophysical Chemistry. 1994;4:51–120. [Google Scholar]
- Bolon PJ, Prestegard JH. COSY cross-peaks from H-1-H-1 dipolar couplings in NMR spectra of field oriented oligosaccharides. J Am Chem Soc. 1998;120:9366–9367. [Google Scholar]
- Bouvignies G, Bernado P, Meier S, Cho K, Grzesiek S, Bruschweiler R, Blackledge M. Identification of slow correlated motions in proteins using residual dipolar and hydrogen-bond scalar couplings. Proc Natl Acad Sci U S A. 2005;102:13885–13890. doi: 10.1073/pnas.0505129102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cai ML, Wang H, Olejniczak ET, Meadows RP, Gunasekera AH, Xu N, Fesik SW. Accurate measurement of H-N-H-alpha residual dipolar couplings in proteins. J Magn Reson. 1999;139:451–453. doi: 10.1006/jmre.1999.1819. [DOI] [PubMed] [Google Scholar]
- Case DA. Calculations of NMR dipolar coupling strengths in model peptides. J Biomol NMR. 1999;15:95–102. doi: 10.1023/a:1008349812613. [DOI] [PubMed] [Google Scholar]
- Clore GM, Gronenborn AM, Bax A. A robust method for determining the magnitude of the fully asymmetric alignment tensor of oriented macromolecules in the absence of structural information. J Magn Reson. 1998a;133:216–21. doi: 10.1006/jmre.1998.1419. [DOI] [PubMed] [Google Scholar]
- Clore GM, Schwieters CD. Concordance of residual dipolar couplings, backbone order parameters and crystallographic B-factors for a small alpha/beta protein: A unified picture of high probability, fast atomic motions in proteins. J Mol Biol. 2006;355:879–886. doi: 10.1016/j.jmb.2005.11.042. [DOI] [PubMed] [Google Scholar]
- Clore GM, Starich MR, Gronenborn AM. Measurement of Residual Dipolar Couplings of Marcomolecules Aligned in the Nematic Phase of a Colloidal Suspension of Rod-Shaped Viruses. J Am Chem Soc. 1998b;120:10571–10572. [Google Scholar]
- Delaglio F, Grzesiek S, Vuister GW, Zhu G, Pfeifer J, Bax A. NMRpipe - a multidimensional spectral processing system based on Unix pipes. J Biomol NMR. 1995;6:277–293. doi: 10.1007/BF00197809. [DOI] [PubMed] [Google Scholar]
- Derrick JP, Wigley DB. The 3rd Igg-Binding Domain From Streptococcal Protein-G - an Analysis By X-Ray Crystallography of the Structure Alone and in a Complex With Fab. J Mol Biol. 1994;243:906–918. doi: 10.1006/jmbi.1994.1691. [DOI] [PubMed] [Google Scholar]
- Eisenmesser EZ, Millet O, Labeikovsky W, Korzhnev DM, Wolf-Watz M, Bosco DA, Skalicky JJ, Kay LE, Kern D. Intrinsic dynamics of an enzyme underlies catalysis. Nature. 2005;438:117–121. doi: 10.1038/nature04105. [DOI] [PubMed] [Google Scholar]
- Engh RA, Huber R. Accurate Bond And Angle Parameters For X-Ray Protein-Structure Refinement. Acta Crystallographica Section A. 1991;47:392–400. [Google Scholar]
- Geen H, Freeman R. Band-selective radiofrequency pulses. J Magn Reson. 1991;93:93–141. [Google Scholar]
- Griesinger C, Sorensen OW, Ernst RR. Two-Dimensional Correlation Of Connected Nmr Transitions. J Am Chem Soc. 1985;107:6394–6396. [Google Scholar]
- Griesinger C, Sørensen OW, Ernst RR. Correlation of connected transitions by two-dimensional NMR spectroscopy. J Chem Phys. 1986;85:6837–6852. [Google Scholar]
- Hall JB, Fushman D. Characterization of the overall and local dynamics of a protein with intermediate rotational anisotropy: Differentiating between conformational exchange and anisotropic diffusion in the B3 domain of protein G. J Biomol NMR. 2003;27:261–275. doi: 10.1023/a:1025467918856. [DOI] [PubMed] [Google Scholar]
- Hansen MR, Mueller L, Pardi A. Tunable alignment of macromolecules by filamentous phage yields dipolar coupling interactions. Nat Struct Biol. 1998a;5:1065–1074. doi: 10.1038/4176. [DOI] [PubMed] [Google Scholar]
- Hansen MR, Rance M, Pardi A. Observation of long-range H-1-H-1distances in solution by dipolar coupling interactions. J Am Chem Soc. 1998b;120:11210–11211. [Google Scholar]
- Harbison GS. Interference Between J-Couplings and Cross-Relaxation in Solution NMR-Spectroscopy - Consequences For Macromolecular Structure Determination. J Am Chem Soc. 1993;115:3026–3027. [Google Scholar]
- Hu KF, Vogeli B, Clore GM. Interference between transverse cross-correlated relaxation and longitudinal relaxation affects apparent J-coupling and transverse cross-correlated relaxation. Chem Phys Lett. 2006;423:123–125. [Google Scholar]
- Ishima R, Torchia DA. Protein dynamics from NMR. Nature Structural Biology. 2000;7:740–743. doi: 10.1038/78963. [DOI] [PubMed] [Google Scholar]
- Koradi R, Billeter M, Wuthrich K. MOLMOL: a program for display and analysis of macromolecular structures. J Mol Graph. 1996;14:51–55. doi: 10.1016/0263-7855(96)00009-4. [DOI] [PubMed] [Google Scholar]
- Lindorff-Larsen K, Best RB, DePristo MA, Dobson CM, Vendruscolo M. Simultaneous determination of protein structure and dynamics. Nature. 2005;433:128–132. doi: 10.1038/nature03199. [DOI] [PubMed] [Google Scholar]
- Lipari G, Szabo A. Model-free approach to the interpretation of nuclear magnetic resonance relaxation in macromolecules. 1. theory and range of validity. J Am Chem Soc. 1982;104:4546–4559. [Google Scholar]
- Losonczi JA, Andrec M, Fischer MWF, Prestegard JH. Order matrix analysis of residual dipolar couplings using singular value decomposition. J Magn Reson. 1999;138:334–342. doi: 10.1006/jmre.1999.1754. [DOI] [PubMed] [Google Scholar]
- Meiler J, Prompers JJ, Peti W, Griesinger C, Bruschweiler R. Model-free approach to the dynamic interpretation of residual dipolar couplings in globular proteins. J Am Chem Soc. 2001;123:6098–6107. doi: 10.1021/ja010002z. [DOI] [PubMed] [Google Scholar]
- Montelione GT, Wagner G. Accurate Measurements Of Homonuclear H-N-H-Alpha Coupling-Constants In Polypeptides Using Heteronuclear 2d Nmr Experiments. J Am Chem Soc. 1989;111:5474–5475. [Google Scholar]
- Mulder FAA, Mittermaier A, Hon B, Dahlquist FW, Kay LE. Studying excited states of proteins by NMR spectroscopy. Nature Structural Biology. 2001;8:932–935. doi: 10.1038/nsb1101-932. [DOI] [PubMed] [Google Scholar]
- Ottiger M, Bax A. Determination of relative N-H-N N-C ', C-alpha-C ', andC(alpha)-H-alpha effective bond lengths in a protein by NMR in a dilute liquid crystalline phase. J Am ChemSoc. 1998;120:12334–12341. [Google Scholar]
- Palmer AG, Kroenke CD, Loria JP. Nuclear magnetic resonance methods for quantifying microsecond-to-millisecond motions in biological macromolecules. Nuclear Magnetic Resonance Of Biological Macromolecules. 2001;339(Pt B):204–238. doi: 10.1016/s0076-6879(01)39315-1. [DOI] [PubMed] [Google Scholar]
- Pellecchia M, Vander Kooi CW, Keliikuli K, Zuiderweg ERP. Magnetization transfer via residual dipolar couplings: Application to proton-proton correlations in partially aligned proteins. J Magn Reson. 2000;143:435–439. doi: 10.1006/jmre.2000.2058. [DOI] [PubMed] [Google Scholar]
- Peng JW, Wagner G. Mapping of spectral density functions using heteronuclear NMR relaxation measurements. J Magn Reson. 1992;98:308–332. [Google Scholar]
- Peti W, Griesinger C. Measurement of magnitude and sign of H, H-dipolar couplings in proteins. J Am Chem Soc. 2000;122:3975–3976. [Google Scholar]
- Peti W, Meiler J, Bruschweiler R, Griesinger C. Model-free analysis of protein backbone motion from residual dipolar couplings. J Am Chem Soc. 2002;124:5822–5833. doi: 10.1021/ja011883c. [DOI] [PubMed] [Google Scholar]
- Prestegard JH, Al-Hashimi HM, Tolman JR. NMR structures of biomolecules using field oriented media and residual dipolar couplings. Q Rev Biophys. 2000;33:371–424. doi: 10.1017/s0033583500003656. [DOI] [PubMed] [Google Scholar]
- Rexroth A, Schmidt P, Szalma S, Geppert T, Schwalbe H, Griesinger C. New Principle For The Determination Of Coupling-Constants That Largely Suppresses Differential Relaxation Effects. J Am Chem Soc. 1995;117:10389–10390. [Google Scholar]
- Sass H-J, Musco G, Stahl SJ, Wingfield PT, Grzesiek S. Solution NMR of proteins within polyacrylamide gels: Diffusional properties and residual alignment by mechanical stress or embedding of oriented purple membranes. J Biomol NMR. 2000;18:303–309. doi: 10.1023/a:1026703605147. [DOI] [PubMed] [Google Scholar]
- Shaka AJ, Keler J, Freeman R. Evaluation of a new broadband decoupling sequence: WALTZ-16. J Mag Res. 1983;53:313–340. [Google Scholar]
- Tian F, Bolon PJ, Prestegard JH. Intensity-based measurement of homonuclear residual dipolar couplings from CT-COSY. J Am Chem Soc. 1999;121:7712–7713. [Google Scholar]
- Tian F, Fowler CA, Zartler ER, Jenney FA, Adams MW, Prestegard JH. Direct measurement of 1H-1H dipolar couplings in proteins: A complement to traditional NOE measurements. J Biomol NMR. 2000;18:23–31. doi: 10.1023/a:1008384904380. [DOI] [PubMed] [Google Scholar]
- Tjandra N, Bax A. Direct measurement of distances and angles in biomolecules by NMR in a dilute liquid crystalline medium. Science. 1997;278:1111–4. doi: 10.1126/science.278.5340.1111. [DOI] [PubMed] [Google Scholar]
- Tjandra N, Marquardt J, Clore GM. Direct refinement against proton-proton dipolar couplings in NMR structure determination of macromolecules. J Magn Reson. 2000;142:393–396. doi: 10.1006/jmre.1999.1985. [DOI] [PubMed] [Google Scholar]
- Tolman JR. A novel approach to the retrieval of structural and dynamic information from residual dipolar couplings using several oriented media in biomolecular NMR spectroscopy. J Am Chem Soc. 2002;124:12020–12030. doi: 10.1021/ja0261123. [DOI] [PubMed] [Google Scholar]
- Tolman JR, Al-Hashimi HM, Kay LE, Prestegard JH. Structural and dynamic analysis of residual dipolar coupling data for proteins. J Am Chem Soc. 2001;123:1416–1424. doi: 10.1021/ja002500y. [DOI] [PubMed] [Google Scholar]
- Tolman JR, Ruan K. NMR residual dipolar couplings as probes of biomolecular dynamics. Chem Rev. 2006;106:1720–1736. doi: 10.1021/cr040429z. [DOI] [PubMed] [Google Scholar]
- Tycko R, Blanco FJ, Ishii Y. Alignment of Biopolymers in Strained Gels: A New Way To Create Detectable Dipole-Dipole Couplings in High-Resolution Biomolecular NMR. J Am Chem Soc. 2000;122:9340–9341. [Google Scholar]
- Ulmer TS, Ramirez BE, Delaglio F, Bax A. Evaluation of backbone proton positions and dynamics in a small protein by liquid crystal NMR spectroscopy. J Am Chem Soc. 2003;125:9179–9191. doi: 10.1021/ja0350684. [DOI] [PubMed] [Google Scholar]
- Vogeli B, Ying JF, Grishaev A, Bax A. Limits on variations in protein backbone dynamics from precise measurements of scalar couplings. J Am Chem Soc. 2007;129:9377–9385. doi: 10.1021/ja070324o. [DOI] [PubMed] [Google Scholar]
- Vuister GW, Bax A. Measurement of four-bond HN-Hα J-couplings in staphylococcal nuclease. J Biomol NMR. 1994;4:193–200. doi: 10.1007/BF00175247. [DOI] [PubMed] [Google Scholar]
- Wang AC, Bax A. Determination of the backbone dihedral angles phi in human ubiquitin from reparametrized empirical Karplus equations. J Am Chem Soc. 1996;118:2483–2494. [Google Scholar]
- Wu Z, Delaglio F, Tjandra N, Zhurkin VB, Bax A. Overall structure and sugar dynamics of a DNA dodecamer from homo- and heteronuclear dipolar couplings and 31P chemical shift anisotropy. J Biomol NMR. 2003;26:297–315. doi: 10.1023/a:1024047103398. [DOI] [PubMed] [Google Scholar]
- Yao L, Vogeli B, Torchia DA, Bax A. Simultaneous NMR study of protein structure and dynamics using conservative mutagenesis. J Phys Chem B. 2008;112:6045–6056. doi: 10.1021/jp0772124. [DOI] [PubMed] [Google Scholar]
- Zhang Q, Sun XY, Watt ED, Al-Hashimi HM. Resolving the motional modes that code for RNA adaptation. Science. 2006;311:653–656. doi: 10.1126/science.1119488. [DOI] [PubMed] [Google Scholar]
- Zweckstetter M, Bax A. Evaluation of uncertainty in alignment tensors obtained from dipolar couplings. J Biomol NMR. 2002;23:127–137. doi: 10.1023/a:1016316415261. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.