Abstract
Control of the longitudinal magnetization in fast gradient echo sequences is an important factor enabling the high efficiency of balanced Steady State Free Precession (bSSFP) sequences. We introduce a new method for accelerating the return of the longitudinal magnetization to the +z-axis that is independent of externally applied RF pulses and shows improved off-resonance performance. The Accelerated Radiation damping for Increased Spin Equilibrium (ARISE) method uses an external feedback circuit to strengthen the Radiation Damping (RD) field. The enhanced RD field rotates the magnetization back to the +z-axis at a rate faster than T1 relaxation. The method is characterized in gradient echo phantom imaging at 3T as a function of feedback gain, phase, and duration and compared with results from numerical simulations of the Bloch equations incorporating RD. A short period of feedback (10ms) during a refocused interval of a crushed gradient echo sequence allowed greater than 99% recovery of the longitudinal magnetization when very little T2 relaxation has time to occur. Appropriate applications might include improving navigated sequences. Unlike conventional flip-back schemes, the ARISE “flip-back” is generated by the spins themselves, thereby offering a potentially useful building block for enhancing gradient echo sequences.
Keywords: Fast imaging, radiation damping, feedback, steady state free precession
INTRODUCTION
The efficient use of longitudinal magnetization is a key consideration in pulse sequence design, since the amount of longitudinal magnetization available for excitation directly affects image sensitivity. In conventional crushed multi-shot sequences, the longitudinal magnetization must either be used sparingly, with only a small amount tipped away from the z-axis per excitation (as in the Fast Low-Angle Shot experiment, FLASH), or fully excited but with a lengthy repetition period (TR) to ensure sufficient T1 recovery of the magnetization before the next excitation. Not all sequences benefit by having a large initial magnetization, and some sequences, e.g., T1-weighted imaging, depend on T1 recovery for contrast. Nevertheless, if T1 weighting is not desired, the efficient use of longitudinal magnetization in sequences with crushed transverse magnetization requires either very low flip angles (with subsequent loss of sensitivity), or very long TR periods, which can greatly increase the scan time and reduce sensitivity per unit time.
Several approaches have been introduced to hasten the return of the longitudinal magnetization to the +z-axis over that achieved by natural T1 relaxation. Radio-frequency (RF) “flip-back” pulses can be applied to rotate coherent transverse magnetization back to the +z-axis and thereby bolster sensitivity for acquisitions with short TR. These “Driven Equilibrium” (DE) (1-3) and “Fast Return” (FR) (4,5) sequences seek to rotate the magnetization back to equilibrium after the readout. They have been most successfully applied in conjunction with spin echo sequences or as a spin echo preparatory sequence (2-5). The return of the magnetization to the +z-axis thus occurs quickly on the time-frame of the added RF pulses and crusher gradients (∼10ms) rather than on the time-scale of T1 (typically ∼500ms to 3s in biological tissue). For example, an additional refocusing pulse has been used at the end of Rapid Acquisition with Relaxation Enhancement (RARE) sequences to refocus the transverse magnetization after the last readout, followed by a 90° pulse applied during the center of the echo formation (4). The spin echo refocuses phase errors that accumulate in off-resonant regions. This is an important consideration since the “flip-back” pulse only properly returns the magnetization if the RF pulse has the correct phase relationship relative to the transverse magnetization. Magnetization with phase shifts deviating from the proper value will not be fully returned, and may even be rotated away from the +z-axis. Thus, while FR and DE sequences allow TR to be reduced without loss of sensitivity or increased T1-weighting, their performance is contingent on the relative phase between the magnetization and the applied flip-back pulse.
Achieving precise flip-back of the transverse magnetization is particularly problematic in gradient echo pulse sequences since off-resonance effects are not refocused as in spin echo sequences. For example, the off-resonance banding artifacts in balanced Steady-State Free Precession (bSSFP) sequences can be viewed as resulting from an incorrect phase relationship between the RF pulse and the transverse magnetization as it exists just prior to the pulse. Balanced SSFP sequences with the excitation frequency set to the pass-band of the bSSFP response do achieve considerable recycling of the longitudinal magnetization in that a steady state of up to 50% of the equilibrium magnetization is preserved in high flip-angle sequences even though TR ≪ T1. In a uniform magnetic field, the magnetization is fully refocused after the readout period and exists as a coherent transverse magnetization vector at the phase of its initial excitation. The subsequent excitation is phased to rotate the spins back toward the z-axis and into the mirror position in the xy-plane (6). By using the RF pulse to manipulate the coherent magnetization about the z-axis rather than requiring T1-mediated return, a steady state equilibrium magnetization is preserved that is much higher than would exist in the equivalent crushed FLASH sequence. If T1 = T2 and 90° pulses are used, an equilibrium magnetization of 50% is achieved, “yielding the highest [signal-to-noise ratio] SNR per unit time of all known sequences” (6).
Nevertheless, bSSFP methods are often plagued by banding artifacts that arise due to magnetic field inhomogeneity (off-resonance effects). An example where such an off-resonant condition might develop includes simple misadjustments of the transmit frequency, or cases where the adjustment is initially correct, but the magnet B0 drifts due to instrumental of physiological processes (like respiration). The banding artifacts improve at ultra-short TR (TR < 5ms) for which there is less time for off-resonance phase errors to accumulate. At TR ≥ 5 ms, the banding artifacts significantly diminish the utility of bSSFP in the body. While ultra-short-TR bSSFP is useful for producing fast images and is efficient in that a high fraction of the sequence is spent sampling the signal, the need to keep TR < 5ms also limits resolution and places high demands on the gradient hardware.
We have devised an approach to allow the magnetization to be recovered in a high flip angle sequence with a wide range of TR values. Rather than an externally applied RF flip-back pulse, we strengthen the otherwise weak Radiation Damping (RD) field (7) and exploit this RD field to rotate the magnetization quickly to the +z-axis. It must be stressed that RD does not bring restore equilibrium; only T1 relaxation can achieve this. Instead, RD rotates the magnetization vector without altering its length. Therefore, magnetization that has been dephased by T2 processes can only be recovered by T1 relaxation. Accelerated RD is a controlled and accelerated method to flip-back magnetization to the longitudinal direction that automatically correctly sets the average phase of the “flip-back” pulse by using the phase and magnitude of the transverse magnetization. The self-generated nature of the RD field ensures the appropriate phase and frequency needed to rotate the spins back to the +z-axis, thus potentially improving the off-resonance problems incurred by balanced SSFP. Since the RD effect is normally weak in MRI, we strengthen its effect by using an external circuit that returns some of the amplified MR signal back to the RF coil to provide positive feedback enhancement of the RD field. We refer to this enhanced RD effect produced by the positive feedback circuit as accelerated RD. The external control of the gain of the feedback loop also provides precise control of the timing and duration of the accelerated return to the z-axis.
Here we describe the construction of an external feedback device that amplifies RD and demonstrate its ability to accelerate the return of the transverse magnetization to the +z-axis in phantom experiments at 3T. We show that nearly 100% of the longitudinal magnetization can be recovered by activating the feedback device for durations as short as 10ms even though T1 was 865ms in the phantom in the case where little T2 dephasing was allowed to occur. We also characterize the effect by modulating the feedback phase, amplitude, and duration and demonstrate the robustness of the effect to off-resonance effects.
THEORY
Understood for decades, RD is a phenomenon whereby the nuclear magnetization acts back on itself via the induced currents in the radio-frequency (RF) coil. (7) The RF field generated by the current induced by the spins in the receive coil is referred to as the RD field. It therefore provides a resonant excitation of the spins, in a manner similar to an external RF excitation pulse, except that the RD field is generated by the spins themselves. Thus, a feature of the RD effect compared to external RF pulses is that the excitation maintains the correct frequency and phase needed to rotate the coherent transverse magnetization back to z-axis. Secondly, unlike a flip-back pulse, the feedback field effectively turns itself off when the magnetization reaches the +z-axis since the transverse magnetization producing the field diminishes as the longitudinal magnetization (Mz) grows. The return to equilibrium occurs at a characteristic rate that is distinct from T1 relaxation. But unlike T1 relaxation, which restores the length of the magnetization vector to its equilibrium value, the RD field rotates but does not alter the length of the magnetization vector. Thus, the amount of magnetization returned to the z-axis is limited to the coherent magnetization in the xy plane. This limits the efficiency of RD in preserving Mz if the feedback occurs at a time greater than T2* after the initial transverse magnetization is generated. Additionally, the amount of magnetization returned to the z-axis will be reduced if the strength and duration of the RF feedback field are too small to induce a 90° rotation.
The macroscopic feedback field induced by the coil exerts a torque to rotate the normalized magnetization vector m(r,t) ≡ M(r,t)/M0 back to the +z-axis at a rate proportional to the magnitude of the average transverse magnetization ⟨m+⟩, where m+ ≡ m+ imy (7). For a sample on resonance in a well-tuned coil, the RD field Br can be approximated in S.I. units as:
| [Eq.1] |
where the RD time constant τr is given by:
| [Eq.2] |
Here γ is the gyromagnetic ratio, μ0 is the magnetic permeability of vacuum, η is the coil filling factor, Q is the coil quality factor, and ϕ is the phase of the RD field. Normally, the relative phase of the RD field with respect to the magnetization is dictated by Lenz’s law (7). In this case, the RD field lags the net transverse magnetization by 90° (corresponding to ϕ = 0° in Eq. 1) (8). Equation 1 provides the generalized formula for the RD field, allowing the RD phase to assume values other than ϕ = 0°, e.g., if the circuit is mistuned. Thus, the magnetization is expected to be driven toward to +z most effectively for ϕ = 0° and toward -z for ϕ = 180°.
The interaction of the RD field with the spins can be described by the modified Bloch equations:
| [Eqs.3] |
Equations 3 also incorporate the effects of transverse (T2) and longitudinal (T1) relaxation.
The RD effect is routinely encountered in high-resolution liquid-state NMR, in which high fields and small coils filled with bulk solvents allow the RD field to become quite significant. Usually considered a nuisance in this regime, RD effectively shortens T1 recovery and thus broadens spectral lines (9). It has also been demonstrated as a mechanism to enhance susceptibility-based contrast in high-field microimaging (10). Several authors have discussed reducing the RD effect in high-resolution NMR through an external feedback device (9,11,12). The external device senses the current induced by the spins in the circuit and uses electronic feedback to cancel or reduce this current. Reducing the induced current in this way reduces the RD feedback field and thus its effect on the magnetization.
For clinical MRI scanners operating at 1.5 or 3 T, the sensitivity and quality factor (Q) of the RF coil are insufficient to induce a strong intrinsic RD field. RD thus plays little role in most MRI experiments. However, besides suppressing RD, a feedback circuit could utilize positive feedback to the RF coil to enhance the RD effect. If the gain of the feedback circuitry is under pulse sequence control, the degree of RD can be modulated from essentially zero (feedback circuit inactive or providing negative feedback) to a higher value than would normally occur (feedback circuit active and providing positive feedback). The ability to control the strength and timing of the RD effect is an important feature contributing to its potential use in imaging sequences.
The enhancement of RD through active feedback is achieved by taking part of the free-induction decay (FID) signal from the coil, amplifying it, and feeding it back into the coil with the appropriate gain and phase relationship. If the feedback is in-phase with the existing current (positive feedback), this contribution adds to the intrinsic RD field generated by the spins alone and increases the strength of the RD effect. In an equivalent view, the negative feedback reduces the value of Q in Eq. 2, and positive feedback can be used to increase Q and thus decrease the time-scale of the RD induced return of the magnetization to the +z-axis.
In order to estimate the expected accelerated RD field acting on the spins, Br, we first estimate the transmit efficiency of the surface coil, B1, in Tesla per unit current, which is given by the Biot-Savart Law as B1=μ0/2r at the center of a circular surface coil with radius r. We first use this coil efficiency to estimate the voltage and current induced in the coil by the spins after a 90° pulse and then use it again to estimate the Br field produced by the current in the coil. The voltage induced by the magnetization M0 is Vc = B1ωM0vs, where ω is the Larmor frequency and vs is the sample volume. (13) M0 is given by:
| [Eq.4] |
where N is the total number of spins in the sample, ħ is Planck’s constant, I = 1/2 is the spin quantum number for protons, B0 is 3T for this experiment, k is the Boltzmann constant, and T the sample temperature. The current in the coil, Ic, is related to the induced voltage by Vc = IcRc where Rc can be determined from the coil Q measurement: Rc = ωLc/Q where Lc is the coil inductance. The RD field experienced by the spins is then calculated from the induced current in the coil using the transmit efficiency Br = B1Ic:
| [Eq. 5] |
The coil inductance was estimated empirically as Lc = μ0r*ln(4.6r/d-3)*10-3 where r is given in mm and d is the width of the coil trace (in mm).
METHODS
Feedback System
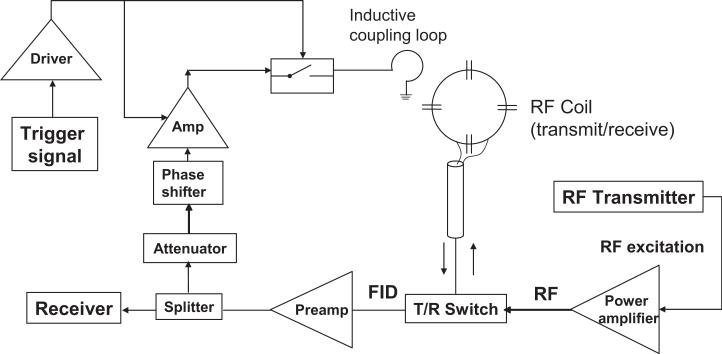
A schematic diagram of the feedback device is shown in Fig. 1. A 90-mm outer diameter (80-mm inner diameter) transmit-receive surface coil was tuned to the Larmor frequency and matched to 50Ω in the presence of a cylindrical water phantom that was 60mm in diameter and 10cm long. The coil was used in conjunction with a standard TR switch (home-built) and preamplifier (Advanced Receiver Research, Burlington, CT, USA) with 23dB of gain. The received signal was split with an RF power splitter. Part of the receive signal then continued on to the receiver plug on the MR scanner, and the remaining part was routed into the feedback device. The bulk of the feedback device was placed outside the scanner room to allow the use of ferromagnetic components.
FIG. 1.
Schematic diagram of a feedback device for enhancing the radiation damping (RD) field in an MR scanner. The received MR signal was split following amplification by the preamplifier, with a portion of the acquired signal continuing to the receiver and the remaining signal being diverted to the feedback device. The MR signal entering the feedback device was then attenuated, and the attenuated signal served as the input of a phase shifter. The signal was amplified via a low-noise amplifier and applied to the input of a switch. The amplifier and switch were powered by a driver, which was in turn triggered by the pulse sequence (Fig. 2). The feedback field was inductively coupled to the sample through a small wire loop.
The feedback pathway consisted of an amplification stage, an attenuation stage, a phase shifter, switches to open or close the feedback loop, and finally an untuned coupling loop to allow the amplified, phase-shifted RD field to induce current in the RF coil. A logic signal under pulse sequence control was used to modulate the gain of the feedback loop by controlling the RF switch in the pathway as well as by turning the power supply to the amplifier on and off. A variable attenuator with 1dB steps from 0dB to 10dB was used in conjunction with additional fixed attenuators placed as needed to control the gain of the feedback.
In addition to the amplitude gain introduced by the feedback loop the RF wave feedback to the coil underwent a net phase shift of ψ degrees. This was accomplished via lengths of coaxial cable and a voltage-controlled phase shifter (Mini-Circuits, Brooklyn, NY, USA, model JSPHS-150). The phase shifter adjusted the phase by up to 240° via a variable direct current (DC) voltage supply (0-12V). For phase shifts above this value, we manually added lengths of coaxial cable corresponding to a 90° or 180° phase shift at the Larmor frequency.
After phase-shifting, the RF signal was amplified by a small signal amplifier (Mini-Circuits, model MAN-1HLN). This amplifier was characterized by gain = 12dB with a 12V power supply, noise figure = 3.7dB, and maximum power output at 1dB compression = 15dBm. The amplifier was followed by standard PIN diode RF switches (3x) in series (MiniCircuits, model PSW-1211). A home-built switch comprised of λ/4 sections followed by PIN diodes to ground was also employed. Finally, the amplified, phase-shifted RF signal was coupled back to the coil with a 35-mm outer diameter (30-mm inner diameter) un-tuned loop approximately 25 mm below the center of the coil. The switches were controlled by the logic level produced by the scanner’s pulse sequence through an OP-amp driver circuit. This same driver was used to supply the power to the amplifiers so that they produced zero gain when the feedback device was in the “off” state. The feedback circuit was only in the “on” state for a short period of time TFB (0 to 40ms) determined by the pulse sequence. A high level of isolation was desired in the off state to prevent the possibility of significant feedback during the MR image readout (at which time the feedback circuit was always in the “off” state.) Thus, the device was essentially transparent to the system if left in the off state.
The construction of an external feedback device makes it possible to manipulate the RD field’s strength and phase. The RD time-constant in Eq. [1] is modified through the feed-back circuit’s effect on the Q of the system. With positive feedback, the system Q is significantly increased. If the feed-back gain exceeds losses in the system, the device will oscillate (infinite Q.) The RD time-constant, τr, in Eq. [1] may then replaced by γGM0, where G is the net gain factor for the feedback path. The gain of the feedback field can be adjusted electronically over a wide range, and the phase angle ψ can also be varied to cover a range of 360°. With our device the feedback gain corresponding to a 0dB attenuator setting (not including the preamplifier gain) was 6.5dB.
The Q value of the RF coil plus active feedback device was measured by loosely coupling into the coil with two un-tuned pickup probes and measuring the S12 parameter between the two probes. The probes were decoupled from each other by geometric overlap. When placed near the coil, the S12 measure peaks at the resonance frequency of the coil. The Q was measured as f/Δf, where Δf was the full width at -3dB from the peak and f was the peak frequency. The measurement was made with the feedback loop in both the open-loop and closed-loop states. In addition to the width of the peak (related to Q), the center frequency of the circuit’s response was also measured as a function of the feedback phase ψ.
The feedback device was tested on a 3T Magnetom Trio, a Tim system (Siemens Medical Solutions, Erlangen, Germany). All experiments were performed on the 60mm-diameter cylindrical phantom (285 mL in volume) filled with an aqueous solution of Magnevist (Berlex Laboratories, Montville, NJ, USA). The concentration of gadolinium contrast agent was adjusted to produce a T1 of 865ms as measured by an inversion recovery turbo-spin echo sequence (TR = 10s, echo time TE = 80ms) using a standard bird-cage head coil to minimize intrinsic RD effects, which were small but observable using the transmit-receive surface coil. The effective transverse relaxation time T2* was measured to be 130ms with a gradient echo sequence using the transmit-receive coil after shimming with the system’s second-order resistive shims.
Sequence Parameters
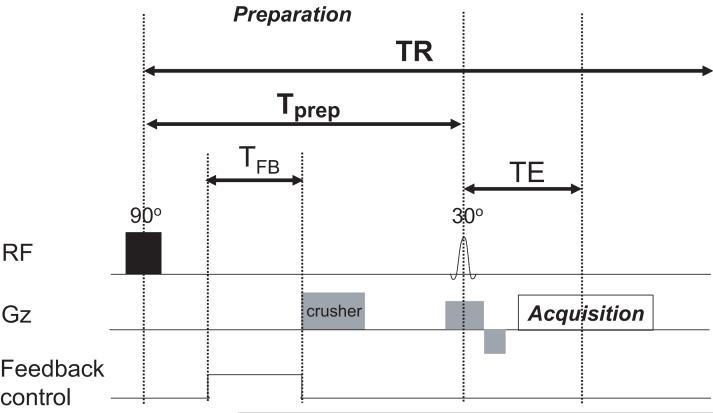
Figure 2 shows the modified gradient echo FLASH sequence with a 90° (1.2 ms) rectangular preparation pulse designed to null the longitudinal magnetization prior to excitation with the slice-selective FLASH excitation pulse. The cylindrical sample was placed standing upright in the surface coil, and single coronal slices of thickness 5 mm were imaged by gradient echo imaging TR/TE = 3000ms/4.8 ms with an FOV of 120mm and a 64×64 image matrix. The duration of each scan using the demonstration sequence was 3.2 min.
FIG. 2.
Modified gradient echo demonstration sequence. Following a 90° rectangular pulse (duration 1.2ms), the magnetization evolved for a fixed preparation time Tprep = 50 ms. Within Tprep, the feedback field was switched on for a duration TFB. A strong crusher gradient was applied after the TFB period to eliminate any residual net transverse magnetization, and the longitudinal magnetization was read out by a 30° slice-selective pulse and gradient echo imaging sequence. A TR of 3 seconds (≫T1 = 865 ms) was used to ensure that the longitudinal magnetization was fully recovered prior to the application of the hard 90° pulse.
The time between the two RF pulses (Tprep) was kept short (50ms) to ensure only minor recovery due to T1. The expected recovery for these conditions is only 6% of M0 (14). The feedback device was turned on for TFB, immediately following the 90° preparation pulse. At the end of the feedback time TFB, a crusher gradient (10ms duration, 20mT/m amplitude) was applied to ensure that no net transverse magnetization remained prior to the slice-selective FLASH excitation pulse. As the TFB was adjusted in length, the start time of the logic pulse was held in a constant position relative to the initial preparation pulse. Thus, the endpoint of the TFB logic pulse as well as the position of the crusher was allowed to vary. Since the natural RD effect (with no feedback present) depends on the net transverse magnetization, the position of the crusher defines the length of time the RD effect can operate for both the accelerated and non-accelerated cases.
The longitudinal magnetization remaining at the end of the preparation period was subsequently imaged with a 30° slice-selective pulse and readout (TE = 4.8ms, BW = 390 Hz/pixel). To assess the fully relaxed longitudinal magnetization (maximum signal in the 30° FLASH excitation), the preparation pulse was set to 0°. In this conventional TR = 3s, α = 30° FLASH excitation, we expected the percentage of longitudinal magnetization in the steady state to be 99.6% of M0, indicating that the measurement sampled the fully recovered M0.
Using the magnetization preparation sequence described above, the image intensity was evaluated as a function of the feedback parameters. Image intensities were measured in a central circular ROI. Image intensity (S) is reported as a fraction relative to the intensity of the fully relaxed image (S0) (no feedback and 0° preparation pulse). The relative image intensity was studied as a function of feedback duration (TFB), feedback gain (by adjusting the attenuator setting), and feedback phase ψ. With the feedback phase optimized to produce maximum imaging intensity in the magnetization prepped sequence, the relative image intensity was studied as a function the MR system’s offset frequency (transmit and receive) to study off-resonance effects as well as a function of shim current offset to assess the effect in inhomogeneous fields.
The effect of the accelerated RD on the spin system was studied by simulating the modified Bloch equations. The sample magnetization was modeled as a normalized magnetization vector m to represent the uniform water magnetization in the phantom sample. Following a 90° pulse, the dynamics of the magnetization were obtained through numerical integration of the modified Bloch equations incorporating RD and relaxation effects (Eqs. 3). The integration was carried out using the finite-difference method and Runge-Kutta (4,5) formula with a relative error tolerance of 1×10-4. The RD time constant τr was varied to reproduce the experimental curves. T1 and T2 were set to experimentally determined values: T1 = 865 ms, while T2 was set to 130 ms in order to model the decrease in transverse magnetization due to T2* relaxation. The RD phase was set to ϕ = 0° unless otherwise noted.
RESULTS
Characterization of Feedback Device
The induced field, Br, and expected response of the spins within a typical feedback time TFB=10ms were estimated from knowledge of the coil geometry, sample and feedback parameters (Eq. 5). The Q measured in the S12 bench test of the coil + feedback system was 130 when the feedback device was off (open circuit). When the feedback device was turned on (full gain) and the phase set for positive feedback, the measured Q increased 10 fold (to 1300). The frequency of the S12 response was observed to change with the feedback phase. The frequency shift observed in the response peak was about 17kHz per degree of shift in ψ.
Based on the measured Q under accelerated RD conditions (feedback loop closed), Br was estimated using Eq. 5 to be 4.98μT at the center of the coil. In reality, Br is expected to be smaller due to the distribution of the field across the sample. Estimating an average value of Br over the sample to be roughly half the value at the center of the loop, an external pulse of this amplitude applied for 10ms would rotate the spins by 380°. Unlike an externally applied field, however, the accelerated RD field is expected to turn itself off as the magnetization vector approached the +z-axis. Thus, the estimated Br under accelerated RD is sufficient to rotate the magnetization from the transverse plane to the +z-axis. On the other hand, under the natural RD field and Q = 130, Br is 10 times smaller, leading to a smaller effect.
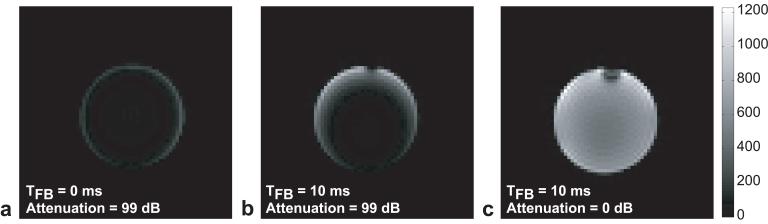
In order to characterize the performance of the feedback device, the phantom was imaged using the demonstration sequence shown in Fig. 2. Figure 3 shows representative images taken with significant feedback attenuation and with optimal accelerated RD. Figure 3a was acquired with the standard 50ms preparation time, but with the transverse magnetization crushed immediately after the initial hard pulse (TFB = 0ms) and the feedback significantly attenuated (attenuation = 99 dB). Figure 3b shows the image acquired the same way but with the crusher shifted by 10ms (TFB = 10ms). In this case, the transverse magnetization created by the hard 90° excitation had 10ms to induce an RD field acting on the spins. As in Fig. 3a, the active feedback circuit was attenuated (attenuation = 99 dB), such that any RD effect observed represented the natural, un-accelerated RD effect. Comparing the intensities in Figs. 3a and 3b shows that the unassisted RD effect corresponded to an increase in the imaged magnetization from 6% of M0 to 10% of M0.
FIG. 3.
Representative phantom images acquired using the demonstration sequence of Fig. 2. (a) Phantom image with no RD effect. Feedback circuit attenuation = 99 dB and TFB = 0.1 ms, thus even natural RD effects are not expected since transverse magnetization is crushed. The average image intensity was 0.06M0 (see Fig. 4). (b) Phantom image with unaccelerated RD. Feedback attenuation = 99 dB and TFB = 10 ms, thus even though the feedback device does not reinforce the induced currents in the coil, un-accelerated RD acts for the 10ms TFB period prior to destruction of the transverse magnetization by the crusher. The average image intensity was 0.1M0 (see Fig. 4). (c) Phantom image with accelerated RD. The feedback circuit was optimized in both phase and gain (maximum gain; attenuation = 0 dB) and TFB = 10 ms. Comparison of the image intensity with a fully relaxed image (hard pulse set to 0°) shows that the accelerated RD effect was sufficient to return 99% of the longitudinal magnetization to the +z-axis.
Figure 3c shows an image utilizing TFB=10ms of accelerated RD in which the feedback gain was maximized (attenuation = 0dB) and the feedback phase ψ was optimized to give maximum image intensity. The noise levels were constant across the two experiments, rendering image intensity and SNR proportional. Compared to the image in Fig. 3a (no RD) the image intensity increased by more than 16 fold. Compared to the image in Fig. 3b (natural RD) the increase was 10 fold, consistent with the measured change in Q. The feedback device allowed for nearly full recovery of the longitudinal magnetization. Compared to the fully relaxed case (no preparation hard pulse and TR = 3s) the accelerated RD effect was able to recover 99% of the longitudinal magnetization compared to 6% for the no RD case (Fig. 3a) and 10% for the un-accelerated RD case (Fig. 3b).
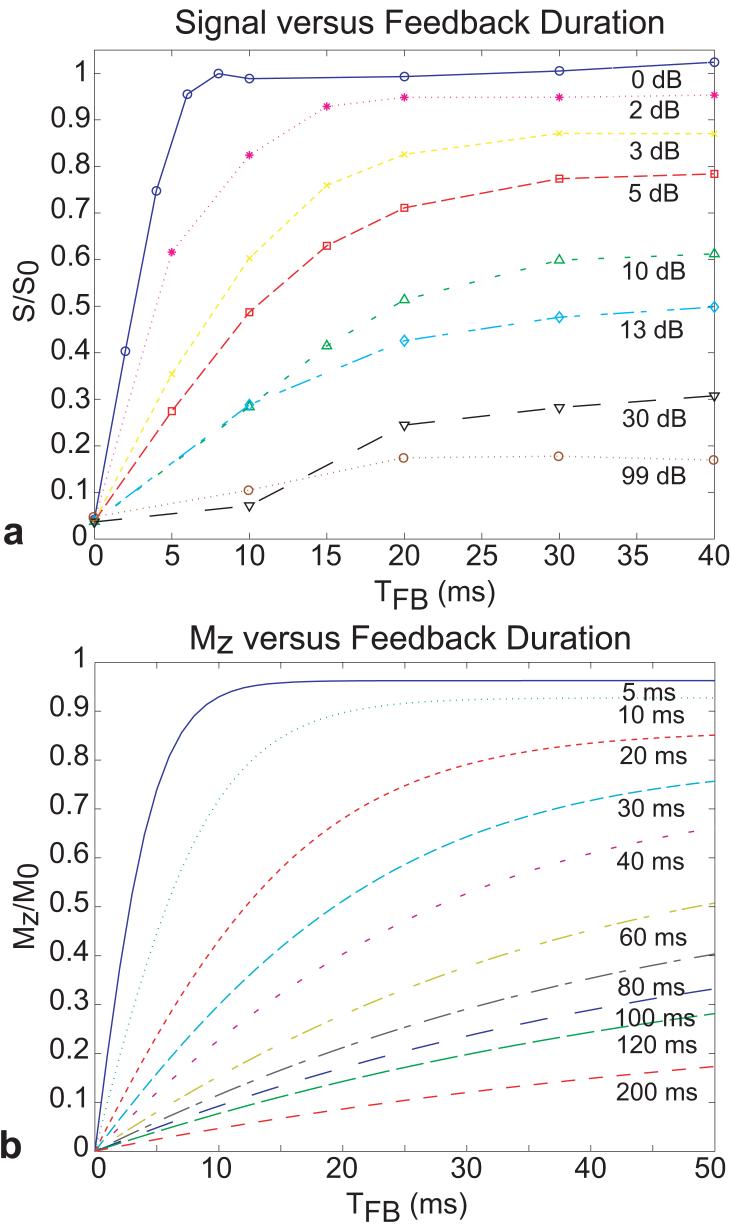
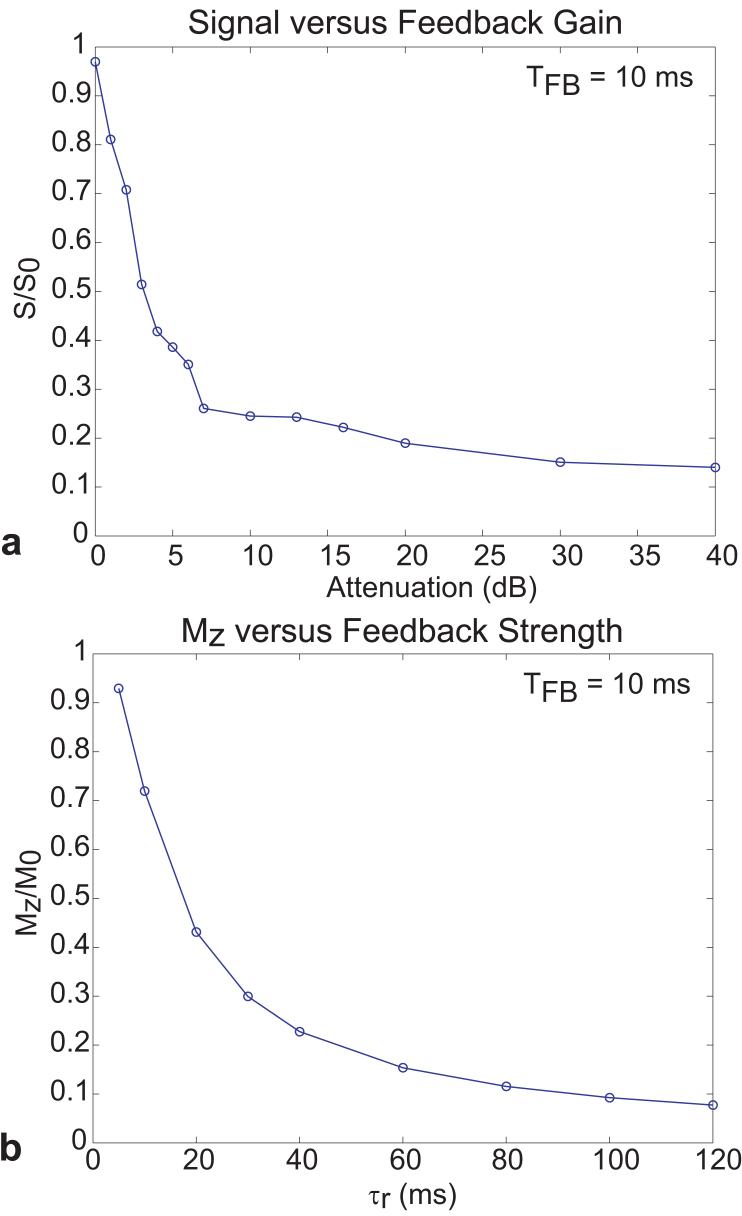
Figure 4 shows simulated and experimental plots of the amount of recovered longitudinal magnetization as a function of feedback duration for a fixed, optimized feedback phase and different feedback strengths. The experimental data showed the expected exponential recovery of the longitudinal magnetization with longer feedback times TFB. Furthermore, attenuation of the feedback strength caused the growth of longitudinal magnetization to decrease. As the gain of the feedback circuit was increased, a higher percentage of the magnetization was recovered. With the highest gains, more than 95% of M0 was recovered for TFB ≥ 10ms.
FIG. 4.
(a) Normalized experimental signal as a function of TFB for different levels of attenuation (in dB) acquired with the demonstration sequence in Fig. 2. The signal S was normalized with respect to signal S0 obtained by setting the first pulse (shown as a hard 90° pulse in Fig. 2) to 0°, with the feedback circuit in open-loop (no feedback). (b) Simulated longitudinal magnetization Mz (normalized to the equilibrium magnetization M0) as a function of TFB for varying radiation damping field strengths, parameterized by the radiation damping time constant τr.
Figure 4b shows simulation results as a function of the time the RD effect was allowed to act (TFB) for different RD time constants, τr. Comparison with the experimental data suggests that maximal feedback corresponds to τr of about 3ms. Comparison of the τr = 200ms simulation showed that this value was in rough agreement with the experimental data corresponding to 99dB of attenuation in the feedback circuit. Figure 5a shows the measured recovered signal plotted as a function of the feedback attenuation (0dB attenuator corresponded to 21dB gain) for TFB=10ms. The simulated data in Fig. 5b shows the recovered magnetization as a function of the RD time constant τr for TFB=10ms. The simulated data followed an exponential decay as τr grew longer.
FIG. 5.
(a) Normalized experimental signal as a function of feedback gain, given in terms of levels of attenuation (in dB). TFB was held constant at 10 ms for each measurement acquired with the demonstration sequence in Fig. 2. (b) Simulated longitudinal magnetization as a function of τr for TFB = 10 ms.
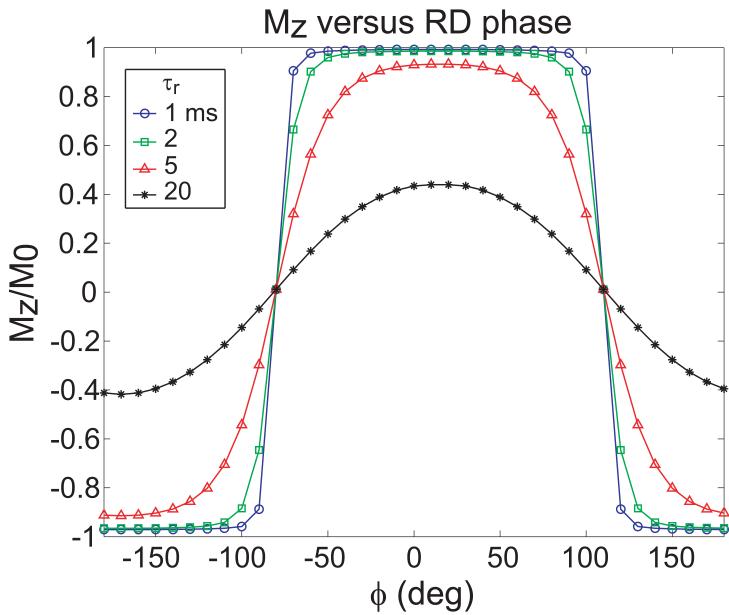
In addition to exploring the dependence on feedback amplitude, the recovered magnetization was mapped as a function of feedback phase. Figure 6 shows the simulated dependence of Mz on the phase of the RD field, ϕ. Relatively broad extrema were found at ϕ = 0° and 180°, with ϕ = 0° corresponding to return of the longitudinal magnetization to the +z axis and 180° corresponding to inversion of the magnetization. Both of these cases would give a maximum in signal intensity in the magnitude image. These phases corresponded to feedback fields that would be exactly orthogonal to the transverse magnetization, leading to the greatest torque exerted by the feedback field on the magnetization. For ϕ = 90° and ϕ = 270°, the feedback field would be aligned with the magnetization and essentially act as a feedback-induced spin lock. For 0° < ϕ < 90° and 270° < ϕ < 360°, the magnetization would be driven toward +z to varying degrees of efficacy, depending on the component of the feedback field orthogonal to the transverse magnetization.
FIG. 6.
Simulated longitudinal magnetization as a function of RD phase ϕ for TFB = 10 ms and different τr.
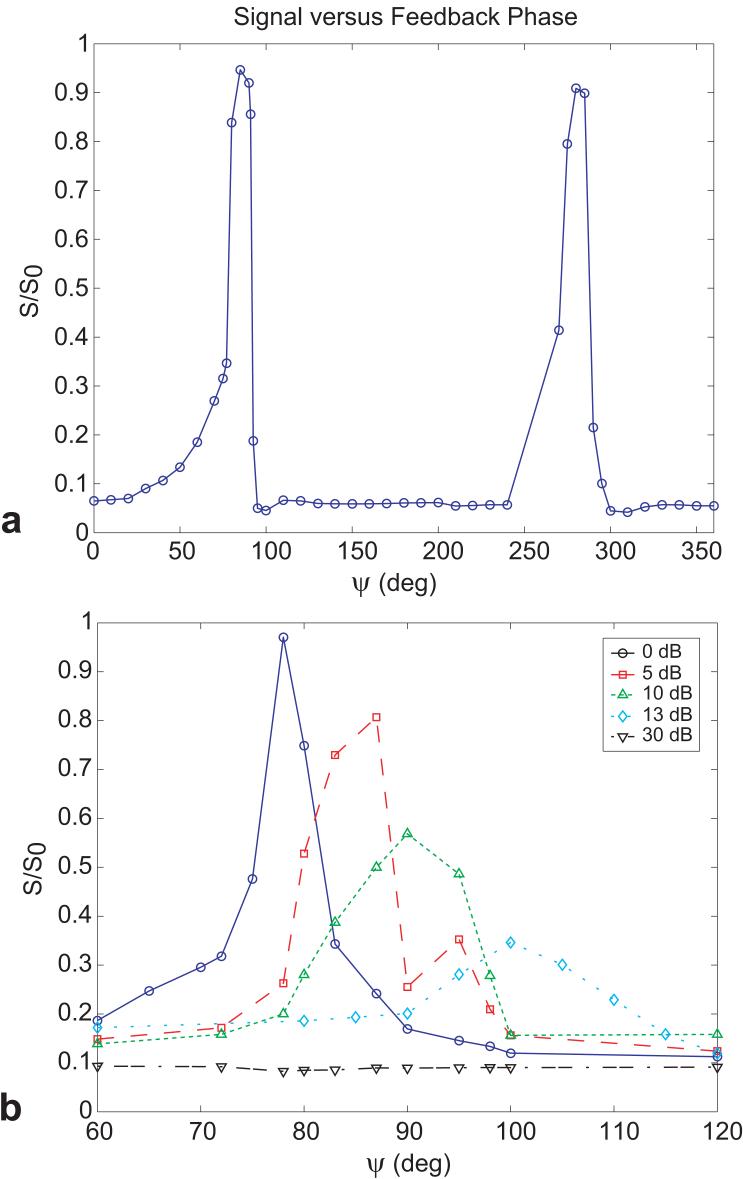
Figure 7 shows the experimental measurements as a function of the RF phase shift in the feedback circuit, ψ. Instead of showing the expected smooth and relatively broad dependence on feedback phase, the magnitude of the recovered magnetization peaked sharply at phases roughly corresponding to ψ = 80° and ψ = 280°, with little recovery observed for all other phases even under the strongest feedback setting. The width of observed peaks in the phase calibration plots corresponds roughly with the expected effect of the frequency shifts observed in the S12 bench measures. For example, with full feedback gain, the half width at half maximum of the peaks in the phase response curve of Fig. 7 is about 5 degrees. Given Q=1300, the S12 response curve of the feedback device is 100kHz in width. Thus if altering ψ shifts the response of the feedback device by 100kHz, the expected feedback field is reduced by half. The S12 bench measurements of the frequency pulling of the response peak as a function of ψ showed a shift of 17kHz per degree of ψ, suggesting that a phase change of 5 degrees corresponds to the frequency shift needed to reduce the feedback field by half.
FIG. 7.
(a) Normalized experimental signal as a function of feedback phase ψ for TFB = 10 ms, acquired with the demonstration sequence in Fig. 2. (b) Normalized experimental signal as a function of feedback phase ψ and different levels of attenuation for TFB = 10 ms.
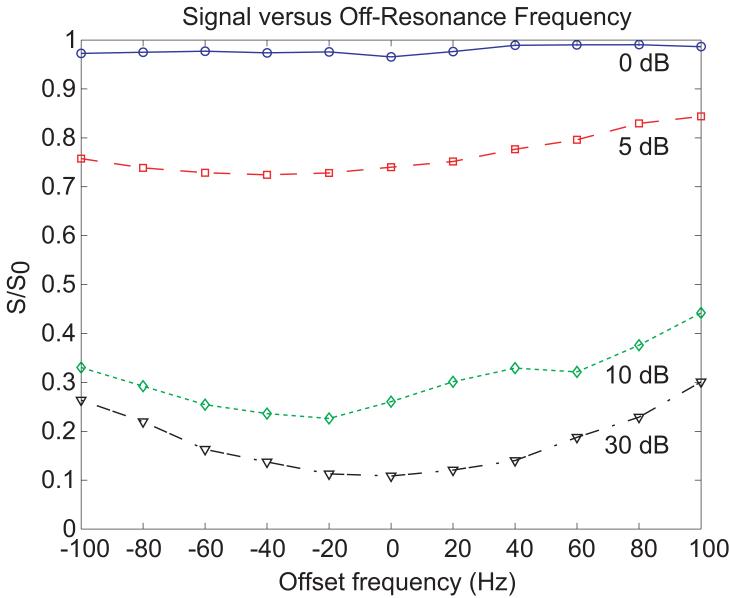
Figure 8 shows the recovered longitudinal magnetization as a function of transmit frequency over a range of ±100 Hz for each feedback gain setting. The recovered longitudinal magnetization was expected to be relatively insensitive to offsets in frequency since the frequency of the RD field is set by the spins themselves. Figure 8 demonstrates that for the strongest RD field, the longitudinal magnetization returned to +z with a variation of less than 3% for the range of offset frequencies (±100 Hz) tested.
FIG. 8.
Normalized experimental signal as a function of off-resonance frequency for TFB = 10ms and different levels of feedback gain acquired with the demonstration sequence in Fig. 2.
DISCUSSION
The modified gradient echo demonstration sequence (Fig. 2) demonstrates the ability of ARISE to expedite the return of the spins to the z-axis at a specified time in the sequence. As pointed out by Bloembergen (7), it is important not to confuse RD with relaxation. Thus, the accelerated RD effect is viewed as the effect of the self-generated resonant RF fields on the spin systems, but not as a component of T1. Only T1 relaxation is able to convert any magnetization state to M0. The RD field simply rotates the coherent magnetization back to +z. As such, RD does not convert T2-dephased magnetization to M0 and thus does not serve as a mechanism for achieving equilibrium magnetization. The test sequence shown in Fig. 2 allowed very little T2 loss between excitation and flip-back. Perhaps even more importantly, the T2 losses did not accumulate from TR to TR since sufficient T1 relaxation occurred within the TR period (TR = 3s). Similar to other flip-back methods, such as bSSFP, if employed in a bSSFP type sequence, the steady-state magnetization would not exceed 0.5M0 unless the flip-back occurred immediately after the excitation. .
Thus, an application in which accelerated RD flip-back might aid in improving Mz usage is a preparation sequence that allows a motion navigator to precede a FLASH or echo-planar imaging (EPI) acquisition. Typically, the preparation sequence would use a small flip angle excitation followed immediately by the navigator measurement, then followed immediately by a 90° excitation for the image acquisition. Our experience with motion navigators suggests they are signal-to-noise limited and can benefit from full use of the available magnetization. This scenario would more closely resemble the sequence of Fig. 2.
Since the Br field depends on the net transverse magnetization, the timing of the accelerated RD must coincide with points in the sequence at which transverse magnetization is present. Thus, if accelerated RD is applied after the image readout, the magnetization must be at least temporarily refocused when the feedback loop is activated. Any net transverse magnetization remaining after the feedback period can be subsequently crushed if required. Since the RD effect acts to return the transverse magnetization to the +z-axis, it is in effect self-regulating in that the RD field will turn itself off when the magnetization has reached the z-axis (i.e., no more transverse magnetization remaining to drive current in the coil).
While the “flip-back” pulse is perhaps the best analogy, the self-generated nature of the effect imposes some important differences. A potential strength of the self-generated nature of RD is that the Br field is always on-resonance and at the correct phase for the spins that generate it. If more than one spectral line is present in the sample due to chemical shift or field inhomogeneity, then each line can be thought of as generating a separate current in the RF coil at its own frequency. If the lines are spectrally farther apart than the effective bandwidth of the flip-back pulse (which depends on TFB, the strength of the Br, and the T2* of the sample), then the effect acts on each line independently. The strength of the effect on a given line, however, depends on the size of the MR signal induced in the coil by that spectral line. For all spectral lines to be returned to the z-axis, the feedback strength and duration must be set to provide enough RD to achieve sufficient recovery of the longitudinal magnetization for the weakest line. Thus, if a sufficient RD effect can be generated, the longitudinal magnetization available is not modulated by off-resonance effects. Nevertheless, as the shim deteriorates, dephasing across the active coil volume may cause a significant loss of the coherence that is required for effective return to the z-axis. While increasing the feedback gain may help expedite the recovery of the weakened coherent magnetization, the current in the coil is no longer correctly phased for all of the spins within the excitation volume.
The off-resonance problem associated with a globally applied RF excitation (by an RF transmit coil) at a single RF phase which acts on a transverse magnetization with a spatial phase variation is common to all flip-back methods (including bSSFP). In this case the phase of the RF flip-back pulse is only correct for one or a few locations within the sample. Unlike signal dephasing in the image, it is not the dephasing across the voxel that is relevant, but rather the global dephasing across the region of the sample inside the RF transmit coil. A possible method for reducing the burden of this “global” dependence is to break the region into smaller transmit volumes using a transmit array. Additionally, some aspects of the self-generated nature of accelerated RD, suggest that the effects of this local phase shift are relatively benign if sufficient feedback gain is used. For example, if only a mild phase roll, e.g., ϕ = 0-180°, exists across the active coil volume, a coherent current will still be generated at the average phase of the sample. The resulting RD field (at this average phase ϕ) will only have the correct phase relationship for certain parts of the sample. But as shown in the Bloch equation simulations of Fig. 6, with sufficient feedback, Mz can be completely restored over a relatively wide range of ϕ for a simple phase shift between magnetization and Br.
Although acclerated RD could in principle be used in applications similar to balanced SSFP to achieve similar steady state magnetizations, the off-resonance behavior of RD flip-back differs from that of balanced SSFP in two important ways. First, in the case of a spatially global off-resonance, the self-generated flip-back pulse sets itself on-resonance while pulses of balanced SSFP would remain off-resonance. Examples of situations in which such an off-resonant condition might develop would include a simple misadjustments of the transmit frequency or cases of global B0 drifts, for example, due to heating of the shim coils by the gradient coils or nearly global B0 drifts due to physiological processes like respiration. While there may be other ways to address this simple global off-resonance issue, RD handles the problem elegantly in offering a simple, self-generated excitation. Second, as shown in Fig. 6, the RD generated flip-back is relatively insensitive to the phase difference between the magnetization and the average induced current in the coil,.
A similar effect to RD could in principle be achieved with conventional flip-back pulses. Such a sequence would require short acquisitions prior to flip-back in order to measure the phase and the relative Mz and Mxy components of the magnetization. Armed with these measurements, the proper phase and excitation angle of the conventional flip-back pulse could be calculated. These additions to conventional flip-back pulses could, in principle, produce a very similar effect to the accelerated RD method.
We have chosen to implement these initial accelerated RD experiments with a surface coil transmit to enable the use of low power RF components. For example, the maximum power output (at 1dB compression) of the amplifier chain was 30mW. The use of a small coil also allowed us to detect and thus compare accelerated RD with the unassisted RD effect. While transmit coils of this approximate size are found in transmit head arrays (15), they are not common in clinical practice. The RF power capabilities of the feedback circuit will thus need to be enhanced for implementation in a birdcage head coil or body coil. As shown in Eq. 5, the Br field scales with QB0B12/Lc. Thus, a birdcage transmit-receive head coil with 10 fold lower B1efficiency and 10 times higher inductance than the surface coil used here will require that the feedback circuit produce a 10 fold greater effective Q than that generated here.
With sufficiently high gain, the feedback device will begin to oscillate spontaneously. The active switching in the feedback loop, however, ensures that the oscillations will only occur during TFB. The oscillations are thus limited to a specified duration and timing in the sequence. If a signal is present that dominates noise components, the oscillation will be locked to the correct phase and frequency relative to the transverse magnetization. In this respect, it is not important whether the positive feedback overcomes the losses and produces oscillations. Use of a high-power feedback loop also has implications for the specific absorption rate (SAR) and will require power monitoring of this pathway. For a coil with an inhomogeneous B1 excitation field such as the one used here, the feedback gain must be high enough to provide sufficient Br to the whole sample. Thus, like the multi-spectral case, it must be designed for the “worst-case” scenario (the weakest B1 region of interest).
The validation studies presented here were performed on simple water phantoms. Extending the method to in vivo imaging will thus require addressing additional issues related to both the sample and the coil. In vivo samples will likely show larger B0 susceptibility variations, chemical shift variations, and increased loading. As referred to earlier, increasing the feedback gain may aid in returning all spectral lines to the z-axis and mitigating the effect of dephasing under B0 susceptibility. This approach may also overcome the decrease in B1r field generation efficiency expected from larger RF coils or the reduction of Q associated with increased coil loading. In addition, many receive coils used in MRI utilize preamplifier decoupling, which introduces a large impedance in the coil loop, reducing current flow. Preamplifier decoupling is designed to reduce inductive coupling between coils by reducing induced currents but has the effect of reducing the current induced by the magnetization (in short turning the MR measurement into a voltage measurement) and thus the RD effect as well. In order to incorporate the RD feedback effect into existing receive systems, the preamplifier decoupling must be switched off during the RD feedback period. The small magnitude of the natural RD effect in vivo may be beneficial in that the effect can essentially be switched on and off by controlling the feedback gain, without needing to suppress any natural, background RD effects. Finally, in vivo application will require SAR monitoring of the power applied by the feedback system.
CONCLUSION
We have developed a new method that returns the magnetization to the z-axis using self-generated flip-back. The ARISE method exploits and strengthens the RD field through an external feedback circuit. Experimental characterization of the feedback circuit as a function of feedback duration, gain, and phase produced results consistent with predictions by the modified Bloch equations. The accelerated RD field can return the full coherent magnetization available prior to RD period back to the +z-axis in 10ms. In the sequence implemented where very little T2 loss occurred prior to the RD period, this resulted in nearly full restoration of the magnetization. The ARISE method provides a self-regulating, resonant, and correctly phased excitation that is relatively insensitive to off-resonance effects. This method thus offers a functional module for accelerating magnetization recovery in a wide variety of sequences.
ACKNOWLEDGMENTS
We thank Andreas Potthast of Siemens for helpful discussions.
Grant support:
National Institutes of Health; NIBIB Grant No. R01EB006847 and R01ED000790; NCRR Grant No. P41RR14075; Siemens Medical Solutions; and the Mental Illness and Neuroscience Discovery (MIND) Institute.
Footnotes
| LIST OF SYMBOLS |
|---|
| O: upper-case oh |
| o: lower-case oh |
| 0: zero |
| l: ell |
| 1: one |
| M0: upper-case em sub zero |
| B0: upper-case bee sub zero |
| B1: upper-case bee sub one |
| vs: lower-case vee sub ess |
| Vc: upper-case vee sub cee |
| Ic: upper-case eye sub cee |
| Rc: upper-case ar sub cee |
| Lc: upper-case ell sub cee |
| γ: gamma (Greek) |
| ψ: psi (Greek) |
| ω: omega (Greek) |
| ϕ: phi (Greek) |
| ≡: equivalent to (Symbol) |
| ⟨: left angular bracket (Symbol) |
| ⟩: right angular bracket (Symbol) |
| <: less than |
| τ: tau (Greek) |
| η: eta (Greek) |
| °: degree (Symbol) |
| ×: times (Symbol) |
| x: ecks |
| ∼: tilde |
| μ0: mu sub zero (Greek) |
REFERENCES
- 1.Becker ED, Ferretti JA, Farrar TC. Driven Equilibrium Fourier Transform Spectroscopy. a New Method for Nuclear Magnetic Resonance Signal Enhancement. Journal of the American Chemical Society. 1969;91(27):7784. doi: 10.1021/ja50001a068. &. [DOI] [PubMed] [Google Scholar]
- 2.Vanuijen CMJ, Denboef JH. Driven-Equilibrium Radiofrequency Pulses in Nmr Imaging. Magnetic Resonance in Medicine. 1984;1(4):502–507. doi: 10.1002/mrm.1910010409. [DOI] [PubMed] [Google Scholar]
- 3.Maki JH, Johnson GA, Cofer GP, Macfall JR. Snr Improvement in Nmr Microscopy Using Deft. Journal of Magnetic Resonance. 1988;80(3):482–492. [Google Scholar]
- 4.Melhem ER, Itoh R, Folkers PJM. Cervical spine: Three-dimensional fast spin-echo MR imaging - Improved recovery of longitudinal magnetization with driven equilibrium pulse. Radiology. 2001;218(1):283–288. doi: 10.1148/radiology.218.1.r01ja38283. [DOI] [PubMed] [Google Scholar]
- 5.Hargreaves BA, Gold GE, Lang PK, Conolly SM, Pauly JM, Bergman G, Vandevenne J, Nishimura DG. MR imaging of articular cartilage using driven equilibrium. Magnetic Resonance in Medicine. 1999;42(4):695–703. doi: 10.1002/(sici)1522-2594(199910)42:4<695::aid-mrm11>3.0.co;2-z. [DOI] [PubMed] [Google Scholar]
- 6.Scheffler K, Lehnhardt S. Principles and applications of balanced SSFP techniques. European Radiology. 2003;13(11):2409–2418. doi: 10.1007/s00330-003-1957-x. [DOI] [PubMed] [Google Scholar]
- 7.Bloembergen N, Pound RV. Radiation Damping in Magnetic Resonance Experiments. Physical Review. 1954;95(1):8–12. [Google Scholar]
- 8.Huang SY, Anklin C, Walls JD, Lin YY. Sizable concentration-dependent frequency shifts in solution NMR using sensitive probes. Journal of the American Chemical Society. 2004;126(49):15936–15937. doi: 10.1021/ja046208s. [DOI] [PubMed] [Google Scholar]
- 9.Hobson RF, Kaiser R. Some Effects of Radiation Feedback in High-Resolution Nmr. Journal of Magnetic Resonance. 1975;20(3):458–474. [Google Scholar]
- 10.Huang SY, Wolahan SM, Mathern GW, Chute DJ, Akhtari M, Nguyen ST, Huynh MN, Salamon N, Lin YY. Improving MRI differentiation of gray and white matter in epileptogenic lesions based on nonlinear feedback. Magnetic Resonance in Medicine. 2006;56(4):776–786. doi: 10.1002/mrm.20987. [DOI] [PubMed] [Google Scholar]
- 11.Broekaert P, Jeener J. Suppression of Radiation Damping in Nmr in Liquids by Active Electronic Feedback. Journal of Magnetic Resonance Series A. 1995;113(1):60–64. [Google Scholar]
- 12.Louisjoseph A, Abergel D, Lallemand JY. Neutralization of Radiation Damping by Selective Feedback on a 400-Mhz Nmr Spectrometer. Journal of Biomolecular Nmr. 1995;5(2):212–216. doi: 10.1007/BF00208813. [DOI] [PubMed] [Google Scholar]
- 13.Oppelt A. Imaging systems for medical diagnostics: fundamentals, technical solutions, and applications for systems applying ionizing radiation, nuclear magnetic resonance, and ultrasound. Publicis Corporate Pub.;Siemens;; Erlangen, [Germany] Berlin: 2005. p. 996. [Google Scholar]
- 14.Bernstein MA, King KF, Zhou ZJ. Handbook of MRI pulse sequences. Elsevier Academic Press; Burlington, MA: 2004. p. 1017. [Google Scholar]
- 15.Alagappan V, Nistler J, Adalsteinsson E, Setsompop K, Fontius U, Zelinski A, Vester M, Wiggins GC, Hebrank F, Renz W, Schmitt F, Wald LL. Degenerate mode band-pass birdcage coil for accelerated parallel excitation. Magnetic Resonance in Medicine. 2007;57(6):1148–1158. doi: 10.1002/mrm.21247. [DOI] [PubMed] [Google Scholar]