Single-molecule FRET measures bends and kinks in DNA

Abstract

We present advances in the use of single-molecule FRET measurements with flexibly linked dyes to derive full 3D structures of DNA constructs based on absolute distances. The resolution obtained by this single-molecule approach harbours the potential to study in detail also protein- or damage-induced DNA bending. If one is to generate a geometric structural model, distances between fixed positions are needed. These are usually not experimentally accessible because of unknown fluorophore-linker mobility effects that lead to a distribution of FRET efficiencies and distances. To solve this problem, we performed studies on DNA double-helices by systematically varying donor acceptor distances from 2 to 10 nm. Analysis of dye–dye quenching and fluorescence anisotropy measurements reveal slow positional and fast orientational fluorophore dynamics, that results in an isotropic average of the FRET efficiency. We use a nonlinear conversion function based on MD simulations that allows us to include this effect in the calculation of absolute FRET distances. To obtain unique structures, we performed a quantitative statistical analysis for the conformational search in full space based on triangulation, which uses the known helical nucleic acid features. Our higher accuracy allowed the detection of sequence-dependent DNA bending by 16°. For DNA with bulged adenosines, we also quantified the kink angles introduced by the insertion of 1, 3 and 5 bases to be 32° ± 6°, 56° ± 4° and 73 ± 2°, respectively. Moreover, the rotation angles and shifts of the helices were calculated to describe the relative orientation of the two arms in detail.

In recent years, fluorescence energy transfer experiments (FRET) have shown great potential for subnanometer analysis of biomolecular structures and their dynamics that can even be applied to single molecules (1–5). Calculation of absolute FRET distances between a donor and acceptor fluorophore is complicated because of several “calibration” factors such as detection efficiencies, spectral cross-talk and fluorescence quantum yields (6) that are difficult to determine accurately. Multiparameter Fluorescence Detection (MFD) (7) avoids most pitfalls (5) by simultaneously collecting all fluorescence parameters (intensity, lifetime and anisotropy in both spectral ranges) at the single-molecule level.

However, determination of absolute distances remains a major challenge because of the uncertainty in the fluorophore positions. This uncertainty is due to the use of the long linkers through which the fluorophores are attached to the biomolecules. Orientational freedom is a prerequisite to safely assume an orientation factor (κ²) of 2/3 (8); however, this prevents a defined fluorophore position, which is needed for fitting data to a geometric model. Here, we present a new conversion function for experimental FRET efficiencies that considers the dynamics of the movement of the fluorophore-linker system and takes into account the fluorophores volume of occupancy derived from molecular dynamics (MD) simulations.

To date, the handedness, helicity (9–11), and sequence-dependent bending (12) of DNA has only been studied by FRET in a qualitative manner. In this work, we were able to determine unique 3D structures of DNA by triangulation of a set of accurate FRET distance constraints in combination with a rigorous analysis of errors. This allowed characterization of sequence-dependent bending of double-stranded DNA and gave structures of DNA kinks introduced by bulged A-loops. We performed MFD studies of various DNA constructs with systematic donor-acceptor distances that varied between 2 and 10 nm to benchmark the spatial resolution of our method.

Results and Discussion

MFD Measurements.

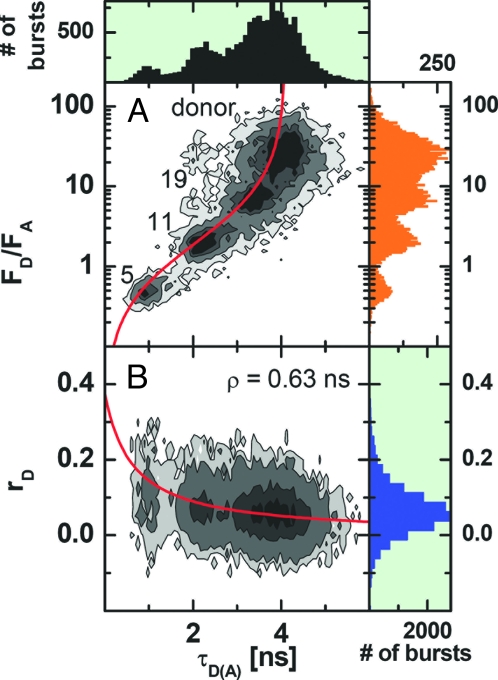
We investigated 12 distances within a double-stranded DNA sequence ranging from 5 to 27 bp in steps of 2 bases. To obtain a set of 12 appropriately double-labeled sample molecules, we combined each of 3 DNA oligonucleotides labeled with the donor fluorophore Alexa Fluor 488 at different positions with each of 4 complementary strands, labeled with the acceptor Cy5 at different positions. Taking a set of 3 samples with interfluorophore distances at 5, 11, and 19 bp, bursts of freely diffusing molecules measured by MFD were arranged into one joint histogram. Fig. 1A shows a 2D frequency histogram of the donor-acceptor fluorescence intensity ratio F_D/F_A versus the donor fluorescence lifetime (in presence of the acceptor) τ_D(A) calculated for all single-molecule events. The 3 FRET-species and the donor-only species can be clearly distinguished. Single-molecule MFD-FRET allows one to take into account all experimental corrections that affect accurate distance measurements, such as detection efficiencies and cross-talk (5). The red line in Fig. 1A shows the expected relation between the donor-acceptor intensity ratio and τ_D(A) when only FRET is changing. The fact that all species fall on this red line, proves that the observed differences are only due to a FRET change. For a given donor-acceptor distance R, the transfer efficiency is given by E = R₀⁶/(R₀⁶+ R⁶) where R₀ is the Förster radius (in ångstroms), which accounts for the system properties. It is calculated by R₀ = (c_FT J κ² Φ_{FD (0)} n⁻⁴)^(1/6), where J is the overlap integral of the donor emission spectrum with the acceptor absorption spectrum with the units [M⁻¹·cm⁻¹·nm⁴], κ² accounts for the relative orientation of donor and acceptor, Φ_FD(0) is the donor fluorescence quantum yield in absence of transfer, and n is the refractive index of the medium (n = 1.33). For the given units, the constant c_FT equals 8.79 10⁻⁵ mol (5). To check that no orientation effects influence the FRET efficiency, the anisotropy r is recorded simultaneously for each detected molecule (Fig. 1B). The short mean rotational correlation time ρ_D = 0.63 ns obtained by a fit with the Perrin equation (red line) shows the high mobility of the donor dye. Moreover, the mobility of Cy5 is also known to be high, which is in agreement with the steady-state (r_A = 0) and time-resolved anisotropy (see supporting information (SI) Fig. S1e) of the sensitized acceptor fluorescence. This justifies as a first approximation the assumption that the mean orientation factor κ² = 2/3 (for more details, see Comparison of Experimental FRET Data with the MD-Simulation), which allows one to calculate a Förster radius given by R₀ = 51.8 Å. Thus, MFD confirms without need of additional ensemble measurements that the observed distinct FRET efficiencies E are only due to differences in distance and are not affected by orientation effects.

Fig. 1.

Two-dimensional frequency histogram of single-molecule data of a mixture of 3 distinct samples with interfluorophore distances of 5, 11, and 19 bp, where frequency increases in gray scale from white to black. The ratio of donor and acceptor fluorescence (F_D/F_A) and the donor anisotropy (r_D) are both plotted against τ_D(A). F_D and F_A are determined from green and red signals by correcting for background counts, B_G and B_R, detection efficiencies, g_G and g_R, and spectral cross-talk α according to equation 3 in ref. 5. (Typical values are B_G = 2.9 kHz, B_R = 0.9 kHz, g_G = 0.36 and g_R = 0.53 and α = 0.019). The direct acceptor excitation is negligible. (A) The red curve shows the FRET relationship F_D/F_A = τ_D(A)φ_FD/((τ_D(0) − τ_D(A))·φ_FA) with τ_D(0) = 4.1 and the fluorescence quantum yields of the donor and acceptor Φ_FD = 0.8 and Φ_FA = 0.43, respectively. (B) The red curve shows the Perrin equation r = r₀/(1 + τ/ρ) with a fundamental anisotropy r₀ = 0.375 and a mean rotational correlation time ρ = 0.63 ns.

Development of an Appropriate Geometric Model.

In previous FRET investigations on double-stranded DNA, a simple straight helix was used as a geometric model that accounts for the helicity of DNA (9, 10). It was then assumed that both fluorophores are positioned at a fixed mean distance from the axis of the DNA, on a helical path according to the DNA rise (3.38Å) and twist (ß = 36°) per base pair (see Fig. 2B and SI Appendix, Eq. 13). However, in this work, MD simulations provide individual dye positions, which are used to test different averaging models.

Fig. 2.

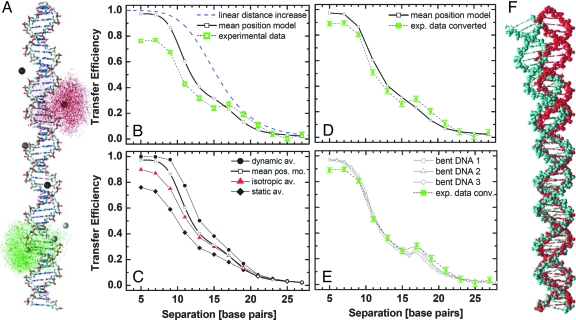
Comparison of modeled and measured FRET distances. (A) MD simulation of fluorophores on B-DNA. The distribution of the donor (green) and acceptor (red) fluorophores is shown for the 21 bp distance, as represented by 5,157 positions of the reference atoms (O7 in Alexa Fluor 488 and C27 in Cy5, respectively). The average positions of the fluorophores for all of the donor and acceptor labels are shown as big spheres. (B) Transfer efficiencies of 12 measured distances as calculated from the donor lifetime. The standard deviations were obtained from 10 subsequent single-molecule measurements. The helicity of the DNA is reflected in the data and can be seen compared with a model of linear distance increase with 0.34 nm per base pair and to the mean position model calculated from the MD-simulated fluorophore positions at a B-DNA (see SI Appendix Eq. 13). (C) From the dataset of the MD simulation, transfer efficiencies were calculated by applying the 3 different averaging regimes (Eq. 2–4): dynamic, isotropic, and static averages. On average the mean position model fits best to the data. (D) To obtain E_mp for a straight DNA, we calculated a conversion function (E_mp = 0.008 + 0.679x + 1.470x² − 1.141x³) by plotting the efficiencies as calculated from the mean position model against the isotropic average that reflects the experimental data. Here, 〈E〉_iso = x (see Fig. S3). (E) The bent DNA-structures 1, 2, and 3 are obtained from the program DIAMOD, using the parameters of Gabrielian and Pongor (19), Goodsell and Dickerson (20), and Ulyanov and James (21), respectively. By modeling the average positions (SI Appendix) of the fluorophores at the according bases in sequence, we obtain specific distance data corresponding to the mean position model (bent DNA 1, 2, and 3). (F) Overlay of B-helix (red) and sequence-dependent structure [Goodsell and Dickerson (21)], (cyan) of the examined DNA. The bending can be approximated by a single kink angle of 16°.

MD Simulation of the Fluorophore-Linker System on a Straight DNA Model.

Here, the fluorophores were allowed to move within the sterically allowed space confined by the straight B-DNA and the length of the linkers. Because we are interested in the maximum range of possible dye positions and not in the actual dynamics, the DNA was kept fixed in the simulation by harmonic potentials, electrostatic interactions were neglected, and the sampling efficiency was increased by elevating the temperature to 2000 K. Fig. 2A shows the structural model of a double-stranded B-DNA together with the computed clouds of 5,157 sterically allowed positions of the donor and acceptor fluorophore, respectively, at a distance of 21 bp. For each fluorophore, the resulting mean dye positions are marked by big spheres (mean position model). More complex models are described in Correct Averaging Procedure. Because of the long linkers, the κ² calculated for all combinations of donor-acceptor positions ranged from 0.65 to 0.69 with an average of 0.67 and a standard deviation of 0.01; this is in close agreement with the value of 2/3 for fully flexible linkers.

Comparing the Experiment with Simple Models.

The dependence of the experimental FRET efficiencies on the number of separating base pairs Δ_bp is given in Fig. 2B (open green squares). Curves of the mean position model of the MD data (black solid line) and a linear distance increase model (blue dashed line) are also shown. Comparison of the experimental data with the 2 basic models shows significant deviations. First, efficiencies measured for small distances are smaller than is predicted by the mean position model for a straight helix, and second, DNA helicity alone is apparently not sufficient to produce the sinusoidal features observed in the experimental curve. Especially at a distance of 17 bp, a much higher than expected efficiency is measured. Thus, both the mean position model and the assumption of a perfect shape of a B-DNA are questionable.

Correct Averaging Procedure.

Knowing the τ_D(0) without transfer, 2 molecular constraints influence the FRET rate constant k_FT = 1/τ_D(0) (R₀/R)⁶(6, 13, 14): (i) orientation fluctuations with the reciprocal rotational correlation time k_R = 1/ρ, which are reflected in the effective orientation factor κ²; (ii) diffusion of the dyes in the sterically allowed volume with characteristic diffusion rate constant k_d, which influences the actual distance R. By averaging all fluorophore positions the information on the width of the position distribution is lost, i.e., the distance between the centres of the clouds of donor and acceptor positions converges to zero for zero base pair distance, whereas the average distance between donor and acceptor does not (15). Thus, neglecting the positional distributions would overestimate the short range distances. Moreover, it is k_FT ∝ κ²/R⁶, and not the distance, that is the relevant physical parameter for averaging. Considering individual distances R_i and individual orientation factors κ_i², 3 extreme cases with distinct mean FRET efficiencies 〈E〉 are computed using R₀ calculated with κ² = 2/3 (for sketches, see Fig. S2 A–C).

Dynamic average: k_R, k_d≫ k_FT:

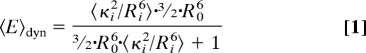Static average: k_R, k_d ≪ k_FT:

Isotropic average: k_R ≫ k_FT ≫ k_d:

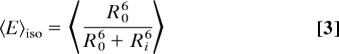To generate geometric models, distances between mean fluorophore positions (R_mp) are needed (SI Appendix). However, flexible fluorophore linkage prohibits direct measurement of R_mp and the corresponding FRET efficiency E_mp (Eq. 4).

Comparison of Experimental FRET Data with the MD Simulation.

Based on the distribution of fluorophore positions and their dipole orientations obtained from the MD simulation, we calculated the 3 different FRET efficiency averages. They indeed show a strong dependence on the fluorophore dynamics (Fig. 2C). The slower the dynamics is with respect to the fluorescence lifetime, the lower is the resulting efficiency. As the calculated distances significantly depend on the choice of averaging model, we have to determine k_R and k_d.

Subensemble and ensemble fluorescence spectroscopy consistently revealed (see Fig. S1 a–e) that both dyes are very mobile. The donor anisotropy decay is described by a sum of 3 exponential decays with the following rotational correlation times ρ_x and the components (r_0x): 0.28 ns (0.250), 1.36 ns (0.076) and 14.3 ns (0.014). Using the fundamental anisotropy of Alexa Fluor 488 r₀ = 0.375, the decay is dominated by fast relaxation rate k_R = 1/ρ₁ = 3.6 × 10⁹ s⁻¹. The slowest component reflecting mainly the rotation of the DNA has only a fraction of 4% of the total donor anisotropy decay. The acceptor anisotropy decay under direct excitation can be described by the sum of 2 exponential decays with ρ_x and (r_0x): 0.682 ns (0.206) and 14.3 ns (0.126) indicating significant local mobility. The rapid rotation of the donor alone is evidence enough for adopting the value of 2/3 for κ².

Based on dye-dye quenching in experiments with varying numbers of intervening base pairs, we can estimate the rate constant of 2D diffusion on the sterically allowed area defined by a distance of approximately ±4 bp to be k_d = 5 × 10⁵ s⁻¹ (A.K.W., C.A.M.S., and F.O., unpublished data). Based on the FRET efficiencies shown in Fig. 2B (and Table 2) and τ_D(0) = 4.1 ns, the computed FRET rate constants k_FT range from 7.9 × 10⁸ to 8.3 × 10⁶ s⁻¹. The order of the k values, k_R > k_FT > k_d indicates that the isotropic average 〈E〉_iso should describe the experimentally observed FRET efficiency best. Comparing the 3 different averages with the experimental data, we indeed found the best agreement for the isotropic average.

FRET Detects Sequence-Dependent Bending of DNA.

The ultimate aim of MFD-FRET measurements is to obtain structural information. This can only be achieved by deriving distances R_mp between 2 fixed points from the data, in our case between the mean fluorophore positions. However, as stated in Comparing the Experiment with Simple Models, this is not measured in a FRET experiment. Based on the simulation data, we generated an empirical polynomial function, that converts the isotropic average 〈E〉_iso into E_mp, which is needed for the geometric description (Fig. S3). This function now permits us to calculate the correct distance between the average donor and acceptor position from any measured FRET efficiency.

The corrected experimental efficiencies are in reasonable agreement with the values calculated for a straight B-DNA helix with a fixed position of the fluorophores, even at small distances (Fig. 2D). However, systematic deviations centered at 17 bp are still visible and much larger than the experimental errors. The deviations are too large to result solely B-DNA helicity, indicating that additional structural features are contained in the FRET data.

It is well known that DNA can adopt different conformations. The most prominent, the A, B, and Z helixes are deduced from crystals, and thus reflect average conformations. Beyond this, each DNA sequence shows an individual bending, which has been investigated extensively by other techniques (16–18). These studies resulted in different models providing sets of bending parameters for any triplet or quartet of consecutive bases, and, thus, can be used to describe the bending of any longer DNA sequence. Based on the 3 alternative sets of bending parameters from Gabrielian and Pongor (19), Goodsell and Dickerson (18), and Ulyanov and James (20), we used the open source program DIAMOD (21) to generate 3 structures of our DNA showing the sequence-dependent bending. Although the authors above provide different sequence related bending parameter sets, these parameters result in a similar overall bending. The difference between the structure of our DNA sequence predicted by Goodsell and Dickerson (cyan) and a B-DNA structure (red) is displayed in Fig. 2F. To compare the bent DNA structures with our data, we modeled the fluorophore position clouds obtained from the MD simulation to the respective bases in the bent DNA (see SI Appendix). Subsequently, we calculated the FRET efficiencies for the distance between the mean fluorophore positions. Fig. 2E shows a superposition of the converted experimental transfer efficiencies and E_mp calculated for the 3 bent DNA structures. Without any additional fitting all models within their variation are in excellent agreement with the experimental data. Both the absolute values and the shape of the experimental transfer efficiency curve are well described by the mean position model of the bent DNA. Small deviations at shortest distances of 5 and 7 basepairs originate from acceptor quenching due to fluorophore collisions, which change their photophysical properties as detected by fluorescence correlation spectroscopy (22). In conclusion, single-molecule FRET is sensitive enough to detect DNA bending that can be approximated by a single kink angle of only 16°. The data presented here clearly show that by taking into account the correct average for the fluorophore dynamics and their positional variability, molecular distances can be calculated with an accuracy of a few percent, using the method of single-molecule multi parameter fluorescence detection.

Kinked DNA.

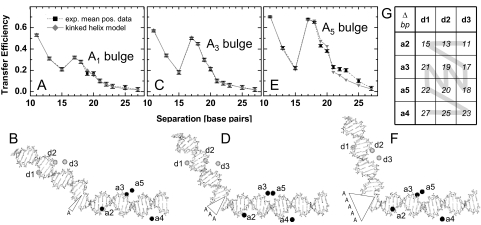
Our single-molecule MFD FRET technique was also applied to measure kinked DNA of unknown structure. We induced kinks into the same DNA sequence as was used above by insertion of unpaired adenosines, so-called A bulges (see Material and Methods). Samples containing 1, 3, and 5 adenosines (A₁, A₃, and A₅ bulge) in the donor strand of the DNA above were investigated. By choosing proper donor and acceptor positions the helical wheel could be studied in 1 or 2 base pair steps (see Fig. 3G). Fig. 3 A, C, and E show the converted transfer efficiencies from single-molecule MFD measurements on DNA samples containing the A₁, A₃, and A₅ bulges. All 3 samples show a significantly higher efficiency for the distance of 17 bp compared with the 15-bp distance. Because of the cross combination of the donor and acceptor labeling positions (Fig. 3 B, D, and F), the relative location of the kink varies for each base pair separation. If a kink is not located symmetrically between the 2 fluorophores, its influence on the interfluorophore distance is much smaller than in the symmetric case. Here, donor d3 and acceptor a2 are closer to the kink than d1 and a3. Accordingly, the 15-bp distance (d1-a2) is hardly affected by the kink, whereas the 17-bp distance (d3-a3) is significantly decreased. This effect becomes more pronounced with increasing number of bulged As, indicating a strong increase of the kink angle. Finally, for the A₅ bulge, the 17-bp distance (d3-a3) is almost as short as the 11-bp distance (d3-a2).

Fig. 3.

Fitting DNA structures to the measured distances. (A, C, and E) FRET-efficiencies of converted experimental data (black) from kinked DNAs. By varying the torsion angles in the kink site (backbone opposite to the inserted adenosines, see Fig. S4a) a kinked 3D helix model (gray) was fitted to the converted experimental data (black). (B, D, and F) Corresponding 3D structures resulting from the best fit (PDB files are given in SI Appendix). The labeling positions for the donor (d) and acceptor (a) are enumerated as described in Materials and Methods. The structures were modeled using bent DNA sequences according to (18). (G) Different DNA oligonucleotides labeled with the donor fluorophore (d3 to d1) and acceptor fluorophore (a2 to a5), respectively, are combined to yield a set of sample molecules with a continuous distance increase (gray line, see Materials and Methods). The interfluorophore distances in the table are given in number of separating base pairs Δ_bp.

Quantitative 3D FRET Structure Analysis of Kinked DNA.

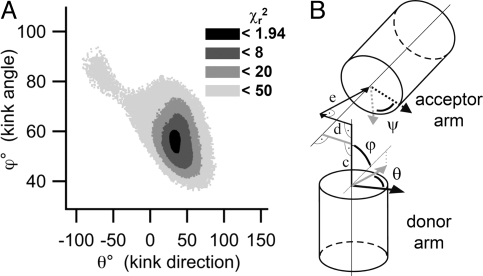
To characterize the structural arrangement of the helical segments, we fitted a detailed molecular model to sets of measured distances. This model takes into account the sequence-dependent bending of the 2 helical arms (18) and fits the kink by the rotation of all 5 backbone torsion angles of the acceptor strand opposite to the position where the A-bulges are inserted, while assuming the donor strand as being cleaved at the respective position (see Fig. S4a). For a geometric description of the overall fitted structure, we calculated the kink angle, ϕ, and the angles of rotation, θ and ψ, of the 2 helical arms around their individual axes. In addition, we calculated 3 shifts of the acceptor-carrying arm, 1 parallel and 2 perpendicular to the axis of the donor-carrying arm (Fig. 4 and Fig. S4b).

Fig. 4.

Kink parameters. (A) The χ_r² surface is shown for the kink angle ϕ and kink direction θ induced by the A₃ bulge. (B) Visualization of the parameters describing the kink. ϕ denotes the kink angle between the donor and the acceptor axis. θ and ψ denote the angle of rotation around the helical axes of the donor and the acceptor arm, respectively. The gray lines define the x and y directions of the initial coordinate system. (c–e) The shift of the acceptor helix is given by the components of a trihedron, along the helical axis of the donor arm (c), perpendicular to the donor and acceptor axis (d), and in direction of the kink (e). Note, that the kink direction is equivalent to the angle of rotation of the donor arm. For a more detailed description see Fig. S4b.

The use of a random search algorithm with a rigorous and quantitative reduced χ² (χ_r²) criterion (see Material and Methods and SI Appendix) allowed us to find the best molecular conformations (Fig. 3 B, D, and F) for a fit of the detailed molecular model to the converted experimental FRET distances. Despite not having included steric hindrance in the fitting routine for the 2 double-stranded DNA segments, structures without any steric conflicts are obtained. The χ_r² surfaces (Fig. 4A and Fig. S5) made it possible to calculate errors for the parameters (angles and displacement) in the geometric model. For all parameters well-defined single minima were found, i.e., the FRET data resulted in unique structures for the different A bulges. The pdb files of these structures are provided in SI Appendix.

The complete sets of parameters that describe the kinks according to the geometric model are listed in Table 1. The kink angles increase with the number of bulged As. Our values are in good agreement with conformations that have already been measured with other techniques: Qualitative transient electric birefringence studies estimate a kink angle of 10–20° in RNA per unpaired base (23). The kink angle we measured for the A₅ bulge is in good agreement with 73 ± 11° obtained by detailed NMR measurements (24). Qualitative FRET measurements conducted by Gohlke et al. (25) were done under ensemble conditions and led to an estimation of the kink angle between 81 and 105°, using 1 and 2 measured distances (26).

Table 1.

Parameters fitted to the kinked DNA

	A1	A3	A5
ϕ, °	32 ± 6	56 ± 4	73 ± 2
θ, °	47 ± 14	34 ± 6	50 ± 4
ψ, °	26 ± 11	38 ± 9	15 ± 5
c, Å	1.6 ± 2	3.7 ± 1.3	5.2 ± 1.1
d, Å	−0.3 ± 3	−3.2 ± 2.5	1.4 ± 1.9
e, Å	−3.7 ± 1.8	−0.16 ± 1.9	−1.9 ± 0.7
χr2	2.72	0.94	70.6

Determined kink parameters with errors and minimal χ_r² values for the analysed kinked DNA structures containing the one-, three- and five-A bulge. For a more detailed discussion of errors, see SI Appendix.

In contrast, we generated a complete 3D model based on kink angles that were calculated taking the bending of the helical arms into account. This leads to different helix axes for the donor and acceptor arm. We have already seen bending of ≈16° of the linear helix (Fig. 2f), which now acts as a “frame” for the bulge. Depending on the relative orientation of the kinking and bending direction, both angles may add up or partially compensate in the experimentally determined values. Thus, in general, different sequences in the helical arms may lead to different measured kink angles for the same number of bulged As.

The reference for rotation of the helical arms and for the direction of kinking is defined as the direction of the phosphor atom P (see Fig. S4) in the strand opposite to the bulged As, when seen from the Center of the helix. The resulting angles of rotation reveal an average kink direction given by (θ + ψ)/2 for all bulges of ≈35° with a variation of ±10° for the A₁ and ±20° for the A₅ bulge. Interestingly, for the A₁ and the A₅ bulges, the rotation of the donor arm is stronger than that of the acceptor arm, such that the bases before and after the kink overlap stronger than in the B-DNA conformation.

The resulting gap in the bulge-carrying strand is 8, 12, and 15 Å for the A₁, A₃, and A₅ bulges, respectively. With 1 base occupying ≈5 Å in the helical backbone, the gap is well sized to harbor all of the bulged bases, implying that the backbone itself can bulge out when containing more than one A. The transfer efficiencies corresponding to the distances calculated from the fitted DNA structures are superimposed in Fig. 3a, c and e, showing the high quality of the fit to the A₁ and A₃ bulge data, which is also reflected in the resulting minimal χ_r² of 2.72 and 0.94. This also justifies the assumption of our molecular model that only the backbone atoms opposite to the bulged As are forming the kink whereas the rest of the DNA structure remains unchanged. However, the distances calculated for the A₅ bulge could not be fitted perfectly by our molecular model, as reflected in the higher χ_r². This indicates that the structures of the DNA helical arms may be distorted by the inserted As. Such distorting influence of additional bases on the double helical structure was previously shown by NMR measurements on an A₅ bulge in another DNA sequence, where the bases were found to be tilted relatively to the helix axis (25).

Conclusion

Significant advances in absolute single-molecule distance measurements via FRET have been achieved by considering positional and orientational fluorophore dynamics and by taking advantage of known helical nucleic acid features in combination with triangulation methods. These improvements in FRET analysis allowed us to determine quantitatively DNA bending and kinking in all 3 dimensions. We emphasize that the given conversion function, which maps the measured to the corrected FRET efficiency may be applied to any other double-stranded DNA structure with the same fluorophore-linker system in a comparable environment. For that purpose we provide the files of the simulated fluorophore positions and a detailed application protocol (see SI Appendix). In view of the fact that protein- or damage-induced DNA bending has been shown to regulate the assembly and function of DNA-multiprotein complexes, structural FRET studies harbor the potential to provide fascinating insights in structural and molecular biology. Moreover, the same approach can be directly transferred to the study of the arrangement of α-helices in proteins.

Materials and Methods

Samples.

All oligonucleotides were synthesized and fluorescently labeled by IBA. The dyes (Alexa Fluor 488 NHS as donor and Cy5 NHS as acceptor) were coupled via 5-C₆-aminoallyl-deoxythymidines. The sequence and labeling positions (superscript numbers) for the donor are 5′-d(X GGA CTA GTC TAG GCG AAC GTT TAA GGC (A_1,3,5) GAT CTC T³GT² TT¹A CAA CTC CGA), whereas those for the acceptor are 5′-d(TCG GAG TTG TAA ACA GAG AT¹C GCC TT²A AAC GT³T⁵ CGC CT⁴A GAC TAG TCC). The single strands are referred to as d3, d2, and d1 and a1, a2, a3, a5, and a4, respectively. X denotes over-hanging bases AATT in case of the sequences including the bulged As, which are given in brackets. Four different series of FRET labeled duplexes are generated by combination of each donor labeled DNA strand with each acceptor carrying strand. The double-strand series without bulged As is labeled at the acceptor positions 1, 2, 3, and 4. Those including the A, A₃ or A₅ bulge are labeled at the acceptor positions 2, 3, 5, and 4. The length of the DNA of 48 bp ensured a minimum of 10 bases adjacent to all fluorophore sites and thus a comparable environment for all dyes. The measurements were performed in a buffer with 50 mM Tris·HCl, 150 mM NaCl, 1 mM EDTA, 5 mM MgCl₂, 0.4 mM ascorbic acid (pH 7.6).

Ensemble and single-molecule fluorescence spectroscopy.

See ref. 7 and SI Appendix.

Simulations.

The calculation of the cloud of possible fluorophore positions was done via MD simulations, using the Gromacs simulation software (27) as described in ref. 28. The model structures were assembled in VMD 1.8.2 (29).

The formulas for calculating the kink and rotation angles and the shifts between the helical arms are given in SI Appendix. We calculated the errors of the fitted parameters that correspond to the standard deviation of the experimental distances by determining the maximal and minimal values for all conformations with a χ_r² less than the minimal χ_r² +1. This was done by using the same algorithm that we used to find the minimal χ_r² with 2 differences: (i) all conformations with a χ_r² less than the minimal χ_r² +1 were collected and not further varied and (ii) the random variation was applied to next 10,000 best conformations. This procedure was repeated until we obtained a set of at least 50,000 conformations with a χ_r² less than the minimal χ_r² +1 (SI Appendix).