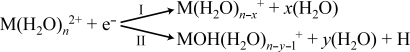Nanocalorimetry in mass spectrometry: A route to understanding ion and electron solvation

Abstract

A gaseous nanocalorimetry approach is used to investigate effects of hydration and ion identity on the energy resulting from ion–electron recombination. Capture of a thermally generated electron by a hydrated multivalent ion results in either loss of a H atom accompanied by water loss or exclusively loss of water. The energy resulting from electron capture by the precursor is obtained from the extent of water loss. Results for large-size-selected clusters of Co(NH₃)₆(H₂O)_n3⁺ and Cu(H₂O)_n2⁺ indicate that the ion in the cluster is reduced on electron capture. The trend in the data for Co(NH₃)₆(H₂O)_n3⁺ over the largest sizes (n ≥ 50) can be fit to that predicted by the Born solvation model. This agreement indicates that the decrease in water loss for these larger clusters is predominantly due to ion solvation that can be accounted for by using a model with bulk properties. In contrast, results for Ca(H₂O)_n2⁺ indicate that an ion–electron pair is formed when clusters with more than ≈20 water molecules are reduced. For clusters with n = ≈20–47, these results suggest that the electron is located near the surface, but a structural transition to a more highly solvated electron is indicated for n = 47–62 by the constant recombination energy. These results suggest that an estimate of the adiabatic electron affinity of water could be obtained from measurements of even larger clusters in which an electron is fully solvated.

Ion–solvent interactions are fundamental to many important phenomena in chemistry and biology, including ion transport across cell walls, salt-bridge formation, surface tension, and protein stability, yet many aspects of such interactions are still not well understood. Mass spectrometry is an important tool for probing ion–solvent interactions and has been widely used to obtain valuable thermochemical information. The ability to form gaseous hydrated clusters of many di- (1) and trivalent (2) ions has greatly expanded the capabilities of mass spectrometry to investigate important ion solvation problems. Structural information of hydrated ions has been obtained from a variety of thermochemical methods (3–5) and spectroscopy (6–9). From these studies, information about how water molecules organize around ions and how water can affect the structures of ions themselves can be obtained (8, 9).

Investigating the most fundamental aqueous ion, the hydrated electron, is challenging because of its powerful reducing nature (E_1/2⁰ = −2.87 V) (10) and high reactivity. Solvated electrons have been observed in many different solvents (11) and are important intermediates in radiation chemistry, electron transfer processes, and many biological processes, including those that can lead to irreversible cell damage. The structure of the hydrated electron has been investigated by several methods, including electron spin resonance (12) and Raman spectroscopy (13), but many details about the structure of the solvent cavity that traps the electron remain elusive.

Information about hydrated electrons and electron–water interactions has been obtained from studies of the structures and dynamics of stable water clusters containing an electron. Since the first observation of (H₂O)_n⁻ by mass spectrometry (14), the structures of these clusters have been hotly debated (15–24). Evidence for both externally and internally solvated electrons has been reported. Electron vertical detachment energies (VDEs) of (H₂O)_n⁻ clusters have been measured for n between 2 and 69 by using photoelectron spectroscopy (15). Based on the dependence of the solvation energy on cluster size, which proceeds as n^1/3, these data extrapolate to a value of 3.3 eV at infinite cluster size. This value is consistent with the photoelectric threshold of water obtained from a thermocycle involving the hydrated electron in ice (3.2 eV) (15) and computational values that range from 3 to 4 eV (25), suggesting that a bulk-like interior electron state for these clusters was probed. However, subsequent calculations suggest that surface state data would also proceed linearly with n^1/3 (16, 26). From mixed quantum-classical simulations of hydrated electron clusters with between 20 and 200 water molecules, Turi et al. (16) concluded that surface states were most consistent with results from all previous experimental studies. In contrast, photoelectron data obtained by Neumark and coworkers (17, 18) for n up to ≈150 indicate that at least three cluster isomers can be produced via supersonic expansion and clusters with both surface and internal electrons could be identified based on their VDEs. Results from femtosecond resolved photoelectron imaging of the electron dynamics in (H₂O)_n⁻ (19, 20) suggest that an interior electronic state was probed (19). Recent infrared spectroscopy data of such clusters provide important insights into electron–water interactions, but do not resolve the electron location debate (27).

An alternative approach to investigating interactions between ions, electrons, and water is to measure recombination energies (REs) resulting from electron capture (EC) by nanometer-sized hydrated ions in the gas phase (28). In this ion nanocalorimetry method, gas-phase nanodrops that contain charged metal ions are reduced by thermally generated electrons (28–31). For large clusters, the RE is deposited into internal modes of the reduced cluster resulting in cluster heating and evaporation of water molecules (28, 29). An estimate of the RE can be obtained from the sum of the sequential threshold dissociation energies for the maximum number of water molecules that are lost. More accurate REs may be obtained from the average number of water molecules lost, in combination with threshold dissociation energies derived from a discrete Thomson liquid drop model (32) and estimates of the translational, rotational, and vibrational energy released into the products (31). Because solvent reorganization after EC takes place on a time scale that is significantly faster than that for these nanocalorimetry measurements, the solvent reorganization energy that is released because of reduction of the precursor should be reflected in the overall number of water molecules lost from this cluster (30, 31). Thus, the REs obtained from these experiments should correspond to the adiabatic ionization energies of the reduced clusters. This nanocalorimetry method has recently been used to obtain absolute REs of gaseous clusters containing different redox-active species that can be related to reduction potentials in bulk solution. By comparing these absolute reduction potentials to relative values measured in solution, an absolute value for the standard hydrogen electrode potential of 4.2 ± 0.4 V was obtained (31).

Here, the effects of size and ion identity on the reactivity of nanodrops with electrons are investigated. Data supporting ion–electron pair formation on EC by large gaseous Ca(H₂O)_n2⁺, n up to 62, clusters is presented. The trend in REs with cluster size is consistent with a transition from an ion–electron pair in which the electron is delocalized at or near the surface to a more fully solvated electron with increasing size. Analysis of the REs as a function of solvation suggests that at larger cluster sizes, thermodynamic values in aqueous solution may be obtained by extrapolating results from these nanocalorimetry experiments to infinite size.

Results and Discussion

Effects of Cluster Size and Metal Ion Identity on EC Reactivity.

Reduction of aqueous nanodrops can result in dissociation by two pathways depending on cluster size and ion identity (Scheme 1). Results from EC experiments of isolated Cu(H₂O)_n2⁺ for n = 15, 21, and 29, which show these pathways, are given in Fig. 1. EC by Cu(H₂O)₁₅²⁺ results predominantly in loss of a H atom accompanied by loss of either 8 or 9 water molecules (pathway II), although a single low-abundance product ion corresponding to the loss of 11 water molecules is also observed (pathway I; Fig. 1A). In contrast, EC by Cu(H₂O)₂₉²⁺ results in the loss of primarily 16 or 17 water molecules from the reduced precursor (pathway I; Fig. 1C). No ions from pathway II are observed from this or larger clusters. For Cu(H₂O)₂₁²⁺, fragment ions from both reaction channels are formed with comparable abundances, but the extent of water loss via each pathway differs dramatically (Fig. 1B); an average of 15.2 and 10.4 water molecules are lost via pathways I and II, respectively. The change in the dissociation pathway and the significant difference in the number of water molecules lost from reduced Cu(H₂O)_n2⁺ for these two pathways at n ≈ 21 is remarkable. For Ca(H₂O)_n2⁺, n ≤ 22, loss of a H atom accompanied by loss of water molecules is exclusively observed, whereas only loss of water molecules occurs for n ≥ 30. A sharp transition in the dissociation pathways occurs at about n = 24 (29). A similar number of water molecules are lost for both pathways.

Scheme 1.

Fig. 1.

Mass spectra resulting from electron capture of isolated Cu(H₂O)₁₅²⁺ (A), Cu(H₂O)₂₁²⁺ (B), and Cu(H₂O)₂₉²⁺(C). Expansions are indicated on each spectrum. Noise peaks are represented by asterisks.

The difference in the energetics of pathways I and II corresponds to the H atom affinity of the M(H₂O)_n⁺ cluster. These results suggest that the H atom affinity of a Cu⁺-containing cluster is much greater than that containing Ca⁺ within these size ranges. These results are consistent with the observation that the loss of water molecules occurs on thermal activation of Cu(H₂O)_n⁺, for n up to 50 (33, 34), whereas loss of H from Ca(H₂O)_n⁺ occurs for 4 < n < 13 (35).

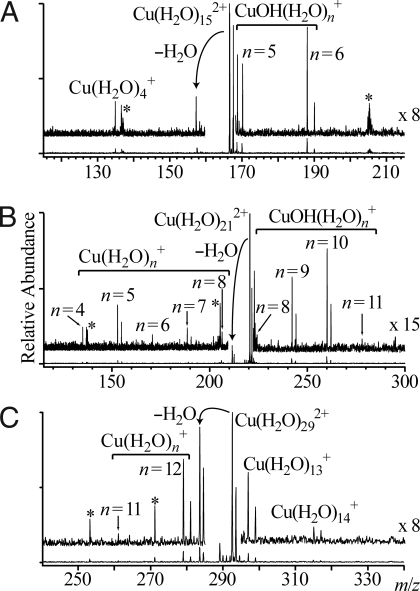
The average number of water molecules lost on EC by M(H₂O)_n2⁺, M = Ca, Mg, Sr, Ba, and Cu, and Co(NH₃)₆(H₂O)_n3⁺ for both pathways combined are shown in Fig. 2. Fewer water molecules are lost from the smaller clusters because of higher water-binding energies with decreasing cluster size. This effect predominates over any increasing RE that may occur with decreasing cluster size (36). In addition, nonergodic H atom loss may occur, at least for smaller clusters (29). The average number of water molecules lost from the reduced Ca²⁺ precursor reaches a broad maximum of ≈10.2 for cluster sizes between n = 24 and 31 and decreases slightly with increasing cluster size (29), but remains nearly constant between n = 47 and 62. Data obtained for Mg(H₂O)_n2⁺ (n ≤ 32) follows a similar trend with only minor differences observed primarily for the smaller clusters, which can be attributed to differences in water-molecule-binding energies to Mg⁺ vs. Ca⁺ containing clusters at these sizes. For both Cu(H₂O)₁₅²⁺ and Ca(H₂O)₁₅²⁺, the average number of water molecules lost is nearly the same (Fig. 2). However, a dramatic difference between nanodrops containing Cu²⁺ and Ca²⁺ is observed for larger clusters, where the average number of water molecules lost from Cu-containing clusters is ≈16.3 compared with ≈10.2 for Ca with n = 26–33.

Fig. 2.

The average number of water molecules lost from the reduced precursor via both dissociation pathways I and II as a function of the precursor size, for Co(NH₃)₆₃⁺, Cu²⁺, Ca²⁺, Mg²⁺, Sr²⁺, and Ba; data used in Fig. 4 are enclosed by dashed squares. Data for M(H₂O)_n2⁺, M = Mg, Sr, Ba, Ca(H₂O)_n2⁺, n < 47, Cu(H₂O)₃₂²⁺, and Co(NH₃)₆(H₂O)₅₅³⁺ are from refs. 28, 29, and 31.

For Co(NH₃)₆(H₂O)_n3⁺, the average number of lost water molecules decreases for n ≥ 40. This can be attributed predominantly to improved ion stabilization with increasing solvation. In addition to the effect of ion solvation, surface energy effects, in which the binding energy of a water molecule to a cluster increases slightly with increasing size, and a degrees of freedom effect, in which larger ions dissociate more slowly with increasing size for a fixed amount of deposited energy, may also contribute. Because the degrees of freedom effect would lead to a decrease in the average number of water molecules lost and because surface energy effects should be similar for the Co(NH₃)₆(H₂O)_n3⁺ data at these cluster sizes, the near constant number of water molecules lost for Ca(H₂O)_n2⁺ with n between 47 and 62 is surprising and indicates that an additional factor, such as a structural change, must contribute to the observed water loss in this size regime.

Ion–Electron Pair Formation.

Several pieces of evidence suggest that an ion–electron pair is formed on EC of Ca(H₂O)_n2⁺ over the range of cluster sizes in which water loss is exclusively observed. For M(H₂O)₃₂²⁺, M = Mg, Ca, Sr, and Ba, EC results in nearly the same number of water molecules lost (Fig. 2), corresponding to a RE of ≈4.5 eV, despite the 5 eV difference in second ionization energies of the bare Mg and Ba atoms (15.0 and 10.0 eV, respectively) (28). In contrast, the RE for Cu(H₂O)₃₂²⁺ is ≈7.1 eV (31) and the second ionization energy of bare Cu is 20.3 eV. These results show that relatively few water molecules have a significant effect on ionization energies. The REs of many other divalent transition metal ions (data not shown) and M(NH₃)₆₃⁺ (31) containing water clusters result in significantly higher and different RE values than those for the alkaline earth dications. Furthermore, the gas-phase reduction of Cu²⁺- and M(NH₃)₆₃⁺-containing clusters can be related to one-electron reduction potentials in aqueous solution (31). These results show that Cu²⁺ and M(NH₃)₆₃⁺ in the larger nanodrops are reduced. In contrast, the constant REs for the larger nanodrops containing the divalent alkaline earth metal cations strongly indicate that an ion–electron pair is formed. By comparison, reduction of alkaline earth dications in aqueous solution occurs via a two-electron process. A one-electron process is not observed presumably because the monovalent cations are relatively unstable in solution because of solvent effects, whereas a one-electron oxidation is observed in aqueous solution for Cu⁺ (37).

Computational studies of Mg(H₂O)_n⁺ indicate that for n = 6–8, the most stable structures correspond to a divalent ion with six water molecules in the first solvation shell and a diffuse electronic surface state in which the electron density is shared by many water molecules (36). For larger clusters (n between 9 and 19), the electron density is dispersed between two water molecules in a molecular “tweezers” structure with the electron interacting with the H atoms of two surface-exposed water molecules. A solvated electron and M²⁺ pair has also been proposed for M(H₂O)_n⁺, M = Mg (35, 38) and Ca (35), at n ≈ 15 or greater, based on a change in dissociation reactivity that occurs for clusters this size. An ion–electron pair structure has also been proposed for neutral water clusters containing individual alkali metals (39, 40). These results are all consistent with the formation of an ion–electron pair for the larger reduced alkaline earth metal ion containing clusters investigated here. An analogous structure is an electride, which is an ionic salt where the electron is the anion. Although such electrides have been investigated for many years (41), it was not until relatively recently that a single crystal electride that is both thermally stable and unreactive was reported (42). Results for size-selected clusters, such as those reported here, may provide insights into the stabilities of electrides.

There are intriguing parallels between these EC results and those from infrared multiphoton dissociation experiments of size-selected (H₂O)_n⁻ clusters measured for n = 15–50 (27). For clusters with up to n = 20–25, the spectra indicate that the electron interacts primarily with a single water molecule that is oriented so that the H atoms are in the electron cloud. For clusters with n between 20 and 50, additional water molecules directly interact with the electron. The spectra for the larger clusters indicate that the electron density of the excess electron is delocalized over multiple water molecules. At n ≈ 25, there is also a change in the slope of the electron VDEs (17, 18) and excited-state lifetimes (21) that was suggested to be the result of a transition between an externally to internally solvated electron (18, 21). Interestingly, infrared multiphoton dissociation results in electron detachment and water loss for n ≤ 24, whereas only water loss occurs for larger clusters (27). By comparison, a relatively abrupt change in dissociation pathways resulting from EC by Ca(H₂O)_n2⁺ occurs for clusters this size as well. The transition from the loss of an H atom and water molecules to loss of exclusively water molecules in these EC experiments is suggestive of a transition from a cluster structure where the electron interacts predominantly with just a single water molecule to one in which the electron is delocalized over many molecules with increasing cluster size.

H Atom Loss Mechanisms.

It is interesting to speculate why the presence of a metal ion in the smaller gaseous clusters catalyzes H atom loss on EC. Loss of a H atom and water molecules from the smaller reduced clusters could occur by three different mechanisms illustrated in Fig. 3. In the salt-bridge mechanism (A), a M²⁺OH⁻ and a H₃O⁺ pair may be formed by shuttling a proton from an inner- to an outer-shell water molecule. EC by the H₃O⁺ results in formation of neutral H₃O, which is marginally stable and in the excited clusters formed by EC, should spontaneously dissociate to a H atom and water; the barrier for H₃O radical dissociation (H₃O → H₂O + H) is calculated to be 0.004 eV (43), although this species can survive on the microsecond time scale when hydrated (44). Analogous salt-bridge structures to those involved in mechanism A can be stable intermediates in charge separation reactions (45). The salt bridge may be transient or its formation may be induced by a captured electron in a high-n Rydberg state. In the direct attachment mechanism (B), the electron attaches to a water molecule resulting in ejection of a H atom and shuttling of a proton from an inner to an outer-shell water molecule to form the stable M²⁺OH⁻. Dissociative electron attachment to an isolated water molecule results in the fragments carrying away the majority of the dissociation energy in the form of kinetic energy (46). Although negatively charged water clusters are stable, the presence of the metal ion could reduce the barrier to H loss via direct attachment. In the direct metal ion reduction mechanism (C), the electron directly reduces the metal ion and prompts a cascade of radical-site-initiated cleavages, resulting in the formation of M²⁺OH⁻ and the loss of a H atom from the cluster. A similar mechanism has been proposed for H atom loss from Mg(H₂O)_n⁺ clusters, in which an intracluster reaction is induced on the direct reduction of the metal ion by the delocalized electron (38).

Fig. 3.

Mechanisms for loss of a H atom and water molecules from reduced precursor nanodrops containing metal ions. (A) Salt-bridge mechanism in which a M²⁺OH⁻ and H₃O⁺ pair are formed and the electron is captured by H₃O⁺, (B) direct dissociative attachment mechanism in which the electron is captured by an outer shell water molecule resulting in H₃O radical dissociation, and (C) direct metal ion reduction followed by a radical-site-initiated intracluster reaction.

Relating Nanodrop Chemistry to the Condensed Phase.

Adiabatic REs are obtained from the average number of water molecules lost from the reduced precursors, where the sequential threshold dissociation energies of water molecules to these extensively hydrated cluster ions are derived from a discrete Thomson liquid drop model (32) and combined with the estimated translational, rotational, and vibrational energy released into the products (31). For reduced Ca(H₂O)₆₂²⁺, the energy removed for each sequential water molecule lost ranges from 9.3 to 10.3 kcal/mol. For reduced Co(NH₃)₆(H₂O)₅₈³⁺, this range is 10.0–11.3 kcal/mol. When the metal ion inside the nanodrop is reduced, the absolute reduction energy in a discrete gas-phase nanodrop can be related to that in bulk solution by using a Born solvation model, which has been done for M(NH₃)₆(H₂O)₅₅³⁺, M = Ru, Co, Os, Cr, and Ir, and Cu(H₂O)₃₂²⁺ to obtain absolute reduction enthalpies for the corresponding redox couples in the condensed phase (31). From experimental measurements of entropy in solution, free energies are obtained and by comparing these values to relative values in solution, the absolute potential of the standard hydrogen electrode can be obtained (31).

An alternative approach to relating these gas-phase measurements to thermochemical values in bulk solution is to obtain data as a function of cluster size and extrapolate these data to infinite size as done previously for measurements of electron VDEs (15). For sufficiently large clusters, where specific cluster effects, that is, “magic numbers,” are minimal, and solvation approaches that in bulk solution, the REs reported here should also progress toward bulk as n^1/3 because the solvation enthalpies are inversely proportional to the cluster radii.

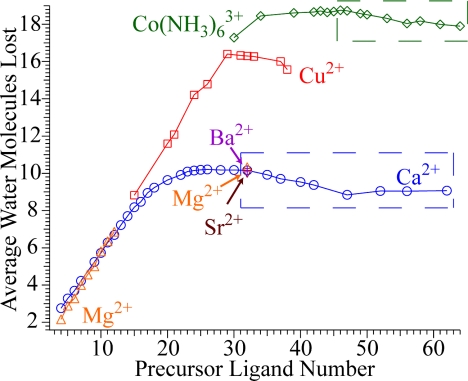
To determine the extent for which the decreasing REs for the larger clusters can be accounted for by a bulk solvation model, the average water molecule loss from the reduced nanodrops are converted to RE values as described (31), and REs for the larger-size clusters of Co(NH₃)₆(H₂O)_n3⁺ and Ca(H₂O)_n2⁺ are plotted as a function of (n + 6)^1/3 and n^1/3, respectively, over a cluster size ranging from ≈1.2 to 1.6 nm in diameter (Fig. 4). As a simplification, ammonia molecules are treated as water molecules for Co(NH₃)₆(H₂O)_n3⁺ in this analysis. For Co(NH₃)₆(H₂O)_n3⁺, there is slight curvature in these data. A linear regression over the range of n + 6 = 46–64 results in a slope of 35 eV, but the slope for the largest clusters (n + 6 = 56–64) is 22.5 eV. A slope of 18.5 eV is obtained from the Born solvation model (47) calculated with a point charge embedded in a homogenous dielectric medium. The larger slope for the experimental values suggests that other factors in addition to ion solvation contribute to the REs for the smaller clusters, but the majority of the decrease in REs with increasing cluster size >n + 6 ≈ 56 can be accounted for with the Born solvation model. This suggests that the absolute reduction potential of Co(NH₃)₆^3+/2+ may be obtained by extrapolating the REs of these and larger clusters to infinite size.

Fig. 4.

Ion–electron recombination energies obtained from the number of water molecules lost from the reduced precursor as a function of n^−1/3 for hydrated Ca²⁺ and (n + 6)^−1/3 for Co(NH₃)₆₃⁺; as a simplification, ammonia is treated as water in this analysis.

For Ca(H₂O)_n2⁺, the data are linear from n = 32 to 47, with a slope of 16.5 eV (Fig. 4). The expected slope from the Born equation is ≈11.1 eV, although this is calculated for a single point charge and may not be directly comparable with the experimental data. The linearity and slope of the data suggest that the decreasing REs with increasing droplet size in this size regime can be attributed largely to bulk solvent effects. However, the RE values are greater than the extrapolated line for n > 47, which clearly indicates that a greater amount of energy is deposited into these nanodrops than the amount expected by this solvation model at these larger sizes. This suggests that the nanodrop changes to a more stable structure in this size regime resulting in a higher RE than expected based on a single structure and a simple solvation model. Initially, Ca²⁺ is in the center of the nanodrop (6) and on EC, the electron is delocalized near the droplet surface with Ca²⁺ remaining in the center, although distortion of the nanodrops may occur to accommodate the ion pair. The deviation of the Ca(H₂O)_n2⁺ data for n = 47–62 in Fig. 4 can be explained by a change in structure from one in which the electron is delocalized near the surface of the nanodrop to one where the electron is increasingly solvated by water. Orientation of water molecules around the e⁻ would result in an increased RE than that expected by the Born solvation model extrapolation. Although the orientation of the water molecules is strongly influenced by the presence of Ca²⁺ in the nanodrop interior, this effect should decrease with increasing droplet size and orientation of water molecules by the electron should become increasingly favored, as should a more interior electron state. The observed trend in RE versus n^1/3 for the largest clusters indicates that the transition between these two structures is not complete at the largest cluster size studied. The onset of a fully solvated electron in these nanodrops should be indicated by a progressive decrease in RE as n^1/3 with even larger cluster sizes toward the bulk value for the adiabatic solvation energy of the electron.

To the extent that the reduced Ca²⁺-containing nanodrops in the size range of n = 32 to 47 form ion–electron pairs in which the electron is delocalized, an upper limit to the energy required to promote such a delocalized electron into vacuum from bulk water can be obtained by extrapolating these data over this limited size range to infinite cluster size. This is a likely upper limit because the observed slope is greater than the expected Born solvation energy slope. The calcium data in Fig. 4 are linear over this range of cluster sizes (R² = 0.998), with a y intercept of −0.6 eV, corresponding to an upper limit of + 0.6 ± 0.6 eV for forming a comparable delocalized electron in bulk water from the vacuum level. This value should be comparable to the upper limit for the conduction band edge of water, V₀, which is the energy of forming a delocalized quasi-free electron in bulk water from the vacuum level with zero kinetic energy. Despite the importance of V₀ toward understanding water band structure and the stability of the hydrated electron, its value remains controversial with reported values as low as −1.3 eV (48) to a proposed upper limit of + 1.0 eV (49), although estimates for a V₀ value closer to zero (50) appear to be more widely accepted. It is difficult to ascertain how the calcium ion in these nanodrops influences the value obtained from this extrapolation compared with bulk solution where ion effects are negligible, but some indication may be obtained by similar studies of other alkaline earth metal ions that should also form ion pairs.

Conclusions

Although this ion nanocalorimetry method is a somewhat unorthodox and indirect route to investigate electron–water interactions, there are several advantages to this approach, including the potential for high accuracy, the ability to investigate transitions from a localized to a delocalized electron, and ultimately to a fully solvated electron for sufficiently large clusters. For these latter clusters, it should be possible to obtain a direct measure of the adiabatic electron affinity of water by extrapolating these data to infinite cluster size. Unlike in aqueous solution where the lifetime of a solvated electron can be fleetingly short, the lifetime of the ion–electron pair in these experiments should extend for the lifetime of the nanodrop, which can be many seconds, depending on cluster size, making structural studies of a delocalized or solvated electron accessible by a host of methods. By investigating clusters containing other divalent alkaline earth metal ions in which the metal ion is not directly reduced, effects of the metal ion on the electron–solvent interaction energy not accounted for in a Born solvation model may be determined. Although there is still significant uncertainty about the nature of the ion–electron pair in these nanodrops, insights from theory and ion spectroscopy may provide important new structural information that would aid interpretation of these data.

For clusters containing metal ions that are directly reduced, adiabatic quantities, such as absolute reduction free energies in bulk solution, could be obtained by extrapolating the corresponding cluster data to infinite size. This could provide an alternative route to establishing both an absolute electrochemical redox scale and an absolute ion solvation energy scale that eliminates uncertainties from specific solvation models. For sufficiently large clusters, both uncertainties in energy partitioning and in water-binding energies are reduced, making it a potentially more accurate method than the method previously demonstrated (31). Extension of these measurements to significantly larger clusters would be greatly enhanced at higher magnetic field strength. Many instrumental performance features for the apparatus used in these experiments increase with the square of the magnetic field, including accessible mass range (51). By using state-of-the-art instruments with 12 T or even 15 T magnets, investigations of clusters with well over 1,000 water molecules should be possible, and should enable bridging the divide between studies of ions in isolated clusters and ions in aqueous solution.

Method

Experiments were performed by using a 2.7 T Fourier transform ion cyclotron resonance mass spectrometer (2) with the ion cell cooled to 130 K with a controlled flow of liquid N₂ (52). Hydrated ions are formed from aqueous solutions by using nanoelectrospray ionization. Electrons are produced by using a 1.0 cm-diameter heated cathode (Heatwave Labs) positioned 20 cm from the cell center and are introduced into the cell for EC experiments by pulsing the cathode housing to −1.4 V for 40–120 ms (29). A detailed description of how RE values are obtained from the average number of water molecules lost from the reduced precursor is given elsewhere (31).