Comparison of Residence Time Estimation Methods for Radioimmunotherapy Dosimetry and Treatment Planning—Monte Carlo Simulation Studies

Abstract

Estimating the residence times in tumor and normal organs is an essential part of treatment planning for radioimmunotherapy (RIT). This estimation is usually done using a conjugate view whole body scan time series and planar processing. This method has logistical and cost advantages compared to 3-D imaging methods such as Single photon emission computed tomography (SPECT), but, because it does not provide information about the 3-D distribution of activity, it is difficult to fully compensate for effects such as attenuation and background and overlapping activity. Incomplete compensation for these effects reduces the accuracy of the residence time estimates. In this work we compare residence times estimates obtained using planar methods to those from methods based on quantitative SPECT (QSPECT) reconstructions. We have previously developed QSPECT methods that provide compensation for attenuation, scatter, collimator-detector response, and partial volume effects. In this study we compared the use of residence time estimation methods using QSPECT to planar methods. The evaluation was done using the realistic NCAT phantom with organ time activities that model ¹¹¹In ibritumomab tiuxetan. Projection data were obtained using Monte Carlo simulations (MCS) that realistically model the image formation process including penetration and scatter in the collimator-detector system. These projection data were used to evaluate the accuracy of residence time estimation using a time series of QSPECT studies, a single QSPECT study combined with planar scans and the planar scans alone. The errors in the residence time estimates were <3.8%, <15%, and 2%–107% for the QSPECT, hybrid planar/QSPECT, and planar methods, respectively. The quantitative accuracy was worst for pure planar processing and best for pure QSPECT processing. Hybrid planar/QSPECT methods, where a single QSPECT study was combined with a series of planar scans, provided a large and statistically significant improvement in quantitative accuracy for most organs compared to the planar scans alone, even without sophisticated attention to background subtraction or thickness corrections in planar processing. These results indicate that hybrid planar/QSPECT methods are generally superior to pure planar methods and may be an acceptable alternative to performing a time series of QSPECT studies.

I. Introduction

Accurate organ residence time estimation is an essential part of treatment planning dosimetry for radioimmunotherapy (RIT), especially for high dose therapy. In many clinical trials of RIT agents, the cumulated organ activity has been estimated using a conjugate view whole body scan time series. The individual planar whole body scans are processed using planar quantitation methods including scatter compensation using methods such as dual energy window or triple energy window (TEW) subtraction [1], [2], attenuation compensation using the geometric mean method [3], and manual segmentation of organs in the planar projections. We term the combination of a set of these methods to be a planar processing method.

Applying a planar processing method to each set of planar images provides a time-activity curve (TAC) for each organ of interest. The organ TACs are then typically fitted with a mono-or bi-exponential curve, which is integrated to give the cumulated activity and residence time. The set of residence times and MIRD methodology [4], [5], as implemented in the software codes such as OLINDA [6], are used to estimate the absorbed dose to each organ.

The quantitative accuracy of planar processing methodology is degraded by several physical effects [7]–[9]. These include the overlap of the organ regions of interest (ROIs) with each other and with the background in the planar projection, incomplete compensation for scatter and attenuation of photons in the patient, scatter and penetration in the collimator, and partial volume (PV) effects [10].

There has been significant effort to improve the quantitative accuracy of cumulated organ activity estimates for RIT dosimetry. Koral et al., have used a hybrid planar/SPECT method to determine tumor dosimetry for ¹³¹I-tositumomab in clinical trials and showed a somewhat improved dose-response relationship for some subsets of patients in their study [11]–[13]. Quantitative SPECT (QSPECT) methods based on iterative reconstruction techniques with compensation for attenuation and scatter were used [14]–[17] for the intratherapy SPECT imaging 2–3 days after the therapy administration. Absolute quantitation calibration factors to convert reconstructed image intensities to activities were obtained from phantom experiments using various sized spheres at various depths inside a water-filled torso phantom. Tang and Hasegawa have also developed methods for improved quantitation in RIT for ¹³¹I imaging. These methods are based on iterative reconstruction with compensations for attenuation and the geometric collimator-detector response function (GCDRF) [18], [19]. They also developed template-based methods for estimating overlap in planar images and PV compensation (PVC) in SPECT [20]. These methods have been applied to a clinical study [21], but the focus of the evaluation was on estimation of tumor activity, not activity in normal organs. Ljungberg et al. have developed and validated methods for improved planar and planar/SPECT dosimetry estimation [22]–[24]. They used a deconvolution method to compensate for scatter and septal penetration. They used registered computed tomography (CT) and transmission images to do attenuation correction, and provided a method for background activity and overlapping organs correction in planar images analysis.

In this work, we used the realistic 3-D NCAT phantom [25] with organ time-activities that model the pharmacokinetics of ¹¹¹In-Zevalin. Projection data were obtained using a previously validated MCS code that realistically models the image formation process including penetration and scatter in the collimator-detector system [26], [27]. In addition, rather than evaluating activity quantitation at a single time point, the proposed methods were evaluated in terms of the accuracy and precision of residence time estimation using data from three acquisition protocols: a time series of planar scans, a time series of QSPECT scans, and a single QSPECT study combined with a planar time series. The QSPECT method has been previously developed and validated; it includes model-based compensations for attenuation, scatter, collimator-detector response, and PV effects [28]–[34]. Since we did not simulated other potential sources of errors (e.g., breathing and heart motion blur, misregistration of images at different time points), the residence time estimation accuracy and precision will depend solely on the activity estimation accuracy of the method themselves and precision due to statistical noise at each time point. The hybrid planar/SPECT method used in this study is similar to that proposed by Koral in [12]. In both, cases the time-activity curve obtained from the planar imaging is rescaled based on an activity estimate from SPECT. The major difference is that in this work we use a model-based QSPECT reconstruction that includes model-based compensation for scatter and the collimator-detector response function whereas their approach used energy window-based scatter subtraction. In their work, the focus was on the tumor dosimetry using intratherapy ¹³¹In imaging. The application in this work is estimation of organ doses for pretherapy treatment planning using ¹¹¹In imaging.

II. Materials and Methods

A. NCAT Phantom and Monte Carlo Simulation

The 3-D NCAT phantom was used to provide a realistic and flexible model of human anatomy, physiology, and pharmacokinetics. In order to study the effects of nonuniform uptake on quantitative accuracy, a version of the NCAT phantom containing airways in the lungs was used. In this model, the activity and attenuation in the airways were set to zero. The activity concentrations at time zero and the effective half-lives for activity simulated in the heart, lungs, liver, spleen, kidneys, bone marrow, blood vessels, and background were based on average values determined from six clinical ¹¹¹In-Zevalin studies. The organ volumes, total activities, and activity concentrations at time 0, as well as the half-lives and residence times, are shown in Table I.

TABLE I.

NCAT Phantom Organ Volumes, Activities, and Concentrations at Time 0, Effective Half Life, and Residence Times

Organs	Volume (cm3)	Total Activities at time 0 (MBq)	Concentration at Time 0 (kBq/cm3)	Half life (hr)	Residence time (hr)
Heart*	762	78.78	129	43.13	4.12
Lungs **	3512	79.19	28	47.24	4.54
Liver	1899	143.42	94	83.21	14.48
Kidneys	375	18.22	61	79.48	1.76
Spleen	249	18.44	93	57.48	1.29
Marrow ***	998	64.92	81	61.30	4.83
Bloodvessels	474	66.18	175	33.01	2.65
Remainder	51,732	720.00	17	65.02	56.79

^*Activities in the heart were not uniform. The activity concentration in the myocardium was 107 kBq/cm³ and in the blood pool was 130 kBq/cm³.

^**Activities in the lungs were not uniform. The activity in airways was 0. The activity concentration shown above is the average value and the volume includes airway.

^***Only bone marrow in pelvis area was modeled in this version of NCAT phantom.

A modified version of the SimSET MCS [27] code combined with an angular response function (ARF) based simulation of the interactions in the collimator and detector was used to simulate the projection data. The ARF method is based on full simulations of the collimator-detector point response function using MCNP and has been previously validated [27]. The accuracy of the SimSET/PHG and MCNP simulations in modeling the image formation of a gamma camera has been previously demonstrated in [26] and [31].

The simulations were performed using parameters appropriate for a GE Discovery VH/Hawkeye SPECT/CT system with a 2.54-cm-thick crystal and a MEGP collimator. Both ¹¹¹In photopeaks (171 and 245 keV) were simulated with the appropriate abundances. Low-noise projection images were generated in 128 transaxial and 170 axial projection bins at 120 views over 360° using a 0.442 cm projection bin size. The counts in two 14% wide energy windows centered at 171 and 245 keV were summed together. Two additional energy windows, 145.9–158.1 keV and 184.5–225.5 keV were acquired for use in TEW scatter compensation.

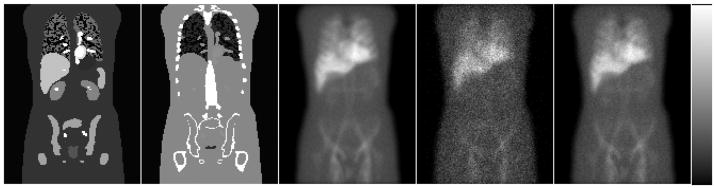
All seven major organs listed in Table I plus the background were simulated separately (total of 14.9 billion simulated photon histories) from a pixelized representation of the NCAT phantom having a pixel size of 0.221 cm. Note that each photon was analyzed for its potential contribution to each projection view, so this is equivalent to 14.9 billion histories per view in terms of the noise level, but the noise in the different views is correlated. Since the simulation method included variance reduction, the noise in the projections was much lower than from a brute force simulation using 14.9 billion simulated photons. This number of simulated photons was thus sufficient to generate low noise projections, as shown in Fig. 1.

Fig. 1.

From left to right the images are coronal slice through activity distribution, same coronal slice through attenuation map, low-noise anterior projection, the noisy anterior SPECT projection, and the noisy anterior planar projection.

The resulting organ and background projection images were scaled to represent organ activities at different time points (1, 5, 24, 72, and 144 h) based on the average organ time activity curves obtained from six patient studies and summed to form a low-noise set of projections for each time point. The scan times were assumed to be the same for both planar and SPECT scans at the five different time points. Fifty different Poisson noise realizations were simulated after scaling the low-noise projections to realistic count levels to generate SPECT projections and anterior and posterior planar images. The average of total counts in the sinogram for the 24 h SPECT projections was 1.37 × 10⁵ (approximately 1.09 times a typical clinical count level for a 30 min scan time).

To generate data simulating planar scans, we scaled the anterior and posterior projections to take into account the difference in acquisition time for the SPECT and planar scans in order to produce data corresponding to a 20 min scan time (3.1 × 10⁶ total counts in the anterior planar image at the simulated 1 h time point). We then created 50 independent Poisson noise realizations at each time point. Fig. 1 shows one coronal slice through the NCAT phantom and the corresponding attenuation map as well as the low-noise 0 h projection data, one sample noisy SPECT projection, and one sample noisy anterior planar image.

B. Planar Processing Method

For the planar processing method, the anterior and posterior images were first scatter compensated using the TEW method. In applying this method, it was assumed that the counts in the scatter window above the 245-keV photopeak were zero and the middle (184.5–225.5 keV) window served as both the lower window for the 245-keV photopeak and the upper window for the 171-keV photopeak. With this assumption, the scale factor for the lower and middle scatter windows were w₁₇₁/2w_l, and (W₁₇₁ + W₂₄₅)/2w_m respectively, where w₁₇₁, w₂₄₅, w_l, and w_m are the widths of the 171-keV photopeak, 24–keV photo-peak, lower scatter and middle scatter windows, respectively. These scale factors were derived based on applying TEW to each photopeak independently, then combining the resulting factors for the two scatter windows to reflect the summing of the data from the photopeaks into one projection dataset. Only two windows were used for the TEW scatter compensation in order to model the limitation on the number of energy windows that can be acquired on the GE Millenium VH system simulated in this study. The total geometric mean (GM) counts in the image obtained at time t after injection in the ROI corresponding to the organ i was computed using

$$\text{GM}(i,t)=\sum _{x,y\in {\text{ROI}}_i}f(x,y)\sqrt{P_A(x,y,t)\times P_P(x,y,t)}$$ (1)

where P_A(x, y, t) and Pp(x, y, t) are the counts in the scatter-compensated anterior and posterior projections, respectively, in pixel (x,y), and ROI_i is the set of pixels in the planar projection that represent the 2-D ROI defined to cover organ i. The function f(x, y) is a correction factor for object thickness.

In geometric mean attenuation compensation, object thickness correction can be performed by setting the correction factor f(x,y) equal to e^{μ (x,y)/2}, where μ(x,y) is the attenuation factor through the entire body for the given pixel. The attenuation factor can be measured by a transmission scan or using a registered CT image. Even with this thickness correction, the Geometric mean method is exact only when the activity is located at a single depth for each projection pixel. If all the activity contributing to a pixel in the projection image is assumed to reside in a single organ with constant activity, a source thickness correction can be applied. The organ thickness can be estimated from a registered CT scan. However, if there are multiple organs contributing to a pixel in the planar images, higher order corrections are needed.

To partially account for the effects of source thickness, we also used a calibration factor that converts GM counts to activity [35]. The conversion factor is based on the ratio of the total object-thickness-corrected geometric mean counts in the body in the 0–1 h image (which is obtained before the patient has voided) divided by the injected activity. Use of this method implicitly assumes that all the administered activity is still inside the patient at the time of the first planar scan, that the relative activity distribution does not change for all subsequent scans, and that the object and source thickness corrections for each organ would be the same. The estimated activity in organ i at time t, A_planar(i, t), using planar processing is

$$A_{\text{planar}}(i,t)=GM(i,t)\times \frac{A_{\text{inj}}\times e^{-{\lambda }_{\text{In}-111}\times t_{1\text{hr}}}}{GM(\text{wb},1\text{hr})}$$ (2)

where A_inj × e^{−λIn −111×t_l hr} is the total administrated activity decay corrected to the time of the 0–1 h scan, t_{1 h} The decay constant for ¹¹¹In is λ_{In − 111}.

The 2-D organ ROIs were all drawn manually based on a display that simultaneously shows and allows ROI definition on anterior, posterior, and fused anterior-posterior images. They were drawn to avoid overlap with other regions and, to some extent, overlap with underlying organs. The projections of the 3-D VOIs from true phantom configurations were also used as a guide to help in drawing the planar ROIs. For the patient studies where the true 3-D VOIs of organs are not available, the projections of manually-drawn 3-D VOIs from registered SPECT and CT slices can be used. The method used to define the planar ROIs is similar to what we do clinically: we compute the simple projection of a SPECT/CT image and manually align it with the planar images. We then project the SPECT/CT VOIs and use as a guide for drawing the planar ROIs. In the VOI projections we can see areas of overlap, which we then manually avoid in defining the planar ROIs.

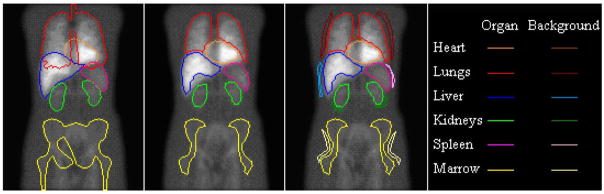
As shown in Fig. 2, the planar ROIs shown on the left image are the outlines of the 2-D projections of the 3-D true organ VOIs. These ROIs clearly demonstrate the problem of organ overlap for this phantom configuration.

Fig. 2.

Two-dimensional projections of the 3-D true organ VOIs (first image) and the manually defined planar ROIs used in Planar Method 1 (second image), and organ ROIs with their associated background ROIs (third image) used in Planar Method 2.

Table II demonstrates the percentage of organ volume that projected into each of the manually defined ROIs (as shown in the middle image of Fig. 2). These data show that the 2-D manually-defined ROIs did not overlap with other organs except for the heart and liver ROIs.

TABLE II.

Percentage of Organ 3-D Volume That Projected Into Each of the Manually Defined 2-D ROIs

Organs\ROIs	Heart ROI	Lungs ROI	Liver ROI	Kidneys ROI	Spleen ROI	Marrow ROI
Heart	90.77%	0.00%	0.18%	0.00%	0.94%	0.00%
Lungs	10.93%	73.22%	5.91%	0.00%	0.39%	0.00%
Liver	0.05%	0.00%	86.36%	0.00%	0.00%	0.00%
Kidneys	0.00%	0.00%	0.00%	89.25%	0.00%	0.00%
Spleen	0.00%	0.00%	0.00%	0.10%	91.00%	0.00%
Marrow	0.00%	0.00%	0.00%	0.00%	0.00%	36.88%

In this work, three different methods for planar processing were used. In the first method (referred to as Planar Method 1), we applied TEW scatter compensation, computed the geometric mean counts with the correction factor term equal to one, used the GM counts-to-activity conversion factor described in (2), and used the manually defined 2-D ROIs, as shown in Fig. 2. No explicit overlap and background corrections were performed.

In the second method (referred to as Planar Method 2), we applied TEW scatter compensation, object thickness correction using a projected attenuation map, and background compensation based on background ROIs using a method similar to that recommended in MIRD Pamphlet 16 [36]. In the background correction, we defined background regions for each organ (as shown in the third image of Fig. 2) on geometric mean images after converting them into activities, and subtracted the mean background activities times the background thickness factor estimated from the NCAT phantom attenuation map. The total organ activities were then estimated as the total corrected activities in each manually defined ROI divided by the fraction of the organ’s volume that projected into the organ’s ROI (the diagonals of Table II). In a clinical study, estimating the background thickness fractions would require a registered CT image. If one is not available, then another method, such as using thickness fractions obtained from a standard phantom, could be used [22]. Since this would be approximate, Planar Method 2 would likely perform better than a typical clinical planar method.

In the third method, referred to as Planar Method 3, we took advantage of the fact that each organ projection was separately simulated. We used the separate organ projections to estimate the organ activities; there was thus no overlap with other organs and background activity. This is an ideal case and no real planar method can perform better than this in terms of overlap compensations.

C. QSPECT Reconstructions

In this work, the reconstructions were performed using the iterative ordered-subsets expectation-maximization (OS-EM) algorithm [37]. Attenuation, scatter, and the collimator-detector response function (CDRF) were modeled during the iterative process using a rotation-based projector.

The true attenuation map was used for the simulation study. The simple average of the attenuation maps for the 171-keV and 245-keV photons emitted by ¹¹¹In was used in the reconstruction. Rigorous calculation of the detection-weighted average need take into account the abundance of the photons, the source depth, crystal thickness, energy window, and energy resolution [38]. According to [38] the difference of attenuation coefficient between using simple average, abundance-weighted or detection-weighted average is small (<0.3%) for the range of source depths, energy resolution, crystal thickness, and energy windows used in this work.

Scatter was modeled using the effective source scatter estimation (ESSE) method [29]. This method is exact for single scatter in a uniform object and includes approximations for nonuniform attenuators and multiple scatter. A fast implementation described in [30] was used to speed up the scatter estimation process.

The CDRF was estimated by MCS of point sources at various distances from the face of the collimator; these simulations included propagation of photons in the collimator and detector [31].

A perturbation-based geometric transfer matrix (pGTM) method was used for both “spill-in” and “spill-out” partial volume compensations [32]. In the pGTM method, the geometric transfer matrix is computed by projecting and reconstructing the original reconstructed image plus a perturbation, where the perturbation is a scaled version of the organ template, as well as the initial reconstructed image. The projection and reconstruction steps include modeling of the desired resolution degrading effects. The region response is computed as the difference between the reconstructed images with and without the perturbation. The projection, reconstruction and subtraction steps are repeated for each organ, and the resulting set of region response images is used to calculate the pGTM. The pGTM is then inverted and used to perform PVC. The perturbation process allows one to take into account the nonlinearity of the iterative reconstruction process during the partial volume compensation. A detailed description and validation of the QSPECT methods can be found in [34].

All 50 sets of noisy projection images were reconstructed using QSPECT methods (30 iterations, five angles per subset). The VOIs for the six organs studied were defined based on the true configuration in the phantom (0.221 cm pixel size). Organ total activities were estimated by summing pixel values in VOIs and scaling these sums by a calibration factor which was calculated from the measured geometric sensitivity of the imaging system. The geometric sensitivity is defined as the number of detected photons that pass through the collimator holes per emitted photon and was determined by simulating a point source in air. The QSPECT-based estimate of the activity in the ith organ at time t, A_QSPECT(i,t) for the simulations was given by

$$A_{\text{QSPECT}}(i,t)=\frac{C_{\text{QSPECT}}(i,t)\times k}{S_{\text{Geom}}}=\frac{C_{\text{QSPECT}}(i,t)\times k}{C_{\text{ptsrc}}/N_{\text{ptsrc}}}$$ (3)

where C_QSPECT (i, t) is the total reconstructed QSPECT image intensity in the 3-D VOI for the ith organ at time t, k is a constant that includes an implicit acquisition time and converts counts to the desired units of activity, S_Geom is the geometric sensitivity of the imaging system which is calculated by C_ptsrc/N_ptsrc where N_ptsrc is the number of simulated photons for the that point source and C_ptsrc is the total counts of geometrically collimated photons in the point source projection image. The factor k was determined so that count levels in the simulated projections matched those in patient projections. In the results of this paper, we computed relative errors. In computing these expressions, the factor k cancels and it did not affect those results, but did affect the activity values reported in Table I.

D. Three Residence Time Estimation Methods

Using the time series of SPECT and planar studies and the processing methods described above, ¹¹¹In organ activities were estimated using planar processing (to estimate A_planar(i, t)) or QSPECT methods (to estimate A_SPECT(i, t)) at each time point. For the simulated data, three methods, pure planar, planar/QSPECT hybrid, and pure QSPECT, were used to estimate the residence times from these series of data.

For the pure planar or QSPECT methods, the residence time was estimated using only the planar or SPECT scan data, respectively. The fraction of injected activity (FIA) in the ith organ at time t, computed using method m (i.e., planar or QSPECT), FIA^m(i, t), was computed using

$${\text{FIA}}^m(i,t)=\frac{A_m(i,t)}{A_{\mathit{inj}}}$$ (4)

where A_m (i, t) is the activity in the ith organ at time t estimated using processing method m.

To estimate the residence time, the FIA for each organ was fitted to a mono-exponential function of time of the form

$${\text{FIA}}^m(i,t)={\text{FIA}}^m(i,0)\times e^{-{\lambda }_m(i)t}$$ (5)

where λ_m(i) is the effective elimination constant (including physical and biological decay) for the ith organ obtained from fitting the data processed using method m.

Finally, the residence time for the ith organ, τ_m(i), was calculated from the fitted function using

$${\tau }_m(i)=\frac{{\text{FIA}}^m(i,0)}{{\lambda }_m(i)}.$$ (6)

For the hybrid method, one QSPECT image (from a SPECT acquisition acquired 24 h postinjection) was used to rescale the TAC obtained from the whole body planar time series as follows. The planar images were used to compute the decay constant for each organ, λ(i), in the same way as for the pure planar method, e.g., using (4)–(6). The SPECT activity in each organ, A_SPECT(i, t_SPECT), at the time of the SPECT acquisition, t_SPECT, was calculated using (3). The FIA at time 0 was then rescaled so that the planar time activity curve passed through the SPECT activity at the time of the SPECT acquisition using

$${\text{FIA}}^{\text{hybrid}}(i,0)=\frac{{\text{FIA}}^{\text{planar}}(i,0)\times {\text{FIA}}^{\text{QSPECT}}(i,t_{\text{SPECT}})}{{\text{FIA}}^{\text{planar}}(i,t_{\text{SPECT}})}$$ (7)

where FIA^hybrid(i;0) is the FIA obtained using the hybrid/SPECT method, FIA^planar(i, 0) is the FIA at 0 h obtained from the fit of the planar images, FIA^planar(i, t_SPECT) is the FIA at the time of the SPECT acquisition calculated from the fit of the planar time-activity-curve. Three hybrid methods were investigated with hybrid methods 1, 2, and 3 based on planar methods 1, 2, and 3, respectively.

III. Results

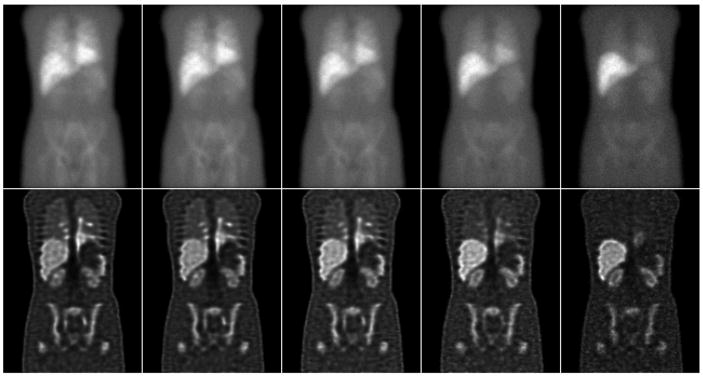
Fig. 3 shows the GM images and a sample coronal slice of reconstructed SPECT images at five different time points, illustrating the differences in relative organ uptake and the quality of the QSPECT images.

Fig. 3.

Top row (left to right) shows the average of 50 noise realizations of the geometric mean images computed from the anterior and posterior whole body scan images at times of 1, 5, 24, 72, and 144 h. Bottom row shows sample coronal slices (the same coronal slice as Fig. 1) through the images obtained by averaging 50 SPECT reconstructions of noisy projection data. The images represent acquisitions obtained at times of (left to right) 1, 5, 24, 72, and 144 h and demonstrate the quality and resolution obtained in the QSPECT images.

A comparison of the percent error in estimated organ activities (mean ± standard deviation) for the 24 h time point obtained using three planar and QSPECT methods is shown in Table III. Planar Method 1 generally overestimated the organ activities, likely due to overlap of the organ projections with those of other organs and the background, as demonstrated in Fig. 2. For a relatively isolated and large organ like the liver, this planar method worked relatively well, as might be expected. For smaller organs like the kidneys and spleen, overlapping and background activity were still important factors even when using the smaller ROIs. Planar Method 2, which used more sophisticated background compensation, gave more accurate activity estimates, especially for the lungs and kidneys where overlapping and background activity are relatively more important. However, these methods used the true 3-D organ VOIs information, and are thus upper limits on the performance in a clinical situation. Planar Method 3 provided the most accurate estimates for most organs among the three planar processing methods, but still resulted in up to 12% error, even though it has ideal (and practically unachievable) overlap and background activity compensation. The activity estimates for the QSPECT method had errors of less than 3.4% for all organs. Note that the precisions of the QSPECT and Planar methods (as measured by the relative standard deviation) were, in all cases, less than 2.3% of the mean. Statistical significances of the differences between planar and QSPECT activities were determined by computing the ensemble mean and standard deviations of the differences in the activity estimates. The alterative hypothesis (QSPECT performed better than planar methods) was then tested using a 1-tailed t-test and the differences for each organ were found to be statistically significant with all p-values less than 0.01 (except for kidneys in Planar Method 3). No multiple comparison corrections were performed.

TABLE III.

Percent Errors and Standard Deviations of Errors in 24 h Organ Activity Estimates for Planar and QSPECT Methods

Error*±Stdev (%)	Heart	Lungs	Liver	Kidneys	Spleen	Marrow
Planar Method 1 **	11.4±0.3%	91.9±0.4%	−13.3±0.2%	100.9±0.8%	80.0±0.8%	7.5±0.4%
Planar Method 2 **	5.4±0.7%	−22.2±0.4%	−3.8±0.2%	−5.0±2.3%	13.0±2.2%	−24.7±0.5%
Planar Method 3 **	7.2±0.3%	−2.4±0.2%	11.6±0.2%	−2.1±0.5%	−1.8±0.6%	−6.0±0.3%
QSPECT Method	−0.5±0.7%	−1.8±0.9%	−1.3±0.4%	−3.4±1.5%	−0.4±1.2%	2.1±0.7%

^*Calculated as (estimate activity – true activity)/true activity * 100%. Negative signs indicate underestimation compared to the true activity.

^**Methods 1, 2, and 3 are without, with approximate, and with ideal background subtraction, respectively.

Table IV shows the mean and standard deviations of the estimates of the organ half-lives obtained using the three planar and QSPECT methods (the half-life for the hybrid methods were the same as for the planar methods). Good estimates of the half-life require a good estimate of the shape of the TAC. From Table IV we see that the half-life estimates from the Planar Method 3 and QSPECT methods are within 3% of the true value for all organs, however the ideal background subtraction of the Planar Method 3 is not clinically achievable. Errors for the first two planar methods were somewhat larger, being on the order of 1 %–16% for most organs. QSPECT performed better than these two planar methods for most organs, and the differences in the half-lives were statistically significant with p-values less than 0.01 (except for lungs in Planar Method 2). However, the errors in the planar estimates of the organ half-lives were relatively small compared to the errors in estimating the organ activities. This indicates that the errors in estimating the activities did not change the shape of the time activity curve and provides a motivation for the use of the hybrid method where an activity estimate from a QSPECT acquisition is combined with the estimate of the half-life from the planar method.

TABLE IV.

Percent Errors and Standard Deviations of Errors in Organ Half-Life Estimates for Planar and QSPECT Methods

Error*±Stdev (%)	Heart	Lungs	Liver	Kidneys	Spleen	Marrow
Planar Method 1 **	9.5±0.4%	11.7±0.3%	−8.6±0.2%	−16.0±0.5%	6.4±0.5%	4.1 ±0.4%
Planar Method 2 **	3.2±1.0%	1.0±0.7%	−7.7±0.2%	−13.5±2.9%	1.5±2.0%	3.1 ±1.0%
Planar Method 3 **	−0.5±0.3%	−1.2±0.2%	−0.3±0.3%	−2.1±0.7%	−1.7±0.6%	−2.1±0.4%
QSPECT Method	−0.0±0.6%	2.9±1.8%	−1.2±0.7%	−2.1±1.4%	0.2±1.2%	0.1 ±1.0%

^*Calculated as (estimate half – life – true half – life activity)/true half – life * 100%. Negative signs indicate underestimation compared to the true half-life.

^**Methods 1, 2, and 3 are without, with approximate, and with ideal background subtraction, respectively.

For half-life estimation, if a method consistently over or under estimates an organ’s activity by a fixed multiplicative amount (i.e., spleen and marrow for Planar Method 1 and 2), the half-life estimate can be good even if there are large errors in estimating its activity at each time point. This could happen, for example, if the ROIs only encompass a fixed fraction of the organ’s activity. Also note that, even though Planar Method 2 gave good activity estimations for liver and kidneys at 24 h scan, their errors for later time points were larger. Thus, the half-life estimates were worse for these organs than for other organs with larger errors at 24 h, but more consistent error levels at the other time points.

Finally, we compared estimates of the organ residence times, as shown in Table V. For Planar Method 1, the residence time estimates were overestimated by at least 11 % for all organs except the liver, where the activity was underestimated by 19%. For Planar Method 2, the errors were smaller but still in range of −23% to 14%. For Planar Method 3, the errors were smallest among the three pure planar methods (in range of −7.6% to 11%), but still resulted in 11 % overestimation of liver residence time. For the hybrid methods and the QSPECT method, the errors were less than 15% and 4%, respectively, for all organs.

TABLE V.

Percent Errors and Standard Deviations of Errors in Organ Residence Time Estimates for Planar, Hybrid, and QSPECT Methods

Error*±Stdev(%)	Heart	Lungs	Liver	Kidneys	Spleen	Marrow
Planar Method 1 **	18.5±0.3%	107.3±0.5%	−19.1±0.2%	76.3±0.8%	88.3±0.9%	10.6±0.4%
Planar Method 2 **	7.7±0.8%	−21.4±0.5%	−9.6±0.2%	−14.2±2.4%	14.0±2.1%	−23.0±0.6%
Planar Method 3 **	6.8±0.3%	−3.3±0.2%	11.3±0.2%	−3.8±0.6%	−3.1 ±0.6%	−7.6±0.3%
Hybrid Method 1 **	5.8±0.3%	6.1±0.2%	−8.0±0.2%	−15.3±0.4%	4.2±0.5%	5.2±0.4%
Hybrid Method 2 **	1.7±0.8%	−0.8±0.6%	−7.2±0.2%	−12.8±2.5%	0.5±1.8%	4.5±0.8%
Hybrid Method 3 **	−0.8±0.3%	−2.7±0.2%	−1.6±0.2%	−5.1±0.6%	−1.7±0.6%	0.4±0.3%
QSPECT Method	−0.9±0.6%	−0.2±1.4%	−1.2±0.5%	−3.8±1.5%	−0.7±1.2%	1.9±0.9%

^*Calculated by (estimate – true)/true * 100%. Negative signs indicate underestimation compared to the true.

^**Methods 1,2, and 3 are without, with approximate, and with ideal background subtraction, respectively.

The differences in residence time for each pair of methods were tested for statistical significance as described above. In all cases, the hybrid methods performed better than their corresponding planar methods for all organs, and the differences were all statistically significant (p < 0.01). Hybrid Method 1 performed better than Planar Method 2 for all organs except for the kidneys, but did not require the sophisticated background subtraction and object thickness correction. These differences were also statistically significant (p < 0.01). The QSPECT method performed better than all three hybrid methods for all organs (p < 0.01) except for the spleen, where Hybrid Method 2 was slightly better, and the heart and marrow, where Hybrid Method 3 was slightly better.

IV Discussion

In this work, a simulation experiment using a realistic anatomical phantom, ¹¹¹In organ time-activity curves based on ¹¹¹In ibritumomab tiuxetan patient data, and Monte Carlo simulated projection data including modeling of interactions in the collimator-detector system were used to evaluate residence time estimation methods based on a series of conjugate view whole body scans without (pure planar) and with QSPECT (hybrid planar) and a series of QSPECT scans. The acquisition of quantitative SPECT images at each time point gave the most accurate estimates of organ residence times. For the planar and hybrid methods, three planar quantitation methods were used with Planar Method 2 (also used with Hybrid Method 2) having more realistic object thickness, overlap and background corrections. However, hybrid planar/SPECT methods gave much more accurate estimates than those obtained from a series of planar scans, and slightly worse than those obtained from a series of SPECT scans with the advantage that they required the acquisition, reconstruction, and analysis of a SPECT image at only a single time point. The hybrid methods performed well because the accuracy of estimating the half life of the activity in an organ using both planar methods was relatively good. This indicates that the shape of the time activity curve was estimated relatively well by the series of planar scans. However, the planar methods, in general, provided poor estimates of the residence time. This is because the estimates of the FIA at the time of injection were very poor. In other words, while the shape of the TAC was well estimated, its absolute scale was not. Whether this observation holds in general will depend on patient anatomy, the differences in half-life for the organ and overlapping regions as well as the relative activities in the organ of interest and other tissues that overlap in the planar ROIs.

There are several reasons why the planar estimates of the activity were likely not very good. A major problem was overlap of organ ROIs with activity in other organs and with activity in the background. In the first planar method, we used a relatively simple method of handling organ overlap: ROIs were drawn smaller than the actual organ in order to avoid regions of overlap. While this is partially effective in reducing organ overlap, it does result in missing some activity that is actually in the organs. In the second method, a more sophisticated method was used to reduce the organ overlap and effects of background activities. However, these methods often involve subjective estimates of background and organ thickness that may increase the variability of accuracy of planar activity estimates. Please note that for clinical studies without registered SPECT or CT images, it would be difficult to gain the 3-D information such as those listed in Table II. Thus a clinical implementation of the second planar method would most likely perform worse than the results presented in this simulation study. The third planar method had ideal overlap and background activity compensation. The estimates obtained with this method are thus substantially more accurate than with the first two planar methods for most organs, but this is the ideal case and no real method can perform better than this in terms of organ overlap and background activity compensation.

Another factor limiting the accuracy of the planar activity estimates is the use of geometric mean attenuation compensation. In the first planar method, source and object thickness corrections were not explicitly applied. The effects were approximately taken into account through the use of a geometric-mean count to activity conversion factor derived from the 0–1 h image. In the second planar method, with the object thickness corrections, the errors in the planar activity estimates were greatly reduced for lung and kidneys. However, object thickness correction is not always performed clinically due to the extra time and difficulty required to obtain the requisite transmission images or to obtain registered CT images. Similarly, source thickness correction requires estimation of organ thickness in each pixel in the organ’s 2-D planar ROI and is usually not performed. In addition, even with both organ and source thickness corrections, geometric mean attenuation compensation is only approximate. The errors obtained with the third planar method (with ideal overlap compensation) illustrate the limitation of the geometric mean method. However, a full investigation of the factors limiting accuracy in the planar method was beyond the scope of the present study.

It might be argued that implementation of the TEW scatter compensation method used in this study, which made use of only two additional energy windows, was somewhat crude. More accurate scatter compensation might be obtained using two smaller windows in place of the wide intermediate (184.5–225.5 keV) energy window. However, using narrow windows would reduce the precision of the scatter estimates. The reason that we used only two scatter energy windows was to model the limitation in the number of energy windows of our GE Millennium VG and VH systems. Newer systems may not have this limitation. To get a rough idea of the potential impact of using a wide energy window, we used Monte Carlo simulation and physical experiments to generate energy spectra for both a point source and simple phantom (hot sphere in a cold elliptical phantom) [39]. In both cases, we found the energy spectrum to be very flat in the range (184–225 keV). While this provides some validation for the use of the wide energy window, the window was clearly not optimized and there is the potential to improve the planar method by using more optimal energy windows in the TEW scatter compensation.

One interesting result from this study is that combining less sophisticated planar quantitation, i.e., using Hybrid Method 1, which is based on Planar Method 1, resulted in estimates of the residence time that were as good as, and usually better than, the estimates obtained with Planar Method 2, where sophisticated attention was paid to background subtraction and thickness corrections. Recall that Planar Method 1 did not explicitly use either object or source thickness corrections or background subtraction. This indicates that a single QSPECT study can improve planar quantitation as least as much as very sophisticated planar quantitation at every time point.

While the accuracy of the planar methods can be improved by the use of improved overlap and attenuation compensation, these require additional imaging time to acquire transmission scans, user effort and skill in drawing the ROIs. However, the hybrid method, with the acquisition of QSPECT images at only a single time point, provided accuracy approaching that of the pure QSPECT method even without object thickness, background and overlap corrections. In addition, the SPECT/CT acquisition provided the data needed to perform organ volume compensation which would not be available for the planar method without the use of an additional CT study. The hybrid method has the advantage, compared to the pure QSPECT method, in that it requires significantly fewer SPECT acquisitions. Thus, the hybrid method seems a viable alternative for clinical studies and was thus adopted for an ongoing dose escalation study to determine the MTD for myeloablative Y-90 ibritumomab tiuxetan therapy [40].

Another interesting aspect of this study is that the precision, for the vast majority of cases, was better than the accuracy, even for the images representing the longest times postinjection. The loss of precision, due to the statistical noise in the projection data, was less than 1.5% for all organs and methods. This indicates that it may be possible to reduce the acquisition time below the levels simulated in this study without major increases in error of activity estimates for a single patient.

The overall purpose of this study was to investigate the precision and accuracy of quantitative imaging methods for residence time estimation. We can summarize the rankings of the various methods in terms of residence time estimation as follows: QSPECT ≈ Hybrid Method 3 > Hybrid Method 2> Hybrid Method 1 ≈ Planar Method 3> Planar Method 2 ≫ Planar Method 1. In this ranking, > indicates “better than,” ≈ indicates “about the same as” and ≫ indicates “much better than.” However, it should be kept in mind that these studies did not model clinical problems such as intraorgan variation in activity and bio-kinetics, intrapatient variation in organ size and uptake, misregistration and misdefinition of ROIs and VOIs, and limitation of field-of-view for the SPECT studies. These effects will clearly impact the accuracy and precision of the methods. We are currently engaged in studies to investigate the relative importance of these effects.

V. Conclusion

This paper presents the results of a simulation study used to investigate the accuracy of organ residence time estimates for myeloablative ¹¹¹ In/90 Y ibritumomab tiuxetan therapy. In particular, differences between pure planar, hybrid planar/QSPECT, and pure QSPECT methods were evaluated. The quantitative accuracy was worst for pure planar processing and best for pure QSPECT processing. Hybrid planar/QSPECT methods, where a single QSPECT study was combined with a series of planar scans, provided a large and statistically significant improvement in quantitative accuracy for most organs compared to the planar scans alone, even without sophisticated attention to background subtraction or thickness corrections in planar processing. These results indicate that hybrid planar/QSPECT methods are generally superior to pure planar methods and may be an acceptable alternative to performing a time series of QSPECT studies.