Theoretical Study of Beloussov's Hyper-Restoration Hypothesis for Mechanical Regulation of Morphogenesis

Abstract

Computational models were used to explore the idea that morphogenesis is regulated, in part, by feedback from mechanical stress according to Beloussov's Hyper-restoration (HR) Hypothesis. According to this hypothesis, active tissue responses to stress perturbations restore, but overshoot, the original (target) stress. To capture this behavior, the rate of growth or contraction is assumed to depend on the difference between the current and target stresses. Stress overshoot is obtained by letting the target stress change at a rate proportional to the same stress difference. The feasibility of the HR Hypothesis is illustrated by models for stretching of epithelia, cylindrical bending of plates, invagination of cylindrical and spherical shells, and early amphibian development. In each case, an initial perturbation leads to an active mechanical response that changes the form of the tissue. The results show that some morphogenetic processes can be entirely self-driven by HR responses once they are initiated (possibly by genetic activity). Other processes, however, may require secondary mechanisms or perturbations to proceed to completion.

1 Introduction

Embryogenesis involves a carefully coordinated series of morphogenetic events, which are carried out by a relatively limited number of basic cellular processes, including migration, multiplication, and the stretching and folding of epithelia (cell sheets). These events are regulated by a dynamic interaction between genetic and environmental factors (chemical and mechanical), with adjustments being made continually through feedback mechanisms. The nature of this interaction remains a central question of developmental biology.

The developmental biologist L.V. Beloussov has postulated that mechanical stress plays a key role in regulating morphogenesis. Based on more than three decades of observations and experiments on embryos, he has proposed the following Hyper-restoration (HR) Hypothesis (Beloussov, 1998; Beloussov et al., 1994; Beloussov and Grabovsky, 2006):

Whenever a change is produced in the amount of local stress applied to a cell or local region of tissue, the cells or tissue will respond by actively generating forces directed toward the restoration of the initial stress value, but as a rule overshooting it. Whenever such changes in stress are unevenly distributed or are anisotropic, then the responses induced will be directed toward reducing (with an overshoot) whichever deviations were greatest.¹

In other words, embryonic tissues respond to load perturbations by actively generating forces that return the current stress σ toward (but overshooting) a target stress σ₀. The overshoot leads to additional perturbations, which induce a new response, and so on until the proper form is created. This idea suggests that embryos are capable of a certain amount of self-assembly, possibly governed by a set of construction rules or morphogenetic laws.

While some attempts have been made to formulate the HR Hypothesis in quantitative terms (Belintsev et al., 1987; Beloussov and Grabovsky, 2006; Beloussov and Grabovsky, 2007), most of the supporting evidence is qualitative in nature. For example, Beloussov and colleagues have used tissue dissection to map regions of tension and compression in embryos (Beloussov et al., 1975; Beloussov et al., 1990; Beloussov et al., 2000; Beloussov et al., 2006; Beloussov, 1998; Beloussov et al., 1994).² These researchers also have proposed qualitative models that illustrate how a series of HR responses can, in theory, drive a number of basic morphogenetic processes, including gastrulation, neurulation, and convergent extension (Beloussov, 1998; Beloussov et al., 1994). While these models seem plausible, intuition can be misleading in highly nonlinear systems such as the embryo (as will be demonstrated). Hence, there is need to test whether such models are consistent with physical laws.

The purpose of the present study is to explore whether morphogenesis based on the HR Hypothesis is consistent with the fundamental principles of mechanics. The HR Hypothesis is formulated within a continuum mechanics framework and applied to mathematical models for several representative problems in epithelial morphogenesis, including stretching and bending of sheets, invagination of cylindrical and spherical shells, and formation of the global shape of the early embryo. Limitations of the HR concept and the importance of the stress overshoot are illustrated. Our models show that the HR response is sensitive to inhomogeneities in system parameters, which, we speculate, may be controlled by regional genetic activity. Comparisons between numerical and experimental results show mixed success in the ability of the HR Hypothesis to capture actual morphogenetic behavior.

2 Methods

Physical consequences of the HR hypothesis are illustrated through a series of examples taken from epithelial morphogenesis. To fix ideas, we first describe the analytical method used to model growth and contraction in one dimension. Then, the method used to solve each problem is detailed, along with any needed extensions of the 1-D analysis.

It is important to realize that epithelia use several mechanisms to actively change their dimensions. For example, they can shorten via cell intercalation,³ programmed cell death (apoptosis), or cytoskeletal (CSK) contraction. In the embryo, CSK contraction is the most common mechanism for shortening. For convenience, we do not distinguish between specific processes and herein refer to any type of active lengthening as “growth” and any type of active shortening as “contraction.”

One-dimensional Theory for Morphomechanics

Volumetric growth is modeled using the theory of Rodriguez et al. (1994), where further details can be found. Briefly, the total deformation of an infinitesimal material element is decomposed into a non-stress-generating growth relative to the current zero-stress configuration and a stress-generating elastic deformation due to loading and to enforcing geometric compatibility between growing elements. For a pseudoelastic bar, the decomposition of the total stretch ratios in Cartesian (x, y, z) coordinates can be written in the form

$${\lambda }_x={\lambda }_{ex}{\lambda }_{gx},{\lambda }_y={\lambda }_{ey}{\lambda }_{gy},{\lambda }_z={\lambda }_{ez}{\lambda }_{gz}$$ (1)

where the λ_gi (i = x, y, z) are growth stretch ratios relative to the reference zero-stress state (e.g., at t = 0), and the λ_ei are elastic stretch ratios (due to stress) relative to the current zero-stress state. With x being the axial direction, we do not consider transverse growth of the bar and set λ_gy = λ_gz = 1. Moreover, contraction is simulated by negative growth. According to the terminology discussed above, therefore, growth and contraction are given by λ_gi > 1 and λ_gi < 1, respectively.

In this theory, stress depends only on the elastic deformation, which, for an incompressible bar, is constrained by the condition J_e = λ_exλ_eyλ_ez = 1. The constitutive relation for Cauchy stress is (Taber, 2001)

$${\sigma }_i=\frac{{\lambda }_{ei}}{J_e}\frac{\partial W_e}{\partial {\lambda }_{ei}}-p$$ (2)

where W_e (λ_ei) is the strain-energy density (SED) function and p is a Lagrange multiplier, which is needed to enforce isovolumic elastic deformation. (Summation is not implied for repeated subscripts.) Material testing has indicated that the stress-strain response of embryonic epithelia is relatively linear for moderately large stretching (Zamir and Taber, 2004; Wiebe and Brodland, 2005). In the present study, therefore, we assume neo-Hookean behavior with

$$W_e=C({\lambda }_{ex}^2+{\lambda }_{ey}^2+{\lambda }_{ez}^2-3)$$ (3)

where C is a material constant. Setting σ_y = σ_z = 0 provides p, and the axial stress in the bar becomes

$${\sigma }_x=2C({\lambda }_{ex}^2-{\lambda }_{ex}^{-1}).$$ (4)

Morphomechanical Laws in One Dimension

The specific mechanical stimulus for growth is a subject of ongoing debate (Humphrey, 2001; Taber, 1995; Cowin, 1996; Omens, 1998). Here, we assume that the local one-dimensional growth/contractile response (in the x-direction) depends on stress through the morphomechanical law

$$D_{gx}=\frac{{\dot{\lambda }}_{gx}}{{\lambda }_{gx}}=a({\sigma }_x-{\sigma }_0)$$ (5)

where D_gx is the growth rate per unit length of an element in the current zero-stress state, σ₀ is the target (homeostatic) stress, and a is a positive constant. According to this equation, the tissue lengthens when σ_x > σ₀ and shortens when σ_x < σ₀, consistent with experimental observations of Beloussov (1998). Hence, if an epithelium is stretched and held at a fixed length, it grows to reduce the elevated stress back toward the value of the target stress. If it is shortened and held, the cells contract, increasing the stress back toward σ₀.

In his writings, Beloussov emphasizes the importance of the observed overshoot of target stress following mechanical perturbation (Beloussov, 1998). One possible cause of such an overshoot is a delay in the active cellular response. In this case, however, either the stress would eventually return to the original value of σ₀ after some oscillations, or sustained oscillations would occur (Ramasubramanian and Taber, 2007). Any “permanent” changes in morphology likely would be quite limited. Recently, Ramasubramanian et al. (2007) showed that substantial permanent changes in form can be induced by specifying regional changes in target stress and suggested that genes may set its value. Here, we consider another possibility: the value of σ₀ itself depends on the current level of stress, evolving through the relation

$${\dot{\sigma }}_0=-b({\sigma }_x-{\sigma }_0)$$ (6)

where b is a positive constant. The sign in front of b is chosen so that σ₀ increases when σ_x falls below σ₀. According to Eq. (5), therefore, the tissue will respond to a drop in stress by contracting to increase σ to a value above the original value of σ₀, and vice versa.

Analysis of Bars in Series and Parallel

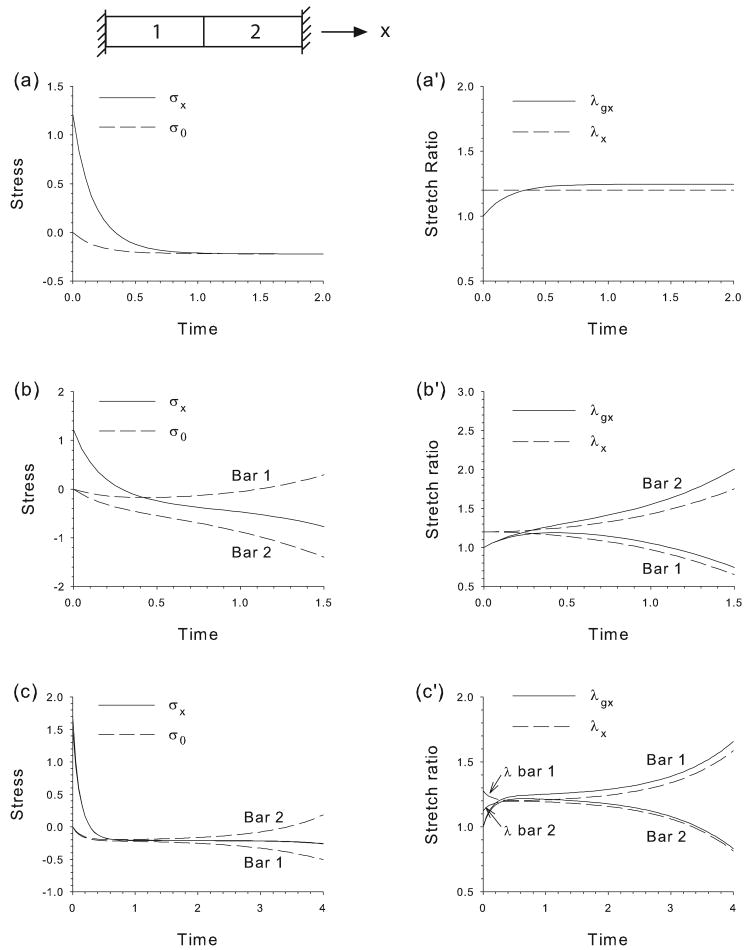
For two bars of equal initial length connected in series (Fig. 1), geometrical and equilibrium considerations give λ₁ + λ₂ = 2λ₀ and F₁ = F₂, where λ_n is the total stretch ratio and F_n the axial force in bar n, and λ₀ is the combined (average) stretch ratio of the bars. Since there is no transverse growth, changes in cross-sectional area are due solely to the elastic deformation. For an incompressible bar, the undeformed area A₀ and deformed area A are related by A = A₀λ_eyλ_ez = A₀/λ_ex. Therefore, the equilibrium condition becomes

Figure 1.

Stretching of bars in series. Bars grow/contract according to the HR Hypothesis after being stretched and held at a fixed total length. Temporal plots of axial stress (σ_x), target stress (σ₀), growth stretch ratio (λ_gx), and total stretch ratio (λ_x) are shown for three cases. (a,a′) Both bars have same properties. Bars grow to new equilibrium as initial tension is converted to compression, illustrating hyper-restoration (HR) of stress. (b,b′) HR response is faster in bar 2 (b₁ = 1, b₂ = 2). Bar 1 shortens and bar 2 lengthens without bound. (c,c′) Bar 2 is stiffer than bar 1 (C₁ = 1, C₂ = 2). Bar 1 lengthens and bar 2 shortens without bound.

$${\sigma }_1/{\lambda }_{e1}={\sigma }_2/{\lambda }_{e2}$$ (7)

where σ_n and λ_en are axial Cauchy stresses and elastic stretch ratios, respectively, in bar n.

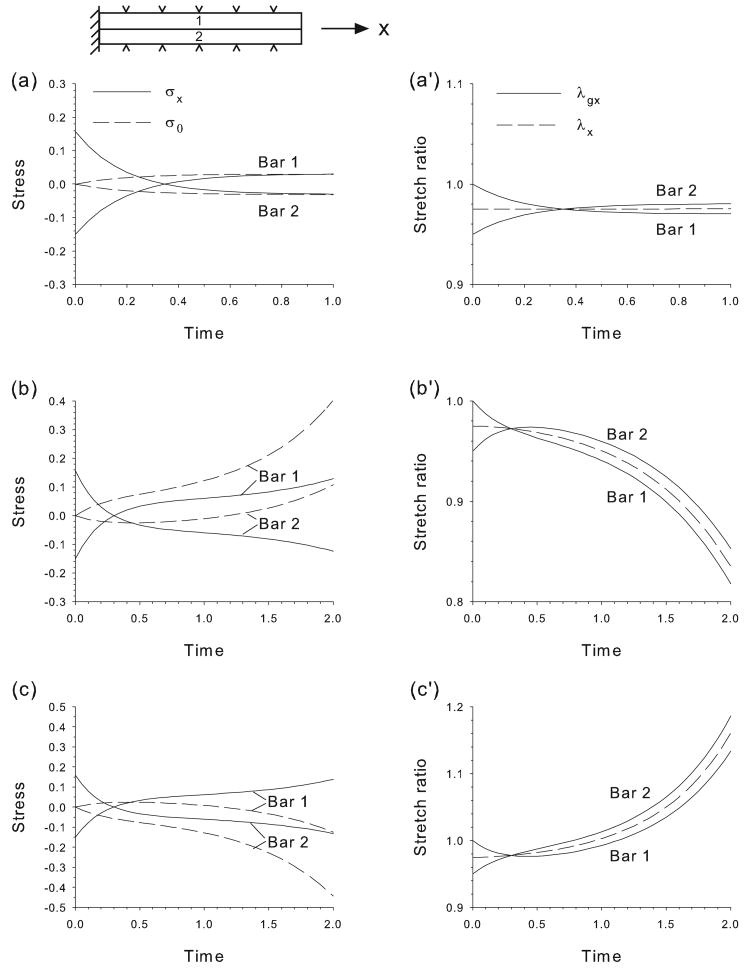
We also consider two bars connected in parallel, with bending prevented by roller supports along the lateral surfaces (Fig. 2). For this problem, λ₁ = λ₂ and σ₁/λ_e1 = −σ₂/λ_e2 (1-D approximation). For simplicity, the transverse stresses applied by the rollers are ignored as small in comparison with the axial stresses.

Figure 2.

Stretching of bars in parallel. Bars grow/contract according to the HR Hypothesis after initial 5% contraction of bar 2. Temporal plots of axial stress (σ_x), target stress (σ₀), growth stretch ratio (λ_gx), and total stretch ratio (λ_x) are shown for three cases. (a,a′) Both bars have same properties. Bar 1 contracts and bar 2 grows until new equilibrium length is established. (b,b′) HR response is faster in bar 1 (b₁ = 2, b₂ = 1). Both bars contract without bound. (c,c′) HR response is faster in bar 2 (b₁ = 1, b₂ = 2). Both bars lengthen without bound.

For both problems, the governing equations were reduced to a single algebraic equation to solve for λ_e1, once the growth stretch ratios λ_g1 and λ_g2 were known. In the computations, the initial values of the λ_gn were set to unity, and the stresses were computed immediately following a prescribed perturbation at t = 0. Then, finite-difference integration of Eqs. (5) and (6) yielded the λ_gn and σ₀ for the next time step, the stresses were updated, and so on. A MATLAB program provided the solution, with the routine fzero used to find λ_e1 at each time step.

Analysis of Other Models

All other problems (bending of plates, invagination of shells, development of amphibian embryo) were solved using the finite element program COMSOL Multiphysics (v 3.3; Comsol, Inc.). This code allows access to the governing equations, which were modified to include growth via the three-dimensional analog of Eq. (1), i.e.,

$$\text{F}={\text{F}}_e\cdot {\text{F}}_g$$ (8)

where F is the total deformation gradient tensor, F_g is the growth tensor, and F_e is the elastic deformation gradient tensor. In this paper, we assume that growth occurs along three orthogonal directions given by the unit vectors e₁, e₂, and e₃ relative to the initial geometry and take

$${\text{F}}_g={\lambda }_{g1}{\text{e}}_1{\text{e}}_1+{\lambda }_{g2}{\text{e}}_2{\text{e}}_2+{\lambda }_{g3}{\text{e}}_3{\text{e}}_3.$$ (9)

Growth laws for the λ_gi are included in COMSOL as supplementary differential equations to be solved along with the equations of solid mechanics. Further details of the analysis relevant for implementation in COMSOL are given in Appendix A. More complete discussions of the general theory for growth can be found elsewhere (Rodriguez et al., 1994).

In the multidimensional models, growth was assumed to occur in specified directions, with the morphomechanical laws for each direction taken in the forms of Eqs. (5) and (6). For cylindrical bending of plates, the analysis is plane strain, and growth was included in the x-direction only. A similar analysis was used for invagination of cylindrical shells, with only circumferential growth included (θ-direction). For invagination of spherical shells, the deformation is axisymmetric with growth occurring in both the circumferential (θ) and meridional (φ) directions, i.e.,

$$\begin{array}{ll}{D}_{g\theta }=\frac{{\dot{\lambda }}_{g\theta }}{{\lambda }_{g\theta }}=a_{\theta }({\sigma }_{\theta }-{\sigma }_{0\theta }),\hfill & D_{g\phi }=\frac{{\dot{\lambda }}_{g\phi }}{{\lambda }_{g\phi }}=a_{\phi }({\sigma }_{\phi }-{\sigma }_{0\phi })\hfill \\ {\dot{\sigma }}_{0\theta }=-b_{\theta }({\sigma }_{\theta }-{\sigma }_{0\theta }),\hfill & {\dot{\sigma }}_{0\phi }=-b_{\phi }({\sigma }_{\phi }-{\sigma }_{0\phi })\hfill \end{array}$$ (10)

Relations for the amphibian embryo are discussed later. In all problems, appropriate symmetry conditions were used to reduce computation time.

One difficulty in the numerical implementation of stress-dependent growth is that small errors in stress can build into large errors as morphomechanical laws are integrated. This is particularly true for incompressible or nearly incompressible materials, which are notoriously problematic from a numerical viewpoint. To reduce these errors, we considered the tissue as slightly compressible in all finite-element problems, with the SED function taken in the modified neo-Hookean form

$$W_e=C({\overline{I}}_1-3)+\kappa {(J_e-1)}^2/2$$ (11)

where C is a material constant, κ is the bulk modulus, J_e = det F_e, and ${\overline{I}}_1=J_e^{-2/3}\text{tr}{\text{C}}_e$ is a modified first invariant of the right Cauchy-Green deformation tensor, ${\text{C}}_e={\text{F}}_e^T\cdot {\text{F}}_e$. We checked the effects of this assumption by running the models with different bulk moduli. In all cases, the results changed slightly quantitatively but were similar qualitatively, so the effects on the present qualitative study should not be significant.

To model an internal fluid in the shell problems, an auxiliary weak constraint condition was included to hold the cavity volume constant. In this formulation, the fluid pressure was represented by a Lagrange multiplier.

3 Results

The main purpose of this paper is to investigate the behavior of epithelia governed by the HR Hypothesis and the fundamental principles of mechanics. The present study is qualitative in nature. Thus, physical units are immaterial, and we take C = a = b = 1 (and κ = 100) in all regions of all models, unless stated otherwise. In addition, for simplicity, all models begin with zero residual stress, and the initial value of the target stress is set to zero. Hence, the models are initially in a stress-free homeostatic state to be perturbed at t = 0.

Because the results from even these relatively simple models can be relatively complex and not always intuitive, specific mechanisms are described below in sometimes unabashed detail. Comparisons to experimental data also are discussed below. For readers who want only an overview, the main results are summarized at the end of each of the following subsections, and the general behavior of the models can be gleaned by studying the figures and accompanying captions.

Bars in Series

To illustrate some basic consequences of the HR Hypothesis, we consider the response of two bars in series that are stretched instantaneously at t = 0 and held at λ₀ = 1.2. Both bars then grow and contract according to Eqs. (5) and (6). Results are shown for three cases (Fig. 1).

In the first case, both bars have identical properties (Fig. 1a,a′), i.e., this is the special case of a single bar. The initial tension induces the target stress to become compressive (Fig. 1a), and the bars respond by growing longer relative to their zero-stress state (λ_gx > 1, Fig. 1a′), thereby lowering the stress. Growth ceases as σ_x → σ₀. The key point here is that the initial tension is transformed into compression, illustrating overshoot of the original target stress of σ₀ = 0, a major tenet of the HR Hypothesis.

Once a new equilibrium is achieved in the above example, continued changes in form await a new perturbation, or possibly a new chemical or molecular signal. Things can change dramatically, however, when the bars have different properties. For example, consider the problem in which the HR response is faster in bar 2 [b₁ = 1 and b₂ = 2 in Eq. (6)]. In this case, the target stress in bar 2 drops below that in bar 1 (Fig. 1b). Both bars then try to meet their individual target stresses, but this is not possible, as equilibrium demands that both bars carry the same stress. Eventually, the stress comes to lie between the two target stresses, with bar 1 contracting (λ·_g < 0) and bar 2 growing (λ·_g > 0) (Fig. 1b′). A new morphogenetic equilibrium is never attained, as bar 1 continues to shorten while bar 2 lengthens to create a simple pattern.

A similar response occurs when the bars have different stiffnesses but the same morphogenetic parameters. Here, we consider the problem where bar 2 is twice as stiff as bar 1 (C₁ = 1, C₂ = 2). When loaded, bar 1 stretches or compresses more than bar 2, and therefore undergoes a greater change in cross-sectional area. Because the axial force must be the same in both bars, the Cauchy stress in bar 1 always is slightly above that in bar 2 (in tension or compression), and integrating Eq. (6) leads to diverging target stresses, one on either side of the (slightly different) stresses in the bars, as in the previous problem (Fig. 1c). Again, a new morphogenetic equilibrium is never reached, as the more compliant bar 1 lengthens indefinitely while bar 2 shortens (Fig. 1c′).

In summary, if two bars in series have different morphogenetic or mechanical properties, the HR response can produce pattern with one bar lengthening while the other shortens without bound. If the bars have the same properties, however, a new morphogenetic equilibrium is achieved.

Bars in Parallel

The early embryo contains three epithelia (germs layers) that spread and slide relative to each other while being constrained initially to a smooth surface (Gilbert, 2003). To examine the basic HR behavior of such a system, we consider the stretching of two bars in parallel that undergo uniaxial deformation without bending. Here, we assume that the bars are “glued” together (no slippage), with the left end of the structure being fixed and the right end free. The initial perturbation is a 5% contraction of bar 2, i.e., λ_g2(0) = 0.95, after which both bars grow and contract according to Eqs. (5) and (6). Again, results are shown for three cases (Fig. 2).

First, we consider the case where all parameters are the same for both bars. Initially, the contraction generates tension in bar 2 and equal compression in bar 1 (Fig. 2a). Consequently, the HR response sends the target stresses to tension in bar 1 and compression in bar 2. Bar 1 then contracts while bar 2 grows (on top of the initial contraction, Fig. 2a′), bringing the stress in each bar toward their corresponding values of σ₀. The system eventually reaches a new morphogenetic equilibrium in which the bars are shorter by an amount equal to half of the initial contraction in bar 2.

If the bars have different stiffnesses, the behavior is similar. However, if the HR response rates differ, both bars grow or contract together without bound. For example, when bar 1 responds faster (b₁ = 2, b₂ = 1), the contraction of bar 1 dominates the initial growth response of bar 2, and the bars begin to contract together (Fig. 2b,b′). The opposite occurs if the HR response of bar 2 is faster (b₁ = 1, b₂ = 2), as both bars eventually grow longer without bound (Fig. 2c,c′).

In summary, if the growth/contraction rates of two bars in parallel differ, the HR response to mechanical perturbation can induce unbounded lengthening or shortening of the bars. If the bars have the same properties, however, a new morphogenetic equilibrium is achieved.

Bending of Bilayered Plates

Epithelial bending plays a prominent role in a number of morphogenetic processes, including neurulation, cardiogenesis, and foregut formation. This section considers cylindrical bending of rectangular plates composed of two layers. The left end of the plate is fixed, the right end is free to move, and the initial perturbation is either an external load or contraction of one layer.

First, we consider the response of a uniform plate, i.e., both layers have the same properties (Fig. 3a–d). The plate is subjected to a temporary bending moment, given by applying equal and opposite forces to a relatively rigid block attached at the right end (Fig. 3). In this example, the perturbing forces change parabolically in time from zero at t = 0 to a peak at t = 0.1 and back to zero for t ≥ 0.2. Both layers grow or contract according to Eqs. (5) and (6) for all t ≥ 0. The amount of bending is quantified by the normalized curvature near the center of the plate (see Appendix B).

Figure 3.

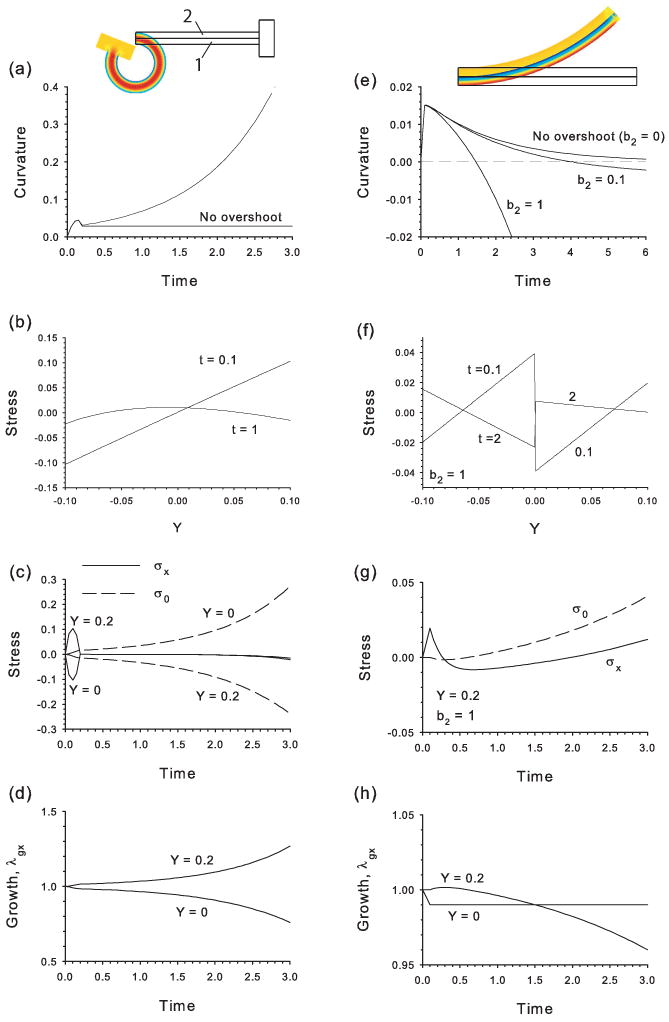
Cylindrical bending of biayered cantilever plate. Layers grow/contract according to the HR Hypothesis after plate is perturbed by temporary bending moment (a–d) or contraction of lower layer (e–h). (a,e) Plate curvature versus time (positive curvature = downward bending). (b,f) Bending stress distributions across beam thickness at center of beam. (c,g) Stress at bottom of plate (Y = 0) and top of plate (Y = 0.2) as function of time. (d,h) Growth stretch ratio at bottom of plate (Y = 0) and top of plate (Y = 0.2) as function of time. Overshoot of target stress can lead to unbounded bending (see text for discussion). The figures show beams at relatively late times, with thin black lines indicating undeformed geometry.

If there is no stress overshoot (b₁ = b₂ = 0), then the bending stress returns to zero, thereby matching the target stress (σ₀ = 0), immediately after the load is removed. Growth has occurred before that time, however, and the beam remains bent in a new homeostatic configuration (Fig. 3a). (Note that downward bending corresponds to positive curvature.) In contrast, stress overshoot (b₁ = b₂ = 1) produces renewed and unbounded bending after load removal, behavior that can be explained by observing how σ_x, σ₀, and λ_gx evolve.

It is important first to note that the bending stress distribution across the plate thickness changes from nearly linear to roughly parabolic when the applied load is removed (Fig. 3b). This reflects the equilibrium requirements of zero axial force and bending moment in the absence of external loads. Moreover, the stresses are nearly equal at the lower and upper surfaces (Y = 0 and Y = 0.2, respectively).

To explain the continued bending, we examine the temporal changes in σ_x and σ₀ (Fig. 3c). The initial perturbation causes compression at Y = 0 and tension at Y = 0.2, inducing target stresses of opposite signs to develop at these locations. In response, the plate contracts at Y = 0 and grows at Y = 0.2 (Fig. 3d), causing a resumption of downward bending after the load is removed. The bending continues indefinitely (Fig. 3a), because the equilibrium constraints discussed above keep the stresses at the top and bottom of the beam nearly equal, thereby preventing them from approaching their diverging targets. These results illustrate the conceptual complexity of the bending problem.

Next, we consider a problem in which contraction of the lower layer provides the initial stimulus (Fig. 3e–h), which bends the beam downward (positive curvature, Fig. 3e). The morphogenetic response initially is turned off, and the lower layer contracts gradually by 1% (to λ_gx = 0.99) for 0 ≤ t ≤ 0.1 (Fig. 3h). Then, with the contraction of this layer held constant (a₁ = 0) for t ≥ 0.1, the upper layer responds according to Eqs. (5) and (6). For the case of no overshoot (b₂ = 0), the plate gradually unbends (Fig. 3e). If overshoot occurs, however, the unbending eventually transforms into bending in the opposite direction. For relatively small values of b₂, a new equilibrium is attained with negative curvature, but the negative (upward) bending continues unbounded if b₂ is large enough (see Fig. 3e, curves for b₂ = 0.1 and 1). In this problem, the discontinuous growth between layers causes relatively complex stress distributions, which must satisfy the equilibrium conditions of zero axial force and bending moment at all times (Fig. 3f).

Hence, depending on the parameter values, the HR response can lead to perpetual bending in both problems. However, whereas the bending is in the same direction as the perturbation caused by an external load, bending occurs in the opposite direction when the initial perturbation is generated internally. To understand the behavior of the second model, we examine plots of σ_x, σ₀, and λ_g at the top of the plate as functions of time. (Recall that only the upper layer responds to stress in this model.) Contraction of the lower layer initially bends the plate downward, causing tension to develop at the top (Fig. 3g). This tension induces growth that unbends the plate. Eventually, this growth generates compression at the top that sends σ_x below σ₀, and the top of the plate then begins to contract (Fig. 3h), forcing the plate to start to bend upward. If the HR response is relatively slow, σ_x eventually catches σ₀, and bending stops. Otherwise, e.g., for b₂ = 1, the contraction and upward bending continue. Interestingly, a similar unbounded response occurs whenever both layers grow with b₁ ≠ b₂. In fact, the plate bends opposite to the direction of the perturbation no matter which layer has the larger value of b (results not shown).

In summary, when external loads cause a bending perturbation of a bilayered plate, the HR response leads to unlimited bending in the same direction as the perturbation. When contraction of one layer perturbs the plate, however, unlimited bending occurs in the direction opposite the initial perturbation. When there is no overshoot of the target stress, the plate reaches a new morphogenetic equilibrium.

Invagination of Shells

Next we consider the problem of invagination, i.e., the inward folding of epithelia. This problem plays a central role, for example, in gastrulation (formation of the primitive gut) and neurulation (formation of the spinal cord). These processes are crucial to proper development after the first cell divisions create the blastula, which is essentially a fluid-filled epithelial shell. To a first approximation, neurulation can be modeled as the formation of a longitudinal groove in a cylindrical shell, while gastrulation in the commonly studied sea urchin embryo can be treated as axisymmetric dimpling of a spherical shell.

For the neurulation problem, we consider deformation of a circular cylindrical shell in plane strain relative to the longitudinal direction (Fig. 4). To include regional morphogenetic activity, the apical region is divided into two layers, where the relatively thin upper layer (layer 1) contains either contractile apical microfilaments or swelling gel (Davidson et al., 1995).

Figure 4.

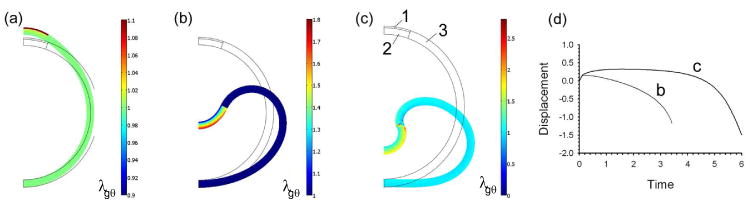
Invagination of cylindrical shell with three regions defined in (c). Colors represent circumferential growth stretch ratio (λ_gθ). (a) 10% constant circumferential expansion in region 1 provides initial stimulus in both cases (configuration at t = 0.1 is shown). (b) Region 2 grows while region 3 remains passive. Unbounded invagination occurs (t = 3.4 shown). (c) Regions 2 and 3 grow. More localized unbounded invagination occurs (t = 6 shown). (d) Displacement of shell apex versus time for both cases. Thin black lines indicate undeformed geometry.

Experiments have shown that neurulation involves contracting apical microfilaments, which cause the cells to become wedge-shaped (Burnside, 1973; Schoenwolf and Smith, 1990). Odell et al. (1981) presented a cylindrical (ring) model based on this premise and the assumption that the microfilaments are stretch-activated, i.e., they contract when stretched beyond a certain threshold value. In their model, contraction of a single cell initiates a contractile wave that travels away from the source in either direction, producing inward bending with the contracting sides of the cells located along the concave side of the invagination. Appropriate choices for model parameters yielded results in good qualitative agreement with observed morphology.

For neurulation governed by the HR Hypothesis, however, results for the plate problem of Fig. 3 suggest a different result. In that simulation, initial contraction in one layer eventually led to bending with the contracted layer on the convex side of the bent plate. Because circumferential bending of a cylindrical shell is similar mechanically to cylindrical bending of a plate, we would expect similar behavior for a shell. Our model confirmed that such contraction produced evagination, rather than invagination (results not shown).

The results from the plate bending problem suggest two possibilities: either contraction of the inner layer or expansion of the outer layer provides the initial perturbation. Contraction of the inner layer (main cell body) seems unlikely, as most actin is concentrated in rings around the apex. In contrast, swelling of an outer layer of gel is theoretically possible, as suggested by experiments and models for sea urchin gastrulation (Davidson et al., 1995), although not neurulation to our knowledge.

Illustrative results are shown for two cases (Fig. 4). Here, the shell is divided into three regions: an upper inner region (1), a lower inner region (2), and an outer region (3) (see Fig. 4c). In both simulations, the initial perturbation is provided by a prescribed circumferential expansion in region 1, as given by ramping λ_gθ up to a value of 1.1 during 0 ≤ t ≤ 0.1 and holding it constant thereafter (with λ_gr = 1). In the first simulation, region 2 grows for t ≥ 0 according to the θ-direction equations of (10), while region 3 remains passive. In the second simulation, both regions 2 and 3 grow, with the growth coefficients being the same for both layers (a_θ = b_θ = 1). After the initial expansion (Fig. 4a), both models undergo unbounded invagination (Fig. 4b–d), as region 2 grows indefinitely. The invagination is more localized in the second model, as growth of region 3 tends to close the tube being created by the invagination (Fig. 4c). This behavior suggests that growth (or other deformation) in neighboring regions is required for complete neural tube closure, consistent with results from other published models of neurulation (Clausi and Brodland, 1993; Brodland and Clausi, 1995).

In the spherical shell model for sea urchin gastrulation, the cross-sectional geometry is the same as for the cylindrical model (Fig. 5h), but axisymmetric deformation is assumed. First, we solved the axisymmetric analog of the first cylinder model above, with a 10% expansion of region 1 specified in both the circumferential and meridional directions during 0 ≤ t ≤ 0.1 (λ_gθ = λ_gφ = 1.1 with λ_gr = 1), while only region 2 grows (t ≥ 0) according to Eqs. (10). Interestingly, the behavior of this model is dramatically different from that of the cylinder, as the region nearest the apex of the shell continues to evaginate and never turns inward (Fig. 5a–c). The source of the difference is the hoop stress σ_θ. The initial upward bending of the shell apex draws the shell inward circumferentially, producing compressive hoop stresses. The HR response then kicks in with circumferential contraction that inhibits downward dimpling while forcing further evagination (Fig. 5b).

Figure 5.

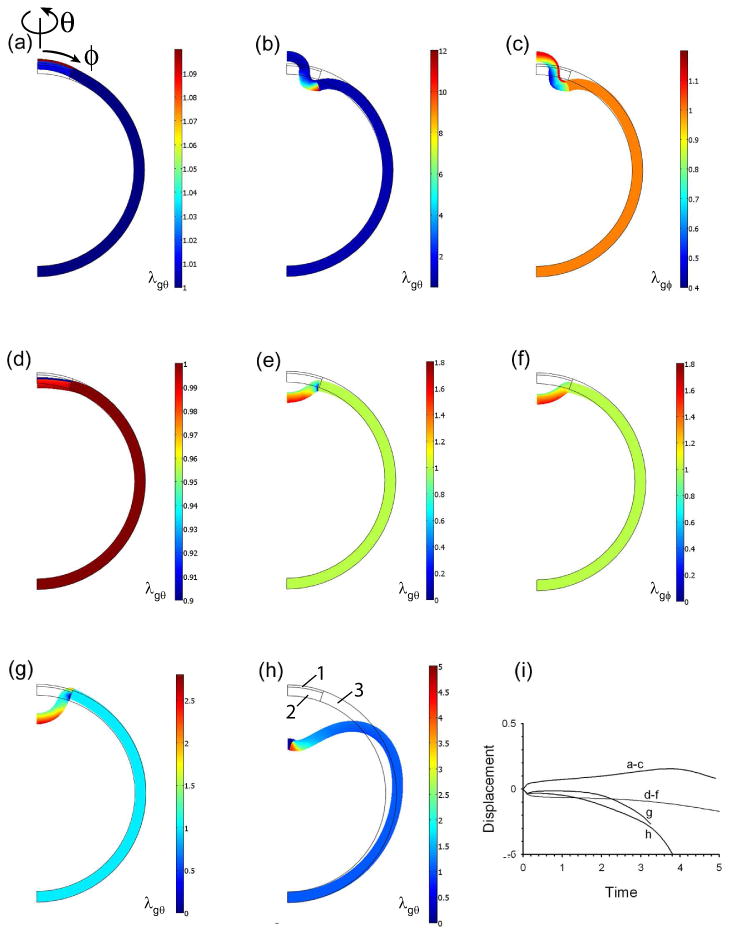
Axisymmetric invagination of spherical shell with three regions defined in (h). Colors represent circumferential growth stretch ratio (λ_gθ) or meridional growth stretch ratio (λ_gφ). (a–c) After 10% constant circumferential and meridional expansion in region 1 (a), HR response in region 2 induces evagination. (d–f) After 10% constant circumferential and meridional contraction of region 1 (d) HR response in region 2 induces invagination. (g) Pressure in internal fluid added to model of d–f changes shape of dimple and allows more invagination. (h) More invagination occurs in fluid-filled shell when region 3 also responds to stress. (i) Displacement of shell apex versus time for all cases. Thin black lines indicate undeformed geometry.

For similar reasons, an initial contraction of region 1 leads to invagination (Fig. 5d–f), contrary to the cylinder problem. Hoop stress effects also cause the deformation of the sphere to be more local than that of the cylinder (compare Figs. 4c and 5e). In these models, the solution stopped converging as the growth stretch ratios became very small in the tightly bent corners of the dimple. The presence of an internal fluid altered the shape of the dimple enough to allow a little more invagination (Fig. 5g), and letting region 3 also grow allowed even more, although the shape of the invagination is not realistic (Fig. 5h). Using other methods to improve convergence, we found that further growth leads to a spherical ballooning of the dimple (not shown), which also is an unrealistic result for gastrulation. The difficulty of deforming a spherical shell may be one reason why a secondary process after the initial dimpling is required to complete gastrulation in the sea urchin (Hardin and Cheng, 1986).

In summary, a local initial contraction or expansion of the outer layer of a cylindrical shell elicits an HR response that causes evagination or invagination, respectively. The same perturbations induce the opposite responses in a spherical shell.

Early Amphibian Development

In his book, Beloussov (1998) discusses how some aspects of embryonic development can be considered as a succession of mechanical events driven and linked by hyper-restoration of stress. For illustration, he describes in qualitative terms the steps involved in amphibian gastrulation. To test his ideas, models are presented here for two parts of this process: (1) the initial stage of gastrulation and (2) early shaping of the head and body of the embryo.

Gastrulation in amphibians is more complex than in sea urchins. The amphibian blastula contains a relatively large volume of yolk that limits the size of the fluid-filled cavity (blastocoel, BC in Fig. 6a). This makes the geometry asymmetric (Fig. 6a), and gastrulation involves invaginating epithelia that slide relative to each other as they pass through a slit-like opening (blastopore, BP) (Gilbert, 2003). Beloussov (1998) speculates that this process is initiated by tension in the roof (R) of the blastocoel due to fluid pressure. The roof then spreads to relieve the tension, and additional spreading due to the HR response compresses cells near the outer edge of the roof. In response, these cells near the edge contract to begin the invagination that creates the blastopore.

Figure 6.

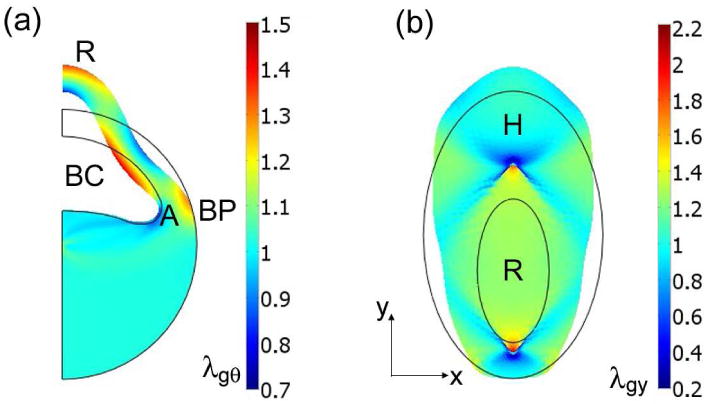
Models for early amphibian development. (a) First phase of gastrulation (t = 4), initiated by added fluid volume in blastocoel (BC). Shape of blastocoel roof (R) is not realistic. Only circumferential growth/contraction (λ_gθ) in included. (BP = blastopore) (b) Formation of basic shape of head and body on surface of embryo (t = 1.74). Active growth/contraction is included only in vertical direction Vertical forces along boundaries of blastocoel roof (R) induce convergent extension that compresses head region (H), which then contracts vertically and expands laterally to produce head shape. Thin black lines indicate undeformed geometry.

A plane-strain model for the blastula was used to test this hypothesis (Fig. 6a). The cavity was assumed to be filled with an incompressible fluid. At the beginning of the simulation (0 ≤ t ≤ 0.5), the fluid volume was gradually increased by 10% and held fixed thereafter. Throughout the embryo for all time, circumferential growth was included, as governed by the left sides of Eqs. (10) with a_θ = b_θ = 1. Consistent with Beloussov's speculation, the model predicts a building region of circumferential contraction near the edge of the blastocoel (Fig. 6a, point A). However, the blastocoel roof begins to bend and extend upward in an unrealistic fashion, causing a region of extension where the blastopore would form (BP), rather than the contraction presumably needed for invagination. A fully 3-D model may hinder this bending, but such a model is outside the scope of the present study.

In addition to triggering invagination, Beloussov (1998) suggests that stretching the blastocoel roof also induces convergent-extension of the cells in the roof, i.e., active vertical extension and lateral contraction within the inner elliptical region (R) of the model shown in Fig. 6b. This model represents a portion the surface of the embryo where the head and body begin to take shape. Both regions have identical properties, with growth in the vertical (y) direction governed by Eqs. (5) and (6) with x replaced by y. To model intercalation, the zero-stress surface area is assumed to remained fixed, and so we set λ_gx = 1/λ_gy and λ_gz = 1. The process is begun by a vertical (y-direction) stretching of the roof region R, given by specifying small vertical forces along the boundary of R.

Via the HR response, the initial vertical tension in the roof region induces active elongation within R, which, as Beloussov speculates, compresses the region immediately above it. This causes the region above R to actively contact in the vertical direction and passively elongate laterally, forming the laterally expanding head region (H, Fig. 6b). This behavior is consistent with Beloussov's proposed mechanism.

In summary, the HR response to cavity pressure in a deforming blastula leads to unrealistic bending of the roof of the blastocoel. In general, however, the predicted shape of the head and body of the embryo are correct.

4 Discussion

Researchers have made great inroads into uncovering the genetic and molecular factors that regulate morphogenesis (Alberts et al., 2002). Considerably less is known, however, about the mechanical mechanisms that drive developmental processes, as well as those mechanisms that may play a regulatory role via mechanotransduction (Ingber, 2006). The objective of the present study is to explore the physical viability of Beloussov's Hyper-restoration Hypothesis as a governing law for morphomechanics.

The basic idea of the HR Hypothesis is that a particular morphogenetic process is initiated by an externally or internally generated stress perturbation, which elicits an active cellular response aimed at restoring the original stress value. This response overcompensates, however, causing a stress overshoot that elicits another active response, and so on, until the process either is complete or awaits another perturbation. Our models clearly show that, following a relatively small perturbation, the HR Hypothesis can indeed lead to some of the large epithelial deformations that characterize morphogenesis. Models based on the HR Hypothesis can generate pattern (alternating long and short regions, Fig. 1b′,c′), spreading (Fig. 2c′), bending (Fig. 3a,e), invagination (Figs. 4 and 5), and the basic form of the early embryo (Fig. 6b). Moreover, the behavior appears to be relatively robust, as the morphogenetic parameters generally affect the speed and possibly the magnitude of the deformation, but not the overall shape.

The accuracy of some of our models, however, is mixed when evaluated using experimental data. For example, invagination of our cylindrical model for neurulation requires (unexpectedly) that the initial perturbation be a regional expansion of cell apexes (Fig. 4), rather than the apical contraction that is known to be a major player in this process (Burnside, 1973; Schoenwolf and Smith, 1990). It is possible that the HR response transforms the expansion into a contraction, but this would need to be confirmed experimentally. On the other hand, a mechanism based on apical swelling has been proposed for sea urchin gastrulation (Davidson et al., 1995), but our model for an invaginating sphere shows that apical contraction works just fine in this case (Fig. 5d–f).

Our models for amphibian development also provide mixed support for the HR Hypothesis. In particular, the model for the initial phase of gastrulation (Fig. 6a) exhibits bending of the blastocoel roof that does not conform to reality, while the head and body patterns form as Beloussov (1998) suggests (Fig. 6b). Perhaps more realistic models would provide more realistic results.

Taken together, our results show that the HR Hypothesis can explain many of the observed changes in shape that occur during morphogenesis. However, it seems improbable that HR can, by itself, produce a comprehensive series of morphogenetic events such as those postulated by Beloussov et al. (1994) for amphibian gastrulation. Genes likely need to occasionally step in to make mid-course corrections or initiate new deformations based on mechanical feedback. In other words, the genes are responsible for providing the overall game plan, setting parameter values, and issuing general instructions to intermittently initiate or correct specific morphogenetic processes, but the nuts and bolts of creating biological form are left to the cells to figure out.

Primary Ingredients of the Hyper-restoration Hypothesis

All models presented in this paper are based on Beloussov's Hyper-restoration Hypothesis (Beloussov, 1998; Beloussov et al., 1994; Beloussov and Grabovsky, 2006). The models are relatively simple and phenomenological in nature, but they are based rigorously on the fundamental principles of nonlinear solid mechanics. Hence, they reveal both the physical plausibility, as well as the limitations, of the HR response in controlling morphogenesis. Ultimately, however, gaining a complete understanding of mechanical morphoregulatory mechanisms will require conducting quantitative experiments and analyses spanning multiple scales from the molecular to the organ level.

The HR Hypothesis, as stated in the Introduction, contains several key assumptions. First, it implies the existence of biophysical laws that govern the behavior of developing tissues. Here, we have proposed relatively simple HR-type morphomechanical laws, expressed in quantitative form. Clearly, biological systems must obey the quantitative laws of physics, but is it not clear whether they also obey quantitative laws of biology. In fact, some authors have dismissed this idea as not plausible. For example, Forgacs and Newman (2005) note that, in contrast to inanimate systems, living systems reproduce and strive for advantages under the auspices of natural selection. Moreover, different tissues serve different functions and likely are optimized to carry out these functions. On the other hand, some data suggest that quantitative rules may exist for some systems, at least within the constraints of natural biological variability. Consider, for instance, the relatively narrow range of fluid shear stress exerted on the walls of arteries of widely varying size (Kamiya et al., 1984). There also is evidence of a quantitative theory for bone development (Carter, 1987). Thus, at least within certain limits, there may indeed be mathematical laws or “construction rules” for morphogenesis.

Second, the HR Hypothesis is based on the idea that mechanical forces play a major role not only in driving, but also in regulating, morphogenesis. Obviously, forces are required to generate the large deformations that occur in the embryo, but the actions of these forces may be dictated entirely by hard-wired genetic and molecular signals. On the other hand, feedback loops would foster communication between genes and cells, allowing each to adjust as circumstances may warrant. Supporting this latter view, recent work has shown that mechanical strain can induce changes in gene expression, and researchers have shown that the nucleus deforms with the cell through CSK attachments between the nucleus and cell membrane (Hu et al., 2005; Maniotis et al., 1997). This mechanism could provide a direct link between mechanical and genetic activity.

The HR Hypothesis takes this idea a step further. Rather than genes being involved in each step of development, tissues are assumed to be capable of a certain amount of self assembly, i.e., they respond actively to perturbations in the mechanical environment without direct intervention by genes.

Third, the HR Hypothesis suggests that stress is the primary mechanical factor that controls cell behavior. Not all investigators accept this view, and some have postulated that growth and remodeling depend on strain, strain rate, or strain-energy density (Cowin, 1996; Omens, 1998; Carter et al., 1987). Some argue that cells contain no mechanism to directly sense the level of stress, just as there is no way for humans to experimentally measure stress inside a material. On the other hand, other researchers argue that Cauchy stress and strain rate are more likely candidates because, unlike strain, these quantities do not depend on a reference geometry, which may be somewhat arbitrary (Taber, 1995). To more clearly define a reference state for strain, Cowin (2004) recently proposed using the zero-stress configuration, but cells may never actually experience this configuration. Addressing this issue in some detail, Humphrey (2001) suggests that the concepts of stress and strain have no real meaning on a molecular level, where the actual transduction mechanisms occur. Rather, he recommends using the terminology that cell behavior correlates with these mechanical measures.

Within this context, Beloussov (1998) is quite clear in stating his view that embryonic cells respond to changes in stress, and not strain. Mechanical considerations show that stress-based morphogenesis can differ considerably from strain-based morphogenesis. In the highly inhomogeneous tissues of the embryo, for example, stress fields often are more complex than the accompanying strain fields, which must satisfy constraints imposed by geometric compatibility. A simple example is stretching of an epithelium with two layers of different stiffness. Although the strain is the same in both layers, the stiffer layer carries more stress. Similarly, the layers of a blastula (or an artery) may stretch similar amounts due to internal fluid pressure, but their stresses may be considerably different. Thus, a stress-based response can produce richer morphogenetic behavior. More evidence favoring stress can be found in mature tissues. For example, skeletal muscles grow thicker when they undergo isometric contraction, which generates stress but not strain (Taber, 1995), although there is strain relative to the zero-stress state.

If stress is in fact the main morphomechanical regulatory quantity, then what is the sensory mechanism? We suggest the following possibility. Suppose that, as postulated by Ingber (1997), the CSK is the primary determinant of the mechanical properties of the cell and connects focal adhesions to the nuclear membrane. Then, consistent with experimental observations (Maniotis et al., 1997; Hu et al., 2005), stretching the cell (and CSK) would transmit forces that deform the nucleus. And since deforming the nucleus requires a certain level of force, gene expression may depend on the force, or average stress, transmitted by the CSK, as opposed to the strain in the CSK. To transmit the same force, a relatively stiff CSK would require less stretch than a more compliant CSK. Experiments by Chen et al. (2001) tentatively support this idea. These investigators found that expression of endothelin-1 increases when integrin receptors in endothelial cells are twisted by attached microbeads, but this response is abolished when drugs are used to block cytoskeletal contraction. Presumably, the more compliant passive CSK transmitted less force to the nucleus. In this context, it would be interesting to see whether applying larger CSK deformations could overcome the loss of CSK stiffness. In other words, does endothelin-1 expression require that a certain level of force be transmitted to the nucleus?

Even in this scenario, however, gene expression ultimately depends on nuclear deformation. Hence, the critical morphomechanical factor may depend on scale. While stress may be the important factor at the cell or tissue level, strain may be the fundamental factor at the molecular level. This idea is consistent with arguments of Humphrey (2001).

Finally, a key feature of the HR Hypothesis is the stress overshoot. As our models have shown, without an overshoot, self-perpetuating morphogenesis is quite limited with deformation soon grinding to a halt as a new equilibrium state is readily established (e.g., see Fig. 3a,e). With an overshoot, however, more substantial deformations are possible, and instabilities can lead (theoretically) to unbounded changes in form. Of course, in real embryos, such unbounded deformation would be limited by internal or external constraints, or exhaustion of the supply of new material. Nevertheless, as shown by Murray (2002) in studies of biological pattern formation, instability may be a cornerstone of morphogenesis. Mechanical instabilities can induce substantial morphogenetic changes in form without continual micromanagement by genes.

Previous Models for Epithelial Morphogenesis

During the past 25 years, several mathematical models for epithelial morphogenesis have been published. Some of these models include feedback, while others do not. Historically, pattern formation has been a popular subject for modelers (Oster et al., 1983; Murray and Oster, 1984; Manoussaki et al., 1996; Namy et al., 2004; Taber, 2000). In fact, Belintsev et al. (1987) proposed an HR-type model for pattern formation. Although this is not the focus of the present study, the model in Fig. 1 can be considered as a simple 1-D model for epithelial pattern formation.

In a pioneering paper, Odell et al. (1981) considered invagination in a blastula modeled as a circular ring of viscoelastic truss-like cells, with deformation driven by contracting microfilaments located at the apex of each cell. This model includes mechanical feedback, as contraction is triggered when the microfilaments are stretched beyond a given threshold. At the beginning of the simulation, contraction is specified in a single cell, which then stretches neighboring cells until they also contract, and so on, generating a contractile wave that travels around the circumference of the ring. This response causes the formation of a local region of invagination, and the authors found parameter values that yield deformed shapes similar to those of a blastula undergoing gastrulation, ventral furrow formation, and neurulation.

It is important to note that stretch-activated contraction runs contrary to the HR Hypothesis, where stretch induces active elongation. Beloussov (1998) realized this contradiction and proposed that stretch activation occurs for relatively small amounts of stretch, while the HR response kicks in for larger deformations.

In a number of other models, morphogenetic forces were specified a priori. These include the models for invagination of Davidson et al. (1995) and Munoz et al. (2007), as well as the finite element model for cardiac looping of Ramasubramanian et al. (2006). In addition, Hardin and Cheng (1986) used a model to study secondary invagination during gastrulation in the sea urchin. After the initial dimpling of the sea urchin blastula (primary invagination), filopodia extend from the tip of the dimple, which elongates until it reaches the opposite wall of the blastula (secondary invagination) to form the archenteron. It is likely that the mechanism that forms the dimple is not strong enough to overcome the relatively high stiffness of the spherical shell, necessitating the need for the secondary process to complete gastrulation. This is clearly shown by our models.

Recently, we studied models for epithelial bending similar to those presented here (Ramasubramanian and Taber, 2007). In those models, however, the value of the target stress was specified a priori, rather than being governed by evolution equations like those of Eqs. (10). The main hypothesis of that paper is that genes directly set and adjust the values of the target stresses on a regional basis, thereby controlling the morphogenetic response. In the present study, we assume that the genes initiate morphogenesis through a mechanical perturbation, which then triggers changes in target stress through mathematical laws. In this respect, morphogenesis is, in part, a problem in self-assembly, rather than being a slave to genetic instructions. The model of Odell et al. (1981) is based on a similar idea.

Limitations and Concluding Remarks

Physical intuition sometimes is misleading in nonlinear mechanics problems. Indeed, some of the results given by our models were unexpected, e.g., the reversal of bending direction in a plate (Fig. 3e). Hence, it is crucial to test whether a hypothesis for morphogenesis is consistent with physical principles.

It is important to note that the models presented here are only for illustration. More realistic models for specific embryos would affect the results quantitatively, if not qualitatively.

In conclusion, this study represents a first attempt to formulate in quantitative terms a general law for morphomechanics. The results are mixed. Our models show that the HR Hypothesis can describe much of the behavior observed in embryos, but some aspects appear to conflict with experimental data. One possibility is that the hypothesis is incorrect, incomplete, or valid only for certain processes. Another is that our proposed functional form of the morphomechanical law is incorrect or incomplete. Clearly, further study is warranted, both in the lab and on the computer.

Appendix A: Implementation in COMSOL

In the following, we describe how finite volumetric growth can be implemented in COMSOL Multiphysics (v 3.3).⁴ Only aspects of the theory directly relevant to this task are presented here. The following analysis applies to 2-D and 3-D problems.

As discussed above, the basic idea is to decompose the total deformation gradient tensor F into growth (F_g) and elastic (F_e) components according to the relation

$$\text{F}={\text{F}}_e\cdot {\text{F}}_g.$$ (A.1)

For a nonlinear hyperelastic material, the stress depends on F_e, and a SED function W_e(F_e) of any form can be entered directly. COMSOL then computes derivatives with respect to displacement gradients to obtain the components of a pseudo first Piola-Kirchhoff stress tensor

$$\overline{\text{P}}=\frac{\partial W_e}{\partial \text{F}}.$$ (A.2)

The FE formulation, however, requires the stress P per unit reference area. In terms of the Cauchy stress tensor σ, this is given by

$${\text{P}}^T=J{\text{F}}^{-1}\cdot \sigma$$ (A.3)

where J = det F. Note that P is the transpose of the usual first Piola-Kirchhoff stress tensor. The software is set up to handle both compressible and nearly incompressible materials. For both cases, the Cauchy stress is given by

$$\sigma =J_e^{-1}{\text{F}}_e\cdot \frac{\partial W_e}{\partial {\text{F}}_e^T}$$ (A.4)

where Eq. (A.1) gives ${\text{F}}_e=\text{F}\cdot {\text{F}}_g^{-1}$ and J_e = det F_e. Substituting Eq. (A.4) into (A.3), taking the transpose, and noting Eq. (A.1) yields

$$\text{P}=J{J}_e^{-1}\frac{\partial W_e}{\partial {\text{F}}_e}\cdot {\text{F}}_g^{-T}.$$ (A.5)

This relation can be simplified by noting that the chain rule gives

$$\frac{\partial W_e}{\partial {\text{F}}_e}=\frac{\partial \text{F}}{\partial {\text{F}}_e}:\frac{\partial W_e}{\partial \text{F}}.$$ (A.6)

Expressing all tensors on the right-hand side in dyadic form and working in Cartesian coordinates, we can show that this equation can be written in the form

$$\frac{\partial W_e}{\partial {\text{F}}_e}=\frac{\partial W_e}{\partial \text{F}}\cdot {\text{F}}_g^{-T}.$$ (A.7)

Finally, inserting this expression into Eq. (A.5) yields

$$\text{P}=J{J}_e^{-1}\frac{\partial W_e}{\partial \text{F}}=J{J}_e^{-1}\overline{\text{P}}.$$ (A.8)

Appendix B: Computation of Plate Curvature

The amount of bending for simulations involving cantilever plates is quantified by the curvature. Let (X, Y) and (x, y) be the Cartesian coordinates of a point near the center of the plate before and after deformation, respectively. The nondimensional curvature is given by (Yang and Feng, 1970)

$$\kappa =H\frac{(w{u}^{\prime }-u{w}^{\prime })}{u^2{(u^2-w^2)}^{1/2}}$$ (B.1)

where

$$\begin{array}{cc}u\hfill & \hfill ={(x^{\prime 2}+y^{\prime 2})}^{1/2}\hfill \\ w\hfill & \hfill =x^{\prime }.\hfill \end{array}$$ (B.2)

In these expressions, prime denotes differentiation with respect to X, and H is the undeformed plate thickness. To avoid end effects, the curvature was computed near the center of the plate.