Direct Three-Dimensional Myocardial Strain Tensor Quantification and Tracking using zHARP

Abstract

Images of myocardial strain can be used to diagnose heart disease, plan and monitor treatment, and to learn about cardiac structure and function. Three-dimensional (3-D) strain is typically quantified using many magnetic resonance (MR) images obtained in two or three orthogonal planes. Problems with this approach include long scan times, image misregistration, and through-plane motion. This article presents a novel method for calculating cardiac 3-D strain using a stack of two or more images acquired in only one orientation. The zHARP pulse sequence encodes in-plane motion using MR tagging and out-of-plane motion using phase encoding, and has been previously shown to be capable of computing 3D displacement within a single image plane. Here, data from two adjacent image planes are combined to yield a 3-D strain tensor at each pixel; stacks of zHARP images can be used to derive stacked arrays of 3D strain tensors without imaging multiple orientations and without numerical interpolation. The performance and accuracy of the method is demonstrated in-vitro on a phantom and in-vivo in four healthy adult human subjects.

1 Introduction

Magnetic resonance imaging (MRI) of regional function in the heart has gained wide acceptance in the study and diagnosis of cardiac diseases that are related to abnormal cardiac mechanics. Although cardiac function can be assessed using ultrasound imaging by techniques like speckle tracking, MRI is leading in terms of spatial resolution, soft tissue contrast, and signal-to-noise ratio (SNR). In addition, computerized tomography (CT) is currently limited by a relatively high radiation dose that limits repeated studies or studies in healthy subjects. Mechanical strain quantifies the relative deformation within a myocardial region and is the most commonly used quantity in characterizing regional cardiac function. There are three methods that are commonly used to directly image strain in MRI: MR tagging (Zerhouni et al., 1988; Axel and Dougherty, 1989) with harmonic phase (HARP) analysis, displacement encoded stimulated echo (DENSE) imaging (Aletras et al., 1999; Kim et al., 2004), and strain encoded (SENC) imaging (Osman et al., 2001; Osman, 2003).

Although HARP, DENSE, and SENC are quite useful for the quantification and visualization of regional cardiac function, their use has been largely limited to the computation of 2D in-plane strains (HARP and DENSE) and 1D through-plane strains (SENC). Extending these methods to 3-D has been problematic due to the lengthy time that is needed to gather sufficient data for 3-D volumetric strain analysis. For example, MR tagging methods have been used to quantify 3-D strain through the use of multiple orthogonal image slices covering the volume of interest (O’Dell et al., 1995; Denney and McVeigh, 1997; Young, 1999; Denney et al., 2003; Deng and Denney, 2005; Pan et al., 2005; Sampath and Prince, 2007). Aside from patient discomfort due to many successive breathholds required to acquire these data, long imaging times promote artifacts or inaccuracies due to image registration errors caused by patient motion, breathing, and/or heart rate variation occurring among the scans. On the other hand, if the overall imaging time is shortened, then the acquired data are sparse, and 3-D strain tensor reconstruction requires aggressive interpolation. Interpolation is generally undesirable due both to the potential for inaccuracies caused by interpolation assumptions and due to the requirement for user interaction in determining myocardial boundaries that restrict or guide the interpolation process.

Two more direct methods to image 3-D regional cardiac function have been reported in the literature. Ryf et al. (2002) used a 3-D tagging sequence and a natural 3-D extension of the HARP concept to directly track any point in 3-D (from which 3-D strain can be computed). This approach is conceptually elegant, but imaging times are prohibitively long since the entire 3-D k-space must be imaged. Sampath et al. (2004) combined SENC and HARP in a fast imaging method that enables calculation of both in-plane and through-plane strains at every pixel in the imaged slice. Unfortunately, this method is not capable of imaging two of the six unique components in the 3-D strain tensor; also, it acquires images of spatially fixed image planes, yielding a time sequence of strains that actually arise from different tissues due to through-plane motion. This latter issue is a limitation of all of the methods described above, and can only be addressed by slice-following or 3-D displacement encoding techniques.

A fast method to image and track the 3-D displacement of all points in a single slice (requiring only two breath-holds) was recently reported (Abd-Elmoniem et al., 2005, 2007a). This approach, called zHARP, uses MR tagging to encode in-plane motion and phase encoding to encode through-plane motion using slice-following where adverse effects of through-plane motion can be avoided. The present paper describes the application of zHARP to compute and track the 3-D strain tensor at any material point in a 3-D stack of parallel zHARP images. It is possible to compute 3-D strain tensors over the whole left ventricle in as few as fourteen breath-hold scans with no spatial interpolation. This approach provides an unprecedented approach to the rapid, automated, volumetric imaging of 3-D strain in the heart. Results from both a compressible phantom and in-vivo experiments show a strong correlation between the proposed method and a conventional 3-D method both visually and statistically from linear regression and Bland-Altman statistics.

2 Background

2.1 Motion, Deformation, and Strain

A region S in Euclidean space 𝔼³ is assumed to be the reference configuration of a moving body and points p ∈ S are called material points. A motion of S is a class C³ function (Gurtin, 1981) X : S × ℝ → 𝔼³, and for each fixed time t, X(·, t) is a deformation of S. The spatial position occupied by the material point p at time t is given by the motion

$$\mathbf{x}=\mathbf{X}(\mathbf{p},t),$$ (1)

where x ≡ [x, y, z]^T. The region of space occupied by the object at time t is given by S_t = X(S, t).

At each t, X(·, t) is a one-to-one mapping of S onto S_t; hence, it has an inverse P(·, t) : S_t → S, which is called the reference map. It follows that P(X(p, t) , t) = p and X(P(x, t) , t) = x.

Figure 1 depicts a slice of tissue occupying a reference configuration S that is taken to be the position S₁ of the slice at time t₁. At a later time t_q, the slice occupies the set S_q. The relationship between a material point p and its position x at time t_q is described by the spatial displacement vector u(·, t) : S_t → 𝔼³, which is given by

$$\mathbf{u}(\mathbf{x},t)\equiv {[u_x,u_y,u_z]}^{\mathbf{T}}=\mathbf{x}-\mathbf{P}(\mathbf{x},t),$$ (2)

Figure 1.

The motion of a tissue slice and the trajectory of a material point within the slice.

Generically, strain is the change in length per unit length. The 3-D analog of this concept is defined using the displacement gradient, which is given by

$$\nabla \mathbf{u}(\mathbf{x},t)=\left(\begin{array}{c}\frac{\partial u_x}{\partial x}\frac{\partial u_x}{\partial y}\frac{\partial u_x}{\partial z}\hfill \\ \frac{\partial u_y}{\partial x}\frac{\partial u_y}{\partial y}\frac{\partial u_y}{\partial z}\hfill \\ \frac{\partial u_z}{\partial x}\frac{\partial u_z}{\partial y}\frac{\partial u_z}{\partial z}\hfill \end{array}\right).$$ (3)

Then the deformation gradient F is given by

$$\mathbf{F}(\mathbf{x},t)={(\mathbf{I}-\nabla \mathbf{u}(\mathbf{x},t))}^{-1},$$ (4)

and, finally, the 3-D Eulerian strain tensor is defined by (Lai et al., 1993)

$$\epsilon (\mathbf{x},t)=\frac{1}{2}\left[\mathbf{I}-{\left({\mathbf{F}}^{-1}(\mathbf{x},t)\right)}^T{\mathbf{F}}^{-1}(\mathbf{x},t)\right].$$ (5)

2.2 zHARP Pulse Sequence

zHARP (Abd-Elmoniem et al., 2005, 2007a) is an MRI tagging pulse sequence that extends slice-following CSPAMM (SF-CSPAMM) (Fischer et al., 1993, 1994) by using phase encoding to encode through-plane displacement. This extension permits the 3-D tracking of any point in an image plane. As shown in Fig. 2, zHARP is a segmented k-space pulse sequence that requires 4 × R heartbeats where R is the number of segments per cine data set. Each cine data set contains Q time-frames.

Figure 2.

Single-slice zHARP pulse sequence.

The four cine data sets are tagged with vertical positive cosine, vertical negative cosine, horizontal positive cosine, and horizontal negative cosine tag patterns, respectively. A gradient with an area G_enc in the slice-select direction is turned on before the acquisition with positive and negative polarities in the vertical and horizontal tagging direction, respectively. After the complex addition of the vertical and the horizontal data sets, separately, we end up with the two data sets

$$\begin{array}{cc}{I}_{\upsilon }(x,y,t)\approx \hfill & \hfill \rho (\mathbf{x},t)e^{j{\phi }_e(\mathbf{x})}{e}^{+j\kappa u_z}\text{cos}(\omega (x-u_x(\mathbf{x},t))),\hfill \\ \hfill =& \hfill \frac{\rho (\mathbf{x},t)}{2}\left[e^{j({\phi }_e+\kappa u_z+\omega u_x-\omega x)}+e^{j({\phi }_e+\kappa u_z-\omega u_x+\omega x)}\right],\hfill \end{array}$$ (6a)

$$\begin{array}{cc}{I}_h(x,y,t)\approx \hfill & \hfill \rho (\mathbf{x},t)e^{j{\phi }_e(\mathbf{x})}{e}^{-j\kappa u_z}\text{cos}(\omega (y-u_y(\mathbf{x},t))),\hfill \\ \hfill =& \hfill \frac{\rho (\mathbf{x},t)}{2}\left[e^{j({\phi }_e-\kappa u_z+\omega u_y-\omega y)}+e^{j({\phi }_e-\kappa u_z-\omega u_y+\omega y)}\right],\hfill \end{array}$$ (6b)

where ρ is the spin density, ω is the tag frequency, κ ≡ γG_enc is the z-encode frequency, γ is the gyromagnetic ratio, and φ_e is the artifactual phase caused by susceptibility and general field inhomogeneity.

2.3 Harmonic Phase Images

The Fourier transform of either I_υ or I_h comprises two distinct harmonic spectral peaks and no peaks at the origin. Therefore, applying HARP filtering (Osman et al., 1999) to these four peaks (two from each image), yields four distinct complex images

$$I_{\upsilon }^{-}\approx \frac{\rho (\mathbf{x},t)}{2}{e}^{j({\phi }_e+\kappa u_z-\omega u_x)},$$ (7a)

$$I_{\upsilon }^{+}\approx \frac{\rho (\mathbf{x},t)}{2}{e}^{j({\phi }_e+\kappa u_z+\omega u_x)},$$ (7b)

$$I_h^{-}\approx \frac{\rho (\mathbf{x},t)}{2}{e}^{j({\phi }_e-\kappa u_z-\omega u_y)},$$ (7c)

$$I_h^{+}\approx \frac{\rho (\mathbf{x},t)}{2}{e}^{j({\phi }_e-\kappa u_z+\omega u_y)}.$$ (7d)

It was shown in (Abd-Elmoniem et al., 2007a) how to use these images to compute 3-D pathline trajectories for all points originating in the image plane. In the following section, we show a new approach that not only improves on the previous computation for 3-D tracking, but yields an elegant expression for the 3-D strain tensors of these tracked points as well.

3 Theory

The previous section provided background on motion, the zHARP pulse sequence, and the harmonic phase images derived from zHARP data. We now describe how zHARP data acquired from two or more adjacent and parallel slices can be used to compute the 3-D strain tensors of all pixels associated with each adjacent image pair.

3.1 zHARP 3-D Displacement Gradient

In theory, the displacements u_x, u_y, and u_z are contained within the phases of the complex images in (7), as follows

$${\varphi }_{\upsilon }^{+}={\phi }_e+\kappa u_z+\omega u_x$$ (8a)

$${\varphi }_{\upsilon }^{-}={\phi }_e+\kappa u_z-\omega u_x$$ (8b)

$${\varphi }_h^{+}={\phi }_e-\kappa u_z+\omega u_y$$ (8c)

$${\varphi }_h^{-}={\phi }_e-\kappa u_z-\omega u_y$$ (8d)

This set of linear equations can be solved, yielding

$$u_x=\left({\varphi }_{\upsilon }^{+}-{\varphi }_{\upsilon }^{-}\right)/2\omega ,$$ (9a)

$$u_y=\left({\varphi }_h^{+}-{\varphi }_h^{-}\right)/2\omega ,$$ (9b)

$$u_z=\left({\varphi }_{\upsilon }^{+}+{\varphi }_{\upsilon }^{-}-{\varphi }_h^{+}-{\varphi }_h^{-}\right)/4\kappa .$$ (9c)

(We discard the solution for φ_e, which is not needed for this application.) These equations form the basis for 3-D point tracking from a single zHARP image, as described in (Abd-Elmoniem et al., 2007a).

Although conceptually straightforward, the computational process described by (8) and (9) is problematic due to the phase wrapping that occurs during the computation of individual phases in (8) from the complex images. Since the phases in (8) can only be computed in the interval [π, π) (using the atan2 operator, for example), the direct use of these wrapped phases in (9) can lead to erroneous results due to the mixing of individual phase wrappings as well as the additional phase wrapping caused by addition and subtraction. Further, the application of a finite difference gradient operator to these results (in order to compute the displacement gradient) is just plain wrong in many locations in the image due to the aforementioned phase-wrapping discontinuity. For example, phase wrapping can occur in ϕ_υ between two points x₁ and x₂ if, for $\delta >0,{\varphi }_{\upsilon }^{+}({\mathbf{x}}_{\mathbf{1}})-\pi <\delta$ and u_x(x₂) − u_x(x₁) > δ/ω, which results, upon using finite difference, in an erroneous abrupt change in the calculated displacement gradient. Therefore, we have developed an alternative approach that handles both the solution of (8) and local phase unwrapping.

The key to this technique is to note that the adding and subtracting of phases that are required in (9) can be handled by multiplication of the complex data. We define the vector Φ of phases as follows

$$\mathbf{\Phi }\equiv \left(\begin{array}{c}{\varphi }_x\hfill \\ {\varphi }_y\hfill \\ {\varphi }_z\hfill \end{array}\right)=\left(\begin{array}{c}𝒲\left(2\omega u_x\right)\hfill \\ 𝒲\left(2\omega u_y\right)\hfill \\ 𝒲\left(4\kappa u_z\right)\hfill \end{array}\right)=\left(\begin{array}{c}\hfill \angle \left(I_{\upsilon }^{+}\times \overline{I_{\upsilon }^{-}}\right)\hfill \\ \hfill \angle \left(I_h^{+}\times \overline{I_h^{-}}\right)\hfill \\ \hfill \angle \left(I_{\upsilon }^{+}\times I_{\upsilon }^{-}\times \overline{I_h^{+}}\times \overline{I_h^{-}}\right)\hfill \end{array}\right),$$ (10)

where the bar represents complex conjugate and 𝒲 is the phase wrapping function given by

$$𝒲(\theta )=\text{mod}(\theta +\pi ,2\pi )-\pi .$$ (11)

This equation makes it clear that the phase computation implied by the operator ∠ yields a wrapped phase value.

Rather than solving for the displacements at this point and then taking the gradient operator, we reverse the order of operations. The gradient of the phases in (10) can be computed without error using the same operator reported in (Osman et al., 1999)

$${\nabla }^{*}\varphi \equiv \{\begin{array}{cc}\nabla \varphi \hfill & \parallel \nabla \varphi \parallel \le \parallel \nabla 𝒲(\varphi +\pi )\parallel \hfill \\ \nabla 𝒲(\varphi +\pi )\hfill & \text{otherwise}\hfill \end{array}$$ (12)

where the gradient operator ∇ is carried out using finite differencing (see Section 3.2). Applying this operator to ϕ_x, ϕ_y, and ϕ _z yields the vector of phase gradients

$${\nabla }^{*}\mathbf{\Phi }\equiv \left(\begin{array}{c}{\nabla }^{*}{\varphi }_x\hfill \\ {\nabla }^{*}{\varphi }_y\hfill \\ {\nabla }^{*}{\varphi }_z\hfill \end{array}\right).$$ (13)

Referring back to equation (10), it is straightforward to solve for the displacement gradient, yielding

$$\nabla \mathbf{u}(\mathbf{x},t)=\left(\begin{array}{c}\nabla u_x(\mathbf{x},t)\hfill \\ \nabla u_y(\mathbf{x},t)\hfill \\ \nabla u_z(\mathbf{x},t)\hfill \end{array}\right)=\left(\begin{array}{ccc}\frac{{\omega }^{-1}}{2\mathrm{\Delta }x}\hfill & 0\hfill & 0\hfill \\ 0\hfill & \frac{{\omega }^{-1}}{2\mathrm{\Delta }y}\hfill & 0\hfill \\ 0\hfill & 0\hfill & \frac{{\kappa }^{-1}}{4\mathrm{\Delta }z}\hfill \end{array}\right){\nabla }^{*}\mathrm{\Phi }(\mathbf{x},t),$$ (14)

where Δx, Δy, and Δz are the physical spacings between the adjacent points in the x–, y–, and z–directions, respectively. The dependence of various quantities on x and t has been restored to remind the reader that these computations are done at every spatial location and all image frames in the acquired sequence.

3.2 zHARP 3-D Strain Algorithm

The following steps are used to calculate the pixel-wise 3-D strain tensor ε (x, t).

Step 1

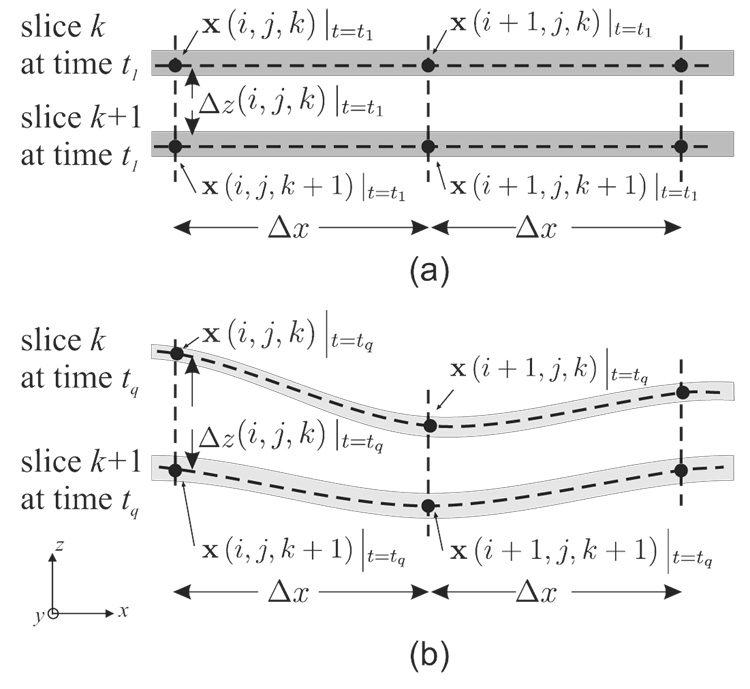
Given a stack of K equally separated zHARP images at time t₁, create an N × N × K rectilinear mesh of points ℳ covering a region of interest (e.g., left ventricular myocardium). The K points in the z-direction (the through-plane direction) always lie on the acquired zHARP image positions, but the locations of the points within the image planes need not lie on pixel locations. Let x(i, j, k) describe a 3-D spatial position defined by the mesh, where i = 1,…,N, j = 1,…,N, and k = 1,…,K.

In this case Δx and Δy do not change since the mesh points only move “up and down”; however, the value of Δz is temporally and spatially varying and is computed at each mesh point according to the computed z positions of the pair of points involved in the finite difference computation (Fig. 3)

$$\mathrm{\Delta }z(i,j,k){|}_{t_q}=\frac{{\nabla }^{*}{\varphi }_z}{4\kappa }+\mathrm{\Delta }z(i,j,k){|}_{t_1},$$ (15)

and Δz (i, j, k)|_t1 is the slice spacing at the reference time t₁.

Figure 3.

A stack of two zHARP slices and the placement of the 3-D mesh ℳ at the reference time t₁(a) and at a later time t_q (b). The physical spacings Δx and Δy are the same everywhere throughout the cardiac cycle while Δz is temporally and spatially varying.

Although zHARP is capable of tracking all the points in ℳ in 3-D, for the purposes of the present algorithm we will not do this. Instead, as shown in Fig. 3, the x and y positions of the points in ℳ will remain constant throughout all time frames, and only their z-positions will change. In this way, the points in ℳ always remain on the tag slices from which the tagged image data is generated (recall that this is a slice following technique), and the points always remain in a fixed relationship to the (Eulerian) x-y coordinates of the acquired image pixels. This is a very important point that underlies the methodology reported in this paper.

Step 2

Using the harmonic phases computed for the underlying images, compute the 3-D harmonic phase vector maps Φ (x (i, j, k) , t) and Φ (x (i, j, k + 1) , t) for all i, j, and k within the mesh ℳ. Use bilinear interpolation of the underlying phase values — ϕ_x, ϕ_y, and ϕ_z — if the x-y positions of the mesh points are not located at pixel locations. Because of the particular way of constructing the mesh in Step 1, this process yields accurate phase maps for the underlying tissue points at all the mesh vertices.

Step 3

Compute ∇*Φ (x (i, j, k) , t) at all grid points using (13) and the following finite differencing scheme

$$\nabla {\varphi }_x=\left[\varphi \left(\mathbf{x}\left(i+1,j,k\right),t\right)-\varphi \left(\mathbf{x}\left(i,j,k\right),t\right)\right]$$ (16a)

$$\nabla {\varphi }_y=\left[\varphi \left(\mathbf{x}\left(i,j+1,k\right),t\right)-\varphi \left(\mathbf{x}\left(i,j,k\right),t\right)\right]$$ (16b)

$$\nabla {\varphi }_z=\left[\varphi \left(\mathbf{x}\left(i,j,k+1\right),t\right)-\varphi \left(\mathbf{x}\left(i,j,k\right),t\right)\right]$$ (16c)

Step 4

Compute ε (x, t), the Eulerian strain tensor, at each mesh point by substituting ∇*Φ (x (i, j, k) , t) into (14) and that result into (5).

3.3 3-D Strain Tensor Tracking

The above procedure yields the strain tensor ε (x, t) at each point on the spatial mesh ℳ. This result is an interesting “mix” of an Eulerian result (in x and y) with a Lagrangian result (in z). Since it is possible to track points using zHARP a more natural result would be to report the 3-D strain associated with a collection of material points in the reference configuration as they move through space. The following algorithm explains how to do this for the single material point p, and this can be repeated for any collection of points in the reference configuration.

Step 1

Compute ∇*Φ (x, t_q) for all x ∈ ℳ and for all cardiac phases t_q = 1,…,Q, as described in Sec. 3.2. This provides a spatiotemporal array of phase gradients covering the region of interest.

Step 2

The reference configuration is taken to be the slice positions at t₁. Track a material point p in the reference configuration using the methods reported in (Abd-Elmoniem et al., 2007a), yielding its 3-D pathline (trajectory), as shown in Fig. 1 and given by

$$𝒯\left(\mathbf{p}\right)\equiv \left\{\left(\mathbf{x},t_q\right)|\mathbf{P}\left(\mathbf{x},t_q\right)=\mathbf{p},1\le q\le Q\right\},$$ (17)

Step 3

The material point p originates within a particular image slice, so it corresponds to a particular k in ℳ. At a later time, the x-y position of the point will put it between an i and i + 1 and a j and j + 1 in ℳ. All three values of the phase gradient vector ∇*Φ (x, t_q) can therefore be determined using bilinear interpolation from the previously computed mesh values (Step 1).

Step 4

Compute the strain tensor ε (x, t), by substituting ∇*Φ (x, t_q) into (14) and that result into (5).

Step 5

Repeat Steps 2–4 for all material points p of interest and all points (x, t_q) within their pathlines.

The mesh ℳ is a convenient collection of material points over which to compute and track the 3-D strain; this is what we do in the experiments described below. But it should be kept in mind that the mesh is serving two distinct purposes.

4 Methods

The zHARP pulse sequence was implemented on a Philips 3.0T Achieva MRI scanner (Philips Medical Systems, Best, NL). A six-channel phased array cardiac receiver coil was used in all the experiments. Surface coils for signal reception were positioned at the anterior and posterior chest wall. A similar coil positioning was used for phantom experiments. Tag spacing ranged from 6 to 8 mm. HARP filtering was applied as described in (Osman et al., 2000) to every harmonic peak with a circular filter with σ = 0.05, and r_A = r_B were such that the effective voxel size after filtering amounts to 7×7×8 mm³ (with slice thickness=8 mm).

4.1 Phantom Experiments

The goal of these experiments was to show the feasibility of measuring and tracking the 3-D strain tensor from parallel image slices using the proposed technique in Sec. 3.2 and Sec. 3.3, respectively.

4.1.1 Setup

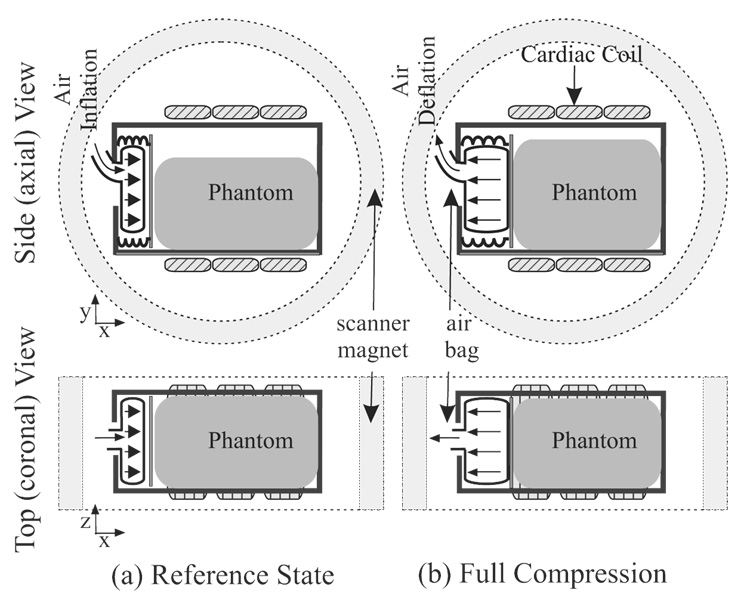
A gel phantom was built using Sylgard® 527 Silicone Dielectric Gel (Dow Corning, Midland, Michigan) with 33% of material A and 67% of material B, which experimentally possesses magnetic properties (T1 and T2) and elasticity similar to in vivo muscular tissues.

As shown in Fig. 4, the deformable phantom had a rectangular shape with the dimensions (70 × 50 × 60)mm³ and was tightly contained in a rigid plastic box except on one side and the top. An air bag was positioned on the side and made to periodically inflate and deflate in the x-direction at a fixed rate of 30 cycles/min. The top of the plastic box was left open so that the gel could bulge in the y-direction when was compressed by the air bag. A TTL pulse simulating the R-wave of the heart was generated at the beginning of each compression cycle in order to trigger the air bag inflation and the MRI scanning simultaneously.

Figure 4.

Phantom Setup in the original and the full-compression states.

4.1.2 Data Acquisition

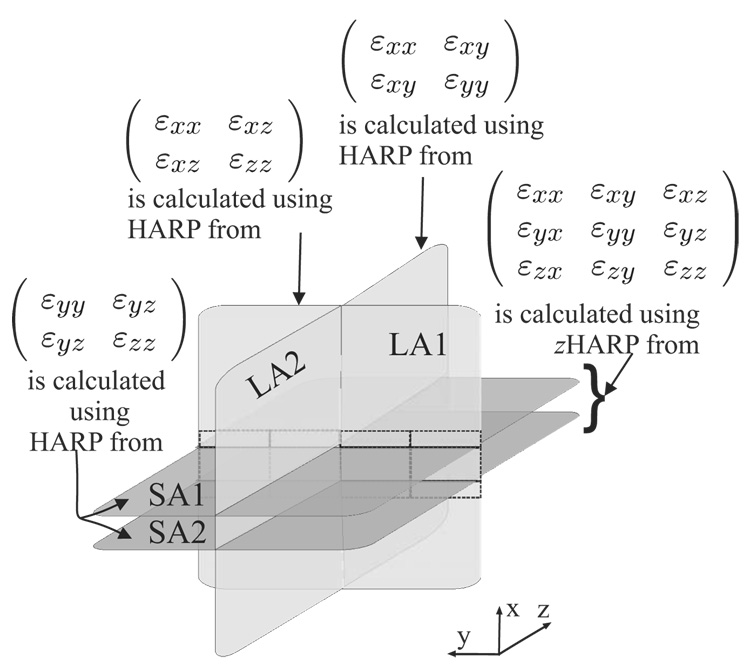
Two phantom experiments were conducted in which the images were acquired in three orthogonal orientations, as shown in Fig. 5.

Figure 5.

Strain tensor validation scheme in a phantom. 3-D strain tensors were calculated from the two parallel SA slices. In-plane components were also computed from the same SA slices using HARP. Through-plane strain components were also computed using LA slices at the intersection with the SA slices.

The imaging orientations were sagittal, coronal, and the axial planes. Sagittal planes are orthogonal to the x-direction are called short-axis (SA) planes. Axial and coronal planes are orthogonal to the SA plane and are called long-axis (LA) planes. Ten contiguous SA zHARP slices were acquired with $\kappa =\frac{2\pi }{33}$ rad/mm, field-of-view (FOV)=160 mm, and slice-thickness=8 mm. For validation of the through-plane strain components, twenty contiguous LA SF-CSPAMM slices were also acquired (10 axial and 10 coronal).

4.1.3 Analysis and Validation

A fine mesh ℳ of points covering the phantom within the acquired image stack was defined. The 3-D strain tensor ε (x, t) was then calculated and tracked for each point in the mesh, as described in Sec. 3.3. For validation, the intersection region between every SA slice and LA slice was divided into three segments. The 3-D strain in each segment was calculated as the average 3-D strain from all the points in the segment. The segmental though-plane strain (calculated from the SA slice) was again calculated from the corresponding LA slice using conventional HARP (see Fig. 5 and Fig. 6). To quantify the method’s performance, linear regression and Bland-Altman plots were generated comparing the through-plane strain component ε_zz as calculated from SA and LA slices using zHARP and regular HARP, respectively.

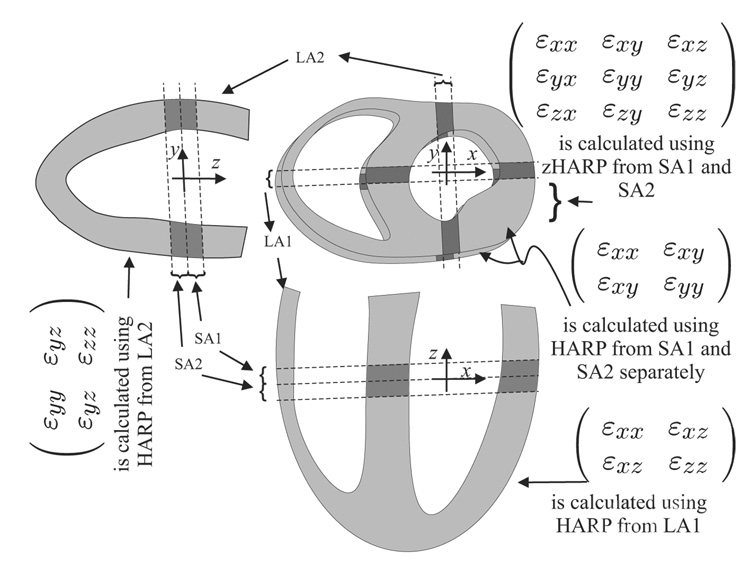
Figure 6.

In-vivo strain tensor validation scheme. 3-D strain tensor was calculated in the SA slices using zHARP and validated from HARP processing of the LA slices.

4.2 In-Vivo Experiments

Four normal subjects were scanned. From each subject, three or four SA zHARP slices were acquired from the basal to the apical positions. Slices were 8 mm thick and spaced 8 mm apart (center-to-center) and had a 35 ms temporal resolution, a FOV of 300 mm, and 15 cardiac phases. Data were acquired using spiral imaging with a 9 ms acquisition window per spiral arm and 10 spiral readouts. Four radially-arrayed LA SF-CSPAMM were acquired for validation. A fine mesh ℳ was fixed in the contiguous SA stack, and the strain tensor ε (x, t) was computed and tracked throughout the cardiac cycle. The intersection regions between SA and LA slices were used for comparison and validation in a similar fashion to the phantom procedure.

5 Results

5.1 Phantom Results

Images of the SA and LA slices are shown in Fig. 7(a, b). Note that the air bag is located to the left of the LA slice and below the plane of the SA slice. We observe that the phantom compression is revealed in the SA slice as a bulging and bending of the tag lines. In the LA slice, however, the phantom compression is revealed as an in-plane narrowing of the tag lines.

Figure 7.

Visual validation of ε_xx (through-plane strain) in SA slices and the equivalent ε_xx (in-plane strain) in an orthogonal LA slice. SA and LA magnitude cine images at different time are shown in (a) and (b), respectively. (c) Through-plane strain ε_xx in the SA slice. (d) In-plane strain ε_xx in the orthogonal LA slice. The dotted lines in (c) and (d) represent the location of the LA and the SA slices, respectively.

As shown in 7(c, d), ε_xx in the SA slice agrees visually with ε_xx from the LA slice at the intersection line (shown dotted). The six unique elements of the 3-D strain tensor on a SA slice, evaluation on the mesh ℳ, are shown in Fig. 8. Notice the bulging of the phantom is represented in the SA slice as stretching in the ε_yy and ε_zz components. The 3-D pathline tracking of representative material points in a SA slice is shown in Fig. 9(a). Strain tensor elements that correspond to the tracked points were evaluated along the pathlines and the ε_zz components is shown in 9(a) as an example. A mesh of two SA slices and an orthogonal LA slice are shown in 9(b) at three different time points with the value of ε_zz is superimposed. Notice that through-plane compression near the balloon (SA1) is higher than far away (SA2) in agreement with the values of ε_zz calculated in the LA slice.

Figure 8.

The six unique elements of the 3-D strain tensor in a SA sagittal slice of the compressible phantom. Balloon inflation and phantom compression are in the through-plane x–direction. Note the blue coloration of ε_xx compression and the in-plane bulging of the tags. The remaining components represent shear stresses in different orientations.

Figure 9.

(a) 3-D representation of ε_zz and pathline tracking in a compressible phantom SA slice. (b) ε_zz calculated in two SA slices and the corresponding ε_zz in an orthogonal LA slice (vertical slice). The balloon is located above the plane of the topmpst SA slice. Note the compression in the phantom near the ballon is higher than the compression of regions far from the ballon. Also, note the visual agreement between ε_zz from LA slice and the corresponding ε_zz from SA slices.

The agreement is further shown quantitatively using linear regression and Bland-Altman plots (Fig. 10).

Figure 10.

Linear regression and Bland-Altman plots for the compressible phantom SA ε_zz strain and the corresponding LA ε_xx.

5.2 In Vivo Results

The 3-D strain tensor components in a basal SA are shown in Fig. 11. A 3-D representation of ε_zz in the SA slice and the corresponding ε_xx in the LA slice are shown in Fig. 12. Finally, the quantitative comparison shows a strong correlation (R > 0.85) between ε_xx, ε_yy, ε_zz calculated using zHARP and conventional HARP, as shown in Fig. 13.

Figure 11.

In-vivo tagged SA slice and its 3-D strain tensor components.

Figure 12.

(a) 3-D representation of ε_zz in the SA slice and the motion pathlines of selected points. (b) The strain component ε_zz as measured from a pair of SA slice using the proposed zHARP 3-D strain algorithm and the same strain component as measured from the LA slice using traditional HARP in-plane strain calculations.

Figure 13.

In-vivo linear regression and Bland-Altman plots for the three diagonal strain tensor components. Y₁, Y₂ and Y₃ are the ε_zz, ε_xx, and ε_yy during systole in zHARP SA slices with $\kappa =\frac{2\pi }{33}$ rad/mm.

6 Discussion

We presented a cine multi-slice zHARP imaging scheme for rapid 3-D strain tensor quantification and tracking in the heart using only SA slices. The method yields both 3-D displacement vectors and 3-D strain tensors throughout the heart muscle at arbitrary material points. Strain tensor results are readily computed at each pixel in adjacent slices without the need for interpolation. This is an advantage over previous methods which could only calculate faithful 3-D strain values at the lines of intersection between SA and LA slices and calculate the rest of the map using interpolation. Because slice following is used, the proposed method yields 3-D measurements associated with true material points in the heart without requiring integration over time.

The method was validated against the SF-CSPAMM approach, which combines LA and SA slices. The in-plane and through-plane strain components compare well with that measured from conventional tagging in both compressible phantom and in-vivo. SF-CSPAMM was used for comparison because of its accurate representation of the in-plane strain even in the existence of through-plane motion. Another approach for validation would be using a model that incorporates measuring the material properties of the phantom and the applied forces. However, this would require the measurement of the exact force distribution during the MR imaging, which would add to the complexity of the imaging setup.

In addition to saving imaging time, a complete slice-following 3-D strain tensor map for a pair of zHARP slices is calculated in less than two seconds on a personal computer using Matlab® (Mathworks, Natick, MA) on a 2.33GHz CPU with 4GB of RAM. Thus, the 3-D strain mapping of the whole heart can be calculated in less than 20 seconds. The proposed algorithm does not require extensive post-processing to estimate 3-D motion at the intersection of LA and SA slices as it is the case with other 3-D strain quantification methods.

Although 3-D MRI provides inherently higher SNR than multi-slice 2-D imaging, zHARP has been shown to have adequate SNR for reproducible myocardial strain quantification (Abd-Elmoniem et al., 2007a) at 3 Tesla MR systems.

The original implementation of zHARP required two breath-holds for every imaged slice. However, scan time can be abbreviated significantly using reduced field-of-view techniques and limited k-space acquisition, which were successfully implemented for real-time strain monitoring using HARP (Sampath et al., 2003; Abd-Elmoniem et al., 2007b) and SENC (Pan et al., 2006). Current works in progress include the fast acquisition of conventional 3-D tagging data of the whole heart in three breath-holds (Rutz et al., 2007) as well as reducing zHARP acquisition from two breath-holds per slice to two breath-holds for the whole heart (Abd-Elmoniem et al., 2008).

Correlation plots suggest that strain components calculated with the proposed method are strongly correlated with the strain components calculated using the conventional HARP analysis. However, more rigorous testing and validation may be required but experimental hurdles related to the MRI environment have to be considered.

The approach presented here should have clinical application when 3-D functional quantification and full coverage of the heart is required. It should also prove useful in scientific investigations in 3-D cardiac modeling. Difficulties with the registration of LA and SA slices, occurring in some existing methods, are now eliminated. As well, the combination of point tracking with 3-D strain measurement, inherent in our method, allows the computation and display of strain for every material point as it moves throughout the cardiac cycle, providing a strong connection and exciting new possibilities for the validation of existing finite element cardiac models.