Assessment of Renal Function with Dynamic Contrast Enhanced MR Imaging

Abstract

MRI is a promising non-invasive modality that can provide a comprehensive picture of renal anatomy and function in a single examination. The advantages of MRI are its high contrast and temporal resolution and lack of exposure to ionizing radiation. In the past few years, considerable progress has been made in development of methods of renal functional MRI and their applications in various diseases. This article reviews the key factors for acquisition and analysis of dynamic contrast-enhanced renal MRI (MR renography) and the most significant developments in this field over the past few years.

Introduction

The primary functions of the kidneys are to filter and excrete metabolic waste products and maintain homeostasis by regulating acid-base balance, blood pressure, and fluid volume. Assessment of the renal function is often required in radiological diagnosis, mainly for assessment of renal insufficiency, renovascular disease, metabolic disorders, renal transplants, and abdominal trauma. Non-invasive tests of renal function can be also helpful in longitudinal and translational studies.

Several non-invasive tests of renal function have been developed. These include measurements of serum creatinine level and endogenous creatinine clearance, renal scintigraphy and contrast-enhanced (CE) computed tomography (CT). However, these methods have serious drawbacks. Creatinine indicators are imprecise and depend on body mass and age and cannot assess a single-kidney function. Renal scintigraphy requires radioactive tracers and provides little information about the kidney anatomy. CT has excellent spatial resolution, but exposes the patient to radiation and potentially nephrotoxic contrast agents.

Magnetic resonance imaging (MRI) provides highly detailed anatomical information and has shown a great promise in noninvasive assessment of the renal function (1-4). Dynamic contrast-enhanced (DCE) MRI of the kidney, or magnetic resonance renography (MRR) monitors the transit of contrast materials, typically gadolinium (Gd) chelates, through the intrarenal regions, the renal cortex, the medulla, and the collecting system (Figure 1). Most gadolinium contrast agents are cleared by glomerular filtration and pass from the renal vasculature into the renal tubules while enhancing the signal of the renal tissues. Typically, the kidney enhancement shows the following stages: (1) bolus arrival in the large vessels; (2) cortical enhancement (20-30 s after administration of contrast) that mostly reflects the contrast within renal vasculature (Figure 1b); (3) medullary enhancement that usually occurs about a minute later and is dominated by the contrast in renal tubules (Figure 1c); and (4) enhancement of the collecting system several minutes afterwards (Figure 1d). By analyzing the enhancement of the renal tissues as a function of time (Figure 2), one can determine such clinically important single-kidney parameters as the renal blood flow (RBF), glomerular filtration rate (GFR), and cortical and medullary blood volumes (5).

Figure 1.

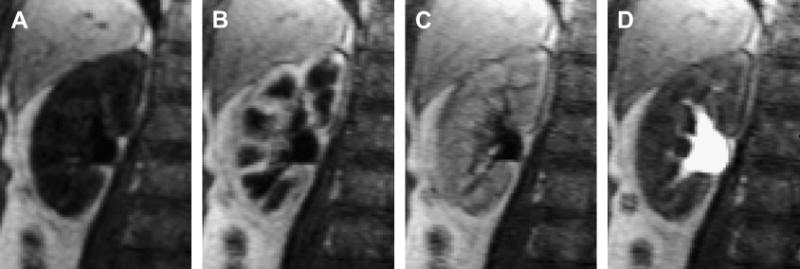
Representative MR renography images of the right kidney of a 65-year-old female patient with normal kidney function showing progressive enhancement of kidney tissue (injected dose 4 mL of Gd-DTPA at 2 mL/s; 3D FLASH, TR/TE/FA=2.84/1.05/12°, voxel volume 1.7×1.7×2.5 mm³): a) unenhanced, b) maximum cortical enhancement, c) maximum medullary enhancement, d) collecting system enhancement.

Figure 2.

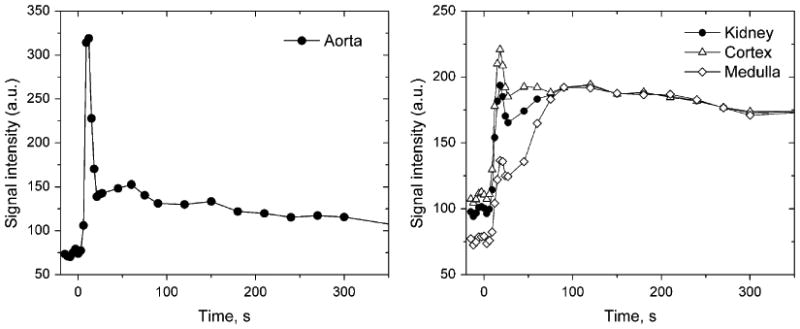
Signal intensity measured in abdominal aorta (a) and cortex and medulla (b) for the same patient as in Figure 1. Rapid first-pass signal changes in aorta and kidneys are sampled every 3 s during the first 30 s. The cortical and medullary signal intensity curves show sharper peaks due to renal vasculature followed by broader peaks due to the contrast in the renal tubules.

The most widely used gadolinium contrast agent is gadopentetate dimeglumine (Gd-DTPA) (6). It is freely filtered by the glomerulus and is neither reabsorbed nor secreted by the renal tubules, which makes it a suitable marker of glomerular filtration. Until recently, gadolinium contrast agents have been considered safe for all patients. However, in the past few years, these contrast agents have been linked with the risk of developing nephrogenic systemic fibrosis (NSF), a debilitating and potentially fatal condition that affects mostly patients with renal insufficiency (with total GFR<30 ml/min/1.73m²) (7,8). So far, about 260 cases of NSF have been reported world-wide (9,10). Therefore, MRR should be performed with caution in patients with decreased renal function, and whenever possible, such patients should be studied with alternative, contrast-free methods.

The MRR studies performed to date have accumulated a wealth of physiological and methodological information relevant for dynamic studies of the kidneys and other abdominal organs. Several excellent reviews of functional renal imaging using MRI have been published by Huang et al (11), Michoux et al (12), Prasad (13), and Michaely et al (14). This article provides an update of the recent developments in T₁-weighted, gadolinium-enhanced MRR and quantification of renal perfusion and filtration based on MRR data.

MR Renography: Key Steps

Numerous MRR studies have been published in the past few years. While there is no consensus regarding the optimal procedure, MRR examination usually consists of the following steps: 1) acquisition of dynamic image series; 2) image post-processing for motion correction and tissue segmentation; 3) quantification of contrast concentration; and 4) analysis of the concentration versus time data leading to derivation of renal functional parameters. These steps are discussed below.

Acquisition

Current MRR studies usually employ T₁-weighted, gradient recalled echo (GRE) sequences. Three-dimensional (3D) acquisitions provide continuous whole-kidney coverage and thus enable assessment of the whole-kidney function, but require longer acquisition times. Two-dimensional (2D) images can be acquired with higher temporal and spatial resolution but sample only selected slices. Also, 2D acquisition of limited number of slices precludes the use of spatial alignment (see below, Image Analysis section) because there is some anterior-posterior renal motion, i.e. perpendicular to the customary coronal acquisition plane.

While most of the published work has been done at 1.0-1.5 T, higher field (3 T) offers better signal-to-noise ratio (SNR) (15). The flip angle is usually selected to maximize SNR and the contrast between the enhanced and unenhanced kidney tissues (16,17). This approach favors lower flip angles. For example, for GRE sequence with repetition time TR=3 ms, the cortical signal with unenhanced T₁=1000 ms is estimated to be about three times higher at flip angle of 12° than at 40°. For expected maximum cortical contrast concentration of 0.4 mM, the contrast between the enhanced and unenhanced cortical signals will be 2.3 times higher for 12° than for 40°. The downside of using lower flip angles is the strong nonlinearity of signal with gadolinium concentration. As an alternative, the flip angle may be chosen to maximize the range and accuracy of the linear relationship between signal and concentration (18,19).

One of the greatest challenges in quantitative functional imaging is the measurement of the signal in arterial blood, which plays the role of arterial input required by majority of tracer kinetic models. The arterial signal is usually sampled in the abdominal aorta and may be affected by the flow-related artifacts. To minimize these effects, imaging can be done in the coronal plane (16,17), or magnetic preparation (saturation or inversion) can be added to axial acquisitions (20-25).

After collecting several unenhanced images for a reliable estimate of baseline signal, dynamic images are acquired every few seconds during free breathing, at separate breath-holds, or a combination of both. Rapid changes of blood and tissue signal intensities during the first-pass enhancement are best captured during breath-holding, while slower-changing subsequent stages may be acquired with quiet breathing or respiratory triggering (17,25). Parallel imaging may be employed to improve temporal resolution of MRR, especially for imaging of the rapid signal changes during the first-pass perfusion, but may provide decreased image quality and therefore is most suitable for imaging when high SNR is expected (26). The temporal resolution used in published MRR studies varies from 1 s during the first-pass phase to 60 s during later (excretion) stages. In experiments on healthy volunteers performed with 1 s resolution, Michaely et al (27) have shown that the temporal resolution of at least 4 s is required to achieve 10% precision in estimates of renal perfusion and filtration rates. Parameters describing the plasma and tubular volumes proved to be more tolerant to temporal resolution and require 9 s sampling interval to reach 10% precision. Note, however, that estimating the precision of renal functional parameters is a complex task, as the precision depends on many factors, including contrast dose and injection rate, arterial sampling scheme, and the choice of the model for parameter identification.

The total acquisition time of MRR series is 3–10 min, with longer time needed to characterize more distal portions of the nephrons. Shorter acquisition time (20-30 s) is sufficient for estimates of renal perfusion, intermediate acquisition time of 2–5 min for assessment of the filtration and tubular properties, and the longest acquisition time is required for characterization of the collecting system. In healthy volunteers, Michaely et al (27) estimated that acquisition time of at least 35 s is required to characterize plasma flow, acquisition time of 85 s is needed for plasma volume, 230 s for tubular flow, and 255 s is needed for tubular volume characterization with precision of 10% or better. Longer acquisition times are needed in patients with decreased renal plasma flow and GFR.

T₁-mapping is sometimes performed prior to MRR to determine the unenhanced T₁ values of the renal tissue for quantification of contrast concentration (Figure 3). Since 3D T₁-mapping within one breath-hold is technically challenging, this measurement is frequently done on a single representative slice through the kidney. Available T₁ measurement methods include dual flip angle technique (17), conventional inversion recovery methods (28), inversion-recovery prepared low-flip angle TrueFISP (29), the Look-Locker method (30), and T₁ fast acquisition relaxation mapping (T₁-FARM) (31).

Figure 3.

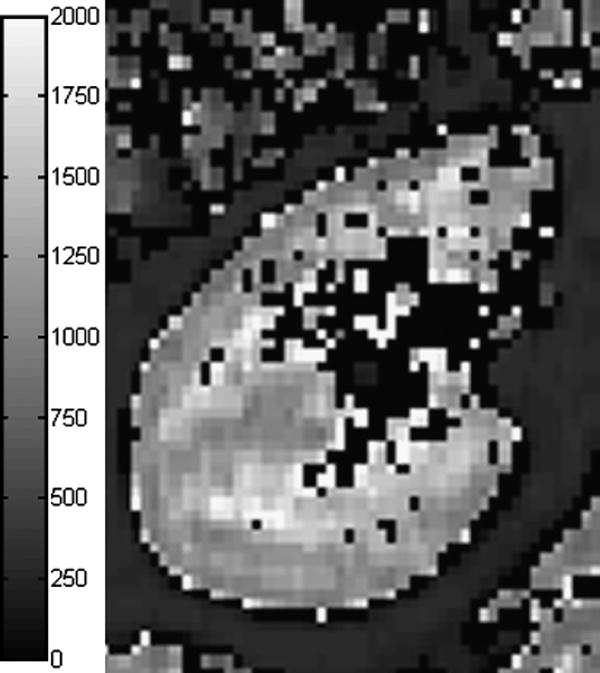
Kidney T₁-map measured with single breath-hold, segmented, inversion-recovery prepared TrueFISP with flip angle of 10° (29). Cortical T₁ is about 1050 ms and medullary T₁ is about 1400-1500 ms. T₁ was set to zero in voxels where fitting failed or yielded T₁ above 2000 ms.

Contrast Dose Selection

Most groups use standard doses of gadolinium for MRR (0.1–0.2 mmol/kg). There is considerable evidence, however, that lower contrast doses do not compromise the precision of renal functional parameters. Using Monte Carlo simulations, our group determined the relationship between the contrast dose and the precision of renography-derived GFR (32). According to this analysis, injected doses of Gd-DTPA above approximately 1.5-2 mmol do not result in increased precision of GFR (Figure 4). The highest GFR precision is achieved at approximately 0.02 mmol/kg dose in normal patients, and approximately 0.025 mmol/kg in patients with decreased renal function. Several studies demonstrated the feasibility of MRR with ultra-low doses, i.e., doses that are up to 10 times lower than the standard ones, and showed that these doses help to avoid the susceptibility effects associated with concentrated gadolinium in renal medulla and collecting system (33,34).

Figure 4.

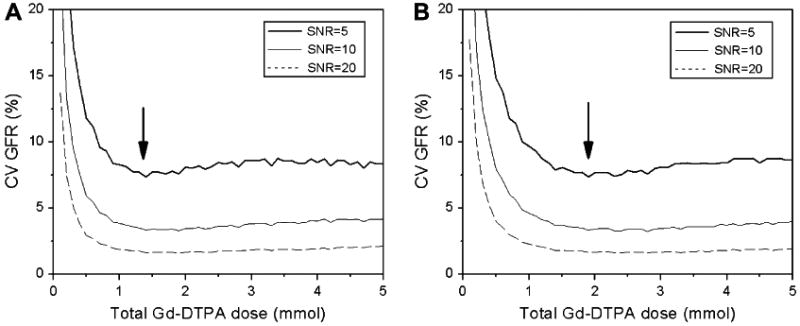
The effect of gadolinium dose on precision of GFR measurement with MRR. Coefficient of variation (CV) of GFR was estimated by Monte Carlo simulations for normal (a) and diseased (b) kidney versus the total injected dose. Arrows indicate the minimum of CV.

Quantification of Contrast Concentration

Kinetic modeling requires that the MRR signal be converted into gadolinium concentration ([Gd]). This conversion presents a challenge because in addition to contrast concentration, MR signal intensity varies with the pulse sequence parameters, the pre-contrast relaxation times, and in the case of blood, the flow velocity (33). Moreover, the relationship between signal and concentration is in general non-linear. At higher contrast concentrations, the susceptibility may cause the signal intensity to decrease with increasing concentration.

The simplest approach is to express gadolinium concentration as the relative enhancement

$$[Gd]=k\frac{S(t)-S(0)}{S(0)}$$ (1)

where S(0) and S(t) are the baseline (at time t=0) and the contrast-enhanced (t>0) signal intensities, respectively. The tissue-dependent constant k can be derived from phantom measurements. However, as the concentration increases, this linear relationship is associated with progressively increasing errors.

Gadolinium concentration can also be computed from analytic expressions of signal intensity. For example, the spoiled gradient echo signal intensity is given by (35):

$$S(t)=S_0\text{sin}\alpha \frac{1-e^{-R_1(t)TR}}{1-\text{cos}\alpha \cdot e^{-R_1(t)TR}},$$ (2)

where S₀ is the equilibrium signal, α is the flip angle, TR is the repetition time, and R₁=1/T₁ is the longitudinal relaxation rate. Eq. (2) can be solved for R₁(t), enabling [Gd] to be derived from the relationship:

$$R_1(t)=R_1(0)+[Gd]r_1$$ (3)

where R₁(0) is the longitudinal relaxation rate of tissue before contrast injection and r₁ is the specific relaxivity of the contrast agent. The specific relaxivity of a contrast agent required by Eq. (3) may depend on the surrounding medium (36), and in vivo measurements of relaxivities are particularly challenging. Specific relaxivities of commonly used contrast agents were recently measured at different fields, temperatures, and in different media (water, saline, plasma, whole blood) (37,38). The resulting relaxivities were somewhat lower than the commonly used values. Rohrer et al (37) found for Gd-DTPA at 1.5T and 37°C, r₁=4.1 (mmol/L)^-1 s^-1 in plasma and 4.3 (mmol/L)^-1 s^-1 in whole blood. At 3T and 37°C, the plasma r₁ was decreased to 3.7 (mmol/L)^-1 s^-1. Pintaske et al (38) obtained similar values, also for Gd-DTPA at 37°C in plasma: at 1.5 T r₁ was 3.9 (mmol/L)^-1 s^-1, and at 3T r₁ decreased to 3.3 (mmol/L)^-1 s^-1.

Alternatively, the relationship between the signal intensity and T₁, denoted f(T₁), may be determined empirically by imaging a gadolinium-doped water phantom, either imaged separately or together with the subject (20,21,25,39). The tissue signal intensity is assumed to be proportional to f(T₁) scaled by a numerical factor g which depends on system gain, coil sensitivity, and patient habitus:

$$S=g\cdot f(T_1).$$ (4)

The coefficient g can be found from a pair of closely matched signal and T₁ measurements, for example, acquired before the injection of contrast. We have shown that for 3D FLASH sequence the phantom-derived f(T₁) dependence is similar to this relationship in human tissues (Figure 5) (39). Compared with the concentrations determined by direct T₁-mapping, concentrations calculated from in vivo MRR signal intensity measurements agreed on average within 13% (r=0.99) up to 1.4 mM when the phantom-based conversion method was employed; whereas the relative enhancement conversion progressively underestimated the concentrations above 0.8 mM by 20% or more.

Figure 5.

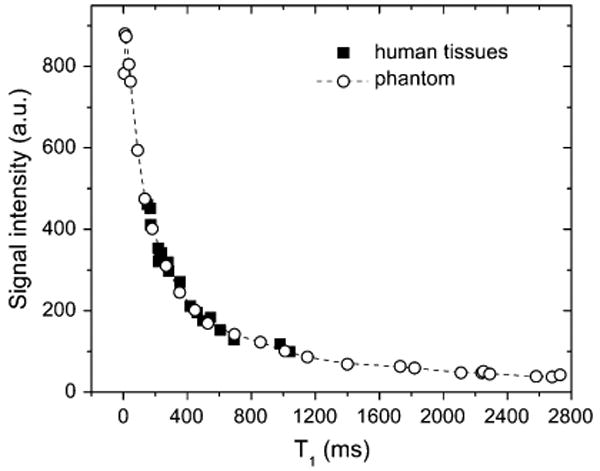
Signal intensity versus T₁ relationship derived from imaging a gadolinium-doped water phantom and in vivo human tissues (after Ref. (29)). The signal versus T1 dependence in the phantom and human tissues appears to be similar.

However, signal calibrations with static phantoms do not account for the variations of the signal intensity due to rapid flow in large blood vessels. The inflow of fresh blood with fully polarized spins causes the flow-related signal enhancement which may result in incorrect arterial concentration and errors in renal functional parameters. To account for inflow effects, Ivancevic et al (40) performed signal intensity versus concentration measurements at varying flow velocity in flow phantoms and applied this calibration to renal perfusion imaging. The calibration had a particularly strong effect on the concentration at the bolus peak. In the phantom, the bolus peak concentration obtained with static calibration was 3.2 times higher than the flow-corrected value, which was not significantly different from the directly measured concentration. In axial fast gradient echo acquisitions performed in patients, without the flow correction, the peak aortic concentration measured at systole was 2.5 times larger than at diastole; but when flow-corrected conversion was employed, the difference between systolic and diastolic measurements became insignificant. The discrepancy between systolic and diastolic measurements of the bolus peak concentration was reduced from 180±37% with static calibration to 21±15% with flow correction.

Coronal acquisitions may help minimizing the inflow effect; however, the problem persists in patients with tortuous aorta. As an alternative, some groups have investigated the use of population-based arterial curves (41-43). Parker et al (41) derived an average aortic curve from 67 MRI examinations of 23 cancer patients and obtained 40% narrower confidence intervals in repeated intraindividiual measurements of perfusion parameters than with the individually measured arterial input. Wang et al (42) reported an excellent correlation (r>0.99) and no significant differences between perfusion parameters derived with individually measured and averaged arterial input functions sampled in femoral arteries of patients with osteosarcomas.

Image Analysis

MRR image post-processing typically consists of image co-registration and segmentation. Co-registration involves spatial aligning of the renal images at different time points, and segmentation is often required to identify the anatomical subregions of the kidney. The analysis of dynamic images is a time-consuming and laborious task, which is particularly demanding for free-breathing acquisitions and larger 3D datasets. Although image registration and segmentation algorithms have been actively researched in recent years, few of them have been applied to the kidney. Absence of reliable image analysis software is one of the factors that limit implementation of MRR in clinical practice.

Outside the brain, co-registration often involves identification of the image features, such as anatomical landmarks or surfaces (44-46). Segmentation may simply involve manual drawing of regions of interest (ROIs) (17,20,21). However, manual segmentation is tedious, time-consuming, and requires anatomical expertise. Moreover, if only small subregions are sampled, the total renal volume required for GFR and RPF estimates remains unknown and the resulting enhancement curves may not be representative of the entire organ. Alternatively, using automated or semi-automated algorithms, the entire kidney may be segmented from the surrounding tissues and collecting system, and the renal parenchyma may be further divided into cortex and medulla (5,47-50) (Figure 6).

Figure 6.

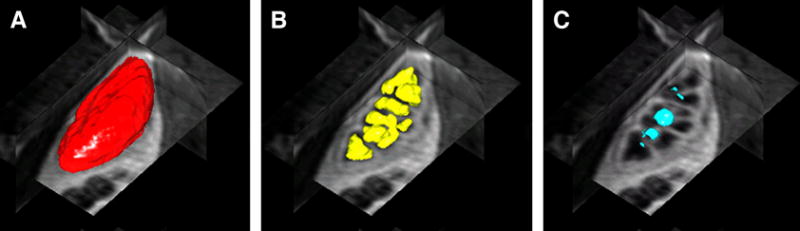
3D renderings and orthogonal views of renal tissue segmented using level sets algorithm of Song et al (47) (a) whole kidney (b) medulla (c) renal pelvis.

A semi-automated tissue segmentation algorithm developed by Boykov et al (51) enables segmentation of MRR images into cortex, medulla, and collecting system regions based on an interactive graph cuts approach. Rusinek et al (52) assessed the accuracy and precision of segmentation with this algorithm applied to simulated and in vivo data in comparison with manual segmentation performed by experienced readers. The semi-automatic segmentation produced a slight systematic oversegmentation of cortex at the expense of medulla (volume errors of about 10% in the cortex and 21% in the medulla relative to their true volumes). The precision of the segmentation was on average 5% in the cortex and 7% in the medulla. Renal plasma flow (RPF) and glomerular filtration rate (GFR) derived from these data using a tracer kinetic model were determined with clinically acceptable accuracy and precision (both below 10% for RPF and below 15% for GFR). The processing time was reduced from 2-3 hours required for manual processing to about 21 minutes per kidney using semi-automatic segmentation.

As an alternative to tissue segmentation, a voxel-by-voxel analysis has also been applied to MRR (19,24,25). With this approach, the signal intensity in each voxel is traced across all time points and analyzed with an appropriate method. This approach provides local information about the kidney function and usually eliminates the need for a separate segmentation step, but is more computationally intense and more susceptible to misregistration errors and signal noise than segmentation-based analysis. Also, voxel-based analysis does not evaluate the whole-kidney function, unless followed by further processing steps.

Renal perfusion quantification: clinical applications

Assessment of renal perfusion is helpful in several renal diseases: for assessment of renal artery stenosis (RAS) and in renal transplant dysfunction (chronic ischemic nephropathy, and drug nephropathy). Several methods have been used to quantify the renal perfusion from MRR, such as the upslope method, the semi-quantitative parametric methods, deconvolution methods, and various compartmental models. It has to be noted, however, that low molecular weight contrast agents, such as Gd-DTPA (molecular weight 590 Da), quickly leak from the bloodstream into the extracellular extravascular space and may provide incorrect estimates of perfusion. More accurate perfusion measurements may be obtained using intravascular contrast agents described in the next section.

The upslope method has been initially devised by Peters et al (53) for nuclear medicine and adapted for MRI. It is based on a simplified picture of contrast behavior akin to microspheres: the tracer flowing into the kidney is assumed to remain in the kidney vasculature. This “inflow only” approximation is valid until the contrast begins to flow from the renal vasculature into the renal tubules. RBF can be found as the maximum slope of the kidney curve divided by the peak arterial concentration:

$$\text{RBF}=\frac{\text{max slope}(K(t))}{\text{max}(A(t))}.$$ (5)

Montet et al (23) used the upslope method to estimate the cortical RBF from dynamic MRI in 9 rabbits. Reference RBF values were measured in the renal artery using an ultrasound (US) flow probe. Experiments were performed at baseline and after a modification of the renal blood flow by an intervention, either by mechanical renal artery stenosis (ipsilateral to the flow probe) or administration of medications. The results demonstrated the benefits of taking into account the arterial input as opposed to using the maximum upslope of the kidney concentration curve alone as a measure of renal perfusion. The US RBF measurements correlated considerably better with the absolute RBF estimates (r=0.80) than the maximum upslope of the kidney curve (r=0.53).

Valée et al (22) applied the upslope method to quantifying renal blood flow in 27 subjects with normal kidneys, well-functioning renal transplants, and kidneys with RAS and renal failure. For functioning kidneys, the average blood flow was found to be 2.54 ± 1.16 mL/min/g in the cortex and 1.08 ± 0.50 mL/min/g in the medulla. In transplanted kidneys both cortical and medullary flows were increased by 30-40% compared to native kidneys. Compared to all functioning kidneys (native and transplant), cortical and medullary flows were 50-60% lower in kidneys with RAS and 70-80% lower in patients with renal failure.

Pedersen et al (54) compared the upslope estimates of RBF in rats subjected to either unilateral renal artery occlusion or partial ureteral obstruction against rats in which the left ureter was dissected 1 hr before MRI (sham-operated). Normalized to the intact side, RBF on operated side was the lowest in kidneys with arterial occlusion (0.35±0.02), slightly higher in kidneys with obstructed ureters (0.40±0.03) and the highest in sham-operated kidneys (0.49±0.01).

The advantage of the upslope method is its simplicity, while its main drawback is the need to measure the maximum of the arterial concentration, which is unreliable. The limited amount of data used for analysis, usually the first 20-30 s after injection, makes it more susceptible to errors, especially at low temporal resolution. The inflow-only approximation may be invalid in well-perfused kidneys beyond the first few seconds after the bolus arrival.

Feasibility of semi-quantitative, parametric evaluation of patients with renal artery stenosis (RAS) was reported by Michaely et al (24). The 2D data were acquired with saturation-recovery TurboFLASH sequence at 1 s temporal resolution for at least 4 min. High resolution MR angiography (MRA) served as the reference technique for detection and grading of RAS. Kidney enhancement curves were fitted with an empirical expression that consisted of a gamma variate function to describe the first-pass perfusion and a double-exponential function to describe the filtration. Four curve parameters were derived from voxel-by-voxel fitting: time to peak (TTP), mean transit time (MTT), maximum upslope (MUS), and maximum signal intensity (MSI). Significant differences were observed in MUS, MTT and TTP between the combined group of normal and low-grade RAS versus the high-grade RAS, but kidneys without RAS and those with low-grade RAS could not be distinguished. MTT and TTP correlated strongly (r=0.96), and TTP and MUS showed moderate negative correlation (r=-0.6). Highly significant, but moderate correlations were found between all four parameters and serum creatinine (|r|∼0.4-0.5). MUS voxel maps enabled detection of segmental perfusion deficits in 3 kidneys in areas confirmed to be ischemic by biopsy.

Deconvolution approach to calculation of renal perfusion and filtration was employed by Hermoye et al (21). The MRR experiments were carried out in six rabbits with a saturation-prepared turbo field echo sequence at 1.1 s temporal resolution. After phantom-based conversion, the arterial input was numerically deconvolved from the cortical curve. The resulting cortical impulse response function (IRF) was expected to exhibit three peaks corresponding to the contrast passing sequentially through the glomeruli, proximal convoluted tubules and distal tubules. The vascular and the proximal tubules peaks were fitted by a sum of two gamma variate functions. The fractional plasma volume (FPV) and the vascular mean transit time (MTT) were determined from the area under the curve and the washout rate of the vascular curve. The renal perfusion was found as the ratio of FPV to MTT and correlated well with the results of the upslope method (r=0.9). As expected for numerical deconvolution, the errors in RPF and other parameters were shown to increase dramatically with noise level. At 5% noise, the error in RPF was about 20% relative to the ideal value, and at 10% it was about 50%.

The feasibility of voxel-based deconvolution analysis of MRR in human kidneys was demonstrated by Dujardin et al (19). The perfusion parameters were determined in 14 volunteers and 1 transplant patient using inversion-recovery prepared TurboFLASH sequence. A flip angle of 50° was used to improve the linearity of the signal versus concentration. The arterial input function was numerically deconvolved from the renal curves to determine the IRF in every voxel. The maximum of the IRF, the area under the IRF curve, and the ratio of the integral to the maximum were respectively interpreted as RBF, renal volume of distribution (RVD), and MTT. The average shape of observed IRF was similar to that obtained by Hermoye et al (21). In native kidneys RBF was 1.6 mL/min/mL and ranged from 0.8 and 4.5 mL/min/mL. Cortical RBF was found to be three times higher than the medullary RBF. Both the perfusion and the cortex-to-medulla ratio were lower than those reported elsewhere (55,56). This underestimation was attributed to deconvolution errors, dispersion of the aortic bolus, and the inflow artifact in the aorta.

A two-compartment model proposed by Annet et al (20), in which the concentration in renal vascular compartment is determined by dispersion and delay of the aortic bolus, enables calculation of vascular volume and RBF (Figure 7). However, the experiments of Annet et al focused on assessing renal filtration, and perfusion estimates were not reported.

Figure 7.

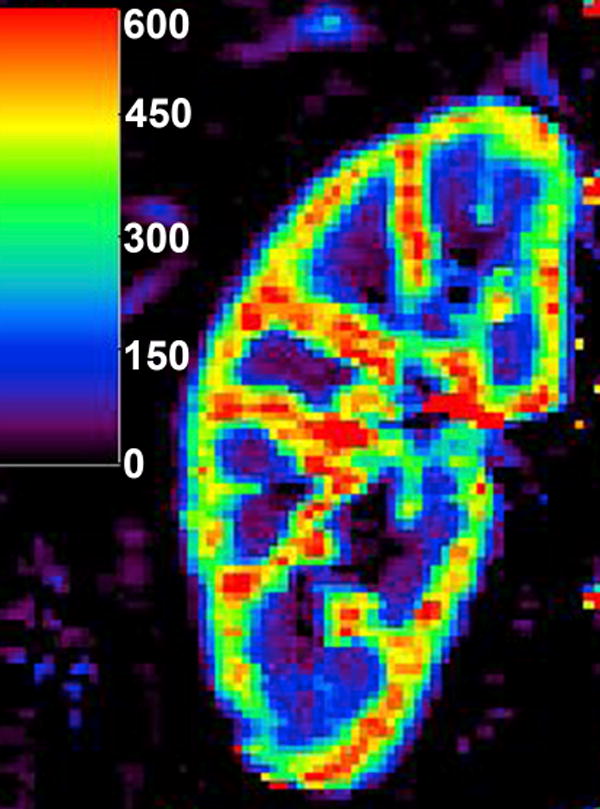
Perfusion map calculated with two-compartment model of Annet et al (20) in a normally functioning kidney. The units of the color bar are mL/min/100mL. The regions of extremely high flow (red) are likely to reflect the renal vessels.

The reviewed results suggest that both semi-quantitative and fully quantitative measures of perfusion can be useful in assessment of renal function. Semi-quantitative parameters, such as the time to peak and maximum upslope, are usually robust and easy to assess, but have limited physiological interpretation and cannot always be compared across different patients. The quantitative perfusion methods include simple inflow models, compartmental models, and deconvolution methods. The upslope method is simple, but relies on the initial part of the first-pass peak, which often contains just few data points, and on the inflow-only approximation, which may not be valid in the kidney beyond the first few seconds after the bolus arrival. The numerical deconvolution methods are sensitive to noise, more so than the compartmental models. All of the quantitative methods require measurements of the arterial input function AIF, which may be unreliable because of sampling errors and inflow artifacts. Because AIF is usually sampled in the aorta, the dispersion and delay of the bolus confounds the modeling. As a result, renal perfusion estimates are highly sensitive to the variations of the arterial input. Further comparisons of the MRR-derived perfusion against other established methods are needed.

Renal Perfusion Imaging Using Intravascular Contrast Agents

Unlike the low molecular weight contrast agents, such as Gd-DTPA, which quickly distribute over the interstitial space, the so-called intravascular contrast agents stay in the bloodstream for a considerably longer time. Since these agents have not yet been approved for clinical use, data mostly from animal experiments are available, although few human studies have been also reported.

Prasad et al (57) reported perfusion measurements using MS-325 (EPIX Medical, Cambridge, MA), a gadolinium-based intravenous contrast agent that binds to serum albumin in plasma. Protein binding reduces leakage of contrast out of the vasculature and thus increases the half-life of contrast in plasma. Pigs with surgically induced RAS were injected with MS-325 and imaged with turbo-FLASH sequence, and cortical blood flow and mean transit time were estimated from the first-pass perfusion data using the upslope method. The resulting perfusion measurements agreed well with the reference microsphere experiments (258 mL/100 g/min versus 198 mL/100 g/min, respectively), but neither indicated any significant reduction in cortical perfusion over 5 weeks after surgery, which may be attributed to the ability of the kidney to regulate blood flow.

Aumann et al (55) employed the intravenous ultrasmall particle iron oxide (USPIO) contrast agent NC100150 to measure perfusion in eight dogs with ultrasound flow probes implanted at the origin of the left renal artery. This agent is cleared from blood by reticuloendothelial system and is not filtered by the kidney at all. As a result, the kidney enhancement reflects only perfusion and is free from the effects of filtration and excretion. Dynamic imaging was performed with a T₂*-weighted FLASH sequence (TR/TE/FA=15/6/12°, temporal resolution 1.92 s), and US flow measurement was done immediately prior to and after the MR measurement. Voxel-based renal perfusion yielded RBF of 524 ± 47 mL/min/100g versus the US-measured value of 403 ± 72 mL/min/100g with moderate correlation (r=0.71). The renal blood volume was found to be 27 ± 3.6 mL/100g and the MTT was 3.4 ± 0.5 s. Thus, the MR perfusion measurements overestimated both the blood flow and the blood volume compared to generally accepted values.

In a subsequent study, Schoenberg et al (56) applied a similar measurement technique and the same contrast agent to dogs with surgically induced RAS and in humans with longstanding RAS. The baseline RBF in dogs was 496 mL/min/100 g and remained almost unchanged for stenosis up to 50% and decreased to 379 mL/min/100 g at stenosis of 80%. At further reduction of renal artery diameter to above 90%, RBF dropped to 151 mL/min/100 g. In human kidneys with parenchymal damage due to RAS RBF was considerably lower than in normal kidneys (166 mL/min/100 g versus 379 mL/min/100 g, respectively), while the blood volume was slightly lower in kidneys with RAS than in normal ones.

Glomerular Filtration Rate

A variety of methods have been proposed for quantification of renal filtration, ranging from simpler upslope models, to more complex compartmental models (Figure 8). Published GFR estimates from tracer-kinetic analysis of MRR data are summarized in Table 1. These models share some common assumptions. The kidney is usually represented as a combination of at least two homogeneous compartments, vascular and tubular, and GFR is found as the flow of contrast from the vascular into the tubular compartment.

Figure 8.

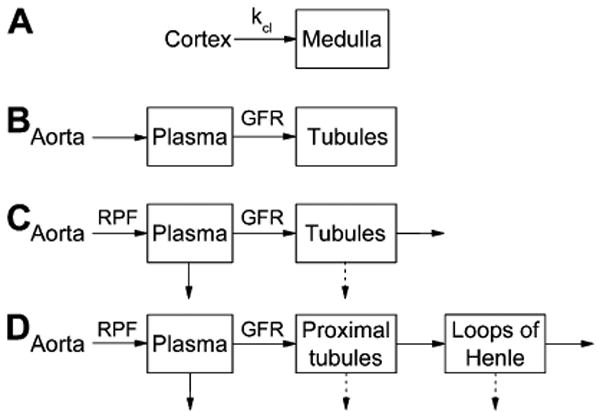
Tracer kinetic renal models for GFR calculation: a) Baumann-Rudin model; b) Patlak-Rutland model; c) two-compartment models of Annet et al (20) and Buckley et al (17); d) three-compartment models of Lee et al (5) and Zhang et al (63). In (a), k_cl is the clearance coefficient related to GFR. Ao is the aortic concentration; Cx and Med are cortical and medullary concentrations. A, P, and L are the arterial, proximal tubules and loops of Henle compartments, respectively. Solid arrows indicate the flow of contrast, and dashed arrows indicate the flow of contrast-free fluid.

Baumann and Rudin proposed an inflow-only model in which the contrast flows from cortex to medulla with the rate given by the filtration coefficient (Figure 8a) (58). The cortex plays the role of the vascular compartment, and the medulla of the tubular compartment. The outflow of contrast from the medulla is ignored. In experiments on rats, Laurent et al (59) have shown that the filtration coefficient correlated with GFR measured by inulin clearance (r=0.75). A development of this model has been recently proposed by Zhang et al (60). Both Baumann-Rudin and Zhang models have an attractive property of not requiring the arterial input function.

Adapted from cerebral perfusion, Patlak-Rutland method has been applied for GFR calculations. This method is based on a two-compartment model, in which the outflow from the second, tubular compartment is ignored (Figure 8b). In its traditional graphical implementation, the ratio of kidney K(t) to aortic concentration Ao(t) is plotted versus the ratio of the integral of Ao(t) to Ao(t). GFR is found as the slope of the linear regression to this curve and the vascular volume fraction as its intercept. Resulting GFR depends on the choice of the time interval used in computing the linear regression. In MRR experiments on healthy volunteers and using slower contrast injections, Hackstein et al (61) found that GFR values determined from the interval of 30-90 s correlated best with reference measurements. This interval coincides with the uptake of contrast by the renal tubules in a normal kidney (Figure 1). The correlation of Patlak-Rutland GFRs with the reference improved considerably at higher contrast doses and reached r=0.83 at 16 mL of Gd-DTPA (in commercially available 500 mM dilution). This finding suggests that Patlak-Rutland method may not be optimal for low-dose MRR experiments or for protocols that provide lower number of acquisitions within the tubular uptake interval.

Buckley et al (17) compared GFRs estimated with Patlak-Rutland method and its extension, a two-compartment model (inspired by the widely-used cancer perfusion models (62)) in which the outflow from the tubules is accounted for (Figure 8c). Both methods were applied to 35 patients with atherosclerotic renovascular disease. Dynamic 3D images were acquired with GRE sequence during free breathing at 4.5 s temporal resolution for up to 3.5 min. Data were extracted from an ROI drawn around the kidney parenchyma on a single mid-coronal slice. Arterial input was measured in the abdominal aorta. Single-kidney GFR values obtained by both methods correlated significantly with the reference GFRs measured by ⁵¹Cr-EDTA clearance and renal scintigraphy: Spearman correlation coefficient was ρ=0.81 for Patlak-Rutland and ρ=0.71 for the extended model. The extended model overestimated GFR by almost 100%, while Patlak-Rutland method overestimated them by about 30%. Such overestimation may be due to the use of a single mid-kidney slice, in which the volume fraction of medulla is higher than in peripheral slices. The subjects' mean global reference GFR was only 35 mL/min, which suggests severely decreased renal function. In such patients, the kidney uptake is low and slow, and the interval of 3.5 minutes may not be sufficient to characterize the outflow from the tubules, which may cause unreliable fitting with the compartmental model.

Higher GFR values produced by a compartmental model relative to Patlak-Rutland model were first observed by Annet et al (20). Experimenting on rabbits, this group analyzed the cortical concentration curves with Patlak-Rutland method and a two-compartment model that accounts for tubular outflow and the spread of the bolus in the renal vasculature (Figure 8c). Unlike Buckley et al (17), GFR obtained from Annet's model underestimated the reference GFR measured by ⁵¹Cr-EDTA clearance. The extended model correlated better with reference GFRs (r=0.82) than Patlak-Rutland method (r=0.74). The relationship between the two methods was similar to that found by Buckley et al, i.e., lower GFRs were obtaind with Patlak-Rutland method compared to the extended model. The latter is likely due to neglecting the outflow in Patlak-Rutland method.

Similar results were obtained by Sourbron et al (25) in 15 healthy volunteers, whose MRR images were analyzed voxel-wise with both Patlak-Rutland model and the two-compartment model similar to that of Annet et al (20). Both cortical and whole-kidney perfusion and filtration flows were determined. In agreement with Annet et al (20) and Buckley et al (17), the full inflow-outflow model applied to whole-kidney data provided higher rates of perfusion (229 mL/min/100 mL) and filtration (31 mL/min/100 mL) than Patlak-Rutland model (210 mL/min/100 mL and 24 mL/min/100 mL, respectively). Cortical data provided higher perfusion, but lower filtration flow values (340 and 21 mL/min/100mL with compartmental model; 331 and 15 mL/min/100 mL with Patlak-Rutland model).

A three-compartment model proposed by our group (5) makes use of separate cortical and medullary curves derived from segmented 3D kidney images (Figure 8d). Each tissue is thought to include the contributions from two compartments: a shared vascular compartment and a tubular compartment, proximal tubules in the cortex, and loops of Henle in the medulla. As in other renal models, the concentration in abdominal aorta provides the input function and is used to infer the concentration in the vascular compartment, from which the contrast passes into the proximal tubules and then into the loops. Besides RPF and GFR, this model also yields cortical and medullary vascular volume fractions and fractions of contrast-free flow reabsorbed in proximal tubules and loops. Applied to 3D MRR data of 10 patients (20 kidneys) imaged using 3D FLASH (TR/TE/FA=2.84/1.05/12°), the model produced GFRs in good correlation with the reference measurements from ^99mTc-DTPA clearance and scintigraphy (r=0.84; or r=0.93 without one outlier kidney with multiple renal cysts) and a slight underestimation of GFR. As estimated by Monte Carlo simulations, for 5% concentration noise, the errors in RPF and GFR were approximately 10% and 5%, respectively, for a well-functioning kidney, and slightly lower for a dysfunctional kidney. The errors were below 12% for vascular volumes, but much higher in reabsorbed fractions (23-30% in healthy case and over 300% in dysfunctional kidney). The model was also shown to provide robust estimates of GFR for different widths of aortic inputs.

To account for non-instant mixing of contrast, we extended this model by considering a minimum transit time that is required for tracer to traverse each compartment into a model based on the same arrangement of compartments as the previous model (63) (Figure 8d). The model provides seven free parameters, including RPF, GFR, minimum transit times and mean transit times. Zhang's model yields significantly better curve fits: the average relative root mean square error was 11.6% versus 15.5% obtained by the model of Lee et al (5). Importantly, the model of Zhang et al provided substantially more reliable fitting of the data from dysfunctional kidneys (Figure 9). Despite the higher number of parameters, their stability in the presence of the data noise was also improved, with errors in both RPF and GFR lower than 3% for both well-functioning and diseased kidneys. There was a good correlation of model-derived GFRs against radionuclide measurements (r=0.82) similar to that obtained with Lee et al model, although the GFR values were more strongly underestimated (on average by 41% versus 34% by Lee et al model) (Figure 10).

Figure 9.

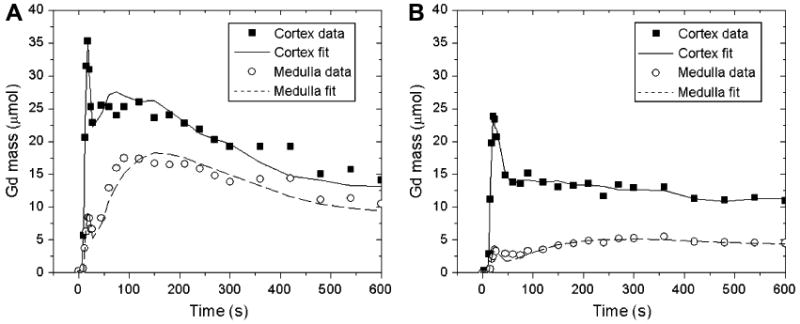
Gadolinium residue (mass) in the cortex and medulla of a functioning kidney (a) and a diseased kidney (b) fitted by the three-compartment model of Zhang et al (63). Cortical and medullary residues are considerably lower in diseased kidney (b) than in the functioning kidney (a), but Zhang's model provides good curve fits in both cases.

Figure 10.

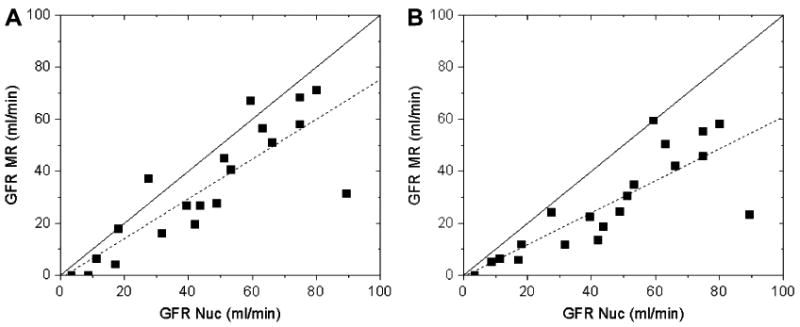
Single-kidney GFRs obtained from the same data using models of Lee et al (5) (a) and Zhang et al (63) (b) versus the GFR values from the same-day nuclear medicine measurements. Both models underestimate GFR, especially Zhang's model, but provide comparable correlations with radionuclide measurements. The linear regressions (dashed lines) are y = 0.76x -1.14 (r = 0.84) (a) and y = 0.61x − 0.32 (r = 0.82) (b). Solid lines are the identity lines.

GFR Quantification from Clearance Measurements

Choyke et al (1) compared GFR measured from clearance of ^99mTc-DTPA (GFR_Tc) with GFR determined from clearance of Gd-DTPA (GFR_Gd) in 90 patients based on three urine and blood samples calculated using the standard clearance equation

$${\text{GFR}}_{\text{contrast}}=\frac{F\cdot U}{P}$$ (6)

where F is the urine flow rate, and U and P are the concentrations of contrast in urine and plasma, respectively. The concentrations of Gd-DTPA in urine and plasma were determined by measurements of the T₁ values of both fluids using nuclear magnetic resonance (NMR) spectrometer and an experimentally derived relationship to convert T₁ into Gd-DTPA concentration. The correlation of GFR_Gd and GFR_Tc was high (r=0.94) and the coefficient of variation of their differences was only 3.6%. A similar study was performed by Ros et al (2) to determine GFR from plasma clearance of Gd-DTPA with MR angiography and MR renography. Again, the correlation between GFR_Gd and GFR_Tc was found to be high (r=0.98) and the standard error was 3.85 mL/min.

Boss et al (64) measured GFR by capturing the clearance of gadobutrol from kidney and liver tissues of healthy volunteers over a long period of time (70 min) using a navigator-gated turbo-FLASH sequence. The rate of exponential decrease of MR signal intensity with time is equal to the ratio of GFR and extracellular fluid volume, with the latter estimated from the weight and height of the subjects. The best estimates of GFR were obtained from measurements between 40 and 65 min after the injection of contrast, as compared to the simultaneous measurements of iopromide clearance from plasma, and were found to be within 5.9±14.6 mL/min from the reference values. The mean half life time of gadobutrol in renal cortex was found to be 92.6±23.7 min. This approach to measurements of GFR has a number of limitations, such as the long imaging time and resulting susceptibility to motion artifacts, the reliance on the subject's height and weight to estimate the extracellular fluid volume, and inability to provide the differential renal function.

Limitations and future directions

MRR suffers from several limitations. The fundamental limitation of MRR is the decrease of SNR with decreasing kidney function, since the uptake of contrast in diseased kidneys is reduced compared to normal kidneys. Thus, MRR studies of diseased kidneys may not be able to provide as much information as those of well-functioning kidneys. Determination of physiological parameters from MRR data requires several steps, including acquisition, image analysis, signal-to-concentration conversion, and tracer kinetic modeling. Each of these steps may contribute errors to the final results. Currently, there is no agreement regarding the best acquisition scheme. The tools for image analysis of dynamic data are lacking. Tracer kinetic models for analysis of renal data provide varying results despite many shared assumptions and these variations have not been reconciled. Most tracer kinetic models require measurements of arterial input function which requires acquisitions with high temporal resolution and may suffer from inflow artifacts. Studies verifying MRR derived kidney parameters against reference measurements are scarce.

Future work includes overcoming these challenges and designing optimal protocols and tools for comprehensive analysis of MRR data, including co-registration, segmentation, and voxel-based modeling.

Conclusions

Quantitative evaluation of renal function, most importantly, perfusion and filtration, is often required for diagnosis and monitoring of vascular diseases, hypertension, obesity, diabetes, renal transplantation, and obstruction of the urinary tract. In research settings, MR renography has been shown to provide excellent anatomical detail and functional information in a single examination. MRR has been researched since the late 1990s and particularly actively in the past few years when the imaging technology has matured to provide dynamic acquisitions with adequate spatial resolution and temporal resolution of few seconds. Numerous studies reported measurements of renal perfusion and filtration with promising results. The results tend to vary greatly among groups and are difficult to compare as there is little agreement regarding the optimal experimental technique. Also lacking are the image analysis tools for post-processing of large dynamic datasets. Greater understanding of the analytical methods, such as tracer kinetic models, is essential as well as the validation studies comparing the MRR-derived functional parameters with those determined by established measurement techniques. Nevertheless, recent developments in MRR are highly encouraging and will hopefully lead to a consensus methodology. However, the implementation of MRR in clinical practice has been hindered because of the recently established connection between exposure to gadolinium contrast agents and developing NSF in patients with renal insufficiency. Such patients may be evaluated using MRR enhanced with macrocyclic contrast agents or by contrast-free methods, such as arterial spin labelling (ASL) and blood oxygenation level dependent (BOLD) imaging.

With the development of reliable methods, MRI can become a one-stop modality that combines morphological assessment with quantitative functional measures. While further research is clearly needed to develop a clinically useful strategy, MRR has the potential to become the leading diagnostic method for renal impairments.