Abstract
RNA tertiary motifs play an important role in RNA folding and biochemical functions. To help interpret the complex organization of RNA tertiary interactions, we comprehensively analyze a data set of 54 high-resolution RNA crystal structures for motif occurrence and correlations. Specifically, we search seven recognized categories of RNA tertiary motifs (coaxial helix, A-minor, ribose zipper, pseudoknot, kissing hairpin, tRNA D-loop/T-loop, and tetraloop–tetraloop receptor) by various computer programs. For the nonredundant RNA data set, we find 613 RNA tertiary interactions, most of which occur in the 16S and 23S rRNAs. An analysis of these motifs reveals the diversity and variety of A-minor motif interactions and the various possible loop–loop receptor interactions that expand upon the tetraloop–tetraloop receptor. Correlations between motifs, such as pseudoknot or coaxial helix with A-minor, reveal higher-order patterns. These findings may ultimately help define tertiary structure restraints for RNA tertiary structure prediction. A complete annotation of the RNA diagrams for our data set is available at http://www.biomath.nyu.edu/motifs/.
Keywords: RNA tertiary motif, RNA structure, annotation
INTRODUCTION
In recent years, many exciting discoveries have exposed the versatility of RNA. Besides the long-recognized functional properties of messenger RNA, transfer RNA, and ribosomal RNA, many new noncoding RNAs are now known to perform fundamental catalytic regulatory roles. Small interference RNAs have a remarkable role in gene silencing (Hannon 2002); microRNAs can repress translation (Vasudevan et al. 2007); transfer-messenger RNAs (tmRNAs) direct the addition of tags to peptides on stalled ribosomes, thereby affecting protein stability and transport (Gillet and Felden 2001); and other small noncoding RNAs regulate messenger RNA stability and translation by base-pairing at various positions with their target messenger RNAs (Ruvkun 2001; Masse and Gottesman 2002). These unique properties of RNA have also been exploited for nanodesign for biomedical and technological applications (Chworos et al. 2004; Jaeger and Chworos 2006; Nasalean et al. 2006). Clearly, more discoveries are yet to come, given the many novel non-protein-coding transcripts identified in the human genome (The ENCODE Project Consortium 2007); many of these RNAs have yet unknown functions.
Although significant progress has been made in RNA secondary structure prediction, present three-dimensional (3D) RNA folding algorithms require manual manipulation or are generally limited to simple structures. For example, the extensive 3D modeling tools developed by the Westhof (Massire and Westhof 1998) and Harvey (Malhotra and Harvey 1994; Mears et al. 2002) groups rely on manual application of expert knowledge. Unfortunately, there are only a few of these experts. Automated 3D prediction tools were reported recently by Das and Baker (2007), who used a 3-nucleotide (nt) fragment library of 3D structures along with simple energy functions to find the lowest energy structure for a given RNA sequence using Monte Carlo sampling. However, this method is still limited to 50-nt sequences. More recently, Parisien and Major (2008) described a method for modeling 3D structures using energy minimization that builds upon earlier work using predicted cyclic building blocks (St Onge et al. 2007). Although this method represents an advance in modeling RNA helical regions, the modeling of nonhelical regions and long-range interactions still requires improvement.
Toward the goal of understanding RNA folding, many teams have analyzed important repetitive 3D structural patterns (called RNA tertiary motifs) that are established during RNA's folding. RNA tertiary motifs are conserved structural patterns formed by pairwise interactions between nucleotides. These include base-pairing, base-stacking, and base–phosphate interactions (Leontis et al. 2006; Nasalean et al. 2008). The variety of RNA's base-pairing interactions can be classified into 12 geometric base-pairing families in terms of pairs of interacting edges, which can be Watson–Crick (W), Hoogsteen (H), Sugar (S), and glycosidic bonds orientation cis (c) and trans (t) (Leontis et al. 2002). Tertiary interactions that are formed by isosteric base pairs can then be presented as interaction networks (Lescoute and Westhof 2006b).
The folded 3D structures of structural RNA molecules are stabilized by a variety of tertiary motifs such as A-minors (Nissen et al. 2001), ribose zippers (Tamura and Holbrook 2002), and coaxial helices (Kim et al. 1974) that produce compact forms (Batey et al. 1999; Hermann and Patel 1999; Moore 1999; Hendrix et al. 2005), and many studies have been devoted to the understanding of RNAs tertiary motifs. For instance, Nissen et al. (2001) first described the abundance and natural preferences of the A-minor motif in the ribosome, and Tamura and Holbrook (2002) classified the ribose zipper according to interaction patterns. Aalberts and Hodas (2005) studied the structure of pseudoknots and found a high tendency to be asymmetric in loop and stem lengths. More recently, Lescoute and Westhof (2006c) compiled and analyzed the topology of three-way junctions, describing rules to predict coaxial helices for this case. The very recent discovery of long pauses during RNA transcription, to guide RNA folding by preventing formation of stable misfolded regions (Wong et al. 2007), also suggests that tertiary anchors in the pathway are essential for generating correct final folded states, rather than merely providing folding efficiency. Hence, these tertiary contacts are important to understand RNA folding in great depth.
Despite the great effort in describing a variety of motifs, many questions remain. What are the major tertiary motifs, and how are they distributed among the universe of RNAs? Questions of motif diversity and redundancy are also interesting to explore. Do motifs function independently or in a cooperative way with other motifs?
Here we begin to address some of these intriguing questions by analyzing a representative set of 54 RNA high-resolution crystal structures. For this data set, we compile a list of occurrences of the seven major tertiary motifs and present the results as two-dimensional (2D) diagrams. The set composed of seven tertiary interaction motifs was chosen based upon the elements listed in the Structural Classification of RNA Database, or SCOR (http://scor.lbl.gov/) (Klosterman et al. 2002), and based upon several reviews on tertiary motifs (Batey et al. 1999; Hermann and Patel 1999; Hendrix et al. 2005).
We emphasize that the term “motif” is a loose concept and there is an infinite number of motifs for RNA, as for proteins. What we use in our annotation study are “motifs” that have been defined in the literature and available for searching in existing programs. This does not mean that alternative definitions for the same motifs are wrong or that other patterns in RNA are not important—it is just a defined starting point, which will expand as we understand more about RNA structure and function. Function, of course, is important in this connection because ultimately we want to work with motifs that can be correlated to RNA function.
Our method for searching tertiary motifs entails: (1) constructing a nonredundant data set; (2) using available computer programs to search the motifs; and (3) annotating and analyzing. Note that because the starting point is the 3D structure, our analysis cannot account for interactions with water molecules, ions, or folding kinetics.
RESULTS
Our data set of 54 high-resolution (≤3.0 Å) RNA crystal structures is derived from a set of representative sequences as described in Materials and Methods. The seven tertiary motifs we search for are coaxial helix, A-minor, ribose zipper, pseudoknot, kissing hairpin, tRNA D-loop/T-loop, and tetraloop–tetraloop receptor as defined in the literature (see, also, the Glossary in Materials and Methods). Note that the A-minor motif definition we use in this analysis is based on the work of Nissen et al. (2001). Later, Lescoute and Westhof (2006a) instead suggested renaming what Nissen et al. (2001) defined as the A-minor motif as the “A-minor interaction,” and that only when a pair of consecutive A-minor interactions co-occur, can an A-minor motif form. Such definitions may be explored in future work.
We use various computer programs to search for these seven tertiary motifs (see the motif search protocol), as detailed under Materials and Methods. Our statistical results are presented next, followed by analysis of motifs and motif correlations.
Statistics of annotated tertiary motifs
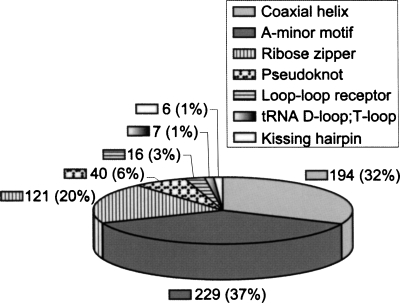
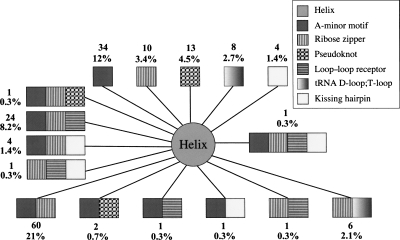
For the nonredundant 54-structure data set (see the structural data set in Material and Methods), we found 613 RNA tertiary interactions in seven major motif classes. The seven motifs are unevenly distributed in RNA structures (Fig. 1). Structural RNAs fold in compact shapes by packing helices using a variety of interactions, including helix stacking and long-range interactions. This requirement is reflected by the dominance of A-minor motifs (37%), coaxial helices (32%), and ribose zippers (20%). Together, these motifs account for 89% of the total tertiary motifs.
FIGURE 1.
The distribution of RNA tertiary motifs in the nonredundant data set of 54 high-resolution crystal structures.
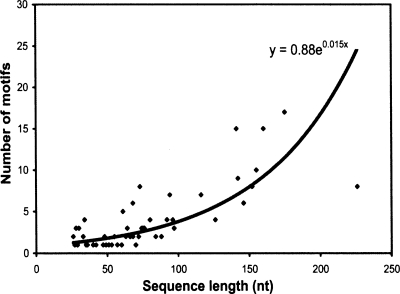
Figure 2 shows a scatterplot of the sequence length (<300 nt) versus the number of motifs. Although the values vary, the growth can be roughly estimated by an exponential function 0.88e 0.015x (R-squared value = 0.6). In other words, the number of tertiary motifs grows exponentially with increasing sequence length.
FIGURE 2.
The increasing number of RNA tertiary motifs for each molecule with sequence (length <300 nt).
The A-minor motif is the tertiary interaction that occurs most often among the seven selected motifs. Four types of A-minor motifs have been defined (see Glossary), namely, types I, II, III, and 0 (Nissen et al. 2001).
More than half (52%) of the A-minor motifs we found belong to type I, which corresponds to the strongest interaction in terms of number of hydrogen bonds formed with the helix receptor. A-minor type II, the second strongest interaction, appears 31% of the time, and the weakest forms (in terms of hydrogen-bond interactions) correspond to type 0 and type III, which are also the least frequent (10% and 7%, respectively).
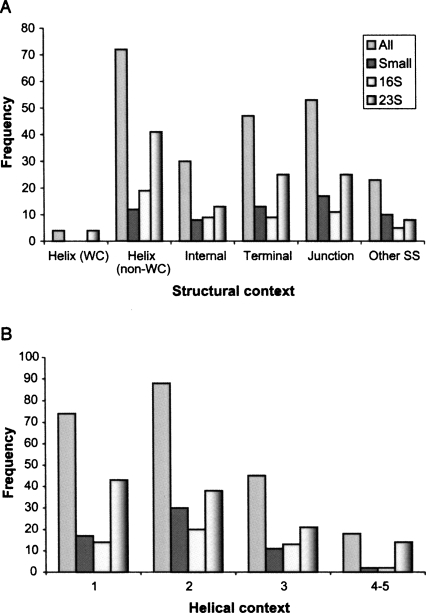
The A-minor motif interacts with other secondary and tertiary motifs as well. Figure 3 illustrates the structural context of both the inserted adenosine and the helix receptor for four categories of RNAs, all RNAs with A-minor motifs, small RNAs, and the 16S and the 23S rRNAs. In particular, Figure 3A shows the distribution of the inserted adenosine in A-minor in different structural contexts. In most of the structural contexts, the 16S and 23S rRNAs show similar trends with small RNAs. Note that, for the 16S and 23S rRNAs, there is a strong preference for the inserted A to be embedded in 3D motifs of noncanonical base-pairing. Additionally, ∼67% of the adenosines in all RNAs are located in single-stranded regions forming 3D motifs in hairpin, internal, or junction loops. Moreover, the helix receptor of the A-minor motif, typically a GC/AU Watson–Crick pair, tends to occur at the end of the helical domain, near the interface with another 3D motif. We count the position (from end to center of the helix) for all A-minor motifs found and show the frequency distribution in Figure 3B. A clear preference for positions 1 and 2 emerges, and no position greater than 5 is observed. This suggests that the helix receptor of A-minor motifs strongly prefers the end site of helices.
FIGURE 3.
Structural context of the A-minor motif. (A) The inserted adenosine is classified into six groups: internal loops, terminal loops, Watson–Crick base pairs (WC) in coaxial helix/helix, non-Watson–Crick base pairs (non-WC) in coaxial helix/helix, junctions, and other types of single-stranded regions (other SS). Internal loops and terminal loops here indicate loops in coaxial helices/helices. (B) The Watson–Crick pair is classified according to its position relative to the end site of a helix.
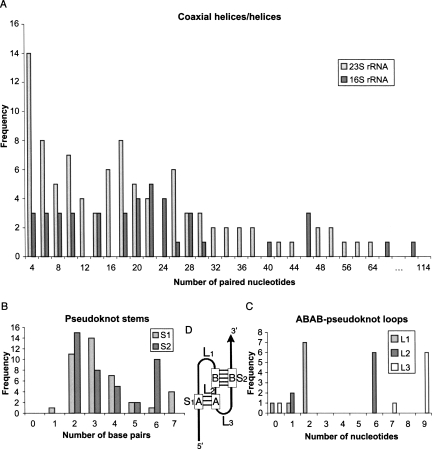
Figure 4A shows the characteristic frequency distributions of the number of paired bases in coaxial helices/helices of the 16S and 23S rRNAs. The 23S has a large peak at four paired bases and a few moderate peaks around six and 18. The 16S has a moderate peak at 22. The large difference between the 23S and 16S rRNAs is the frequency of short helices made by four paired bases. The 23S rRNA includes 14 examples of such a helix, while the 16S has three. Additionally, the 16S rRNA can form larger coaxial helices, up to 112 paired bases.
FIGURE 4.
(A) Histogram of the number of paired bases in the 16S and 23S ribosomal RNAs. (B) Histogram of the number of base pairs in the two stems of pseudoknot. (C) Histogram of the number of nucleotides in the three loops of pseudoknot. (D) Sketch of the pseudoknot: (L1–L3) loops; (S1 and S2) stems.
The simplest pseudoknot we find belongs to the ABAB class according to the pseudoknot classification of Aalberts and Hodas (2005), which consists of an RNA chain starting at the 5′-site, forming a stem S1 at the site A and a stem S2 at the site B, then back to S1 at A, and finally to S2 at B (Fig. 4D). Interestingly, eight out of 40 (20%) pseudoknots we found belong to the ABAB-pseudoknot variety, which differs from the data shown in the database Pseudobase (van Batenburg et al. 2000), where >96% of a nonredundant set are of the ABAB type (Aalberts and Hodas 2005). Figure 4B shows the histogram distribution of the length of the two stems (S1 and S2) that form the pseudoknot. In agreement with previous studies (Aalberts and Hodas 2005), S1 peaks at 3 bp, and S2 favors 2 or 6 base pairs (bp) (Fig. 4B). Also of interest, eight examples of symmetric pseudoknots (length S1 = length S2) are found, but these examples do not correspond to the ABAB-pseudoknot variety. Figure 4C describes the frequency (in terms of sequence length) of the loops that form ABAB-pseudoknots. Although the loops (L1, L2, and L3) can take small values from 0 to 1, their peaks form at 2, 6, and 9, respectively.
The seven tRNA D-loop/T-loop interactions we identified in five structures (1EFW, 1EHZ, 1N78, 1U0B, TRNA05) in our nonredundant data set reveal conservative base–base interactions, namely, cWW interaction between a guanosine and cytosine, and tWS interaction between a guanosine and pseudouridine or uridine. More T-loop interactions have been observed in viral RNAs, tmRNAs, and local regions of the rRNAs (Nagaswamy and Fox 2002).
The ribose zipper is the third most abundant tertiary interaction, with 121 instances found in our set. Each of these tertiary interactions is a combination of sugar-edge base pairs formed when two adjacent Watson–Crick base pairs in a helix interact with two stacked “loop” nucleotides. The most common types of ribose zippers are canonical (52%), single (26%), and cis (13%). Other types, such as pseudo-cis and pseudo-single, are only found once each.
Diversity of A-minor motif and related interactions
Based on Nissen et al. (2001), the A-minor motif forms when minor-groove adenosines (or other) insert into the minor groove of neighboring helices, where they form hydrogen bonds with one or both of the 2′-OHs of the receptor pairs. In this subsection, we show how diverse A-minor motifs are and that more than the four types (I, II, III, 0; see first statistics subsection) (Nissen et al. 2001) occur.
Among the 229 A-minor motifs we found, 18% interact with the GC base pair at the helix receptor region, 62% with CG, 5% with AU, 9% with UA, and the remaining can be attributed to the less common helix receptors formed by GU (UG) wobble and noncanonical base pairs. These observations are consistent with reports of A-minor motif interactions (Nissen et al. 2001; Battle and Doudna 2002), which show that the helix receptor in A-minor motifs strongly prefers Watson–Crick base pairs. On the other hand, the inserted adenosine occurs in a variety of structural elements, including noncanonical base pairs, loops, junctions, and other single-stranded regions (Fig. 3). In our search, we encounter cases of A-minor type I interactions such as in the 16S rRNA (PDB ID: 2J00), where the interaction can be described as A1080A919 tWS or possibly tSS, A1080A16 cSS and A919A16 cWW (Fig. 5D). A-minor motif interactions involving GA cWW base pairs at the helix receptor are also observed. In the 23S rRNA (PDB ID: 1VQO), uridine U121 is docked into the minor groove of the G51C110 Watson–Crick base pair (Fig. 5E). This interaction is an A-minor type I with a uridine rather than adenosine involved.
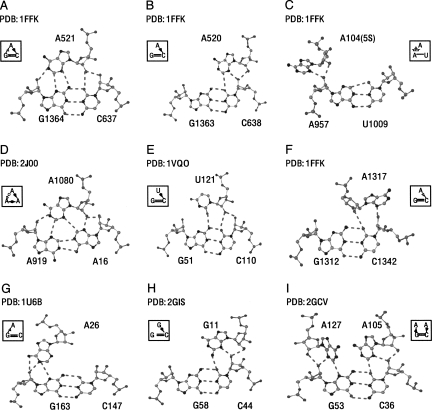
FIGURE 5.
Examples of A-minor and other similar interactions. The symbolic (Leontis/Westhof) notation is used. (A–C) Typical examples of A-minor I, II, and 0, respectively. (D) An unusual A-minor type I with an adenosine (A1080) docked into the minor groove of an AA cis Watson–Crick base pair. (E) A uridine inserting into the minor groove of a GC cis Watson–Crick base pair making an A-minor type I. (F) A trans version with an adenosine (A1317) inside the minor groove of GC cis Watson–Crick base pair. (G) An adenosine A26 interacting in the minor groove of a GC Watson–Crick base pair in an unusual presentation. (H) G-minor type II. (I) Double A-minor motif type II.
Other interactions similar to A-minor motifs also arise. In Figure 5F, a contact consisting of adenosine, in trans configuration, interacting with the minor groove of a helix receptor is shown. This contact can be compared to a “trans version” of the A-minor type II interaction (Fig. 5B). Figure 5G shows a “rotated” adenosine that could be described by a tWS base pair, except for the lack of (A26)N3/(G163)N2 interaction.
As mentioned above, A-minor motifs are not limited to adenosine residues, and several examples of C-minor and U-minor motifs (type 0) have been observed. Previous studies (Nissen et al. 2001; Lescoute and Westhof 2006a) have observed that A-minor type II is only restricted to adenosines; however, Figure 5H shows a clear example of a G-minor type II. The last diagram, Figure 5I, reveals that a helix receptor can interact as an A-minor type II with two adenosine residues simultaneously, and the two adenosines are ∼6.5 Å apart. Because these interactions have been encountered in our minimal, nonredundant RNA data set, more examples of the interactions can be expected. No relevant information is observed in A-minor type III interactions.
Tetraloop–tetraloop receptor and other loop–loop receptor motifs
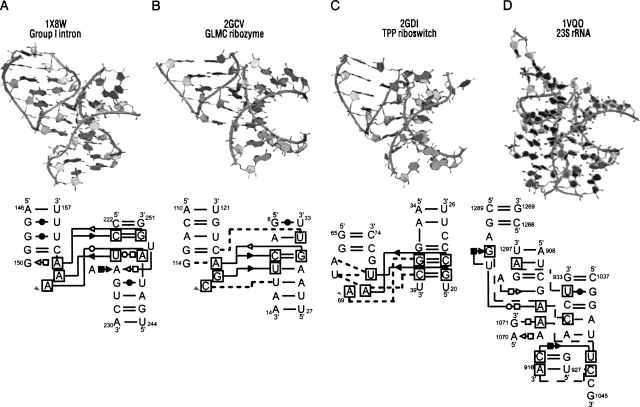
The tetraloop–tetraloop receptor (Costa and Michel 1995) is a conserved interaction occurring between a GNRA tetraloop and a receptor region (Fig. 6A). The tetraloop receptor contains an internal loop with an adenosine–adenosine platform and a looped-out uridine. During the search for tetraloop–tetraloop receptors by FR3D, we encounter an interesting array of loop–loop receptor interactions. Five loop–receptor interactions are observed in the 16S rRNA (PDB ID: 2J00), six in the 23S rRNA (PDB ID: 1VQO), and other examples are found in ribozymes. Such interactions show a diversity beyond the classic tetraloop–tetraloop receptor; some have weaker but clear long-range interactions, and these loop–loop receptors show discrepancy numbers (a measure similar to RMSD) (see Sarver et al. 2007) ranging from 0.33 to 0.67 from the traditional tetraloop–tetraloop receptor. The closest instance to the tetraloop–tetraloop receptor is found in the GLMC ribozyme (Fig. 6B), where the lack of internal loop in the receptor leads to weaker loop–receptor contacts; however, it has a small discrepancy (0.33) from the 1Y0Q tetraloop–tetraloop receptor (described in Materials and Methods). Figure 6C shows an example of an interaction between a hexaloop and its receptor, where the four residues U68–U71 form a tetraloop. Another interesting example is found in a junction–helix interaction (Fig. 6D). A single-stranded region from a junction docks into a helical receptor.
FIGURE 6.
Loop–loop receptor interactions. (A) A typical tetraloop–tetraloop receptor motif. (B) A near tetraloop–tetraloop receptor in a riboswitch. (C) A loop–loop receptor between a hexaloop and its loop receptor. (D) A loop–loop receptor of a single-stranded region in a junction interacting with a loop receptor. For each example, we illustrate its 3D structure and corresponding planar network diagrams with the Leontis/Westhof nomenclature.
These loop–loop receptor interactions are not tetraloop–tetraloop receptors in the strict sense because they lack the AA-platform element and other characteristic features. However, both interactions help organize helical packing and stabilize the tertiary structure. Although similar GNRA loop–loop receptor interactions have been reported (Abramovitz and Pyle 1997; Geary et al. 2008), these interactions show a diversity beyond GNRA loop interactions.
Correlations between tertiary motifs
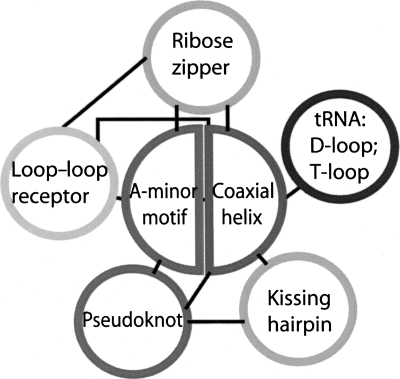
We term RNA correlated motifs as motifs that consistently occur together in RNA molecules; they can interact with each other directly or indirectly. In our data set, every loop–loop receptor contains at least one ribose zipper motif, and the ribose zipper motifs often (73%) contain nucleosides involved in A-minor motifs. We thus consider two motifs to be correlated when one contains all or part of the other motif. Although we observe correlations between most of the seven motifs, the A-minor and coaxial helix/helix define two “traffic hubs” (hotspots) that organize with other motifs.
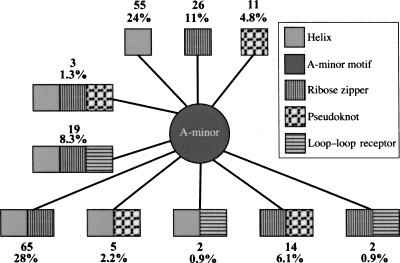
A-minor rarely forms as an isolated motif; in fact, it often occurs with coaxial helix/helix, ribose zipper, pseudoknot, and loop–loop receptor motifs. Figure 7 describes such motif correlations with A-minor motifs. Notably, 24% of the total A-minor motifs (55 examples) are correlated with coaxial helices only, 28% (65 examples) are correlated with both helix and ribose zipper, and 8.3% (19 examples) are correlated with helices, ribose zippers, and loop–loop receptors. Two correlation patterns, A-minor/helix and A-minor/helix/ribose-zipper, occupy >50% of the A-minor motif interactions found in the nonredundant data set (Fig. 7). Specifically, 149 out of 229 A-minor examples (65%) occur in helical regions (including internal and terminal loops) (Fig. 7). The example in Figure 8A demonstrates these correlations.
FIGURE 7.
Correlations between A-minor and four other tertiary motifs. (Squares) Tertiary motifs; (lines) correlations. Numbers and percentages correspond to the number and proportion of A-minor motifs correlations found in our data set analysis.
FIGURE 8.
Examples of A-minor-related correlations. (A) A-minor and coaxial helix/ribose zipper (PDB ID: 2J00). (B) A-minor and pseudoknot (PDB ID: 1L2X). (C) A-minor and junction (PDB ID: 2J00). (Framed boxes) A-minor motifs; (solid gray boxes) ribose zippers; (columns) coaxial helices; (light font letters) pseudoknots. These representations are a subset of our annotation diagrams available in color at http://www.biomath.nyu.edu/motifs.
We also observe two types of interactions with respect to the distance between helices. First, A-minor motifs link two adjacent or sequentially proximal helices; second, A-minor motifs link two long-range helices. In the latter type of correlation, more than one A-minor motif on average is associated with one coaxial helix.
The A-minor motif (56%) also associates with ribose zippers in a different correlation pattern (Fig. 7). One ribose zipper usually associates with one or two A-minor motifs. Moreover, A-minor, coaxial helix/helix, and ribose zipper motifs tend to appear together as one of the major correlation patterns.
Besides the two major correlation patterns for A-minor motifs mentioned above, A-minor motifs are also correlated with pseudoknots and loop–loop receptors. For example, a viral RNA pseudoknot (PDB ID: 1L2X) (Egli et al. 2002) has a pseudoknot and A-minor type I motif (Fig. 8B). There are also A-minor motifs that are not correlated with tertiary motifs; instead, the inserted adenosine of the A-minor associates with single-stranded regions, such as junctions (Fig. 8C). The structural contexts of the inserted adenosine shown in Figure 3A also support this type of correlation.
Since the A-minor motif is highly correlated with both the coaxial helix and ribose zipper motif, it is not surprising to observe the major correlation pattern helix/A-minor/ribose-zipper by using a helix as a hub (Fig. 9). Here, our helix represents both conventional and coaxial helical interactions. Note that some minor helix-correlation patterns have interesting features. We find that 15 out of 16 loop–loop receptors associate with helices because the loop corresponds to the terminal loop of a helix and thus its receptor is located in another helix. Our data show that 53% of identified pseudoknots in our data set form coaxial helices. All the tRNA D-loop/T-loop examples are found in two terminal loops of tRNA structures, which, in turn, form correlations with coaxial helices.
FIGURE 9.
Correlation between coaxial helix/helix and six other tertiary motifs. See legend of Figure 7 for notation.
Motif correlation features
Coaxial-helix/A-minor-centered view
To understand the relationship between tertiary motifs, we propose a coaxial-helix/A-minor-centered view (Fig. 10) based on the above analysis. The following features may serve as guidelines to predict RNA structures from sequences and to build RNA 3D models.
FIGURE 10.
Cooperative interactions among RNA tertiary motifs. (Black lines) Correlations between motifs.
The adenosine in the minor groove of an A-minor motif has 31% possibility to occur in noncanonical base pairs in a helix, 23% to occur in junctions, and 21% to occur in terminal loops.
The Watson–Crick pair of an A-minor motif tends to be found at the end of a helix, i.e., the second to the last pair (39%) or the last pair (33%).
Sixty-five percent of A-minor motifs are correlated with a helix, while 38% are correlated with helix/ribose-zipper motifs.
Seventy-three percent of ribose zippers are correlated with A-minor motifs, and 88% of loop–loop receptors with A-minor motifs.
Higher-order motifs
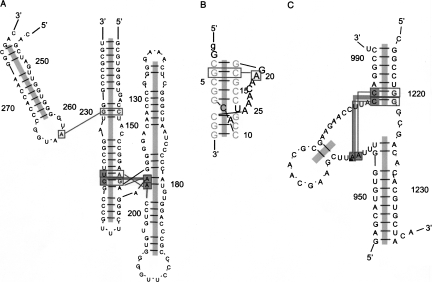
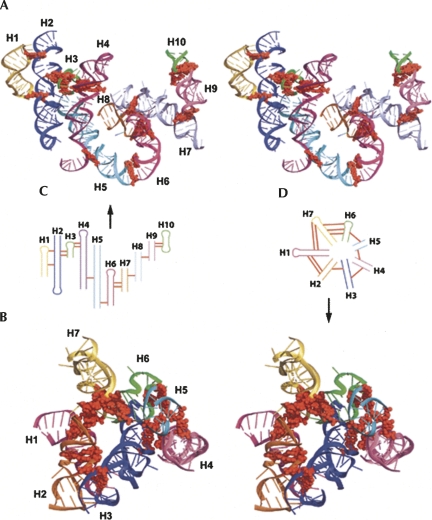
The correlations analyzed above suggest a cooperative interacting mode among RNA tertiary motifs (Fig. 10). We define this kind of interaction as a higher-order motif. Two core tertiary motifs—coaxial helices and A-minor motifs—interact with each other and also with five other motifs. The most abundant higher-order motif is formed by coaxial helices and A-minor motifs (the A-minor–coaxial-helix higher-order motif central circle in Fig. 10). This motif connects helices to form helical networks. The largest helical network of this kind in the nonredundant data set consists of 13 coaxial helices/helices (in 23S rRNA, PDB ID: 1VQO). The A-minor–coaxial-helical network has two modes: linear and circular. The example in Figure 11A shows a 10-helix network linked by A-minor motifs in a linear fashion. Another example in Figure 11B shows a helical network in a circular fashion. Both examples come from the Haloarcula Marismortui 23S rRNA (PDB ID: 1VQO). Coordinates are available upon request.
FIGURE 11.
Stereoview of (A) a linear helical network formed by 14 A-minor motifs and 10 coaxial helices (H1–H10) and (B) a circular helical network formed by 11 A-minor motifs and seven coaxial helices (H1–H7) (PDB ID: 1VQO). (A,B, red ball-and-stick) A-minor motifs; (color-coded ribbons) coaxial helices. (C,D) Simplified diagrams corresponding to the 3D structures in A and B, respectively. (C,D, red lines) A-minor motifs. Helices in the linear network and the circular helical network correspond to conventional helix numbers (Ban et al. 2000). Specifically, helices 1–10 in the linear helical network correspond to conventional helices 25, 41/45, 40, 36/29/46, 2/3/4, 11, 32, 74/75, 68, and 69; helices 1–7 in the circular helical network correspond to conventional helices 11, 32, 74/75, 68, 66, 66, and 52.
DISCUSSION
Advances in RNA structure prediction depend on our understanding of the modular nature of RNAs and their intricate interactions. To understand the complexity of RNA interaction networks, it is important to analyze in detail a number of known examples. By generating a nonredundant data set of RNA crystal structures, we have annotated seven different motifs into RNA diagrams. The data have been analyzed from various perspectives.
RNA 3D structures can be thought of as a set of interaction networks, where base pairs are represented by nodes and hydrogen-bond interactions are the connectors. Although such networks contain a large amount of information, the resulting diagrams become complex as the size of RNA molecules increases. Lescoute and Westhof (2006b) propose that RNA tertiary interactions can also be expressed as interaction networks, by encapsulating base-pairing interactions into isosteric classes in terms of the Watson–Crick, Sugar, and Hoogsteen edges (Lescoute and Westhof 2006b). This classification leads to 12 different types of base-pairing interactions, which simplifies the level of complexity of the network. However, such networks can become complicated, particularly in the ribosomal 16S and 23S rRNAs. Here we attempt to reduce complexity by grouping noncanonical base pairs into elements of known 3D motifs such as the A-minor motif, ribose zipper, and pseudoknot. For instance, an A-minor type I encapsulates a cSS, a tSS, and a cWW base-pairing interaction (see Glossary). This simplified annotation approach, combined with the Leontis/Westhof notation, can help define a multilevel understanding of RNA tertiary motif interactions.
Our statistical survey of RNA tertiary motifs indicates that ribose zippers, coaxial helices, and A-minor motif interactions are highly abundant. They are important in folding possibly due to RNA helical packing into compact shapes. Overall, the number of RNA 3D motifs grows exponentially with size. Not surprisingly, the 16S and 23S rRNA molecules account for more than half of the data considered.
From all the 3D motifs considered here, the importance of A-minor and coaxial helices is reflected in their diversity of interaction with other motifs. In fact, the A-minor motif is more diverse than originally described, and the initial four types can be extended or generalized. Other interactions of adenosines in different conformations at the minor groove also occur. Similarly, the tetraloop–tetraloop receptor is only the first of this type of more general loop–loop receptor interactions. These interactions provide the same functional properties as their original counterparts, that is, RNA stability through helical packing.
The simplified notation also exposes information concerning RNA interaction networks. Coaxial helix and A-minor motifs are two major components among the seven selected motifs. We propose a coaxial-helix/A-minor-centered view to understand the interaction network formed by the seven tertiary motifs. RNA motifs organize in a higher-order fashion and function in a collaborative way (Brion and Westhof 1997). The specific correlations between motifs we observe here may lead to a hierarchical mode of the role of RNA motifs during the folding pathway. For example, canonical Watson–Crick base pairs are strong forces formed initially during folding. Similarly, base stacking represents strong forces, which can initially induce coaxial helices. Although the full RNA folding pathway is still unknown, coaxial helices interact in collaboration with A-minor motifs in the final folding state, and A-minor motifs can function with other motifs, such as ribose zippers and loop–loop receptors, to stabilize the 3D structure. Pseudoknots, as well, may lead to coaxial helices, and then the loop regions of the pseudoknot, often composed of adenosines, tend to interact with the helix (see Fig. 8B) through A-minor motifs.
As noted in the beginning of the Results, a more stringent definition of A-minor motif (as a pair of “A-minor interactions”) (Lescoute and Westhof 2006a) may also help clarify high-order correlations in tertiary RNA structures. Also, given the many motifs that exist in RNA, future analyses should consider other motifs that can also be searched in automated software or manually.
Having available annotated motifs for RNA provides an opportunity to further study the diversity of known RNA tertiary motifs, and to analyze correlations between motifs, including cooperation among motifs. Such derived 2D/3D structure restraints might, in turn, contribute to the prediction of RNA tertiary structure, especially in conjunction with excellent graphical viewing and manipulation packages of 3D structures (Martinez et al. 2008). Ultimately, extensions of our analysis concerning motif diversity, motif correlation, and higher-order motifs might help predict RNA 3D structures from sequence. The color versions of the figures and annotated color diagrams are available in PDF and EPS format, and can be downloaded at http://www.biomath.nyu.edu/motifs/.
MATERIALS AND METHODS
Structural data set
Our RNA structures are taken from the Nucleic Acid Database (NDB) (Berman et al. 1992), March 2007. To generate a nonredundant RNA data set, we use a selection algorithm that has been employed to screen protein data sets (Hobohm et al. 1992). Specifically, RNA structures are selected based on the following criteria: (1) high-resolution (≤3.0 Å); (2) structure size (>2 nt/strand); (3) representative sequences (≤55% sequence identity); and (4) tertiary interactions (structures should have at least one tertiary motif). Note that one large RNA structure (ribosomal RNA small subunit, PDB ID: 2J00) has resolution of 2.8 Å. To include this structure, we set the resolution for the nonredundant data set to be 3.0 Å or higher.
The nonredundant RNA data set contains 54 high-resolution crystal structures (Supplemental Table S1). They belong to different types of biological molecules (simple duplex, single-stranded RNA, tRNA, ribozyme, riboswitch, protein/RNA complex, and ribosomal RNA) and span a wide range of sequence lengths (25–2879 nt).
Terminology for RNA secondary and tertiary motifs
We define three major categories for secondary structural elements: internal loops, hairpin loops, and multihelix junctions: internal loops represent unpaired regions in helices flanked by Watson–Crick base pairs on both ends; hairpins are single-stranded regions that are covalently linked with helix ends. Junctions—unpaired regions connecting multiple helices—are classified as three-way, four-way, and higher-order junctions (Lilley et al. 1995). There are other minor single-stranded regions, such as 5′- and 3′-single-stranded regions. The helical region is formed by coaxial stacking of Watson–Crick. Frequently, internal or hairpin loops contain non-Watson–Crick base pairs that stack continuously with adjacent helices. We define the coaxial helix/helix pattern as an object containing conventional and coaxial helices (helical regions) and their attached loops (internal loops and hairpins), when these are continuously stacked.
Within these categories, we select seven tertiary motifs to search for in our nonredundant data set (see Glossary): coaxial helices (Kim et al. 1974), A-minor motifs (Nissen et al. 2001), ribose zippers (Cate et al. 1996), tetraloop–tetraloop receptors (Costa and Michel 1995), pseudoknots (Pleij et al. 1985), kissing hairpins (Chang and Tinoco 1994), and tRNA D-loop/T-loop motifs (Holbrook et al. 1978). These motifs are well described in the literature; some are highly recurrent in nature and considered to play an important role in RNA folding. The coaxial helix is formed by quasi-continuous helical regions (see, for example, Fig. 8).
A-minor motifs represent interactions between the minor-groove edge of an adenosine and the minor groove of a helix receptor. Specifically, an A-minor type I corresponds to simultaneous formation of a cSs base pair (see Leontis and Westhof 2001 for base-pair nomenclature) and a tSs or tWS base pair between the base in the minor groove (usually but not always an A) and two Watson–Crick paired bases in the helix (Fig. 5A), while the A-minor type II has a csS interaction (Fig. 5B). The A-minor type 0 is equivalent to helix packing (Fig. 5C), and the A-minor type III has a weaker interaction comparable (but not necessarily equal) to the Sugar/Sugar edge interactions.
The ribose zipper forms zipper-like interactions between backbones of two strands (Fig. 8A,C).
The pseudoknot motif is formed by a hairpin or internal loop (Watson–Crick) base-pairing with a single-strand region outside of the hairpin or internal loop stem (Fig. 8B). The kissing hairpin describes a pseudoknot formed by two (Watson–Crick) complementary hairpins (see, for example, diagram of 1ZCI structure in the Supplemental Material), and the tRNA D-loop/T-loop denotes interactions between the two specific loops in tRNA (diagram of 1EHZ structure in the Supplemental Material). More detailed definitions of the seven tertiary motifs are described in the Glossary.
Motif search protocol
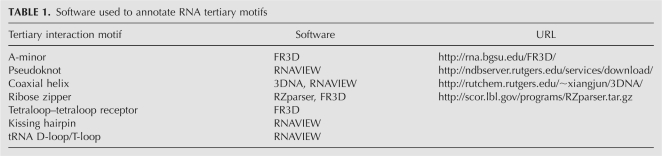
We used various computer programs available in the public domain (Table 1) for each motif search. When appropriate, we set a maximum hydrogen-bond distance between donor and acceptor to be 4 Å (Lu and Olson 2003).
TABLE 1.
Software used to annotate RNA tertiary motifs
For coaxial helices, we use a semiautomatic method for searching. We define a coaxial helix based on the distance between origins of two base pairs less than 7.5 Å (Lu and Olson 2003) and require a consensus between RNAVIEW (Yang et al. 2003) and 3DNA (Lu and Olson 2003). Namely, if both programs produce a consistent coaxial helix description, the motif is accepted; if the programs disagree, we visually inspect the structures by two independent raters to assign the correct configuration.
For A-minor motifs, we use FR3D's geometric search approach (Sarver et al. 2007). The required templates for each A-minor type are listed in Supplemental Table S2. Based on the search result of FR3D, we independently computed a set of hydrogen-bonding constraints as described by Nissen et al. (2001) to obtain the final list of A-minor motifs.
We search for ribose-zipper motifs primarily using RZparser (Tamura and Holbrook 2002), a program designed for this purpose. FR3D was also used to verify the results and to search for motifs that might have been missed using the hydrogen-bond criteria above. The templates built in FR3D (see Supplemental Table S3) are sufficient to find all seven known types of the ribose-zipper motifs.
For tetraloop–tetraloop receptor motifs, we employ a geometric search, also using FR3D (see Supplemental Table S4 for templates). The search produces a number of interesting loop–helix interactions, which we describe in the Results.
Finally, we identify pseudoknots, kissing hairpins, and tRNA D-loop/T-loop motifs by visual inspection using RNAVIEW, since they are much less frequent.
Prediction accuracy by FR3D
To assess the accuracy of the geometric motif search by FR3D, we compiled an independent and complete list of A-minor motif type I for a 23S rRNA (PDB ID: 1S72) (Klein et al. 2004) based on the following criteria: (1) the motif contains a cWW base pair; (2) the motif contains an adenosine inserting into the minor groove of the Watson–Crick base pair; (3) the hydrogen bonds between the adenosine and the Watson–Crick pair are within 4.0 Å; (4) the three nucleotides are nearly coplanar (the maximum angle between base normals is <65°). We then use positive predictive value (PPV) and sensitivity (defined below) to assess the accuracy of prediction by FR3D. The PPV and sensitivity values we obtained for 52 cases are 96% and 100%.
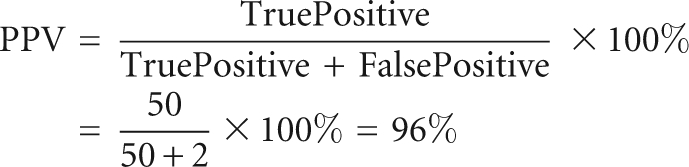 |
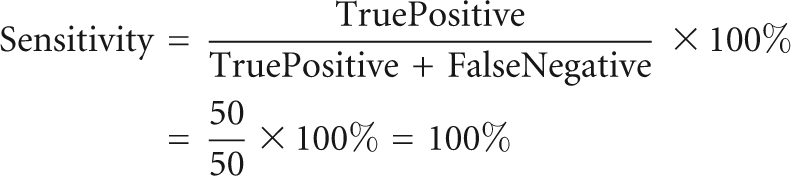 |
This result suggests that FR3D is an efficient and reliable program to search for A-minor motifs.
GLOSSARY
Coaxial helix (Kim et al. 1974)
Two separate helical regions stack to form coaxial helices as a pseudo-continuous (quasi-continuous) helix. Coaxial helices are highly stabilizing tertiary interactions and are seen in several large RNA structures, including tRNA, pseudoknots, the group I intron P4–P6 domain, and in the Hepatitis Delta Virus ribozyme.
A-minor motif (Nissen et al. 2001)
The A-minor motif involves the insertion of minor-groove edges of adenosines into the minor groove of neighboring helices. It has four subtypes depending on the position of the adenosine to the interacting Watson–Crick base pair.
Type 0
The N3 of the A (or other) residue is outside the O2′ of the far strand of the receptor helix. The A-minor type 0 can be viewed as a helix packing interaction (Fig. 5C).
Type I
The O2′ and N3 atoms of the A residue are inside the minor groove of the receptor helix. The inserted base for the Type I interaction must be an adenine. The A-minor type I motif corresponds to simultaneous formation of a cSs base pair and a tSs or tWS base pair (Leontis and Westhof 2001) between the base in the minor groove (usually but not always an A) and two Watson–Crick paired bases in the helix (Fig. 5A).
Type II
The O2′ of the A residue is outside the near-strand O2′ of the helix, and the N3 of the A residue is inside the minor groove. The inserted base for the type II interaction must be an adenine. The A-minor type II has a csS interaction (Fig. 5B).
Type III
The O2′ and N3 of the A (or other) residue are outside the near-strand O2′ of the receptor helix. The A-minor type III has a weaker interaction comparable (but not necessarily equal) to the Sugar/Sugar edge interactions.
Note: The Lescoute and Westhof (2006a) redefinition of the A-minor motif considers the four A-minor motifs defined by Nissen et al. (2001) as A-minor interactions, so that A-minor motifs become a pair of these interactions in the minor groove.
Ribose zipper (Cate et al. 1996)
The ribose zipper is a tertiary interaction formed by consecutive hydrogen-bonding between the backbone ribose 2′-hydroxyls from two regions of the chain interacting in an antiparallel manner.
Pseudoknot (Pleij et al. 1985)
When bases pair between nucleotide loops (hairpin or internal) and bases outside the enclosing loop, they form a pseudoknot. This structure often contains coaxial helices. It can be a very stable tertiary interaction.
Loop–loop receptor
The tetraloop–tetraloop receptor was identified by comparative sequence analysis (Costa and Michel 1995). This tertiary interaction is characterized by specific hydrogen-bonding interactions between a tetraloop and a 11-nt internal loop/helical region that forms the receptor. Other kinds of loop and receptor interactions, such as penta-loop/receptor and hexa-loop/receptor, are observed in our tertiary motif search. Thus, this motif is called the loop–loop receptor.
tRNA D-loop/T-loop (Holbrook et al. 1978)
The D-loop in tRNA contains the modified nucleotide dihydrouridine. It is composed of 7 to 11 bases and is closed by a Watson–Crick base pair. The TψC-loop (generally called the T-loop) contains thymine, a base usually found in DNA and pseudouracil (ψ). The D-loop and T-loop form a tertiary interaction in tRNA.
Kissing hairpin (Chang and Tinoco 1994)
The kissing hairpin complex is a tertiary interaction formed by base-pairing between the single-stranded residues of two hairpin loops with complementary sequences.
SUPPLEMENTAL DATA
Supplemental material can be found at http://www.rnajournal.org.
ACKNOWLEDGMENTS
The work was supported by the Human Frontier Science Program (HFSP) and by a joint NSF/NIGMS initiative in Mathematical Biology (DMS-0201160). We also thank the NSF-funded Institute for Mathematics and Its Applications (IMA) for bringing all authors together to an inspiring RNA workshop (“RNA in Biology, Bioengineering and Nanotechnology,” October 29–November 2, 2007). Funds from the RNA Ontology Consortium, supported by Research Coordination Network (RCN) grant from the National Science Foundation (grant no. 0443508), were also crucial in allowing C.L. to work at the Leontis Laboratory. We thank Hin Hark Gan for valuable comments.
Footnotes
Article published online ahead of print. Article and publication date are at http://www.rnajournal.org/cgi/doi/10.1261/rna.1249208.
REFERENCES
- Aalberts D.P., Hodas N.O. Asymmetry in RNA pseudoknots: Observation and theory. Nucleic Acids Res. 2005;33:2210–2214. doi: 10.1093/nar/gki508. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Abramovitz D.L., Pyle A.M. Remarkable morphological variability of a common RNA folding motif: The GNRA tetraloop–receptor interaction. J. Mol. Biol. 1997;266:493–506. doi: 10.1006/jmbi.1996.0810. [DOI] [PubMed] [Google Scholar]
- Ban N., Nissen P., Hansen J., Moore P.B., Steitz T.A. The complete atomic structure of the large ribosomal subunit at 2.4 Å resolution. Science. 2000;289:905–920. doi: 10.1126/science.289.5481.905. [DOI] [PubMed] [Google Scholar]
- Batey R.T., Rambo R.P., Doudna J.A. Tertiary motifs in RNA structure and folding. Angew. Chem. Int. Ed. 1999;38:2327–2343. doi: 10.1002/(sici)1521-3773(19990816)38:16<2326::aid-anie2326>3.0.co;2-3. [DOI] [PubMed] [Google Scholar]
- Battle D.J., Doudna J.A. Specificity of RNA–RNA helix recognition. Proc. Natl. Acad. Sci. 2002;99:11676–11681. doi: 10.1073/pnas.182221799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berman H.M., Olson W.K., Beveridge D.L., Westbrook J., Gelbin A., Demeny T., Hsieh S.H., Srinivasan A.R., Schneider B. The Nucleic-Acid Database—A comprehensive relational database of three-dimensional structures of nucleic-acids. Biophys. J. 1992;63:751–759. doi: 10.1016/S0006-3495(92)81649-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brion P., Westhof E. Hierarchy and dynamics of RNA folding. Annu. Rev. Biophys. Biomol. Struct. 1997;26:113–137. doi: 10.1146/annurev.biophys.26.1.113. [DOI] [PubMed] [Google Scholar]
- Cate J.H., Gooding A.R., Podell E., Zhou K., Golden B.L., Kundrot C.E., Cech T.R., Doudna J.A. Crystal structure of a group I ribozyme domain: Principles of RNA packing. Science. 1996;273:1678–1685. doi: 10.1126/science.273.5282.1678. [DOI] [PubMed] [Google Scholar]
- Chang K., Tinoco I., Jr Characterization of a “kissing” hairpin complex derived from the human immunodeficiency virus genome. Proc. Natl. Acad. Sci. 1994;91:8705–8709. doi: 10.1073/pnas.91.18.8705. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chworos A., Severcan I., Koyfman A.Y., Weinkam P., Oroudjev E., Hansma H.G., Jaeger L. Building programmable jigsaw puzzles with RNA. Science. 2004;306:2068–2072. doi: 10.1126/science.1104686. [DOI] [PubMed] [Google Scholar]
- Costa M., Michel F. Frequent use of the same tertiary motif by self-folding RNAs. EMBO J. 1995;14:1276–1285. doi: 10.1002/j.1460-2075.1995.tb07111.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Das R., Baker D. Automated de novo prediction of native-like RNA tertiary structures. Proc. Natl. Acad. Sci. 2007;104:14664–14669. doi: 10.1073/pnas.0703836104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Egli M., Minasov G., Su L., Rich A. Metal ions and flexibility in a viral RNA pseudoknot at atomic resolution. Proc. Natl. Acad. Sci. 2002;99:4302–4307. doi: 10.1073/pnas.062055599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- The ENCODE Project Consortium. Identification and analysis of functional elements in 1% of the human genome by the ENCODE pilot project. Nature. 2007;447:799–816. doi: 10.1038/nature05874. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geary C., Baudrey S., Jaeger L. Comprehensive features of natural and in vitro selected GNRA tetraloop-binding receptors. Nucleic Acids Res. 2008;36:1138–1152. doi: 10.1093/nar/gkm1048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gillet R., Felden B. Emerging views on tmRNA-mediated protein tagging and ribosome rescue. Mol. Microbiol. 2001;42:879–885. doi: 10.1046/j.1365-2958.2001.02701.x. [DOI] [PubMed] [Google Scholar]
- Hannon G.J. RNA interference. Nature. 2002;418:244–251. doi: 10.1038/418244a. [DOI] [PubMed] [Google Scholar]
- Hendrix D.K., Brenner S.E., Holbrook S.R. RNA structural motifs: Building blocks of a modular biomolecule. Q. Rev. Biophys. 2005;38:221–243. doi: 10.1017/S0033583506004215. [DOI] [PubMed] [Google Scholar]
- Hermann T., Patel D.J. Stitching together RNA tertiary architectures. J. Mol. Biol. 1999;294:829–849. doi: 10.1006/jmbi.1999.3312. [DOI] [PubMed] [Google Scholar]
- Hobohm U., Scharf M., Schneider R., Sander C. Selection of representative protein data sets. Protein Sci. 1992;1:409–417. doi: 10.1002/pro.5560010313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holbrook S.R., Sussman J.L., Warrant R.W., Kim S.H. Crystal-structure of yeast phenylalanine transfer-RNA. 2. structural features and functional implications. J. Mol. Biol. 1978;123:631–660. doi: 10.1016/0022-2836(78)90210-3. [DOI] [PubMed] [Google Scholar]
- Jaeger L., Chworos A. The architectonics of programmable RNA and DNA nanostructures. Curr. Opin. Struct. Biol. 2006;16:531–543. doi: 10.1016/j.sbi.2006.07.001. [DOI] [PubMed] [Google Scholar]
- Kim S.H., Sussman J.L., Suddath F.L., Quigley G.J., Mcpherson A., Wang A.H.J., Seeman N.C., Rich A. General structure of transfer-RNA molecules. Proc. Natl. Acad. Sci. 1974;71:4970–4974. doi: 10.1073/pnas.71.12.4970. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klein D.J., Moore P.B., Steitz T.A. The roles of ribosomal proteins in the structure assembly, and evolution of the large ribosomal subunit. J. Mol. Biol. 2004;340:141–177. doi: 10.1016/j.jmb.2004.03.076. [DOI] [PubMed] [Google Scholar]
- Klosterman P.S., Tamura M., Holbrook S.R., Brenner S.E. SCOR: A structural classification of RNA database. Nucleic Acids Res. 2002;30:392–394. doi: 10.1093/nar/30.1.392. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leontis N.B., Westhof E. Geometric nomenclature and classification of RNA base pairs. RNA. 2001;7:499–512. doi: 10.1017/s1355838201002515. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leontis N.B., Stombaugh J., Westhof E. The non-Watson–Crick base pairs and their associated isostericity matrices. Nucleic Acids Res. 2002;30:3497–3531. doi: 10.1093/nar/gkf481. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leontis N.B., Lescoute A., Westhof E. The building blocks and motifs of RNA architecture. Curr. Opin. Struct. Biol. 2006;16:279–287. doi: 10.1016/j.sbi.2006.05.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lescoute A., Westhof E. The A-minor motifs in the decoding recognition process. Biochimie. 2006a;88:993–999. doi: 10.1016/j.biochi.2006.05.018. [DOI] [PubMed] [Google Scholar]
- Lescoute A., Westhof E. The interaction networks of structured RNAs. Nucleic Acids Res. 2006b;34:6587–6604. doi: 10.1093/nar/gkl963. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lescoute A., Westhof E. Topology of three-way junctions in folded RNAs. RNA. 2006c;12:83–93. doi: 10.1261/rna.2208106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lilley D.M.J., Clegg R.M., Diekmann S., Seeman N.C., von Kitzing E., Hagerman P.J. A nomenclature of junctions and branchpoints in nucleic acids. Nucleic Acids Res. 1995;23:3363–3364. doi: 10.1093/nar/23.17.3363. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu X.J., Olson W.K. 3DNA: A software package for the analysis, rebuilding and visualization of three-dimensional nucleic acid structures. Nucleic Acids Res. 2003;31:5108–5121. doi: 10.1093/nar/gkg680. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Malhotra A., Harvey S.C. A quantitative model of the Escherichia coli 16 S RNA in the 30 S ribosomal subunit. J. Mol. Biol. 1994;240:308–340. doi: 10.1006/jmbi.1994.1448. [DOI] [PubMed] [Google Scholar]
- Martinez H.M., Maizel J.V., Shapiro B.A. RNA2D3D: A program for generating, viewing, and comparing 3-dimensional models of RNA. J. Biomol. Struct. Dyn. 2008;25:669–683. doi: 10.1080/07391102.2008.10531240. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Masse E., Gottesman S. A small RNA regulates the expression of genes involved in iron metabolism in Escherichia coli . Proc. Natl. Acad. Sci. 2002;99:4620–4625. doi: 10.1073/pnas.032066599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Massire C., Westhof E. MANIP: An interactive tool for modeling RNA. J. Mol. Graph. Model. 1998;16:197–205. doi: 10.1016/s1093-3263(98)80004-1. [DOI] [PubMed] [Google Scholar]
- Mears J.A., Cannone J.J., Stagg S.M., Gutell R.R., Agrawal R.K., Harvey S.C. Modeling a minimal ribosome based on comparative sequence analysis. J. Mol. Biol. 2002;321:215–234. doi: 10.1016/s0022-2836(02)00568-5. [DOI] [PubMed] [Google Scholar]
- Moore P.B. Structural motifs in RNA. Annu. Rev. Biochem. 1999;68:287–300. doi: 10.1146/annurev.biochem.68.1.287. [DOI] [PubMed] [Google Scholar]
- Nagaswamy U., Fox G.E. Frequent occurrence of the T-loop RNA folding motif in ribosomal RNAs. RNA. 2002;8:1112–1119. doi: 10.1017/s135583820202006x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nasalean L., Baudrey S., Leontis N.B., Jaeger L. Controlling RNA self-assembly to form filaments. Nucleic Acids Res. 2006;34:1381–1392. doi: 10.1093/nar/gkl008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nasalean L., Stombaugh J., Leontis N.B., Zirbel C. 2008. RNA 3D structural motifs: Definition, identification, annotation, and database searching . Sringer, Berlin. [Google Scholar]
- Nissen P., Ippolito J.A., Ban N., Moore P.B., Steitz T.A. RNA tertiary interactions in the large ribosomal subunit: The A-minor motif. Proc. Natl. Acad. Sci. 2001;98:4899–4903. doi: 10.1073/pnas.081082398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parisien M., Major F. The MC-Fold and MC-Sym pipeline infers RNA structure from sequence data. Nature. 2008;452:51–55. doi: 10.1038/nature06684. [DOI] [PubMed] [Google Scholar]
- Pleij C.W.A., Rietveld K., Bosch L. A new principle of RNA folding based on pseudoknotting. Nucleic Acids Res. 1985;13:1717–1731. doi: 10.1093/nar/13.5.1717. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ruvkun G. Molecular biology—Glimpses of a tiny RNA world. Science. 2001;294:797–799. doi: 10.1126/science.1066315. [DOI] [PubMed] [Google Scholar]
- Sarver M., Zirbel C.L., Stombaugh J., Ali M., Leontis N.B. FR3D: Finding local and composite recurrent structural motifs in RNA 3D structures. J. Math. Biol. 2007;56:215–252. doi: 10.1007/s00285-007-0110-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- St Onge K., Thibault P., Hamel S., Major F. Modeling RNA tertiary structure motifs by graph-grammars. Nucleic Acids Res. 2007;35:1726–1736. doi: 10.1093/nar/gkm069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tamura M., Holbrook S.R. Sequence and structural conservation in RNA ribose zippers. J. Mol. Biol. 2002;320:455–474. doi: 10.1016/s0022-2836(02)00515-6. [DOI] [PubMed] [Google Scholar]
- van Batenburg F.H.D., Gultyaev A.P., Pleij C.W.A., Ng J., Oliehoek J. PseudoBase: A database with RNA pseudoknots. Nucleic Acids Res. 2000;28:201–204. doi: 10.1093/nar/28.1.201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vasudevan S., Tong Y., Steitz J.A. Switching from repression to activation: MicroRNAs can up-regulate translation. Science. 2007;318:1931–1934. doi: 10.1126/science.1149460. [DOI] [PubMed] [Google Scholar]
- Wong T.N., Sosnick T.R., Pan T. Folding of noncoding RNAs during transcription facilitated by pausing-induced nonnative structures. Proc. Natl. Acad. Sci. 2007;104:17995–18000. doi: 10.1073/pnas.0705038104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang H.W., Jossinet F., Leontis N., Chen L., Westbrook J., Berman H., Westhof E. Tools for the automatic identification and classification of RNA base pairs. Nucleic Acids Res. 2003;31:3450–3460. doi: 10.1093/nar/gkg529. [DOI] [PMC free article] [PubMed] [Google Scholar]