Introduction
Intra-articular fractures can cause long-term changes in the loading environment within the affected joint, resulting in post-traumatic arthritis 1–3. Post-traumatic arthritis is a debilitating disease, affecting a disproportionate percentage of younger patients who fare poorly 4. Understanding the etiology of post-traumatic arthritis is important to try to prevent injured joints from degeneration. Injury-associated changes in articular surface congruity 1,5 or in joint stability 6–8 contribute to a chronic pathomechanical loading environment that ultimately leads to cartilage degeneration. However, the specific aspect(s) of injury-associated pathomechanical change(s) at the joint level that are the most potent stimulators of cartilage degeneration are not known.
It has been shown that transient contact stresses in intact joints are relatively uniformly distributed over the contact region, and are low in magnitude throughout the entire duty cycle 9. Such a stress distribution results in contact stress directional gradients that are low-magnitude and randomly-oriented 10. Injury-associated changes in contact stress distribution can cause pathologic changes in contact stress directional gradients which may be important pathomechanical changes that cause posttraumatic arthritis.
Little is known of the clinical consequences of increased contact stress directional gradients. However, several basic scientific investigations suggest that increased gradients may play an important role in post-traumatic arthritis 11,12. In a static model of articular surface incongruity, it was shown that incongruity-associated increases in contact stress were small in contrast to much larger corresponding increases in contact stress directional gradients around degenerative lesions in canine knees 11. In a live rabbit patellofemoral impact model, regions of increased contact stress directional gradients were the best predictors of acute mechanical damage to the cartilage 12. More recently, under dynamic loading conditions, it has also been shown that articular surface incongruity in human cadaveric ankles led to greatly increased contact stress directional gradients 9,10.
While incongruity-associated changes in contact stress directional gradients have been quantified, the effect of instability on contact stress directional gradients is unknown. Clinically, these two pathomechanical entities can coexist, since unstable motion can arise from joint incongruity. This study was designed to quantify changes in contact stress directional gradients that occur due to articular surface incongruity with or without articular instability. The study quantified incongruity- and instability-associated changes in transient contact stress directional gradients in human cadaveric ankles. It was hypothesized that an instability event, superimposed on an already incongruous ankle, would significantly increase transient contact stress directional gradients.
Methods
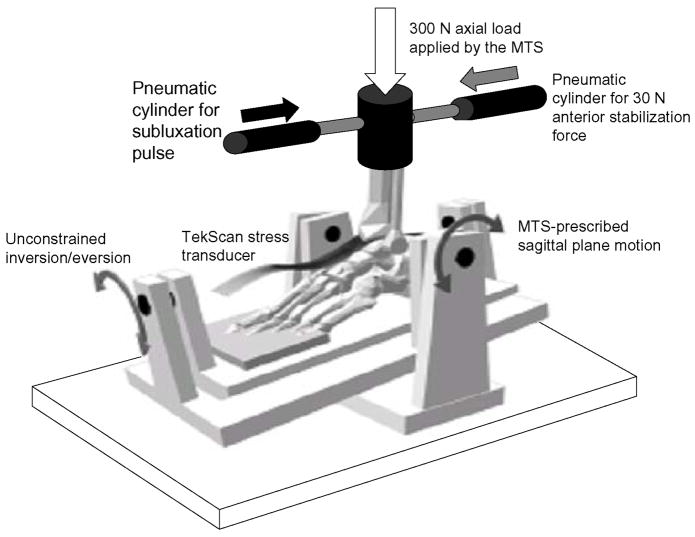
Seven fresh frozen human cadaveric foot and ankle specimens (donor ages 44 to 92 years) were prepared and mounted into an MTS machine (MTS Corporation, Eden Prairie, MN) using an established testing model protocol 9,10,13,14. Quasi-physiologic forces and motion (scaled to mimic stance-phase motion and forces) were applied to the specimens via a custom-fabricated testing fixture that allowed unconstrained motion in the ankle, hindfoot, and midfoot joints (Fig. 1). Ankles were screened for obvious preexisting abnormalities, and had to have a minimum of 20 degrees of both plantar and dorsiflexion. Contact stresses were sampled via a custom-designed transient stress transducer inserted through anterior and posterior capsulotomies. Sagittal translation between the tibia and talus was tracked using a linear potentiometer. Previous work had demonstrated no changes in ankle kinematics resulting from this preparation sequence 13.
Figure 1.
An MTS applied a constant 300 N axial load and directed sagittal plane plantar/dorsiflexion to specimens. A posterior pneumatic cylinder applied a constant 30 N anteriorly-directed stabilization force (gray arrow) to prevent spontaneous anterior talar subluxation. A second anterior pneumatic cylinder applied the posteriorly-directed subluxation pulses (black arrow) causing talar subluxation. The testing setup allowed unconstrained motion of the ankle, midfoot, and hindfoot.
The custom-designed ankle contact stress transducer (TekScan Inc., Boston, MA) used to measure the intra-articular contact stress distribution during motion reported instantaneous stress measurements from a 46 × 32 (1472) orthogonal grid of sensels arrayed over the ankle joint. The insert covered a 27 mm by 39 mm area, yielding a testing density of 0.694 mm2 per sensel. The inserts reported stresses at 132 Hz. Each sensor was calibrated on a sensel by sensel basis to minimize error inherent to sensor discrepancies.
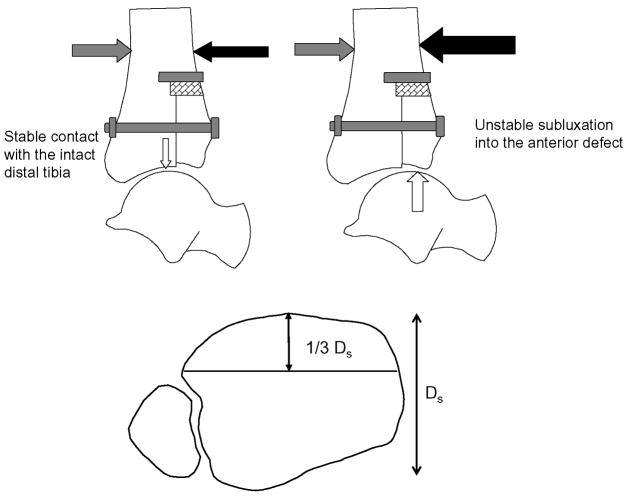
The present study was designed to measure abnormalities in transient ankle contact stress directional gradients that resulted from an articular surface incongruity, and to subsequently measure how incongruity-associated abnormalities in transient directional gradients were exacerbated by an instability event. Therefore, a metastable model of ankle incongruity was developed, i.e. a situation in which an instability event could arise with minimal additional perturbation of extrinsic loading between stable and unstable conditions, in the presence of an articular surface incongruity. Metastable incongruous conditions were created by displacing the entire anterior one-third of the distal tibia 2.0 mm proximal to the ankle joint, in combination with transection of the anterior talofibular ligament (Figure 2). In previous testing of human cadaveric ankles with a displaced osteotomy of the anterolateral quarter of the distal tibia, specimens were successfully subjected to a 600 N axial force 9,10,13,14. However, in the current test, with the osteotomy extending across the entire coronal width of the distal tibia, specimens consistently fractured under 600 N of axial load. Therefore, the axial load was reduced to 300 N. Under these conditions, minor modulation of anterior/posterior forces applied during motion determined whether the talus remained in a reduced position under the intact posterior two-thirds of the distal tibia throughout the duty cycle, or whether it temporarily subluxated into the anterior defect during loading.
Figure 2.
The incongruous ankle was created by displacing the anterior one-third of the distal tibial articular surface proximally 2.0 mm, and rigidly securing the stepoff with a lag bolt. Under axial load, a 30 N anteriorly directed force (gray arrow) had to be applied to the tibia to prevent spontaneous talar subluxation. During testing, the posteriorly-directed subluxation pulse (black arrow) was randomly varied between 0 and 120 N, in 20 N increments. Each specimen subluxated into the anterior defect (large white arrow) once a specimen-specific subluxation pulse was reached (instability threshold pulse). The ankle articulation remained stable (small white arrow) in each specimen when the metastable limit pulse (20 N less than the instability threshold pulse) was applied.
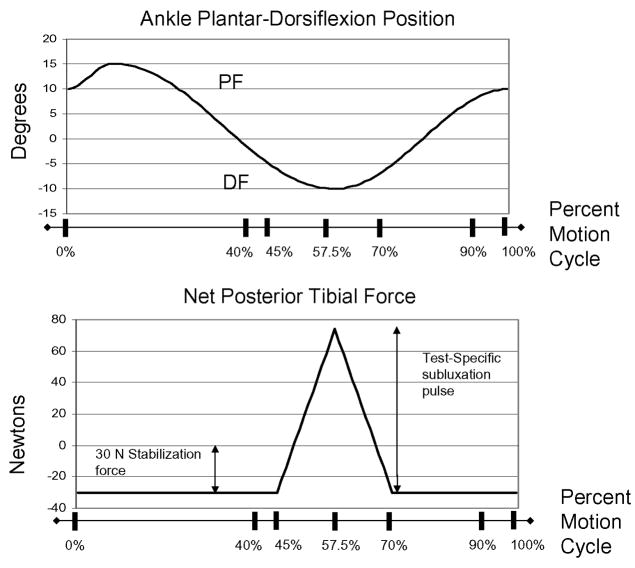
All specimens spontaneously subluxated into the anterior distal tibial defect under metastable conditions when subjected to purely axial load. Therefore, a 30 N anteriorly-directed stabilization force (Figure 1) was applied to the tibia via a pneumatic cylinder (Airpot Corporation, Norwalk CT) throughout the entire motion cycle, which succeeded in preventing spontaneous subluxation in all specimens. Specimen-specific subluxation events were created by superimposing a separate posteriorly-directed subluxation pulse to the tibia, via a second pneumatic cylinder during motion (Figure 1). The subluxation pulse onset was at the 45% instant (0.9 sec) of the gait cycle (corresponding to the instant of heel-off) (Figure 3). This pulse was linearly ramped from 0 N at the 45% instant of the duty cycle to a test-specific peak magnitude at the 57.5% instant of the duty cycle (ankle near maximum dorsiflexion), and back down to zero at the 70% instant of the duty cycle (ankle coursing from dorsiflexion toward neutral position) (Figure 3).
Figure 3.
The tibia coursed through stance-phase range of motion (top graph). Data were analyzed between the 40% to 90% instants of the duty cycle. The net posterior tibial force (bottom graph) was the sum of the constant 30 N anteriorly-directed force and the subluxation pulse. The subluxation pulse onset was at the 45% instant of the duty cycle. The pulse peak was reached at the 57.5% instant of the duty cycle, and the pulse ramped back down to zero at the 70% instant of the duty cycle.
Initially, all specimens were loaded under intact conditions over a two-second testing period, during which the ankle was rotated through stance-phase range of motion, beginning at 10 degrees plantarflexion, coursing to 15 degrees plantarflexion, reversing to 15 degrees dorsiflexion, and finally coursing back to 10 degrees plantarflexion at toeoff (Figure 3). Both a 300 N axial load applied by the MTS and the 30 N anteriorly-directed stabilization force applied by the first pneumatic cylinder were held constant throughout the entire duty cycle. Subsequently, subluxation pulses between 0 N and 120 N, in 20 N increments, were randomly applied as described. No subluxation occurred in any of the intact specimens over this entire range of subluxation pulses. Testing was repeated with all subluxation pulse increments randomly applied in a different order to confirm the repeatability of the results.
The anterior one-third of the distal tibia was then osteotomized, displaced proximally 2.0 mm, and rigidly stabilized with an anterior-to-posterior lag bolt (Figure 2). The anterior talofibular ligament was then cut. The testing sequence was repeated: a 300 N axial force, a 30 N anteriorly-directed stabilization force, and random application of posteriorly-directed subluxation pulses (0 N to 120 N in 20 N increments). All seven specimens subluxated once a specimen-specific subluxation pulse magnitude was exceeded. The lowest-magnitude subluxation pulse that caused the specimen to subluxate was defined as that specimen’s instability threshold, and the trial with a subluxation pulse 20 N less than the instability threshold was defined as that specimen’s metastable limit. Testing was repeated with a different sequence of random application of subluxation pulses, to determine the repeatability of testing. In all specimens, the instability threshold and metastable limit subluxation pulse magnitudes were unchanged in repeated testing. Therefore, each specimen had its contact stress distribution history sampled while intact, and while under incongruous conditions with random application of posteriorly-directed subluxation pulses. These loading parameters defined four conditions: intact specimens subjected to the metastable limit subluxation pulse, intact specimens subjected to the instability threshold subluxation pulse, stable-incongruous specimens (those with the 2.0 mm step-off, subjected to the metastable limit subluxation pulse, that remained stable), and unstable-incongruous specimens (those with the 2.0 mm step-off, subjected to the instability threshold subluxation pulse, that subluxated).
Instantaneous contact stresses for all specimens under each condition were collected at 132 Hz. Contact stress values were mask-filtered to exclude spurious peak values resulting from local sensor irregularities resulting in turn from abnormal sensor deformation around the stepoff. Mask-filtering was done by considering the nine concurrent stress measurements in a 3 × 3 sensel mask centered around each sensel at each time frame. The six highest values in the nine sensel mask were averaged, yielding the mask-filtered value for the central sensel (the sensel of interest) within the 3 × 3 grid.
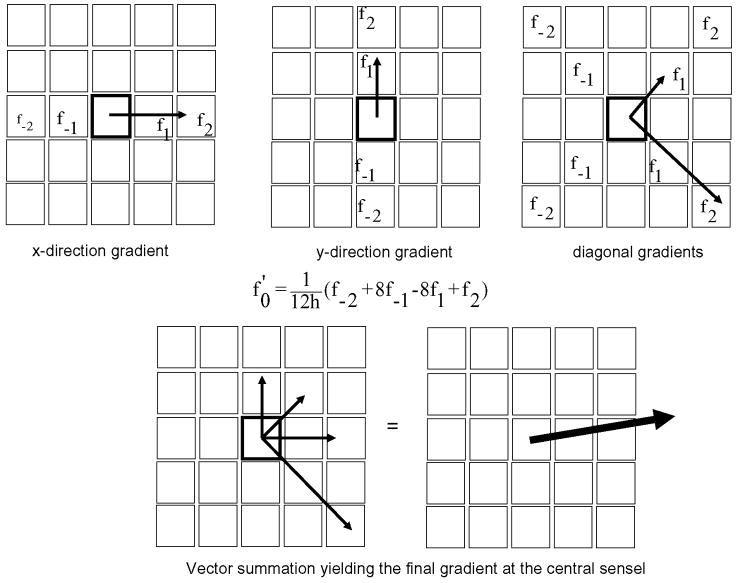
The focus of this study was to calculate transient contact stress directional gradients at each sensel under the various test conditions to quantify instantaneous topographical variations in the contact stress distribution over the articular surface. The directional gradients were calculated using a Lagrange four-point central differencing formula, based on stress measurements (mask-filtered) from neighboring sensels 15. To make maximal use of local stress data, the Lagrange formula (f′0 = (1/12h) × (f −2 + 8f −1 − 8f 1 + f 2) was applied to local sensel information in four distinct directions: along the x-axis (perpendicular to the sagittal axis of the distal tibia), the y-axis (parallel to the sagittal axis of the distal tibia), and along two 45° diagonals. Here the value f′0 is the calculated gradient, h is the sensel width, and the values f −2, f −1, f 1, and f 2 represent neighboring stress measurements along the axis of interest (Figure 4). These four respective directional samplings were vectorially averaged to calculate the transient contact stress directional gradient at each sensel.
Figure 4.
Transient contact stress directional gradients were calculated at each individual sensel at each time frame by applying the Lagrange Central-Differencing Formula. Neighboring sensel stress values (f−2, f−1, f1, f2) were used to calculate x-direction, y-direction, and two diagonal gradients at the central sensel (highlighted). Vector addition of the four individual gradients calculated the final transient gradient at the center sensel.
Data analysis was performed on transient directional gradient values calculated between the 40% (0.8 sec) and 90% (1.8 sec) time points of the duty cycle, to focus on the instability event (Figure 3). Therefore, each data set consisted of 194,304 directional gradient calculations (1472 measurements × 132 samplings). Gradient data sets for each condition were rank ordered, and the 95th percentile values were determined. The 95th percentile values were chosen to avoid over-interpretation of peak values, which may have been influenced by sensor sampling error, or by magnification secondary to the numerical differentiation used to calculate gradient values. To control for overall type I error, a global test for a difference between any pair of groups was first performed using a repeated measures MANOVA (multivariate ANOVA) analysis (p = 0.0037). Significant follow-up paired comparisons, based on paired t-tests, between intact and experimental conditions were then performed.
Results
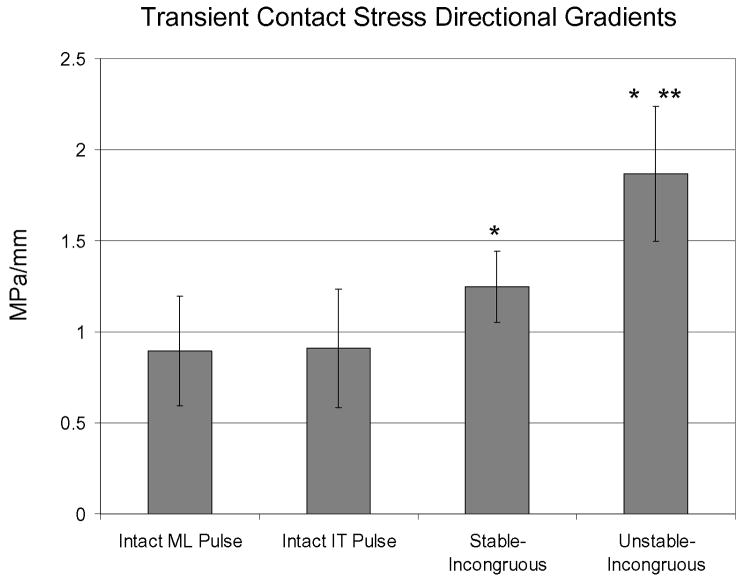
Under intact conditions, 95th percentile transient contact stress directional gradients were indistinguishable for specimens subjected to the instability threshold pulse versus the metastable limit pulse, measuring 0.9 MPa/mm (Figure 5). This value increased to 1.2 MPa/mm under stable-incongruous conditions (1.3X intact conditions, p = 0.004). Under unstable-incongruous conditions, 95th percentile transient contact stress directional gradients increased to 1.9 MPa/mm (1.6X stable-incongruous conditions, p = 0.0008; 2.0X intact conditions, p = 0.0004).
Figure 5.
Transient contact stress directional gradients were identical in intact specimens subjected to the metastable-limit and instability-threshold level subluxation pulses. Compared to intact conditions, 95th percentile transient contact stress directional gradients increased 30% in stable-incongruous conditions and 100% in unstable-incongruous conditions (* denotes significantly increased (p < 0.05) compared to intact conditions). Compared to stable-incongruous conditions, transient contact stress directional gradients increased 60% in unstable-incongruous conditions (** denotes significantly increased (p < 0.05) compared to stable-incongruous conditions).
Throughout the entire duty cycle under intact conditions, contact stress directional gradient vector format plots consistently demonstrated low-magnitude and randomly oriented stress gradients. In contrast, under incongruous conditions (stable or unstable), the vector format plots were nearly identical with preferentially-oriented gradients aligned along the osteotomy border radially directed away from the incongruity-related stress concentration while the talus remained stable and reduced under the distal tibia. Representative vector format plots of transient contact stress directional gradients during subluxation (taken at the same instant coincident with the instant of peak subluxation in unstable-incongruous conditions), highlight feature differences between intact, stable-incongruous, and unstable-incongruous conditions (Figure 6). Under intact conditions, the gradient vectors remain low-magnitude and randomly oriented. In contrast, under incongruous conditions, there is preferential orientation of higher-magnitude stress gradient vectors aligned along the entire border of the osteotomy on the intact distal tibial articular surface. In addition, the sharp focus of stress gradient vectors on the anterior fragment is clearly evident under unstable conditions when the talus has subluxated.
Figure 6.
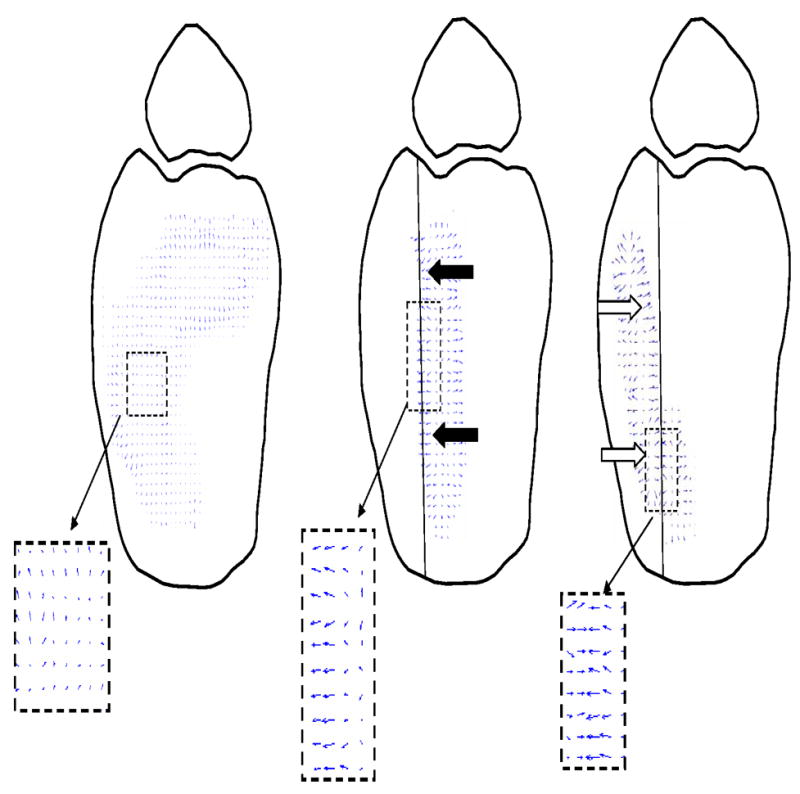
Representative transient contact stress directional gradient vector plots show low-magnitude and randomly-oriented transient vectors under intact conditions. Higher magnitude gradients, radially directed away from the high stress region at the osteotomy border, are seen in stable-incongruous conditions (black arrows). During subluxation, high-magnitude polarized gradient vectors are distributed on the displaced anterior fragment under unstable conditions (white arrows).
Discussion
It was hypothesized that superimposing an instability event on already incongruous ankles would lead to significant increases in transient contact stress directional gradients. Under stable-incongruous conditions, the 95th percentile values of transient contact stress directional gradients increased by 30% compared to intact conditions. With an identical articular incongruity and only small changes in extrinsic loading, occurrence of a subluxation event caused the corresponding values to increase by an additional 60% compared to stable-incongruous conditions, strongly supporting the hypothesis that instability significantly increased contact stress directional gradients. The effect of instability under these testing conditions was significantly greater than the effect of incongruity alone in increasing contact stress directional gradients.
In previous testing, elevated contact stress directional gradients have been shown to be predictive of acute cartilage fissuring in a live rabbit patellofemoral impact model 12. Rabbit patellofemoral joints were impacted and the contact footprint was recorded on pressure sensitive film. Regions with the highest contact stress directional gradients had the greatest amount of fissuring. In statically loaded cadaveric canine knees, contact stress directional gradients increased four-to-six-fold adjacent to circular full-thickness cartilage defects, as compared to intact conditions. In contrast, peak contact stresses only increased by roughly 25% in the same defect specimens, compared to intact knees 11.
Recently, using the same quasi-physiologic human cadaveric ankle testing system as in the present study, incongruity of the anterolateral quarter of the distal tibia, with presumably stable motion, resulted in greater percentage increases in transient contact stress directional gradients compared to the stable-incongruous conditions in the current experiment 9. Peak transient gradients increased by nearly 140% in specimens with a 2.0 mm stepoff in that earlier series, compared to only a 30% increase in stable-incongruous specimens, in the current test. In the previous test, the loading regimen was different, with 600 N axial loads and a different anterior/posterior loading protocol (specimens in the previous test were stable and no baseline stabilization force was necessary). In the current test, specimens loaded to 600 N consistently fractured along the osteotomy border, so the axial load was reduced to 300 N. However, at either 300 N or 600 N axial load, the morphology of the contact stress distribution under intact conditions was nearly identical throughout the entire duty cycle. Furthermore, the contact stress morphology under intact conditions in the previous and current ankle tests was also similar to recent ankle contact distributions determined by stereophotographic methods 16.
In the previous ankle experiment 9, the incongruous fragment had an orthogonal apex at the corner of the osteotomy border, with focal regions of high gradients were encountered immediately adjacent to the apex. Finally, the values reported in the previous test were 99th percentile values, compared to 95th percentile values in the current test. The lesser values were chosen in this test to avoid reporting spurious values resulting from experimental error or numerical differentiation. While the differences in the calculations between the two tests may have been affected by different loading regimens and differences in data reduction, the results between the two experiments demonstrate the mechanical idiosyncrasies of articular surface incongruity, with incongruities of roughly the same magnitude resulting in substantially diifferent pathomechanical changes of contact loads.
While the physical effects of increased contact stress directional gradients on cartilage are not known, the premise that elevated stress gradients can lead to cartilage degeneration is supported by the biphasic nature of the tissue 17. The majority of load transmitted through cartilage is via pulses of pressurized interstitial fluid, minimizing shear deformation in the tissue 17,18. The skeletal elements of the cartilage (the collagen lattice and interspersed proteoglycan molecules) resist compression-induced expansion, thereby facilitating interstitial pressurization 17–19. The biphasic arrangement also minimizes interstitial shear strains, which must be supported by the collagen/proteoglycan scaffold 17,20. Aberrant loads, such as those that would occur in regions with elevated directional gradients, could potentially reverse the physiologic loading strategy of cartilage, leading to increased shear deformation and decreased interstitial fluid pressurization. Therefore, regions with grossly elevated contact stress directional gradients are at risk to overload the collagen/proteoglycan scaffold, potentially disrupting the interstitial skeleton of the cartilage 20. Multiple studies have shown elevated levels of aggrecan in synovial fluid from patients with osteoarthritis, presumably from disrupted bonds between the aggrecan chains and the hyaluronic acid core of the proteoglycan 21,22. The non-covalent bonds between aggrecan and the hyaluronic core are tenuous when compared to other non-covalent bonds, and are several orders of magnitude weaker than covalent bonds 23. In addition, multiple studies have demonstrated that chondrocytes subjected to elevated shear stress respond by increased production of catabolic mediators including nitric oxide and several metalloproteinases, which have been associated with cartilage degeneration 24,25. Therefore it is plausible that elevated stress gradients, transmitted as shear stresses through the cartilage interstitium, could physically disrupt the cartilage skeleton and affect chondrocyte metabolism, leading to degeneration.
The premise of this experiment was to create a metastable ankle that could either remain stable or be rendered unstable with minimal changes in extrinsic loading in the presence of an articular surface incongruity. Under such conditions, injury-associated changes in contact stress directional gradients that resulted from incongruity either with or without subsequent instability could be quantified. This was done with admittedly a somewhat contrived loading regime, and at subphysiologic loads. Nevertheless, all specimens were subjected to the same set of forces, and underwent similar motion. It is obvious that the increases in contact stress directional gradients under unstable-incongruous conditions compared to stable-incongruous conditions did not result simply from the superimposition of an additional 20 N of posteriorly-directed force: The resultant vector of the anterior-posterior loads, when combined with the axial load in the unstable-incongruous specimens, was only 4 N greater than corresponding values in the stable-incongruous specimens. Moreover, under intact conditions, specimens subjected to instability-threshold and metastable-limit subluxation pulses had indistinguishable 95th percentile transient contact stress directional gradients.
Numerical differentiation of the contact stress scalar values, to calculate the directional gradients, obviously involved differentiation-associated artifact. To minimize this artifact, the contact stress values were smoothed by digitally filtering low-level noise (< 0.25 MPa) and by removing potential spurious peaks due to local sensel idiosyncracies by mask-filtering. Mask-filtering presumably muted some of the peak values, but again, all cases were subjected to the same data reduction techniques. Also, each sensor was individually calibrated, on a sensel-by-sensel basis, by subjecting all sensels to a uniform load and determining calibration curves for each individual sensel.
In conclusion, instability in the presence of incongruity caused dramatically greater increases in transient contact stress directional gradients compared to incongruity alone.
Acknowledgments
Financial assistance was provided by grant R49CCR 721745 from Center for Disease Control and Prevention, and P50 AR48939 from the National Institutes of Health. We would like to thank Dr. Stephen Hillis for statistical assistance.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Contributor Information
Todd O. McKinley, Department of Orthopaedic Surgery, University of Iowa., 200 Hawkins Drive, Iowa City, Iowa 52242, 319-384-8253, todd-mckinley@uiowa.edu.
Yuki Tochigi, Orthopaedics Biomechanics Laboratory, Department of Orthopaedic Surgery, University of Iowa.
M. James Rudert, Orthopaedics Biomechanics Laboratory, Department of Orthopaedic Surgery, University of Iowa.
Thomas D. Brown, Orthopaedics Biomechanics Laboratory, Department of Orthopaedic Surgery, University of Iowa
References
- 1.Honkonen SE. Indications for surgical treatment of tibial condyle fractures. Clin Orthop Relat Res. 1994;302:199–205. [PubMed] [Google Scholar]
- 2.Letournel E. Acetabulum fractures: classification and management. Clin Orthop Relat Res. 1980;151:81–106. [PubMed] [Google Scholar]
- 3.Matta JM. Fractures of the acetabulum: accuracy of reduction and clinical results in patients managed operatively within three weeks after the injury. J Bone Joint Surg Am. 1996;78:1632–45. [PubMed] [Google Scholar]
- 4.Brown TD, Johnston RC, Saltzman CS, Marsh JL, Buckwalter JA. Posttraumatic osteoarthritis: a first estimate of incidence, prevalence, and burden of disease. J Orthop Trauma. 2006;20:739–44. doi: 10.1097/01.bot.0000246468.80635.ef. [DOI] [PubMed] [Google Scholar]
- 5.Mitchell N, Shepard N. Healing of articular cartilage in intra-articular fractures in rabbits. J Bone Joint Surg Am. 1980;62:628–34. [PubMed] [Google Scholar]
- 6.Daniel DM, Stone ML, Dobson BE, Fithian DC, Rossman DJ, Kaufman KR. Fate of the ACL-injured patient. A prospective outcome study. Am J Sports Med. 1994;22:632–44. doi: 10.1177/036354659402200511. [DOI] [PubMed] [Google Scholar]
- 7.Harrington KD. Degenerative arthritis of the ankle secondary to long-standing lateral ligament instability. J Bone Joint Surg Am. 1979;61:354–61. [PubMed] [Google Scholar]
- 8.Rasmussen PS. Tibial condylar fractures. Impairment of knee joint stability as an indication for surgical treatment. J Bone Joint Surg Am. 1973;55:1331–50. [PubMed] [Google Scholar]
- 9.McKinley TO, Rudert MJ, Koos DC, Pedersen DR, Baer TE, Tochigi Y, et al. Contact stress transients during functional loading of ankle stepoff incongruities. J Biomech. 2006;39:617–26. doi: 10.1016/j.jbiomech.2005.01.036. [DOI] [PubMed] [Google Scholar]
- 10.McKinley TO, Rudert MJ, Koos DC, Pedersen DR, Baer TE, Tochigi Y, et al. Stance-phase aggregate contact stress and contact stress gradient changes resulting from articular surface stepoffs in human cadaveric ankles. Osteoarthritis Cartilage. 2006;14:131–8. doi: 10.1016/j.joca.2005.09.010. [DOI] [PubMed] [Google Scholar]
- 11.Brown TD, Pope DF, Hale JE, Buckwalter JA, Brand RA. Effects of osteochondral defect size on cartilage contact stress. J Orthop Res. 1991;9:559–67. doi: 10.1002/jor.1100090412. [DOI] [PubMed] [Google Scholar]
- 12.Haut RC, Ide TM, De Camp CE. Mechanical responses of the rabbit patello-femoral joint to blunt impact. J Biomech Eng. 1995;117:402–8. doi: 10.1115/1.2794199. [DOI] [PubMed] [Google Scholar]
- 13.Fitzpatrick DC, Otto JK, McKinley TO, Marsh JL, Brown TD. Kinematic and contact stress analysis of posterior malleolus fractures of the ankle. J Orthop Trauma. 2004;18:271–8. doi: 10.1097/00005131-200405000-00002. [DOI] [PubMed] [Google Scholar]
- 14.McKinley TO, Rudert MJ, Tochigi Y, Pedersen DR, Koos DC, Baer TE, et al. Incongruity-dependent changes of contact stress rates in human cadaveric ankles. J Orthop Trauma. 2006;20:732–8. doi: 10.1097/01.bot.0000211150.00919.0e. [DOI] [PubMed] [Google Scholar]
- 15.Kreyszig E. Numerical Analysis. In: Kreyszig E, editor. Advanced Engineering Mathematics. 3. Vol. 1. New York: John Wiley and Sons, Inc; 1972. pp. 859–61. [Google Scholar]
- 16.Millington S, Grabner M, Wozelka R, Hurwitz S, Crandall J. A stereophotographic study of ankle joint contact area. J Orthop Res. 2007;25:1465–73. doi: 10.1002/jor.20425. [DOI] [PubMed] [Google Scholar]
- 17.Mow VC, Kuei SC, Lai WM, Armstrong CG. Biphasic creep and stress relaxation of articular cartilage in compression? Theory and experiments. J Biomech Eng. 1980;102:73–84. doi: 10.1115/1.3138202. [DOI] [PubMed] [Google Scholar]
- 18.Oloyede A, Flachsmann R, Broom ND. The dramatic influence of loading velocity on the compressive response of articular cartilage. Connect Tissue Res. 1992;27:211–24. doi: 10.3109/03008209209006997. [DOI] [PubMed] [Google Scholar]
- 19.Li LP, Buschmann MD, Shirazi-Adl A. Strain-rate dependent stiffness of articular cartilage in unconfined compression. J Biomech Eng. 2003;125:161–8. doi: 10.1115/1.1560142. [DOI] [PubMed] [Google Scholar]
- 20.Wilson W, van Burken C, van Donkelaar C, Buma P, van Rietbergen B, Huiskes R. Causes of mechanically induced collagen damage in articular cartilage. J Orthop Res. 2006;24:220–8. doi: 10.1002/jor.20027. [DOI] [PubMed] [Google Scholar]
- 21.Lohmander LS, Neame PJ, Sandy JD. The structure of aggrecan fragments in human synovial fluid. Evidence that aggrecanase mediates cartilage degradation in inflammatory joint disease, joint injury, and osteoarthritis. Arthritis Rheum. 1993;36:1214–22. doi: 10.1002/art.1780360906. [DOI] [PubMed] [Google Scholar]
- 22.Struglics A, Larsson S, Pratta MA, Kumar S, Lark MW, Lohmander LS. Human osteoarthritis synovial fluid and joint cartilage contain both aggrecanase-and matrix metalloproteinase-generated aggrecan fragments. Osteoarthritis Cartilage. 2006;14:101–13. doi: 10.1016/j.joca.2005.07.018. [DOI] [PubMed] [Google Scholar]
- 23.Liu X, Sun JQ, Heggeness MH, Yeh ML, Luo ZP. Force-mediated dissociation of proteoglycan aggregate in articular cartilage. Biorheology. 2006;43:183–90. [PubMed] [Google Scholar]
- 24.Das P, Schurman DJ, Smith RL. A stereophotographic study of ankle joint contact area. J Orthop Res. 1997;15:87–93. [Google Scholar]
- 25.Jin G, Sah RL, Li YS, Lotz M, Shyy JY, Chien S. Biomechanical regulation of matrix metalloproteinase-9 in cultured chondrocytes. J Orthop Res. 2000;18:899–908. doi: 10.1002/jor.1100180608. [DOI] [PubMed] [Google Scholar]