A Network Model for Activity-Dependent Sleep Regulation

Abstract

We develop and characterize a dynamical network model for activity-dependent sleep regulation. Specifically, in accordance with the activity-dependent theory for sleep, we view organism sleep as emerging from the local sleep states of functional units known as cortical columns; these local sleep states evolve through integration of local activity inputs, loose couplings with neighboring cortical columns, and global regulation (e.g. by the circadian clock). We model these cortical columns as coupled or networked activity-integrators that transition between sleep and waking states based on thresholds on the total activity. The model dynamics for three canonical experiments (which we have studied both through simulation and system-theoretic analysis) match with experimentally-observed characteristics of the cortical-column network. Most notably, assuming connectedness of the network graph, our model predicts the recovery of the columns to a synchronized state upon temporary overstimulation of a single column and/or randomization of the initial sleep and activity-integration states. In analogy with other models for networked oscillators, our model also predicts the possibility for such phenomena as mode-locking.

1 Introduction

Sleep is a fundamental process in human and animal life, that comprehensively impacts both our day-to-day existence and our long-term growth and development. The fundamental importance of sleep has fostered extensive study on its neurological characteristics and mechanisms (e.g., [1,2]). This research has been complemented by efforts to mathematically model the sleep-wake cycle as a homeostatic (regulation) process, with the aim of giving predictive descriptions of sleep dynamics (e.g., [3–5]). In the activity-dependent or use-dependent theory for sleep [2, 6], the fundamental units that transition between sleep and wake states (as reflected by functional changes in these units) are groups of tightly-connected neurons in the cortex known as cortical columns. The biochemical and bioelectrical mechanisms underlying the sleep/wake transition in each cortical column are modulated by local activity, i.e. by electrical and biochemical drives that project a particular function (e.g., the twitching of a particular whisker on a rat) onto an individual cortical column. The transition is also modulated by loose network couplings among the columns, and by sleep regulatory circuitry. Our aim here is to develop a mathematical model for this network of cortical columns, that captures the fundamentals of the activity-dependent mechanism of sleep.

It is worthwhile to connect our modeling efforts with the existing models concerned with sleep regulation. Sleep has been extensively modeled at the behavioral level (e.g., [3]). These simple models capture 1) the projection of the circadian rhythm into sleep dynamics and 2) some homeostatic regulation of the sleep state, at a whole-organism level. However these models do not capture either the spatial structure or the biochemical/bioelectrical pathways underlying activity-dependent sleep. Cortical columns (and more generally neuronal assemblies) are well-known to be basic building blocks for sleep and memory, and there has been some interest in modeling their dynamics. In particular, a variation of the classical Wilson-Cowan model has been shown to display the periodic responses characteristic of excitatory/inhibitory processes in cortical columns [7]. Recently, a more complicated model for cortical column dynamics has been developed, that explicitly codes the notion of a sleep state as well as the activity-dependent evolution of assembly dynamics [8]. While these models represent the regulatory role played by cortical columns, they cannot capture the translation of local activity (activity at one or a small number columns) into a global sleep state. Also of interest, network models (often comprising excitatory/inhibitory agents as components) have been used to capture a variety of neuronal dynamics in e.g. the thalamus and subthalamic nucleus including in sleep regulatory circuitry (e.g., [9–12]). In this direction, Hill and Tononi have developed a circuit-level model of the thalamocortical system, that permits examination (through simulation) of the nominal sleep-wake transition and the slow-wave sleep dynamics [13]. Massimini and coworkers have put forth and tested the hypothesis that the network connectivity changes between waking, REM, and NREM sleep, respectively; their effort can be viewed as an explicit modeling of the network topology’s evolution, and hence complements our efforts to model overlayed dynamics [14]. The evolution of synaptic weights (connectivities) is also explored using a mean-field analysis of a network model, in [15]. Meanwhile, cortical activity has also been represented using continuum models rather than networks with discrete elements, see e.g. [16]. On the other hand, activity-dependence has also recently been considered in the sleep modeling literature [17], though only at the level of detail of a two-process model. The current work advances the existing modeling efforts by making explicit the role played by the cortex in sleep and its regulation, in particular by 1) making explicit the incorporation of local activity in sleep regulation through the cortical columns and 2) capturing networked interactions among the columns.

The biochemical and electrical mechanisms of sleep include the processes by which local activity, coupling of neighboring cortical columns, and regulatory circuits modulate sleep regulatory substances (SRSs), as well as the mechanisms by which accumulated SRSs cause the functional changes associated with sleep-state change. Here, we abstractly view each column’s intricate dynamics as an activity-integrator that modulates a functional sleep state; using this abstraction, we represent the cortical columns as a network of activity-integrators with associated functional states, that further interact through loose coupling and through regulatory circuitry. With this coarser or network-level model, we are able to study how the local dynamics of the columns can foster formation of a global sleep state.

Specifically, our modeling efforts contribute to ongoing research in the following ways:

1. From the perspective of sleep research, our network model captures analytically the combined roles of local activity inputs, coupling between cortical columns, and regulatory circuitry in formation and evolution of a global sleep state. As such, it is depictive of the activity-based theory for sleep developed by Krueger and co-workers [2, 6], and permits exploration of the sleep-state dynamics under the premises of the theory. While our primary aim here is to give a plausible description and analysis of activity-dependent sleep, the model holds promise in the long run as a tool for prediction and design, for instance in characterizing the effects of sleep deprivation and/or designing drugs that impact regulation.

2. In that we study regulatory dynamics defined on a graph, our work also explicitly connects sleep modeling with the ongoing effort to model and in turn control dynamical networks, e.g. [20–22]. We note here that the activity-dependent theory for sleep regulation matches the developing paradigm for control in modern engineered networks, wherein highly limited agents interact through localized network couplings (with possibly rather complex or arbitrary coupling topologies) to achieve a global regulation task (see, e.g., the overviews [23,24] or the articles [25, 26]). Within this broad domain, our efforts are especially connected with ongoing research in both the physics and electrical engineering communities on synchronization or agreement in oscillator networks (see e.g [27–30] in the physics and natural-sciences literature, and [20,31–36] in the engineering community). From this perspective, the key contributions of the work are the 1) introduction and characterization a general network model for synchronization with external inputs, and 2) the study of a novel nonlinear dynamic model for oscillators.

The article is organized as follows. In Section 2, we motivate and formulate the network model. Section 3 characterizes the model and illustrates its predictive capability, through both simulation and analysis.

2 Network Model Formulation

In this section, we propose a network model for the interaction of cortical columns, which shows promise in predicting activity-dependent regulation of sleep. Specifically, we represent individual cortical columns as very simple but interacting activity-based regulators, and explore the role played by the network interactions in translating local activity inputs as well as global regulatory-circuit signals into whole-animal sleep. Our model captures both the spatial structure and temporal characteristics of sleep identified in the activity-dependent theory [2, 6].

In the model that we propose, the interactions among the cortical columns are critical to the rapid formation of a global sleep state. This paradigm of local interactions leading to a global state has been of considerable interest to the complex-systems modeling community (e.g., [20, 40]) as well as the network-control community (e.g., [21–23]). A key feature of the networks considered in this literature is that they are built of agents with very simple internal dynamics, but quite complicated interactions that lead to interesting global dynamics. We note that the model developed here is of the same form, and hence indicates a new application for this complex networks theory. Also of interest, the model described here can be viewed as having an intrinsic mechanism for the emergence of a global state, but complementarily also can be viewed as using both external inputs and feedback through network coupling to achieve regulation. In this sense, this study connects the modeling paradigm pursued in the complex-system community with the regulator-design paradigm of the network-control community.

The following are the key points of the activity-dependent theory for sleep used in model development [2, 6]. During awake periods, individual cortical columns integrate (store) activity information (or energy for activity relative to available energy) through biochemical and electrical means, in entities known as sleep regulatory substances; when this integrated activity becomes large enough, the cortical column transitions to a sleep state (a state exhibiting unresponsiveness to sensory stimuli, certain increases in synaptic plasticity, etc). It is postulated that the transition to a sleep state is also impacted by spatially-close cortical columns that are already in a sleep state. These columns tend to drag the awake column toward the sleep state through biochemical and electrical means, and hence foster the formation of a global sleep state. Similarly, a cortical column in the sleep state can be viewed as containing processes that gradually return to a waking state (either through inhibition of the processes inducing sleep, or through other integrative processes); again, nearby columns that are in an awake state have an impact. Besides the activity-dependent dynamics and couplings, sub-cortical global regulatory circuits impose a circadian rhythm and also permits rapid waking under stimulus.

Based on the above description, we abstractly model each cortical column using a sleep state variable and an activity variable, which evolve in time due to integration of local activity, as well as interactions with other columns and global regulation. Precisely, let us consider a network of n cortical columns. Each cortical column i is described by a binary sleep state variable S_i(t), where S_i(t) = 1 indicates that the column is in the sleep state, while S_i(t) = 0 indicates a wake state. We also associate a continuous-valued total activity variable (or simply activity variable in short) x_i(t) with the cortical column i, which indicates the total activity since waking when the column is in the wake state, and indicates the total restoration effort in the sleep state.

In addition to the internal variables for each column, the model comprises a network topology describing the strengths of interactions between cortical columns. In particular, for each pair of cortical columns i and j, we use a fixed nonnegative weight w_ij to capture the strength of the effect of cortical column i on cortical column j. We find it convenient to assemble the weights into a (possibly asymmetric) topology matrix $W\stackrel{\mathrm{\Delta }}{=}[w_{ij}]$. Also, we draw a network graph comprising n vertices labeled 1,…,n, with an edge drawn from i to j if and only if w_ij > 0. One can postulate several plausible formative odels for the network topology; however, the fundamental observed behaviors of the model are not dependent on the specifics of the network topology beyond its connectedness, so we leave the representation general.

We also assume the existence of a global clock signal, which eventually enforces (under normal activity conditions) that the cortical columns not only synchronize but transition between the sleep state and wake state at environmentally-appropriate times, i.e. according to a circadian rhythm. In humans, the clock signal is maintained by the suprachiasmatic nuclei (SCN), and distributed globally through neuronal connections, see e.g. [5] for details and modeling methods. Here, we denote the scalar clock signal by C(t), where C(t) = 1 indicates that the organism should be awake, C(t) = −1 indicates that sleep is desirable, and C(t) between −1 and 1 indicates weaker proclivities for waking/sleep.

Now we are ready to describe the evolution of the sleep state variables and the activity variables. Broadly, the activity variable gradually increases for each column during awake periods (depending on activity at the column), and gradually decreases during asleep periods. The sleep state variable changes when the activity relative to provided energy reaches thresholds; this threshold conceptually represents either an energy-deficit level, or a biochemical state, such that sleep occurs. Specifically, let us first consider the evolution of a cortical column i that is currently in the awake state (S_i(t) = 0). We model the activity variable x_i(t) and sleep state variable S_i(t) as evolving as follows:

• $x_i(t)=+u_i(t)+{\sum }_{j=1}^n{S}_j(t)\mathit{step}(x_j(t)-E_j)w_{ji}+{\alpha }_i(1-C(t))$

• S_i(t) → 1 if x_i(t) − E_i > T_i,

where u_i(t) is the activity input at the cortical column i at time T, E_i(t) is the energy available during the awake period, T_i is the sleep threshold, and step() is a function that equals 1 for positive arguments and 0 for negative arguments. We notice that, nominally, the activity variable x_i(t) integrates the activity at the column over time, but the cortical column is more quickly driven toward the sleep state when connected cortical columns have recently entered the sleep state (S_j (t)step(x_j (t) − E_j ) > 0). The strength of this interactive response scales with the weight w_ji.

Similarly, the activity variable and sleep state variable evolve during the asleep period, as follows:

• $x_i(t)=-r_i(t)+{\sum }_{j=1}^n(1-S_j(t))\mathit{step}(E_j-x_j(t))w_{ji}+{\alpha }_{i}C(t)$

• S_i(t) → 0 if E_i − x_i(t) > T_i,

where r_i(t) is called the recovery input to cortical column i, and represents restoration of the activity variable prior to waking (which is connected to the repair and synaptic development occurring during sleep). Again, we note that the activity variable integrates both local input and signals from nearby cortical columns that have recently entered the awake state.

We holistically refer to the model as the activity integrator-network (AIN). Let us reiterate the connection of the AIN with the extensive literature on network control. Over the several years, there has been extensive research concerned with analyzing dynamics defined on a graph, and relating characteristics of such dynamics with structural characteristics of the underlying graph, see [24, 41, 42] for overviews of some important aspects of this analysis. Recently, control theorists have realized that understanding network structure further is critical to controlling/designing dynamics on a network, in such diverse fields as autonomous vehicle team formation, sensor networking, and virus-spreading control [21–23, 26]. What these various works have in common is that individual agents with very simple internal dynamics achieve a global task through network interactions. The AIN falls within this paradigm, in that cortical columns with essentially integration and thresholding capabilities achieve global sleep regulation. Within this broad class, the AIN is most closely connected to models for oscillator networks and rotational agreement, though the specifics of the dynamics differ from the models in the literature, e.g. [31–34]. One very significant novelty in our development, from a modeling and control-theory standpoint, is that we consider the impact of external input signals (disturbances) on the dynamics.

Let us conclude our formulation of the AIN by noting two limitations of the model. First, we have entirely excluded modeling of the humoral mechanisms for sleep, see e.g. [44], because our efforts are focused on the local couplings in the cortex that underly sleep. Second, we have not attempted yet to model all the time- and state-dependent variations of the network structure/parameters that are observed in the sleep cycle (e.g. [6]). Most prominently, the coupling parameters between the cortical columns would be expected to change between the sleep and wake states, and also during sub-intervals of sleep and waking (e.g., REM sleep, high-activity waking periods).

3 Prediction of Whole-Animal Sleep: Simulations and Analysis

We illustrate that the AIN dynamics match the predictions of the activity-dependent sleep theory through simulations (System 3.1) and system-theoretic analysis (Section 3.2). We note that our efforts characterize both the internal dynamics and the input-to-state behavior of the AIN.

3.1 Illustrative Simulations

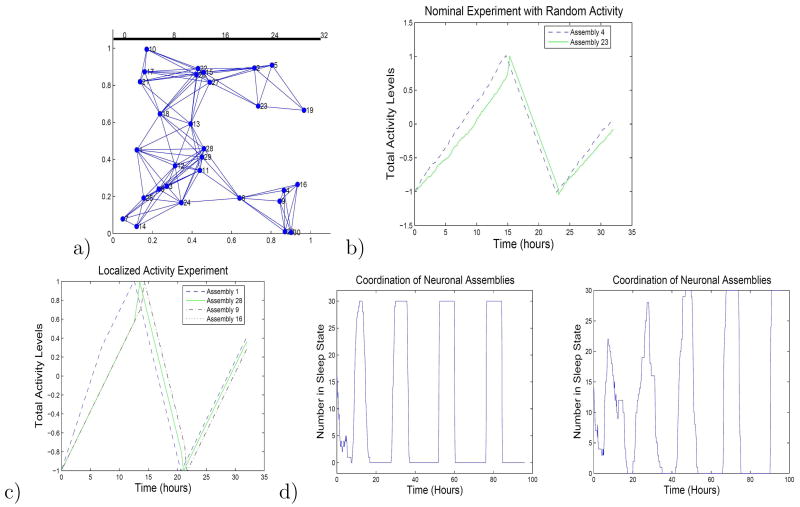
We illustrate the combined role of the activity inputs and network interactions in the AIN dynamics, using several canonical simulations. We present simulation results using a network with 30 cortical columns with identical internal dynamics, see Figure 1.

Figure 1.

a) The network topology for the 30-cortical-column example is illustrated. b) The baseline activity simulation is shown. c) The local overstimulation experiment is simulated; activity variables for five representative cortical columns (neuronal assemblies) are shown. d) The coordination experiment is simulated, for two different interaction strengths. Higher interaction strengths yield faster coordination.

Baseline Activity Simulation

Under normal rest or light activity conditions, a reasonable assumption is that the cortical columns are initially synchronized, and the activity inputs at each column are independent stochastic signals with identical statistics. In Figure 1, we show time-traces of two columns’ total activity variables in the example AIN, under baseline activity conditions. The simulation illustrates that the loose couplings between columns are needed for maintaining coordination: because of the loose coupling, we see that the transition to the sleep state flows in a wave-like fashion through the network.

Local Overstimulation Experiment

Experiments in which one or a small number of cortical columns are overstimulated have been of particular interest in the sleep community, because they permit evaluation of the claim that sleep is activity dependent. For instance, the impact on a rat’s sleep response of repeatedly moving a single whisker has been studied [43]. We simulate such an experiment, by driving one or a small number of cortical columns with an input that is significantly larger than the nominal. In particular, we overstimulate one cortical column for a period, causing it to quickly enter the sleep state. Once the column has entered the sleep state, nearby columns begin to rapidly transition toward a sleep state, with the rate of transition become more pronounced as more columns enter the sleep state, see Figure 1. Thus, the sleep state spreads rapidly throughout the network, before the nominal falling-asleep time. We also note that the columns become even further coordinated during the subsequent transition from sleep to waking.

Coordination Experiment

It has been postulated that cortical columns with initially uncorrelated sleep states eventually achieve coordination, because of the interactions between the columns. To capture this instance in our model, we initialize each cortical column with a random total activity variable value and a random sleep state, and observe the responses of the columns over several days. Our simulations indicate that, indeed, the cortical columns become coordinated over time, with the duration needed for coordination depending on the strengths of interactions between the columns (Figure 1).

The simulations together highlight the critical role played by both the activity inputs and the network couplings in regulating sleep, in the presence of varying activity inputs.

3.2 System-Theoretic Analysis

We conclude our study of the AIN with a preliminary system-theoretic analysis of its dynamics. Explicit analysis of the AIN dynamics is both difficult and valuable from a system-theory standpoint. The novelty (and complexity) in the analysis stems from three aspects of the model: 1) the (novel) nonlinear dynamics, 2) the fact that the model represents a distributed system or network defined on an arbitrary graph, and 3) the need for characterizing the response to (deterministic or stochastic) external signals. Our analysis here characterizes, largely at a qualitative level, the dual role played by the activity inputs and the network couplings in governing sleep-state evolution. We stress here that the this study is, to the best of our knowledge, the first effort to characterize the external (disturbance rejection) properties of a complex-network model such as this one. Specifically, we pursue two analyses:

1. We study the internal stability properties of the system, i.e. we study the approach to synchronization (coordination) from an initially-uncoordinated state (and assuming identical activity inputs).

2. we study the external stability or disturbance-response properties of the AIN, in particular verifying that the network coupling permits the AIN to remain coordinated in the presence of activity-input variations.

We characterize the AIN’s dynamics for arbitrary network topologies, but for convenience we shall assume that the cortical columns in the AIN have identical internal dynamics (that is, E_i, T_i, and α_i are the same for all cortical columns); it is easy to see that the results naturally transfer to an inhomogeneous network with scaled inputs.

3.2.1 Internal Dynamics: Approach to Synchronization

Here, we analyze the approach to synchronization (perfect coordination) of the AIN when the activity/recovery inputs are all the same, i.e. we study the internal stability of the AIN¹. We notice that this analysis characterizes return-to-synchronization of the AIN upon local over-stimulation, as well as the coordination when e.g. a lesion has caused the cortical column to become unsynchronized. We shall study the approach to synchronization in two steps, first in the case where the perturbation of the cortical columns from their synchronized state is small (i.e., local syncronization) and second in the general case. In the general (large-perturbation) case, we will only give a preliminary illustration of the analysis through a simple two-assembly example.

Let us begin by formally defining synchrony for the AIN. To do so, we first find it convenient to define relative activity variables. WLOG, we define these relative states with respect to the integrated activity of cortical column 1. In particular, we define the relative activity variable z_i for agent i, i = 2,…,n, as z_i = x_i − x₁. We also define the relative sleep state y_i as y_i = S_i − S₁. Synchrony is naturally defined in terms of the relative activity variables and relative sleep states:

Definition 1 The AIN is said to be synchronized at time t if z_i(t) = 0 and y_i(t) = 0 for i = 2,…,n.

As a preliminary step, we formalize that the syncronized cortical columns remain so when the activity inputs to the columns are the same; that is, we note that any synchronized state is a (relative) equilibrium in this case:

Theorem 1 Consider an AIN whose cortical columns have identical internal dynamics (E_i, T_i, and α_i are the same for all i). If the AIN is initially synchronized and the activity/recovery inputs to the cortical columns are identical, then it remains synchronized at all time t ≥ 0.

Proof: From the fact that the cortical columns and activity inputs are identical, it follows automatically that ż_i = 0 for i = 2,…,n whenever the columns are synchronized. Thus, synchronization is maintained.

To present the small-perturbation result, we find it convenient to combine the sleep state variable and activity variable into a single angular state, which describes the “distance” along the sleep-wake cycle traveled by the cortical column from a reference point (say the occurrence of waking). Formally, let us define the angle θ_i of column i as follows:

• When the cortical column is awake, ${\theta }_i=180\frac{x_i-(E_i-T_i)}{2T_i}$.

• When the cortical column is asleep, ${\theta }_i=180+180\frac{E_i+T_i-x_i}{2T_i}$.

Notice that the cortical column’s angle moves from 0 to 180 during the wake state, and from 180 to 360 during the sleep state. This notion of an angle is a clever way to incorporate both the activity variable and sleep state variable into a single scalar, and hence to differentiate between asleep and awake columns that have equal activity variables.

We also find it useful to define angle differences, to describe the “distance” along the sleep-wake cycles between two cortical columns. Specifically, for two cortical columns with angles θ_i and θ_j, we define the angular distance d(θ_i,, θ_j ) as follows: d(θ_i, θ_j ) = (θ_i − θ_j + 180)mod360 − 180. This measure equals the shorter of the two angles between the two columns’ angles. We note that the network is synchronized at time t if and only if d(θ_i(t), θ_j (t)) = 0 for all i, j.

Let us now present the asymptotic-synchronization result in the case where the cortical columns are perturbed only a small amount from synchronization. For simplicity in presentation, we describe only the case where the identical input to each cortical column is a positive constant during the wake period and a negative constant during the sleep period, although the analysis generalizes naturally to the case where the columns have identical but non-constant nominal inputs. To highlight the role played by the network, we also exclude the SCN input in the analysis. Here is the result:

Theorem 2 Consider an AIN whose cortical columns have identical internal dynamics (E_i and T_i are the same for all i, and α_i̇ = 0), and have identical constant activity inputs u_i(t) = ū and recovery inputs u_i(t) = −ū. Also assume that the AIN has a connected network topology. Then there exists M > 0 such that if |d(θ_i(t₀), θ_j (t₀))| ≤ M for all i, j at some time t₀, then the synchronized state is attractive, i.e. d(θ_i, θ_j) → 0 as t → ∞ for all i and j.

Proof: Choose any M less than 90, and let r(t) and s(t) be the pair of cortical columns for which |d(θ_r(t)(t), θ_s(t)(t))| is largest², and assume WLOG that d(θ_r(t)(t), θ_s(t)(t)) > 0. Notice that the angle of cortical column r can be viewed as “leading” the angles of the other cortical columns, while the angle of s can be seen as “lagging”. Now let us consider the time-derivative of d(θ_r(t)(t), θ_s(t)(t)). Let us separately consider four cases. If both cortical columns r(t) and s(t) are awake (Case 1) or asleep (Case 2), then all the columns are awake (respectively, asleep). In this case, ẋ_i is identical for all columns including r(t) and s(t), and so the time-derivative of d(θ_r(t), θ_s(t)) is zero. Now consider the case where column r(t) is in the sleep state and column s(t) is in the wake state (Case 3). From the activity-variable update, it is clear that the angle of s(t) is increasing at least as quickly as the angle of r(t) (see Figure 3). We find the same result in the case that r(t) is in the sleep state and s(t) in the wake state. We thus immediately find that the time-derivative d(θ_r(t)(t), θ_s(t)(t)) is always nonpositive. In turn, we recover that d(θ_r(t)(t), θ_s(t)(t)) is a non-increasing function of time that is also lower-bounded. We thus recover that d(θ_r(t)(t), θ_s(t)(t)) approaches a limit.

What remains to be proved is that, in fact, the limiting value of d(θ_r(t)(t), θ_s(t)(t)) is 0 and hence the AIN is attractive to a synchronized state. Let us prove this by contradiction. In particular, assume that the limiting value is some θ ≠ 0. Next, notice that the leading column r(t) is the same one for all t ≥ t₀, since when it is in either the sleep or wake part of the cycle, no other (lagging) column in the same state can overtake it. Now, consider the ordered sequence of lagging columns r₂(t),…, r_n(t) = s(t), and consider the measure ${\sum }_{i=2}^n\mid d({\theta }_{r(t)}(t),{\theta }_{r_i(t)}(t))\mid$. It is easy to see that, during each sleep/wake cycle, this measure strictly decreases by at least a fixed positive amount (which incidentally is linear in γ). Since each relative angle |d(θ_r(t)(t), θ_ri(t)(t))| is non-negative, we thus recover that all such relative angles, including |d(θ_r(t)(t), θ_s(t)(t))|, eventually decrease. Thus, we have a contradiction.

Next, let us study the asymptotics of the AIN for arbitrary initial conditions (i.e., for large perturbations). The global stability of nonlinear-oscillator networks such as this one are well-known to be complicated, see e.g. [31–33]. One prominent characteristic of these oscillator networks is the possibility for mode-locked trajectories, or in other words equilibrium trajectories that do not correspond to synchronized states. Here, let us demonstrate using a two-cortical-column example that the AIN also can have such mode-locked trajectories, although in this case the mode-locked trajectory is not attractive.

Theorem 3 Consider an AIN with n = 2 cortical columns with identical internal dynamics (E_i and T_i are the same for all i, and α_i = 0), and identical constant activity inputs u_i(t) = ū and recovery inputs u_i(t) = −ū. Also assume WLOG that w₂₁ ≥ w₁₂ > 0. Now consider that cortical column 2 has an initial angle θ₂(t₀). Then there is exactly one initial angle for cortical column 1 such that the AIN does not synchronize and instead reaches a periodic orbit; for all other initial angles, the AIN synchronizes.

Proof: First we notice that, as proved in Theorem 2, once we have |d(θ₁(t), θ₂(t))| ≤ 90, then |d(θ₁(t), θ₂(t))| is monotonically non-increasing and in fact decreases during each cycle; thus, the two columns become synchronized. Hence, we only need to consider 90 < |d(θ₁(t), θ₂(t))| < 180. In the case that cortical column 2 is “leading”, we can easily see that |d(θ₁(t), θ₂(t))| also decreases by at least a fixed amount with each cycle. Thus, there exists a time t such that |d(θ₁(t), θ₂(t))| ≤ 90, which implies synchronization.

In the case that cortical column 1 is leading, |d(θ₁(t), θ₂(t))| may change non-monotonically. For instance, when the two columns are in different sleep states and both network couplings are activated, |d(θ₁(t), θ₂(t))| increases (enlarges); and then when they are still in opposite states and only column 1 drives column 2, |d(θ₁(t), θ₂(t))| decreases (shortens). Thus, we expect the possibility for extension-shrinkage-constant half-cycles, which would imply that the cortical columns do not synchronize. In fact, based on the initial angles of the two columns, we have three different outcomes. First, if θ₂(t₀) is larger than a particular angle, after a half-cycle the distance enlarged is bigger than that shortened, and hence the overall |d(θ₁(t), θ₂(t))| increases. Eventually the distance increases beyond 180° after some half-cycles, and column 2 leads instead. Synchronization then is achieved as proved above. Second, if θ₂(t₀) is smaller than this angle, the distance shrinks after a half-cycle, and eventually decreases below 90°. Again, synchronization is guaranteed. Third, the distance enlarged is exactly the same as that shortened for a half-cycle. In this case, we have mode-locking; in particular, |d(θ₁(t), θ₂(t))| is periodic. Simple calculation shows that the initial angle of column 2 that delineates the three outcomes is ${\theta }_2(t_0)=270-90°\frac{w_{12}}{w_{21}}$.

Since the mode-locked state is not an attractive one, we notice that in practice the cortical columns will not evolve to this state. However, the existence of the mode-locked state indicates the possibility that the cortical columns will remain away from synchronization for an extended period. This possibility for extended asynchronization may be reflective of such phenomena as part-brain sleep in e.g. dolphins.

3.2.2 Disturbance Response of the AIN

A key postulate of the activity-dependent theory for sleep is that the cortical columns maintain coordination for variable activity levels and inputs, but their sleep state dynamics are also modulated by the activity inputs. This dual task is fundamentally achieved through the interplay of local activity integration at individual columns and network couplings among the columns. Here, we verify that coordination among the columns in the AIN is maintained in the presence of persistent variations in the activity inputs, but the predicted durations of sleep/waking are dependent on the local inputs. The verification of coordination in this case fundamentally requires study of the disturbance-rejection (or external stability) properties of the AIN. We stress that a disturbance-rejection analysis constitutes an entirely new focus in the study of oscillator networks (see e.g. [45] for a discussion of why the disturbance rejection of even simple nonlinear systems, let alone networks, is so complicated).

For the AIN, verification of coordination in the presence of input variations (disturbances) follows naturally from the initial-condition analysis of the AIN. In particular, we obtain the following:

Theorem 4 Consider an AIN comprising identical cortical columns that are driven by activity inputs u_i(t) = ū + du_i(t), where ū is a strictly positive constant. Let us call the angle difference between the leading column s(t) and the lagging column r(t) at an initial time t₀ by θ_init. For each θ_init < 90, there exists β̂ > 0 such that for all β < β̂, if ||du_i(t)||_∞ ≤ β for all t, then 1) |d(θ_r(t)(t), θ_s(t)(t))| < 90° for all t ≤ t₀, and 2) |d(θ_r(t)(t), θ_s(t)(t))| ≤ Cβ for all sufficiently large t and for some constant C.

The proof of the theorem follows automatically from the proof of Theorem 2: specifically, the observation that the decrease in ${\sum }_{i=2}^n\mid d({\theta }_{r(t)}(t),{\theta }_{r_i(t)}(t))\mid$ over a cycle is linear in its value, together with the fact that the absolute integral of du_i(t) over one cycle is bounded, yields the desired results. We thus omit the details.

The above theorem points out the critical role played by the network coupling in achieving and maintaining a coordinated sleep state: without the coupling, the columns would lose coordination over time. While the columns remain coordinated through the couplings, however, the sleep-state evolution nevertheless is modulated by the activity input.