Liquid and surfactant delivery into pulmonary airways

Abstract

We describe the mechanisms by which liquids and surfactants can be delivered into the pulmonary airways. These are instilled and transported throughout the lung in clinical therapies such as surfactant replacement therapy, partial liquid ventilation and drug delivery. The success of these treatments is contingent on the liquid distribution and the delivery to targeted regions of the lung. The targeting of a liquid plug can be influenced by a variety of factors such as the physical properties of the liquid, the interfacial activity, the gravitational orientation, instillation method and propagation speed. We provide a review of experimental and theoretical studies that examine these effects in single tubes or channels, in tubes with single bifurcations and in the whole lung.

1. Introduction

Airways are liquid-lined, flexible tubes and closure of airways can occur by a Rayleigh instability of the liquid lining, or an instability of the elastic support for the airway as the surface tension of the air-liquid interface pulls the tube shut, or both. (See the article by Heil et al. (2008) in this special issue for a review on airway closure). Airway closure may occur in normal lungs at low lung volumes resulting in liquid plugging (Kamm and Schroter, 1989). Liquid plugs may also form in diseases such as respiratory distress syndrome when the surface tension at the air-liquid interface is too high, asthma when there is extreme narrowing of the airways due to inflammation, pulmonary edema when too much liquid becomes accumulated in the lung, and emphysema due to loss in elastic recoil. Regardless of the mechanism, the airway is closed because the liquid lining has created a plug that prevents gas exchange. Once closed the primary option for reopening an airway is by inspiration. This maneuver will pull the flexible airways open and force the liquid plug to flow distally by the incoming air stream. Airway reopening depends to a large extent on this plug flow. As the plug deposits its contents on the airway walls, it can eventually rupture and gas exchange is again possible.

The liquid plug propagation which occurs in airway reopening is also a phenomenon seen in other pulmonary applications. For example, treatment of certain diseases involves instillation of drugs mixed with liquid directly into the trachea and forced throughout the lung by imposed ventilation. This is the common method of delivering surfactants into the lungs of prematurely-born neonates who suffer from surfactant deficiency (hyaline membrane disease, also called respiratory distress syndrome of the newborn). Liquid plugs are formed during these procedures and blown distally by mechanical inspiration. The resulting spatial distribution in the lung depends on the system parameters governing the basic plug flow phenomenon. Delivery of genetic material and other drugs into the lung can also be accomplished by liquid instillation techniques. The liquid layer that is left behind the propagating bolus may advance due to a combination of gravitational drainage and surface tension gradients generated by a non-uniform surfactant distribution. In smaller airways, surfactant may form a surface layer that spreads due to these surface-tension gradients.

Another pulmonary example of plug propagation is liquid ventilation, a way of ventilating a critically ill patient with perfluorocarbon liquid. The process of filling the lung with the perfluorocarbon, as well as the development and motion of plugs are essential to the effectiveness of the treatment.

The remainder of the paper is organized as follows. In the next section we provide a short review of surface tension effects on flows which are needed to describe the plug propagation and surfactant spreading models reviewed in section 3–section 6. Experimental and theoretical models for liquid and surfactant delivery to the whole lung are reviewed in section 3. Section 4 reviews theoretical models of plug propagation in single tubes or channels, while section 5 covers models of plug propagation through a single bifurcation. Surfactant spreading on thin liquid layers is reviewed in section 6.

2. Surface tension effects on flow

The types of flows described above are all examples of interfacial flows which are affected by surface tension. We provide a brief overview since surface tension and surfactants are also discussed in the articles by Gaver and Ghadiali (2008) , Heil et al. (2008) and Hall et al. (2008) found in this special issue. Molecules within a liquid layer are attracted equally from all sides. However, those near an air-liquid interface experience unequal attractions. The intermolecular attractive forces between nearest neighbors along the interface are stronger. This increase of forces is called surface tension. Those molecules near the surface experience a net force which tends to pull them back into the liquid and attempts to reduce their exposed surface to the smallest possible area.

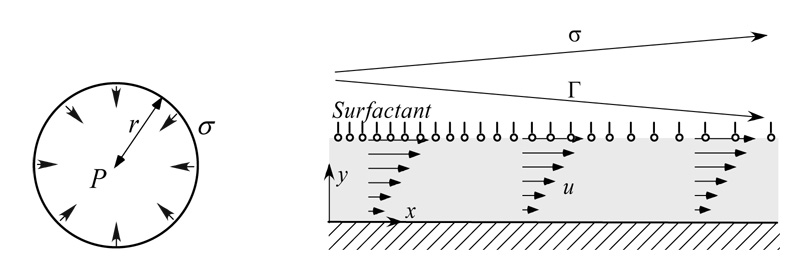
Consider a gas bubble in a quiescent fluid. The surface of the bubble contracts as much as possible as it can. It turns out that a sphere has the smallest possible surface area for a given volume as shown in Fig. 1. A pressure P is generated in the bubble, and according to the Young-Laplace law it is given by

$$P=\sigma \kappa =2\frac{\sigma }{r}$$

where σ is the surface tension, κ is the curvature and r is the bubble radius. (For a sphere κ=2 / r.) This law has several repercussions. A smaller bubble can blow up a larger bubble because it generates a larger pressure. So there is tendency for alveoli to collapse due to this destabilizing effect of surface tension. Another example is the break up of a liquid layer coating the inner surface of a cylinder. Flows within the liquid layer due to the jump in pressure across the interface may result in the occlusion of an airway if the volume of liquid is sufficiently large. This occlusion is known as airway closure. These instabilities are affected by the presence of pulmonary surfactants, which are surface-active molecules produced by type II alveolar cells that like to migrate to air-liquid interfaces. Their proteins and lipids have both a hydrophilic head and a hydrophobic tail. The most favorable energetic configuration is for the heads to be in the layer with the tails sticking out in the air. Surfactants reduce the surface tension by interacting with the cohesive force between water molecules at the air-liquid interface, and can have a stabilizing effect. For example, the tendency of a smaller bubble to empty into a larger one is reduced because as the bubble radius decreases the surfactant molecules are more closely packed thus lowering the surface tension.

Figure 1.

Surface tension effect on the pressure in a soap bubble (left) and a flow induced by the Marangoni stress due to the gradient in surfactant concentration, Γ that induces a flow within the liquid layer (right).

Another important aspect is the fact that a non-uniform surfactant distribution along an interface gives rise to the development of a surface tension gradient, as shown in Fig. 1. The interface can then support a shear stress, commonly known as the Marangoni stress, which is balanced by this gradient. Mathematically, this balance of tangential forces is given by the following equation:

$$\frac{\partial \sigma }{\partial x}=\mu \frac{\partial u}{\partial y}$$

The surface tension σ is normally a decreasing function of interfacial surfactant concentration Γ, so that σ = f(Γ). The function f that relates σ to Γ is known as the surfactant equation of state. A simple example is a linear relationship of the form

$$\sigma ={\sigma }_0-E(\mathrm{\Gamma }-{\mathrm{\Gamma }}_0)$$

where σ₀ is a uniform surface tension corresponding to a uniform surfactant concentration Γ₀ about which the surfactant concentration is perturbed, and E = −(∂σ / ∂Γ)_Γ0 is the surfactant elasticity. The Marangoni stress can have a stabilizing effect in airway closure by opposing the capillary driven instability (Halpern and Grotberg, 1993; Otis et al., 1993). This can be understood by considering the stability of a uniform liquid layer lining the inner surface of a tube with a uniform surfactant distribution coating the air-liquid interface. A disturbance to the air-liquid interface grows due to the destabilizing effect of surface tension explained earlier. The induced flow causes surfactant to be swept from troughs to the peaks of the disturbance, resulting in a surface tension gradient that opposes the surface-tension driven instability. It has been that surfactant can delay closure by approximately a factor of four compared to a clean interface (Halpern and Grotberg, 1993; Otis et al., 1993; Cassidy et al., 1999). More recently, Hideki et al. (2007) have considered the effects of a viscoelastic liquid layer, and have shown that such a layer can be more unstable than a Newtonian liquid layer. This is because the effective viscosity is smaller for a viscoelastic layer leading to a faster liquid flow into the growing bulge (which eventually turns into a plug).

Fig.2 illustrates the formation of a liquid plug as a result of the surface tension instability described above (Cassidy et al., 1999). Surface tension also plays an important role in plug propagation and airway reopening. The thickness of the film left behind the moving plug is determined by a balance of viscous and surface tension forces, and is a function of the capillary number Ca = μU / σ where μ is the viscosity of the film and U is the speed of the plug. Analytical results exist for a semi-infinite air-bubble or a large volume plug (so that there is no interaction between the leading and trailing menisci). When the flow is slow and surface tension is the dominant effect so that Ca ≪ 1, h / R ~ 1.337Ca^2/3 (Bretherton, 1961) where h is the film thickness and R is the tube radius. For Ca ≫ 1, the ratio h / R is independent of Ca and is approximately equal to 0.361. Numerical results obtained from direct numerical simulations bridge the gap between small and large capillary numbers (Reinelt and Saffman, 1985; Halpern and Gaver, 1994; Giavedoni and Saita, 1997; Heil, 2001). Another important parameter is the Bond number, Bo, which measures the importance of gravity with respect to surface tension, and is given by ρgR² / σ, where ρ is the fluid density, and g is the gravitational constant. In large airways it is also important to consider the effects of inertia, which is characterized by the Reynolds number, Re = ρUR / μ, denoting the ratio of inertial to viscous effects. In small airways, viscous effects are dominant and so Re ≪ 1, but in large airways Re ≫ 1 indicating the importance of inertial effects.

Figure 2.

Creation of a liquid plug due to the surface tension induced capillary instability. (A) Less viscous core fluid is injected into tube, displacing the more fluid already in the tube, and leaving behind a uniform film whose thickness depends on Ca ; (B) The injection described in (A) is stopped, and the surface-tension instability ensues as shown in (C)–(F). From Cassidy et al. (1999).

3. Experimental and theoretical models for liquid and surfactant delivery to the whole lung

There are many clinical applications in which a liquid bolus is instilled into the lung. Examples include the delivery of surfactant in surfactant replacement therapy, the delivery of perfluorocarbon liquids in liquid ventilation to treat patients with respiratory distress syndrome, and the delivery of other types of drugs or genetic material. It is important for a clinician to come up with a line of attack that optimizes liquid delivery for a specific treatment. In some cases, a homogeneous liquid distribution throughout the lung may be desirable, while in others it may be preferable to target specific regions of the lung. The targeting of a liquid bolus can be influenced by a variety of factors.

Cassidy et al. (2001a) investigated two delivery methods to instill liquid containing surfactant in a rat lung model. In the first method, the instilled liquid is initially driven by gravitational drainage, followed by inspiration, and in the second method, a liquid plug is allowed to form in the trachea which is then driven to the distal parts of the lung by ventilation. They found that in the second method the instilled liquid reached the distal parts of the lung very quickly, in a few breaths, and resulted in a more uniform liquid distribution throughout the lung. In the first method, the liquid drainage at a bifurcation is dependent on the orientation of the airways with respect to gravity, the branch angle and the relative size of parent to daughter tubes. Anderson et al. (2004) also used an excised rat lung model to investigate the effect of breathing frequency on the liquid plug distribution, with the goal to understand the interaction between gravitational drainage and the dynamics of plug propagation discussed at the end of the previous section. They found that a plug instilled into a vertical oriented lung at a slow ventilation rate would not rupture in the larger airways unlike one instilled at a fast rate, and therefore was able to reach the deep into the gravity-dependent regions of the lung relatively quickly. The plug instilled at a fast rate of 60 breaths/minute ruptured quickly (during the first inspiration) because it left behind a thicker film, and the liquid coating the upper airways was then found to slowly drain down into the distal parts of the lung as a result of gravity. After a fixed number of breaths it was found that a more uniform vertical distribution of liquid throughout the lung was obtained with the higher ventilation rate. The implication for surfactant delivery is that using a slow rate of ventilation could result in a non homogeneous surfactant distribution, which is not the desired outcome. This could lead to over-inflation of the parts of the lung receiving the surfactant and result in bronchopulmonary dysplasia (Ueda et al., 1994). In models of airway reopening in which a semi-infinite bubbles propagates through a liquid filled compliant airway, it has also been shown that greater epithelial cell injury can occur at slower propagating speeds (Bilek et al., 2003; Kay et al., 2004; Gaver and Ghadiali, 2008).

Bull et al. (2004), motivated by an interest in liquid ventilation by instilling perfluorocarbon liquids into the lung, explored the effects of plug propagation speed and gravity. They found that liquid plugs could be formed in the larger airways by instilling the perfluorocarbon at faster rates, and obtained more homogeneous liquid distributions throughout the lung in upright animals, consistent with the experiments described above. Compared with the supine position, the upright animals normally had lower homogeneity indices because it is harder to fill the upper regions of the lung. Tredici et al. (2006) showed that liquid viscosity is another important controlling factor affecting the distribution of perfluorocarbon in the lung. They found that the more viscous liquid yielded a more homogeneous distribution, and, by estimating the center of mass of the distribution of the instilled liquid delivered, that the less viscous plug penetrated more deeply into the distal airways. The results of these experiments, together with those of Bull et al. (2004), can be explained in terms of the theory for the thickness of the trailing film deposited behind an advancing liquid plug. The film thickness increases with Ca. So, if the speed of plug propagation and the surface tension are the same, then Ca is higher for the more viscous plug, or if the viscosity and the surface tension, then Ca is higher for the plug instilled at a faster rate. The results of these studies indicate how specific areas of the lung could be targeted by designing perfluorocarbons with specific rheological properties, by using different instillation and ventilation rates and by posture. Nevertheless, there is still debate as to what the optimal properties of perfluorocarbons are for total liquid ventilation. On the one hand, the more viscous liquid plug can produce a more homogeneous distribution, but a less viscous one could prevent airway collapse (Bull et al., 2005).

The propagation of a liquid bolus of surfactant throughout the lung in surfactant replacement therapy has been studied theoretically by Halpern et al. (1998), Espinosa et al. (1999), and Zhang et al. (2003). The latter also considered the simultaneous transport of a passive solute such as a therapeutic drug. These studies comprise of a sequence of different mechanisms by which instilled liquid, initially in the form of a liquid bolus, may reach the distal parts of the lung. First, ventilation can push the plug into the lung, and as it propagates through the tracheobronchial tree, it leaves behind a trailing liquid film coating the airways. As previously discussed, the thickness of this layer depends on the capillary number, Ca. Because of the increase in total surface area, the local thickness of the deposited layer actually decreases with airway generation. The plug may eventually rupture if it picks up less liquid than it deposits, and may not reach the alveolar regions of the lung. However, gravitational drainage and, later, surface tension gradients once the film becomes sufficiently thin, can assist in the transport of surfactant contained in the deposited liquid layer to the distal regions of the lung where surfactant is needed. Halpern et al. (1998) also include an alveolar clearance model of the surfactant. These studies show that transit and delivery times depend on plug volume, lung geometry, gravity, the amount of endogenous surfactant, surfactant kinetics, and shear stress due to airflow. The exogenous surfactant takes in the order of minutes to reach the alveoli, but the lowering of surface tension at the distal ends occurs very rapidly, within seconds, as the result of the compression of the endogenous surfactant (Grotberg et al., 1995). The delivery of therapeutical chemical is slower than the exogenous surfactant since it is approximately convected with the mean flow which is typically twice as slow as the surface flow that the exogenous surfactant experiences. More details on surfactant spreading are given in section 6. Finally, it is worth pointing out some of the limitations of the above theoretical models that need to be addressed in future work. They all have assumed that the layer coating the airways consists of a single Newtonian fluid, discarding the fact that it is a bilayer consisting of a water periciliary layer with a mucous layer on top of it, and have also assumed a symmetric lung model consisting of rigid tubes.

4. Liquid plug propagation in single channel or tube

In this section, we focus our attention on the propagation of a finite volume plug through a liquid-filled channel or tube. We review several analytical and computational studies that have considered the effects of compliance, surfactant, inertia, gravity, plug volume and the stability of steady propagation.

Howell et al. (2000) modeled the propagation of a liquid bolus through a compliant channel in the limit of Stokes flow and small capillary number, and obtained expressions for the pressure drop across the bolus and the trailing film thickness as functions of the wall properties of the channel quantified by a compliance parameter (dependent on the wall's Young modulus) and a longitudinal tension parameter, the capillary number, and the precursor film thickness. This study showed that rupture (or reopening) is more likely to occur in a more compliant channel coated with a pre-existing thicker film, that increasing longitudinal wall tension decreases the likelihood of rupture and that there is a critical pressure drop above which rupture occurs. Waters and Grotberg (2002) considered the effect of soluble surfactant on plug propagation through a single tube. Assuming bulk equilibrium conditions (where bulk surfactant is constant) and rapid surface adsorption kinetics, it was found that the pressure drop across the plug needed to move it at a prescribed velocity and the trailing film thickness increase with surfactant elasticity.

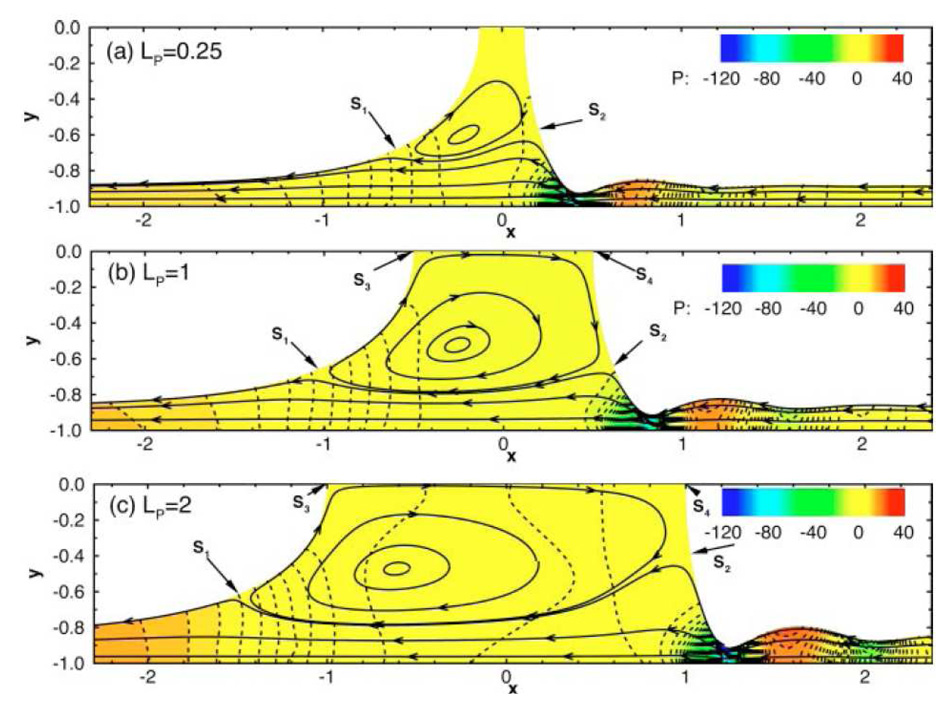
Fujioka and Grotberg (2004) used a finite volume method which enabled them to investigate larger capillary numbers and consider the effects of inertia that are important in large airways. When the plug width is smaller than the channel width, the trailing film thickness is smaller than that for a semi-infinite bubble, and there is significant interaction between the leading and trailing interfaces that affects the plug core flow field for finite Re. In this region, a recirculation flow develops which skews towards the rear meniscus as Re increases. Fig. 3 shows how the flow within the plug is affected by plug length. The motion is from left to right, but the streamlines (the solid lines with arrows) are drawn in a frame of reference fixed with the plug. Lines of constant pressure are denoted by the dotted lines, with a reference pressure set to zero at the far right edge of the domain. The three panels illustrate a flow region near the channel walls where flow goes from the precursor film to the trailing film, and a recirculation region in the core which is skewed due to inertia effects. A large amplitude capillary wave is also seen in the front film. This is where the film is thinnest and where there are large variations in pressure. The macroscopic pressure gradient, defined to be the pressure drop between the two gas phases divided by the plug length, is found to contain terms proportional to U and U², where U is the propagation speed, with the quadratic term being dominant when the plug length is small. The front meniscus has a capillary wave whose amplitude increases with Re. This can cause large variations in wall shear stresses and pressures, and in turn have a detrimental effect on the cells lining the airways.

Figure 3.

The effect of inertia on the flow in a liquid plug for three different plug lengths. Re=80 and Ca=0.08, (A) L_P=0.25, (B) L_P=1.0, (C) L_P=2.0. Lines with arrows are streamlines. Colored contours represent the pressure field, p=p^*/(μU/H), where μ is the viscosity, U is the plug speed and H is the channel half width. S₁~S₄ are stagnation points. From Fujioka & Grotberg (2004).

In Suresh and Grotberg (2005) the effect of plug propagation speed and gravity on the quasisteady motion of a liquid plug in a two-dimensional liquid-lined channel oriented at an angle α with respect to gravity was studied. It was assumed that the capillary number Ca was small while the Bond number Bo was arbitrary. The thickness of the trailing films left behind by the plug and the pressure drop across it were determined as functions of Ca, Bo, α and the thickness of the precursor films using matched asymptotic expansions and lubrication theory. When Bo is small, the trailing film thickness and the flow contribution to the pressure drop scale as Ca^2/3 at leading order with coefficients that depend on Bo and α. The correction to the film thickness occurs at O(Ca) as opposed to O(Ca^4/3) in the Bo = 0 case. By computing the ratio of liquid volumes above and below the centerline of the channel, V_R the asymmetry in the liquid distribution was quantified. The distribution is equal, V_R = 1 at Bo = 0. It was found that V_R decreases with Bo and Ca, but increases with the plug length L_p. The decrease of V_R with Ca suggests that higher propagation speeds in small airways may result in less homogenous liquid distribution, which is in contrast to the expected effect in large airways. For given values of the other parameters, a maximum capillary number Ca_c was identified above which the plug will eventually rupture. When Bo becomes equal to an orientation-dependent critical value Bo_c, the scalings of the film thickness and pressure drop change to Ca^1/2 and Ca^1/6, respectively. This scaling is valid for small increments of the Bond number over its critical value, Bo = Bo_c + BCa^1/6, but for higher Bond numbers the asymptotic approach breaks down.

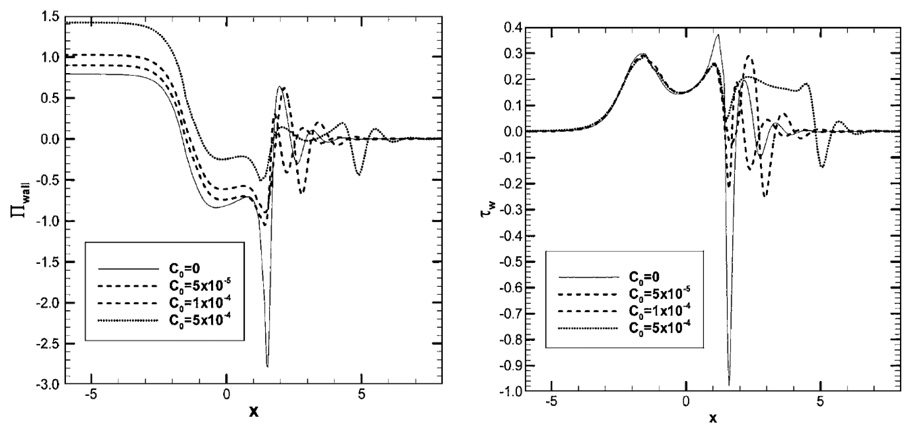
Fujioka and Grotberg (2005) extended their previous work (Fujioka and Grotberg, 2004) by considering the effects of surfactant. A finite volume numerical scheme was used to solve the Navier-Stokes equations with free-surface boundary conditions and the surfactant transport equations. Pulmonary surfactant properties were used to describe the adsorption/desorption process. As the plug propagates forward, surfactant accumulates on the front meniscus interface as it is swept from the precursor film. The surfactant concentration is a maximum somewhere in the front meniscus, and a surface tension gradient is established that opposes flow out of the film region. In this region, the surface velocity almost vanishes, and this results in the precursor film thickness near the meniscus being thicker than the leading film thickness. Because of an increase in the minimum film thickness, there is a reduction in the peaks of wall pressure and shear stress as shown in Fig. 4. However, in the thicker film region, the drag forces are actually larger than the surfactant free case. Therefore, the overall pressure drop across the plug increases as the result of the increasing surfactant concentration. A recirculation flow forms inside the plug core, which becomes more skewed toward the rear meniscus as the Reynolds number increases. When there is no surfactant, the recirculation flow is in contact with both the front and the rear interfaces. As the surfactant concentration increases, the Marangoni stress causes the front interface to become rigidified and forces the recirculation flow away from the front meniscus. Subsequently, the recirculation flow is directed away from the rear interface in a manner similar to that for the front interface. When the plug length is shorter, this change in recirculation pattern occurs at a smaller surfactant concentration.

Figure 4.

Wall pressure (left) and shear stress (right) induced by the propagation of a liquid plug of length L_P=2 (plug core: −1<x<1). Here C₀ is the bulk surfactant concentration sufficiently far ahead of the plug in the precursor film. The wall pressure and shear stress are normalized by the surface tension, [Π_wall, τ_wall] = [p^*_wall, τ^*_wall]/(σ/H). From Fujioka & Grotberg (2005).

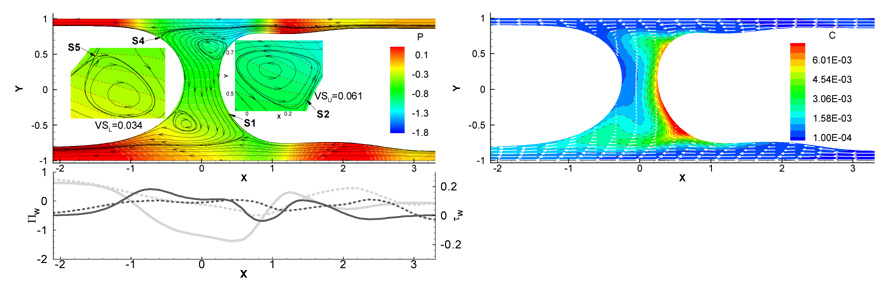
In Zheng et al. (2007) a numerical model of steady plug propagation driven by gravity and pressure in a 2-D liquid-lined channel oriented at an angle α with respect to gravity was developed. The important parameters in this problem were the Bond number, Bo, α, the capillary number, Ca, the Reynolds number, Re, the plug length L_p, and the surfactant concentration C₀. An example illustrating the effect of gravity on the velocity and pressure fields, the wall mechanical stresses, and the bulk surfactant concentration is shown in Fig. 5. If gravity is neglected the plug is symmetric, and in this case there are two flow regimes: two wall layers and two trapped vortices in the core. Also, there is no flow interaction between the upper and lower half plug domains. The number of vortices can be zero, one, or two when Bo ≠ 0 and α ≠ 0,π, as fluid flows from the upper precursor film, through the core and into the lower trailing film. When C₀ = 0, the vortices have stagnation points on the interface, but for C₀ > 0 the vortices detach from the interface and create saddle points inside the core. A capillary surface wave develops on the front meniscus that extends into the precursor film. In this region the film is thinnest and the wall shear stress attains its peak value, as high as ~ 100 dyne / cm² in adult airways. This indicates a significant risk of pulmonary airway epithelial cell damage. The peak magnitude of the shear stress can be reduced by the addition of surfactant, thus diminishing the risk of cell damage. The volume ratio parameter V_r, representing the ratio of the liquid above to that below the center line of the channel, can be used to describe the pre-bifurcation asymmetry of the plug. V_r was found to increase with L_p, Ca, Re and C₀, but to decrease with Bo.

Figure 5.

Effect of gravity on (a) streamlines, pressure field and wall mechanical stresses, and (b) bulk surfactant concentration for Ca=0.05, Re=0, Bo=0.6, L_P=0.5, α=π/2 and C₀=10⁻⁴. The solid lines with arrows in (a) are streamlines and the dashed lines are lines of constant pressure. S1~S5 are stagnation or saddle points. The dashed lines in (b) are for constant concentrations and the solid lines with arrows are velocity vectors. From Zheng et al. (2007).

Campana et al. (2007) investigated numerically the stability of the motion of a liquid plug. This was achieved by perturbing the plug volume of a steady solution and examining whether or not the plug length and trailing film thickness h_∞ returned to their steady values. Also, a stability criterion was given based solely on the steady problem for fixed Ca and Re : For a given L_p, if dh_∞ / dL_p > 0(< 0) the steady plug is stable (unstable) to small perturbations. However, the scope of this study was somewhat limited in that only one capillary number was considered. Also, in the future, the role of surfactant on the stability of plug propagation also needs to be investigated.

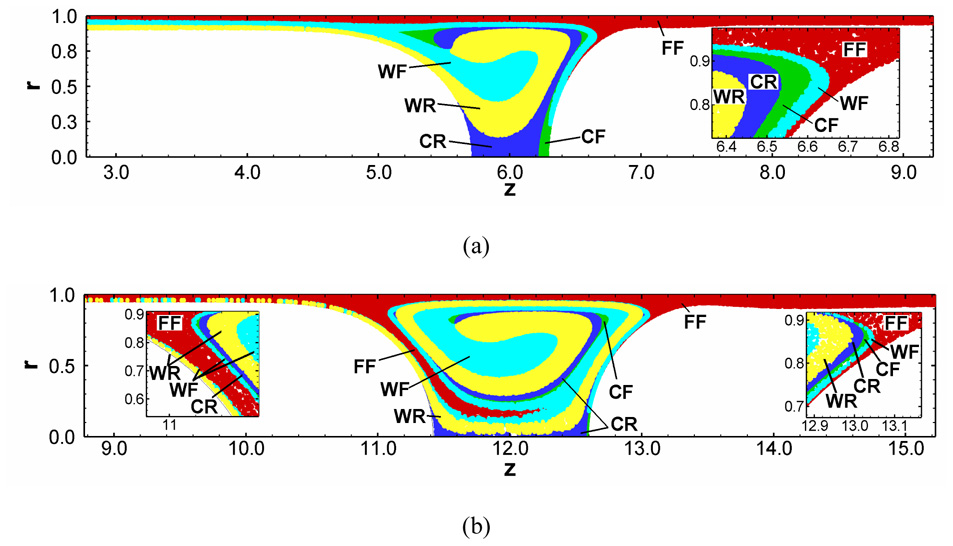
Recently, Fujioka et al. (2008a; 2008b) investigated unsteady liquid plug propagation numerically. They considered the propagation of a liquid plug within a rigid axisymmetric tube coated by a thin liquid film with or without surfactant. A liquid plug is initially static with a uniform surfactant concentration and begins to propagate by a constant pressure difference between front and rear air-phases. The magnitudes of the wall pressure and wall shear stress are greatest in the front meniscus region, and they increase with a thinner precursor film. If the trailing film is thicker (thinner) than the precursor film, the plug volume decreases (increases) as it propagates. To investigate how a liquid plug loses (gains) mass during it propagates, they computed path of many marked particles. This particle has no mass so that a particle represents the Lagrange fluid transport (fluid particle). As a liquid plug loses mass, the fluid particles near the front meniscus go to the trailing film (Fig. 6(a)). But as a plug gains mass, the fluid particles from the precursor film come into the plug core through the rear transition region (Fig. 6(b)). When the plug length (L_P) becomes short, the Marangoni stress increases the hydrodynamic viscous friction and causes L_P to plateau. The strength of the wall pressure and shear stress in the front transition region increases as the precursor film thins. The magnitude of these stresses is much larger than those in the rear transition region. During the period of L_P plateau, since the meniscus surface curvature near the wall becomes strong, the pressure gradients and shear stress within the transition regions increase (Fig. 7).

Figure 6.

Particle transport in a surfactant-laden plug for (a) losing and (b) gaining mass for h₂=0.05, C₀=5×10⁻⁴. Each particle has a tag which indicates its initial location: film front (FF), film rear (FR), wall front (WF), wall rear (WR), core front (CF), and core rear (CR). Initially, a liquid plug of L_P=1 begins to propagate driven by a constant pressure drop (a) ΔP=1 and (b) ∆P=0.5. From Fujioka et al. (2008).

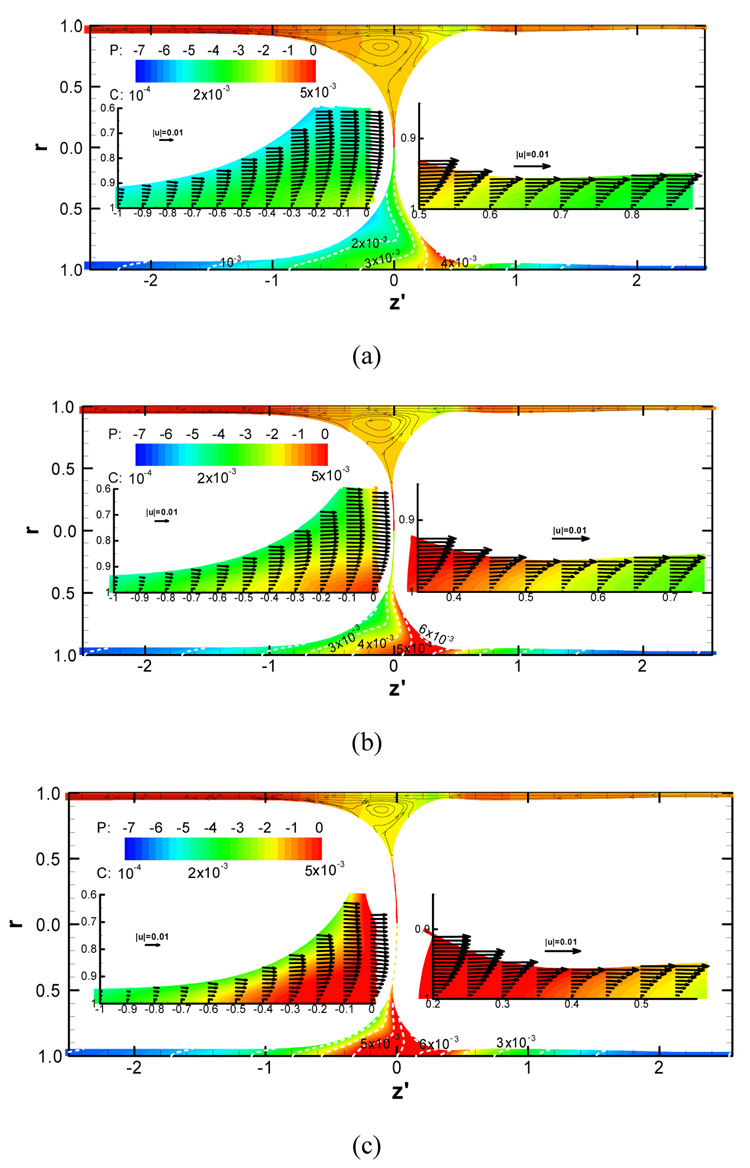
Figure 7.

Flow, pressure (upper half) and bulk surfactant concentration (lower half) fields for the precursor film thickness of h₂=0.03, the initial L_P=1, ΔP=1 and C₀=5×10⁻⁴ at (a) t=900, (b) t=1200 and (c) t=1500. Upper half of each panel displays the pressure contours and streamlines. Lower half of each panel shows the surfactant concentration contours. The magnified plots within both transition regions are shown with the velocity vectors. From Fujioka et al. (2008).

5. Plug splitting at a bifurcation

In this section, we review several experiments and simple theoretical models on liquid plug propagation through a single bifurcation. These examine the effects of effects of flow rate, gravitational orientation and liquid blockages.

Cassidy et al. (2001b) were the first to investigate the propagation of a liquid plug through a symmetric bifurcation. They considered one case where the plug propagated from the parent tube into the two daughter tubes, and another case where one of the daughter tubes was blocked by a second liquid plug. They showed that for the first case the volume of fluid entering each daughter tube was equal, and that the trailing film thickness was smaller in the daughter tubes (at the same capillary number). It was suggested that this difference could be due to geometrical effects near the bifurcation. For the second case of a blocked daughter tube, they showed that the unblocked daughter collects a larger fraction of the volume from the parent tube. This implies that the plug in the unblocked tube propagates faster because of the lower flow resistance, and could have an important consequence as far surfactant replacement therapy is concerned, where the delivery of repeated surfactant doses could take the same path as the previous doses.

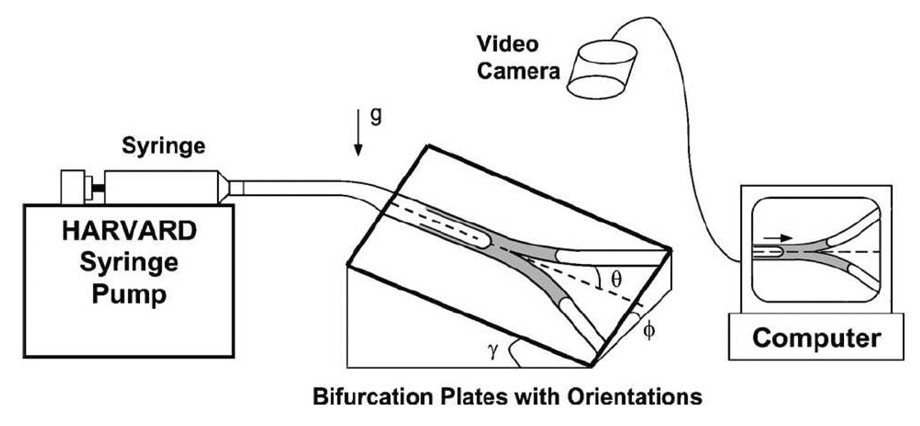
In Zheng et al. (2005) a bench top model of a symmetrically bifurcating airway was used to investigate the effect of gravity on the distribution of instilled liquids (as shown in Fig. 8). A liquid plug was instilled into the parent tube and driven through the bifurcation by a syringe pump. The influence of gravity was varied by adjusting the roll angle ϕ and pitch angle γ of the bifurcation, where ϕ determines the relative gravitational orientation of the two daughter tubes and γ determines the component of gravity acting along the axial direction of the parent tube. An important quantity is the splitting ratio R_s which is the ratio of the liquid volume in the upper daughter to the lower just after plug splitting. It is a function of the parent-tube capillary number (Ca_p), the Bond number (Bo), ϕ, γ, and the presence of pre-existing plugs initially blocking either daughter tube. Below a critical capillary number Ca_c no liquid entered the upper daughter (R_s = 0), and above which R_s increased and leveled off with Ca_p. Ca_c increased while R_s decreased with increasing Bo, ϕ, and γ for blocked and unblocked cases at a given Ca_p > Ca_c. Compared to the nonblockage cases, R_s decreased (increased) at a given Ca_p while Ca_c increased (decreased) with an upper (lower) liquid blockage. More liquid entered the unblocked daughter with a blockage in one daughter tube, and this effect was larger with larger gravity effect. A simple theoretical model was developed that predicts R_s and Ca_c. It uses macroscopic mass balances and pressure drops between parent and daughter tubes, neglecting the effects of inertia, gravity and entrance effects. In addition, the relationship between deposited film thickness and Ca appropriate for semi-infinite bubbles is applied, and the pressure drop across the plug follows Poiseuille’s law. Despite these assumptions, their theory is in qualitative agreement with the experiments over a wide range of parameters.

Figure 8.

Experimental apparatus and definition of the roll angle ϕ and pitch angle γ of the bifurcation. From Zheng et al. (2005).

Zheng et al. (2006) extended their previous work, and investigated the effects of inertia and gravity on liquid plug splitting in an airway bifurcation model to simulate the liquid distributions in large airways by conducting bench top experiments and theoretical studies. The splitting ratio, R_s, the ratio of the plug volume entering the upper (gravitationally opposed) daughter tube to the lower (gravitationally favored) one, was measured as a function of parent tube Reynolds number Re_p, gravitational orientations for roll angle, ϕ, and pitch angle, γ, parent plug length L_p, and the presence of pre-existing plug blockages in downstream daughter tubes. Results showed that increasing Re_p causes more homogeneous splitting. It was found that there is a critical Reynolds number Re_c such that no liquid enters the upper daughter tube. This occurs when Re_p ≤ Re_c, R_s = 0. Re_c increased while R_s decreased with increasing ϕ and γ. When a blockage exists in the lower daughter Re_c is only found at ϕ = 60° for the range of Re_p studied, and the total mass ratio can be as high as 6. Inertia was further demonstrated to cause more homogeneous plug splitting when compared with a study of R_s versus Ca_p (another characteristic speed). A theoretical model based on entrance flow for the plug in the daughters was developed from which R_s can be predicted as a function of Re_p. The frictional pressure drop was estimated and shown to be linearly dependent on Re_p. This theory provides a good prediction on liquid plug splitting and well simulates the liquid distributions in the large airways of human lungs. Important effects such as wall compliance and film rheology remain to be investigated.

6. Surfactant spreading dynamics

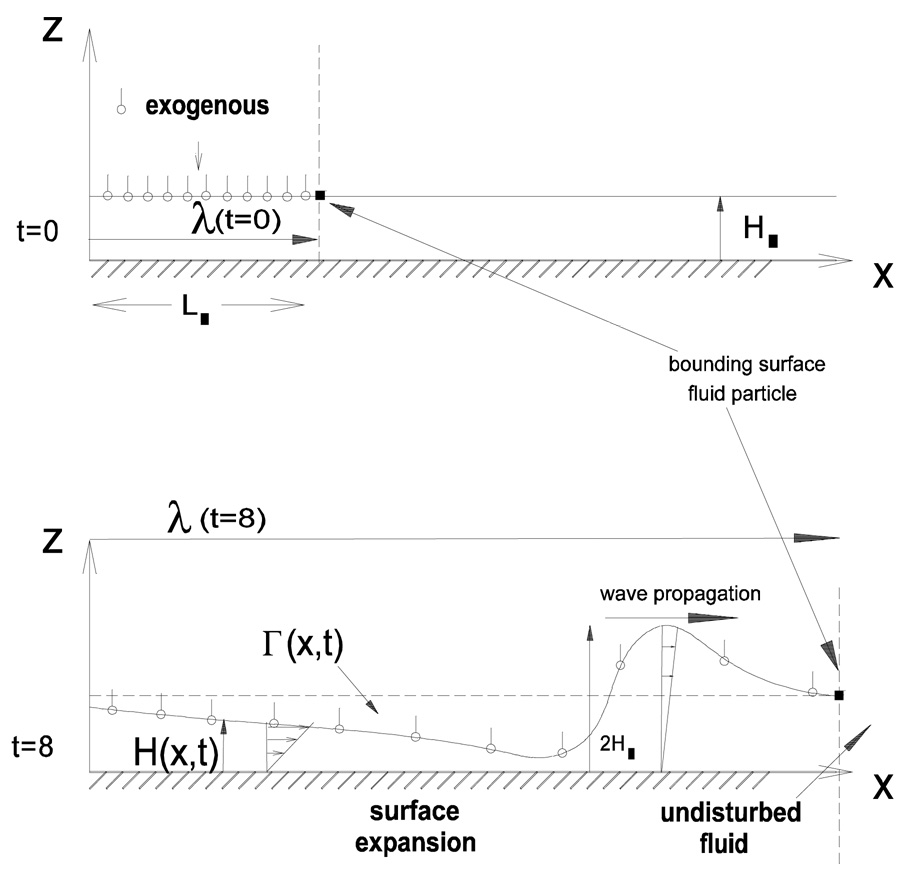
Surfactant replacement therapy (SRT) is often used to treat premature neonates with respiratory distress syndrome (RDS). One form of treatment consists of instilling a bolus of surfactant into the trachea. Initially the bolus is displaced by the airflow and gravity (Halpern et al., 1998; Espinosa and Kamm, 1999). As it propagates down the airways, the bolus deposits a liquid layer that coats the airways. The bolus may rupture because it may not pick up as much fluid as it is depositing, and therefore it may not reach the distal areas of the lung where the surfactant is needed. Still, the deposited liquid layer that is left behind may advance due to gravitational drainage and/or surface tension effects. The latter become dominant once the liquid layer is thin enough. In this section we focus our attention on the spreading of surfactant due to surface tension effects. Reviews of surfactant spreading on thin liquid layers can be found in Grotberg (1994), Grotberg (2001), Afsar-Siddiqui et al. (2003) and Gaver et al. (2005). Earlier theoretical models considered the spreading of an insoluble surfactant monolayer that comes into contact with a clean (surfactant-free) Newtonian liquid layer of constant thickness (Gaver and Grotberg, 1990). Lubrication theory was used to approximate the momentum equations and interfacial conditions, and enabled a system of partial differential equations for the thickness of the liquid layer and the surfactant concentration to be derived. It was found that large deformation of the layer is possible near the leading edge of the advancing surfactant front, and that near center of the drop the layer could thin considerably, sometimes even rupturing causing spreading to stop (Fig. 9). In SRT it is important to know how fast a planar front of surfactant spreads along the lining of the airways and how fast a drop of surfactant spreads radially along the liquid film coating the alveoli. A power law relationship of the form R(t) = kt^α can be used to describe the location of the advancing front or drop, R, as a function of time, t. The exponent α can be equal to 1/4 for a drop (Gaver and Grotberg, 1990; Gaver and Grotberg, 1992; Dussaud et al., 2005), it can be equal to 1/3 for a planar strip (the equivalent of a 2D drop) (Jensen and Grotberg, 1992; Espinosa et al., 1993), or it can be equal to ½ for a planar front corresponding to the case when there is a fixed surface tension gradient for all time (Ahmad and Hansen, 1972; Jensen and Grotberg, 1992; Espinosa et al., 1993). In all these cases, the effects of endogenous surfactant and surfactant solubility were not taken into account. These are discussed next.

Figure 9.

Exogenous surfactant spreading on a thin liquid layer. The top panel shows a thin liquid layer of constant thickness which is partially coated with a surfactant monolayer. The ensuing film deformation and surfactant transport due to the Marangoni stress at the interface are shown in the bottom panel. From Halpern et al. (1998).

Surfactant spreading on a clean interface in which the surfactant is also soluble in the liquid layer have can be significantly different from the insoluble case because of differences between bulk and surface flows, and the inclusion of adsorption and desorption effects between the interface and the bulk (Halpern and Grotberg, 1992; Jensen and Grotberg, 1993). It was found, depending on boundary conditions, that film deformation could be greater in the soluble case as compared to the insoluble case, and that wall uptake of surfactant could result in the slowing down or reversal of the propagation of the leading edge of the surfactant front.

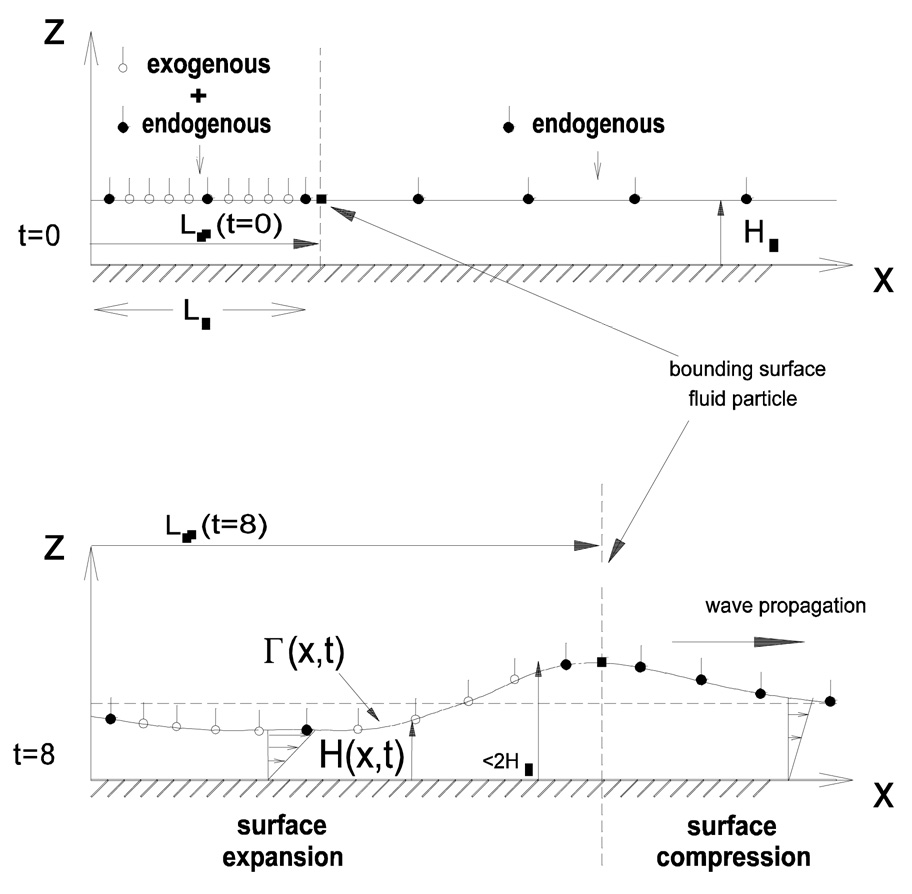
Grotberg et al. (1995) showed, using a two-dimensional model of planar spreading, that pre-existing surfactant could slow down the spreading of new surfactant, but, in addition, the new surfactant could induce a disturbance through the existing surfactant that propagated faster than the leading edge of the new surfactant (Fig. 10). The propagating speed of the compression wave was found to be inversely proportional to the endogenous surfactant concentration (Bull et al., 1999a). Bull et al. (1999b) obtained similar results for axisymmetric droplet spreading. As explained in section 3, the level of endogenous surfactant could have important consequences in SRT. Increased levels of endogenous could hinder the delivery to the distal parts of the lung of exogenous surfactant or a passive solute such as therapeutic drug which piggybacks onto the exogenous surfactant (Jensen et al., 1994; Zhang et al., 2003).

Figure 10.

The top panel shows a surfactant monolayer being placed on film already contaminated with a pre-existing (endogenous) surfactant. The bottom panel shows the resulting film deformation and spreading of the exogenous and endogenous surfactants. From Halpern et al. (1998).

Espinosa and Kamm (1997), Bull and Grotberg (2003) and Wei et al. (2003) have taken into account the periodic airway stretching that occurs during the breathing cycle. These studies are applicable to fluid clearance from the lungs and flows within the lining coating the alveoli. In (Espinosa and Kamm, 1997), the time-dependent evolution of a liquid layer over a stretchable membrane in the presence of soluble surfactant was modeled using lubrication theory. A linear strain wall model was used, with the trachea being the stiffer end compared to the distal end of the lung. The surfactant was assumed to be constant in the bulk, and allowed to squeeze out from the interface into the bulk. It was found that an optimal frequency that maximized the flow towards the stiffer end. Increasing the amplitude of the strain had the effect of decreasing liquid transport, and sometimes the transport was directed to the less stiff end. In (Wei et al., 2003), compared to (Espinosa and Kamm, 1997), the effect of capillarity was included to model the high surface tension situation when there is a deficiency in surfactant, and no flux boundary conditions were applied at the stiffer end of the domain. It was found that capillarity could decrease the clearance process by increasing the flow towards the less stiff end.

Halpern et al. (1998) and Espinosa and Kamm (1999) developed a model for surfactant and liquid transport through the airways that included the increase in area due to airway branching which have been previously described in the context of liquid plug propagation. Zhang et al. (2003) used a similar model to study the transport of a therapeutic substance such as a drug or a gene vector. Halpern et al. (2004) extended the model of Halpern et al. (1998) by incorporating the effects of breathing, and showed that surfactant transport towards the alveolar end could be enhanced by using larger tidal volumes and breathing cycle periods. However, care must be taken in using larger tidal volumes to avoid potential ventilator induced injury (Dreyfuss and Saumon, 1998; Tremblay and Slutsky, 1998; Tremblay et al., 1998)

The non-Newtonian characteristics of the lung’s liquid lining have been considered by Craster and Matar (2000) and Zhang et al. (2002). In Craster and Matar (2000), two cases were analyzed: a single layer modeled as a Herschel-Bulkley fluid with shear-thinning and yield stress characteristics; and a bilayer consisting of a Newtonian periciliary liquid layer and a Herschel-Bulkley fluid modeling a mucus layer. Zhang et al. (2002) have considered the effect of weak viscoelasticity on surfactant spreading by using the Oldroyd-B constitutive equation to model the viscoelastic liquid layer. In both models, the spreading rate of surfactant could be smaller than the corresponding Newtonian case. In some cases, the surface-tension gradients could not overwhelm the yield stress and the transport is very slow and due solely to surface diffusion.

The two-dimensional spreading of a surfactant laden drop over a liquid layer has been recently investigated by Jensen and Naire (2006). They showed that initial conditions can have a significant impact on spreading rates since they have an impact on the dynamics in the very thin film just ahead of the drop’s contact line. Also, the severe thinning that can happen in the neighborhood of the contact line due to a large initial surfactant gradient could prevent the transport of a passive solute ahead of the droplet.

7. Summary

This review highlights some of the essential mechanisms that influence the instillation of liquids and surfactants into the lung. The models discussed above represent significant steps towards the development of a coherent strategy to achieve targeted liquid delivery by, for example, controlling ventilation, posture and instillation methods that enhances or deters liquid plug formation in the distal airways of the lung, without generating excessive mechanical stresses on the airway walls that could possibly damage the lung. These models do have their limitations and there is room for improvement. The small airways have been modeled as rigid tubes or channels. In reality, the small airways are compliant and may buckle and collapse. In surfactant replacement therapy, the liquid plug most likely consists of a colloid suspension of micelles, and the viscosity exhibits a non-Newtonian behavior, with a yield stress that depends on the micelle concentration, as opposed to the Newtonian model described above which is reasonable if the surfactant concentration is low. In order to consider higher surfactant concentrations, micelle production and transport will have to be incorporated in present models.