Bacteriophage Therapy and the Mutant Selection Window

Abstract

We use kinetic models to investigate how to design antimicrobial phage therapies to minimize emergence of resistant bacteria. We do this by modifying the “mutant selection window” hypothesis in a way that accounts for the ongoing self-replication of the phage. We show that components of combination phage therapies need to be appropriately matched if treatment is to avoid the emergence of resistant bacteria. Matching of components is more easily achieved when phage dosages are high enough that ongoing phage replication is not needed for the clearance of the bacteria. Theoretical predictions such as ours need to be tested experimentally if applications of phage therapy are to avoid the problems of widespread resistance that have beset chemical antibiotics.

In recent years, there has been renewed interest in bacteriophage therapy as an alternative antimicrobial approach (1, 3, 8, 12, 15). Bacteriophages are able to selectively infect and kill susceptible bacteria, in the process producing large numbers of progeny that are similarly capable and therefore have considerable potential for use as self-replicating pharmaceuticals (21). It has been argued that threshold phenomena determine the success and mode of action of phage therapies (11, 21-23, 29), and the predictions of various pharmacokinetic and pharmacodynamic (PK/PD) models have been tested against in vitro data for a variety of bacterial species (2, 11, 16, 17, 24, 28). These models are broadly consistent with phage-bacterium interactions observed experimentally, but they do not address the issue of how to prevent or alleviate the possible emergence of phage-resistant bacteria. In the context of antibiotic chemotherapies, efforts to address the problem of antibiotic resistance often focus on PK and PD. Here we extend those PK/PD approaches to look at the potential problem of phage-resistant bacteria in phage therapy.

Bacteria have evolved a number of mechanisms of resistance to virulent phage, and in general resistance to phage strains is readily acquired. Protocols for phage treatments that do not give consideration to bacterial resistance mechanisms may be likely to fail, and resistance must be taken into account in both theoretical and experimental phage therapy studies (2, 12). While bacterial resistance to phage treatments is usually studied as a short-term problem, resistance may also be important in the longer term, just as it has become for chemical antibiotics. If phage therapy is to achieve its full potential, and in particular as it continues to move from in vitro to in vivo contexts, both short- and long-term resistance will need to be addressed.

For antibiotic therapies, the mutant selection window (MSW) hypothesis of Zhao and Drlica (32, 33) highlights the role of dosing-to-cure treatment strategies in promoting antibiotic resistance. If the effective antibiotic dose is just enough to kill susceptible bacteria, then it will be selective for single mutations conferring antibiotic resistance, whereas there might be a higher dose that is sufficient to suppress these single-step mutants. Between these two doses is the “window” in which single-step mutants are selectively amplified in the bacterial population. It has been proposed that by “closing the window” one may, in the future, mitigate some of the problems with antibiotic resistance (32). One way of doing this is to use combination therapies, and this also fits with recent empirical studies that have examined “cocktails” of phages, testing their ability to kill bacteria in cultures or experimental infections and examining their potential for preventing the rise of resistant bacteria (10, 13, 18, 19, 26, 27, 31). In this paper, we examine how to adapt the MSW hypothesis to make it applicable to phage as self-replicating pharmaceuticals. We find that the MSW hypothesis has novel implications for treatment strategies in phage therapies.

Threshold theory of antimicrobials.

PK and PD theories of antimicrobials point to threshold phenomena that determine their effectiveness (Fig. 1). In the case of antibiotics, the drug concentration must be high enough to prevent the growth of the target bacterial population at the site of infection; that is, the antibiotic must exceed a MIC. Giving antibiotics at doses designed simply to cross this threshold has been termed the “dosing-to-cure” strategy. Awareness that dosing to cure might not be the best approach has led to the concept of the MSW as a framework for considering the effect of antibiotic dose on the rise of resistant mutants (5, 6). The MSW for an antibiotic-bacterium pair is the range of concentrations of the antibiotic within which bacteria that have acquired resistance by a single mutation are selectively enriched. The lower bound of the window is the MIC, and the upper bound is termed the “mutant prevention concentration” (MPC) (4). Below the MIC, and thus beneath the MSW, the antibiotic concentration is not sufficient to prevent the growth of the wild-type bacteria. Inside the MSW (Fig. 1A), growth of susceptible bacteria is suppressed but resistant mutants can still proliferate. Above the MPC and thus beyond the MSW (Fig. 1B), the antibiotic concentration is high enough that multiple resistance-conferring mutations are required for growth (4). The MSW hypothesis therefore states that to avoid promoting resistance, single antibiotics should be given at concentrations above the MPC. If such a high concentration is not feasible, then combination therapies of two or more antibiotics, each requiring the bacterium to acquire different, independent mutations in order to become resistant, should be given such that the times coincide during which the concentration of each antibiotic is within its respective MSW. The MICs and MPCs have been found for a range of bacterium-drug combinations, and together with knowledge of the PK/PD provide important predictors of therapeutic outcomes and resistance prevention (9).

FIG. 1.

A schematic of important thresholds in the PK/PD theory of antibiotic and phage therapies. (A) “Dosing to cure.” Under the MSW hypothesis, the pharmacodynamic properties of antibiotics imply that antibiotic-resistant mutants are selectively enriched when the antibiotic concentration (solid line) is in the MSW between the MIC and the MPC. With a dose-to-cure strategy, the MSW is open as long as the antibiotic is effective (I). (B) “Closing the window.” With higher doses, the antibiotic concentration passes through the MSW quickly (II) and remains above the MPC (III) long enough to ensure that susceptible cells are suppressed, before passing through the MSW once more as it declines (IV). This approach reduces the probability that single-step resistant mutants will acquire additional resistance-conferring mutations. (C) “Passive” phage therapy. At sufficiently high doses, the phage concentration (solid line) rapidly exceeds the IT, and so the treatment will have a therapeutic effect without requiring the phages to replicate (V). The IT for a phage is analogous to the MIC for a chemical antibiotic, and in passive therapy the phage is treated much like a chemical antibiotic. It is unclear whether there must be an analogue of the MPC for phage therapies, but if not then the MSW would be open whenever the phage concentration is above the IT. (D) “Active” phage therapy. Phages can actively proliferate only when the bacterial concentration (dashed line) is at or becomes greater than the PT. Then, even at low doses, a phage (solid line) can grow (VI), eventually exceeding the IT to become effective at suppressing susceptible bacteria (VII).

As with antibiotics, therapeutic phages must achieve a concentration sufficient to prevent bacterial growth. This concentration is the analogue of the MIC, but it has previously been called the “inundation threshold” (IT): the concentration of phage at which the rate of bacterial growth is equaled by the rate of phage infection (22 [see Appendix]). Susceptible bacteria will be suppressed when the concentration of a virulent phage is above its IT, which depends on the rate of growth of bacteria and the adsorption rate of phage particles to bacterial cells, but not directly on the bacterial concentration. In this respect, phage antimicrobials might be treated much like antibiotics, without special consideration to the concentration of the bacterial population. However, a novel aspect of phage therapy is the potential for low-dose phage treatments, relying on self-replication to bring the phage concentration up above the IT at the site of infection. In order that the phage concentration can increase, the rate of phage replication must exceed the rate at which phage degrade or are otherwise lost. This condition depends not on the phage concentration but on the concentration of the susceptible bacteria: if there are too few bacteria, phage will be too likely to degrade or be lost before they find a bacterial cell in which to complete their life cycle. The bacterial concentration is therefore an important consideration where phage must be administered at a low dose; if the bacterial concentration is low, the phage will not be able to replicate up to a therapeutically effective concentration. Analysis of the dynamics of phage-bacterium interactions yields a “proliferation threshold” (PT): the concentration of bacteria above which the total phage population increases and below which it decreases.

The IT and PT delimit two different, but not mutually exclusive, modes of phage therapy (22). If the initial phage dose is above the IT and can be maintained there during treatment, then the therapy is principally passive (Fig. 1C). In this mode, therapy is achieved because the phages infect and lyse bacteria without necessarily relying on the production of progeny phage. In contrast, if the dose is lower it may be possible to achieve active therapy if the bacterial concentration reaches the PT before too many phage degrade or are lost (Fig. 1D). Thereafter, replication may enable the phage concentration to cross the IT, at which time the susceptible bacteria will be suppressed.

A significant problem for phage therapies is that bacteria that are or have become insensitive to a particular phage are readily found both in vitro and in vivo. There are many mechanisms by which bacteria can become insensitive or resistant to phage, which may be classified into several types: (i) genetic changes in bacteria, including mutation, recombination, and horizontal transfer of genetic material containing resistance genes; (ii) activation of existing restriction-modification or abortive infection systems; and (iii) stationary or other phases of growth that confer temporary resistance to phages. We focus on genetic determinants of resistance to phage infection, and unless otherwise stated hereafter, “resistance” will refer to phage insensitivity of any sort that is acquired more or less at random.

The existence of an IT is all that is required for some form of mutant selection window, since it establishes that there are a range of concentrations in which mutant populations are selectively enriched. There might also be an analogue for phage therapies of the MPC, which would put an upper bound on the MSW, although determination of an MPC for a phage therapy is likely to be complicated by the many mechanisms of resistance to phages that bacteria possess. If some single-step mutants are highly resistant to the phage treatment—as for example can occur with rifampin treatment of Staphylococcus aureus (33)—there may be no measurable MPC.

MATERIALS AND METHODS

We formulated a PK/PD model of the effect of two antimicrobials on a growing bacterial population. It was assumed that individual bacteria were initially susceptible but could acquire total resistance to either antimicrobial consistent with random mutation or recombination. The probability of a singly resistant mutant acquiring resistance to both antimicrobials was also incorporated into the model. The complete model can be expressed as a set of delay differential equations (see Appendix). Although in principle, the equations allow for MPCs, we assumed that resistance is total so that the antimicrobials were in their respective mutant selection windows whenever they were above their MICs/ITs.

We investigated the effects of combining two antimicrobials into a single treatment using computer simulations: either two phage strains used in the same mode (active or passive), or a “mixed-mode” combination of a phage in the active mode together with either a phage in the passive mode or a chemical antibiotic. Antibiotic and exclusively passive phage therapies were assumed to be functionally identical for the purposes of this numerical study. When comparing combinations of two phages used in the same mode, we examined how the probability that doubly resistant mutants will arise relates to differences in life cycle parameters, dosage, and timing of the component phages. Phage life cycle and dose parameters were modified as noted from base values given in the Appendix.

RESULTS

When two phage strains are introduced at low doses, both may proliferate, but the treatment will be dominated by whichever is the first to undergo explosive growth (Fig. 2). The “faster” phage will essentially outcompete the “slower” phage by growing more rapidly, reaching its IT earlier, and, overall, infecting and killing more bacteria (Fig. 2A). The dominance of the faster phage does not have any negative implications for the suppression of susceptible bacteria, but it does affect the rise of phage-resistant cells. If resistance to each phage is acquired by bacteria independently, then bacteria resistant to one phage will remain susceptible to the other. When a faster phage dominates the overall treatment, the slower phage will be unable to suppress fast-phage-resistant bacteria, and these cells will be selectively enriched. One solution to this problem is to better match the faster and slower phages, so that both contribute to treatment and both reach their respective ITs (Fig. 2B). When well matched, each phage will be effective against bacteria that are susceptible to the other, and both populations of singly resistant cells will be wiped out along with the totally susceptible initial population.

FIG. 2.

Simulations of active phage therapy of an initially susceptible bacterial strain with a combination of two infective phage strains used in the active mode. (A) A “faster” phage (adsorption rate of 3.0 × 10⁻⁹ [black dashed line]) together with a substantially “slower” phage (adsorption rate of 0.6 × 10⁻⁹ [gray dashed line]). Both phages replicate within the susceptible bacteria (solid line). The faster phage also infects mutants resistant to the slower phage (gray dotted and dashed line), while the slower phage infects mutants resistant to the faster phage (black dotted and dashed line). (B) Better-matched faster (adsorption rate of 1.2 × 10⁻⁹ [black dashed line]) and slower (adsorption rate of 0.87 × 10⁻⁹ [gray dashed line]) phages.

Even when two phage strains are well matched for combination therapy in an active mode, it will always remain possible that multiply resistant bacteria could arise by chance before all singly resistant cells are killed. We find, however, that if the growth properties of the phage are well matched then the probability of finding multiply resistant cells is relatively small. We varied the adsorption rate in particular (Fig. 3A), but similar results may be observed by varying the latent periods, burst sizes, or loss rates of the component phages (results not shown). Conversely, when the life cycle properties of the two phages are sufficiently different it becomes highly likely that multiply resistant bacteria will arise before all singly resistant cells can be wiped out.

FIG. 3.

Probability (Pr) of multiple resistance arising by a fixed time after phage therapy with a cocktail of two phage strains. (A) Both phages are introduced at the same low concentration so that treatment is principally active, but the adsorption rates are varied. The adsorption rates at the marked ratio (ratio = 5 [dashed line]) are the same as for Fig. 2A and are used again in plots B and C. (B) A cocktail of one “faster” and one “slower” phage is introduced at a fixed, high dose (20 times the average IT of the two strains at time 14 h) so that treatment is passive but the proportion of each strain in the cocktail is varied. Active replication of phage is ignored by assuming that the burst sizes are zero. (C) Alternatively, the same phages are introduced at identical high doses (10 times the average IT) but at different times (14 h and between 11 h and 17 h).

By use of passive therapy, phage strains that would be poorly matched for active therapy might still be useful for treatment. Component phage strains in a passive combination treatment should ideally be matched for dose (Fig. 3B). The probability of multiple resistance is not particularly sensitive to differences in the doses of component phages, but this depends to some degree on the total dose, and in general, the higher the total dose, the greater the flexibility in the proportions of component phage (results not shown). With regard to timing of phage treatments, earlier inoculation is generally preferable, but the probability that multiple resistance will arise depends most strongly on the time at which the last phage is introduced (Fig. 3C). The greatest reduction in the probability of multiple resistance is achieved by administering the last component phage sooner.

DISCUSSION

Optimizing active phage therapy.

Our results suggest that although active phage therapies could be very effective at suppressing susceptible bacteria, difficulties can arise when it is necessary to avoid the rise of cells that are resistant to the phage treatment. Phage-resistant bacteria are readily found both in vitro and in vivo and are a particular problem when the bacterial population is large or growing. Unless there is an analogue of the MPC not much above the IT—which does not seem probable—single-strain active phage therapies are unlikely to avoid problems of resistance. If the MPC for a single phage-microbe pair is large or of unknown magnitude, that is, where single-step mutants can be highly or totally resistant to infection by the phage, combinations of multiple phages for which cross-resistance does not arise will probably be the only option for closing the mutant selection window.

Combinations of phages that are used in an active mode must be closely matched for their various life cycle properties in order to suppress resistant mutants. When the phages are not well matched, the “faster” phage will dominate the treatment and the combination treatment will be little more effective than the faster phage would have been alone (Fig. 2). In particular, as the differences between phage strains increase, there is a rapid transition from a relatively low probability that multistrain-resistant cells emerge to a very high probability (Fig. 3A). The suddenness of this transition reflects how important it is for both the strains to cross the IT and thereby close the MSW. Whether such matching is practical is unknown, although manipulations of in vivo phage loss rates have previously been demonstrated (14). Optimization of active combination phage therapies might also be possible by altering the dosage and timing of the component phage treatments (Fig. 4A and C). Repeated phage doses may, in principle, help ensure that all component phages remain near their desired concentration until replication can commence (23).

FIG. 4.

Schematic of unoptimized versus optimized combination therapies where at least one component is active phage therapy. (A) When a combination of two active-mode components has not been optimized, the faster phage (solid line) dominates the slower phage (dashed line) until the concentration of faster-phage-resistant mutants grows large enough to support the slower phage. The MSW is open, encouraging the growth of resistant mutants, whenever the concentration of one but not both components is above the IT. (B) Similarly, when an antibiotic or passive phage (gray line) is introduced too early, growth of the active phage (solid line) will be delayed, again leaving the MSW open. (C and D) In either of the above situations, the timing and dosage of components may be adjusted to ensure that the MSW is closed during most of the time in which the treatment has a therapeutic effect.

One alternative to purely active-mode combination therapies would be to use phages with a combination of active and passive modes. Mixed-mode treatments would still need to be carefully matched, and because the components work in different ways, optimization would principally be a matter of dosage and timing (Fig. 4B and D). It remains uncertain whether successful treatment would be any easier to achieve when only one phage is actively replicating.

Resistance and passive therapy.

Some of the problems with bacterial resistance could be avoided by using passive phage therapies, provided sufficiently high concentrations can be delivered. Our results show how for combination passive phage therapies, the concentration of each phage should be greater than its corresponding IT, and remain so until all susceptible bacteria are infected (Fig. 3B). The phages should also be administered as early as possible and at the same time (Fig. 3C). This will effectively close the mutant selection window provided that resistance to one component phage does not confer resistance to all. Repeated doses might also be useful to ensure that the phage concentration can be maintained above the IT (23), and empirical studies are beginning to address the effects of such a dosing strategy for passive phage therapies (26).

One particular example of what appears to be a passive-mode combination phage treatment is a cocktail of six phages, LMP-102 (Intralytix, Inc.), that is effective against a range of pathogenic strains of Listeria monocytogenes (10, 25). LMP-102 was recently approved by the FDA for use in the United States as a food additive (7). Each phage in this cocktail is included at the same concentration (10⁹ PFU/ml); our results suggest that such an equal-concentration formulation could be effective in practice, provided L. monocytogenes concentrations are not very high and the ITs for each combination of phage and target bacterial strain are well below 10⁹ PFU/ml. Six phage strains seems to be more than enough to construct a successful treatment, although single mutations that confer resistance to multiple phage strains could reduce the effectiveness of the preparation. Notably, a second preparation comprising 14 different phage strains, LMP-103, was not found to have a statistically different effect on the concentration of L. monocytogenes (10), suggesting that although many phage strains can feasibly be combined in a single cocktail, a limit in the effectiveness of the cocktail is soon reached as further strains are added. Leverentz et al. (10) rightly suggested that the variety of strains in LMP-102 and LMP-103 could reduce the potential for development of resistant bacteria, but they did not investigate this experimentally.

There are other significant advantages of using phages in the passive rather than the active mode. First, restriction-modification and abortive infection mechanisms, and even interference between phages in multiply infected cells, should not cause significant practical difficulties, since in passive therapy the phages are not required to undergo replication. Active phage therapies, on the other hand, might be rendered less effective or even fail if infected bacterial hosts can modify or reduce production of progeny phages or if there is interference between component phage strains. Second, because passive therapies rely on delivering a large number of phages directly to the problem bacteria, growing bacterial populations are less likely to be able to avoid phage predation by entering stationary phase or other phase of growth that may be refractory to phage infection. Thus it seems likely that passive combination phage therapies can better address the potential pitfalls of phage antimicrobials than those that use active phage replication.

Combining phages and antibiotics.

The few previous studies that have looked at combination phage and antibiotic therapies suggest that they can yield fewer positive outcomes than phages used alone (1). Nonetheless, there are, at present, too few data on such mixed therapies, and in principle they could provide several possible benefits. Mechanisms of bacterial resistance to phages are likely to differ from those to antibiotics, and so combinations of phages and antibiotics could ensure the independence of resistance-conferring mutations, facilitating closure of the MSW and thereby giving better control of resistant bacteria than phage-only or antibiotic-only treatments. For example, the β-lactam antibiotics, which inhibit cell wall synthesis, might be particularly good partners for phages because the typical mechanisms of bacterial resistance to these compounds seem unlikely to correspond to mechanisms of resistance to phage. In addition, the IT of the phage component might be lowered due to slower bacterial growth in the presence of an antibiotic, thereby enhancing the effect of phages used in passive-mode therapy. Other incidental benefits could include lower side effects, such as renal damage, as compared with combination antibiotic therapies (20), and a greater potential for use against pathogens for which the choice of antibiotics is restricted due to multidrug resistance.

On the other hand, there are potential disadvantages of combined phage and antibiotic therapies. First, antibiotics might directly inhibit phage activity by interfering with the bacterial processes needed for phage replication and cell lysis. Second, antibiotic dosage and timing would have to be carefully managed, since premature administration of antibiotics could defeat an active-mode phage treatment by preventing the bacterial concentration from crossing the PT (22). Third, it is possible that where antibiotic resistance is already prevalent, continued use of antibiotics with the addition of phages may encourage genetic linkage of antibiotic resistance genes with phage resistance genes, negating the potential advantage of combining the two types of antimicrobials. Finally, in terms of the MSW the two treatment components will need to be carefully matched (Fig. 4). This might not be straightforward but is likely to be easier to achieve with passive than with active phage therapy.

Concluding remarks.

Effective phage therapy will need to take into account the speed with which target bacteria acquire resistance to phage. We have applied PK/PD models of both antibiotic and phage treatments to develop a theory of the therapeutic use of bacteriophages that incorporates bacterial resistance. No phage-based treatment will be exempt from the type of problems of resistance that occur with chemical antibiotics, and this must be accounted for if the full potential of phage therapy is to be realized. The simpler dynamics of passive therapies suggest that they are likely to be easier to apply than active therapies, provided issues of phage delivery can be overcome. The greater difficulties for active therapies in dealing with resistance reinforce this conclusion. There is also considerable scope for combination therapies that utilize both phages and antibiotics. Such treatments might maximize the independence of resistance-conferring mutations and minimize the incidence of harmful side effects, although there could be unwanted interference between treatment components. A focus on passive-mode phage cocktails, and perhaps also phage-antibiotic combination treatments, appears to be the best course for developing phage therapies in the near future.

APPENDIX

Simulations.

The idealized dynamics of two phage strains and one susceptible bacterial strain with possible resistant mutants in a well-mixed system are assumed to follow a system of delay differential equations:

(A1)

(A2)

(A3)

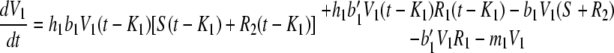(A4)

(A5)

Here, the variables are the concentration of the wild-type bacteria, S, that is susceptible to both phages; the concentrations of phage strain 1, V₁, and of phage strain 2, V₂; and the concentrations of bacteria that are at least partially resistant to phage 1, R₁, and to phage 2, R₂. We do not include here the concentration of cells infected by each phage strain, although this could be derived from the infection rates at times t, t − K₁ and t − K₂. The parameters are the growth rate, a, of completely susceptible wild-type bacteria and a′ of resistant bacteria; the rate of acquisition of mutations conferring resistance to phage 1, f₁, and to phage 2, f₂; the adsorption rates, b₁ and b₂, of phage 1 and phage 2, respectively, to wild-type bacteria and to mutants resistant to the other phage; the burst size at lysis in numbers of phage particles for phage 1, h₁, and for phage 2, h₂; the delays between infection and lysis for phage 1, K₁, and for phage 2, K₂; and the rates of degradation or loss from the system for phage 1, m₁, and phage 2, m₂. Each singly resistant bacterial type is totally resistant to its corresponding phage only if the adsorption rates b₁′ of phage 1 and b₂′ of phage 2 to their corresponding resistant cells are equal to zero. Units are (nominally) hours for time and CFU or PFU per milliliter for concentrations, with parameter values chosen to be plausible but not derived from data. Base parameters for each simulation are those given in Table A1.

TABLE A1.

Base parameters for simulations plotted in Fig. 2 and 3

Parameter	Value
a	0.8
a′	0.76
f1	1.0 × 10−6
f2	1.0 × 10−6
b1	1.0 × 10−9
b1′	0.0
b2	1.0 × 10−9
b2′	0.0
K1	1.0
K2	1.0
h1	30.0
h2	30.0
m1	1.0 × 10−2
m2	1.0 × 10−2
V1(0)	1.0 × 104
V2(0)	1.0 × 104
S(0)	1.0 × 105

In this model, we assume a best-case scenario with respect to resistance. Point mutations or other randomly occurring genetic changes are assumed to be the only mechanisms that confer resistance—an assumption that is not realistic but which allows us to examine the role that the design of a phage treatment may play in preventing heritable resistance. We also assume that resistance is specific to each phage strain, so that in order to acquire resistance to two phages, a bacterium must acquire two resistance-conferring mutations. We do not include superinfection in our model. Superinfection of a single cell by two different phage strains could lead to interference between the strains or recombination during phage replication that produces progeny phage that are a mixture of the two original strains. The effects of such events are uncertain but could violate the assumptions of the independence of each phage in the treatment.

The probability that a multiply resistant cell appears that is resistant to both phage strains is calculated according to the hazard function f₂R₁(t) + f₁R₂(t). If this probability is P(t), then

(A6)

This formulation corresponds to the assumption that multiply resistant bacteria arrive at random at rates proportional to the concentrations of singly resistant cells. If P(t) = 1 − exp{-r(t)}, then P(t) can be found from r(t), the solution to

(A7)

Simulations were performed using the PyDDE solver for delay differential equations with switches (http://pypi.python.org/pypi/PyDDE), based on Simon N. Wood's Solv95 (30). The algorithm is an adaptively stepping Runge-Kutta 2(3) scheme with lagged-state variables calculated using cubic Hermite interpolation. Except as noted, simulations were started at time 0 h, with phage assumed to be introduced at time 1 h and the phage and bacterial concentrations and the probability of multiple resistance followed for a further 20 h.

IT and PT.

The IT is the phage concentration at which bacteria tend to be infected before they can replicate. According to equation A1, the IT can be estimated from the growth rate, a, of the bacteria and the rate constant, b, of the specific adsorption rate of phage to bacteria:

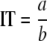(A8)

The PT is the concentration of bacteria at which sufficient progeny are produced by replicating phage to account for those virions that degrade or are lost from the system. The PT depends on a number of factors, including the number of phage h released at lysis (the “burst size”), the adsorption rate b, and the phage loss rate m. From these parameters, and a simple argument for the increase in the concentration of the total (free plus latent) phage (21), we find

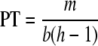(A9)

Both the IT and the PT depend on the precise characters of the phages and bacteria, but any model that includes phage replication and infection and lysis of bacteria will entail some form of each of these thresholds. In principle, the model also incorporates mutant prevention concentrations for each treatment component at the new ITs for resistant cells. For example, the MPC for phage 1 is equal to a₁′/b₁′ according to equations A2 and A8.