Abstract
The current system of radiation protection for humans is based on the linear-no-threshold (LNT) risk-assessment paradigm. Perceived harm to irradiated nuclear workers and the public is mainly reflected through calculated hypothetical increased cancers. The LNT-based system of protection employs easy-to-implement measures of radiation exposure. Such measures include the equivalent dose (a biological-damage-potential-weighted measure) and the effective dose (equivalent dose multiplied by a tissue-specific relative sensitivity factor for stochastic effects). These weighted doses have special units such as the sievert (Sv) and millisievert (mSv, one thousandth of a sievert). Radiation-induced harm is controlled via enforcing exposure limits expressed as effective dose. Expected cancer cases can be easily computed based on the summed effective dose (person-sievert) for an irradiated group or population. Yet the current system of radiation protection needs revision because radiation-induced natural protection (hormesis) has been neglected. A novel, nonlinear, hormetic relative risk model for radiation-induced cancers is discussed in the context of establishing new radiation exposure limits for nuclear workers and the public.
Keywords: hormesis, radiation, adaptive response, risk assessment
INTRODUCTION
The current system of limiting human exposure to ionizing radiation is based on the premise that the risk of deleterious stochastic effects such as cancer increases as a linear-no-threshold (LNT) function of the absorbed radiation dose (i.e., radiation energy deposited in tissue divided by the tissue mass). This is known as the LNT hypothesis and has no scientific basis. The linearly increasing risk function is also often called the LNT model. Such a linear relationship, if correct, means that doubling the radiation dose doubles the risk of harm. Conversely, reducing the dose one million-fold is supposed to reduce the risk by the same factor.
Some basic terminology is explained below to facilitate following the later sections of this paper.
High- and Low-LET Radiations
Two types of radiation (high and low linear energy transfer [LET]) are usually distinguished in characterizing radiation risks to humans. High-LET forms include alpha particles, neutrons, and heavy ions that produce intense ionization patterns when interacting with biological tissue. Considerable energy is deposited when traversing a narrow thickness of tissue. Low-LET forms include x and gamma rays and beta particles that deposit far less energy when traversing a narrow thickness of tissue.
Units for Expressing Radiation Doses
Radiation dose is expressed in different ways depending on the intended usage. A fundamental unit is the absorbed radiation dose, which is a measure of energy deposited in tissue (or other material) divided by the mass irradiated. Typical units of absorbed dose are the gray (Gy) which is equal to 1 joule/kg, and the milligray (mGy), which is one thousandth of a gray. These units can be applied when characterizing any type of radiobiological damage.
For regulating radiation exposure of humans (e.g., setting radiation exposure limits) and for low-dose risk assessment, special radiation dose units have been established that are based on the linear-no-threshold [LNT] hypothesis. These units are the result of applying statistical weights called radiation weighting factors (WR) to radiation-specific doses and are expressed in units such as the sieverts (Sv) and millisieverts (mSv). These weighted doses are called equivalent doses and can be added for a given tissue. To account for differing sensitivities of different tissue, a second set of weights called tissue weighting factors (WT) are employed to the equivalent doses. The resulting weighted doses can also be added and the resultant dose is called effective dose and expressed in sieverts or millisieverts. Under presumed LNT dose-response functions for all cancer types, the effective dose represents the uniform gamma-ray dose to the total body that would incur the same overall cancer risk as is associated with the person’s actual exposure, irrespective of its nonuniformity and irrespective of the type and energies of the radiations that are involved.
Radiation Dose Limits
Human radiation exposures are limited for nuclear workers, the public, and other groups based on limiting the effective dose. For example, the effective dose limit for nuclear workers is 50 mSv/y and for the public is 1 mSv/y based on U.S. Department of Energy and Nuclear Regulatory Commission regulatory policies (Metting 2005). The U.S. Environmental Protection Agency’s regulatory policy limits on release of radioactivity to air is based on limiting the effective dose to humans to 0.1 mSv/y, and for public drinking water the corresponding limit is 0.04 mSv/y. For a point of reference, natural background radiation doses in the United States are associated with an effective dose of about 3 mSv/y (radon exposure included) (Metting 2005). For Ramsar, Iran, the corresponding dose associated with natural background radiation is about 200 mSv/y. Interestingly, such high background radiation doses appear to be associated with radiation hormesis-related protection against cancer (Frigèrio and Stowe 1976; Nambi and Soman 1987), i.e., a reduction in cancers.
Low Dose/Dose Rate Cancer Risk Assessment within the LNT Framework
Under the LNT risk assessment framework, effective doses for individuals can be added to obtained person-sievert (a collective dose) for population exposure, and the collective dose can be used to calculate the expected number of cancers among an irradiated population. Similarly, effective dose can be used to assign an individual specific cancer risk. However, low doses are often delivered at low rates and a correction is made for a reduction in harm after low-rate exposure as compared to high-rate exposure. For low doses and dose rates, a low-dose and dose-rate effectiveness factor (DDREF) is used to reduce the slope of the cancer risk curve by a fixed amount, usually a factor of 2 (Mitchel 2006). However with the LNT framework, reducing the effective dose by a factor of 2 has the same effect. By using the LNT-based DDREF approach for low-dose, low-dose-rate risk assessment, one essentially dismisses the possibility of radiation-induced protective effects (hormesis), as the dose-response curve slope is constrained to be positive.
Hormetic Dose-Response Curves
With hormesis, low doses of radiation protect against cancer, leading to a negative slope in the low-dose region for the dose-response curve. High doses, however, inhibit protection causing risk to then increase as dose increases. This yields what has often been called a U- or J-shaped dose-response curve (Calabrese and Baldwin 2001; Calabrese 2004, 2005; Calabrese et al. 2006).
DIFFERENT CLASSES OF RADIATION-ASSOCIATED HORMESIS
This paper distinguishes three classes of radiation hormesis based on the recent recommendations of Calabrese et al. (2007):
Radiation conditioning hormesis: This form of hormesis relates to circumstances where a small radiation dose (mild stress) or moderate dose administered as a low rate (prolonged mild stress) activates protective processes that in turn suppress harm from a subsequent damaging large radiation dose.
Radiation hormesis: A small radiation dose (mild stress) or a moderate dose given at a low rate (recurring mild stresses) activates protective processes and reduces the level of biological harm to below the spontaneous level.
Radiation post-exposure conditioning hormesis: Damage normally caused by a large radiation dose or large dose of some other agent is reduced as a result of a subsequent exposure to a small radiation dose (mild stress) or a moderate dose delivered at a low rate (repeated mild stresses).
Sheldon Wolff’s group (Olivieri et al. 1984; Wolff 1989, 1996) were the first to demonstrate and publish radiation conditioning hormesis data. When human lymphocytes were cultured with tritiated thymidine, which was a source of low-level chronic beta radiation, and then briefly exposed to 1500 mGy of x rays, the yield of chromatid aberrations from the x-ray exposure was suppressed. In a 1988 publication (Wolff et al. 1988) by his group, it was also demonstrated that human lymphocytes exposed to low doses of ionizing radiation (mild stress) became refractory to chemical mutagens that induced double-strand breaks in DNA. Howard Ducoff (1975) was the first to demonstrate radiation hormesis in insects. This author benefited greatly by participating in some of Dr. Ducoff’s research as a graduate student at the University of Illinois. Members of this research group are now known as the Irradiating Illini.
T.D. Luckey, in his 1991 book entitled Radiation Hormesis, reported extensive data on the indicated topic, including data showing that repeated mild stresses associated with chronic low-rate exposure (involving low-LET radiation or low- plus high-LET radiation) significantly reduced the cancer incidence or mortality to below the level for spontaneously occurring cancers. Recently, such chronic radiation hormesis has been demonstrated for lung cancer in a very large number of epidemiological and ecological studies (Sanders and Scott 2007).
Ullrich et al. (1976) were the first to demonstrate a pronounced radiation hormesis effect (for lung cancer) in gamma-ray irradiated female RFM mice. The mice had a high spontaneous frequency of cancer implicating high genomic instability burdens. The pronounced radiation hormesis effect was similar in magnitude to the radiation hormesis demonstrated for neoplastic transformation by Azzam et al. (1996) for mouse embryo fibroblast cells exposed to x rays in vitro. Further, dose-response curves for neoplastic transformation were remarkably similar to those reported by Ullrich et al. (1976) for lung cancer. Just as in the Ullrich et al. study with high spontaneous lung cancer, there was a high spontaneous frequency of transformations for the mouse embryo fibroblasts, implicating a high genomic instability burden for the unirradiated cells. Such hormetic observations now are thought to relate to a dependency of protective intercellular signaling on the concentration of cells bearing genomic instability (Bauer 1996, 2000; Portess et al. 2007; Scott 2007a,b,c). Protective signaling intensity for protective apoptotic pathways is thought to increase with increasing numbers of genomically unstable cells (Scott 2004; Scott et al. 2007), i.e., a form of natural protection. The distribution of mild radiation hits among the target cell population appears also to be an important determinant of the protective signaling intensity (Bond et al. 1987; Feinendegen et al. 2004; Rithidech and Scott 2007), including signaling related to induced immunity (Laster et al. 2007).
Ullrich and Storer (1979) apparently attributed the radiation-hormesis-like observation for lung cancer in mice to systematic errors in lung cancer detection based on the methodology used. However, such a systematic error should operate at all dose levels, including those for the controls; and thus correcting such an error would not be expected to eradicate the hormetic dose-response curve shape. This can be demonstrated by assigning an arbitrary large systematic error (e.g., 50%) to each dose group including the controls and correcting the data. When evaluating relative risk, the correction is canceled so the hormetic curve shape remains. In addition, the study by Ullrich et al. (1976) not only demonstrated radiation hormesis for lung cancer, but it was also demonstrated for reticulum cell sarcoma for both gamma-ray and neutron exposures.
Edouard Azzam (Azzam et al. 1996) and colleagues were the first to demonstrate radiation hormesis in vitro by exposing mouse embryo fibroblasts in culture to low doses of x-rays. Their findings were later confirmed by Redpath et al. (2001, 2003). Studies by Dr. Redpath’s group also demonstrated the importance of the type of radiation as well as dose rate in radiation hormesis response (Redpath et al. 2001, 2003; Ko et al. 2004, Elmore et al. 2005; Redpath and Elmore 2007). At the encouragement of this author, Day et al. (2007) performed the first studies demonstrating radiation post-exposure conditioning hormesis in mice (prostate gland). Chromosomal inversions associated with a large radiation dose were completely prevented by a subsequent small radiation dose (mild stress). Now there are many publications related to the indicated classes of radiation-associated hormesis (e.g., Liu et al. 1987, 1994; Hosoi and Sakamoto 1993; Cohen 1995; Howe 1995; Khokhryakov et al. 1996; Wolff 1996; Jaworowski 1997, 2001; Rossi and Zaider 1997; Hashimoto et al. 1999; Tokarskaya et al. 1995, 1997, 2002; Redpath et al. 2001, 2003; Nyström et al. 2002; Wei and Sugahara 2002; Liu 2003, 2004, 2007; Mitchel et al. 2003; Pollycove and Feinendegen 2003; Sakai et al. 2003; Chen et al. 2004, Feinendegen et al. 2004; Hooker et al. 2004; Ko et al. 2004; Mitchel 2004, 2005, 2006, 2007; Scott 2004, 2005a,b, 2007a,b,c; Scott et al. 2004; Zaichkina et al. 2004; Elmore et al. 2005; Ina and Sakai 2005; Tubiana 2005; Tubiana et al. 2005; Boreham et al. 2006; Mothersill and Seymour 2006; Redpath 2006; Pollycove 2007; Portess et al. 2007; Sanders and Scott 2007; Scott and Di Palma 2007; Scott et al. 2007). For an extensive listing of the many early radiation-associated hormesis publications, see Dr. Luckey’s (1991) book entitled Radiation Hormesis.
The indicated radiation-associated hormesis publications and others collectively demonstrate that low doses/dose rates of low-LET radiation:
Activate protective apoptosis signaling pathways and stimulate immunity.
Protect against spontaneous chromosomal damage, mutations, neoplastic transformation, and cancer.
Protect against high dose chemical- and radiation-induced cancer.
In spite of these now widely published hormetic effects, regulatory agencies still use the LNT-based system for regulating human exposure to ionizing radiation and for low-dose cancer risk estimation. Use of the LNT-based system is considered justifiable by many outside the hormesis community in light of publications such as the BEIR VII Report (NRC 2006), published by the U.S. National Research Council/National Academy of Science. The BEIR VII report concluded that the LNT approach to low-dose risk assessment was valid and essentially dismissed radiation-associated hormesis. A corresponding French Academies report did not come to the same conclusions (Tubiana 2005; Tubiana et al. 2005) when examining essentially the same data that were reviewed in the BEIR VII report. The French report found hormesis to be plausible and the LNT risk function to be invalid for low-LET radiation doses < 100 mGy and especially for doses < 10 mGy.
In the next section, three epidemiological tricks are discussed that when used helps to justify continued use of the LNT framework for low-dose-radiation risk assessment. An approach for accounting for radiation-associated hormetic effects in regulating radiation exposure is then discussed.
EPIDEMIOLOGICAL TRICKS THAT FAVOR A LNT DOSE-RESPONSE CURVE
Trick #1: Throwing Away Radiation Dose
With many previous epidemiological studies of radiation-induced cancer, the researchers somehow came to the conclusion that radiation dose was wasted. Thus, in order to correct for the so-called wasted dose, one has to lag (throw away) some of the dose. However, if the dose-response curve is indeed of the LNT type, then each fixed infinitesimally small increment, dD, in the radiation dose, D, would be expected to be associated with the exact same increment in the cancer risk (i.e., risk per individual). Stated mathematically, if R(D) is the dose-dependent LNT risk function and D is the radiation dose and αis the slope of the LNT dose-response curve, then the fixed increment in risk is dR(D) = αdD; each small increment dD in the dose increases the risk by the amount αdD. Now there is a problem! If each increment in dose is equally effective in increasing risk, how can one conclude that dose is wasted? One cannot in one breath claim the existence of a LNT risk function, then in the next breath claim dose wasting and throw away dose. It is wrong to simply throw away radiation dose in order to obtain a LNT dose-response curve!
When studying DNA double-strand break induction by radiation, one usually observes a LNT-type dose-response curve at low doses (NRC 2006). This seems to be the basis for the expectation by many experts that cancer risk is also a linear function of dose. Interestingly, no dose lagging is used when evaluating DNA double-strand break dose-response curves; possibly because the inappropriateness of doing so would be immediately realized by many if not most radiation researchers.
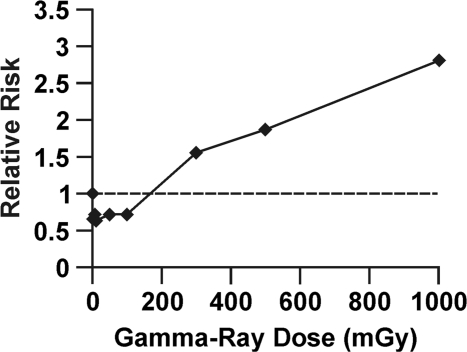
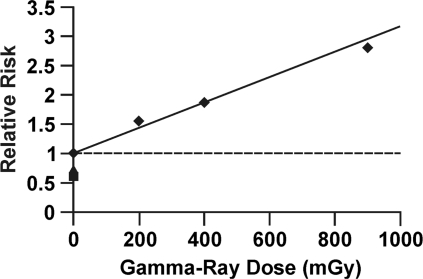
To illustrate how radiation hormesis can be hidden by this dose lagging trick, data are presented in Figure 1 for in vitro neoplastic transformation after brief high-rate exposure to gamma rays, based on studies of Redpath et al. (2001). The cells used were HeLa x skin fibroblast, and relative risk (RR) for these cells has been demonstrated to agree quite well with RR data for cancer (leukemia and solid tumors) induction in humans after brief high-rate exposure (Redpath et al. 2001). Note the hormetic zone between 0 and 100 mGy (which corresponds to the hormetic zone demonstrated by Azzam et al. (1996) using x rays and mouse embryo fibroblast cells) where RR is suppressed to < 1. Figure 2 shows the same data as in Figure 1 with doses lagged by 100 mGy. The radiation hormesis has magically disappeared! There is no longer a hormetic zone. This dose lagging trick is still widely used in epidemiological studies but needs to be stopped. Publishers should no longer allow this trick to be used to deceive the readers and funding agencies. Use of the indicated trick contributed indirectly to the radiation phobia that led to more than 100,000 misinformed physician-recommended abortions of wanted births after the Chernobyl accident (Ketchum 1987).
FIGURE 1.
Relative risk dose-response relationship for gamma-ray induced neoplastic transformation of HeLa x skin fibroblast human hybrid cells by brief high-rate exposure, based on in vitro data from Redpath et al. (2001).
FIGURE 2.
Application of dose lagging (100 mGy) to the data in Figure 1. Analysis based on data from Redpath et al. (2001).
Trick #2: Eliminating the Hormetic Zone via Averaging over Dose Groups
The second trick relates to forming dose groups comprised of persons having received widely varying radiation doses (i.e., the minimum and maximum doses [often reconstructed] for each dose group differs greatly). Such dose groups are usually necessary in case-control studies and are also often used in cohort studies of irradiated populations. Here the focus is on case-control study design and the use of odds ratio (OR) as an estimate of RR.
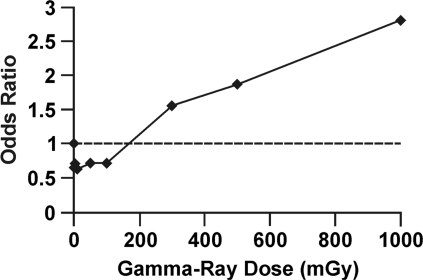
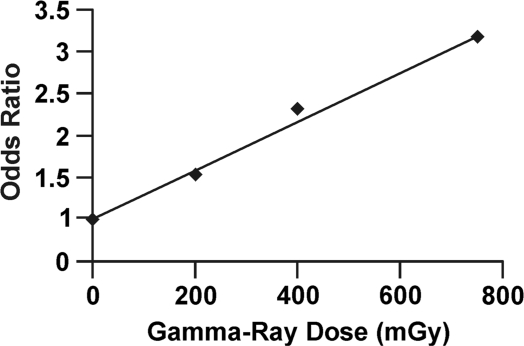
The neoplastic transformation frequency data used for the RR curve presented in Figure 1 can also be converted to odds of neoplastic transformation and the odds used to obtain OR relative to controls which are point estimates (without grouping) as indicated in Figure 3. Note that the hormetic zone is still present and that the dose-response curve is almost identical to the curve in Figure 1. For low frequency stochastic biological effects, OR and RR are quite similar. Dose groups were then formed over the following intervals: 0 to 100 mGy, 101 to 300 mGy, 301 to 500 mGy, and 501 to 1000 mGy. The odds for neoplastic transformation were then averaged over these intervals. Then, these averages were used to calculate OR relative to the lowest dose group, which corresponds to the averaging carried out and methodologies employed in case-control studies of cancer induction. The results obtained are presented in Figure 4, with the lowest dose group plotted at a dose of 0 (as is done in some epidemiological studies) and the results for the other dose groups plotted at the group midrange dose. Note that the hormetic zone has again disappeared. Thus, odds averaging over wide dose groups when evaluating OR can also vanish the hormetic zone. Journal editors and the general public need to be aware of this averaging trick when they are told that the dose-response data from case-control studies are consistent with the LNT hypothesis, which implies that any amount of radiation is harmful no matter how small. Users of the odds averaging trick with no previous knowledge of its hormetic zone vanishing capabilities should be more cautious of how they interpret their research findings.
FIGURE 3.
Odds ratio relative to controls for the neoplastic transformation data presented in Figure 1 for gamma-ray exposure of HeLa x skin fibroblast human hybrid cells.
FIGURE 4.
Ratio of dose-interval-specific average odds for neoplastic transformation based on data in Figure 3. Ratio of average odds evaluated relative to the lowest dose group. The lowest dose group was plotted at dose = 0 mGy. Other data plotted at the midrange of the dose intervals are used.
Dose-grouping in cohort studies of radiation-induced cancer can also vanish the hormetic zone when persons who received low doses are included among the control group (representative of unexposed individuals). This is because the study design has reduced power for demonstrating suppressed risk at low doses when irradiated persons with radiation doses in the hormetic zone are included in the control group (used to represent unirradiated persons).
Trick #3: Constraining the Slope of the Cancer Risk Dose-response Curve to Always Be Positive
A trick often employed in cohort and case-control studies is to constrain the slope of the dose-response curve to be positive while including high-dose, high-risk data in the analysis of the dose-response curve fit. This is especially true when a LNT function has been presumed to apply at low doses by the researchers. Irrespective of the low-dose data, an increase in risk is predicted as dose increases for all such studies. The conclusion that any dose is harmful then follows. Low-dose hormetic (U- and J-shaped) data departing from the LNT characteristic is often simply ignored. It is wrong to portray such data as part of a LNT curve! Low-dose risk assessments should account for the hormetic shape to the dose-response curve.
HORMESIS IMPLICATIONS FOR REGULATORY POLICY
In Zbigniew Jaworowski’s1997 article, Beneficial Effects of Radiation and Regulatory Policy, he states the following:
Adaptive stimulating effects of ionizing radiation occur at near natural doses. This disagrees with linear, no-threshold hypothesis on the dose/effect relationship, which is a basis of the current radiation protection. Vast literature demonstrates that such effects, usually known as hormetic ones, occur at molecular, cellular and population levels, and often result in increased longevity and decreased cancer incidence. . . . After the Chernobyl accident, adverse health effects and vast material losses were induced in the former USSR by practical implementation of the ICRP radiation protection recommendations. A revision of the current approach to managing the risk of ionizing radiation is needed for the public interest.
Here, an approach to regulating radiation exposure is recommended that allows for the existence of a hormetic dose zone just above natural background radiation. The approach relates to the hormetic relative risk (HRR) model previously developed by this author (Scott 2007 a,b,c), which is summarized below in a more general form.
Hormetic Relative Risk Model
With the HRR model for low-dose radiation-induced cancer, doses at or slightly above normal monthly natural background low-LET radiation levels are presumed to fall within the what is currently considered the hormetic zone. This hormetic zone starts at natural background radiation and spans a relative wide dose range, possibly exceeding 1000 mGy of low-LET radiation when radiation dose is delivered at a low rate. However, protective effects associated with hormesis may also occur at below current natural background levels for some individuals. For low-LET radiation doses in the hormetic zone, cancer RR from exposure to low-LET radiation in excess of natural background is expected to remain < 1 for most if not all members of the population. Also, for combined exposure to low doses of low- and high-LET radiations above natural background radiation levels, the low-LET component of the dose activates protective hormetic processes and prevents cancer RR from increasing above 1. The risk may decrease as a result of hormetic processes that are regulated by protective intercellular and intracellular signaling.
The protective signaling, presumed activated with low doses and dose rates of low-LET radiation, relates to removal of aberrant cells from the body via p53-dependent and independent apoptosis signaling pathways and stimulated immunity (Scott 2007 a,b,c; Scott and Di Palma 2007; Scott et al. 2007). The protective signaling can also involve DNA repair pathways if a damage threshold is exceeded (Rothkamm and Löbrich 2003). Possible exceptions to full hormetic protection are the very young and children who may not have significant burdens of genomically unstable cells that participate in the signaling associated with protective p53-independent apoptosis (Scott and Di Palma 2007).
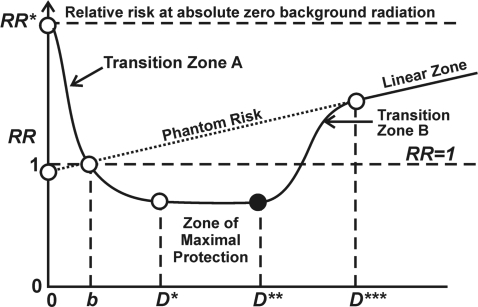
Stochastic thresholds (StoThresh) that vary between different individuals are required in the HRR model for activating the protective signaling. However, somewhat higher doses (also StoThresh) inhibit protection causing an increase in the RR as dose increases up to a point at which protection is suppressed in all individuals. At this point, a linear response that extrapolates to RR = 1 at background radiation b is presumed to apply (Figure 5). This corresponds to use of the LNT model to extrapolate from high to low doses.
FIGURE 5.
Schematic representation of the hormetic relative risk model. The model is presented as a function of the total absorbed radiation dose D to allow for a two-dimensional representation. The dose scale ranges from hypothetical absolute zero natural background radiation dose (D = 0) to doses in excess of the current dose b from natural background. Doses D*, D** and D*** define the different dose zones indicated. The RR at absolute zero radiation is indicated by RR*. The exponential rise as dose decreases below b is supported by epidemiological data (Cohen 1995) for environmentally irradiated humans and is presumed to relate to reduced DNA repair capacity (Rothkam and Löbrich 2003), the loss of protective apoptosis (Scott and Di Palma 2007), and the loss of stimulation of immune functions (Liu et al. 1987).
The mathematical functions discussed in this paper relate to radiation doses equal to or greater than natural background radiation. For this dose range, the indicated nonlinear hormetic RR(D) function (population average) can be evaluated as arising from a weighting between two RR(D) function components: a LNT component (RRLNT) that applies to unprotected individuals and a hormetic component (RRHORM) that applies to protected individuals. The weighting function, PROTEC(D), is the probability function for activated protection (radiation hormesis) as a function of the dose vector, D (called a covariate dose vector by some), which relates to all relevant radiation doses (from low- and high-LET sources) in excess of natural background. PROTEC(D) represents the proportion of the irradiated population that is protected via p53-independent apoptosis and induced immunity and is expected to depend on genetic and other characteristics of the population. The RR(D) for persons with the same nonzero dose vector D, under this model is given by
Equation 1 is used to characterize the population average RR and applies to radiation doses in excess of natural background. Equations that relate to below natural background radiation exposures are not addressed in this paper. The function RRHORM(D) = 1 – PROFAC is for doses in the hormetic zone and equals 1 otherwise (Scott 2007a). The protection factor (PROFAC) gives the expected proportion of cancer cases that are prevented due to radiation hormesis and only relates to the low-LET component of the total radiation dose. The PROFAC relates both to protective apoptosis (presumed p53-independent) and immune functioning but does not relate to DNA repair (Scott 2007a). The function RRLNT(D) simply adds to RR = 1 (with no radiation exposure) the sum K′D, where K′is a row vector of radiation-specific slope factors for excess cancers for matching radiation-specific doses in the dose vector D (a column vector). For a single radiation type K′D = kD, where k is the excess RR per unit dose and D is the individual radiation dose. Components of the vector K′depend on DNA repair capacity (Scott 2007a) which is expected to be greatly reduced in below natural background radiation environments (Rothkam and Löbrich 2003). Components of K′are expected to increase as DNA repair capacity decreases, which is expected to be the case for below natural background radiation exposure. For above natural background radiation exposures, components of K′are currently modeled as being constant.
For just above natural background radiation exposure PROTEC(D) is evaluated presently as 1, decreasing only when one exits the hormetic zone (through a transition zone) at moderate to high doses. For natural background radiation exposure, RR(D) = 1. The RR dose-response curve associated with Equation 1 when plotted as a function of the total radiation dose (indicated by D in this example) has the general features as indicated in Figure 5 for doses ≥natural background b. The figure however presents doses ranging from absolute zero natural background radiation exposure to doses considerably in excess of background radiation exposure.
What has traditionally been considered the hormetic zone comprises the above natural background range of radiation doses for which RR < 1. However, for doses below and above this zone, protective effects can be operational for some individuals. With the HRR model, RR increases above 1 to RR* as the radiation dose decreases below natural background to absolute zero radiation, due to a progressive loss of protected individuals. Over the dose range for which RR < RR*, the dose-response curve is expected to have a U- or J-shape. The schematic exponential increase of RR in Figure 5 as dose decreases below natural background b is supported by data on human lung cancer mortality rates (Cohen 1995) and data revealing a loss of essential DNA repair capacity in low-dose radiation environments (Rothkamm and Löbrich 2003).
Transition Zone A in Figure 5 is where StoThresh for activating protective signaling are progressively exceeded as radiation dose increases. When protective signaling is activated in all members of the population, then the RR is roughly constant through what is called the Zone of Maximal Protection. At doses just above this zone, StoThresh for inhibiting protective signaling (immune system stimulation, protective p53-independent apoptosis, but not p53-related DNA repair) are progressively exceeded as dose increases (Transition Zone B). At somewhat higher doses, protection is suppressed in everyone (except for p53-related DNA repair) and what is called here the Linear Zone then emerges. This zone was previously called the LNT Zone because of intersection of a LNT line (Scott and Di Palma 2007), but this proved to be confusing terminology. The Linear Zone corresponds to the dose region where most epidemiological studies have mainly been conducted that claimed a LNT dose-response curve. For this zone, PROTEC(D) = 0, so that RR(D) = RRLNT(D). For very high doses, departure from linearity can again emerge due to lethal damage to body organs such as the bone marrow.
Over Transition Zone A, PROTEC(D) increases from zero to 1 and remains at 1 over the Zone of Maximal Protection. Over Transition Zone B, PROTEC(D) decreases from 1 to 0.
Regulatory Threshold with Respect to Cancer Induction
It is beneficial to define a regulatory radiation absorbed dose threshold (REGRADT) based on the StoThresh, Tj,i , for loss of protection against cancer in tissue, j, due to dose from the ith radiation type of interest. The indicated REGRADT can be assigned as the radiation-specific dose that corresponds to the minimum individual dose for transitioning from the Zone of Maximal Protection to Zone B. Let Tj,i{min} represent the tissue-j-specific minimum absorbed dose from radiation of the ith radiation type (e.g., x rays, gamma rays, electrons, positrons, protons, muons, neutrons, alpha particles, fission fragments, nonrelativistic heavy nuclei, etc.), for Zone B. The REGRADT is therefore determined by the most sensitive member of the population, related to loss of protection over Transition Zone B. The REGRADT therefore likely depends on the types of radiation involved, dose rates, radiation energies, the population at risk, and the tissue of interest. The dose D** in Figure 5 corresponds to the proposed REGRADT. Higher doses produce harm in part via loss of hormetic protection.
One can then use the normalized stochastic effect dose, Sj , for tissue j as defined below to limit radiation-induced cancers (with respect to preventing excess cancers relative to the spontaneous frequency):
for all tissues j and all n radiations of interest. A value Sj = 0.5 means that only one half of the require radiation exposure for loss of adaptive protection by the most sensitive member of the population has occurred.
This example does not account for genetic effects. However, it is widely known that genetic effects are much less likely to be induced than cancer (NRC 2006). Thus, limiting testicular and ovarian cancer occurrence would be expected to also limit genetic effects. There is also some evidence for dose-response relationships for genetic effects in humans being of the hormetic type with respect to low-rate exposure to gamma rays (Chen et al. 2007). Limiting both cancer and genetic effect occurrences would be expected to also limit shortening of life due to deleterious genetic effects and cancer.
The REGRADT as defined would apply both to population and individual exposures. New, funded research is needed in order to properly assign appropriate values for Tj,i{min} for different radiations, radiation energies (e.g., neutron energy), different cancer types, and for different populations.
CONCLUSIONS
There is abundant evidence for radiation-associated hormesis. However, dismissal of radiation-associated hormesis is in many instances based on epidemiological tricks that include dose lagging, odds averaging over wide dose ranges when evaluating OR, and forcing a positive slope to the RR dose-response curve.
Its time for new, low-dose radiation risk assessment and regulatory paradigms that allow for hormesis. Normalized stochastic effects dose, based on radiation-, radiation-energy-, and dose-rate-specific REGRADTs could be used to limit radiation exposure. For Sj limited to < 1, for all tissues, cancer RR ≤1 would be expected.
Acknowledgments
This research was supported by the Office of Science (BER), U.S. Department of Energy (DOE) Grant DE-FG02-03ER63657. I am grateful to Ms. Vicki Fisher and Ms. Dinese Leonard for editorial assistance and to Ms. Wendy Piper for graphic support. I am also grateful to Dr. Leslie Redpath for his assistance in using published data from his research group and to the journal reviewers for their constructive comments. The views and conclusions contained herein are those of the author and should not be interpreted as necessarily representing the official policies or endorsement, either expressed or implied, of the DOE or of Lovelace Respiratory Research Institute.
REFERENCES
- Azzam EI, de Toledo SM, Raaphorst GP, Mitchel RE. Low-dose ionizing radiation decreases the frequency of neoplastic transformation to a level below the spontaneous rate in C3H 10T1/2 cells. Radiat Res. 1996;146:369–373. [PubMed] [Google Scholar]
- Bauer G. Elimination of transformed cells by normal cells: novel concept for the control of carcinogenesis. Histol Histopathol. 1996;11:237–255. [PubMed] [Google Scholar]
- Bauer G. Reactive oxygen and nitrogen species: efficient, selective, and interactive signals during intercellular induction of apoptosis. Anticancer Res. 2000;20(6B):4115–4139. [PubMed] [Google Scholar]
- Bond VP, Feinendegen LE, Sondhaus CA. Microdosimetric concepts applied to hormesis. Health Phys. 1987;52(5):659–661. doi: 10.1097/00004032-198705000-00019. [DOI] [PubMed] [Google Scholar]
- Boreham DR, Dolling J-A, Somers C, Mitchel R. The adaptive response and protection against heritable mutations and fetal malformation. Dose-Response. 2006;4(4):317–326. doi: 10.2203/dose-response.06-104.Boreham. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Calabrese EJ, Baldwin LA. Hormesis: U-shaped dose-responses and their centrality in toxicology. Trends Pharmacol Sci. 2001;22:285–291. doi: 10.1016/s0165-6147(00)01719-3. [DOI] [PubMed] [Google Scholar]
- Calabrese EJ. Hormesis: from marginalization to mainstream: a case for hormesis as the default dose-response model in risk assessment. Toxicol Appl Pharmacol. 2004;197:125–136. doi: 10.1016/j.taap.2004.02.007. [DOI] [PubMed] [Google Scholar]
- Calabrese EJ. Paradigm lost, paradigm found: the re-emergence of hormesis as a fundamental dose response model in the toxicological sciences. Environ Pollut. 2005;138:379–412. doi: 10.1016/j.envpol.2004.10.001. [DOI] [PubMed] [Google Scholar]
- Calabrese EJ, Staudenmayer JW, Stanek III EJ, Hoffmann GR. Hormesis outperforms threshold model in National Cancer Institute antitumor drug screening database. Toxicol Sci. 2006;94(2):368–378. doi: 10.1093/toxsci/kfl098. [DOI] [PubMed] [Google Scholar]
- Calabrese EJ, Bachmann KA, Bailer AJ, Bolger PM, Borak J, Cai L, Cedergreen N, Cherian MG, Chiueh CC, Clarkson TW, et al. Biological stress response terminology: Integrating the concepts of adaptive response and preconditioning stress within a hormetic dose-response framework. Toxicol Appl Pharmacol. 2007;222:122–128. doi: 10.1016/j.taap.2007.02.015. [DOI] [PubMed] [Google Scholar]
- Chen WL, Luan YC, Shieh MC, Chen ST, Kung HT, Soong KL, Yeh YC, Chou TS, Mong SH, Wu JT, Sun CP, Deng WP, Wu MF, Shen ML. Is chronic radiation an effective prophylaxis against cancer? J Amer Phys Surg. 2004;9(1):6–10. [Google Scholar]
- Chen WL, Luan YC, Shieh MC, Chen ST, Kung HT, Soong KL, Yeh YC, Chou TS, Mong SH, Wu JT, Sun CP, Deng WP, Wu MF, Shen ML. Effects of cobalt-60 exposure on health of Taiwan residents suggest new approach needed in radiation protection. Dose-Response. 2007;5:63–75. doi: 10.2203/dose-response.06-105.Chen. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen BL. Test of the linear-no-threshold theory of radiation carcinogenesis for inhaled radon decay products. Health Phys. 1995;68(2):157–174. doi: 10.1097/00004032-199502000-00002. [DOI] [PubMed] [Google Scholar]
- Day TK, Zeng G, Hooker AM, Bhat M, Scott BR, Turner DR, Sykes PJ. Adaptive response for chromosomal inversions in pKZ1 mouse prostate induced by low doses of X radiation delivered after a high dose. Radiat Res. 2007;167:682–692. doi: 10.1667/RR0764.1. [DOI] [PubMed] [Google Scholar]
- Ducoff HS. Form of the increased longevity of Tribolium after X-irradiation. Exp Gerontol. 1975;10:189–193. doi: 10.1016/0531-5565(75)90031-5. [DOI] [PubMed] [Google Scholar]
- Elmore E, Lao XY, Ko M, Rightnar S, Nelson G, Redpath J. Neoplastic transformation in vitro induced by low doses of 232 MeV protons. Int J Radiat Biol. 2005;81(4):291–297. doi: 10.1080/09553000500140324. [DOI] [PubMed] [Google Scholar]
- Feinendegen LE, Pollycove M, Sondhaus CA. Responses to low doses of ionizing radiation in biological systems. Nonlin Biol Toxicol Med. 2004;2(3):143–171. doi: 10.1080/15401420490507431. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frigèrio NA, Stowe RS.1976Carcinogenic and genetic hazard from background radiation Biological Effects of Low-Level Radiation Pertinent to Protection of Man and His Environment Chicago: November3–71975, 385–393.International Atomic Agency,Vienna [Google Scholar]
- Hashimoto S, Shirato H, Hosokawa M, Nishioka T, Kuramitsu Y, Matsushita K, Kobayashi M, Miyasaka K. The suppression of metastases and the change in host immune response after low-dose total-body irradiation in tumor-bearing rats. Radiat Res. 1999;151:717–724. [PubMed] [Google Scholar]
- Hooker AM, Bhat M, Day TK, Lane JM, Swinburne SJ, Morley AA, Sykes PJ. The linear no-threshold model does not hold for low-dose ionizing radiation. Radiat Res. 2004;162:447–452. doi: 10.1667/rr3228. [DOI] [PubMed] [Google Scholar]
- Hosoi Y, Sakamoto K. Suppressive effect of low-dose total body irradiation on lung cancer metastases: dose dependence and effective period. Radiother Oncol. 1993;26(2):177–179. doi: 10.1016/0167-8140(93)90101-d. [DOI] [PubMed] [Google Scholar]
- Howe GR. Lung cancer mortality between 1950 and 1987 after exposure to fractionated moderate-dose-rate ionizing radiation in the Canadian fluoroscopy cohort study and a comparison with lung cancer mortality in the atomic bomb survivors study. Radiat Res. 1995;142:295–304. [PubMed] [Google Scholar]
- Ina Y, Sakai K. Further study of prolongation of life span associated with immunological modification by chronic low-dose-rate irradiation in MRL-lpr/lpr mice: effects of whole-life irradiation. Radiat Res. 2005;163:418–423. doi: 10.1667/rr3316. [DOI] [PubMed] [Google Scholar]
- Jaworowski Z. Beneficial effects of radiation and regulatory policy. Australas Phys Eng Sci Med. 1997;20(3):125–138. [PubMed] [Google Scholar]
- Jaworowski Z.2001. Ionizing radiation in the 20th century and beyond. Symposium “Entwicklungen im Strahleschutz”. Munich, November 29. Available at: http://www.cns-snc.ca/branches/Toronto/radiation/
- Ketchum LE. Lessons of Chernobyl: SNM members try to decontaminate world threatened by fallout. Newsline. 1987;28(6):933–941. [PubMed] [Google Scholar]
- Khokhryakov VF, Menshikh ZS, Migurova NI.1996Problems of the occurrence of pneumosclerosis and lung cancer among workers exposed by inhalation to plutonium aerosols Radiat Safety 251–55.in Russian [Google Scholar]
- Ko SJ, Liao X-Y, Molloi S, Elmore E, Redpath JL. Neoplastic transformation in vitro after exposure to low doses of mammographic-energy x rays: Quantitative and mechanistic aspects. Radiat Res. 2004;162:646–654. doi: 10.1667/rr3277. [DOI] [PubMed] [Google Scholar]
- Laster B, Nathan I, Gopas J, Kalef-Ezra J.2007Conferral of Immunity to Cancer and Other Diseases by Continuous Low Dose Radiation The 6th International Conference on Hormesis: Implications for Toxicology, Medicine and Risk AssessmentUniversity of Massachusetts, Amherst, MAMay 1–2abstract [Google Scholar]
- Liu S-Z, Liu WH, Sun JB. Radiation hormesis: its expression in the immune system. Health Phys. 1987;52:579–583. doi: 10.1097/00004032-198705000-00008. [DOI] [PubMed] [Google Scholar]
- Liu S-Z, Su X, Zhang YC, Zhao Y. Signal transduction in lymphocytes after low doses of radiation. Int J Occup Med Toxicol. 1994;3:107–117. [PubMed] [Google Scholar]
- Liu S-Z. Nonlinear dose-response relationship in the immune system following exposure to ionizing radiation: mechanisms and implications. Nonlin Biol Toxicol Med. 2003;1(1):71–92. doi: 10.1080/15401420390844483. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu S-Z. Radiation-induced change in lymphocyte proliferation and its neuroendocrine regulation: dose-response relationship and pathophysiological implications. Nonlin Biol Toxicol Med. 2004;2(3):233–244. doi: 10.1080/15401420490507486. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu S-Z. Cancer control related to stimulation of immunity by low-dose radiation. Dose-Response. 2007;5(1):39–47. doi: 10.2203/dose-response.06-108.Liu. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luckey TD. Radiation Hormesis. CRC Press, Boca Raton; Florida: 1991. [Google Scholar]
- Luckey TD. Radiation hormesis: The good, the bad, and the ugly. Dose-Response. 2006;4(3):169–190. doi: 10.2203/dose-response.06-102.Luckey. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Metting N. Ionizing radiation dose ranges chart. Office of Science, U.S. Department of Energy; Washington, DC: 2005. [Google Scholar]
- Mitchel REJ, Jackson JS, Morrison DP, Carlisle SM. Low doses of radiation increase the latency of spontaneous lymphomas and spinal osteosarcomas in cancer prone, radiation sensitive Trp53 heterozygous mice. Radiat Res. 2003;159:320–327. doi: 10.1667/0033-7587(2003)159[0320:ldorit]2.0.co;2. [DOI] [PubMed] [Google Scholar]
- Mitchel REJ. The bystander effect: recent developments and implications for understanding the dose response. Nonlin Biol Tox Med. 2004;2(3):173–183. doi: 10.1080/15401420490507512. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mitchel REJ. Radiation risk prediction and genetics: the influence of the TP53 gene in vivo. Dose Response. 2005;3:519–532. doi: 10.2203/dose-response.003.04.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mitchel REJ. Cancer and low dose responses in vivo: Implications for radiation protection. Proceedings of the 15th Pacific Basin Nuclear Conference; 15–20 October, 2006; Sydney, Australia. 2006. [Google Scholar]
- Mitchel REJ. Low doses of radiation reduce risk in vivo. Dose-Response. 2007;5(1):1–10. doi: 10.2203/dose-response.06-109.Mitchel. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mothersill C, Seymour C. Radiation-induced bystander effects: evidence for an adaptive response to low dose exposures? Dose-Response. 2006;4(4):283–290. doi: 10.2203/dose-response.06-111.Mothersill. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nambi KSV, Soman SD. Environmental radiation and cancer in India. Health Phys. 1987;52:653–657. doi: 10.1097/00004032-198705000-00018. [DOI] [PubMed] [Google Scholar]
- NRC (National Research Council) 2006. Health Risks from Exposure to Low Levels of Ionizing Radiation. The National Academies Press; Report BEIR-VII, Phase 2. Available at: www.nap.edu [PubMed]
- Nyström L, Andersson I, Bjurstam N, Freisell J, Nordenskjöld B, Rutqvist LE. Long-term effects of mammography screening: updated overview of the Swedish randomised trials. The Lancet. 2002;359(9310):909–919. doi: 10.1016/S0140-6736(02)08020-0. [DOI] [PubMed] [Google Scholar]
- Olivieri G, Bodycote J, Wolff S. Adaptive response of human lympocytes to low concentrations of radioactive thymidine. Science. 1984;223(4636):594–597. doi: 10.1126/science.6695170. [DOI] [PubMed] [Google Scholar]
- Pollycove M, Feinendegen LE. Possible effect of inducible protective responses in mitigating endogenous damage. Hum Exper Toxicol. 2003;22:290–306. doi: 10.1191/0960327103ht365oa. [DOI] [PubMed] [Google Scholar]
- Pollycove M. Radiobiological basis of low-dose irradiation in prevention and therapy of cancer. Dose-Response. 2007;5(1):26–38. doi: 10.2203/dose-response.06-112.Pollycove. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Portess DI, Bauer G, Hill MA, O’Niel P. Low-dose irradiation of nontransformed cells stimulates the selective removal of precancerous cells via intercellular induction of apoptosis. Cancer Res. 2007;67(3):1246–1253. doi: 10.1158/0008-5472.CAN-06-2985. [DOI] [PubMed] [Google Scholar]
- Redpath JL, Liang D, Taylor TH, James C, Christie E, Elmore E. The shape of the dose-response curve for radiation-induced neoplastic transformation in vitro: evidence for an adaptive response against neoplastic transformation at low doses of low-LET radiation. Radiat Res. 2001;156:700–707. doi: 10.1667/0033-7587(2001)156[0700:tsotdr]2.0.co;2. [DOI] [PubMed] [Google Scholar]
- Redpath JL, Lu Q, Lao X, Molloi S, Elmore E. Low doses of diagnostic energy x-rays protect against neoplastic transformation in vitro. Int J Radiat Biol. 2003;79(4):235–240. doi: 10.1080/0955300031000096306. [DOI] [PubMed] [Google Scholar]
- Redpath JL. Nonlinear response for neoplastic transformation following low doses of low LET radiation. Nonlin Biol Tox Med. 2005;3:113–124. doi: 10.2201/nonlin.003.01.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Redpath JL. Suppression of neoplastic transformation in vitro by low doses of low LET radiation. Dose-Response. 2006;4(4):302–308. doi: 10.2203/dose-response.06-114.Redpath. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Redpath JL, Elmore E.Radiation-induced neoplastic transformation in vitro, hormesis and risk assessmentDose-Response 2007, in press. Available at http://dose-response.metapress.com [DOI] [PMC free article] [PubMed]
- Rithidech K, Scott B.2007. Evidence for radiation hormesis after in virto exposure of human lymphocytes to low doses of ionizing radiation. Does-Resposne, submitted. [DOI] [PMC free article] [PubMed]
- Rossi HH, Zaider M. Radiogenic lung cancer: the effects of low doses of low linear energy transfer (LET) radiation. Radiat Environ Biophys. 1997;36:85–88. [PubMed] [Google Scholar]
- Rothkamm K, Löbrich M. Evidence for a lack of DNA double-strand break repair in human cells exposed to very low x-ray doses. Proc Nat Acad Sci USA. 2003;100(9):5057–5062. doi: 10.1073/pnas.0830918100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sakai K, Hoshi Y, Nomura T, Oda T, Iwasaki T, Fujita K, Yamada T, Tanooka H. Suppression of carcinogenic process in mice by chronic low dose rate gamma-irradiation. Int J Low Radiat. 2003;1(1):142–146. [Google Scholar]
- Sakai K, Nomura T, Ina Y. Enhancement of bio-protective functions by low dose/dose-rate radiation. Dose-Response. 2006;4(4):327–332. doi: 10.2203/dose-response.06-115.Sakai. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sanders CL, Scott BR.2007Smoking and hormesis as confounding factors in radiation pulmonary carcinogenesisDose-Response, in press. [DOI] [PMC free article] [PubMed]
- Scott BR. A biological-based model that links genomic instability, bystander effects, and adaptive response. Mutat Res. 2004;568:129–143. doi: 10.1016/j.mrfmmm.2004.06.051. [DOI] [PubMed] [Google Scholar]
- Scott BR, Walker DM, Walker VE. Low-dose radiation and genotoxic chemicals can protect against stochastic biological effects. Nonlinearity. 2004;2:185–211. doi: 10.1080/15401420490507602. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scott BR. Stochastic thresholds: a novel explanation of nonlinear dose-response relationships for stochastic radiobiological effects. Dose-Response. 2005a;3(4):547–567. doi: 10.2203/dose-response.003.04.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scott BR.2005bLow-dose radiation risk extrapolation fallacy associated with the linear-no-threshold model BELLE Newsletter 132Part 2; December 2005:22–27. [DOI] [PubMed] [Google Scholar]
- Scott BR. Low-dose radiation-induced protective process and implications for risk assessment, cancer prevention, and cancer therapy. Dose-Response. 2007a;5(2):131–141. doi: 10.2203/dose-response.05-037.Scott. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scott BR. Natural background radiation-induced apoptosis and the maintenance of mammalian life on earth. In: Vinter CV, editor. New Cell Apoptosis Research. Nova Sciences Publishers, Inc.; Hauppage, NY: 2007b. pp. 1–35. [Google Scholar]
- Scott BR. Radiation hormesis and the control of genomic instability. In: Gloscow EJ, editor. New Research on Genomic Instability. Nova Sciences Publishers, Inc.; Hauppage, NY: 2007c. pp. 139–180. [Google Scholar]
- Scott BR, Di Palma J.2007Sparsely ionizing diagnostic natural background radiation are likely preventing cancer and other genomic-instability-associated diseases Dose-Response, Int J low Radiatin press [DOI] [PMC free article] [PubMed]
- Scott BR, Haque M, Di Palma J. Biological basis for radiation hormesis in mammalian cellular communities. Int J Low Radiat. 2007;4(1):1–6. [Google Scholar]
- Sykes PJ, Day TK, Swinburne SJ, Lane JM, Morley AA, Hooker AM. In vivo mutagenic effect of very low dose radiation. Dose Response. 2006;4(4):309–316. doi: 10.2203/dose-response.06-004.Sykes. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tokarskaya ZB, Okladnikova ND, Belyaeva ZD, Drozhko EG. The influence of radiation and nonradiation factors on the lung cancer incidences. Health Phys. 1995;69:356–366. doi: 10.1097/00004032-199509000-00007. [DOI] [PubMed] [Google Scholar]
- Tokarskaya ZB, Okladnikova ND, Belyaeva ZD, Drozhko EG. Multifactorial analyses of lung cancer dose-response relationships for workers at the Mayak nuclear enterprise. Health Phys. 1997;73(6):899–905. doi: 10.1097/00004032-199712000-00003. [DOI] [PubMed] [Google Scholar]
- Tokarskaya ZB, Scott BR, Zhuntova GV, Okladnikova ND, Belyaeva ZD, Khokhryakov VF, Schöllnberger H, Vasilenko EK. Interaction of radiation and smoking in lung cancer induction among workers at the Mayak enterprise. Health Phys. 2002;83(6):833–846. doi: 10.1097/00004032-200212000-00011. [DOI] [PubMed] [Google Scholar]
- Tubiana M. Dose-effect relationship and estimation of the carcinogenic effects of low doses of ionizing radiation: The joint report of The Académie des Sciences (Paris) and of The Académie Nationale de Médicine. Int J Radiat Oncol Biol Phys. 2005;63(2):317–319. doi: 10.1016/j.ijrobp.2005.06.013. [DOI] [PubMed] [Google Scholar]
- Tubiana M, Aurengo A, Averbeck D, Bonin A, Le Guen B, Masse R, Monier R, Valleron A-J, de Vathaire F.2005. Dose-effect relationships and estimation of the carcinogenic effects of low doses of ionizing radiation. Académie des Sciences Report March 30, 2005, Nat Acad Med (France). Académie Nationale de Médicine report
- Ullrich RL, Jernigan MC, Cosgrove GE, Satterfield LC, Bowles ND, Storer JB. The influence of dose and dose rate on the incidence of neoplastic disease in RFM mice after neutron irradiation. Radiat Res. 1976;68(1):115–131. [PubMed] [Google Scholar]
- Ullrich RL, Storer JB. Influence of gamma irradiation on the development of neoplastic disease in mice. II. Solid tumors. Radiat Res. 1979;80:317–324. [PubMed] [Google Scholar]
- Wei L-X, Sugahara T.2002Recent advances of “epidemiological study in high background radiation area in Yangjiang, China.” Proceedings of the International Symposium on Radiation and HomeostasisKyoto, Japan13–16 July 2001International Congress Series123691–99. [Google Scholar]
- Wolff S, Afzal V, Wiencke JK, Olivieri G, Michaeli A. Human lymphocytes exposed to low doses of ionizing radiation become refractory to high doses of radiation as well as to chemical mutagens that induced double-strand breaks in DNA. Int J Radiat Biol. 1988;53(1):39–48. doi: 10.1080/09553008814550401. [DOI] [PubMed] [Google Scholar]
- Wolff S. Are radiation-induced effects hormetic? Science. 1989;245:575–621. doi: 10.1126/science.2762808. [DOI] [PubMed] [Google Scholar]
- Wolff S. Aspects of the adaptive response to very low doses of radiation and other agents. Mutat Res. 1996;358:135–142. doi: 10.1016/s0027-5107(96)00114-5. [DOI] [PubMed] [Google Scholar]
- Zaichkina SI, Rozanova OM, Aptikaeva GF, Achmadieva ACh, Klokov DY. Low doses of gamma-radiation induced nonlinear dose responses in mammalian and plant cells. Nonlin Biol Tox Med. 2004;2(3):213–221. doi: 10.1080/15401420490519861. [DOI] [PMC free article] [PubMed] [Google Scholar]