Abstract
The O2 transport from mixtures of commercially produced hemoglobin-based O2 carriers (HBOCs) and red blood cells (RBCs) flowing through arteriolar-sized (25-μm) conduits is simulated. A generalized treatment of extraluminal O2 transport processes is used to reflect variations in physiological conditions, such as increased O2 consumption. Of the HBOCs considered, polymerized bovine hemoglobin (PolyBvHb, p50 = 54 mmHg), tetrameric cross-linked human hemoglobin (ααHb, p50 = 33 mmHg), and PEGylated human hemoglobin (MP4, p50 = 5 mmHg), only MP4 does not increase O2 extraction ratios when compared to RBC suspensions alone. A reduction in arteriolar O2 extraction is likely to be beneficial for HBOCs by preventing O2-induced vasoactivity and maximizing the supply of O2 available to the capillaries. Results from in vivo HBOC transfusion experiments cannot be predicted by the model, unless PolyBvHb has a significant decrease in extraluminal O2 transport resistance as compared to MP4. This result is consistent with the literature that shows arteriolar O2 consumption to increase with intravascular pO2.
Keywords: Facilitated diffusion, O2 affinity, transport simulation, vasoconstriction, blood substitute
Introduction
This study is a direct comparison of the oxygen transport properties of commercially developed hemoglobin-based O2 carriers (HBOCs) under dynamic, flowing conditions in the absence of biological flow regulation. The tool used in this study is a mathematical model of O2 transport from mixtures of red blood cells (RBCs) and acellular hemoglobin (Hb) flowing through arteriolar-sized gas permeable conduits, which we validate by comparison to in vitro artificial capillary experiments. The techniques we use here have been applied for direct comparisons of commercially developed HBOCs that have been the subject of numerous studies on oxygen transport both in vivo (Nolte et al., 1997; Rohlfs et al., 1998; Tsai et al., 2003b) and in vitro (McCarthy et al., 2001; Page et al., 1998a), and in silico (Cole et al., 2007; Page et al., 1998b). Our current study shows that unless both the O2 affinity and molecular size of HBOCs are increased, the addition of acellular Hb to RBCs is likely to lead to excessive O2 extraction in arteriolar-sized tubes when compared to RBC suspensions alone. Comparisons to in vivo results indicate that O2 delivery by polymerized bovine Hb is increased by processes triggered outside of the lumen.
The HBOCs that have been developed exhibit a large range of oxygen affinities, molecular sizes, and Hb concentrations ([Hb]), variations linked to chemical techniques employed to increase vascular retention time. The modifications made to native Hb include intermolecular cross-linking between Hb subunits, intermolecular polymerization of Hb tetramers, and surface conjugation of Hb molecules to polyethylene glycol (PEG). Each of these processes is similarly intended to reduce Hb dimerization and subsequent renal toxicity, and yet these modified Hb molecules vary significantly in size and O2 binding properties. As Hb chemistry techniques have advanced, increased specificity to the sites of modification (or attachment) has been used to alter O2 affinity and binding cooperativity. We have previously used a mathematical model to study the effect of parameter variations on model Hb when rapidly desaturated while flowing through an arteriolar-sized artificial vessel (Cole et al., 2007).
In general, acellular Hb tends to deliver larger amounts of O2 than RBC suspensions with the same [Hb] when flowing through an arteriole-sized artificial vessel (McCarthy et al., 2001; Page et al., 1998b). A RBC suspension will exhibit a decreased hematocrit near the vessel wall, providing a significant barrier to O2 transport by increasing the average distance required for O2 diffusion out of the vessel. In addition to reducing the resistance effects due to the RBC-depleted layer, extracellular Hb is able to diffuse readily within the lumen, increasing lateral O2 transport by serving as a carrier molecule for bound O2. This phenomenon, facilitated diffusion, is well described in the literature (Kreuzer, 1970; Scholander, 1960; Wyman, 1966). We have found that unless 1) the p50 is much less than that of RBCs (and even < 15 mmHg) and 2) the molecular size is increased compared to native Hb, acellular Hb solutions will deliver more O2 than a RBC suspension at the same [Hb] (Cole et al., 2007).
In this study, we consider three HBOCs that have undergone various stages of clinical study. These HBOCs are human Hb cross-linked between α subunits (ααHb or DCLHb), polymerized bovine Hb (PolyBvHb), and PEG-modified human Hb (MP4). The O2 affinities of HBOCs vary by as much as an order of magnitude (p50 = 5 mmHg for MP4 versus p50 = 54 mmHg for PolyBvHb) (Tsai et al., 2003b). The molecular sizes of PolyBvHb and MP4 are both increased compared to native Hb or ααHb, a modification that leads to decreased molecular diffusivity of the extracellular Hb (DHbO2). A series of in vivo experiments with HBOCs have shown increased efficacy for HBOCs with high O2 affinities and increased molecular size (Rohlfs et al., 1998; Tsai et al., 2003b; Winslow et al., 1998); these data have led to the idea that the ill effects often associated with acellular Hb, namely increased systemic vascular resistance and reduced functional capillary density, may be caused by an excessive supply of O2 in the precapillary microcirculation (Intaglietta et al., 1996; McCarthy et al., 2001).
Mathematical models have been developed to describe O2 transport from acellular Hb (Lemon et al., 1987), RBCs (Nair et al., 1989), and RBC/acellular Hb mixtures (Page et al., 1998a) flowing through arteriolar-sized gas-permeable tubes. These models have been validated by gas-exchange experiments in arteriolar-sized conduits (Boland et al., 1987; Nair et al., 1989; Page et al., 1998b). All of these studies are similar in that they used simple, diffusion-type boundary conditions with minimal extraluminal resistance to describe the outside environment. The comprehensive description of intraluminal processes allowed the subsequent applications of more interesting boundary conditions, such as extraluminal O2 consumption by hepatocytes in a hollow fiber bioreactor (Sullivan et al., 2006; Sullivan and Palmer, 2006).
In vivo, arteriolar extraluminal processes are complex and not described in a manner appropriate for straight-forward modeling. Studies using phosphorescence quenching microscopy by Intaglietta and coworkers have indicated high rates of metabolism by arteriolar walls (Tsai et al., 1998). Recently, Golub et al. proposed that the large arteriolar wall O2 gradients that have previously been interpreted as indicating high wall O2 consumption are largely imposed by extraluminal O2 consumption by the experimental technique (Golub et al., 2008). An as yet undescribed function of O2 supply, NO scavenging, and plasma viscosity regulates arteriolar O2 extraction. In lieu of access to this function, and without consensus agreement of its spatial distribution, we model extraluminal processes in a general way, with a generic extraluminal transport resistance term. Variations in this parameter, the Biot number (Bi), are intended to qualitatively reflect that the properties of the extraluminal environment change with tissue type or metabolic state.
A number of studies have quantified O2 transport from RBCs or RBC/HBOC mixtures for individual capillaries (Dimino and Palmer, 2007; Gundersen and Palmer, 2007; Patton and Palmer, 2006; Vadapalli et al., 2002) and for microvascular networks (Sharan and Popel, 2002; Tsoukias et al., 2007). To date, no study has quantitatively addressed the potentially large difference in arteriolar O2 transport for the particular combination of these three commercially developed HBOCs, particularly since MP4 is a recently introduced product. The most relevant prior work, the HBOC/RBC mixture simulations of Page (Page et al., 1998b), give arteriolar O2 transport from mixtures with varying extracellular [Hb] and p50. However, these simulations were performed over a smaller range of p50 and [Hb] than is spanned by commercially produced HBOCs, and they do not demonstrate the significant effects of cooperative binding and HBOC molecular size. Because of the wide disparity in multiple O2 transport parameters of HBOCs, simulations using the correct values of p50, n, [Hb], and DHbO2 for each are of great use.
In the present work, we describe numerical simulations of O2 delivery in 25-μm diameter conduits for mixtures of commercially developed HBOCs with human RBC suspensions. Two mixture compositions are used, including one set of conditions similar to in vivo microvascular O2 transport measurements (Tsai et al., 2003b). The total O2 transferred from the flowing Hb solution to the surrounding environment is calculated as a function of apparent residence time, which is the longitudinal location normalized by the flow velocity. One test case is chosen to give more detailed information regarding O2 extraction ratios and the desaturation of the RBC component of mixtures.
Methods
Hb solution properties
Calculating O2 transport in Hb solutions requires the accounting of dissolved and Hb-bound O2. The common physiological convention of referring to O2 tension (p) and O2 solubility (α) rather than [O2], and Hb fractional saturation (Y) and total Hb concentration ([HbO2]tot) rather than [HbO2] are followed here. The values for α depend on hemoglobin concentration (Christofordes and Hedley-Whyte, 1969); we use values interpolated between the properties of plasma and erythrocyte intracellular Hb (Christofordes et al., 1969; Christofordes and Hedley-Whyte, 1969) to determine an average α value for any given RBC/HBOC mixture; this allows a simplification of the governing O2 transport equations. The values of α and other parameters used in the simulation are given in Table 1.
Table 1.
Parameters used in the calculations.
| Symbol | Description | Value | Source |
|---|---|---|---|
| r | radial coordinate | independent parameter | |
| z | axial coordinate | independent parameter | |
| R | tube radius | 12.5 μm | simulation parameter |
| Bi | mass transfer Biot number | 1, 3, or 10 | simulation parameter |
| αpl | O2 solubility coefficient, in plasma | 1.33 μM/mmHg | (Christofordes et al., 1969) |
| αrbc | O2 solubility coefficient, inside RBC | 1.47 μM/mmHg | (Christofordes and Hedley-Whyte, 1969) |
| DO2,pl | O2 diffusivity in plasma | 2.75 × 10−5 cm2/s | (Kreuzer, 1970) |
| DO2,rbc | O2 diffusivity inside RBC | 1.48 × 10−5 cm2/s | (Spaan et al., 1980) |
| [Hb]rbc | heme concentration inside RBC | 21.4 mM | (Weibel, 1984) |
| α | O2 solubility coefficient | linearly interpolated between αpl and αrbc by [Hb] | |
| DO2 | O2 diffusivity | linearly interpolated between DO2,pl and DO2,rbc by [Hb] | |
| DHbO2 | HbO2 diffusivity | (1, 3, or 10) × 10−7 cm2/s | simulation parameter |
| [Hb]total | total [Hb] for RBC suspensions | (3.75, 5, 7.5, 9, 15) g/dl | simulation parameter |
| λ | normalized radius of RBC rich core | (0.66, 0.68, 0.71, 0.74, 0.90) | (Tateishi et al., 2001) |
| μc | core viscosity | (1.25, 1.5, 2.0, 2.5, 3) cP | (Pries etal., 1992) |
The Hill equation, Eq. 1, is used to describe Hb-O2 equilibrium binding, where p50 is the p where Y = 0.5 and is a measure of the Hb-O2 binding affinity, and the Hill number, n, is an empirical constant which gives Hb/O2 binding cooperativity (Hill, 1913).
| (1) |
The total O2 content of a Hb/RBC mixture is the sum of the dissolved O2 and Hb-bound O2 within RBCs and bound to extracellular (EC) hemoglobin Eq. 2. In Eq. 2, h is the average hematocrit, the fractional volume occupied by RBCs, and 1- h is the fractional volume occupied by extracellular Hb.
| (2) |
We use mixed-mean or bulk concentrations, cb, as defined in Eq. 3, to describe the average value of p or Y at a given axial position (Rosner, 1986), where u(r) is the flow profile, R is the tube radius, r is the radial position in the tube, and z is the axial position in the tube.
| (3) |
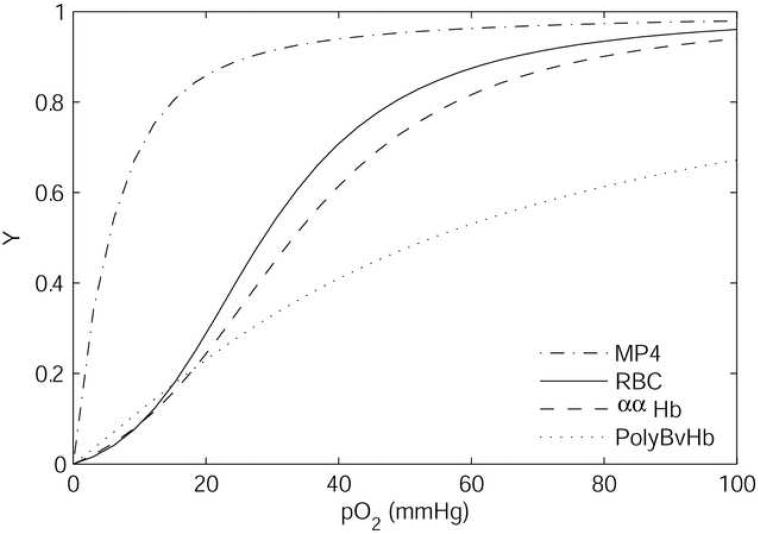
In this study we consider three chemically modified acellular Hb products developed for use as prospective HBOCs. MP4 is a human Hb conjugated with polyethylene glycol produced by Sangart (San Diego, CA); the clinical product of MP4 is called Hemospan®. PolyBvHb is a polymerized bovine Hb produced by Biopure (Boston, MA). ααHb is a human Hb cross-linked between α subunits developed by the U.S. Army and Baxter Heathcare (Round Lake, IL) that has been discontinued from clinical study. The product produced by Baxter (HemAssist™) was mirrored by a functionally identical product produced by the Letterman Army Institute of Research (ααHb), which was used in a large number of academic studies (Winslow, 2000). The properties of the HBOCs are given in Table 2. Figure 1 shows the O2 equilibrium binding curves for MP4, PolyBvHb, ααHb, and human RBCs. The Hb solution properties, as prepared for clinical use, vary significantly. The [Hb] for MP4 (4.3 g/dl) is markedly lower than that for either PolyBvHb (13.1 g/dl) or ααHb (10 g/dl). MP4 has high O2 affinity (p50 ∼5 mmHg (Vandegriff et al., 2003), ααHb moderate O2 affinity (p50 ∼33 mmHg) (McCarthy et al., 2001), and PolyBvHb low O2 affinity (p50 ∼54 mmHg) (Tsai et al., 2003b). The p50 for PolyBvHb has been listed in the literature as 39 mmHg (Page et al., 1998b), but it has been noted that this discrepancy is due to errors in commercial-measurement techniques, where a high pO2 calibration point is erroneously assumed to be fully saturated (Tsai et al., 2003b). MP4 and PolyBvHb are fairly non-cooperative (n ∼1.2), and ααHb has greater cooperativity (n ∼2.4). The low cooperativity and high p50 of PolyBvHb causes it to be only ∼70% saturated at the pO2 of blood leaving the lungs (100 mmHg).
Table 2.
Properties of HBOCs at 37°C. The viscosities are of full concentration HBOCs. The values given for DHbO2 are, in order, 100% HBOC, 50% HBOC/50% RBC, 25% HBOC/25% RBC.
Figure 1.
Oxygen equilibrium curves for the HBOCs at 37°C, pH = 7.4 (McCarthy et al., 2001; Tsai et al., 2003b).
The diffusivity of acellular Hb (DHbO2) of known geometry may be estimated by the Stokes-Einstein equation, Eq. 4.
| (4) |
The friction factor, fr, for a diffusing sphere is 6πμrA, where μ is the solute viscosity and rA is the radius. The HBOC diffusivities used in the simulations are given in Table 2. They assume the HBOCs are mixed with an extracellular fluid with the viscosity of plasma (μ = 1 cp), leading to a different μ than the production-formulated value. The undiluted DHbo2 for ααHb, a roughly spherical molecule, is 7.9 × 10−7 cm2/s according to Eq. 4, using the production-solution viscosity and molecular radius (rA = 3.1 nm, (McCarthy et al., 2001)). Recent small angle x-ray scattering (SAXS) studies have shown that MP4 is an anisotropic molecule that can be represented as an ellipsoid of dimensions 13 nm × 6.5 nm (Svergun et al., 2008). For ellipsoids with aspect ratios < 3, it is adequate to replace the friction factor of the ellipsoid with that of a sphere of equal surface area (Gordon, 2003). The equivalent spherical radius for MP4 is 4.2 nm, giving an undiluted DHbO2 = 2.2 × 10−7 cm2/s. MP4 molecules are also seen to have significant intermolecular repulsive forces, which may lead to physical exclusion from vessel walls (Svergun et al., 2008).
Because PolyBvHb is a heterogeneous product composed of polymers with molecular weights ranging from 64 to 500 kDa and an average molecular weight of 200 kD, it does not lend itself easily to analysis by Eq. 4. The diffusivity of PolyBvHb at production concentration has been measured directly to be 2.8 × 10−7 cm2/s (Budhiraja and Hellums, 2002). If PolyBvHb were composed of spheres of the same size, the equivalent radius according to Eq. 4 would be ∼ 4 nm. The dilution of HBOC with extracellular fluid changes the viscosity and, therefore, the DHbO2 approximately as shown in Table 2. Due to the large degree of heterogeneity for PolyBvHb, it is difficult to ascribe biological effects to the properties of the Hb solution (Winslow, 2007).
Hb reaction kinetics
The rate of O2 liberation from Hb, fHb, is related to HbO2, Hb, and O2 concentrations, as well as the association and disassociation rate coefficients k' and k, respectively (Eq. 5).
| (5) |
Because f is a function of [Hb], p50, and n, we use subscripts RBC and EC on the reaction function to indicate whether the reaction involves RBC or extracellular Hb, respectively. To reflect differences in k' and k due to equilibrium binding effects, Moll developed a technique that holds the association coefficient constant and varies the dissociation coefficient in the Hill equation as a function of saturation, Y (Eq. 6) (Moll, 1968).
| (6) |
The value for k' is given by Gibson as 3.5 × 106 M−1 s−1 for Hb at 37°C (Gibson et al., 1955). The use of constant association and variable dissociation coefficients to define activity for different Hbs is consistent with kinetic measurements for native and chemically modified Hb (Vandegriff et al., 1991; Vandegriff et al., 2004). The underlying assumption for this method is that the offloading of O2 from Hb is not a rate-limiting step and that intraluminal O2 transport rates are primarily dependent on the speeds of lateral diffusive processes. This assumption was validated in our previous work (Cole et al., 2007).
Mathematical Model
The details of the mathematical model of O2 transport are given in the appendix. Briefly, an in vitro O2 exchange experiment can be performed on a hemoglobin solution flowing through a gas-permeable tube. The rate of O2 transport is controlled by the geometry of the tube (including the wall thickness), the permeability of the tube material, and the O2 concentration at the outer surface of the tube. Mathematical models have been developed that accurately predict the results of such experiments, as long as hemoglobin properties and other experimental parameters are known.
Models of this type require simplification of the extraluminal environment that vary from those in vivo. This study uses the mass transfer Biot number (Bi) applied to the radial boundary condition for the pO2 to lump all extraluminal processes together. The values of Bi used are estimated from in vivo O2 transport data as described in the appendix.
Results
Model Validation
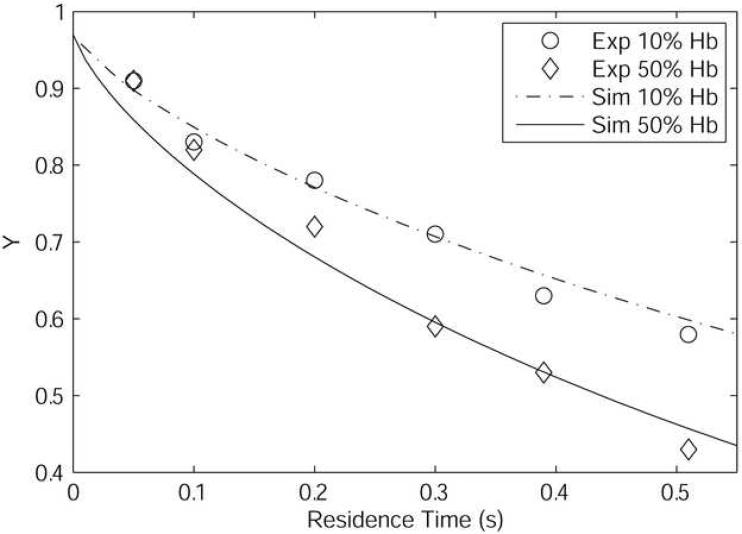
The model was validated by direct comparison with in vitro artificial capillary experiments performed in 27-μm diameter silicone conduits by Page (Page et al., 1998b). This was done to ensure that the modifications made to the Page et al. model still allow for the accurate prediction of experimental results. The mixtures simulated have a total [Hb] = 10.2 g/dl with either 10% or 50% of the total Hb composed of acellular Hb, with the balance contained within RBCs (p50 = 29 mmHg, n = 2.6). The acellular Hb considered was unmodified bovine Hb (p50 = 25 mmHg, n = 2.65, DHbO2 = 5.6 × 10−7 cm2/s) (Page et al., 1998a). Based on the geometry and other parameters such as geometry and O2 permeability given in Page (Page et al., 1998a), we calculated a Bi for this series of experiments as ∼100 to use in our simulations. The viscosity and radius of the cell-rich core were estimated from sources in literature (Pries et al., 1992; Tateishi et al., 2001). For 10% extracellular Hb, μc = 2.5 cP and λ = 0.74 were used; for 50% extracellular Hb, μc = 1.5 cP and λ = 0.68 were used. Figure 2 shows that simulations performed with the model we present here and experiments performed by Page (Page et al., 1998b) are in be in good agreement, indicating that the simplifications we made to the model described by Page (Page et al., 1998a) still allow a correct description of the observed data.
Figure 2.
Results of simulations (Sim) compared to experiment (Exp) in 27μm diameter silicone tubes (Page et al., 1998a). The total Hb concentration is 10.2 g/dl with 10% or 50% of the Hb consisting of acellular Hb (p50 = 25 mmHg, n = 2.65, DHbO2 = 5.6 × 10−7 cm2/s).
Mixtures with 50% RBCs and 50% HBOC
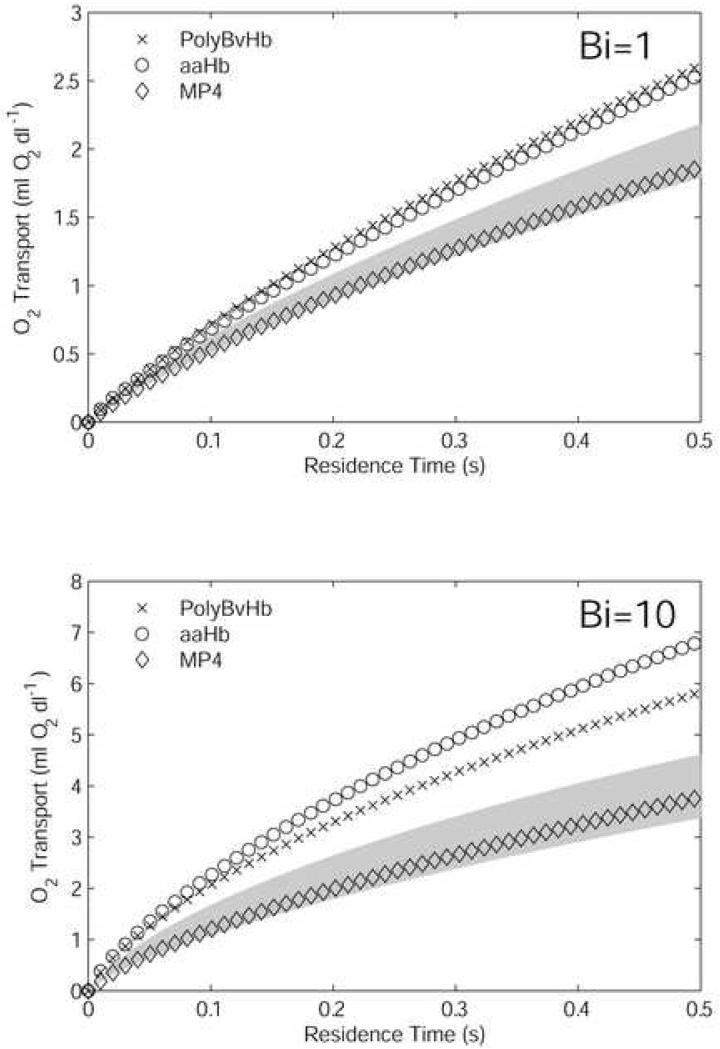
Simulations were performed on mixtures containing 7.5 g/dl RBCs and 50% of the formulated-production [Hb] for each HBOC, with two different extraluminal resistance conditions. The motivation for this set of experiments was to mimic the case of a 50% isovolemic exchange transfusion. The initial O2 content of each mixture is given in Table 3. These values were calculated from Eq. 2, using p = 100 mmHg and the equilibrium fractional saturations for both RBC and HBOC Hb. The cumulative O2 transport from RBCs, acellular Hb, and dissolved O2 into the extraluminal environment is plotted in Figure 3 versus residence time (a surrogate for axial position). This measure is the same as the difference between the initial O2 content and the average O2 content of the mixture flowing through a given axial position, as defined in Eq. 2 and Eq. 3. For each Bi value, the O2 transport by 7.5 g/dl and 15 g/dl (i.e., non-hemodiluted) RBC-only suspensions were calculated, with the region between the two RBC-only cases shaded, for means of comparison. For Bi = 1, the PolyBvHb and ααHb mixtures give ∼50% more O2 transport than 7.5 g/dl RBCs-only, as compared to a ∼25% increase for 15 g/dl RBCs-only. MP4 gives slightly more overall O2 than 7.5 g/dl RBCs.
Table 3.
Initial O2 content of 50% RBC, 50% HBOC mixtures in equilibrium at pO2 = 100 mmHg. [HBOC] and [RBC] are in g/dl, [O2] is in ml O2/dl.
| HBOC | [HBOC] | [RBC] | [O2] RBC | [O2] HBOC | [O2] Total |
|---|---|---|---|---|---|
| - | - | 7.5 | 9.9 | - | 9.9 |
| - | - | 15 | 19.8 | - | 19.8 |
| ααHb | 5.0 | 7.5 | 9.9 | 7.4 | 16.3 |
| PolyBvHb | 6.55 | 7.5 | 9.9 | 7.3 | 16.2 |
| MP4 | 2.15 | 7.5 | 9.9 | 2.9 | 12.8 |
Figure 3.
Oxygen transport out of the vessel by mixtures composed of 7.5 g/dl RBCs and 50% of formulated HBOC [Hb]. The transport is the negative of the difference in luminal O2 content. Results are shown for high (Bi = 1) and low (Bi = 10) extra-luminal resistance cases. The shaded area is the amount of O2 transport spanned by 7.5 g/dl RBCs (lower bound) and 15 g/dl RBCs, i.e., normal hematocrit (upper bound).
When the extraluminal resistance was decreased so that Bi = 10, the total O2 transport of each HBOC mixture increased with respect to the RBC-only suspensions. A larger relative increase in O2 transport by ααHb was a result of facilitated diffusion due to its relatively smaller molecular size. Facilitated diffusion is the process by which small, highly diffusible extracellular HbO2 molecules increase lateral transport by acting as carrier molecules for O2. The increased effect of facilitated diffusion under low extraluminal resistance conditions has been demonstrated in our previous work (Cole et al., 2007). ααHb O2 transport in this case was ∼100% greater than that by 7.5 g/dl RBCs-only and ∼25% greater than that by PolyBvHb. The O2 transport by MP4 was only ∼10% more than that by 7.5 g/dl RBCs-only suspensions, a small increase in transport compared to the situations with ααHb and PolyBvHb. In comparison, doubling [Hb] of RBC-only suspensions from 7.5 g/dl to 15 g/dl, O2 transport was increased by ∼40%. In all cases tested, MP4 fell within the shaded area of RBC-only suspensions.
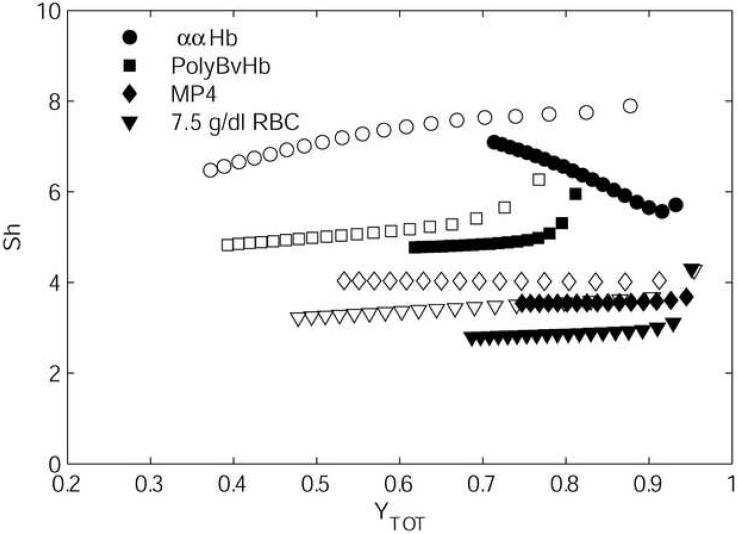
The intraluminal transport resistances were calculated for the set of conditions shown in Figure 3 and are given in Figure 4. The Sherwood number (Sh) was calculated, giving a non-dimensional form of an intraluminal mass-transfer coefficient. Such data typically are used to investigate microvascular networks with geometry too complex to perform detailed intravascular simulations. Sh is defined in Eq. 7, where Jw is the O2 flux at the lumen wall, pw is the pO2 at the wall, and pb is the bulk pO2. The values of α and DO2 used are those for plasma (Table 1).
| (7) |
Figure 4 gives plots of Sh versus the average Hb saturation of the RBC/HBOC mixture (YTOT) for Bi = 1 and Bi = 10. In each case, data are shown until a residence time of 1 second, giving more data than shown in Figure 3, although still not encompassing the entire range of possible (YTOT). For each simulation, there was a rapid change from a large initial Sh to a somewhat lower value, showing gradual changes with YTOT. This effect is an artifact of the large pO2 gradients that form within outer boundary layers until the concentration profiles have had enough time to develop. The Sh values calculated for RBCs are in general agreement with those given in literature (Hellums et al., 1996). For each case studied, Sh was less for Bi = 1 than for Bi = 10. With RBCs-only, MP4, or PolyBvHb, this difference was in the range of 10-20%. This difference was larger for ααHb at high YTOT, although at YTOT = 0.7, the Sh for Bi = 1 approached the relatively small differences exhibited by the other HBOC/RBC mixtures. The increases in Sh between HBOCs are correlated to the quantity DHBO2 × [Hb]EC, which gives a rough measurement of the potential for transport augmentation due to facilitated diffusion. The steepness of the O2 binding curve, dY/dp, also affects facilitated diffusion and causes a cooperative HBOC like ααHb to be at its maximum when it is locally near Y = 0.5. The much lower Sh values for ααHb with Bi = 1 versus Bi = 10 occurred because the HBOC remained highly saturated across the vessel cross-section. The larger intraluminal gradients imposed by Bi = 10 cause significant desaturation near the vessel wall, activating the facilitated diffusion mechanism. These phenomena are discussed in greater depth later in this paper.
Figure 4.
Non-dimensionalized mass transfer coefficient (Sh) for mixtures shown in Figure 3, plotted versus total Hb saturation (black markers are Bi = 1, white markers are Bi = 10).
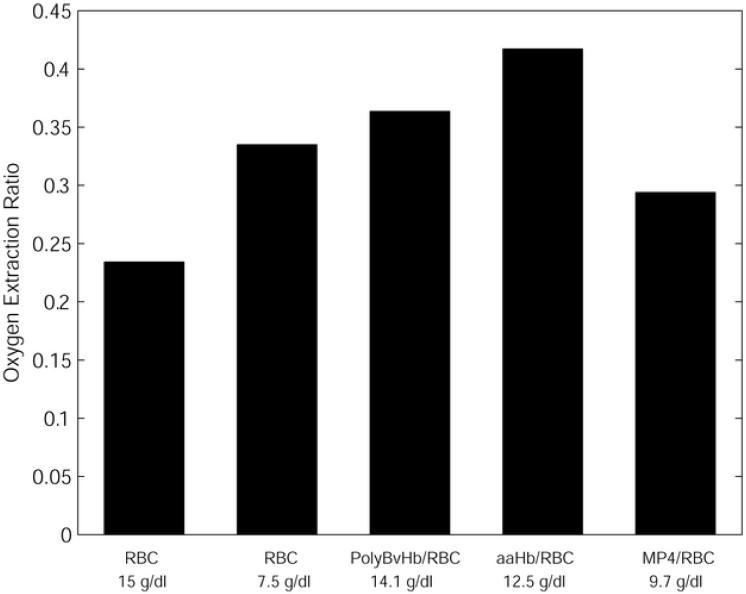
A more in-depth view of the intraluminal processes for the case of Bi = 10 can be seen in Figure 5 and Figure 6. This particular Bi was chosen for an in-depth view because in a previous study (Cole et al., 2007) we found that lower relative values of extraluminal resistance were required to cause O2 fluxes similar to those observed in vivo, although it is likely that the choice of an appropriate extraluminal resistance condition depends on location in the body. Figure 5 shows the O2 extraction ratios (OER) for the HBOC mixtures, defined as the fraction of the initial O2 content delivered in the arteriolar segment. These values are displayed at an arbitrary residence time of 0.5 sec, although similar behavior can be seen for the entire range of residence times as shown in Figure 3. Compared to 15 g/dl RBCs-only, 7.5 g/dl RBCs-only showed an increase of 0.10. This difference in OER would be even greater if not for the increase in O2 transport resistance associated with the thicker cell-depleted layer at the lower hematocrit. Compared to 7.5 g/dl RBCs, PolyBvHb and ααHb showed even higher increases in OER of 0.03 and 0.09, respectively. MP4 alone showed an OER in between those of 7.5 g/dl and 15 g/dl RBCs, with an OER that was 0.03 less than 7.5 g/dl RBCs-only. Thus, the O2 extraction for the MP4-RBC 50:50 mixture fell in a range similar to RBCs, while the extraction by PolyBvHb or ααHb was significantly larger. Strikingly, the addition of more RBCs to the 7.5 g/dl RBC-only solution reduced the OER, while the addition of PolyBvHb or ααHb increased the OER.
Figure 5.
Oxygen extraction ratios of 7.5 g/dl RBCs, 50% HBOC. The lower number is the total [Hb] for the RBC/HBOC mixture.
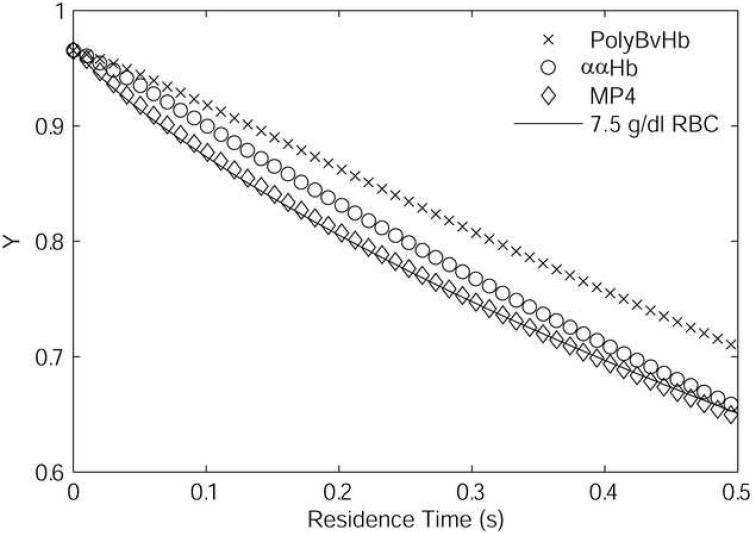
Figure 6.
Desaturation of RBC component of 7.5 g/dl RBCs, 50% HBOC mixtures compared to desaturation of 7.5 g/dl RBCs only.
Figure 6 shows the Hb fractional saturation of the RBC component of the mixtures plotted versus residence time for the results shown in Figure 3 using Bi = 10. For either ααHb or PolyBvHb mixtures, the desaturation of the RBC component was delayed as compared to the 7.5 g/dl RBC-only suspension, with PolyBvHb, which has the highest p50 and [Hb], imparting the greatest slowing of RBC desaturation. In contrast, the desaturation of RBCs was essentially unchanged by the addition of MP4. The ααHb RBC component showed a profile intermediate to those for PolyBvHb and MP4.
Mixtures with 25% RBCs and 25% HBOC - Comparison with in vivo experiment
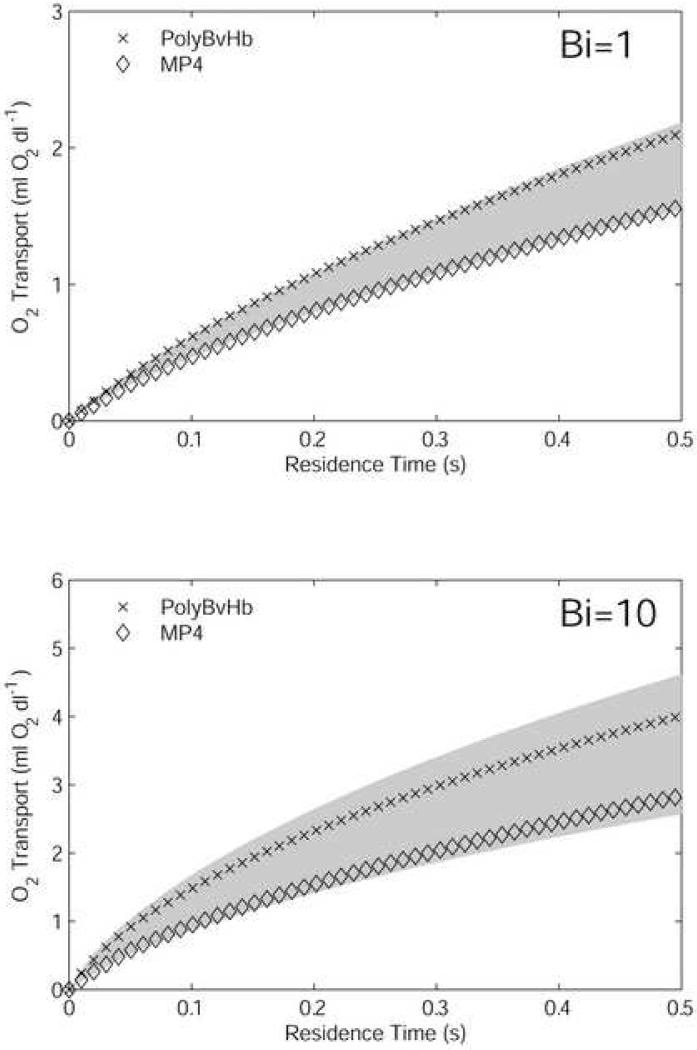
Figure 7 shows the O2 transport from 3.75 g/dl RBC, 25% HBOC mixtures. The motivation for this set of conditions was to compare simulations by our model with in vivo exchange experiments in a hemodiluted hamster model performed by Tsai (Tsai et al., 2003b). In these, the hematocrit was reduced by exchange with Dextran, followed by an additional exchange with MP4, PolyBvHb, or Dextran until the final hematocrit was 11%, and the HBOC content was roughly 25% of the formulated [Hb]. The reported values for tissue pO2 in Tsai (Tsai et al., 2003b) are all < 2 mmHg, so the choice of p∞ = 0 mmHg in Eq. A9 appears reasonable in this instance. The shaded region in Figure 7 gives the calculated range of O2 transport between 3.75 g/dl RBCs and 15 g/dl RBCs. For these calculations, we neglected the slightly higher p50 of hamster RBCs (34 mmHg) compared to human RBCs. For each Bi, the O2 transport from MP4 was similar to that of the diluted RBC component (3.75 g/dl RBCs). For Bi = 1, PolyBvHb showed 30% more O2 than 3.75 g/dl RBCs; for Bi = 10, it showed 50% more O2. The implications of these results in comparison to the in vivo studies are discussed in the next section.
Figure 7.
Oxygen transport out of the vessel by mixtures composed of 3.75 g/dl RBCs and 25% of formulated HBOC [Hb]. Results are shown for high (Bi = 1) and low (Bi = 10) extraluminal resistance cases. The shaded area is the amount of O2 transport spanned by 3.75 g/dl RBCs (lower bound) and 15 g/dl RBCs (upper bound).
Discussion
At the time of writing, the HBOC MP4 is undergoing Phase III clinical trials, while the HBOCs ααHb and PolyBvHb have entered Phase III trials and not been approved. Among these HBOCs, specific in vivo models have shown the greatest efficacy for MP4, a result we believe is due in part to decreased arteriolar O2 delivery. This is the first study that gives the potential arteriolar O2 transport from MP4/RBC mixtures in comparison to ααHb and PolyBvHb, in absence of biological flow regulation.
In vitro, the addition of acellular Hb to a RBC suspension generally increases the fraction of the total O2 that is delivered in arteriolar-sized tubes. This effect can be eliminated by significant reductions in p50 and increases in the molecular size of the HBOC, as compared to native Hb. We show that mixtures containing early-generation blood substitutes, ααHb and PolyBvHb, have the potential for elevated O2 transport in arteriolar-sized tube compared to RBCs alone. This result can be interpreted to correlate with increased in vivo arteriolar O2 delivery. The higher O2 affinity of the new-generation product, MP4, causes it to unload little of its bound O2 in this test model, which indicates limited potential for O2 transport in the arteriolar segment of the microcirculation. This result can be interpreted to correlate with MP4's increased potential for O2 delivery to the capillaries. Despite its low p50 (5 mmHg), the efficacy of MP4 to deliver O2 in the capillaries has been demonstrated in vivo (Tsai et al., 2003b), and our results describe that the design for an HBOC to maintain capillary delivery is inherent in the diffusive and O2 binding properties of the product.
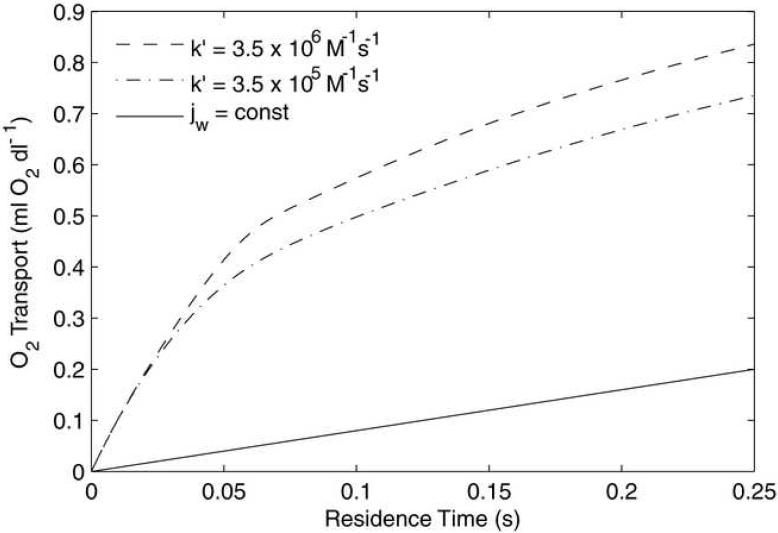
The ability of MP4 to deliver O2 in capillary-sized vessels is shown figure 8. The hematocrit is set to 0%, R = 2.5 μm, [Hb] = 1 g/dl, and Bi = 0.1. At small size scales O2 dissociation kinetics may begin to limit the amount of O2 available to be transported to the peripheral tissue. In this study, reaction kinetics were approximated by holding the association rate constant (k′) steady and varying the disassociation rate constant (k) as a function of p50 and n (Eq. 6). For capillary-sized vessels sensitive to the choice of k′ (or k), more detailed data, specific to each HBOC, would be required. Because these data are not available, simulations were performed with the value of k′ used elsewhere in this study (3.5 × 106 M−1 s−1) and then set one order of magnitude less to demonstrate the potential reduction in capillary O2 transport due to reaction kinetic limitations (Figure 8). In vivo O transport measurements on capillaries give Jw ∼ 1 ×10−6 ml O2/(cm2s) (Ellsworth et al, 1988; Stein and Ellsworth,1992), which is a significantly smaller rate of transport than calculated with either k′ rate used for MP4 in Fig. 8. These results indicate that the ability of MP4 to deliver adequate amounts of O2 on capillary size scales is not in doubt.
Figure 8.
Oxygen transport out of 5-μm diameter tubes for 0% hematocrit MP4 solution. For the case shown, [Hb] = 1 g/dl, Bi = 0.1, and p∞ = 0 mmHg. The slope of each line is proportional to the O2 flux. jw gives the total O2 delivered when O2 is extracted at a constant rate based on published values of capillary O2 flux. An order-of-magnitude reduction in k provides a small reduction in O2 delivery.
This study focuses on the intraluminal O2 transport properties of HBOC/RBC mixtures in precapillary-sized microvessels. We suggest that the delivery of excessive amounts of O2 in the precapillary microcirculation is undesirable because: 1) autoregulatory effects decrease capillary perfusion; 2) arteriolar O2 delivery is inefficient for tissue oxygenation in comparison with capillary O2 delivery. Our previous studies have shown that HBOCs with low p50 and increased molecular size do not lead to increases in mean arterial pressure and vascular resistance generally associated with cell-free Hb (Rohlfs et al., 1998; Winslow et al., 1998). Detailed microvascular measurements have shown increased functional capillary density and tissue perfusion with a low p50 HBOC (MP4) as compared to a high p50 one (PolyBvHb) (Tsai et al., 2003b). These results can be interpreted as the minimization of O2 supply-induced vasoactivity, because increases in O2 affinity and molecular size both trend with decreased O2 transport. It should be noted that besides O2 supply, NO-scavenging by extracellular Hb and/or plasma viscosity may play additional roles in microvascular flow regulation. The relative importance of each is under study (Palmer, 2006), as specific experiments are designed so that each factor becomes a primary flow determinant (Cabrales et al., 2006; Cabrales and Tsai, 2006; Doherty et al., 1998).
In vivo vasoactivity of acellular HBOC products has been shown to be correlated to molecular size (Olson et al., 2004). We have suggested that this effect is due to increases in O2 delivery due to facilitated diffusion, i.e., by the additional O2 transport from lateral diffusion and subsequent O2 release by HbO2 (McCarthy et al., 2001). The reduction in O2 transport resistance due to the addition of HBOC to RBCs is clearly shown in Figure 4. The magnitude of the effect of facilitated diffusion can be estimated from Eq. 8, where JHbO2 is the lateral flux of HbO2, [Hb]EC is the extracellular [Hb], and ∂Y/∂r is the extracellular Hb saturation gradient.
| (8) |
JHbO2 is linearly related to the quantity DHbO2 × [Hb]EC, and thus inversely proportional to molecular size. Of the HBOCs studied here, DHbO2 × [Hb]EC orders as MP4 < PolyBvHb < ααHb, which correlates to the ordering of the observed differences in intraluminal transport resistance (Figure 4). ∂Y/∂r depends on the equilibrium binding properties of the HBOC, and to some extent, extraluminal resistance. Because ∂Y/∂r ≈ dY/dp×∂p/∂r, the local value of JHbO2 is largest when the HBOC has a pO2 near its p50, such that the slope of the O2 binding curve (dY/dp) is sufficiently steep. dY/dp increases with n and O2 affinity, although lowering the p50 has a counteracting effect by decreasing ∂p/∂r. HBOC with appropriately large DHbO2 and [Hb]EC can have a large facilitated diffusion effect even at high average Y if there is a significant difference between the average Y and Y at the vessel wall. This difference allows the Hb in the near-wall region to have a pO2 similar to the p50, elevating the local JHbO2. Because the intraluminal gradients (i.e., the difference between the mean and wall values of pO2 and Y) increase with Bi, the much lower intraluminal resistance for ααHb with Bi = 10 compared to Bi = 1 for Y > 0.7 (Figure 4) is a direct consequence of the smaller applied extraluminal resistance.
The data provided here are useful for network O2 transport studies of RBC/HBOC mixtures, similar to those performed by Sharan and Popel (Sharan and Popel, 2002), Kavdai (Kavdai et al., 2002), and Tsoukias (Tsoukias et al., 2007). We have found that the mass transfer coefficients needed for such studies are functions of the specific properties of the HBOC as well as the extraluminal transport resistance. An HBOC with the most significant potential for facilitated diffusion is most sensitive to the extraluminal conditions when the Hb is highly saturated. This is important when modeling healthy physiological conditions, where only a fraction of the total O2 carried by blood is extracted.
Even with the information provided by accurate modeling of intraluminal processes, the current models do not replicate the arteriolar flow regulation involved with O2 supply, NO scavenging, and plasma viscosity. Because of this, the models are generally used to ascertain the potential effects of varying important parameters. The model we employ here can also be used to interpret in vivo data; by manipulating parameters to mimic experimental data, information can be gained on the relevant physiological phenomenon.
The in vivo study that best explores the differences in microvascular O2 delivery by two of the HBOCs studied was performed by Tsai et al. in the hamster skin-fold model (Tsai et al., 2003b) using phosphorescence quenching microscopy to take intravascular pO2 measurements in the arteries, in the arterioles, and in the post-capillary veins - thus describing O2 transport over the arterioles and the capillaries. Recently, the validity of this method has been questioned because of extraluminal O2 consumption by the technique (Golub et al., 2008). This critique is valid for tissue and slow-moving fluid that reside in an O2 depletion region for a long time. In arteriolar-sized vessels, the blood inside vessels flows fast enough that this has minimal effect.
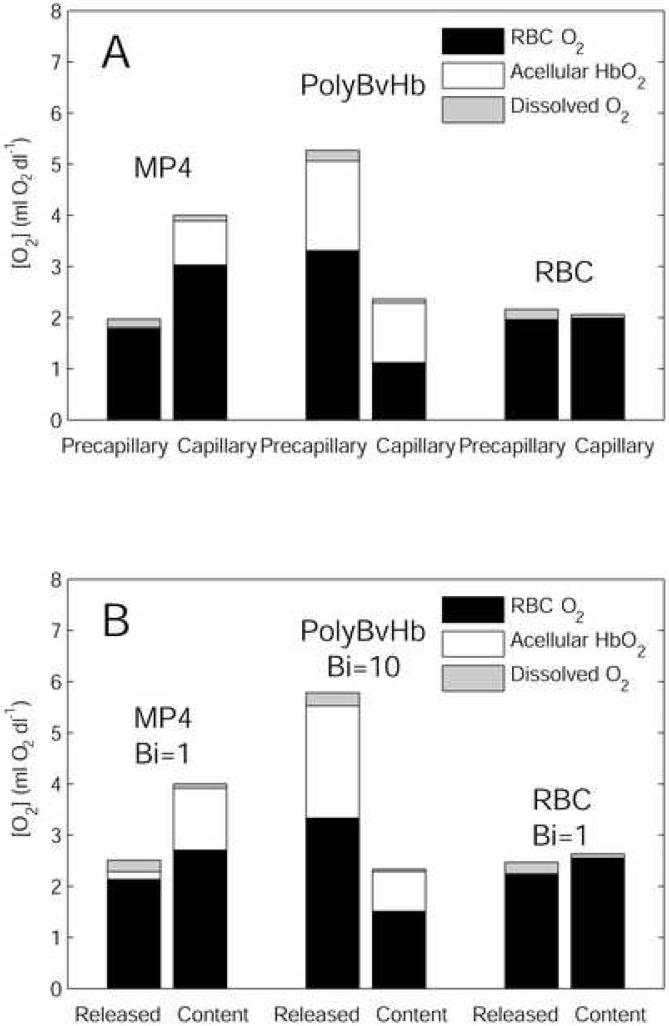
Figure 9A shows experimental data reproduced from the exchange experiments of Tsai (Tsai et al., 2003b). The precapillary delivery was defined as the difference between the arterial and arteriolar O2 content, and the capillary delivery as the difference between arteriolar and venular O2 content. The major finding of that study was the excessive offloading of O2 by PolyBvHb to the arterioles and the “targeting” of O2 transport by MP4 to the capillaries. MP4-treated animals were seen to deliver significantly less O2 (∼30% of total O2) in the precapillary arterioles and significantly more O2 in the capillaries (∼60% of total O2). PolyBvHb displayed the opposite of this trend, with 70% of O2 delivered in the arterioles. The end result was an almost 2-fold increase in capillary O2 delivery for MP4-treated animals as compared to PolyBvHb-treated ones, despite the lower initial O2 content. This study also showed low lactate levels in MP4 animals, indicating adequate tissue oxygenation with this HBOC.
Figure 9.
(A) Precapillary and capillary O2 delivery by RBC/HBOC mixtures in (Tsai et al., 2003a). (B) Cumulative O2 released by t = 1 second (“Released”) and remaining O2 content for 3.75 g/dl RBC 25% HBOC mixtures (“Content”). See text for details.
The simulations in Figure 7 show that, when flowing through identical domains (with identical boundary conditions), O2 transport by PolyBvHb is 30-50% greater than O2 transport from MP4 or RBCs-only, depending on the applied extraluminal resistance condition. This increase is a direct result of the higher p50 and [Hb] of PolyBvHb, indicating that much of the 250% increase in in vivo arteriolar O2 delivery by PolyBvHb in Figure 9A is a consequence of factors not taken into account by parallel comparisons of O2 transport under identical extraluminal conditions. These factors could include increased residence time because of induced microvascular flow regulation, induced changes in tissue pO2 due to differences in functional capillary density, and increased extraluminal O2 consumption, which would cause a decrease in extraluminal O2 transport resistance (i.e., increased Bi in the model). Alone, the observed in vivo O2 transport increase for PolyBvHb mixtures would require doubling the residence time compared to MP4. However, the microvascular measurements do not report statistically significant differences in blood flow velocity (Tsai et al., 2003b). The functional capillary density for MP4 mixtures was observed to be 80% greater than for PolyBvHb (Tsai et al., 2003b), indicating a substantial difference in the hemodynamics at some level, but the observed tissue pO2s are each very low, and the analysis of Golub et al. lead to the conclusion that these values may be questioned.
A large-scale decrease in extraluminal resistance could also cause the type of increase in O2 extraction seen for PolyBvHb (Tsai et al., 2003b). Figure 9B shows data from the simulations in Figure 7 at a residence time of 1 second. This residence time was chosen to give a similar amount of total O2 transferred as Figure 8A; it does not have any particular significance in the much more complex environment of the in vivo model. The “released” label in Figure 8B indicates the total O2 released in the arteriolar test segment, and “content” refers to the remaining O2 content of the HBOC/RBC mixtures after the given residence time. Because the remaining O2 is almost entirely extracted in the capillaries in vivo, the “content” measure is analogous to the capillary O2 delivery in Figure 8A. To fit the in vivo data, a lower extraluminal resistance boundary condition (Bi = 10) is required for PolyBvHb than for MP4 or RBCs-only (Bi = 1), suggesting increased extraluminal O2 consumption with PolyBvHb.
Adding more physiologically detailed boundary conditions to model the extraluminal environment may not produce the same effects as altering the extraluminal resistance. For example, we have simplified far-field tissue pO2 with p∞ = 0 mmHg, which is lower than the actual in vivo pO2 that dictates the O2 gradient. One might assume that p∞ would be higher for PolyBvHb versus MP4 due to the higher p50, giving decreased O2 delivery for PolyBvHb in relation to MP4, according to Eq. A9. Considerations of higher values for p∞ would lead to smaller differences in O2 delivery between MP4 and PolyBvHb than those displayed in Figure 7. A different consideration of boundary conditions that may allow them to be more physiologically relevant (but not account for the differences in O2 transport that we are seeking to explain) would be to apply pO2-dependent O2 consumption in the region surrounding the vessel. To apply this method, other investigators have modeled tissue O2 metabolism using Michaelis-Menton kinetics as given in Eq. 9 (Dimino and Palmer, 2007; Gundersen and Palmer, 2007; Patton and Palmer, 2006).
| (9) |
In this, Mt is the local rate of O2 consumption, Vmax is the maximal rate, and Km is the pO2 where Mt = 0.5Vm. Typically using this method, Km ∼1 mmHg (Patton and Palmer, 2006), so Eq. 9 gives constant Mt for p > 10 mmHg and decreases when [O2] becomes limiting at lower pO2. In the case of low-p50 MP4, in vivo data of Tsai (Tsai et al., 2003b) do not indicate that O2 supply is limited enough to depress Mt, and the measured arteriolar intravascular pO2 for MP4 (39 mmHg) is similar to that reported for blood (p ∼ 40 mmHg) (Vadapalli et al., 2000). Despite its higher p50, the intravascular pO2 for PolyBvHb is significantly lower (23 mmHg). Tsai also reported physiological indicators showing better tissue oxygenation for MP4 than PolyBvHb (Tsai et al., 2003b).
Conclusion
Early-generation blood substitutes were designed to mimic the O2 equilibrium binding properties of whole blood, with regard to p50 and Hb concentrations. The subsequent discovery that significant O2 gradients exist in the precapillary microcirculation (Popel et al., 1989) led to the understanding that the rates of O2 and HbO2 diffusion, as well as the radial distribution of Hb, are important factors to be considered. Due to its particulate nature, the physics of O2 transport from blood are complex; an acellular Hb solution does not exist that will match O2 transport for all potential boundary conditions (Cole et al., 2007). As a general rule, the p50 must be decreased and the molecular size increased, relative to native Hb, for an acellular Hb solution to provide similar O2 transport to RBCs (Cole et al., 2007). Of the HBOCs studied here, MP4 displays such properties and does not release excessive amounts of O2 in the arteriolar model.
We propose that HBOCs are most efficient when they deliver the bulk of their bound O2 to the capillaries and not the arterioles. Because vasoactive processes appear to increase upstream to O2 extraction, this is an especially prudent strategy. The cause of vasoactivity is under some debate (Palmer, 2006), but minimizing NO-scavenging by extravasated Hb and reducing excessive O2 by transport due to facilitated diffusion may both be achieved by increasing the molecular dimensions of the HBOC.
The in silico model we have used here is a simplified technique to study the direct O2 transport properties of HBOCs that have been developed. A more physiologically relevant situation would include a more specific treatment of extraluminal O2 consumption and diffusion processes. Additionally, the intraluminal fluid mechanics have been simplified to assume that steady-state RBC profiles are reached, and that any potential O2 transport enhancements due to RBC motions are negated by the resistance caused by the cell-depleted layer. In vivo, arteriolar segments are relatively short in length, potentially limiting the development of peripheral cell-depleted layers and enhancing the effects of micro-mixing caused by cell motion. Further studies of this phenomenon and incorporation of these data into a transport model are merited.
Acknowledgements
This work was supported in part by the National Institutes of Health Bioengineering Partnership Grant R24 64395 and NHLBI Grant R01 076163. R.C., K.V. and R.W. hold stock options in the company. R.W. is the President, CEO and Chairman of the Board of Sangart.
Appendix
Fluid mechanics
When an initially well-mixed RBC suspension flows through a tube, individual RBCs migrate away from the tube boundary towards the centerline, creating an inhomogeneous distribution of RBCs. Because viscosity is a function of the hematocrit, the viscosity is greatest at the center of the tube and least near the tube wall, leading to a blunted velocity profile. Steady-state velocity and hematocrit profiles are reached after a given amount of transit time inside a tube. Because the basic artificial capillary model is assumed to be long compared the tube diameter, it is assumed that steady-state conditions are obtained. It should be noted that the possibility does exist that, in vivo, steady-state profiles are not reached for a significant portion of an arteriole's length, leading to a smaller average thickness of the RBC depleted layer and greater lateral O2 transport.
We chose to describe the flow field by a two-phase model similar to that described by Sharan and Popel (Sharan and Popel, 2001). This model is a rough estimate of the flow profile of a RBC suspension through a small tube. All of the RBCs are assumed to be contained within a core region of radius λR, where R is the tube radius and 0 ≤ λ ≤ 1. A simple description of hematocrit profile, h(r), is used, with h(r) = hc, a constant value, within the core region (0 ≤ r ≤ λR) and h(r) = 0 in an RBC-depleted shell region (λR ≤ r ≤ R). The general form of the velocity profiles used in each region is given by Eq. A1 and Eq. A2.
| (A1) |
| (A2) |
The velocity fields used in previous models such as those by Nair (Nair et al., 1989) and Page (Page et al., 1998a) assumed a “slip” velocity between the RBCs and the extracellular fluid phase. This assumption was based on calculations by Simha on single spheres in a pressure-driven tube flow (Simha, 1936). More recently, velocity measurements performed in concentrated suspensions in channel flows have shown the velocity of particles and the fluid phase to be statistically indistinguishable (Lyon and Leal, 1998); hence we have neglected particle slip in our velocity profile. The inhomogeneous hematocrit profile coupled with the velocity profile causes a greater average velocity for RBCs compared to the extracellular fluid.
The values for umax, upl, and B are functions of the core viscosity (μc), plasma viscosity (μo), average flow speed (uavg), and λ (which is itself a function of hematocrit). The parameter B is the bluntness of the velocity profile and gives the deviation of the velocity profile from parabolic flow. The values for λ are taken from direct experimental measurements 25-μm diameter tubes by Tateishi (Tateishi et al., 2001). Because only values for 20%, 30%, and 40% hematocrits are available, the values for 11%, 22%, and 45% hematocrit (e.g. 3.75, 7.5, 15 g/dl) are extrapolated linearly from the two nearest data points. (The value used for 11% has the greatest degree of uncertainty, because of its distance from the nearest data point.) Velocity magnitudes in each region use the general form from the two-phase flow model of Sharan (Sharan and Popel, 2001). The values for umax, upl, and B have been defined previously (Sharan and Popel, 2001), and are given in Eq. A3, Eq. A4, and Eq. A5, below.
| (A3) |
| (A4) |
| (A5) |
We have estimated core viscosity values (μc) based on the work of Pries (Pries et al., 1992), and assumed an extracellular viscosity μ0 = 1 cP. Although mixing HBOC with extracellular fluid changes the μo, we ignore any differences in velocity profile at a given hematocrit that may be caused by the addition of HBOCs.
Mathematical model
A coupled system of partial differential equations can be used to predict O2 transport from RBC/HBOC mixtures flowing through thin gas-permeable tubes. The modeling of the fluid mechanics and chemical kinetics of discrete RBCs is a large computational problem, yet the physics allow various simplifying assumptions to be made to reduce the governing equations to a more tractable form. The RBC-depleted layer formed near a tube wall due to shear-induced migration of RBCs creates a significant barrier to lateral O2 transport. This effect is large enough that the RBC-rich core region may be approximated by a continuum with the same volume-averaged properties (Nair et al., 1989). Furthermore, it is necessary only to consider the convection of fluid down the axis of the tube and the lateral diffusion of acellular Hb and dissolved O2. This general method was first proposed by Nair (Nair et al., 1989) for RBC suspensions and then extended to RBC/acellular Hb mixtures by Page (Page et al., 1998a). Each of these models has been validated in 27-μm artificial capillary experiments (Nair et al., 1989; Page et al., 1998b).
The set of equations we employ here is a modified version of those developed by Page (Page et al., 1998b) to describe O2 transport by RBC/acellular Hb mixtures. The compartmentalization of dissolved O2 inside and outside of the RBC phase used by Nair (Nair et al., 1989) is eliminated. Because <5% of the total O2 transport resistance is located near the RBCs, one equation is used to describe the convection and diffusion of both intra- and extracellular dissolved O2. This requires the use of average quantities for α and DO2, which actually vary slightly inside and outside of the RBCs, an approximation that has been used elsewhere (Hellums et al., 1996). The thickness of the cell-depleted layer is taken directly from experimental observation instead of calculated from a set of algebraic equations that involve a number of hydrodynamic assumptions. We validated and explained these approximations for RBC suspensions in our previous work (Cole et al., 2007).
Axial (z-direction) convection and radial (r-direction) diffusion of dissolved O2 is described by Eq. A6.
| (A6) |
Dissolved O2 is allowed to diffuse freely through the RBC phase. The convection, diffusion, and O2 release by cell-free Hb are described by Eq. A7. [Hb]EC is the [Hb] in the extracellular compartment. Both Eq. A6 and Eq. A7 are valid across the entire tube radius. However, the O2 diffusion described in Eq. A6 is valid both inside and outside the RBCs, while the HbO2 diffusion described in Eq. A7 is only valid in the extracellular space.
| (A7) |
Equation A8 gives the convection and O2 release by RBCs flowing in the cell-rich core. Equation A8 does not apply for λR ≤ r ≤ R, and it can be seen in Eq. A6 and Eq. A7 that the influence of RBCs disappears in the outer region. The intracellular RBC Hb concentration, [Hb]RBC, is taken to be 21.4 mM (heme concentration) (Weibel, 1984).
| (A8) |
This model assumes a homogeneous distribution of Hb in the extracellular space. However, flowing Hb molecules tend to migrate away from tube walls by a mechanism similar to that which causes the inhomogeneous RBC profile. For instance, see Ma and Graham for an example of the migration of small polymeric molecules away from solid boundaries (Ma and Graham, 2005). Because the magnitude of particle migration mechanisms, such as those described by Leighton and Acrivos (Leighton and Acrivos, 1987), are proportionate to the square of the particle (or molecular) dimension, a potential acellular Hb depletion layer is likely small compared to the dimensions of the channel. This effect could, theoretically, provide a certain degree of physical exclusion of the HBOC within several molecular radii of a tube or vessel wall. Possible additional effects due to repulsive forces from PEG conjugated to Hb on MP4 (Svergun et al., 2008) cannot be evaluated at this point and are not considered here.
In spirit, the model presented is the same as that proposed by Page (Page et al., 1998a) in that it contains the following features: 1) a two-phase blunted flow profile; 2) a hematocrit profile that depends on the total suspension hematocrit and disappears at the tube wall; 3) volumetric displacement of the extracellular phase; 4) diffusion of HbO2 in the extracellular space.
It should be noted that the model described by Eq. A6-A8 can predict the results of artificial capillary-type experiments with RBC/HBOC mixtures. These steady-state results can be expressed as average values of p or Y as a function of the location z along a given vessel. Because the axial variations in Eq. A6-A8 are proportional to the ratio of flow speed to longitudinal position, the values of p or Y calculated at a given z and average flow speed will be the same as those calculated at a position 2z if the flow speed is doubled. For this reason, the simulation results are plotted versus the apparent residence time t=z/uavg, which is a normalized representation of z. The use of t does not indicate any transient kinetics not described in the model.
Boundary conditions
The solution of Eq. A6-A8 requires entry conditions for p, YEC, and YRBC to be stated, as well as two radial boundary conditions for both p and YEC. At the entry, p is set to 100 mmHg (average p in the lungs), while YEC, and YRBC are set to the appropriate saturation values for p = 100 mmHg, according to the Hill equation. An assumption of axial symmetry allows the radial partial derivatives of p and YEC to be set to zero at the centerline of the domain. The impermeability of the domain wall to the diffusion of Hb requires that the radial derivative of YEC also be zero at r=R. A boundary condition of the form of Eq. A9 dictates the rate at which O2 is transported from the intra- to the extraluminal environment, where pw is the pO2 at the wall, and p∞ is the far-field tissue pO2 assumed to be 0 mmHg.
| (A9) |
The dimensionless parameter Bi, the mass transfer Biot number, is a generalized method to estimate the ratio of intraluminal to extraluminal O2 transport resistances. This is the same boundary condition that occurs as a result of artificial capillary experiments, such as those by Page (Page et al., 1998b). Typical Bi values from previous experiments (Boland et al., 1987; Lemon et al., 1987; Page et al., 1998b) are ∼100, so the extraluminal transport in those cases is essentially negligible.
An estimate of Bi can be made from in vivo experimental data tabulated by Vadapalli (Vadapalli et al., 2000). Following from Fick's law, DO2∂(αp)/∂r=−Jw (Jw = O2 flux through vessel wall), Bi can be approximated as JwR/(αΔpDO2). Because the difference between the p at the wall and the far field are not available, pi, the intravascular p, was be used. From 24 arteriolar studies listed (Vadapalli et al., 2000) with mean diameter 40 μm and range 17-70 μm, an average Bi = 3.2±2.8 was calculated. Given the spread in Bi and our rough estimate that Δp should be less than pi by a factor of 2 or 3 [based on arteriolar wall gradients of 10-20 mmHg (Tsai et al., 2003a)], studying a range of Bi was warranted to describe potential phenomenon. In our previous work (Cole et al., 2007), we performed deoxygenation simulations on 15 g/dl RBC suspensions for Bi = 1 and Bi = 10, and noted that the O2 fluxes provided by each bounded the average Jw (Vadapalli et al., 2000) from similar sized microvessels. In the same studies, we found that increasing Bi to 100 provided a small (10%) increase in O2 transport, and that decreasing Bi to 0.1 gave O2 transport that was essentially negligible. Here we used Bi = 1 and 10, with the implicit admission that in vivo conditions beyond this range are bound to exist.
The physiological relevance of using the simplified boundary condition given in Eq. A9 should not be overstated. Extraluminal processes are treated as pure diffusion, and Eq. A9 does not account for more complex processes such as O2 consumption. The different Bi values used are a qualitative acknowledgement that extraluminal processes will change as a function of geometry, tissue type or metabolic state, and such changes will affect intraluminal phenomena. For instance, if peripheral O2 demand is high, it should follow that the extraluminal resistance will be low, and that rates of O2 delivery will be more limited by the speed of intravascular O2 diffusion.
The choice of the far-field p∞ is another non-physiological simplification required for Eq. A9. The simulations shown here assume p∞ = 0 mmHg, and thus give the maximum rates of O2 transport, given the applied value of extraluminal resistance. For the assumption of a value for p∞ to not be required, a more comprehensive compartmental scheme that accounts for O2 accumulation in the tissues must be used.
Whether the simplified description of extraluminal processes and the presence of an infinite O2 sink accurately reflect in vivo processes is unclear.
Solution method
The system of coupled, nonlinear partial differential equations was solved with Comsol Multiphysics software (Comsol, Palo Alto, CA), a nonlinear, finite-element based solver that is commonly used for chemical/biological engineering applications. An automatic gridding function was used for the initial discretization of the domain, with subsequent grid resolutions applied manually in regions where high spatial resolution was necessary. This was particularly important near the radial boundary at the domain entry because of the occurrence of mass transfer boundary layer-type behavior. A typical grid using ∼5,000 elements caused the convergence of a Galerkin error monitor. Solutions were exported to Matlab (Mathworks, Natick, MA) for post-processing.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Boland EJ, Nair PK, Lemon DD, Olson JS, Hellums JD. An in-vitro capillary system for studies on microcirculatory oxygen transport. J Appl Physiol. 1987;62:791–797. doi: 10.1152/jappl.1987.62.2.791. [DOI] [PubMed] [Google Scholar]
- Budhiraja V, Hellums J. Effect of hemoglobin polymerization on oxygen transport in hemoglobin solutions. Microvasc Res. 2002;64:220–233. doi: 10.1006/mvre.2002.2418. [DOI] [PubMed] [Google Scholar]
- Cabrales P, Tsai AG. Plasma viscosity regulates systemic and microvascular perfusion during acute extreme anemic conditions. Am J Physiol Heart Circ Physiol. 2006;291:2445–2452. doi: 10.1152/ajpheart.00394.2006. [DOI] [PubMed] [Google Scholar]
- Cabrales P, Tsai AG, Intaglietta M. Nitric oxide regulation of microvascular oxygen exchange during hypoxia and hyperoxia. J Appl Physiol. 2006;100:1181–1187. doi: 10.1152/japplphysiol.01105.2005. [DOI] [PubMed] [Google Scholar]
- Christofordes C, Hedley-Whyte J. Effect of temperature and hemoglobin concentration on solubility of O2 in blood. J Appl Physiol. 1969;27:592–596. doi: 10.1152/jappl.1969.27.5.592. [DOI] [PubMed] [Google Scholar]
- Christofordes C, Laasberg L, Hedley-Whyte J. Effect of temperature and hemoglobin concentration on solubility of O2 in human plasma. J Appl Physiol. 1969;26:56–60. doi: 10.1152/jappl.1969.26.1.56. [DOI] [PubMed] [Google Scholar]
- Cole RH, Vandegriff KD, Szeri AJ, Savas O, Baker DA, Winslow RM. A quantitative framework for the design of acellular hemoglobins as blood substitutes: implications of dynamic flow conditions. Biophys Chem. 2007;128:63–74. doi: 10.1016/j.bpc.2007.03.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dimino ML, Palmer AF. Hemoglobin-based O2 carrier O2 affinity and capillary inlet pO2 are important factors that influence O2 transport in a capillary. Biotechnol Prog. 2007;23:921–931. doi: 10.1021/bp0700298. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Doherty DH, Doyle MP, Curry SR, Vali RJ, Fattor TJ, Olson JS, Lemon DD. Rate of reaction with nitric oxide determines the hypertensive effect of cell-free hemoglobin. Nature Biotech. 1998;16:672–676. doi: 10.1038/nbt0798-672. [DOI] [PubMed] [Google Scholar]
- Ellsworth ML, Popel AS, Pittman RN. Assesment and impact of heterogeneities of convective oxygen transport parameters in capillaries of striated muscle: experimental and theoretical. Microvasc Res. 1988;35:341–362. doi: 10.1016/0026-2862(88)90089-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gibson Q, Kreuzer F, Meda E, Roughton F. The kinetics of human haemoglobin in solution and in the red cell at 37 degrees C. J Physiol. 1955;129:65–89. doi: 10.1113/jphysiol.1955.sp005339. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Golub AS, Barker MC, Pittman RN. Microvascular oxygen tension in the rat mesentery. Am J Physiol Heart Circ Physiol. 2008;294:H21–H28. doi: 10.1152/ajpheart.00861.2007. [DOI] [PubMed] [Google Scholar]
- Gordon PA. Characterizing isoparaffin transport properties with Stokes-Einstein relationships. Ind Eng Chem Res. 2003;42:7025–7036. [Google Scholar]
- Gundersen SI, Palmer AF. Conjugation of methoxypolyethylene glycol to the surface of bovine red blood cells. Biotechnol Bioeng. 2007;96:1199–1210. doi: 10.1002/bit.21204. [DOI] [PubMed] [Google Scholar]
- Hellums JD, Nair PK, Huang NS, Ohshima N. Simulation of intraluminal gas transport processes in the microcirculation. Ann Biomed Eng. 1996;24:1–24. doi: 10.1007/BF02770991. [DOI] [PubMed] [Google Scholar]
- Hill AV. The combinations of haemoglobin with oxygen and with carbon monoxide. I. Biochem J. 1913;7:471–480. doi: 10.1042/bj0070471. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Intaglietta M, Johnson PC, Winslow RM. Microvascular and tissue oxygen distribution: Cardiovasc Res. 1996;32:632–643. [PubMed] [Google Scholar]
- Kavdai M, Pittman RN, Popel AS. Theoretical analysis of effects of blood substitute affinity and cooperativity on organ oxygen transport. J Appl Physiol. 2002;93:2122–2128. doi: 10.1152/japplphysiol.00676.2002. [DOI] [PubMed] [Google Scholar]
- Kreuzer F. Facilitated diffusion of oxygen and its possible significance; a review. Respir Physiol. 1970;9:1–30. doi: 10.1016/0034-5687(70)90002-2. [DOI] [PubMed] [Google Scholar]
- Leighton D, Acrivos A. The shear-induced migration of particles in concentrated suspensions. J Fluid Mech. 1987;181:415–439. [Google Scholar]
- Lemon DD, Nair PK, Boland EJ, Olson JS, Hellums JD. Physiological factors affecting oxygen transport by hemoglobin in an in vitro capillary system. J Appl Physiol. 1987;62:798–806. doi: 10.1152/jappl.1987.62.2.798. [DOI] [PubMed] [Google Scholar]
- Lyon MK, Leal LG. An experimental study of the motion of concentrated suspensions in two dimensional channel flow. Part 1. Monodisperse systems. J Fluid Mech. 1998;363:25–56. [Google Scholar]
- Ma H, Graham MD. Theory of shear-induced migration in dilute polymer solutions near solid boundaries. Phys Fluid. 2005;17 Art No. 083103. [Google Scholar]
- McCarthy MK, Vandegriff KV, Winslow RM. The role of facilitated diffusion in oxygen transport by cell-free hemoglobins: Implications for the design of hemoglobin-based oxygen carriers. Biophys Chem. 2001;92:103–117. doi: 10.1016/s0301-4622(01)00194-6. [DOI] [PubMed] [Google Scholar]
- Moll W. The influence of hemoglobin diffusion on oxygen uptake and release by red cells. Respir Physiol. 1968;6:1–15. doi: 10.1016/0034-5687(68)90014-5. [DOI] [PubMed] [Google Scholar]
- Nair PK, Hellums JD, Olson JS. Prediction of oxygen transport rates in blood flowing in large capillaries. Microvasc Res. 1989;38:269–285. doi: 10.1016/0026-2862(89)90005-8. [DOI] [PubMed] [Google Scholar]
- Nolte D, Steinhauser P, Pickelmann S, Berger S, Hartl R, Messmer K. Effects of diaspirin-cross-linked hemoglobin (DCLHb) on local tissue oxygen tension in striated skin muscle: an efficacy study in the hamster. J Lab Clin Med. 1997;130:328–338. doi: 10.1016/s0022-2143(97)90028-7. [DOI] [PubMed] [Google Scholar]
- Olson JS, Foley EW, Rogge C, Tsai AL, Doyle MP, Lemon DD. NO scavenging and the hypertensive effect of hemoglobin-based blood substitutes. Free Rad Biol Med. 2004;36:685–697. doi: 10.1016/j.freeradbiomed.2003.11.030. [DOI] [PubMed] [Google Scholar]
- Page TC, Light WR, Hellums JD. Prediction of microcirculatory oxygen transport by erythrocyte/hemoglobin solution mixtures. Microvasc Res. 1998a;56:113–126. doi: 10.1006/mvre.1998.2088. [DOI] [PubMed] [Google Scholar]
- Page TC, Light WR, McKay CB, Hellums JD. Oxygen transport by erythrocyte/hemoglobin solution mixtures in an in vitro capillary as a model of hemoglobin-based oxygen carrier performance. Microvasc Res. 1998b;55:54–64. doi: 10.1006/mvre.1997.2055. [DOI] [PubMed] [Google Scholar]
- Palmer A. Molecular volume and HBOC-induced vasoconstriction. Blood. 2006;108:3231–3232. [Google Scholar]
- Patton JN, Palmer AF. Numerical simulation of oxygen delivery to muscle tissue in the presence of hemoglobin-based oxygen carriers. Biotechnol Prog. 2006;22:1025–1049. doi: 10.1021/bp060022a. [DOI] [PubMed] [Google Scholar]
- Popel AS, Pittman RN, Ellsworth ML. Rate of oxygen loss from arterioles is an order of magnitude higher than expected. Am J Physiol Heart Circ Physiol. 1989;256:H921–H924. doi: 10.1152/ajpheart.1989.256.3.H921. [DOI] [PubMed] [Google Scholar]
- Pries AR, Niehaus D, Gaehtgens P. Blood viscosity in tube flow: dependence on diameter and hematocrit. Am J Physiol. 1992;363:H1770–H1778. doi: 10.1152/ajpheart.1992.263.6.H1770. [DOI] [PubMed] [Google Scholar]
- Rohlfs RJ, Bruner E, Chiu A, Gonzales A, Gonzales M, Magde D, Magde MD, Vandegriff KD, Winslow RM. Arterial blood pressure responses to cell-free hemoglobin solutions and the reaction with nitric oxide. J Biol Chem. 1998;273:12128–12134. doi: 10.1074/jbc.273.20.12128. [DOI] [PubMed] [Google Scholar]
- Rosner D. Transport processes in chemically reacting flow systems. Dover; New York: 1986. [Google Scholar]
- Scholander PF. Oxygen transport through hemoglobin solutions. Science. 1960;131:585–590. doi: 10.1126/science.131.3400.585. [DOI] [PubMed] [Google Scholar]
- Sharan M, Popel AS. Compartmental model for oxygen transport in brain microcirculation in the presence of blood substitutes. J Theor Biol. 2002;215:1–22. doi: 10.1006/jtbi.2002.3001. [DOI] [PubMed] [Google Scholar]
- Sharan M, Popel AS. A two-phase model for flow of blood in narrow tubes with increased effective. 2001. [PubMed]
- Simha R. Analysis on the viscosity of suspension and solutions7: the viscosity of balls suspension (suspension in Poiseulle's basic flow) Kolloid Z. 1936;76:16–19. [Google Scholar]
- Spaan JA, Kreuzer F, vanWely FK. Diffusion coefficients of oxygen and hemoglobin as obtained simultaneously from photometric determinations of the oxygenation of layers of hemoglobin solutions. Pflug Arch. 1980;384:241–251. doi: 10.1007/BF00584558. [DOI] [PubMed] [Google Scholar]
- Stein JC, Ellsworth ML. Microvascular oxygen transport: impact of a left-shifted dissociation curve. Am J Physiol Heart Circ Physiol. 1992;262:H517–H522. doi: 10.1152/ajpheart.1992.262.2.H517. [DOI] [PubMed] [Google Scholar]
- Sullivan JP, Gordon JE, Palmer AF. Simulation of oxygen carrier mediated oxygen transport to C3A hepatoma cells housed within a hollow fiber bioreactor. Biotechnol Bioeng. 2006;93:306–317. doi: 10.1002/bit.20673. [DOI] [PubMed] [Google Scholar]
- Sullivan JP, Palmer AF. Targeted oxygen delivery within hepatic hollow fiber bioreactors via supplementation of hemoglobin-based oxygen carriers. Biotechnol Prog. 2006;22:1374–1387. doi: 10.1021/bp0600684. [DOI] [PubMed] [Google Scholar]
- Svergun DI, Ekström F, Vandegriff KD, Malavalli A, Baker DA, Nilsson C, Winslow RM. Solution structure of poly(ethylene) glycol-conjugated hemoglobin revealed by small-angle X-ray scattering: implications for a new oxygen therapeutic. Biophys J. 2008;94:173–181. doi: 10.1529/biophysj.107.114314. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tateishi N, Suzuki Y, Cicha I, Maeda N. O2 release from erthrocytes flowing in a narrow O2-permeable tube: effects of erythrocyte aggregation. Am J Physiol. 2001;281:H448–H456. doi: 10.1152/ajpheart.2001.281.1.H448. [DOI] [PubMed] [Google Scholar]
- Tsai AG, Johnson PC, Intaglietta M. Oxygen gradients in the microcirculation. Physiol Rev. 2003a;83:933–963. doi: 10.1152/physrev.00034.2002. [DOI] [PubMed] [Google Scholar]
- Tsai AG, Vandegriff KD, Intaglietta M, Winslow RM. Targeted O2 delivery by low-P50 hemoglobin: a new basis for O2 therapeutics. Am J Physiol. 2003b;285:H1411–H1419. doi: 10.1152/ajpheart.00307.2003. [DOI] [PubMed] [Google Scholar]
- Tsoukias NM, Goldman D, Vadapalli A, Pittman RN, Popel AS. A computational model of oxygen delivery by hemoglobin-based oxygen carriers in three-dimensional microvascular networks. J Theor Biol. 2007;248:657–674. doi: 10.1016/j.jtbi.2007.06.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vadapalli A, Goldman D, Popel A. Calculations of oxygen transport by red blood cells and hemoglobin solutions in capillaries. Art Cells Blood Subs Immobil Biotech. 2002;30:157–188. doi: 10.1081/bio-120004338. [DOI] [PubMed] [Google Scholar]
- Vadapalli A, Pittman RN, Popel AS. Estimating oxygen transport resistance of the microvascular wall. Am J Physiol Heart Circ Physiol. 2000;279:H657–H671. doi: 10.1152/ajpheart.2000.279.2.H657. [DOI] [PubMed] [Google Scholar]
- Vandegriff KD, Bellelli A, Samaja M, Malavalli A, Brunori M, Winslow RM. Kinetics of NO and O2 binding to a maleimide poly(ethylene glycol)-conjugated human haemoglobin. Biochem J. 2004;382:183–189. doi: 10.1042/BJ20040156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vandegriff KD, Le Tellier YC, Winslow RM, Rohlfs RJ, Olson JS. Determination of the rate and equilibrium constants for oxygen and carbon monoxide binding to R-state human hemoglobin cross-linked between the α subunits at lysine 99. J Biol Chem. 1991;266:17049–17059. [PubMed] [Google Scholar]
- Vandegriff KD, Malavalli A, Wooldridge J, Lohman J, Winslow RM. MP4, a new nonvasoactive PEG-Hb conjugate. Transfusion. 2003;43:509–516. doi: 10.1046/j.1537-2995.2003.00341.x. [DOI] [PubMed] [Google Scholar]
- Weibel ER. Structure and function in the mammalian respiratory system. Harvard University Press; Cambridge: 1984. The pathway for oxygen. [Google Scholar]
- Winslow RM. Red cell substitutes. Semin Hematol. 2007;44:51–59. doi: 10.1053/j.seminhematol.2006.09.013. [DOI] [PubMed] [Google Scholar]
- Winslow RM, Gonzales A, Gonzales ML, Magde M, McCarthy M, Rohlfs RJ, Vandegriff K. Vascular resistance and the efficacy of red cell substitutes in a rat hemorrhage model. J Appl Physiol. 1998;85:993–1003. doi: 10.1152/jappl.1998.85.3.993. [DOI] [PubMed] [Google Scholar]
- Winslow R. αα-Crosslinked hemoglobin: was failure predicted by preclinical testing? Vox Sang. 2000;79:1–20. doi: 10.1159/000031200. [DOI] [PubMed] [Google Scholar]
- Wyman J. Facilitated diffusion and the possible role of myoglobin as a transport mechanism. J Biol Chem. 1966;241:115–121. [PubMed] [Google Scholar]