Abstract
A number of human brain diseases have been associated with disturbances in the structure and function of cortical synapses. Answering fundamental questions about the synaptic machinery in these disease states requires the ability to image and quantify small synaptic structures in tissue sections and to evaluate protein levels at these major sites of function. We developed a new automated segmentation imaging method specifically to answer such fundamental questions. The method takes advantage of advances in spinning disk confocal microscopy, and combines information from multiple iterations of a fluorescence intensity/morphological segmentation protocol to construct three-dimensional object masks of immunoreactive (IR) puncta. This new methodology is unique in that high- and low-fluorescing IR puncta are equally masked, allowing for quantification of the number of fluorescently-labeled puncta in tissue sections. In addition, the shape of the final object masks highly represents their corresponding original data. Thus, the object masks can be used to extract information about the IR puncta (e.g., average fluorescence intensity of proteins of interest). Importantly, the segmentation method presented can be easily adapted for use with most existing microscopy analysis packages.
Keywords: Quantitative fluorescence microscopy, immunoreactive puncta, segmentation, synaptic structure, fluorescent immunohistochemistry
Introduction
A number of brain diseases, such as schizophrenia, Alzheimer disease, and Fragile X syndrome, appear to be primarily disorders of synaptic structures (Bear et al., 2004; Mirnics et al., 2001; Selkoe, 2002). In some cases, the abnormality is believed to involve an inability to form and/or maintain normal synaptic densities. Alternatively, aberrations may include reductions in protein levels that affect transmission at the synapse. The resulting changes in neurocytoarchitecture and/or protein levels can be subtle and restricted to the synapses formed by small subsets of neurons. The study of synaptic structures in situ has largely relied on immunohistochemistry to selectively label synaptic components in tissue sections. Markers of axon terminals and dendritic spines appear as immunoreactive (IR) puncta under the light microscope when using immunohistochemistry to visualize them, allowing ready quantification of structure number and density via the application of stereological techniques. To date, this approach has mostly been applied in single label experiments designed to quantify the density/number of IR puncta.
The emergence of the confocal laser scanning microscope (CLSM) has markedly enhanced the simultaneous visualization of multiple markers of synaptic structures by fluorescent immunohistochemistry. One advantage of assessing multiple markers simultaneously is that the frequency with which different antigens colocalize can be determined. Moreover, use of fluorescence allows for the determination of relative antigen concentration within identified structures. Although the CLSM is an excellent research tool for determining the densities of IR puncta that mark synaptic components, it is not necessarily the best tool for quantifying the labeled antigen via measurement of fluorescence intensity for several reasons. For example, the pinhole used in the CLSM, which is responsible for the improved resolution, rejects 100 times more out-of-focus light, some of which originates from the IR puncta of interest, than the conventional fluorescence microscope does (Murray et al., 2007; Sandison and Webb, 1994; Shaw, 2006). Although it is ideal to use wide-field fluorescence microscopy for quantitative fluorescence measurements (Murray et al., 2007; Swedlow et al., 2002), wide-field fluorescence microscopy is not suitable for imaging tissue sections because too much out-of-focus blur is detected. Falling between CLSM and conventional microscopes, spinning disk confocal microscopes collect 10 times more out-of-focus information than CLSM (Sandison and Webb, 1994). When combined with deconvolution algorithms, which provide excellent resolution enhancement for imaging puncta (Benveniste et al., 1989; Hiraoka et al., 1990), spinning disk confocal microscopes are exceptional tools for both quantifying numbers of multiple synaptic components and estimating protein levels in synaptic structures in tissue sections. In addition, the CCD cameras used for image detection in spinning disk confocal microscopes have higher quantum efficiencies (often exceeding 90%) than the relatively low quantum efficiency of photomultiplier tubes (~25%) used as detectors on most CLSM (Murray et al., 2007; Sandison and Webb, 1994; Shaw, 2006; Wang et al., 2005). Furthermore, the process of collecting 3D image stacks with a spinning disk confocal is substantially faster than collection using a CLSM. The increased speed decreases the amount of photobleaching that occurs above and below the focal plane, an effect that is magnified in the sampling of thick tissue sections because large numbers of focal planes are imaged. In addition, increases in speed also facilitate the collection of large data sets required for most stereology sampling schemes.
When using fluorescence immunohistochemistry to determine IR puncta density in tissue sections, two-dimensional (2D) microscopy images are collected at several serial z positions and collated into 3D data sets. Then IR puncta are generally identified using threshold-based segmentation. In this process, pixels are selected according to their brightness by applying lower/upper threshold values. The IR puncta are then counted manually, or with semi-automated or automated segmentation software. In the semi- and automated counting approaches the threshold values of the resulting histogram are masked to create a binary color image of the pixels of interest. All three counting approaches usually use a single threshold for image segmentation that is either visually adjusted or determined by a thresholding algorithm.
The use of a single threshold to select objects of interest works extremely well for images with high signal-to-noise ratios, objects with relatively uniform fluorescence, and/or highly fluorescing objects. However, these scenarios are not usually present when using fluorescence immunohistochemistry to probe brain tissue sections, particularly when they are derived from postmortem human subjects. For example, human postmortem brain tissue has high levels of autofluorescence resulting in a decrease in the signal-to-noise ratio. In addition, proteins differ in their distribution within axon terminals and dendritic spines, creating potential for differences in detectability of these structures across markers. Furthermore, the levels of proteins in these structures can vary drastically during development and as a result of disease states, substantially reducing uniformity or decreasing overall protein levels. Therefore, a single threshold level may be insufficient to mask all the axon terminals or dendritic spines of interest. We present here a methodology that circumvents these limitations.
Results
Segmentation of immunoreactive puncta
The process of segmentation is routinely used to identify and quantify objects of interest in both 2D and 3D data sets. Typically, the segmentation of 3D data sets involves the selection of voxels (the smallest resolution unit in the image) according to their brightness by applying lower/upper threshold values. The threshold values of the resulting histogram are masked to create a binary color image of the voxels of interest. However, this approach fails when target structures have widely varying fluorescence intensities and low signal-to-noise ratios, such as those typically found in postmortem brain tissue. We present here a methodology that uses recurrent segmentations to circumvent these limitations.
Fluorescent microspheres (0.17 μm in diameter; ~ 0.02 μm3) of varying intensity were mixed with mounting medium, placed on a slide, and coverslipped. 3D data sets consisting of sequential images taken 0.1 μm apart were then collected. Prior to segmentation, a flat field processing step was performed to control for differences in illumination over the field of view. The data set was then deconvolved with a constrained iterative algorithm using a calculated point-spread function (PSF, which describes the response of an imaging system to a point source), a maximum of 20 iterations, and 3D frequency filtering. An image projection of the deconvolved data set, which consists of 11 z-planes, is shown in Fig 1A1. The same image in Fig 1A1 is displayed using different intensity levels in Fig 1A2 so that all the microspheres in the image stack can be easily discerned. Deconvolution was followed by background subtraction to establish the low value of the final histogram. The histogram was then renormalized so that the upper limit was set at the intensity of the hottest pixel in the data set. The final processed data set was threshold segmented, masked, and objects in the mask were selected by size using a range of 0.0125 to 0.04 μm3. We performed 20 iterations of this intensity segmentation/mask/morphological segmentation protocol using different low threshold settings that progressively migrated towards the high value, which remained fixed. Although a criterion in which the low threshold setting (xn; where n = the iteration number) per iteration (numbered 1-19) was x1 = y (the low value of the final histogram) + h / 20 (where h is the highest value on the final histogram); x2 = x1 + h / 20; x3 = x2 + h / 20; and so on, worked well, empirically determined criteria ascertained in tissue sections worked better. Specifically, using manual masking techniques we determined the basic fluorescence characteristics (i.e. maximum, minimum, and average fluorescence intensity) of a variety of IR puncta. The data showed that a disproportionate number of the IR puncta had mean intensity values within the lower third of the grey level range of the histogram when non-saturating imaging settings were used. These findings suggested that an iterative approach that used initially smaller changes between iteration in the low threshold value might be necessary to differentiate closely positioned puncta of relatively low mean fluorescence intensity. Thus, through a process of trial and error where the accuracy of different low threshold values to mask IR puncta was visually determined using three dimensionally reconstructed images the following criteria to calculate xn was established: x1 = y + (h / 20) * 0.5; x2 = y + (h / 20) * 0.66; x3 = y + (h / 20) * 0.75; x4 = x3 + (h / 20) * 0.5; x5 = x4 + (h / 20) * 0.75; x6 = x5 + (h / 20); which was similarly repeated to determine x7 through x19. To automate the process of inserting the value xn, the above calculations were performed in Microsoft Excel and automatically copied into the analyses software when needed. After the second iteration, the resulting mask objects were combined with those from the first cycle into a single mask such that completely overlapping objects were represented by one mask object. This new mask containing the combined mask objects was then combined with those selected in the third iteration. This process of combining mask objects into a single mask continued throughout all iterations. The final mask contained a relatively uniform set of object masks that approached the upper size limit of our selection criteria (average volume = 0.033 μm3; STDEV = 0.008; Fig 1A3).
Figure 1. Segmentation of IR puncta using repetitive intensity and morphological gating.

(A) 0.17 μm diameter fluorescently labeled microspheres of varying intensity were mounted on a slide for observation. (A1-A2) Two projection images of the same 11 z-planes (step size = 0.1 μm) from a deconvolved image stack are presented using different intensity values. (A3-A4) The data in A1 were segmented using a new iterative method (A3; see main text for protocol) or the automated Ridler-Calvard technique available in SlideBook 4.2 (A4). (B) Cryostat sections (40 μm) were labeled for synaptophysin. (B1) Projection image of a deconvoled image stack (11 z-planes taken 0.25 μm apart). The data were segmented using our segmentation methodology with a morphological range of 0.0125 to 0.1 μm3 (B2) or 0.0125 to 0.5 μm3 (B3), or using the Ridler-Calvard algorithm (B4). Grid size = 5 μm.
The threshold values are calculated in Microsoft Excel or a similar program (e.g., MATLAB), making it easy to perform uniform or non-uniform incremental division of the histogram and as much iteration as necessary to identify individual puncta or other objects of interest. For example, an approach that uses small uniform increments, similar to one previously described (Bergsman et al., 2006), could easily be implemented. However, when analyzing large data sets (i.e., those needed to perform unbiased stereological counting of IR puncta in tissue sections), use of the minimum number of iterations necessary to mask all objects of interest, which for our data sets was 20, substantially reduces the overall image processing time. Furthermore, the flexibility of our approach similarly allows for additional morphological selection criteria (e.g., after each time masks are combined).
Using the above methodology, microspheres with relative fluorescence mean intensity ranging from 0.03% to 100% were equally masked. In contrast, using currently available semi-automated (ImagePro 6.2, and ImageJ) and automated (SoftWoRx and SlideBook 4.2) software solutions, only microspheres with relative mean intensities from 3.0% to 100% were masked. In addition, our approach was found to correctly identify more than twice as many puncta as these other solutions. For example, our approach correctly found 2.06 times more microspheres than the automated Ridler-Calvard thresholding algorithm in SlideBook 4.2 (Fig 1A4). Furthermore, in contrast to the very uniform set of object masks made using our approach (see above), the masks made using the Ridler-Calvard algorithm were highly variable (average volume = 0.039 μm3; STDEV = 0.047). Importantly, using Automation Anywhere to automate keystrokes and Microsoft Excel for data input our methodology can be easily adapted to work with most software packages. We used SlideBook 4.2 because the morphological operations can be run using gating parameters based on 3D rather than 2D representations of structure. We found that by analyzing all pixels at or below the low threshold setting for each iteration and using size criteria based on μm3 (or voxels) the final 3D mask of a puncta has a three dimensional ovoid shape that better represents the “true” structure. Another advantage to analyzing puncta using 3D masks is that it allows for the quantification of IR puncta number using unbiased stereologic counting principles (Sterio, 1984). These advantages are not present when using methodologies that define segmented objects in μm2 (or pixels) (Bergsman et al., 2006).
To demonstrate the ability of our methodology to identify IR puncta in tissue sections from monkey prefrontal cortex (area 46), cryostat (40 μm) sections were labeled for a marker of presynaptic axon terminals, synaptophysin (SY) (Fig 1). 3D data sets consisting of sequential images taken 0.25 μm apart were collected and processed as described above, except that a 60X 1.42 N.A. oil immersion objective was used and Gaussian noise smoothing was performed during deconvolution. An image projection of 11 sequential deconvolved images is shown in Fig 1B1. The final processed data set was threshold segmented, masked, and objects in the mask were selected by size using a range of 0.0125 to 0.1 μm3 (Fig 1B2) or a range of 0.0125 to 0.5 μm3 (Fig 1B3) with the iterative methodology described above. For each size range, the final mask contained a relatively uniform set of object masks that approached the upper size limit of the selection criteria. Using the smaller size range 332 SY-IR puncta were identified per 1000 μm3, while 295 were identified in the same volume using the larger size range and only 166 were identified using the Ridler-Calvard algorithm (Fig 1B4). As demonstrated in Fig 1B, the segmentation masks made using the larger size range in general cover more of the IR puncta they represent than the segmentation masks made using the smaller size range. However, nearby mask objects may become overlapping during the process of combining masks, resulting in the detection of a smaller number of unique IR puncta by the software (compare panel B2 to B3 in Fig 1). Thus, for counting IR puncta one should use a size range that selects for mask objects that are in general much smaller than the corresponding object as done in Fig 1B2.
Colocalization of proteins in terminals
Here we illustrate the power of our methodology for identifying axon terminals containing two different proteins of interest. For these studies, we chose to study the distribution of GAD65 and GAD67 because it is believed that the major site of function for these proteins is the axon terminal and that they are expressed by all interneurons. However, they are expressed at different levels within some neurons (Esclapez et al., 1994; Feldblum et al., 1993; Feldblum et al., 1995; Stone et al., 1999).
Monkey PFC area 46 cryostat (40 μm) sections were labeled for GAD67 and GAD65 (green and red, respectively; Fig 2). 3D data sets consisting of sequential images taken 0.22 μm apart were collected. A projection image of 21 sequential images is shown in Fig 2A. Image stacks were post-processed as described above for the synaptophysin data. An image projection of a deconvolved data set, which consists of the same z-planes used to construct Fig 2A, is shown in Fig 2B. As described above, after deconvolution a background subtraction was performed and the histogram renormalized. The final processed data set was threshold segmented, masked, and objects in the mask were selected by size (range = 0.0125 to 0.1 μm3) using the iterative segmentation approach described above. As discussed above, using a larger size range resulted in the overlapping of mask objects during the process of combining masks (see white arrow in Fig 2c’). Thus, for counting structures a smaller size range works better. However, to quantify the colocalization of mask objects from different channels (different proteins in the same synaptic structure) it is desirable for mask objects to fully cover the fluorescence puncta they mark. In order to increase the size range, without decreasing the final number of masks, one can perform a final segmentation on the final mask using a watershed algorithm to demarcate objects that do not occupy the same space. However, watershed algorithms can result in over-segmentation (two object masks representing the same real object). Therefore, to confirm that the watershed algorithm is not resulting in over-segmentation one should also make a mask consisting of the smallest mask of each object over the 19 iterations to confirm that the number of identified objects is correct. For example, when a watershed algorithm was applied to the mask in Fig 1B3 the number of mask objects changed from 564 to 631, which is within reason considering that 633 IR puncta were counted using the range in Fig 1B2. Considering the above, for our colocalization study a final segmentation on the final mask using a watershed algorithm was used to demarcate objects that do not occupy the same space. Masks of each channel were then pseudo-colored corresponding to the original data, combined, and made into a projection image. The final masks are displayed either using the full spectrum of a 12bit histogram (Fig 2C and 2c’) or by setting the intensity for all pixels at 100% (Fig 2c”) so that regions of colocalization were easily discerned. Mask operations between channels were then used to identify colocalized GAD67 and GAD65 immunoreactivity. When a new mask is made of the overlapping regions (seen as yellow), size segmentation is performed to eliminate false positives (small yellow region in 2c’ and 2c” denoted by yellow arrow). Using this approach, we determined the proportion of GAD65 puncta that were also labeled for GAD67 in the monkey DLPFC. We found that 93% of the GAD65-IR puncta were also GAD67-IR (n > 40,000 puncta). A random analysis of the data suggested that the 7% of GAD65-IR puncta mask objects that did not colocalize with GAD67-IR puncta mask objects had correctly identified GAD65-IR puncta. Thus, future studies are needed to determine why a higher degree of colocalization was not found.
Figure 2. Colocalization of GAD65 and GAD67 puncta.
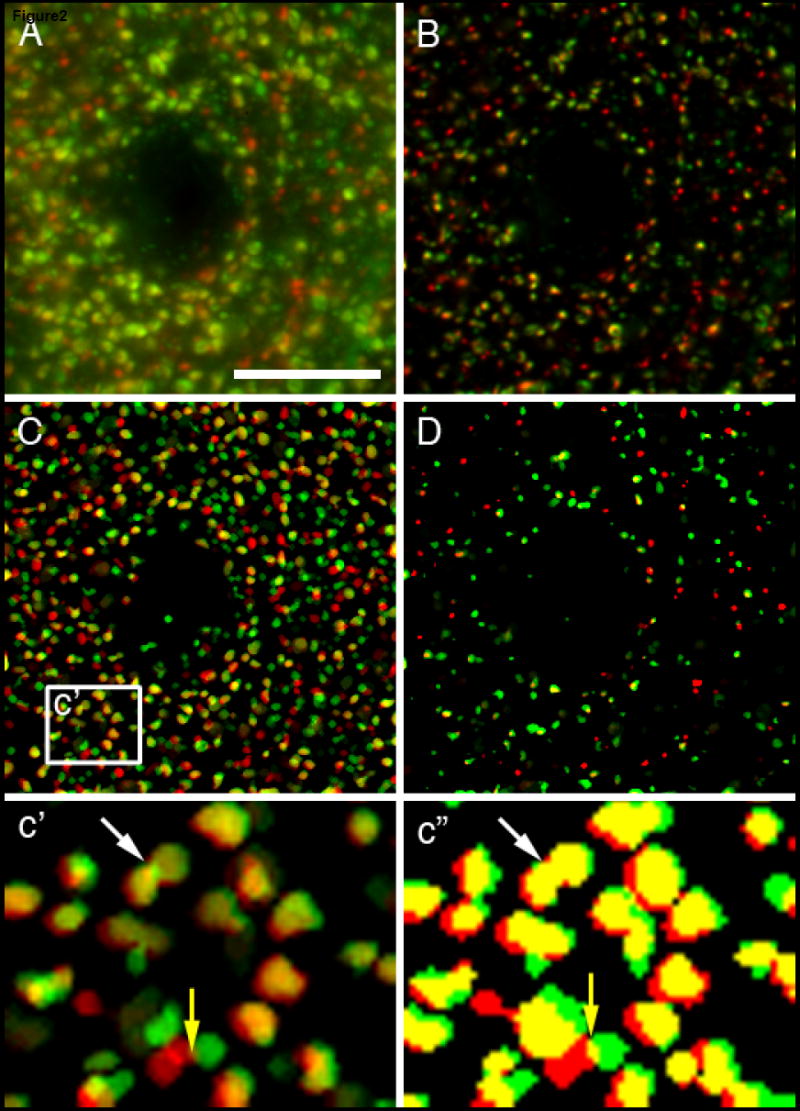
Cryostat sections (40 μm) were labeled for GAD65 (red) and GAD67 (green). (A-D) Projection images of 21 z-planes taken 0.22 μm apart. (A) Original data, (B) processed data, (C) color segmentation masks of B using our approach or (D) the automatic segmentation feature in SlideBook 4.2. (c’) A 4X magnification of the region designated in C. (c”) The data in c’ is presented with all pixel intensities set at 100%. Of the 23 puncta identified in the box in C, 19 were immunoreactive for both GAD65 and GAD67, 3 were immunoreactive for GAD65 only and 1 was immunoreactive for GAD67 only. Bar = 10 μm.
Quantitative analysis of protein levels in terminals
Using the above methodology we measured terminal protein levels of PV in the primate PFC during development. We chose to study the levels of this protein in tissue derived from neonatal (1.3 months) and adolescent (31 months) monkeys because terminal levels of PV have been hypothesized to increase over development (Erickson and Lewis, 2002). For this experiment, we compared the PV fluorescence intensity of puncta that were also immunoreactive for the GABA membrane transporter 1 (GAT1) between the two developmental time points. We included GAT1 in these studies for two reasons. First, the density of GAT1-IR puncta does not appear to change across development (Erickson and Lewis, 2002). Secondly, PV is expressed in axon terminals of a subset of inhibitory interneurons and of excitatory projections from the thalamus (Melchitzky et al., 1999). Thus, by only evaluating puncta that are both PV- and GAT1-IR we can focus our analyses on PV-IR terminals from cortical GABA neurons. In order to have an even more homogenous population of puncta, we chose to only analyze PV positive non-chandelier cell terminals because a previous study of PV-IR chandelier cartridges has shown that the time course of their postnatal development is quite different from that of PV-IR puncta outside of cartridges (CondÇ et al., 1996). For these experiments, we focused on terminals within cortical layers II-IV of the PFC. Tissue from two different monkeys was used for each time point and a total of 16 regions of interest (ROI) were imaged. Within each ROI an area of ~23,748 μm3 was analyzed. The Z axis of the area analyzed began 1 μm below the surface of the tissue that was closest to the objective lens and consisted of 33 z-planes spaced 0.22 μm apart. Mask objects were made for each GAT1-IR and PV-IR puncta using the approach described above. To separate PV-IR puncta that were not part of cartridges from those that were, we used a modification of our segmentation approach to build object masks of GAT1-IR cartridges that were used to eliminate chandelier axon cartridges from our analyses. Specifically, by changing the morphological selection criteria in our masking protocol such that very large masks were kept while smaller masks representing puncta were eliminated, we made object masks that were specific for cartridges (Fig 3B). This is possible since the terminals that are within cartridges reside extremely close to one another. Then, prior to final analyses mask operations were used to exclude any GAT1-PV-IR puncta that were contained in the GAT1-IR cartridge object masks. If it is desirable to extract information within the puncta that form cartridges, a multi-step process can be used to make object masks of these terminals. For example, 1) object masks of cartridges are made (Fig 3B); 2) data within cartridge masks is remasked using the approach described above (Fig 1); and 3) puncta within cartridges cannot always be separated from one another using a watershed algorithm. Thus, the object masks in step 2 are duplicated, and then eroded to a single point that designates the center of intensity of each object. The point masks are then used as “seeds” that are grown within the original object masks (step 2) such that they are as large as possible without touching another object (Fig 3C). In addition to excluding puncta within cartridges, any mask objects that touched an edge were removed prior to the use of mask operations designed to select the GAT1-IR puncta that were also PV-IR. This population of mask objects (GAT1-PV-IR) was used to determine the fluorescence intensities of PV and GAT1 (see below). No difference between the density of GAT1-IR puncta in neonatal (1257/8000 μm3) and adolescent (1271/8000 μm3) monkeys was detected. In contrast, there was a large difference between the densities of PV-IR puncta in neonatal (60/8000 μm3) versus adolescent (237/8000 μm3) monkeys.
Figure 3. Masking of PV-IR cartridges.
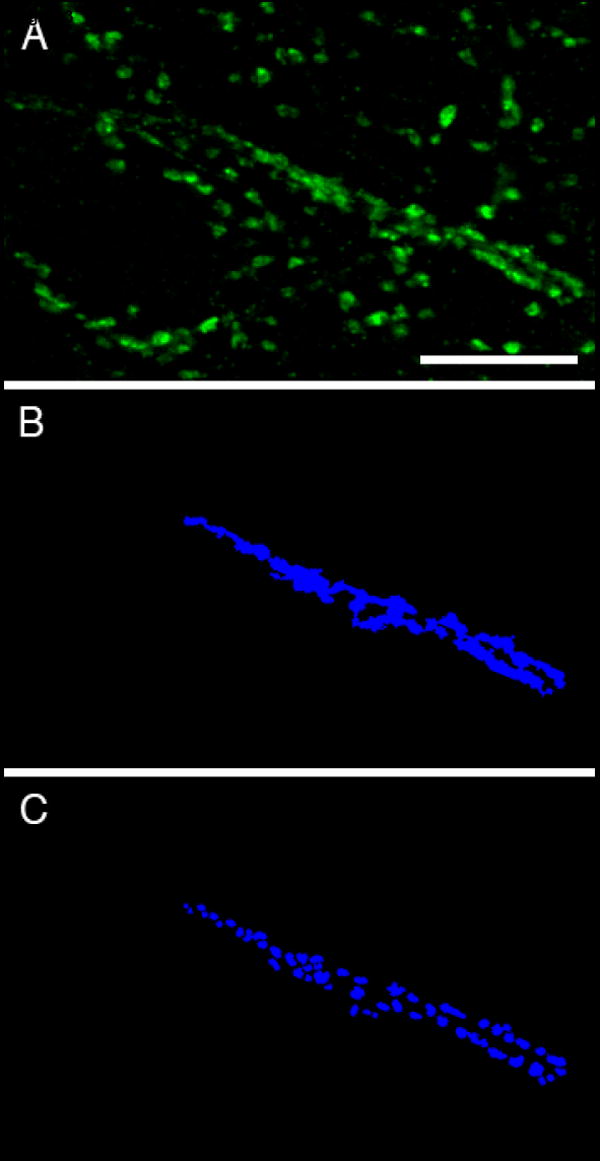
Cryostat sections (40 μm) were labeled for PV. (A) Projection image of deconvolved image stack (13 z-planes taken 0.22 μm apart). (B-C) The PV cartridge in A was masked using a modification of our segmentation approach designed to mask cartridges (B) and designed to mask puncta that make up cartridges (C). Bar = 10 μm.
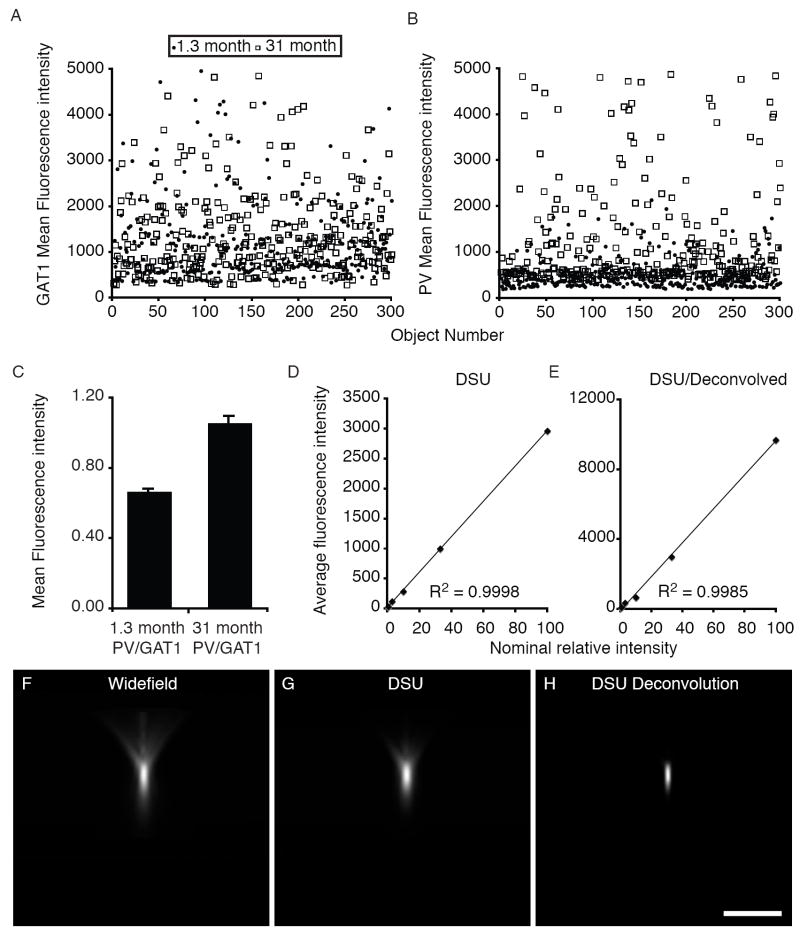
We next determined the average mean fluorescence intensity of PV in puncta that were GAT1-PV-IR using the GAT1 mask objects. The PV average mean fluorescence intensity per IR puncta was 1.73 times greater in adolescent (1394; SEM=18.9) than in neonatal (806; SEM=16.4) animals (Fig 4B). In order to directly compare the mean fluorescence per puncta between the two groups we created a relative intensity curve using fluorescent microspheres of known intensities that cover the dynamic range of our camera when imaged at a single exposure (Fig 4). Using the equation of the microspheres’ trend line (y = 0.0103X + 1.043), individual data points were transformed (Fig 4A-B). The transformed data show that on average there was 1.65 times more PV immunoreactivity in terminals of adolescent animals than neonatal ones. In addition, the average PV/GAT1 mean fluorescence intensity ratio in adolescent monkeys (PV/GAT1=0.94; SEM=0.02) was 1.54 times greater than that in neonatal animals (PV/GAT1=0.61; SEM=0.01; Fig 4C). There were no statistically significant differences in the average fluorescence intensity per z plane within subjects across the Z-axis, indicating that all quantification was from within a Z-axis depth penetrated by our primary and secondary antibodies. Thus, not only is there a large difference between neonatal and adolescent animals in the number of GAT1-IR puncta that are PV-IR, they also differ in average PV fluorescence intensities/puncta.
Figure 4. Analyses of fluorescence intensity changes in PV-IR puncta during development.
Cryostat sections (40 μm) containing the PFC from 1.3 and 31 month old monkeys were labeled for PV and GAT1. (A-B) The mean fluorescence intensities of 300 individual IR puncta that were randomly selected from our transformed data set are shown. (C) The PV/GAT1 mean fluorescence ratio for all puncta collected is shown. (D-E) Fluorescent microspheres of varying intensities were used to examine the linearity and dynamic range of our system. In order to directly compare the average fluorescence intensities of IR puncta from neonatal monkeys to adolescent ones the data were transformed using the equation for the line in E (y = 0.0103X + 1.043). Note that deconvolution of the raw DSU data leads to a substantial increase in the measured average fluorescence intensity (compare D to E). (F-H) A 0.5 μm diameter microsphere was imaged by widefield (F) or confocal (G) microscopy to demonstrate the differences in image blur between the two techniques. (H) The data in G were deconvolved and presented to demonstrate why the average fluorescence intensity increases as a result of deconvolution. Bar = 5 μm; see main text for statistics.
Importantly, the minimum PV intensity value found for puncta from neonatal monkeys was 402.85 (before background subtraction), which is nearly twice as high as the average background intensity (204.5). This value (after background subtraction) is nearly one-third the average terminal PV mean intensity in neonatal monkeys and one sixth that of adolescent monkeys. These findings suggest that sensitivity is not an issue. In support of this suggestion, using fluorescent microspheres of varying intensity placed throughout a section of monkey PFC tissue we empirically determined that the sensitivity of our approach in the Alexa 488 channel used for PV is such that an object with average fluorescence intensity 1.1 times greater than background can be masked. Importantly, this value was obtained while maintaining imaging settings that were non-saturating for the most intensely fluorescing microspheres, which we have found to have average fluorescence intensity values similar to the brightest puncta in our studies. Thus, our methodology has a high dynamic range that allows us to mask small objects that represent a wide range of average intensity values. For example, in the experiment in this section we masked puncta with mean fluorescence intensities (post deconvolution) that ranged from 267 to 10,323 in the same imaging field. These levels span the dynamic range of our camera (Fig 4E).
Discussion
We have presented a new segmentation methodology that can be performed using most image analysis software packages. This methodology, which can be automated, allows for the determination of the number of fluorescently-labeled puncta, the colocalization of different labels in the same small structure, and the quantification of fluorescence intensity in these structures in tissue sections.
Neurons are highly polarized cells with three different biochemically and functionally unique compartments: axon, soma, and dendrites. Immunohistochemistry can be used to separate these compartments using morphological criteria and markers against proteins that are specifically targeted to only one of these compartments. For the most part, the quantification of IR puncta in brain sections has been performed manually or with semi-automated, computer-assisted counting methods, which is tedious and time-consuming. In addition, these approaches to counting puncta depend on the microscopist’s identification of the structures of interest and thus are prone to methodological variability due to differences between microscopists, or between sessions conducted by the same microscopist. Furthermore, manual counting is also influenced by variability in the intensity of immunoreactivity of labeled structures. For example, the use of fixed camera and monitor settings during computer-assisted microscopy is comparable to the use of a single segmentation threshold, and will result in missed counts of faintly labeled structures and in failures to accurately resolve multiple, closely-spaced structures. Although it is possible to implement iterative counts at different imaging and display settings in manual counting, this approach substantially increases the work load and likely enhances measurement variability. Our methodology avoids these problems by probing the full intensity range using an automated iterative approach, which yields exactly the same results each time.
Fluorescence microscopy is a more powerful technique than other types of microscopy for studying synaptic structures because it provides both the ability to analyze the distribution of several proteins simultaneously and to quantify the amount of fluorescent label for each protein. In neuronal cultures, a variety of fluorescence based microscopy techniques have been employed to measure protein levels in synaptic structures (Glynn and McAllister, 2006; Sugiyama et al., 2005). However, the use of quantitative fluorescence microscopy to identify and measure protein levels in synaptic structures in brain sections has been hampered for several reasons. For example, the autofluorescence of brain tissue, particularly in primates, is high. In addition, the hundreds of thousands of fluorescently-labeled molecules of interest in a single section each create out-of-focus blur when illuminated. Combined, these characteristics lead to a less than desirable signal-to-noise ratio. Also, as the density of objects of interest increases it becomes more and more difficult to distinguish them, particularly along the z-axis because of the limited resolution of light microscopes. Furthermore, protein levels, particularly in synaptic structures can vary substantially depending on connectivity, developmental stage, and/or disease state. Combined, these inherent problems make it very difficult to create mask objects that accurately identify small structures (e.g., IR-puncta), which is essential for quantifying their fluorescence intensity. The methodology described here is able to mask IR puncta in order to extract information in samples with low signal-to-noise ratios and when there is non-uniformity of IR puncta fluorescence.
Here, we have demonstrated the utility of the presented methodology using image stacks collected on a spinning disk confocal. Although our methodology works equally well when trying to mask objects of a particular size in data sets collected on other instrumentation (e.g., CLSM), we chose spinning disk confocal microscopy over CLSM to quantitate the fluorescence levels of IR puncta in tissue sections for several reasons. For example, spinning disk confocals can capture full-frame images substantially faster than CLSMs, the CCD cameras they use can have significantly higher quantum efficiencies than the PMTs used on CLSMs, and they can capture 10X more of the photons entering objective than a CLSM. With that said, CLSM systems have the ability to capture higher resolution images with better signal-to-noise ratios than spinning disk confocals. To improve the resolution of images collected by spinning disk confocal microscopy, image stacks can be processed with deconvolution algorithms. The quality of the PSF is critical to the performance of a deconvolution algorithm. Although the described methodology is not necessarily dependent on issues related to deconvolution for puncta masking, the information contained within masks (i.e., voxel intensity) is highly dependent on post processing procedures. Thus, it is important to take precautions to avoid introducing artifacts and aberrations when using deconvolution algorithms. For example, tissue sections need to be thin enough so that the out-of-focus fluorescence (blur) is not too overwhelming and to limit the introduction of spherical aberration, which can be induced gradually as imaging depth increases. The sampling interval, particularly along the z-axis, should be at least twice the resolvable spatial frequency. The upper and lower z-axis boundaries, and the x-y boundaries of each image stack should extend beyond the boundaries of the region of interest. Furthermore, empirical PSFs should be generated at different z-depths even if theoretical ones are being used for image restoration so they can be compared. By taking these precautions along with others we were able to improve the final data to the extent that puncta with average fluorescence intensity 1.3 times greater than background were masked in our development study (Fig. 4). Although these findings suggest that our methodology is highly sensitive, it is plausible that we would have found a higher percentage of GAT1-IR puncta that were PV-IR in the neonatal if our sensitivity was improved. One way to improve sensitivity is to use lasers instead of a metal arc lamp as the excitation source. Lasers provide much more flexibility in power, which when adjusted properly can lead to fluorochromes being fully excited. In addition, background fluorescence is usually less when imaging with a laser because they use a single wavelength for excitation. In conclusion, as the sensitivity of imaging systems improves through the development of new hardware the methodology of masking IR puncta described here will become more powerful.
Experimental Procedure
Antibodies
The following primary antibodies were used in this study: mouse anti-GAD67 (1:1000; Millipore, Billerica, MA), rabbit anti-GAD65 (1:1000; Millipore), mouse anti-PV (1:2500; SWant, Bellinzona, Switzerland), rabbit anti-GAT1 (1:1000; Millipore), and mouse anti-synaptophysin (1:4000; Sigma-Aldrich, St. Louis, MO). All secondary antibodies conjugated to Alexa 405, 488, 568, or 647, and all fluorescent microspheres were from Invitrogen (Carlsbad, CA).
Tissue
All monkey tissue was obtained from 3-4 year old, male, long-tailed macaque monkeys (Macaca fascicularis) or 1.3 month and 31 month old, female, rhesus monkeys (Macaca mulatta) used in other studies (Cruz et al., 2003; Erickson and Lewis, 2002; Melchitzky et al., 1999). Monkeys were anesthetized with ketamine (20 mg/kg) and pentobarbital sodium (30 mg/kg), and then perfused transcardially with 1% paraformaldehyde in phosphate buffer (pH 7.4) at 4°C followed by 4% paraformaldehyde in phosphate buffer, as previously described (Oeth and Lewis, 1993). Brains were immediately removed and coronal blocks (5-6 mm-thick) were postfixed, then cryoprotected and stored as previously described (Oeth and Lewis, 1993). Importantly, immunoreactivity for a number of antigens is unaffected by the protocol used (Cruz et al., 2003). Sections (40 μm) were then cut along the rostral-caudal axis from coronal blocks containing DLPFC area 46 from the left hemisphere.
Tissue Processing
Sections were processed for fluorescence immunocytochemical labeling using procedures that permit labeling throughout the section’s z-axis with limited post-processing shrinkage in this axis (Konopaske et al., 2007; Zaitsev et al., 2005). For the PV expression development study tissue sections from both experimental groups were processed together to eliminate inter-experiment variability. Slides were always coded so that the microscopy and statistical analyses were performed blind to group assignment.
Microscopy
Images were collected on an Olympus (Center Valley, PA) BX51 upright or IX71 inverted microscope equipped with an Olympus DSU spinning disk confocal using a 60X 1.2 N.A. water immersion, a 60X 1.42 N.A. oil immersion objective, or a 60X 1.45 N.A. oil immersion objective. Both microscopes are equipped with Hamamatsu C4742-98 CCD cameras and high precision Prior Scientific motorized XY stages with linear z-encoders (Rockland, MA). The microscopes are controlled by SlideBook 4.2 (Intelligent Imaging Innovations, Inc., Denver, CO), which is the same software used for post-processing. As described in the text, Stereo Investigator software (MicroBrightField, Inc., Williston, VT) was used to determine sampling sites. The program Automation Anywhere (Tethys Solutions, Santa Clara, CA) was used to automate keystrokes in SlideBook during post-processing in order to accelerate the processing steps described in the text. In order to transform intensity data 2.5 μm InSpeck fluorescent microspheres (505ex/515em and 540ex/560em; Invitrogen) of varying relative intensities (100%, 30%, 10%, 3%, 1%, 0.3%) were used to make intensity calibration curves. The relationship between microsphere intensity and excitation exposure durations was linear, resulting in the following equations used to transform Alexa 488 and 568 intensity capture data, respectively: y = 0.0103X + 1.043; y = 0.0104X + 1.7576.
Acknowledgments
Supported by NIH grant MH051234 (DAL), MH071533 (RAS), and University of Pittsburgh CMRF award (KNF). The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institute Of Mental Health or the National Institutes of Health. We are extremely grateful to Mrs. Kelly Rogers and Heidi Scriven for technical assistance. We are also grateful to Olympus American and B&B Microscopes for their advice.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Bear MF, Huber KM, Warren ST. The mGluR theory of fragile X mental retardation. Trends Neurosci. 2004;27:370–7. doi: 10.1016/j.tins.2004.04.009. [DOI] [PubMed] [Google Scholar]
- Benveniste M, Schlessinger J, Kam Z. Characterization of internalization and endosome formation of epidermal growth factor in transfected NIH-3T3 cells by computerized image-intensified three-dimensional fluorescence microscopy. J Cell Biol. 1989;109:2105–15. doi: 10.1083/jcb.109.5.2105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bergsman JB, Krueger SR, Fitzsimonds RM. Automated criteria-based selection and analysis of fluorescent synaptic puncta. J Neurosci Methods. 2006;152:32–9. doi: 10.1016/j.jneumeth.2005.08.008. [DOI] [PubMed] [Google Scholar]
- CondÇ F, Lund JS, Lewis DA. The hierarchical development of monkey visual cortical regions as revealed by the maturation of parvalbumin-immunoreactive neurons. Developmental Brain Research. 1996;96:261–276. doi: 10.1016/0165-3806(96)00126-5. [DOI] [PubMed] [Google Scholar]
- Cruz DA, Eggan SM, Lewis DA. Postnatal development of pre- and post-synaptic GABA markers at chandelier cell inputs to pyramidal neurons in monkey prefrontal cortex. J Comp Neurol. 2003;465:385–400. doi: 10.1002/cne.10833. [DOI] [PubMed] [Google Scholar]
- Erickson SL, Lewis DA. Postnatal development of parvalbumin- and GABA transporter-immunoreactive axon terminals in monkey prefrontal cortex. J Comp Neurol. 2002;448:186–202. doi: 10.1002/cne.10249. [DOI] [PubMed] [Google Scholar]
- Esclapez M, Tillakaratne NJ, Kaufman DL, Tobin AJ, Houser CR. Comparative localization of two forms of glutamic acid decarboxylase and their mRNAs in rat brain supports the concept of functional differences between the forms. J Neurosci. 1994;14:1834–55. doi: 10.1523/JNEUROSCI.14-03-01834.1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feldblum S, Erlander MG, Tobin AJ. Different distributions of GAD65 and GAD67 mRNAs suggest that the two glutamate decarboxylases play distinctive functional roles. J Neurosci Res. 1993;34:689–706. doi: 10.1002/jnr.490340612. [DOI] [PubMed] [Google Scholar]
- Feldblum S, Dumoulin A, Anoal M, Sandillon F, Privat A. Comparative distribution of GAD65 and GAD67 mRNAs and proteins in the rat spinal cord supports a differential regulation of these two glutamate decarboxylases in vivo. J Neurosci Res. 1995;42:742–57. doi: 10.1002/jnr.490420603. [DOI] [PubMed] [Google Scholar]
- Glynn MW, McAllister AK. Immunocytochemistry and quantification of protein colocalization in cultured neurons. Nat Protoc. 2006;1:1287–96. doi: 10.1038/nprot.2006.220. [DOI] [PubMed] [Google Scholar]
- Hiraoka Y, Agard DA, Sedat JW. Temporal and spatial coordination of chromosome movement, spindle formation, and nuclear envelope breakdown during prometaphase in Drosophila melanogaster embryos. J Cell Biol. 1990;111:2815–28. doi: 10.1083/jcb.111.6.2815. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Konopaske GT, Dorph-Petersen KA, Sweet RA, Pierri JN, Zhang ZW, Sampson AR, Lewis DA. Effect of chronic antipsychotic exposure on astrocyte and oligodendrocyte numbers in macaque monkeys. Biological Psychiatry. 2007 doi: 10.1016/j.biopsych.2007.08.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Melchitzky DS, Sesack SR, Lewis DA. Parvalbumin-immunoreactive axon terminals in macaque monkey and human prefrontal cortex: Laminar, regional and target specificity of Type I and Type II synapses. The Journal of Comparative Neurology. 1999;408:11–22. [PubMed] [Google Scholar]
- Mirnics K, Middleton FA, Lewis DA, Levitt P. Analysis of complex brain disorders with gene expression microarrays: schizophrenia as a disease of the synapse. Trends Neurosci. 2001;24:479–86. doi: 10.1016/s0166-2236(00)01862-2. [DOI] [PubMed] [Google Scholar]
- Murray JM, Appleton PL, Swedlow JR, Waters JC. Evaluating performance in three-dimensional fluorescence microscopy. J Microsc. 2007;228:390–405. doi: 10.1111/j.1365-2818.2007.01861.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oeth KM, Lewis DA. Postnatal development of the cholecystokinin innervation of monkey prefrontal cortex. The Journal of Comparative Neurology. 1993;336:400–418. doi: 10.1002/cne.903360307. [DOI] [PubMed] [Google Scholar]
- Sandison DR, Webb WW. Background rejection and signal-to-noise optimization in confocal and alternative fluorescence microscopes. Applied Optics. 1994;33:603–615. doi: 10.1364/AO.33.000603. [DOI] [PubMed] [Google Scholar]
- Selkoe DJ. Alzheimer’s disease is a synaptic failure. Science. 2002;298:789–91. doi: 10.1126/science.1074069. [DOI] [PubMed] [Google Scholar]
- Shaw PJ. Comparison of widefield/deconvolution and confocal microscopy for three-dimensional imaging. In: Pawley JB, editor. Handbook of Biological Confocal Microscopy. Springer; New York: 2006. pp. 453–467. [Google Scholar]
- Sterio DC. The unbiased estimation of number and sizes of arbitrary particles using the disector. J Microsc. 1984;134:127–36. doi: 10.1111/j.1365-2818.1984.tb02501.x. [DOI] [PubMed] [Google Scholar]
- Stone DJ, Walsh J, Benes FM. Localization of cells preferentially expressing GAD(67) with negligible GAD(65) transcripts in the rat hippocampus. A double in situ hybridization study. Brain Res Mol Brain Res. 1999;71:201–209. doi: 10.1016/s0169-328x(99)00185-0. [DOI] [PubMed] [Google Scholar]
- Sugiyama Y, Kawabata I, Sobue K, Okabe S. Determination of absolute protein numbers in single synapses by a GFP-based calibration technique. Nat Methods. 2005;2:677–84. doi: 10.1038/nmeth783. [DOI] [PubMed] [Google Scholar]
- Swedlow JR, Hu K, Andrews PD, Roos DS, Murray JM. Measuring tubulin content in Toxoplasma gondii: a comparison of laser-scanning confocal and wide-field fluorescence microscopy. Proc Natl Acad Sci U S A. 2002;99:2014–9. doi: 10.1073/pnas.022554999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang E, Babbey CM, Dunn KW. Performance comparison between the high-speed Yokogawa spinning disc confocal system and single-point scanning confocal systems. J Microsc. 2005;218:148–59. doi: 10.1111/j.1365-2818.2005.01473.x. [DOI] [PubMed] [Google Scholar]
- Zaitsev AV, Gonzalez-Burgos G, Povysheva NV, Kroner S, Lewis DA, Krimer LS. Localization of calcium-binding proteins in physiologically and morphologically characterized interneurons of monkey dorsolateral prefrontal cortex. Cereb Cortex. 2005;15:1178–1186. doi: 10.1093/cercor/bhh218. [DOI] [PubMed] [Google Scholar]