Beyond statistical inference: A decision theory for science

Abstract

Traditional null hypothesis significance testing does not yield the probability of the null or its alternative and, therefore, cannot logically ground scientific decisions. The decision theory proposed here calculates the expected utility of an effect on the basis of (1) the probability of replicating it and (2) a utility function on its size. It takes significance tests—which place all value on the replicability of an effect and none on its magnitude—as a special case, one in which the cost of a false positive is revealed to be an order of magnitude greater than the value of a true positive. More realistic utility functions credit both replicability and effect size, integrating them for a single index of merit. The analysis incorporates opportunity cost and is consistent with alternate measures of effect size, such as r² and information transmission, and with Bayesian model selection criteria. An alternate formulation is functionally equivalent to the formal theory, transparent, and easy to compute.

Whatever their theoretical orientation, α = .05 is a number that all psychologists have in common. If the probability of their results under the null hypothesis (p) is greater than α, it will be difficult or impossible to publish the result; the author will be encouraged to replicate with a larger n or better control of nuisance variables. If p < α, the effect is called significant and clears a crucial hurdle for publication. How was this pivotal number .05 chosen? Is there a better one to use? What role does effect size play in this criterion?

Null Hypothesis Statistical Tests

The α = .05 yardstick of null hypothesis statistical tests (NHSTs) was based on a suggestion by Fisher and is typically implemented as the Neyman–Pearson criterion (NPc; see Gigerenzer, 1993, among many others). The NPc stipulates a criterion for the rejection of a null hypothesis that keeps the probability of incorrectly rejecting the null, a false positive or Type I error, no greater than α. To know whether this is a rational criterion requires an estimate of the expected costs and benefits it delivers. Table 1 shows the situation for binary decisions, such as publication of research findings, with errors and successes of commission in the top row and successes and errors of omission in the bottom row. To calculate the expected utility of actions on the basis of the NPc, assign costs and benefits to each cell and multiply these by the probability of the null and its alternative—here, assumed to be complementary. The sums across rows give the expected utilities of action appropriate to the alternative and to the null. It is rational to act when the former is greater than the latter and, otherwise, to refrain from action.

Table 1.

The Decision Matrix

	State of Nature
Decision	Null True (N)	Alternative True (A)
Act for the alternative (𝒜) Balk (ℬ); refrain from action	false positive; Type I error true negative	true positive false negative; Type II error

Alas, the NPc cannot be derived from such a canonical decision theory. There are two reasons for this.

1. NHST provides neither the probability of the alternative p(A) nor the probability of the null p(N): “Such a test of significance does not authorize us to make any statement about the hypothesis in question in terms of mathematical probability” (Fisher, 1959, p. 35). NHST gives the probability of a statistic x more extreme than the one obtained, D, under the assumption that the null is true, p(x ≥ D|N). A rational decision, however, requires the probability that the null is true in light of the statistic, p(N|D). Going from p(D|N) to p(N|D) is the inverse problem. The calculation of p(N|D) requires that we know the prior probability of the null, the prior probability of the statistic, and combine them according to Bayes's theorem. Those priors are difficult to estimate. Furthermore, many statisticians are loath to invoke Bayes for fear of rendering probabilities subjective, despite reassurances from Bayesians, M. D. Lee and Wagenmakers (2005) among the latest. The problem has roots in our use of an inferential calculus that is based on such parameters as the means of the hypothetical experimental and control populations, μ_E and μ_C, and their equality under the null (Geisser, 1992). To make probability statements about parameters requires a solution to the inverse problem. Fisher invested decades searching for an alternative inferential calculus that required neither parameters nor prior distributions (Seidenfeld, 1979). Neyman and Pearson (1933) convinced a generation that they could avoid the inverse problem by behaving, when p < α, as though the null was false without changing their belief about the null; and by assuming that which needed proving: “It may often be proved that if we behave according to such a rule, then in the long run we shall reject H when it is true not more than, say, one in a hundred times” (Neyman, 1960, p. 290, emphasis added). When the null is false, inferences based on its truth are counterfactual conditionals from which anything follows—including psychologists’ long, illicit relationship with NHST.

The null has been recast as an interval estimate in more useful ways (e.g., Jones & Tukey, 2000), but little attention has been paid to the alternative hypothesis, generally treated as an anti-null (see Greenwald's [1975] seminal analyses). Despite these difficulties, the NPc constitutes the most common test for acceptability of research.

2. If these tactics do not solve the problem of assigning probabilities to outcomes, they do not even address the problem of assigning utilities to the outcomes, an assignment at the core of a principled decision theory. Observation of practice permits us to rank the values implicit in scientific journals. Most journals will not publish results that the editor deems trivial, no matter how small the p value. This means that the value of a true positive—the value of an action, given the truth of the alternative, v(𝒜|A)—must be substantially greater than zero. The small probability allowed a Type I error, p(𝒜|N) α < .05, reflects a substantial cost associated with false alarms, the onus of publishing a nonreplicable result. The remaining outcomes are of intermediate value. “No effect” is difficult to publish, so the value of a true negative—v(ℬ|N)—must be less than that of a true positive. v(ℬ|N) must also be greater than the value of a Type II error—a false negative, v(ℬ|A)—which is primarily a matter of chagrin for the scientist. Thus, v(True Positive) > v(True Negative) > v(False Negative) > v(False Positive), with the last two being negative. But a mere ranking is inadequate for an informed decision on this most central issue: what research should get published, to become part of the canon.

BEYOND NHST: DTS

The decision theory for science (DTS) proposed here constitutes a well-defined alternative to NHST. DTS's probability module measures replicability, not the improbability of data. Its utility module is based on the information provided by a measurement or manipulation. Together these provide (1) a rational basis for action, (2) a demonstrated ability to recapture current standards, and (3) flexibility for applications in which the payoff matrix differs from the implicit matrices currently regnant. The exposition is couched in terms of editorial actions, since they play a central role in maintaining the current standards (Altman, 2004), but it holds equally for researchers' evaluation of their own results.

The Probability Module

Consider a measurement or manipulation that generates an effect size of

$$D=\frac{M_{\mathrm{E}}-M_{\mathrm{C}}}{s_{\mathrm{p}}},$$ (1)

where M_E is the sample mean of an experimental group E, M_C the sample mean of an independent control group C, and s_p is the pooled within-group standard deviation (see the Appendix for details). The expected value of this measure of effect size has been called d, g, and d′. It has an origin of zero and takes as its unit the root-mean square of the standard deviations of the two samples. To differentiate a realized measurement and a prospective one, the former is denoted d₁, here measured as D, and the latter d₂.

The old way

A strategic problem plagues all implementations of statistical inference on real variables: How to assign a probability to a point such as d₁ or to its null complement. These are of infinitely thin sections of the line with no associated probability mass, so their prior probabilities are 0. This constitutes a problem for Bayesians, which they solve by changing the topic from probabilities to likelihoods. It also constitutes a problem for frequentists, since the probability of an observed datum d₁ is an equally unuseful p = 1. Fisherians solve the problem by giving the null generous credit for anything between d₁ and infinity, deriving p values as the area under the distribution to the right of d₁. This is not the probability of the observed statistic, but of anything more extreme than it under the null. Neyman–Pearsonites set regions of low probability in the null distribution on the basis of the variance of the observed data. This permits determination of whether the inferred p value is below the α criterion, but just how far below the criterion it is cannot enter into the discussion, since it is inconsistent with the NPc logic. No bragging about small p values—setting the smallest round-number p value that our data permit—is allowed (Meehl, 1978), even though that is more informative than simply reporting p < .05. Fisher will not let us reject hypotheses, and Neyman–Pearson will not let us attend to the magnitude of our p values beyond p < α. Neither solves the inverse problem. Textbooks hedge by teaching both approaches, leaving confused students with a bastard of two inadequate methodologies. Gigerenzer has provided spirited reviews of the issues (1993, 2004; Gigerenzer et al., 1989).

The new way

The probability module of DTS differs from NHST in several important ways. NHST posits a hypothetical population of numbers with a mean typically stipulated as 0 and a variance estimated from the obtained results. DTS uses more of the information in the results—both first and second moments—to predict the distribution of replication attempts, while remaining agnostic about the parameters. By giving up specification of states of nature—the truth value of the null or alternative—that cannot, in any case, be evaluated, DTS gains the ability to predict replicability.

The replication of an experiment that found an effect size of d₁ might itself find an effect size d₂ anywhere on the real number line. But the realized experiment makes some parts of the line more probable than others. The posterior predicted distribution of effect sizes is approximately normal, N(d₁, ${\sigma }_{\mathrm{rep}}^2$), with the mean at the original effect size d₁. If the replicate experiment has the same power as the original—in particular, the same number of observations in experimental and control groups drawn from the same population—then its variance is ${\sigma }_{\mathrm{rep}}^2\approx 8∕(n-4)$, where n is the total number of observations in the experimental and control groups (see the Appendix). The probability that a subsequent experiment will find supportive evidence—an effect of the same sign—is called p_rep (Killeen, 2005a). If the effect to be replicated is positive, p_rep is the area under the normal curve in Figure 1 that covers the positive numbers.

Figure 1.

The Gaussian density is the posterior predicted distribution of effect sizes based on an experiment with n = 24 and an effect size d₁ of 0.5. The probability of supportive evidence of any magnitude is the area to the right of zero. The sigmoid represents a utility function on effect size. The expected utility of a replication is the integral of the product of these functions.

The analysis has a Bayesian flavor, but an unfamiliar one (e.g., Killeen, 2006; Wagenmakers & Grünwald, 2006). The probability module of DTS may be derived by using Bayes's theorem to (1) infer the distribution of the parameter δ by updating diffuse priors with the observed data (P. M. Lee, 2004; Winkler, 2003) and then to (2) estimate the distribution of the statistic (d₂) in replication, given the inferred distribution of δ (Doros & Geier, 2005). Fisher attempted to leapfrog over the middle step of inferring the distribution of δ—frequentists such as he maintain that parameters cannot have distributions—but his “fiducial probabilities” were contested (Macdonald, 2005; cf. Killeen, 2005b). Permutation statistics (Lunneborg, 2000) provide another route to DTS's probability module, one that better represents standard experimental procedure. This approach does not rely on the myth of random sampling of subjects from hypothetical populations and, consequently, does not promulgate the myth of automatic generalizability. Under this derivation, p_rep predicts replicability only to the extent that the replication uses similar subjects and materials. To the extent that they differ, a random effects version that incorporates realization variance qualifies the degree of replicability that can be expected.

Informative priors could also be used at the first step in the Bayesian derivation. When those are available, Bayesian updating is the ideal engine for meta-analytic bounding of parameters. But parameter estimation is not the goal of DTS. Its goal is to evaluate a particular bit of research and to avoid coloring that evaluation with the hue of its research tradition. Therefore p_rep and DTS ignore prior information (Killeen, 2005b). DTS goes beyond textbook Bayesian analysis, because it respects the NPc as a special case, it rationalizes current NPc practice, it proposes a particular form for the utility of effects, and it provides a convenient algorithm with which to meld effect size with effect replicability. It thus constitutes an integrated and intuitive foundation for scientific decision making and an easily instrumented algorithm for its application.

The Utility Module

The key strategic move of DTS shifts the outcomes to be evaluated from the states of nature shown in Table 1 to prospective effect sizes shown in Table 2 and Figure 1. The utility of an observation depends on its magnitude, reliability, and value to the community. Reliability is another name for replicability, and that is captured by the distribution of effect sizes in replication described above. But not all deviations from baseline—even if highly replicable—are interesting. Small effects, even if significant by traditional standards, may not be worth the cost of remembering, filing, or publishing. Magnitude of effects may be measured as effect size or transformations of it, such as its coefficient of determination, r², or the information it conveys about the parameters of the populations it was sampled from.

Table 2.

The Payoff Matrix for DTS

	Future Effect (d2)
Decision	Negative With Probability 1 – prep	Positive With Probability prep
Act (𝒜)	u(𝒜 | d2 ≤ 0) = −c|d2|γ	$u(𝒜\mid d_2>0)={\mathit{sd}}_2^{\gamma }$
Balk (ℬ)	u(ℬ) = b	u(ℬ) = b

In this article, the utility of an outcome is assumed to be a power function of its magnitude (see Table 2), where magnitude is measured as effect size (Equation 1). DTS is robust over the particular utility function and measure of magnitude, as long as the function is not convex. The complete analysis may be replicated using r², or Kullback–Leibler (K–L) information, as shown below, with little if any practical differences in outcome. The scale factor c, appearing in Table 2, represents the cost of false positives. It is the cost of a decision to act when the replication then shows an effect one standard deviation in the wrong direction. It is called a false positive because it represents the failure to replicate a positive claim, such as “this treatment was effective.” If the original effect had a positive sign, as is generally assumed here, it is the cost incurred when d₂ = 1. The scale factor s represents the utility of true positives. It is the utility of a decision to act when the replication then shows an effect one standard deviation in a direction consistent with the original result (d₂ = +1). It is the difference between s and c that matters in making decisions, and for now, this is adequately captured by fixing s = 1 and considering the effects of changes in c. Refraining from action—balking—incurs a cost b. The psychological consequences of balking—chagrin or relief, depending on the state of nature—differ importantly. But having balked, one has no entitlement or hazard in the outcome, so the bottom row of this matrix is independent of d. For the moment, b is set to zero. The cost of missed opportunities that may occur when b ≠ 0 will be discussed below.

A representative utility function is shown as the ogive in Figure 1. It is similar to that employed by prospect theory (Kahneman & Tversky, 1979). Its curvature, here shown as γ = ½, places decreasing marginal utility on effect size: Twice as big an effect is not quite twice as good.

The expected utility of a replication attempt

The expected utility (EU) of an action—here, a replication attempt—is the product of the probability of a particular resulting effect and its utility, summed over all effect sizes:

$$\mathrm{EU}(𝒜\mid d_1)={\int }_{-\infty }^{\infty }p(d_2\mid d_1)u\left(d_2\right){\mathit{dd}}_2.$$

The cost, u⁻(d), and benefit, u⁺(d), functions will generally differ. Assuming that the original effect was in the positive direction (d₁ > 0), this is partitioned as

$$\begin{array}{cc}\hfill \mathrm{EU}(𝒜\mid d_1)=& {\int }_{-\infty }^{0}p(d_2\mid d_1)u^{-}\left(d_2\right){\mathit{dd}}_2\hfill \\ \hfill & +{\int }_0^{\infty }p(d_2\mid d_1)u^{+}\left(d_2\right){\mathit{dd}}_2.\hfill \end{array}$$ (2)

Equation 2 gives the expected utility of an attempt to replicate the original results. Evaluators may set a minimal EU to proceed; researchers to move from pilot to full-scale experiments; panelists to fund further research; drug companies to go to the next stage of trials; editors to accept a manuscript.

Recovering the Status Quo

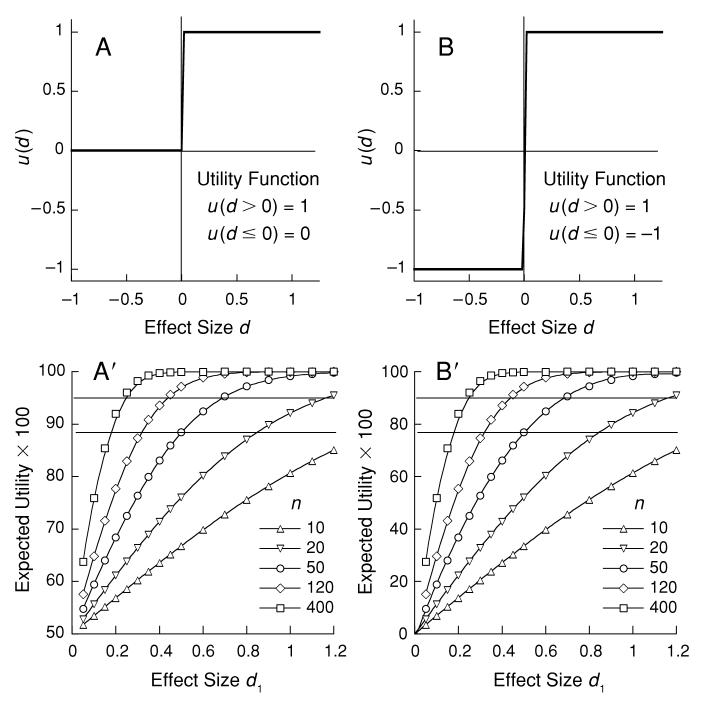
How does this DTS relate to the criteria for evaluating research that have ruled for the last half century? Consider the step utility function shown in panel A of Figure 2; it assigns zero cost for false positives and a maximum (1.0) utility for a positive effect of any size. Its valuation of results is as shown in panel A′ below it. Because this utility function gives unit weight to any positive effect and zero weight to negative effects, weighting the replication distribution (the Gaussian shown in Figure 1) by it and integrating gives the area of the distribution over the positive axis. This area is the probability of finding a positive effect in replication, p_rep. It has a unique one-to-one correspondence with Fisher's p value; in particular, p_rep = N[2^−1/2z(1 − p)], where N is the standardized normal distribution and z its inverse (see the Appendix). Distributions of effect size quickly converge on the normal distribution (Hedges, 1981). For p = .05, .025, and .01, a replication has the probability p_rep ≈ .88, .92, and .95 of returning an effect of the same sign. The horizontal lines in the bottom panels of Figure 2 correspond to p values of .05 and .01. Any result with an n and effect size that yields utilities greater than the criterial p_rep would also be judged significant by NPc; none of those falling below the horizontal lines would be significant. Panel A thus displays a utility function that, along with the inverse transformation on p_rep, recovers the current expert criteria (the horizontal lines) for significance of effects.

Figure 2.

Utility functions and the corresponding expected utility of results below them. Left: The step function returns an expected value of p_rep, the probability of observing d₂ > 0 in replication. The intersection of the curves with the criterion lines marks the first combination of n and d₁ to achieve significance at α ≤ .05 (lower criterion) or α ≤ .01 (upper criterion). Right: A symmetric utility function yielding a set of expected values shown in panel B′ that are congruent with those in panel A′. Note the change of scale, with origin now at 0.

This recovery is unique in the following sense. The NPc gives no weight to magnitude of effect per se, so any admissible utility function must be flat on that variable, or any other measure of strength of effect. The NPc values true positives more than false positives, so the function must be stepped at the origin, as is shown in Figure 2. For any value of α and any values of c and s, there exists a particular criterion $p_{\mathrm{rep}}^{\ast }$ such that $p_{\mathrm{rep}}>p_{\mathrm{rep}}^{\ast }$ iff p < α, as is shown in the Appendix. This generality is exemplified in panel B′ of Figure 2, where c is increased to 1. Under this new costing of false positives, comparable thresholds for action may be recovered by simply adjusting $p_{\mathrm{rep}}^{\ast }$. The analysis is not unique, in that it supports other conventions for replicability; for instance, p_rep could be defined as the probability of replication, with the n in replication going to infinity. But such cases yield similar results and fit easily into the same framework.

This analysis would be of only academic interest if it merely recovered the status quo. Recovery of the existing implicit criteria is the first step toward rationalizing them, taken next. The third step will be to improve them.

Rationalizing the Status Quo

What is the provenance of α = .05? It was chosen informally, as a rule of thumb that provided decent protection against false positives while not militating too heavily against true positives (Skipper, Guenther, & Nass, 1967). Chosen informally, it has nonetheless become a linchpin for the formalisms of inferential statistics. What kind of scientific values does it reflect? In particular, can we ascertain an implicit valuation that makes α = .05 an optimal criterion? Yes, we can; the expected utility of effects under the step functions shown in Figure 2 is easily calculated. Set the utility of a true positive equal to 1.0, as in both panels of the top row, and let the cost for a false positive be c. The expected utility is the area of the posterior distribution to the right of zero (p_rep) times 1, plus the area to the left of zero (1 − p_rep) times −c: EU = p_rep −c(1 − p_rep). The utility function in the right panel of Figure 2 shows the implications of increasing c from 0 to 1. Note the change in the origin and scale of the otherwise congruent curves in this and the panel to its left. This change of the cost of false positives stretches the EUs down to zero as d₁ approaches zero, carrying with them the values of p_rep that correspond to traditional significance levels (the horizontal lines).

For what c is α = .05 optimal?

Where should an evaluator set a criterion in order to maximize utility? Assume that an editor accepts all research with an expected utility greater than the criterion. Move a test criterion from left to right along the x-axis in Figure 1, and the expected utility of those decisions first will increase as costs are avoided and then will decrease as benefits are increasingly avoided. An editor maximizes expected utility by accepting all research whose expected utility is positive. Additional implicit criteria include the judgment of the editor on the importance of the research, the size of the effect, the preference for multiple studies, the preference for new information rather than replication, and a sense of the interests of the readership, all of which allow him or her to reduce the acceptance rate to the carrying capacity of the journal. As the fundamental explicit criterion common to most research endeavors in the social sciences, α is freighted to carry much of the burden of the various implicit criteria, a burden for which it is unsuited (Gigerenzer, 1993; Kline, 2004). DTS provides a better mechanism for incorporating these considerations.

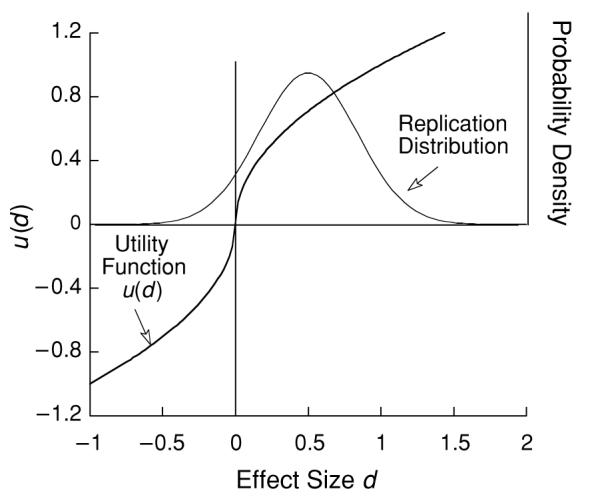
To ask what cost c associated with false positives makes α an optimal choice is tantamount to asking what value of c makes the expected utility of accepting a claim just go positive at the point when p = α. We have seen that the step functions in Figure 2 are utility functions on effect size that are consistent with the NPc; that is, a criterion on p_rep is isomorphic with a criterion on p, but only p_rep lets us calculate the expected utility of various criteria. If the cost of false positives is zero, as in the left panels of Figure 2, the EU can never be less than zero, and any result will have some, perhaps minuscule, value. For c = −1, the symmetric utility function in panel B of Figure 2, d₁ must be greater than zero for EU to be positive. As the cost of false positives increases, the minimal acceptable effect size moves to the right, pulling the left tail of the distribution away from the costly region. What is the cost on false positives that makes the expected utility just go positive at a combination of n and d that generates a p = α? Remembering that EU = p_rep − c(1 − p_rep), set EU = 0 and solve for c. The imputed cost c that rationalizes the criterion is $p_{\mathrm{rep}}^{\ast }∕(1-p_{\mathrm{rep}}^{\ast })$, with $p_{\mathrm{rep}}^{\ast }$ the probability of replication corresponding to α. For α = .05, .025, and .01 (and corresponding p_reps of .88, .92, and .95), the imputed costs of false positives are c ≈ 7, 11, and 19. These are the costs that, in retrospect, make the corresponding values of α a rational (optimal) choice. These increasing penalties increasingly draw down the left treads of the step functions in Figure 2 and, with them, the origin of the utility functions in the curves below them, setting the origins—the threshold for action—at the point where the EU exceeds 0. This is shown in Figure 3 for c = 11, corresponding to p_rep = .917 ( p = .025).

Figure 3.

The expected utility of evidence as judged by current criteria for p < α = .025, corresponding to a cost of false positives of c = 11. All combinations of n and d that yield a positive EU are significant.

Decisions based on p values are (1) isomorphic with decisions based on replicability (p_rep) and (2) rational, if magnitude of effect plays no further role in a decision (the segments of the utility function are flat over d) and the cost of false positives is an order of magnitude greater than the value of true positives. This may not be the utility structure that any reader would choose, but it corresponds to the one our discipline has chosen: NPc with α in the vicinity of .025, as shown in Figure 3.

Getting Rational

The importance of this analysis lies not only in its bringing implicit values to light; it is the possibility that, in that light, they can be redesigned to serve the research community better than our current criteria do. Review the top panels of Figure 2. Most scientists will dislike the discontinuous step functions: Why should an effect size of d = −0.01 be 11 times as bad as an effect size of +0.01 is good, but a d of 1.0 be no better than a d of 0.01? This value structure is not imposed by the current analyses, but by the privileged use of NPc. NPc places the exclusive weight of a decision on replicability, wherein effect size plays a role only as it moves the posterior distribution away from the abyss of d < 0. Figure 3 shows that under the NPc, an effect size of 1.0 with an n of 20, (1, 20), is valued less than (0.8, 40), and (0.8, 40) < (0.6, 80) < (0.4, 200). Effect size may affect editors' decisions de facto, but never in a way that is as crisp or overt as their de jure decisions based on p values. Textbooks from Hays (1963) to Anderson (2001) advise researchers to keep n large enough for decent power, but not so large that trivial effects achieve significance. Apparently, not all significances are equally significant; the utility functions really are not flat. But such counsel against too much power is a kludge. There is currently no coherent theoretical basis for integrating magnitude and replicability to arrive at a decision central to the scientific process.

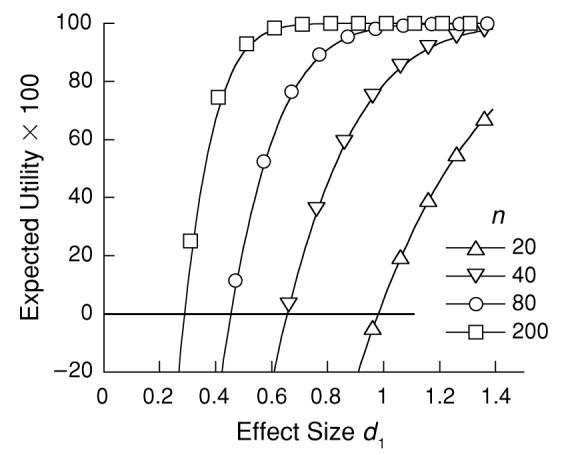
Integration becomes possible by generalizing the utility functions shown in the top of Figures 1 and 2. The functions in the top of Figure 4 are drawn by u⁺(d) = d^γ, d > 0, with values of γ = 1/100, ¼, ½, and 1.0. Potential failures to replicate are costed as u⁻(d) = −c|d|^γ, d ≤ 0. As will be explained below, the exponent gamma, 0 ≤ γ ≤ 1, weights the relative importance of effect size in evaluating research; its complement weights the relative importance of replicability.

Figure 4.

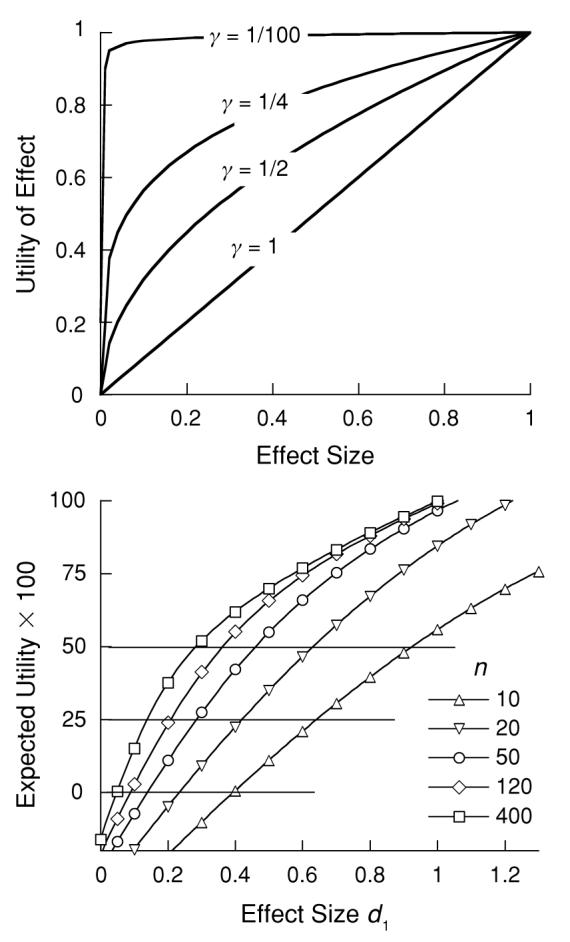
The utility functions in the top panel range from one representing current practice of placing extreme weight on replicability (γ = 1/100) to one that places extreme weight on effect size (γ = 1). The bottom panel shows the expected value of experiments resulting when the utility function is γ = ½ and the cost of false positives is c = 2. The horizontal lines represent criteria appropriate to different opportunity costs.

The proper value for γ must lie between 0 and 1. It is bound to be positive, else an effect in the wrong direction would be perversely given greater positive utility than effects in the predicted direction would be. When γ = 0 (and c ≈ 11), the current value structure is recovered. When γ = 1, the utility function is a straight line with a slope of 1. The expected utility of this function is simply the original effect size (d₁), which is independent of the variance of the posterior predictive distribution: An effect size of 0.50 will have a utility of 0.50, whether n = 4 or n = 400. When γ = 1, therefore, evaluation of evidence depends completely on its magnitude and not at all on its replicability. Gamma is bound to be ≤1; otherwise, the resulting convex utility functions could give small-n experiments with positive effects greater utility than they give large-n studies with the same effect sizes, because the fatter tails of the posterior distributions from weaker experiments could accrue more utility as they assign higher probabilities in the right tail, where utility is accelerating. The wishful thinking implicit in γ > 1 wants no calls for more data.

Utility functions between γ = 0 and γ = 1

The bottom panel of Figure 4 shows the expected utility of replications based on various combinations of d and n for the case in which the scale for false positives is c = 2, with γ = ½. The curves rise steeply as both utility and replicability increase with d; then, as the left tail of the predictive distribution is pulled past zero, the functions converge on a pure utility function with a curvature of ½. These parameters were chosen as the most generous in recognition of the importance of large effect sizes (γ = ½), and the mildest in censure for false positives (c = 2), that are likely to be accepted by a scientific community grown used to γ ≈ 0, c ≈ 11.

What utility function places equal weight on replicability and effect size? The answer depends on a somewhat arbitrary interpretation of equal weight. For the range of effect sizes between 0 and 1, the area of the triangle bounded by γ = 0 and γ = 1 is 0.5 (see the top panel in Figure 4). The utility function drawn when γ = ⅓ bisects that area. This exponent is, therefore, a reasonable compromise between effect size and replicability.

Getting Real: Opportunity Cost

The classic NPc is equivalent to a decision theory that (1) sets the expected utility of successful replications d₂ to u⁺ = s, s = 1, for all d₂ > 0 and (2) penalizes false positives—original claims whose replications go the wrong way—by u⁻ = −c, c ≈ 11, for all d₂ ≤ 0 (Figure 3). Penalizing false positives an order of magnitude more than the credit for true positives seems draconian. Could editors really be so intolerant of Type I errors, when they place almost nil value on reports of failures to replicate? Editors labor under space constraints, with some journals rejecting 90% of submissions. Acceptance of a weak study could displace a stronger study whose authors refuse long publication delays. As Figure 3 shows, adopting small values for α (large implicit c) is a way of filtering research that has the secondary benefit of favoring large effect sizes. Editors know the going standards of what is available to them; articles rejected from Class A journals generally settle into B or C journals, whose editors recognize a lower opportunity cost for their publication. Politic letters of rejection that avoid mentioning this marketplace reality discomfit naive researchers who believe the euphemisms. It is fairer to put this consideration on the table, along with the euphemisms. That can be accomplished by assigning a nonzero value for b in Table 2. It may be interpreted as the average expected utility of experiments displaced by the one under consideration. Opportunity cost subtracts a fixed amount from the expected utility of all reports under consideration. Editors may, therefore, simply draw horizontal criteria, such as the ones shown in Figure 4, representing their journals' average quality of submissions. That is the mark to beat.

Figure 5 gives a different vantage on such criteria. The continuous lines show the combinations of d and n that are deemed significant in a traditional one-tailed NPc analysis. The unfilled triangles give the criteria derived from the utility function shown in Figure 4, with lost opportunities costed at b = 0.5. It is apparent that the proposed, very nontraditional approach to evaluating data, one that values both replicability and effect size (using fairly extreme values of c and γ), nonetheless provides criteria that are not far out of line with the current NPc standards. The most important differences are the following. (1) Large effects pass the criteria with smaller n, which occurs because such large effect sizes contribute utility in their own right. (2) Small effect sizes require a larger n to pass criterion, which occurs because the small effect sizes do not carry their weight in the mix. (3) A criterion, embodied in opportunity cost b, is provided that more accurately reflects market factors governing the decision. Changes in b change the height of the criterion line. The costing of false positives and the steepness (curvature, γ) of the utility function are issues to be debated in the domain of scientific societies, whereas the opportunity costs will be a more flexible assessment made by journal editors.

Figure 5.

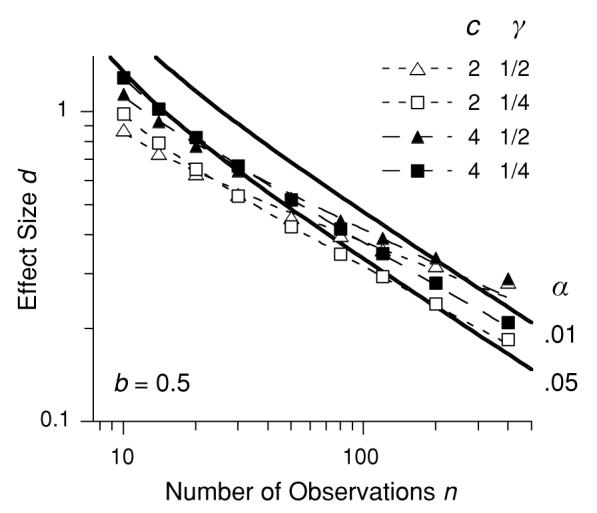
The continuous lines represent traditional criteria (γ = 0). Everything falling above those lines is significant. The symbols show combinations of effect size d and number of observations n that satisfy various costs for false positives (c) and utility functions on effect size, indexed by γ. With a moderate criterion representing opportunity cost (b), this figure shows that even extremely liberal weight on effect size and leniency in costing false positives can support useful criteria. Changes in b shift the criteria vertically. The dashed lines are from Equation 3.

An Easy Algorithm

The analysis above provides a principled approach for the valuation of experiments but wants simplification. An algorithm achieves the same goals with a lighter computational load. Traditional significance tests require that the measured z score of an effect d/σ_d ≥ z_α, where z_α is the z score corresponding to the chosen test size α and σ_d is the standard error of the statistic d. Modify this traditional criterion by (1) substituting the closely related standard error of replication, σ_rep = √2 · σ_d for σ_d, (2) raising each side to the power 1 − γ′, and (3) multiplying by d^γ′. Then d/σ_d ≥ z_α becomes

$$d^{{\gamma }^{\prime }}{\left(d∕{\sigma }_{\mathrm{rep}}\right)}^{1-{\gamma }^{\prime }}\ge d_{\beta }^{{\gamma }^{\prime }}{z}_{\beta }^{1-{\gamma }^{\prime }}.$$

The factor d^γ′ is the weighted effect size, and (d/σ_rep)^1−γ′ the weighted z score. When γ′ = 0, this reduces to a traditional significance criterion d/σ_rep ≥ z_β ≈ d/σ_d ≥ √2 · z_α. The standard z_β is thus the level of replicability necessary if effect size is not a consideration (γ′ = 0), in which case the criterion becomes d/σ_rep ≥ z_β. Conversely, d_β is the effect size deemed necessary where replicability is not a consideration (γ′ = 1), in which case the criterion becomes d ≥ d_β. Gamma is primed because it weights slightly different transformations of magnitude and replicability than does γ.

Effect sizes are approximately normally distributed (Hedges & Olkin, 1985), with the standard error σ_d ≈ √[4/(n − 4)]. The standard error of replication, σ_rep, is larger than σ_d, since it includes the sampling error expected in both the original and the replicate and realization variance ${\sigma }_{\delta }^2$ when the replication is not exact: ${\sigma }_{\mathrm{rep}}\approx \sqrt{}\left[2(4∕(n-4)+{\sigma }_{\delta }^2)\right]$. For the present, set ${\sigma }_{\delta }^2=0$, gather terms, and write

$$\mathrm{EU}=d{[(n-4)∕8]}^{(1-{\gamma }^{\prime })∕2}\ge \kappa ,$$ (3)

where $\kappa =d_{\beta }^{{\gamma }^{\prime }}{z}_{\beta }^{1-{\gamma }^{\prime }}$ and n > 4. Equation 3 gives the expected utility of results and requires that they exceed the criterion κ.

The standard κ is constant once its constituents are chosen. Current practice is restored for γ′ = 0 and κ = z_β = 1.96/√2, and naive empiricism for γ′ = 1 and κ = d_β. Equation 3 provides a good fit to the more principled criteria shown in Figure 5. Once γ′ and κ are stipulated and the results translated into effect size as measured by d, evaluation of research against the standard κ becomes a trivial computation. A researcher who has a p value in hand may calculate its equivalent z score and then compute

$$\mathrm{EU}=\frac{z}{\sqrt{2}}{\left(\frac{d}{z∕\sqrt{2}}\right)}^{{\gamma }^{\prime }}.$$ (4)

Equation 4 deflates the z score by root-2 to transform the sampling distribution into a replication distribution. The parenthetical expression brings effect size in as a consideration: either not at all when γ′ = 0, exclusively when γ′ = 1, and as a weighted factor for intermediate values of γ′.

Other Loss Functions

Coefficient of determination

When γ > 0 the utility function u(d) = d^γ increases without limit. Yet intuitively, there is a limit to how much we would value even perfect knowledge or control of a phenomenon. Utility must be bounded, both from above and from below (Savage, 1972, p. 95). The proportion of variance accounted for by a distinction or manipulation, r², has the attractive properties of familiarity, boundedness, and simplicity of relation to d (Rosenthal, 1994): r² = d²/(d² + 4). By extension of the utility functions on d,

$$u^{-}(r\le 0)=-{\mathit{cr}}^{2\gamma };u^{+}(r>0)=r^{2\gamma }.$$

The circles in Figure 6 show a criterion line using the coefficient of determination r² as the index of merit, with the utility function having a gradient of γ = ¼ and a cost for a false positive of c = 3. When the opportunity cost is b = 0.3, the criterion line lies on top of the function based on effect size. The dashed curve is given by Equation 3, with recovered parameters of γ′ = ¼ and κ = 0.92. Thus, criteria based on the coefficient of determination may be emulated by ones based on effect size (squares) and may be characterized by Equation 3.

Figure 6.

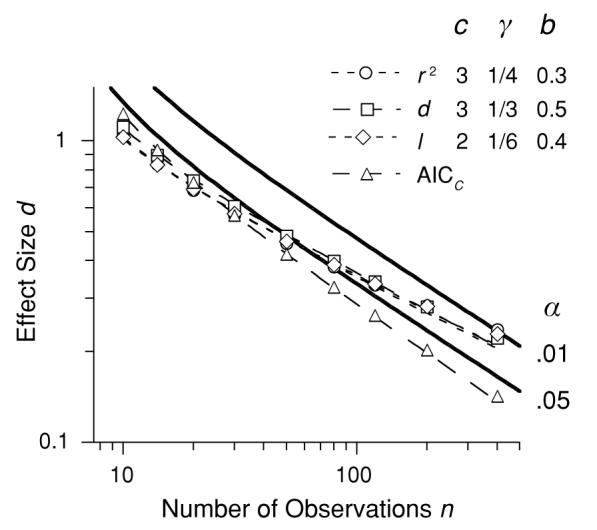
The continuous lines represent traditional criteria (γ = 0). The symbols show combinations of d and n that satisfy various costs for false positives (c), and utility gradients (γ), on the coefficient of determination (r²), effect size (d), K–L distance (I ), and the Akaike information criterion (AIC_c). Note that all may be emulated by utility functions on effect size and by Equation 3 (dashed lines).

The exponential integral, w(1 − e^−γx), is another popular utility function (Luce, 2000). Let x = |d| and w = c for losses and 1 for gains. When c = −3, γ = ½, and opportunity cost b = 0.3, this model draws a criterion line not discriminable from that shown for d, with recovered parameters of γ = ⅕ and κ = 0.98.

Information

The distinction between experimental and control groups is useful to the extent that it is informative. There are several ways to measure information, all of which are based on the reduction of uncertainty by an observation. They measure utility as a function, not of the size of an effect u(d), but of the logarithm of its likelihood, u(log[ f(d)]). In the discrete case, Shannon information is the reduction in entropy, −∑p(d)log[ p(d)], afforded by a signal or other distinction. In the continuous case, information transmitted by a distinction may be measured as

$$I={\int }_{d}f\left(d\right)\log [f\left(d\right)∕g\left(d\right)],$$

the Kullback–Leibler distance. If the logarithm is to base 2, it gives the expected number of additional bits necessary to encode an observation from f(d) using on an optimal code for g(d). The base density g(d) is status quo ante distinction; it may characterize the control group, as opposed to the experimental group, or the prior distribution, or the distribution under some alternate hypothesis. This formulation was alluded to or used by Peirce, Jeffreys, Gibbs, and Turing (Good, 1980). It is closely related to the expected log Bayes factor and to Fisher information gain (Frieden, 1998); it is the basis for the Akaike information criterion.

Figure 6 shows a criterion function (diamonds) using K–L distance as the index of merit, with the utility function on it having a gradient of γ = ⅙ and a cost for false positives of c = 2. For an opportunity cost b = 0.4, the criterion function lies on top of those for effect size and coefficient of determination. The dashed line is given by Equation 3, with recovered parameters of γ′ = ¼ and κ = 0.91. Thus, over this range, a utility function on the information gain associated with a result may, with a suitable choice of parameters, be emulated by ones based directly on effect size and characterized by Equation 3.

Good (1980) calls a symmetric version,

$$I={\int }_d[f\left(d\right)-g\left(d\right)]\ln [f\left(d\right)∕g\left(d\right)],$$

the expected weight of evidence per observation; Kullback (1968) calls it divergence. For Gaussian densities where S and N are the mean transmitted signal power and noise power, it equals the signal-to-noise ratio S/N, a principle component of Shannon's channel capacity (Kullback, 1968). When the distributions are normal, the distinction between experimental and control group provides an information gain of I ≈ r²/(1 − r²) ≈ d²/4 nats per observation (Kullback, 1968), where a nat is the unit of information in natural logarithms. It is obvious that measuring the utility of information as the square root of the weight of evidence expected in replication returns us to our original formulation.

Indecision over fundamental, but somewhat arbitrary, assumptions—here, the form or argument of the utility function—often stymies progress. Why should the utility of evidence increase as, say, a cube root of d? Reasons can be adduced for various other functions. A good case can be made for information as the axis of choice; but the above shows that the more familiar effect size will do just as well. In light of Figure 6, it just does not matter very much which concave utility function is chosen. Once the gatekeepers have set the adjustable parameters, most reasonable functions will counsel similar decisions. Both would be trumped by decision-pertinent indices of merit, such as age-adjusted mortality, where those are available. The appropriate value for γ′ will provide a continuing opportunity for debate, but the generic form of the utility function, and its argument, need not.

Viable null hypotheses

In a thoughtful analysis of the implications of our current prejudice against the null hypothesis, Greenwald (1975) suggested, inter alia, that the use of posterior distributions and range null hypotheses would increase the information transmitted by scientific reporting. The present analysis may exploit his suggestions by adding a row to Table 2 for accepting a “minimal effect,” or nil hypothesis (Serlin & Lapsley, 1985). A second utility function would be overlaid on the function in Figure 1—presumably, an inverted U centered on 0, such as m−|d|^γ, with m measuring the utility accorded this alternative. Computation of the expected utility of actions favoring the nil and the alternative are straightforward. Balking would now occur for combinations of d and n that are too big to be trivial, yet too small to be valuable (Greenwald, 1975; Greenwald, Gonzalez, Harris, & Guthrie, 1996).

Other Criteria

AIC and BIC

By providing an unbiased estimate of K–L distance, Akaike made the major step toward its general utilization. The Akaike information criterion (AIC) is proportional to minus the log likelihood of the data given the model plus the number of free parameters. The AIC is always used to judge the relative accuracy of two models by subtracting their scores. Here, we may use it to ask whether an additional parameter, a (nonzero) difference in the means of E and C, passes the minimal criterion of the AIC. If the distributions are normal with equal variance, the distinction between E and C is not worthwhile when ${\mathrm{AIC}}_c^{\mathrm{N}}<{\mathrm{AIC}}_c^{\mathrm{A}}$. The superscripts denote the null hypothesis of zero effect size and the alternative hypothesis of an effect size large enough to justify adding a separate population mean. The AIC needs additional corrections for small to moderate numbers of observations (Burnham & Anderson, 2002); the corrected version is called AIC_c. For the simple case studied here, this criterion may be reduced to nln(1−r²) < K, K = 2 + 12/(n−3) − 4/(n−2).

The AIC may be used as a decision criterion without reference to DTS, as is shown in Figure 6. The triangles, which give the combinations of n and d that satisfy the Akaike criterion, lie parallel to and below the α = .05 criterion line. Like the NPc, the AIC gives no special concession to larger effect sizes. When Equation 3 is fit to its loci, γ′ is driven to 0. AIC is equivalent to an NPc with α asymptotically equal to .079 (one tailed, as are the NPc shown in Figure 6).

An alternative model selection criterion, Schwarz's Bayes information criterion (BIC; Myung & Pitt, 1997), exacts a more severe penalty on model complexity, relative to error variance, and thereby generates a criterion line that is flatter than any shown in Figure 6. Equation 3 provides an excellent fit to that line, as is shown by Figure 7 and the BIC column interposed in Table 3.

Figure 7.

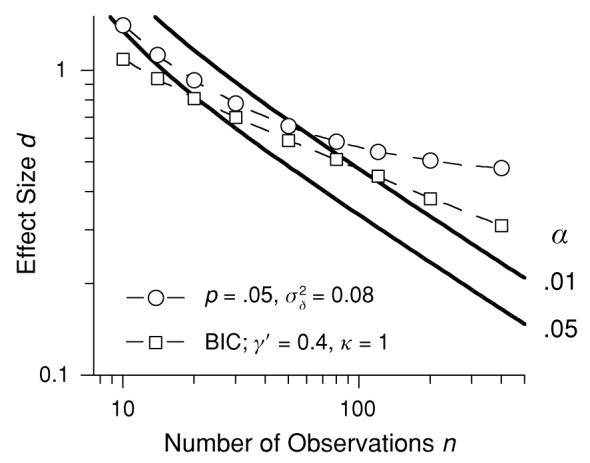
The continuous lines represent traditional criteria (γ = 0). The circles show combinations of d and n that maintain probability of replication constant at .88 (corresponding to significance at α = .05) in a random effects model that respects typical realization variance. The squares show combinations of d and n that satisfy the Bayes information criterion (BIC) for favoring the alternate over the null hypothesis. The dashed line through the squares is given by Equation 3 and accurately emulates the BIC.

Table 3.

Effect Size d Necessary to Satisfy the Criterion d ≥ [8/(n – 4)]^{(1–γ′)/2}

	γ′					γ′
n	0	0.1	0.2	0.3	BIC	0.4	0.5	1
12	1.00	1.00	1.00	1.00	.96	1.00	1.00	1.00
20	.71	.73	.76	.78	.80	.81	.84	1.00
30	.55	.59	.62	.66	.69	.70	.74	1.00
40	.47	.51	.55	.59	.62	.64	.69	1.00
50	.42	.46	.50	.54	.57	.59	.65	1.00
60	.38	.42	.46	.51	.53	.56	.61	1.00
80	.32	.36	.41	.45	.47	.51	.57	1.00
100	.29	.33	.37	.42	.43	.47	.54	1.00
200	.20	.24	.28	.33	.33	.38	.45	1.00
500	.13	.16	.19	.24	.22	.29	.36	1.00
1,000	.09	.11	.15	.18	.17	.24	.30	1.00
10,000	.03	.04	.06	.08	.06	.12	.17	1.00

Note—The parameter γ′ is the weight placed on effect size; 1 – γ′ is the weight placed on replicability. The bars mark values of d below which this criterion is more stringent than a traditional significance test of size α = .05. The BIC column indicates the effect size necessary to justify the addition of an additional parameter (d > 0) by the Bayes information criterion.

Realization Variance

Some of the variance found in replication attempts derives not from (subject) sampling error, but from differences in stimuli, context, and experimenters. This random effects framework adds realization variance as the hyper-parameter ${\sigma }_{\delta }^2$. In a meta-analysis of 25,000 social science studies involving 8 million participants, Richard, Bond, and Stokes-Zoota (2003) report a median within-literature realization variance of ${\sigma }_{\delta }^2=0.08$. ${\sigma }_{\delta }^2$ puts a lower bound on the variance of the replicate sampling distribution and, thus, an upper limit on the probability of replication. This limit is felt most severely by large-n studies with small effect sizes, because increases in n can no longer drive variance to zero, but only to ${\sigma }_{\delta }^2$. This is shown by the circles in Figure 7, where a realization variance of 0.08 is assumed, and the effect size is adjusted so that p_rep is held at the value just necessary to pass a conventional significance test with α = .05. It is obvious that as effect size decreases toward 0.4, the n required to attain significance increases without bound. The magnitude of this effect is somewhat shocking and helps explain both the all-too-common failures to replicate a significant effect, and avoidance of the random effects framework.

Stipulating the appropriate level of realization variance will be contentious if that enters as a factor in editorial judgments. It is reassuring, therefore, that DTS provides some protection against this source of error, while avoiding such specifics: All criterial slopes for DTS are shallower than those for the NPc and, thus, are less willing than the NPc to trade effect size for large n. The loci of the squares in Figure 7 represent the BIC, and the dashed line through them Equation 3 with γ′ = 0.4 and κ = 1. BIC, and this emulation of it, may be all the correction for realization variance that the market will bear at this point.

It should be manifest that Equation 3 closely approximates the principled decision theoretic model DTS. It accommodates utility functions based on effect size, information criteria (AIC and BIC), and variance reduced (r²). It provides a basis for evaluating evidence that ranges from the classic NPc (γ′ = 0) to classic big effects science (γ′ = 1), with intermediate values of γ′ both respecting effect size and providing insurance against realization variance. I therefore anticipate many objections to it.

OBJECTIONS

Publishing unreplicable ‘research’ (γ = 1) is inimical to scientific progress

Giving a weight of 1 − γ = 0 to statistical considerations does not entail that research is unreplicable, but only that replicability is not a criterion for its publication. Astronomical events are often unique, as is the biological record. Case studies (n = 1) adamant to statistical evaluation may nonetheless constitute real contributions to knowledge (Dukes, 1965). Some sub-disciplines focus on increasing effect size by minimizing the variance in the denominator of Equation 1 (Sidman, 1960) or by increasing its numerator (“No one goes to the circus to see an average dog jump through a hoop significantly oftener than chance”; Skinner, 1956), rather than by increasing n. DTS gathers such traditions back into the mainstream, viewing their tactics not as a lowering of standards but, rather, as an expansion of them to include the magnitude of an effect. Values may differ, but now they differ along a continuum whose measure is γ. As long as γ < 1, even Skinner's results must be replicable.

The importance of research cannot be measured by d alone

It cannot; and a fortiori, it cannot be measured by levels of significance, or replicability, alone. The present formulation puts magnitude of effect on the table (Table 2 and Equation 3), to be weighted as heavily (γ → 1) or lightly (γ → 0) as the relevant scientific community desires. It does not solve the qualitative problem of what research is worth doing or worth reporting. A cure for cancer is clearly of greater value than a cure for canker. But if partial or probabilistic cures are being discussed, as is usually the case, effect sizes remain pertinent. The present formulation allows ad hoc editorial value judgments. Depending on perceived significance, the editor can expand or contract the unit value of true positives, s, u(d) = sd^γ, where s now stands for significance as meant in the vernacular. One need not reject DTS to make the relevant value judgment; nor is it even necessary to make an explicit dilation of the scale. Increasing the weight for important effects is both thoroughly consistent with the philosophy of DTS, and tantamount to lowering the threshold κ for exceptional contributions. The converse also holds.

Size is not everything, but it should count for something. Yet currently, only 20 of 1,000 psychology journals require that effect size be reported (Fidler, Thomason, Cumming, Finch, & Leeman, 2004). Psychologists are not unique in their history of placing undue emphasis on significance levels. In the 1990s,

of the 137 papers using a test of statistical significance in the American Economic Review fully 82% mistook a merely statistically significant finding for an economically significant finding. A super majority (81%) believed that looking at the sign of a [regression] coefficient sufficed for science, ignoring size. The mistake is causing economic damage: losses of jobs and justice, and indeed of human lives.

(Ziliak & McCloskey, 2004, p. 527)

The stumbling block has been on assigning utility to size. This article provides a concrete step to the solution of that problem.

Setting a criterion line on expected utility merely dresses the wolf of NPc in more ambiguous clothes

Opportunity cost b, and its pragmatic realization as κ, are expectations for research typical of a journal. The intrinsic utility of a true positive will vary with the subject, with transient needs of a journal or the field, or with an editor's satiation on a particular type of study; the obtained EU should, therefore, not be rigidly held against such a modal criterion. When EU < b, however, the implications of the study should have compensatory importance.

Some may bemoan the loss of a “value-free” criterion such as α = .05. That α criterion was never value free, as has been shown by the present analysis, just cryptic in its values, biased exclusively toward replicability, indifferent to effect size. Too much ink has been spilled on how to live with NHST; it's time to embrace life without it.

Isn't this just a skimmed version of the Bayesian decision theoretic framework of statistical inference?

DTS follows a long tradition of Bayesian scholarship (Jaynes & Bretthorst, 2003, and Robert, 2001, among many others) that may be engaged for more particular statistical questions. What is new is the demonstrated recoverability and rationalization of frequentist criteria, the step away from parameters and thus back from priors, the case for a utility function on effect size, and a pragmatic rule of thumb (Equations 3 and 4) for valuation of research results. It is also a step toward an information theoretic valuation of contributions to knowledge.

I am interested in using statistics to filter fMRI/DNA data. How is analysis of publication criteria relevant?

DTS is consistent with the modern approach to multiple comparisons originating with Benjamini and Hochberg (1995) and elaborated by Williams, Jones, and Tukey (1999), among others (Garcia, 2004). These analyses are based on controlling the false discovery rate (FDR), a statistic akin to 1 − p_rep. Hero and associates (Hero, Fleury, Mears, & Swaroop, 2004) have generalized this approach to take into account both FDR and effect size, with a threshold criterion on biological significance. Because DTS permits biological significance (effect size) to enter as a continuous variable, it promises special utility in such industrial strength arenas, where true and false positives are more easily costed.

OK, I'll try it. How do I analyze my 2 × 3 × 4 repeated measures data?

The first step is for scientific authorities to assign a canonical gradient (γ) that stipulates the relative importance of effect size and the penalty for false positives (c). These decisions will set the origin and curvature of expected utility functions, such as those in Figure 4, and will determine the derived values of γ′ and κ for Equation 3, for some standard value of b*. Given these, journals must estimate their opportunity costs and, thus, set their own threshold (b or κ) for publication. This is all relatively simple. A reasonable choice for γ is around ⅓. A reasonable value for c is around 3—more lenient than the current imputed values of 7–19 but still punitive enough to maintain standards. The resulting criterial function is shown in Figure 6 for an opportunity cost of b = 0.5. Equation 3 gives the curve through the data, with the recovered γ′ = 0.20 and κ = 1. Using these values, data pass muster if d ≥ κ[8/(n − 4)]^0.4, a reasonable standard for an experimental psychology journal, which might even raise γ′ to ¼, or to ⅓. More adventurous journals, or those specializing in large-n effects of some subtlety, might lower their criterial κ. It is a simple matter for researchers to see where their data fall and for editors to experiment with opportunity costs, largely reflected in κ. The implications of various weights on effect size are shown in Table 3, where the effect sizes necessary to satisfy the criterion d ≥ κ[8/(n − 4)]^{(1 − γ′)/2} are displayed as a function of n and γ′, with κ = 1.0.

The next step is to develop and deploy the design-particular analytic schemes that have evolved into the complex stat-packs now available for NHST. The simple transformation between p and p_rep simplifies calculation of replicability, and Equation 4 permits easy calculation of expected utility on the basis of conventional statistical tests. The map to AIC and BIC may open the door to a model comparison framework for inference. Eventually, native applications based on permutation models will be developed. The deck chairs must be rearranged, but now the cruise is through calmer waters to an attainable destination.

APPENDIX

Pooled variance is

$$s_{\mathrm{p}}^2=\frac{s_{\mathrm{C}}^2(n_{\mathrm{C}}-1)+s_{\mathrm{E}}^2(n_{\mathrm{E}}-1)}{n-2},$$ (A1)

where n = n_C + n_E.

The sampling distribution for effect size approaches the normal quickly. Over the range of − 1 < d < 1, the standard error of effect size is approximately σ_d ≈ √[4/(n − 4)]. In predicting replications, sampling error is incurred twice, first in the original experiment and then in replication, so that the standard error of the replicate distribution is σ_rep ≈ √2 · σ_d ≈ √[8/(n − 4)] (Killeen, 2005a).

The probability of replication, p_rep, is the area above the positive line under the distribution shown in Figure 1, as given by

$$p_{\mathrm{rep}}={\int }_0^{\infty }n\left(d_1,{\sigma }_{d_R}\right)={\int }_{-\infty }^{d_1^{\prime }}n\left(0,{\sigma }_{d_R}\right),\text{with}{\sigma }_{d_R}=\sqrt{2}{\sigma }_{d_1}.$$

The logic of p_rep is displayed in the top panel of Figure A1, and the correspondence between p and p_rep is shown in the bottom panel. The curve through the corresponding values may be calculated as N[2^−1/2z(1 − p)], where N[z] is the cumulative normal distribution function and z( p) is its inverse. The prediction is only asymptotically precise, depending in any single application on the representativeness of d₁. See the December 2005 issue of Psychological Science for critiques of this measure of replicability.

Effect size, measured as d, is a simple function of the coefficient of determination, d = 2r(1 − r²)^−1/2, making transformation of the results of correlational studies into a format appropriate for the present analyses straight-forward. For the simple two-independent-group case, d = t[1/n_E + 1/n_C]^1/2, and for a repeated measures t, d = t_r[(1 − r)/n_E + (1 − r)/n_C]^1/2, where r is the correlation between the measures (Cortina & Nouri, 2000; Lipsey & Wilson, 2001).

Empirical (Monte Carlo) sampling distributions avoid problems such as heterogeneity of variances, unequal n, and the assumption of normality, while facilitating the use of permutation models, which are more appropriate to most experimental designs. The resulting values of p may be converted into p_rep and inserted into Equation 3 to evaluate the results.

Figure A1.

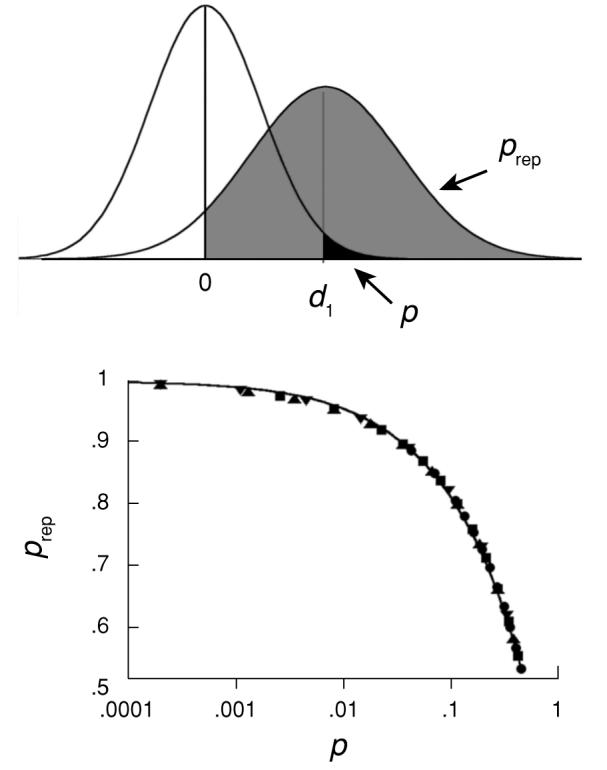
The left curve at top is the sampling distribution for a statistic, such as a mean or effect size (d), under the null hypothesis. The traditional p value is the area to the right of the obtained statistic, d₁, shown in black. Shift this curve to its most likely position (the observed statistic) and double its variance (to account for the sampling error in the original plus that in the replicate) to create the distribution expected for replications. The probability of finding an effect of the same sign (p_rep) is given by the shaded area. The curve at the bottom shows that as power or effect size change, p and p_rep change in complement. From “An Alternative to Null Hypothesis Significance Tests,” by P. R. Killeen, 2005, Psychological Science, 16, p. 349. Copyright 2005 by Blackwell Publishing. Reprinted with permission.