Changes in the structure-function relationship of elastin and its impact on the proximal pulmonary arterial mechanics of hypertensive calves

Abstract

Extracellular matrix remodeling has been proposed as one mechanism by which proximal pulmonary arteries stiffen during pulmonary arterial hypertension (PAH). Although some attention has been paid to the role of collagen and metallomatrix proteins in affecting vascular stiffness, much less work has been performed on changes in elastin structure-function relationships in PAH. Such work is warranted, given the importance of elastin as the structural protein primarily responsible for the passive elastic behavior of these conduit arteries. Here, we study structure-function relationships of fresh arterial tissue and purified arterial elastin from the main, left, and right pulmonary artery branches of normotensive and hypoxia-induced pulmonary hypertensive neonatal calves. PAH resulted in an average 81 and 72% increase in stiffness of fresh and digested tissue, respectively. Increase in stiffness appears most attributable to elevated elastic modulus, which increased 46 and 65%, respectively, for fresh and digested tissue. Comparison between fresh and digested tissues shows that, at 35% strain, a minimum of 48% of the arterial load is carried by elastin, and a minimum of 43% of the change in stiffness of arterial tissue is due to the change in elastin stiffness. Analysis of the stress-strain behavior revealed that PAH causes an increase in the strains associated with the physiological pressure range but had no effect on the strain of transition from elastin-dominant to collagen-dominant behavior. These results indicate that mechanobiological adaptations of the continuum and geometric properties of elastin, in response to PAH, significantly elevate the circumferential stiffness of proximal pulmonary arterial tissue.

pulmonary arterial hypertension (PAH) in neonates, infants, and children is a progressive condition marked by substantial vascular remodeling of the distal pulmonary vasculature, which increases pulmonary vascular resistance (PVR) and pulmonary arterial (PA) pressure. PVR measurement has been the standard diagnostic for evaluating both the significance of PAH and the extent of vascular response to therapies. However, PVR is an inherently limited diagnostic in that it ignores pulmonary vascular stiffness (PVS), an especially important omission, given the inherently pulsatile nature of cardiac function and the importance of robust ventriculo-vascular coupling in maintaining hemodynamic efficiency through the pulmonary vasculature. In fact, many studies of vascular function in systemic hypertension are documenting the substantial role played by the elastic proximal arteries in maintaining systemic vascular hemodynamic efficiency and reducing cardiac workload. Several investigators have shown the significant mechanical advantages conveyed by the elasticity of systemic conduit arteries in reducing overall hydraulic impedance and cardiac workload (29, 32, 37, 38). Other authors have correlated proximal artery stiffness and cardiovascular mortality for patients with systemic hypertension (5, 13, 28). Although less work has been done regarding PA elasticity in PAH, several recent animal studies are beginning to address this topic. In particular, recent work by Kobs and Chesler (26) used fresh artery material testing to correlate increased collagen and elastin content with elevated elastic moduli for the collagen- and elastin-dominant regions of the stress-strain curve, respectively.

In addition, several clinical studies have shown that increased PVS is correlated with patient mortality (12, 18, 31, 43) and can account for as much as 30–40% of the increased load on the heart (40) due to elevated vascular hydraulic impedance and right ventricular afterload. Remodeling of the extracellular matrix (ECM), in particular, appears to be an important aspect of PVS, and a number of studies have examined various biological mechanisms, including inflammatory factors, upregulation of proliferative catalysts, and phenotypic changes in resident cells (2–4, 6, 17, 20–24, 40, 41, 44). Other studies have shown increased collagen content and vascular tone in stiffer arteries (7, 11, 14, 19, 21, 27, 34, 35). In elastin-specific studies, elastolytic activity has been shown to increase during PAH (33), and inhibition of this pathway by the serine elastase inhibitor elafin mitigates hypoxia-induced PAH (46). In recent work from our group coupling a novel orthotropic, hyperelastic, microstructural model of the PA wall to biomechanical studies of PAs from normotensive and hypertensive rats, we suggested that increased ECM structural protein cross-linking may be one mechanism by which these vessels stiffen (47, 48). The next step in addressing this hypothesis is to evaluate experimentally whether the increased stiffness seen in hypoxia-induced PAH can be attributable to increased stiffness of the structural protein matrix. Given that elastin is the ECM protein largely responsible for vascular elasticity, we evaluate here in a well-established PAH neonatal calf model the role of elastin in modulating the stiffness of upstream PA vessels.

In this study, we hypothesize that changes in the functional mechanical properties of elastin are one of the primary causes of the increased stiffness seen in the proximal PAs due to hypoxia-induced PAH. To test this hypothesis, we examined the biomechanics and structure of normotensive and hypertensive neonatal calf proximal PAs and their associated elastin tissue.

MATERIALS AND METHODS

Animal model.

All studies were performed after approval by institutional animal care and use committees. Arterial tissues from three normotensive and six hypertensive male Holstein calves (70–110 lbs.) were used. Hypertension was induced by hypobaric hypoxia, 2 wk, 430 mmHg (4,600-m equivalent air pressure). Hypoxic animals were killed at 430-mmHg pressure after 14 days at hypoxic conditions. All animals were studied and killed at 15 ± 1–2 days of age. PA pressures were obtained with a 5-French Swan-Ganz or Millar catheter, positioned in the main PA (MPA). After death, the right PA (RPA), left PA (LPA), and MPA were excised and stored in nutrient-balanced medium (4°C). Testing was conducted within 24 h of death; material properties of fresh tissues were unchanged for tests conducted up to 4 days postdeath.

Geometric and material property results were calculated using three control and six hypertensive tissues for the LPA and MPA. Two hypertensive RPA tissues were too small and irregularly shaped for stress-strain testing; therefore, three control and four hypertensive RPA tissues were used. We were also unable to accurately measure the PA pressure for one hypertensive animal. Due to this, three control and five hypertensive LPA and MPA and three control and four hypertensive RPA tissues were used for all material property comparisons made at physiological pressure/strain values.

Tissue dissection and processing.

Arteries were inspected for holes, tears, branch points, and localized thickening or other anomalies that may adversely affect test results. Loose connective tissue was removed, and gross anatomic measurements of diameter (1 distal, 1 proximal) and wall thickness (4 distal, 4 proximal) were obtained with digital calipers before axial bisection (see Fig. 1). Circumferential rectangular sections (∼8 × 20 mm) were taken for subsequent material testing. Biopsy samples were taken for histological analysis, three each in the longitudinal and circumferential directions.

Fig. 1.

Thickness measurements, tissue dissection, and biopsy locations (typical). ID, internal diameter; MC, biopsy taken in circumferential direction; ML, biopsy taken in longitudinal direction.

Materials testing.

Fresh tissue stress-strain data were acquired with an MTS, Insight 2 (MTS Systems, Eden Prairie, MN) material testing system, equipped with an ancillary environmental chamber and either 5-N or 2-kN load cell, depending on the maximum expected load for each test (Fig. 2). Stress-strain tests were conducted in calcium and magnesium-free NaCl-PBS buffer (0.01 mol/l, ionic strength 0.15, pH 7.4) at 36°C. Sample width, thickness, and gage length were measured using digital calipers. Stress-strain properties remained consistent for tissue tests performed up to 3 days postdeath.

Fig. 2.

Detail of material testing system (MTS) used to generate stress (σ)-strain (ɛ) data for arterial tissue samples.

Tissues were preconditioned by 10 full extension-relaxation cycles before data were taken. The strain rate for all mechanical tests was 10% strain per second. In this study, force and stress data refer to the loading region of the stress-strain curve. In an effort to avoid damage that may affect elastin-only material tests, tissues were stretched until the collagen-dependent, strain-stiffening response became fully developed, typically 60–80% strain (Fig. 3). Elastin tissue tests were conducted in the same manner as that outlined for fresh arteries, but with a 2- or 5-N load cell. Elastin samples were tested at strains ranging from 60 to 100% at 10% increments or until failure. Data processing was conducted using custom-written software (Matlab R2007a, The Math Works, Natick, MA).

Fig. 3.

Typical loading/unloading curves for fresh and elastin tissue tests. F_n, width-normalized force.

Tissue digestion using formic acid-cyanogen bromide solution.

After fresh artery material testing, tissues were processed into elastin-only scaffolds using the cyanogen bromide (CNBr)-formic acid digestion procedure outlined by Lu et al. (30). Briefly, fresh arteries were submerged in a 70% formic acid, 50 mg/ml CNBr solution and gently stirred for 19 h at room temperature followed by 1 h at 60°C. The samples were then boiled for 10 min to remove any residual CNBr. The digestion solution was then decanted, and the tissue was rinsed with distilled water.

CNBr-formic acid digestion was chosen for elastin purification due to its effectiveness for removing nonelastin components from arterial tissues. Other common elastin purification procedures using hot alkali or autoclaving were rejected due to possible network fragmentation and incomplete elastin purification, respectively (15).

Amino acid analysis was performed on LPA elastin samples (n = 7) to determine the effectiveness of the digestion procedure. After digestion, the samples retain formic acid, and subsequent material testing showed strong pH dependence. NaOH titration was, therefore, used to raise the pH from 2–3 to 7.4. After titration, samples were stored in NaCl-PBS buffer and were tested within 2 wk of animal death. Elastin mechanical properties were unchanged for tests conducted up to 1 mo postdeath.

Histology and elastin area fraction.

Biopsies were fixed in 10% buffered formalin, wax embedded, sectioned, and stained for elastin using Verhoeff's Van Gieson. Bright-field photomicrographs were taken with a Nikon TE-200 (Nikon Instruments, Melville, NY) microscope (×40 magnification, SPOT RT-900 camera; Diagnostic Instruments, Sterling Heights, MI). Elastin area fraction was determined using custom software (Matlab R2007a Image Processing Toolbox, The Math Works).

Calculations.

Fresh artery Cauchy stress (σ_fresh) was calculated with the assumption of incompressibility applied to the width (W) and thickness (T) directions to account for changes in cross-sectional area as a function of engineering strain (ɛ).

(1)

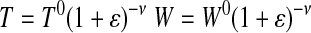(2)

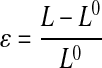(3)

Where F is the applied force; L is the loaded sample length in the direction of applied load; T⁰, W⁰, and L⁰ are the initial thickness, width, and length, respectively; A_elast is the area fraction of elastin; and ν is Poisson's ratio (0.5 for incompressible tissue). Due to the layered structure of the fenestrated elastic sheets, stresses for the digested elastin samples (σ_elast) were calculated with the condition of incompressibility applied to the width direction only. To facilitate modulus (E) calculations, stress-strain data for fresh and elastin samples were fit with ninth- and fourth-order polynomials, respectively. The ninth- and fourth-order polynomials were determined to be the lowest order polynomials necessary to achieve an average squared correlation coefficient R≥ 0.995 for all fresh and elastin data sets, respectively.

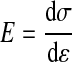(4)

Stiffness (Φ) is the derivative of the width-normalized force (F_n: force divided by current width) by strain, and, as such, stiffness is dependent on thickness geometry and represents the extensive equivalent of elastic modulus.

(5)

The condition of incompressibility was applied to the stiffness calculation to account for any variation in width as a function of imposed strain. F_n data were fit to polynomials in the same manner as was used for the stress. Unless otherwise noted, all results for the material parameters (E, Φ) were calculated at a strain of 35%, so that tissues could be compared. Strains higher than 35% resulted in one or more of the stress-strain curves extending into the collagen-dominant, strain-stiffening region. At strains >35%, any comparison between fresh and elastin stress-strain data would be complicated by the active loading of collagen. Since this collagen component cannot be removed from the fresh artery data set, any comparison of the mechanical properties made at strains >35% would include collagen and, therefore, not allow for the direct comparison of elastin mechanical property changes from the fresh to digested state.

Lame's equation for stress in thick-walled tubes (σ_L) (6) was used to determine the strains that correspond to the measured physiologic pressures.

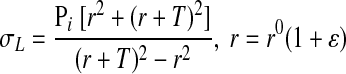(6)

Lame's equation was equated to the polynomial stress-strain function and solved iteratively for the strains that correspond to the in vivo measured systolic, diastolic, and mean pressures (P_i); r and r⁰ are the internal radii of the artery in the loaded and initial state, respectively. The estimated physiological strains were then used to calculate the systolic and diastolic moduli using Eq. 4.

Curvature (κ) of the stress-strain curve was used to determine the onset of collagen engagement (Fig. 4).

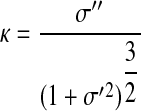(7)

Fig. 4.

Top: typical σ-ɛ behavior of fresh (σ_fresh) and elastin (σ_elast) tissue. ɛ_trans is the ɛ of transition from the elastin-dominant region (A) to the transitional region (B), associated with increasing collagen engagement. Bottom: typical curvature (κ) plot of fresh tissue. H, height; κ_PSS, average prestrain-stiffening κ; κ_trans, κ of the stress-strain curve at the transition strain; κ_max, maximum κ calculated for a given tissue sample; ɛ_H, ɛ associated with maximum curvature minus 20% ɛ; ɛ_L, 20% ɛ; ɛ_PSS, prestrain-stiffening ɛ.

The second-order derivative in the numerator of the curvature equation led to large variances when calculated from the polynomial fit to the original stress-strain data. We, therefore, applied a zero-phase, low-pass, elliptic digital filter to smooth the data. A new ninth-order polynomial was then fit to the filtered data, resulting in reduced curvature variance.

Average prestrain-stiffening curvature (κ_PSS) was calculated for the strain range between ɛ_L and ɛ_H, where ɛ_L equals 20% strain and ɛ_H equals the strain associated with maximum curvature minus 20% strain (Fig. 4). The ɛ_L and ɛ_H were defined in this way so that any curvature associated with the low-strain loading region or high-strain strain-stiffening region would not influence the κ_PSS value. Transition strain (ɛ_trans) was then determined by the relationship:

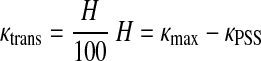(8)

such that ɛ_trans is associated with the onset of curvature elevation; κ_trans is the curvature of the stress-strain curve at the transition strain; and κ_max is the maximum curvature calculated for a given tissue sample. The ɛ_trans results compare favorably with those previously published using both experimental (36), as well as Lorentz distribution functions (45, 49). Stress-strain plots of elastin tissue do not exhibit curvature elevation behavior, and since strain-stiffening is associated with collagen engagement, we defined ɛ_trans as the strain at which collagen begins to carry load. Strains below this value fall within the elastin-dominant region of the stress-strain curve (Fig. 4, top, A), while strains that are greater fall within the transitional or collagen-dominant region (Fig. 4, top, B). We further defined the collagen-dominant region as those strains that result in a fresh artery modulus greater than 10 times the artery modulus calculated within the elastin-dominant region at a strain of 35%. While this is an arbitrary definition for collagen dominance, it seemed logical to suggest that collagen is the dominant load-bearing structural protein when at least 90% of the material modulus can be attributed to collagen.

Equation 9 defines the percentage of the fresh tissue load that is carried by elastin (%F_n-C, %F_n-H) and the percentage of the increased load, due to PAH, that is attributable to the increased stiffness of elastin (%F_n-e,f), calculated at a strain of 35%.

(9)

where F_n-f,C and F_n-f,H are F_n for fresh tissue (control and hypertensive, respectively); and F_n-e,C and F_n-e,H are F_n for elastin tissue (control and hypertensive, respectively). F_n-C and F_n-H were similarly calculated at systolic and diastolic strains to determine the percent load-carrying capacity of elastin at physiological strains.

P values refer to the probability associated with the one-tail, two-sample equal variance, Student's t-test. Results were deemed statistically significant for P values ≤0.05. All error bars represent 1 SD above and below the mean. Standard deviations (SD) were calculated using the “n − 1” method. In all curve fitting, the average of the squared correlation coefficient was deemed statistically significant for R≥ 0.995.

RESULTS

Morphology.

PAH resulted in an increase in vessel wall thickness by 30% (SD = 12%, P = 0.02), 28% (SD = 11%, P = 0.04), and 26% (SD = 8%, P = 0.03) for the RPA, LPA, and MPA, respectively (Fig. 5). There was no statistically significant change in the internal diameter as a result of hypertension. PAH also caused a decrease in the area fraction of elastin by 17% (SD = 2%, P = 0.03), 16% (SD = 2%, P = 0.01), and 16% (SD = 3%, P = 0.03) for the RPA, LPA, and MPA, respectively (Fig. 5). The elastin content factor (ECF) is the product of the elastin area fraction and tissue thickness and is representative of the volume of elastin in a given tissue cross section. The increase in ECF, resulting from PAH, was calculated to be 7.6% (SD = 3.1%), 7.7% (SD = 3.1%), and 5.5% (SD = 2.0%) for the RPA, LPA, and MPA, respectively; average ECF = 6.9% (SD = 1.2%).

Fig. 5.

Comparison of average thickness values and elastin area fractions between control and hypoxic populations. Values are means ± SD. RPA, LPA, MPA: right, left, and main pulmonary artery, respectively. *P < 0.05.

Physiology.

Average systolic/diastolic pressures were 45/18 mmHg (SD = 12/7 mmHg) and 146/71 mmHg (SD = 29/18 mmHg) for control and hypoxic populations, respectively. Control and hypoxic mean pulmonary pressures were 31 mmHg (SD = 12 mmHg) and 106 mmHg (SD = 16 mmHg), respectively. We were unable to collect accurate diameter data for all tested tissues; therefore, the strain at systole and diastole was calculated using Lame's equation (6), with average unloaded internal radii calculated for each MPA, RPA, and LPA, measured from 4 control and 11 hypertensive tissues. The average systolic/diastolic strains for the PAs were 59% (SD = 10%)/34% (SD = 6%) and 72% (SD = 13%)/53% (SD = 11%) for the control and hypoxic populations, respectively. The average strain for the mean pulmonary pressures were 47% (SD = 8%) and 65% (SD = 12%) for the control and hypoxic populations, respectively. The average ɛ_trans was unchanged by PAH: 49% (SD = 8%) for control and 51% (SD = 9%) for hypertensive tissues (P = 0.29). The ɛ_trans values are comparable to the strain corresponding with the onset of collagen engagement published by Zulliger et al. (49). The strain associated with the onset of collagen dominance was calculated to be 69% (SD = 7%) and 74% (SD = 8%) for the control and hypoxic populations, respectively.

Mechanical properties of fresh tissue.

At 35% strain, the average increase in stiffness, due to PAH, was 72% (SD = 30%, P = 0.01), 107% (SD = 56%, P = 0.01), and 63% (SD = 14%, P = 0.01) for the RPA, LPA, and MPA, respectively (Fig. 6). The overall average increase in stiffness was 81% (SD = 23%, P ≪ 0.05). PAH also caused an increase in modulus of PA tissues by 28% (SD = 7%, P = 0.04), 45% (SD = 23%, P = 0.10), and 65% (SD = 18%, P = 0.02) for the RPA, LPA, and MPA, respectively. The average overall increase in fresh tissue modulus was 46% (SD = 18%, P = 0.02). Average stiffness values at physiological strains are shown in Fig. 7, and comparisons between physiological stiffness values are detailed in Table 1.

Fig. 6.

Comparison of mean values for artery stiffness (Φ) and modulus (E) of the RPA, LPA, and MPA for control and hypoxic populations. Values are means ± SD. *P < 0.05.

Fig. 7.

Average control and hypertensive tissue stiffness at systolic and diastolic pressures. Values are means ± SD. Comparative values are presented in Table 1.

Table 1.

Physiological stiffness comparison

	RPA	LPA	MPA	Average
Fresh tissue
ΦDias,Cont to PAH	327*	274*	279*	293*
ΦSys,Cont to PAH	584*	512*	435*	510*
ΦCont,Dias to Sys	151*	125*	158	145*
ΦPAH,Dias to Sys	303*	268*	265*	278*
Elastin tissue
ΦDias,Cont to PAH	151*	243*	124*	173*
ΦSys,Cont to PAH	102*	186	81*	123*
ΦCont,Dias to Sys	41	41	36	39
ΦPAH,Dias to Sys	13	18	10	14
Percent load-carrying capacity of elastin
Fn,Dias,Cont	50	46	87	61
Fn,Dias,PAH	45	43	56	48
Fn,Sys,Cont	45	36	63	48
Fn,Sys,PAH	30	31	35	32

Average change (in %) in stiffness for control and pulmonary arterial hypotension (PAH) tissues at diastolic and systolic pressure and average load-carrying capacity of elastin. Comparative values are based on the data presented in Fig. 7. RPA, LPA, MPA: right, left, and main pulmonary artery, respectively; Φ_{Dias,ConttoPAH} and Φ_{Sys,ConttoPAH}: average increase in stiffness from control to PAH tissues measured at diastole or systole, respectively. Φ_{Cont,DiastoSys} and Φ_{PAH,DiastoSys}: average increase in control or PAH tissue stiffness from diastole to systole, respectively. F_n,Dias,Cont, F_n,Sys,Cont: average percent load-carrying capacity of control tissue measured at diastole or systole, respectively; F_n,Dias,PAH, F_n,Sys,PAH: average percent load-carrying capacity of PAH tissue measured at diastole or systole, respectively.

^*P < 0.05.

Mechanical properties of purified arterial elastin.

At 35% strain, PAH resulted in an increase in the stiffness of the elastin by 57% (SD = 19%, P = 0.04), 109% (SD = 68%, P = 0.03), and 50% (SD = 17%, P = 0.05) for the RPA, LPA, and MPA, respectively (Fig. 8). The overall average increase in the stiffness of elastin was 72% (SD = 33%, P = 0.01). The modulus of elastin increased by 34% (SD = 7%, P = 0.04), 88% (SD = 43%, P = 0.01), and 73% (SD = 36%, P = 0.07) for the RPA, LPA, and MPA, respectively. The overall average increase in the modulus of elastin was 65% (SD = 28%, P ≪ 0.05). Elastin stiffness at physiological pressure is detailed in Fig. 7 and Table 1. Amino acid analysis confirmed that CNBr-formic acid digestion resulted in elastin tissue samples of high purity (25), as evidenced by the high number of residues per 1,000 for alanine (227, SD = 20), valine (127, SD = 6), and glycine (342, SD = 16), along with the lack of methionine and hydroxylysine residues (trace) and the low concentration of hydroxyproline (14, SD = 5).

Fig. 8.

Comparison of mean values for elastin stiffness and modulus for the RPA, LPA, and MPA for control and hypoxic populations. Values are means ± SD. *P < 0.05.

Average values for %F_n-C and %F_n-H are 51% (SD = 16%, P = 0.02) and 48% (SD = 13%, P = 0.003), respectively, meaning that, at a minimum, roughly one-half of the load applied to the fresh arteries is carried by elastin for both control and hypertensive conditions at a strain of 35%. Also, %F_n-e,f indicates that the change in the stiffness of the elastin accounts for an average of 43% (SD = 10%, P = 0.003) of the change in the stiffness of the fresh tissue as a result of hypertension. Changes in elastin load-carrying capacity at physiological strains are detailed in Table 1.

DISCUSSION

Several key issues arise from this study. First, both the physiological pressure and PA stiffness elevation for the hypoxia-induced neonatal calf model mimic the changes we have seen in the human (12) and confirm the value of this model for studying PA stiffness and impedance changes in PAH. Second, the increases in stiffness appear attributable to a significant extent on material rather than purely geometric factors. Third, the changes in material modulus due to PAH appear to be significantly attributable to changes in elastin modulus specifically. Fourth, the physiological tissue strain at diastolic pressure is largely dependent on the stiffness of elastin. Last, a significant component of the mechanical load for both normal and hypertensive conditions continues to be carried by elastin. We comment on each of these issues below.

Use of the neonatal bovine model.

The normal and pathological physiology of the bovine model more closely mimics that of humans than that of the available rodent models. Humans and young calves both have similar body mass, heart rate, blood pressure, and vascular wall thickness. In addition, the cellular composition of the proximal PA wall of the large mammals is similarly complex to humans, incorporating numerous phenotypically distinct smooth muscle cell populations that rapidly proliferate during PAH (40, 41). For these reasons and the fact that we have significant experience with this model, we chose the hypoxic neonatal calf as the in vivo model for understanding how the proximal PA stiffens during hypoxia-induced PAH.

Impact of PAH on physiological strain.

Hypoxic conditions successfully induced PAH, as evidenced by the significant increase in mean PA pressure, vascular wall thickness, and PVS. Due to the stress-strain nonlinearity of arterial tissue, the relative contribution of elastin and collagen is contingent on the strains associated with in vivo physiological pressures. Our results indicate that the physiological region of the stress-strain curve bounds the ɛ_trans, with 62% of the curve residing in the elastin-dominant region and 38% in the transition region for the control population (Fig. 9). Hypertension shifts the physiological strain region to higher strain values, but has no effect on the ɛ_trans. The resulting diastolic strain of hypertensive tissues is roughly equal to the ɛ_trans, 53 and 50%, respectively, and the systolic strain of 72% nearly equals the strain associated with collagen-dominant, stress-strain behavior (74% in PAH tissues). Hypertensive stress-strain curves, therefore, begin at the ɛ_trans and reside entirely within the transition region. This bounding of the ɛ_trans in control tissues and the correlation of transition and diastolic strains for hypertensive tissues suggest that the diastolic strain, and, therefore, baseline slope, of the stress-strain curve is set by the stiffness of elastin, whereas the systolic strain incorporates collagen engagement.

Fig. 9.

Mean pressure-ɛ data for control and hypertensive tissues. Shaded regions indicate the predicted physiological conditions for control (A) and hypertensive (B) tissues. ɛ_cd, Collagen-dominant ɛ.

At diastolic strain, PAH causes a 293% (Φ_{Dias,Cont to PAH}) increase in artery stiffness (Fig. 7, Table 1). Since diastolic strain resides within the elastin-dominant region for control tissues and at the ɛ_trans for PAH tissues, this increase in diastolic stiffness is likely the result of both increased elastin stiffness and the onset of collagen engagement. We calculate that PAH causes a 173% (Φ_{Dias,Cont to PAH}) increase in diastolic elastin stiffness for digested samples. The discrepancy in diastolic stiffness elevation between elastin and fresh tissue is a consequence of the removal of nonelastin material during elastin purification, which will necessarily change the mechanical properties of elastin between its natural and tested state. However, given that the minimum percent diastolic load-carrying capacity of elastin is 61% (%F_{n Dias,Cont}) and 48% (%F_{n Dias,PAH}) for the control and PAH tissues, respectively, and that elastin stiffness values are relatively strain independent, we feel confident in stating that the change in diastolic stiffness, due to PAH, is predominately a result of an increase in elastin stiffness.

The significant strain stiffening response of the transitional region acts to limit the maximum systolic strain at elevated pressure. Our data shows that PAH causes an increase in both fresh tissue and purified elastin systolic stiffness by 510% and 123% (Φ_{Sys,Cont to PAH}), respectively. By comparing the systolic and diastolic stiffness change from control to hypertensive tissues (Φ_{Sys,Cont to PAH} to Φ_{Dias,Cont to PAH}), we see that the systolic stiffness elevation of fresh tissue, resulting from PAH, is nearly double that of the diastolic stiffness elevation, while the elastin stiffness elevation remains relatively constant. This is not surprising, given the linear nature of the elastin stress-strain curve compared with the highly nonlinear fresh tissue curve. This highly nonlinear behavior coupled with the elevated PAH physiological strain results in an increase in stiffness for control and PAH tissue from diastolic to systolic strain of 145% (Φ_{Cont,Dias to Sys}) and 278% (Φ_{PAH,Dias to Sys}), respectively, while the more linear elastin tissue only increased 39 and 14% for control and PAH tissues, respectively. Also, the minimum percent systolic load-carrying capacity of elastin is reduced from 48% (%F_n,Sys,Cont) for control tissues to 32% (%F_n,Sys,PAH) for PAH tissues, indicating that collagen carries more load in the diseased state. However, these data also show that elastin is an important load-carrying material, even at PAH systolic strains. Increased systolic tissue stiffness is, therefore, due to both elevated elastin stiffness, as well as a higher degree of collagen engagement, resulting from the increase in systolic strain due to PAH.

While our results indicate that PAH causes PA tissues to operate at higher strains, the elevated stiffness of the elastin-dominant region mitigates this effect and maintains the physiological strain range within the transitional region. Due to the large strains associated with control fresh tissues operating at PAH physiological pressures, we were unable to consistently stretch the control fresh tissues to strains large enough to attain hypoxic pressure-load values without risk of tissue damage. However, by projecting the fitted polynomial curves of control fresh tissues, we estimate that the PAH diastolic pressure intersects the control fresh tissue curve at a strain of ∼73%. At these high strains, the compliance of arterial tissue is significantly reduced due to elevated tissue modulus, resulting from increased collagen loading. Therefore, the elevated stiffness of the PAH elastin-dominant region of the stress-strain curve maintains the physiological strains of PAH arterial tissues within the transition region of the stress-strain curve by lowering the diastolic strain from ∼73 to 53%. Without this increased stiffness, PAH PA tissues would operate entirely within the high-modulus, collagen-dominant region of the stress-strain curve, which would result in a significant reduction of the windkessel effect. This further underlines the importance of understanding how elastin contributes to the mechanical properties and morphology of PA tissue in response to PAH.

PVS and elastin.

Typically, modulus is calculated with a cross-sectional area determined from microscopic analysis of arterial sections (8–10, 16, 27, 39, 42). This method assumes that the constituent artery materials maintain homogeneity, regardless of pathology or anatomical location. Since stiffness calculations do not require this assumption, the 72% increase in elastin stiffness is an independent result, indicating that elastin carries substantially more load in the pathological state. However, the removal of nonelastin tissue during the digestion process results in experimentally measured material properties that differ between the isolated elastin tissue and elastin in its native state.

Individual elastic fibers are arranged in a network and bound together to form fenestrated elastic sheets, which surround the artery in concentric layers and work to uniformly distribute arterial loads (38). While the individual elastic fibers do not have a linear stress-strain relationship, network effects allow the resulting elastin tissue to obey Hooke's law up to large strains (45). The resulting elastic sheets, which are bound to nonelastin ECM components and smooth muscle cells through glycoprotein and integrin bonds, imbue the artery with a Neo-Hookean load-carrying elastin component that behaves in a near perfectly elastic manner (1). Hypertensive adaptation of these intratissue bonding proteins is thought to play a role in the development of increased arterial stiffness (2–4, 6, 20–22); however, during the CNBr digestion process, the elastin intratissue bonds are broken, and all nonelastin material is extracted. In addition, the removal of bulk, nonelastin, artery material eliminates many of the constraints that resist the movement of elastin sheets relative to one another. The removal of both the intratissue bonds and nonelastin material likely results in experimentally measured stiffness and modulus values that are lower then those of the tissue in its native state. However, any discrepancy between the experimentally determined and native elastin stiffness should have little impact on material property comparisons between control and hypertensive elastin tissues, since both underwent the same digestion process. Due to this discrepancy between the experimentally measured and native stiffness properties, %F_n-C and %F_n-H should be considered as the lower bound for the fresh tissue load fraction carried by elastin, and %F_n-e,f defines the minimum fraction of increased load directly attributable to hypertensive elastin tissue. Hypertension, therefore, causes a significant increase in the stiffness of the elastin material responsible for carrying roughly one-half (%F_n-C, %F_n-H) of the arterial tissue load in the elastin dominant region, at a minimum.

PVS is a function of both the intrinsic material property of modulus and the extrinsic geometric consideration of thickness. Our data show a 46 and 28% average increase in fresh tissue modulus and thickness, respectively, and an 81% average increase in fresh tissue stiffness. For elastin tissues, our data show a 65 and 6.9% average increase in modulus and ECF, respectively, and a 72% average increase in stiffness. Since the width-normalized force, and hence stiffness, scale linearly with changes in both modulus and thickness, it is evident that modulus, rather than geometric tissue thickening, is the dominant factor in determining the stiffness of hypertensive arterial and elastin tissues. Also, it is interesting to note that the stiffness elevation predicted by our fresh tissue modulus and thickness data is 87%, which is close to the measured stiffness increase of 81%, and the stiffness elevation predicted by our increase in elastin modulus and ECF is 76%, which is close to the 72% average increase in measured elastin stiffness.

Elastin modulus.

Our biomechanical tests show that hypertension causes an increase in the modulus of both the fresh and elastin arterial tissues by an average of 46 and 65%, respectively. This increase in elastin modulus supports our thinking that one of the primary structural targets of proximal vascular remodeling during hypoxia-induced PAH is arterial elastin. Changes in fresh artery modulus are comparable to the 30% average increase in the modulus of the PAs in mice published by Kobs et al. (26, 27) and 40% decrease in compliance, identified as the threshold for pediatric hypertension in humans, by Dyer et al. (12).

The increased modulus of elastin, resulting from hypertension, suggests either a change in elastin fibril modulus or a structural adaptation in fibril orientation/interelastin binding. The turnover rate for collagen and elastin is low in healthy arteries, but vascular pathology upsets the regulatory pathways that maintain this balance. In response to hypertension, the overexpression of both proinflammatory and proteinase-inhibitory molecules dramatically increases arterial ECM synthesis (2, 23, 24). Although little is known about the ECM synthesis pathway of hypertensive arterial tissue (2, 40), the upregulation of the tissue inhibitor of matrix metalloproteinase-1 is one method by which ECM synthesis may be enhanced during hypertension (23, 24). However, the ECM proteins synthesized in response to hypertension have a three-dimensional architecture that is functionally less optimal then those deposited during fetal development and may play an important role in determining the modulus of pathological elastin tissue (2, 23, 24). More experimentation is required to determine the underlying cause for the increase in elastin modulus.

Limitations.

Several limitations in these studies must be acknowledged. First, the tissue digestion procedure may alter the mechanical properties of elastin through chemical attack or thermal degradation, although no evidence of this was found in our studies or in the literature. Second, the use of continuum mechanics for discontinuous materials will lead to some degree of error in calculated mechanical properties due to simplifying assumptions; however, this should have little impact on comparison of those properties. Third, uniaxial rather than fully biaxial testing was performed. However, given that the objective of this study was not to investigate the anisotropic behaviors of artery tissues, but rather to determine how such properties of fresh and digested tissue samples change as a result of hypertension, the uniaxial test was deemed sufficient.

Conclusion.

Via biomechanical testing of both fresh and digested elastin tissues of control and hypoxia-induced pulmonary hypertensive animals, we have confirmed that vascular remodeling results in a significant increase in the modulus and stiffness of both the fresh and elastin tissues of the proximal PAs in the circumferential direction. We have further shown that, at 35% strain, a minimum 48% of the load imposed on fresh arterial tissue is carried by elastin, and that, at a minimum, 43% of the change in stiffness of fresh arterial tissue is directly attributable to the change in stiffness of the elastin component of those arteries. We have also shown that PAH causes an increase in the strains associated with the physiological pressure range but had no effect on the strain of transition from elastin-dominant to collagen-dominant behavior. Stress-strain behavior of fresh arterial tissues further revealed that the diastolic strain and baseline slope of the stress-strain curve are determined by elastin mechanics, and the strain at systole becomes increasingly dependent on collagen mechanics as a result of hypertension. The final conclusion drawn from the above statements is that elastin is an important passive material for carrying the load imposed on the proximal PAs at physiological pressure ranges, and that the increase in stiffness of elastin acts to maintain the physiological strain range within the more elastin-dependent region of the stress-strain curve.

GRANTS

This study was supported by National Institutes of Health Grants P50HL84923, T32HL072738, and K24HL081506.