Theoretical model of blood flow autoregulation: roles of myogenic, shear-dependent, and metabolic responses

Abstract

The autoregulation of blood flow, the maintenance of almost constant blood flow in the face of variations in arterial pressure, is characteristic of many tissue types. Here, contributions to the autoregulation of pressure-dependent, shear stress-dependent, and metabolic vasoactive responses are analyzed using a theoretical model. Seven segments, connected in series, represent classes of vessels: arteries, large arterioles, small arterioles, capillaries, small venules, large venules, and veins. The large and small arterioles respond actively to local changes in pressure and wall shear stress and to the downstream metabolic state communicated via conducted responses. All other segments are considered fixed resistances. The myogenic, shear-dependent, and metabolic responses of the arteriolar segments are represented by a theoretical model based on experimental data from isolated vessels. To assess autoregulation, the predicted flow at an arterial pressure of 130 mmHg is compared with that at 80 mmHg. If the degree of vascular smooth muscle activation is held constant at 0.5, there is a fivefold increase in blood flow. When myogenic variation of tone is included, flow increases by a factor of 1.66 over the same pressure range, indicating weak autoregulation. The inclusion of both myogenic and shear-dependent responses results in an increase in flow by a factor of 2.43. A further addition of the metabolic response produces strong autoregulation with flow increasing by a factor of 1.18 and gives results consistent with experimental observation. The model results indicate that the combined effects of myogenic and metabolic regulation overcome the vasodilatory effect of the shear response and lead to the autoregulation of blood flow.

the ability of vascular beds to maintain a relatively constant blood flow over a large range of arterial pressures is known as vascular autoregulation. With increasing arterial pressure, the degree of vascular smooth muscle (VSM) activation, VSM tone, increases in arterioles, resulting in decreased vessel diameter and increased flow resistance. Several mechanisms contribute to changes in vascular tone, including responses to intraluminal pressure (myogenic response), shear stress on the endothelial lining of vessels (shear-dependent response), metabolite concentrations in vessels and/or tissue (metabolic response), and neural stimuli. The cerebral and renal vasculature show the most stable flow over a wide range of arterial pressures (2, 25), whereas in other beds, such as those in the mesentery, autoregulation is less effective.

Several theoretical models for the autoregulation of blood flow have been developed using a multicompartmental approach, in which blood is considered to flow through a number of compartments connected in series representing different types and sizes of vessels. Gao et al. (10) developed a model for the cerebral circulation with four vascular regions, where the vessel size and response in each region were described by empirical equations based on in vivo experimental data (16). Although the model implicitly included all mechanisms acting in vivo, such as myogenic, shear-dependent, and metabolic responses, it did not allow analysis of the relative contributions of these mechanisms to autoregulation. In the model of Cornelissen et al. (5) for the coronary circulation, the myogenic response was included by assuming pressure-diameter relationships in vasoactive segments based on experimental observations on isolated segments. Liao and Kuo (20) considered the effects of only myogenic and shear-dependent responses in an empirically based model. Ursino and Lodi (34) and Cornelissen (4) employed pressure-, flow-, and metabolic-dependent responses in their respective models of cerebral and skeletal muscle tissues; however, these three responses were not present in all of the resistance vessels. For example, in the latter model, vascular segments responded to either pressure and shear stress or metabolic state depending on their position in the vascular tree. None of these studies compared the individual effects of the different responses on autoregulation.

The objective of this study is to analyze the contributions of myogenic, shear-dependent, and metabolic responses to the autoregulation of blood flow. The myogenic response of arterioles to variations of intraluminal pressure is triphasic. At low pressures, arterioles dilate passively with increasing pressure. Increasing pressure from 20 to 120 mmHg elicits myogenic constriction. At very high pressures, above 140 mmHg, the vessel is dilated despite the generation of nearly maximal VSM tone due to the myogenic response, and any additional increase in pressure causes further dilation. VSM tone also depends on the shear stress generated by blood flow. Increased shear stress initiates the endothelial release of nitric oxide (NO), which leads to the relaxation of VSM. In addition, several mechanisms of metabolic response contribute to VSM tone. The present model is based on a mechanism in which low oxyhemoglobin saturation causes red blood cells (RBCs) to release ATP, inducing an upstream conducted vasodilatory response (1, 9, 35). Changes in the diameter of any vascular segment affect flow and, therefore, levels of shear stress, pressure, and oxyhemoglobin saturation in upstream and downstream segments. To take such interactions into account, a multicompartment representative segment model is used, in which several compartments, representing different classes of vessels, are connected in series. Each compartment represents the flow resistance of multiple branched vessels with a range of diameters and consists of a parallel arrangement of segments with identical size, length, and response characteristics. The active responses of arteriolar segments are described by a previously developed model for the myogenic response (3), modified here to include the shear-dependent and metabolic responses. These three responses are separately activated or deactivated to test their effects on predicted pressure-flow relationships.

METHODS

Model for myogenic response.

In a previous model (3), tension in the vessel wall is represented as the sum of a passive component, T_pass, and an active component generated by the VSM. The active component can be expressed as the product of the maximal active tension that is generated at a given vessel circumference, T_act^max, and the degree of activation or VSM tone, A. Therefore, the total tension in the vessel wall, T_total, is given by:

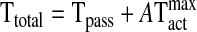(1)

The passive tension is a nonlinear function of diameter, D, and is approximated by the following exponential relationship:

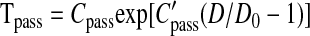(2)

where D₀ is the passive vessel diameter at an intraluminal pressure of 100 mmHg. The maximal active tension generated by the VSM cells in the vessel wall is described by a Gaussian curve (11):

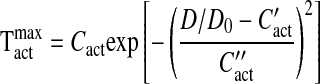(3)

The activation varies between 0 and 1 and is assumed to have a sigmoidal dependence on the stimulus, S_tone, determining the level of VSM tone:

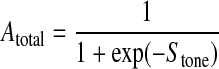(4)

The myogenic response is represented by assuming:

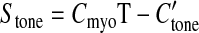(5)

The unknown parameters C_pass, C′_pass, C_act, C′_act, C″_act, C_myo, and C″_tone were estimated as functions of vessel diameter in Ref. 3 based on data from several experimental studies giving pressure-diameter curves for vessels with diameters ranging from 40 to 300 μm.

Model for myogenic and shear-dependent responses.

In this study, the model for the myogenic response is extended to represent responses to shear stress by including a term dependent on shear stress in S_tone. Few experimental studies have examined responses of cannulated vessel segments to changes in both pressure and flow. Here, data of Sun et al. (33) are used to estimate myogenic and shear-dependent contributions to S_tone. Several forms of shear dependence were tested, and a linear relationship between S_tone and vessel wall shear stress, τ_wall, was found to fit the experimental data nearly as well as more complex relationships:

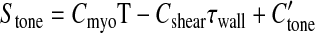(6)

where C_shear determines the sensitivity of S_tone to shear stress. C′_tone differs from its value in Ref. 3 since it is now fit to pressure-diameter data at four flows. These parameter values are given in Table 1. In Eqs. 1–6, the components of tension in the vessel wall are expressed in dynes per centimeters, wall shear stress is expressed in dynes per squared centimeters, and A and S_tone are dimensionless.

Table 1.

Parameter values defining arteriolar activation and diameter

Parameter Value	Large Arteriole	Small Arteriole
Cmyo, cm/dyn	0.0101	0.0359
Cshear, cm2/dyn	0.0258	0.0258
Cmeta, 1 μM/cm	30	30
C′tone	−2.22	−0.53
C″tone	10.11	10.66
Cpass, dyn/cm	1,042.99	259.90
C′pass	8.293	11.467
Cact, dyn/cm	1,596.3	274.193
C′act	0.6804	0.750
C″act	0.2905	0.384
D0, μm	156.49	38.99

C_myo, vascular smooth muscle (VSM) activation tension sensitivity; C_shear, VSM activation shear stress sensitivity; C_meta, VSM activation conducted response sensitivity; C′_tone and C″_tone, VSM constants; C_pass and C′_pass, passive tension strength and sensitivity, respectively; C_act, C′_act, and C″_act, maximally active VSM peak tension, length dependence, and tension range, respectively; D₀, passive reference vessel diameter.

Model for myogenic, shear-dependent, and metabolic responses.

The model for metabolic flow regulation is based on a mechanism in which a decline in oxyhemoglobin saturation in capillaries and venules causes RBCs to release ATP at an increased rate, and the resulting elevated ATP level in plasma induces an upstream conducted vasodilatory response that is transmitted along the vessel wall to the arterioles (1, 9, 35). A theoretical model (1) is used to simulate the variation of oxyhemoglobin saturation and ATP concentration along the length of a vascular pathway. At each point on the pathway, an upstream conducted response is assumed to be generated in proportion to the local plasma ATP level. This response is summed in the upstream direction including the effect of an exponential decay with distance traveled to obtain the conducted response signal, S_CR. Thus S_CR at a given point in a vessel is defined as the integral of the ATP concentrations at each downstream position reduced by the exponential of the distance from the given point. This signal is multiplied by a sensitivity factor, C_meta, to account for its effect on VSM activation with respect to the other contributing regulatory mechanisms. The resulting expression for S_tone is:

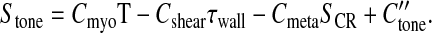(7)

where C″_tone is a dimensionless constant. A detailed description of the model for the metabolic response, including the computation of S_CR, is given in Ref. 1, and parameter values and units are listed in Table 1.

Representative segment model.

Effects of changes in vascular tone on blood flow are estimated using a representative segment model (1), in which the systemic vasculature is divided into seven regions: upstream arteries, large arterioles, small arterioles, capillaries, small venules, large venules, and downstream veins. Each region, which in actuality contains multiple vascular segments with a range of diameters, is represented here by a fixed number of segments of specified length and diameter. The upstream artery, capillary, and venous regions are assumed to have no vasoactive response and, therefore, are represented as fixed resistances to blood flow. In reality, the diameters of capillaries and venules may vary with arterial pressure, but the contribution of these vessels to total flow resistance is relatively small, and their effects on autoregulation are neglected here. The large arteriole and small arteriole regions react actively to changes in pressure, shear stress, and metabolism.

Determination of control state.

A control state is defined based on vascular network geometry, hemodynamic conditions, and model parameters determined from experimental evidence (27). Assumptions are made to define control shear stress, pressure distribution, activation, and symmetry of the representative segment vascular pathway. First, τ_wall in the control state is assumed to be 55 dyn/cm² in the upstream artery, large arteriole, small arteriole, and capillary regions and 10 dyn/cm² in the venules and downstream veins according to experiment (27). An input arterial pressure of 100 mmHg is assumed, and control pressure drops of 10, 15, 40, and 15 mmHg across the upstream artery, large arteriole, small arteriole, and capillary regions, respectively, are defined. These values were chosen to yield midpoint pressures for each vessel that corresponds to compiled experimental intravascular pressures (1, 27). Since this study considers mean pressures, responses to the pulsatile component of pressure are neglected. The control level of activation of the large and small arteriole is assumed to be 50% (A_LA = A_SA = 0.5), where LA is the large arteriole and SA is the small arteriole, so that S_tone = 0 in the control state. Finally, the representative segment vascular network is assumed to be symmetric, defining the same number and length of small arterioles as small venules for one input large arteriole and one output large venule. From these assumptions, the values of control state flow, number of vessels, resistance to flow, pressure drop, length, and diameter of vessels can be calculated for each region (1).

Evaluation of parameters.

Four parameters defining the response of the large arterioles to pressure and wall shear stress (C′_act, C″_act, C_shear, and C′_tone) are determined by minimizing the mean square deviation of predicted vessel diameters from the experimental data in Sun et al. (33) for a single vessel. The data for the four flows observed by Sun et al. (33) are fit simultaneously to yield the best fit to the entire group of data points. The values of C_myo and C_act are estimated from a linear regression of these parameters with vessel reference diameter (3). Values of C_pass and C′_pass are taken directly from Ref. 3. To estimate the parameter values for small arterioles, data of Davis and Sikes (6) are used. However, these data do not include responses to shear stress. In the absence of a suitable data set showing the variation of arteriolar diameter with both pressure and flow for vessels of this size, the value of C_shear for small arterioles is set equal to the value determined for the large arteriole segment. The value of C″_tone for the LA and SA is determined from the condition that S_tone = 0 in the control state. The estimation of the parameter C_meta is previously discussed by us (1). Parameter values for the small and large arterioles are given in Table 1. Oxygen demand is 8.28 cm³ O₂·100 cm⁻³·min⁻¹, which is within the 6.3–8.3 cm³ O₂·100 cm⁻³·min⁻¹ range of oxygen consumption rates in rat cortex (28). Analysis using this level of oxygen demand is appropriate since the model results are compared with experimental data also from cerebral tissue (7, 21). A list of all model variables and parameters is provided in Table 2.

Table 2.

Model variables and parameters

	Description	Units
Variable
Ttotal	Total vessel wall tension	dyn/cm
Tpass	Passive tension	dyn/cm
Tactmax	Maximally active VSM tension	dyn/cm
A	VSM activation	unitless
D	Vessel diameter	μm
τwall	Vessel wall shear stress	dyn/cm2
Stone	VSM activation stimulus	unitless
SCR	Conducted metabolic response signal	μM·cm
Parameter
Cpass	Passive tension strength	dyn/cm
C′pass	Passive tension sensitivity	unitless
Cact	Maximally active VSM peak tension	dyn/cm
C′act	Maximally active VSM length dependence	unitless
C″act	Maximally active VSM tension range	unitless
D0	Passive reference vessel diameter	μm
Cmyo	VSM activation tension sensitivity	cm/dyn
Cshear	VSM activation shear stress sensitivity	cm2/dyn
Cmeta	VSM activation conducted response sensitivity	1/(μM·cm)
C′tone	VSM constant	unitless
C″tone	VSM constant	unitless

Simulation procedure.

To predict pressure-flow relationships under the assumptions of the model, mean arterial pressure (MAP) is varied from 20 to 200 mmHg, and the corresponding flow through the large arteriole is computed and expressed relative to its value under control conditions, 70.9 cm³ O₂·100 cm⁻³·min⁻¹ (MAP = 100 mmHg). A dynamic representation of the vessel response to diameter and VSM activation changes is used to approach the steady-state conditions of both the large and small arteriole segments (1). Several cases are considered in which various responses are activated or deactivated to investigate their relative contributions to autoregulation. The myogenic response is deactivated by holding tension constant at its control state value. The shear-dependent response is deactivated by holding the shear stress constant at its control state value. The metabolic response is deactivated by setting the S_CR constant at its control state value. The effect of varying oxygen demand in the presence of all three regulatory mechanisms is also examined.

RESULTS

Single vessel response to pressure and wall shear stress.

The myogenic and shear-dependent response model is used to predict pressure-diameter curves at four different flows in a single vessel. In these calculations, the time constants governing the rate of change of the diameter and VSM activation, respectively, were both set to 1 s. Other time constants can yield oscillations in diameter and activation in certain pressure ranges. In such conditions, the average of the oscillation is approximately the same as the results shown here.

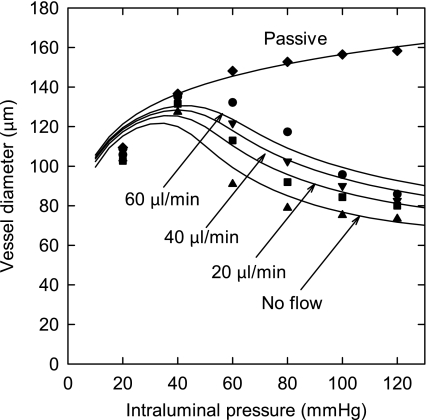
In Fig. 1, the model predictions are compared with experimental data (33) and show a good fit. At pressures above 140 mmHg, the model predicts that the vessel dilates to a diameter close to the passive value (not shown), resulting in a triphasic response (3). Diameter increases with increasing flow in the range of pressures over which the myogenic response is active. This reflects the vasodilatory effect of increasing wall shear stress.

Fig. 1.

Dependence of vessel diameter on pressure and flow. Solid curves are model predictions, with flows as indicated and for the passive case [activation (A) = 0]. Symbols are corresponding experimental results (Ref. 33).

Myogenic, shear-dependent, and metabolic responses in autoregulation.

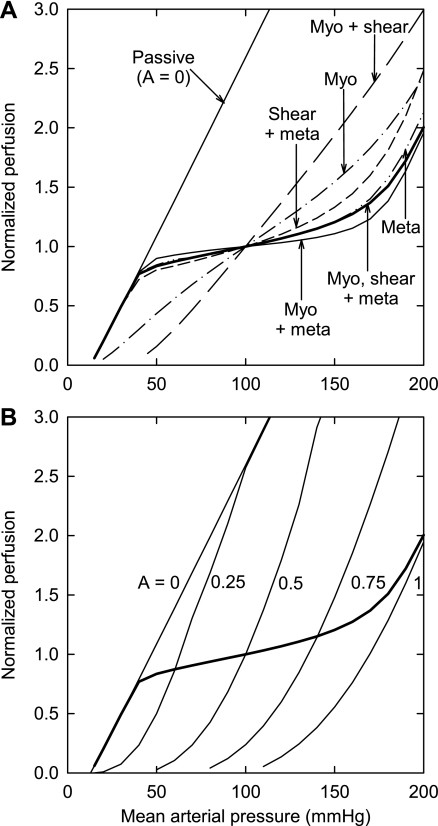
In Fig. 2, the normalized flow as a function of arterial pressure is shown for several different cases. Table 3 gives the factors by which flow increases with changes in pressure of 80 to 130 mmHg and 50 to 150 mmHg. With no responses active and A = 0.5, an increase in MAP from 80 to 130 mmHg causes an increase in flow by a factor of 5.29. Flow increases at a faster rate than linear rate with pressure because increasing pressure causes passive dilation of the large and small arterioles, resulting in decreased flow resistance. When only the myogenic response is active (Fig. 2A, dash dotted), very weak autoregulation is predicted and flow increases by a factor of 1.66 given the same increase in pressure. This decreased factor reflects the constriction induced by the myogenic response over this pressure range. When the shear-dependent response is combined with the myogenic response (Fig. 2A, long dash), autoregulation is abolished. The shear-dependent response counteracts the autoregulatory effect of the myogenic response, leading to an increase in flow by a factor of 2.43. When all three responses are present (Fig. 2A, thick solid), the autoregulatory response is restored with flow increasing by a factor of 1.18. Additionally, if only the metabolic response is active, then strong autoregulation occurs (1.18; Fig. 2A, dashed double dot); the addition of the shear-dependent response to the metabolic response weakens autoregulation (1.28; Fig. 2A, short dash). Combining the myogenic and metabolic responses produces the strongest autoregulation (1.09; Fig. 2A, thin solid). Figure 2B indicates how autoregulation is achieved by a strong increase in activation for pressures above 40 mmHg.

Fig. 2.

Predicted dependence of perfusion on arterial pressure. Perfusion is expressed relative to its value when mean arterial pressure equals 100 mmHg. A: passive results and results including active responses as indicated. B: results for constant activation levels: A = 0, 0.25, 0.5, 0.75, and 1. The predicted curve in the presence of all 3 regulatory mechanisms (heavy line) is also shown. Meta, metabolic; myo, myogenic.

Table 3.

Factors by which blood flow increases with pressure changes

Pressure Ratio (mmHg·mmHg)	Control, A = 0.5	Myogenic	Myogenic And Shear	Myogenic, Shear And Metabolic	Metabolic	Metabolic And Shear	Metabolic And Myogenic
130:80 (1.625)	5.29	1.66	2.43	1.18	1.18	1.28	1.09
150:50 (3.00)	122.99	3.55	12.24	1.44	1.43	1.66	1.23

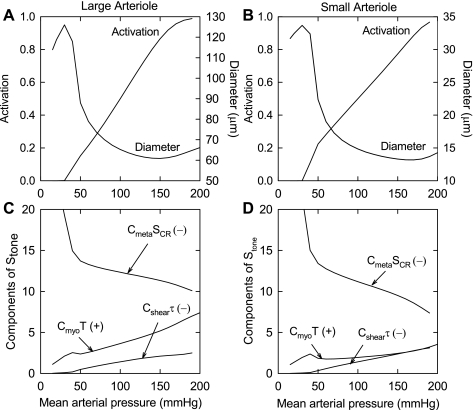
Figure 3, A and B, shows the activation and diameter as functions of MAP in the large and small arterioles with all three responses present. The increases in activation lead to strong decreases in vessel diameter with increasing pressure. Figure 3, C and D, shows the contributions of the three response mechanisms to the increases in vascular tone. The vasodilator effects of increases in shear stress are countered by the vasoconstrictor effects of increasing pressure and decreasing metabolic signal.

Fig. 3.

Top: predicted dependence of activation and diameter on mean arterial pressure with all regulatory responses activated. A: large arteriole. B: small arteriole. Bottom: predicted dependence of the components of the stimulus that dictates the level of VSM tone (S_tone; wall tension, wall shear stress, and conducted response signal) on mean arterial pressure. C: large arteriole. D: small arteriole. (+) and (−), positive and negative contributions, respectively, to S_tone. C_myo, VSM activation tension sensitivity; C_shear, VSM activation shear stress sensitivity; C_meta, VSM activation conducted response sensitivity; S_CR, conducted metabolic response signal.

Comparison with experimental data.

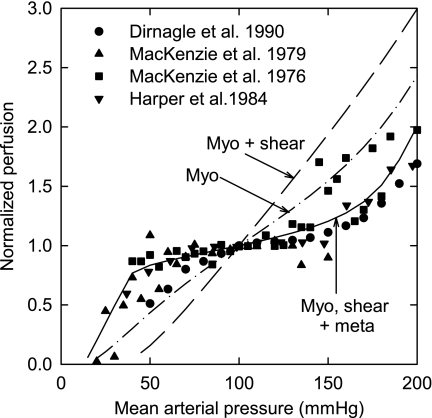
In Fig. 4, model predictions are compared with several sets of experimental data (7, 12, 21, 22). When all three mechanisms are included, the autoregulation predicted by the model is consistent with that seen experimentally. If only the myogenic and shear-dependent responses are present, autoregulation is absent and the predicted curve deviates significantly from experimental observations.

Fig. 4.

Dependence of perfusion on arterial pressure. Curves are model predictions (as in Fig. 2A, with active responses as indicated). Symbols are experimental data (Refs. 7, 12, 21, 22).

Varying oxygen consumption rate.

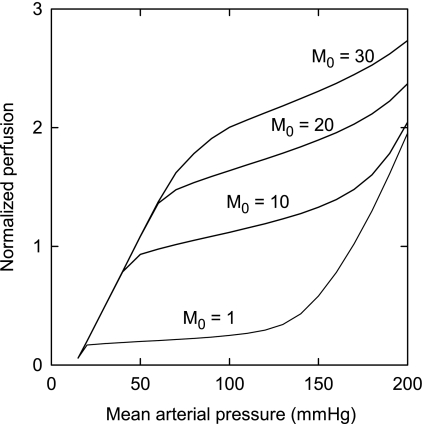
Figure 5 shows the effects of oxygen demand on autoregulatory behavior. As oxygen demand increases, flow increases for a given pressure. The general shape of the autoregulation curve is preserved at low to moderate oxygen demand. At the highest level of demand, autoregulatory behavior is lost.

Fig. 5.

Predicted effect of oxygen demand (M₀; in cm³ O₂·100 cm⁻³·min⁻¹) on autoregulation. Perfusion is expressed relative to its value when mean arterial pressure equals 100 mmHg.

DISCUSSION

The present study extends a previously developed theoretical model for the myogenic response (3) to include shear-dependent and metabolic responses. Terms proportional to wall shear stress and the conducted response signal are included in the quantity S_tone (Eq. 7). The contributions of the three mechanisms to autoregulation are quantitatively analyzed using a mechanistic model that predicts pressure-flow curves when the various responses act alone or in combination with each other. The model supports the concept that information about metabolic tissue status is communicated to upstream vessels by conducted responses and that this plays an important role in the autoregulation of flow.

Comparison with previous model studies.

Two previous modeling studies have considered the contributions of both myogenic and shear-dependent responses to autoregulation (4, 20). In both models, the inclusion of shear-dependent responses led to substantially weaker autoregulation than would be the case with no shear-dependent response. The assumptions of these models differed from those of the present model. Both previous studies used experimental data (19) in which maximal shear-dependent dilation was observed at a shear stress of 4 dyn/cm². Arteriolar wall shear stress is usually >4 dyn/cm² (27). Cornelissen et al. (4) introduced an attenuation factor that effectively shifted the assumed response into a more physiological range of shear stress. The present study is based on data (33) in which maximal sensitivity to wall shear stress occurs in the physiologically relevant range of 10 to 50 dyn/cm². A second difference is that both previous models expressed the myogenic response as a function of intravascular pressure. Liao and Kuo (20) expressed vessel diameter as an explicit function of pressure, whereas Cornelissen et al. (4) expressed the myogenic tone as a sigmoidal function of pressure. In the present study, myogenic tone is assumed to depend on wall tension and not directly on pressure. This assumption is preferable because the dominant stress in the vessel wall is circumferential tension, not pressure. Any shear-dependent vasodilation results in increased wall tension according to the law of Laplace and thereby generates a myogenic response. Finally, neither of these studies (4, 20) considered the myogenic and shear-dependent responses in conjunction with a metabolic response. The main finding of the present study that the combined action of the metabolic and myogenic responses is required to overcome the effect of the shear-dependent response and achieve autoregulation of flow with increasing arterial pressure depends on the analysis of the simultaneous effects of all three mechanisms.

Limitations of present model.

The present model involves several simplifications. The three mechanisms included in this model do not represent all known mechanisms of flow regulation (8). We (1) discuss other possible regulatory mechanisms that could be added to the current model. The model is limited by the available experimental data on simultaneous vascular responses to pressure and wall shear stress. For the myogenic response, data for a wide range of vessel diameters were incorporated in the model (3). However, the response to wall shear stress was based on one study (33), giving information corresponding to the large arteriole in the present model. The effects of flow and pressure on vessel diameter were examined in two other studies (17, 26). In one (17), the shear-dependent vasodilatory response was fully saturated at a level of wall shear stress below typical physiological levels, whereas in the other (26), the variation in diameter was recorded as a function of flow for only one intraluminal pressure. Therefore, data from these studies could not readily be incorporated into the present model.

The parameter governing shear-dependent sensitivity was assumed to be equal in both arteriolar segments. It has been observed that the shear-dependent response is greater in small arteries and large arterioles than in small arterioles (18, 32), and thus this model may overestimate the shear-dependent response in small arterioles. NO scavenging by RBCs is not considered in the model, causing a possibly greater overestimation of the shear stress contribution to autoregulation. In the current model, venular resistance is assumed constant on the basis that venules represent a small fraction of the total flow resistance and that changes in venular resistance would have relatively little effect on overall flow resistance. However, the relative contribution of venules to flow resistance increases when the arterioles are strongly dilated, such that changes in venular resistance might significantly affect flow. Shear-dependent vasodilation has been observed in venules, and this may contribute to the increase in blood flow in exercise (15). Such an effect could readily be incorporated in the model.

The present model is not tissue specific and does not incorporate mechanisms such as tubuloglomerular feedback in the kidneys or variation in intracerebral pressure in the cerebral vasculature, which are factors that likely play important roles in autoregulation in those specific organs. Metabolic demand varies with tissue type, and this may affect the contributions of the considered response mechanisms to autoregulation. The results presented here are for steady-state conditions in skeletal muscle, although the model could also be used to simulate dynamic responses to changes in arterial pressure.

Effect of myogenic response on autoregulation.

The myogenic response is generally considered to play a dominant role in autoregulation (13, 23). In many vascular beds, resistance vessels exhibit a sustained constriction in response to maintained pressure elevation. This is represented in the model by the increase in activation with pressure in Fig. 3, A and B. The present results show that the myogenic response reduces the increase in blood flow when arterial pressure is increased from 80 to 130 mmHg (Fig. 2A and Table 3). Despite the resulting sustained vasoconstriction, the myogenic response acting alone only yields a mild degree of autoregulation.

Effect of shear-dependent response on autoregulation.

The model for myogenic and shear-dependent responses is based on in vitro observations (33) of vascular responses to intraluminal pressure and flow (Fig. 1). A linear relationship between shear stress and S_tone is assumed. A more complicated relationship might be justified if more data were available on the variation of diameter with pressure and flow. If MAP is increased without changes in vascular tone, then pressures and pressure gradients are increased in all segments, causing passive dilation. Wall shear stress, which is proportional to the product of diameter and pressure gradient, is therefore increased. As a result, vessels with a shear-dependent response tend to dilate, counteracting the myogenic constriction in response to increased pressure. As seen in Fig. 2A, the shear-dependent response reverses myogenic autoregulation, with flow rate increasing more rapidly than pressure. The present results are in agreement with findings of previous models (4, 20) in which autoregulation was substantially weaker when shear-dependent responses were included.

Effect of metabolic response on autoregulation.

In this study, the metabolic response was simulated using a model (1) based on ATP release by RBCs and an upstream conducted response. The contribution of the metabolic response to autoregulation has not been previously evaluated. Including the metabolic response with both the myogenic and shear-dependent responses produces a level of autoregulation close to that which is observed in cerebral (7, 12, 21), mesenteric (14), and renal (30, 31) tissue. The current model shows that the combined effects of the myogenic and metabolic responses are necessary and sufficient to generate autoregulatory behavior, despite the contrary effect of the shear-dependent response.

In the presence of only the metabolic response, flow increases by a factor of 1.18 as pressure increases from 80 to 130 mmHg, indicating that the conducted metabolic response acting alone is sufficient for the development of strong autoregulation and that the metabolic response contributes more strongly to autoregulation than the myogenic response. If the conducted metabolic response is combined with the shear-dependent response, then the degree of autoregulation is reduced. These results show that both the myogenic and conducted metabolic responses are required to produce strong autoregulation in the presence of a shear-dependent dilator response. In this model, the metabolic regulation is considered to be achieved purely by the ATP-dependent mechanism as already described. In reality, multiple mechanisms may contribute, including tissue buildup and washout of metabolites such as adenosine. Such metabolites may also act through conducted response pathways (24, 29).

An increase in oxygen demand is accompanied by an increase in flow for a given arterial pressure (Fig. 5). For low to moderate levels of demand, blood flow shows autoregulation at a level that depends on the demand. As oxygen demand increases, autoregulatory behavior is eventually lost, because the flow at pressures under 100 mmHg is insufficient to meet metabolic demand even at maximal dilation.

Interactions among regulatory responses.

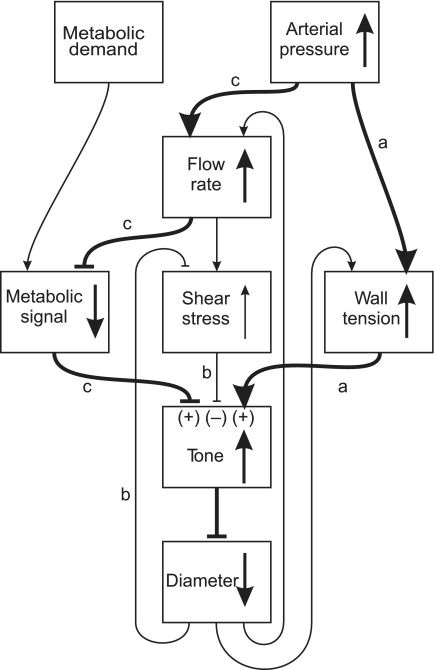
Figure 6 summarizes the contributions of these three regulatory mechanisms to blood flow autoregulation. Pathway a indicates the increase in wall tension and vascular tone that results from increased arterial pressure. The increase in tone is denoted by (+). The resulting vasoconstriction leads to increased shear stress, which decreases vascular tone (−) as described by pathway b. Increased arterial pressure increases the flow and therefore decreases the metabolic signal. The decreased metabolic response results in increased tone (+) and vasoconstriction, defined by pathway c. In summary, the model predicts that the autoregulation of blood flow over a wide range of pressures as observed experimentally results from the combined effects of the myogenic and metabolic responses, which when acting together are sufficient to overcome the competing effect of the shear-dependent response.

Fig. 6.

Schematic diagram illustrating interactions between factors involved in blood flow regulation. Heavy lines and arrows show the primary effects in the system. Blunt-ended arrows denote negative effects. Vertical arrows indicate effects of increasing arterial pressure in the presence of the myogenic, shear stress, and metabolic responses. Pathway a shows the vasoconstriction caused by increased wall tension. Pathway b shows the decrease in tone resulting from increased shear stress in the system. Pathway c shows the vasoconstrictor effect of the metabolic response in the presence of increased pressure and flow. (+) and (−), increase or decrease in tone, respectively, generated by each mechanism as a result of increased arterial pressure.

GRANTS

This work was supported by National Institutes of Health Grants HL-070657 and T32-EB-001650 and National Science Foundation Grant 9870659.