Polarity reversal lowers activation time during diastolic field stimulation of the rabbit ventricles: insights into mechanisms

Abstract

To fully characterize the mechanisms of defibrillation, it is necessary to understand the response, within the three-dimensional (3D) volume of the ventricles, to shocks given in diastole. Studies that have examined diastolic responses conducted measurements on the epicardium or on a transmural surface of the left ventricular (LV) wall only. The goal of this study was to use optical imaging experiments and 3D bidomain simulations, including a model of optical mapping, to ascertain the shock-induced virtual electrode and activation patterns throughout the rabbit ventricles following diastolic shocks. We tested the hypothesis that the locations of shock-induced regions of hyperpolarization govern the different diastolic activation patterns for shocks of reversed polarity. In model and experiment, uniform-field monophasic shocks of reversed polarities (cathode over the right ventricle is RV−, reverse polarity is LV−) were applied to the ventricles in diastole. Experiments and simulations revealed that RV− shocks resulted in longer activation times compared with LV− shocks of the same strength. 3D simulations demonstrated that RV− shocks induced a greater volume of hyperpolarization at shock end compared with LV− shocks; most of these hyperpolarized regions were located in the LV. The results of this study indicate that ventricular geometry plays an important role in both the location and size of the shock-induced virtual anodes that determine activation delay during the shock and subsequently affect shock-induced propagation. If regions of hyperpolarization that develop during the shock are sufficiently large, activation delay may persist until shock end.

defibrillation of the heart by timely application of a strong electric shock is now the only effective means for prevention of sudden cardiac death. However, understanding the mechanisms by which shocks terminate life-threatening arrhythmias has challenged researchers for many years. Despite the significant increase in our knowledge of the basic mechanisms by which a shock defibrillates the heart, several key aspects regarding the interaction between electric shock and the heart remain controversial.

One of these controversies refers to the response of the heart to shocks given in diastole. Understanding the diastolic response is important in resolving the puzzle of defibrillation because, at any time during fibrillation, a portion of the myocardium is not excited. It is now well documented that upon delivery of an electric shock, regions of positive and negative membrane polarization, termed virtual electrodes (VEs), are formed throughout the myocardium (9, 13–15, 24, 30). Some of these VEs, both negative and positive, are expected to be induced in excitable regions within the fibrillating ventricles. Thus understanding the diastolic response of the myocardium to shock-induced VEs of both polarities will help complete the mechanistic insight into the events that take place following a defibrillation shock. This response of the ventricles in diastole to electric shocks is, however, particularly difficult to study. Indeed, diastolic excitation following the shock has been reported to take place within 1 ms of shock onset (25), which renders it difficult to map using optical imaging techniques, the only method that currently allows mapping of the response of the heart to defibrillation shocks with high spatiotemporal resolution.

The existence of negative VEs, i.e., regions of hyperpolarization, during shocks given in diastole also remains controversial. Because these regions are associated with the removal of positive charges from the intracellular space, they can cause a delay in the shock-induced activations following the diastolic shock (23, 31). In an optical mapping study of isolated porcine left ventricular (LV) preparations, Sharifov and Fast (25) did not observe hyperpolarization following diastolic shocks in areas that were clearly negatively polarized when the same shocks were delivered during systole. A later study by the same team (24) reported that, when the preparation was stained with a voltage-sensitive dye only on the surface rather than via coronary perfusion as in the previous study, strong negative polarization was observed in diastole at shock onset. The authors attributed these differences to contributions from intramural VEs. These findings indicate the importance of ascertaining the distribution of VEs within the three-dimensional (3D) volume of a preparation during shocks given in diastole and the subsequent 3D postshock propagation.

Determining the distribution of VEs and the role of hyperpolarization throughout the intact ventricles is of particular importance here. Studies by Fast and colleagues used isolated LV preparations and often recorded from the transmural (cut) surface of the wedge (14, 24–27). However, recording VEs on the surfaces of the preparation does not necessarily reveal the contribution of intramural VEs (19); moreover, the cell damage present on the cut surface is likely to distort shock-induced behavior (12). Furthermore, care must be taken when interpreting optical signals from a cut surface (22).

In the intact heart, due to the differences in chamber geometry, external uniform-field shocks of reversed polarity induce different VE patterns throughout the ventricles. In the rabbit ventricles, for shocks delivered during systole, the main postshock excitable area (caused by negative polarization) was found to be located either in the LV or in the septum, depending on the shock polarity, but never in the right ventricle (RV) (21). These intramural excitable areas have been found to have a profound effect on postshock propagation (3). Similar differences in the 3D distribution of VEs, particularly in hyperpolarized areas, could exist following diastolic shocks, thus resulting in different patterns of activation and postshock behavior.

The goal of the present study is to ascertain the 3D distribution of VEs throughout the rabbit ventricles following diastolic shocks and to test the hypothesis that the locations of the shock-induced regions of hyperpolarization govern the different diastolic activation patterns in the ventricles for diastolic shocks of reversed polarity. Whereas optical mapping techniques provide high-resolution information regarding epicardial activity, the methodology is insufficient in resolving depth information and thus in testing our hypothesis. Therefore, to fully elucidate the effect of diastolic shocks in the 3D ventricular mass, this study uses a combination of optical mapping experiments and 3D bidomain computer simulations.

METHODS

Specimen preparation.

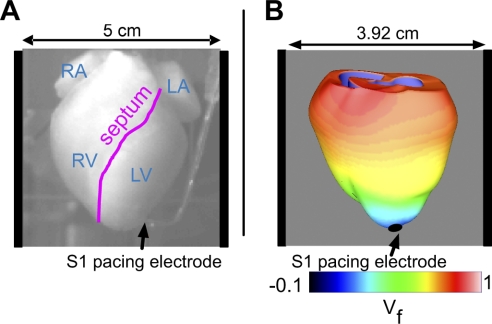
New Zealand White rabbits (2.2–3.6 kg) were preanesthetized with intramuscular ketamine (50 mg/kg). Intravenous heparin (2,000 units) and pentobarbital (60 mg/kg) were then administered. The hearts were excised and immediately Langendorff perfused on a custom-built C-shaped glass arm. The ascending aorta was cannulated and secured for retrograde perfusion of the coronary arteries with an oxygenated Tyrode solution maintained at 37°C. To minimize motion artifacts, diacetyl monoxime (Sigma) was added to the Tyrode solution at a concentration of 15–20 mM. To prevent buoyancy of the heart in the perfusion bath, the heart was secured to the glass arm by two sutures, one at the apex and another through the posterior heart, with care to avoid major vessels. The heart was then positioned in a warmed, oxygenated, circulating bath (15 cm wide) of Tyrode solution such that the anterior heart could be imaged, as shown in Fig. 1A. All experiments were conducted in accordance with the National Institutes of Health regulations for the ethical use of animals in research and were approved in advance by the Vanderbilt Institutional Animal Care and Use Committee.

Fig. 1.

A: view of the anterior rabbit heart in the experimental setup. The locations of the right atrium (RA), left atrium (LA), right ventricle (RV), left ventricle (LV), and septum are marked. The S1 pacing bipolar electrode is located near the apex, and the shock electrodes are positioned at the right and left sides of the perfusing chamber. B: schematic of the three-dimensional model of the rabbit ventricles with computed optical fluorescence signal (V_f) shown during the repolarization of an S1-paced beat. S1 stimuli are delivered via the apical pacing electrode, as indicated by the black arrow; field shocks are administered via plate electrodes located on either side of the ventricles in the chamber (as represented by the vertical black bars).

Optical imaging.

To view changes in transmembrane voltage, 200 μl of the voltage-sensitive fluorescent dye di-4-ANEPPS (0.5 mg/ml dimethyl sulfoxide; Molecular Probes; Eugene, OR) was administered to rabbit hearts (n = 4) via a bolus injection into a bubble trap above the aorta. The anterior heart was illuminated by a diode-pumped, solid-state 532-nm laser (Verdi; Coherent, Santa Clara, CA). The emitted light was passed through a cutoff filter (no. 25 Red, 607 nm, Tiffen). Images were acquired with a high temporal resolution charge-coupled device camera (Redshirt: 26×26 pixels, 5,000 frames/s). Figure 1A shows the view of the anterior rabbit heart. The typical field of view required to image the whole rabbit heart was 5 × 5 cm².

Computational modeling.

Simulations of the response of the ventricles to shocks were conducted using an anatomically realistic model of the rabbit ventricles (Fig. 1B), employed previously by us to study shock-induced vulnerability and defibrillation (3, 20, 21). Detail regarding the model and the numerical approach can be found in these publications. Briefly, the model incorporated realistic rabbit ventricular geometry and fiber orientation and included representations of the surrounding perfusate and the blood in the ventricular cavities. The transmembrane potential (V_m) distribution was calculated throughout the ventricles using the bidomain equations. Membrane kinetics were represented by an augmented version of the Luo-Rudy dynamic model, having a resting membrane potential (V_rest) of approximately −87 mV (4) that is suitable for defibrillation studies and also incorporated the formation of pores in the cardiac membranes (electroporation) due to the high-strength shocks.

To provide meaningful comparisons between experimental and simulation results, we utilized a novel model of optical mapping (7) used in our recent studies of shock-induced VEs (6, 19). To compare the results of the simulations with those obtained experimentally, 3D V_m distributions throughout the rabbit ventricles were used as an input to a model of optical recordings. As described previously (6), the distribution of photon density following uniform epicardial illumination was calculated throughout the ventricles using the steady-state photon diffusion equation. It was then convoluted with the local value of V_m to represent fluorescent emission intensity. The photon diffusion equation was again solved to calculate photon density at the emission wavelength. Fick's Law was used to relate the gradient of this photon density at the imaged surface to the photon flux recorded by the detector. The optical signals for the numerical model (V_f) were thus synthesized solely on the epicardial surface. Tissue optical properties at illumination and emission wavelengths were represented by penetration depths of 0.90 and 2.10 mm, respectively, as measured in rabbit heart experiments (7). The advantage of this approach to simulating the optical maps is that it takes into account photon scattering in 3D, rather than only in the direction normal to the surface, as in earlier attempts to simulate optical mapping (8).

Stimulation protocol.

In experiments, 10 pacing stimuli (S1) were delivered near the apex via an insulated bipolar electrode with <1 mm of the platinum wire tips exposed (0.2 mm diameter, 2-mm spacing between poles). Stimuli (4-ms long, strength twice the diastolic threshold) were provided by a computer-controlled current source (Bloom Associates, Narberth, PA) and were delivered at intervals of 300–350 ms.

To isolate the basic contribution of ventricular anatomy to diastolic shock response, and, in particular, the geometrical differences between the LV and RV, the present study employs a spatially uniform applied field. Field shocks (S2) were produced by a custom high-voltage stimulator (18) and applied via titanium plates positioned at either ends of the bath such that they faced the LV and RV (Fig. 1A). The 2-ms S2 shocks were applied during diastole (S1–S2 coupling interval of 300–350 ms) at strengths of 5, 10, 15, 20, 25, and 30 V/cm; for each shock strength, the polarity of the shock was also reversed. Similar to a previous study (21), shocks for which the cathode faced the RV and the anode faced the LV were labeled RV−; the reverse polarity was referred to as an LV− shock.

In simulations, the ventricles were paced via an apical pacing electrode. Diastolic field shocks of the same strength as in the experiments were applied to the ventricles via plate electrodes located at the vertical boundaries of the perfusing chamber (Fig. 1B). The stimulation protocol in the modeling studies was identical to that in the experiments. The model provided simulation data regarding both the 3D distribution of V_m and the epicardial distribution of V_f.

Data processing and analysis.

When necessary to improve signal quality, the experimental data were spatially filtered with a 3 × 3 Gaussian filter. To preserve the shock timing, no temporal filtering was utilized. Experimental data were normalized on a pixel-by-pixel basis, according to the change in fluorescence (F) during the S1 pacing response. The resulting normalized data ranged from 0 (rest) to 1 (peak) for the S1 response. Pixels corresponding to atrial tissue were digitally removed from the data and subsequent analyses. In simulations, V_f numerical data were normalized to the last S1 paced activation such that data ranged from 0 (rest) to 1 (peak) in a manner similar to experimental normalization.

Total activation time (AT) was defined as the time elapsed between the start of the applied shock and the time at which the last ventricular pixel (experiments) or node (simulations) reached the activation cutoff of F (experiments) or V_f (simulations) equal to 0.5. We then normalized AT to the S1 whole ventricle AT for both experiments and simulations. A paired, one-tailed Student's t-test was employed in both simulations and experiments to test the null hypothesis that there was no difference between the mean ATs for RV− vs. LV− shocks; P < 0.05 was considered significant to disprove the null hypothesis. In experiments, AT variability among different hearts was measured via the SE of the mean.

In simulations, the distributions of V_m and V_f on the epicardial surface were analyzed both during and following shock application. V_m was also evaluated within the 3D bulk of the ventricular myocardium. Analysis of these distributions allowed both examination of epicardial and transmural VE distributions and activation patterns, as well as the calculation of the area or volume occupied by shock-induced hyperpolarization (for V_f and V_m, respectively) at any instant of time.

The total volume occupied by myocardial hyperpolarization in the 3D ventricles was assessed in simulations, for each shock strength and shock polarity, as the percentage of myocardial volume (out of the entire ventricular volume) experiencing a cutoff V_m of less than V_rest at shock end. Since the main shock-end excitable area for RV− and LV− shocks is either in the LV free wall or septum, respectively (21), evaluating regional hyperpolarization in the RV and septum (RV/S) and in the LV separately permitted assessment of the effect of chamber geometry on shock-induced VEs and its subsequent effect on AT. In simulations, the amount of hyperpolarization in RV/S or LV was calculated as the percentage of RV/S or LV volume (out of the total ventricular volume) experiencing V_m of less than V_rest at shock end for a given shock strength and shock polarity. The amount of anterior epicardial hyperpolarization was assessed as the percentage of anterior epicardium (out of the entire epicardial surface) experiencing V_f of less than zero at shock end, and the amount of anterior epicardium activated at a given time was calculated as the percentage of the anterior epicardial surface area experiencing V_f greater than the activation cutoff of 0.5 out of the total anterior epicardial surface area.

RESULTS

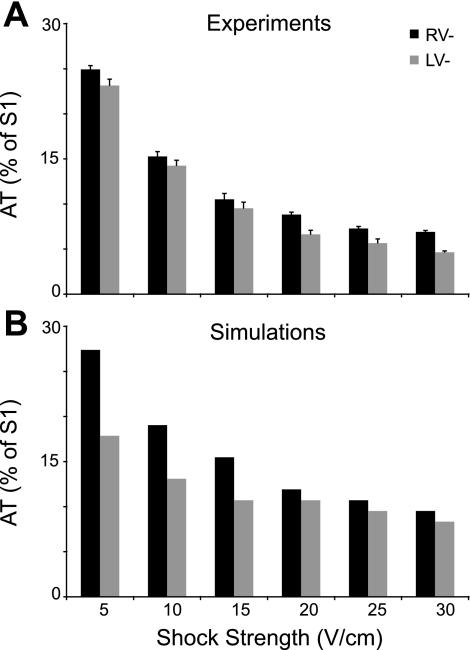
Figure 2 demonstrates the effects of an increase in shock strength, for shocks of both polarities, on AT in experiments (Fig. 2A, average over results in all preparations) and simulations (Fig. 2B, bidomain ventricular model). Clearly, simulation and experimental results exhibit the same trend in the global response of the diastolic ventricles to shocks. In both experiments and simulation, the AT decreases with the increase in shock strength, regardless of shock polarity. This decrease is faster for low shock strengths and slows down for shock strengths in the range of 20 to 30 V/cm. Furthermore, for all shock strengths tested, RV− shocks result in significantly longer ATs compared with LV− shocks of the same strength in both simulations (P < 0.018) and experiments (P < 0.00037). For RV− shocks, ATs were, on average, 17.2% longer in experiments and 21.7% longer in simulations than for LV− shocks. This new finding implicates anatomical differences between ventricular chambers in the diastolic shock-induced polarization and postshock propagation. To determine the role of chamber anatomical differences in VE (and specifically, hyperpolarization) and subsequent propagation within the 3D volume of the ventricles, we examined the distribution of shock-induced V_m and the propagation pattern that ensues on the epicardial surface (by optical imaging and simulations) and throughout the 3D volume of the ventricles (by simulations) during and after the shock.

Fig. 2.

Total epicardial activation time (AT), measured from the onset of the shock until the last pixel (experiment) or myocardial node (simulation) was activated, as a function of shock strength for both RV− and LV− shock polarities in experiments (A) and in simulations (B). Error bars in A indicate the SE of the mean.

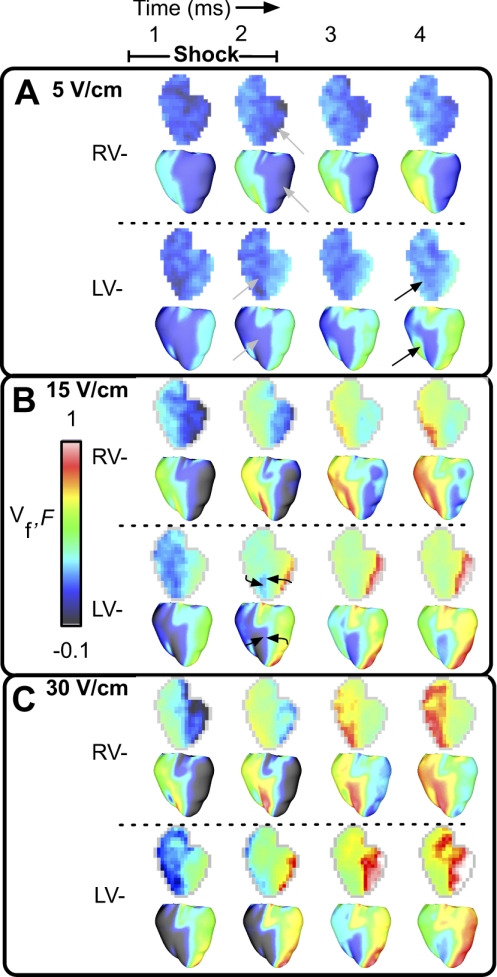
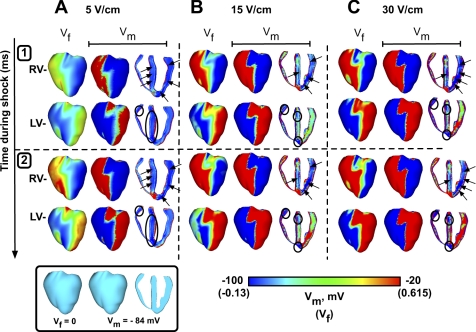
Figure 3 presents optical maps of epicardial surface V_m distribution induced by the diastolic shock in one experiment (F) and in the model (V_f). Figure 3A portrays the effects of RV− and LV− diastolic shocks of strength of 5 V/cm. RV− shocks result in depolarization over the RV epicardium and hyperpolarization at the LV epicardium (gray arrows) during the shock, after which activations emanating from the depolarized RV progress slowly across the epicardial surface in both the experiment (top rows) and the simulation (bottom rows). LV− shocks result in hyperpolarization on the RV epicardium (gray arrows); however, activations ensue not only from the LV epicardium in the vicinity of the cathode, but also on the epicardium near the RV-septal junction in both the simulation and the experiment (black arrows).

Fig. 3.

Optical maps of epicardial surface polarization in experiments [fluorescence (F), top rows] and in simulations (V_f, bottom rows) during and after the shock. Postshock timing is indicated at top. Shock strengths are 5 (A), 15 (B), and 30 V/cm (C).

Figure 3B presents epicardial optical maps of the ventricular response to a shock of strength of 15 V/cm. Both shock polarities are associated with postshock activations that appear to propagate quickly during and after the shock in experiment and simulation. For RV− shocks, activations originate on the RV epicardium; after shock end, these wave fronts progress further toward the LV. LV− shocks elicit activations on both LV and RV epicardial surfaces; these wave fronts propagate from the epicardial RV-septal junction, overrunning the virtual anodes (black arrows). Shock-induced hyperpolarization is present on the LV epicardium for RV− shocks and on the RV epicardium for LV− shocks. The anterior epicardial surface area occupied by hyperpolarization at shock end enlarges with the increase in shock strength from 5 to 15 V/cm. In V_f maps, this area increased from 19.8 and 6.7% to 25.8 and 13.3% of the anterior epicardium for RV− and LV− shocks, respectively.

In Fig. 3C (30 V/cm), the area of shock-induced hyperpolarization on the anterior epicardial surface increased for both shock polarities in the experiment and in the simulation; in V_f maps, 35.1 and 37.8% of the anterior epicardium are hyperpolarized for RV− and LV− shocks, respectively. Activation progresses across the epicardium in a pattern similar to that in Fig. 3B. Simulations show that 40.4 and 41.9% of the anterior epicardium are activated for shocks of 15 V/cm at shock end (Fig. 3B), doubling the shock strength to 30 V/cm results in only 41.4 and 43.1% activated anterior epicardium at shock end (Fig. 3C).

Figure 3 reveals a good qualitative match between F and V_f maps with respect to epicardial events during and immediately following field shocks in diastole. Next, the electrical events within the 3D volume of the ventricles need to be elucidated, which can only be achieved via analysis of the model results. Because shock-induced epicardial hyperpolarization occupies a small area for low-shock strengths (Fig. 3A), whereas it occupies a much larger area following the increase in shock strength (Fig. 3, B and C), we hypothesize that shock-induced virtual anodes are responsible for the decrease in ATs as shock strength increases in Fig. 2. During the shock, activations proceeding from the virtual cathodes may be retarded or even detained when they encounter tissue experiencing shock-induced hyperpolarization, particularly when it occupies a large tissue volume, as a depolarizing wave front bordering a virtual anode may be unable to provide the downstream of positive charge that would be necessary to bring the hyperpolarized area above the threshold for activation. Although virtual anodes dissipate with the removal of a shock, it is probable that retarded wave-front propagation during the shock would affect the whole ventricle AT.

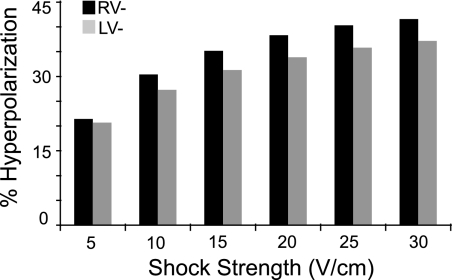
Figure 4 examines the effects of field shock strength and polarity on the 3D global myocardial hyperpolarization (GMH; defined as the total volume of hyperpolarized tissue at shock end as a percentage of the entire myocardial volume), as assessed in simulations. The initial rapid decrease in AT with an increase in shock strength from 5 to 15 V/cm (Fig. 2) corresponds to GMH that encompasses 21.4 and 20.7% of the myocardial volume for RV− and LV− shocks, respectively (5 V/cm, Fig. 4), to GMH of 35.2 and 31.3%, for RV− and LV− shocks, respectively (15 V/cm, Fig. 4). The decrease in AT for shock strengths in the range of 15–30 V/cm (Fig. 2) corresponds to an increase in GMH to 41.6 and 37.2% for RV− and LV− shocks, respectively (Fig. 4). GMH is 9.7% larger for RV− shocks compared with LV− shocks, as averaged among all shock strengths.

Fig. 4.

The total volume of hyperpolarized ventricular myocardium (expressed as a percentage of the total myocardial volume) as a function of shock strength, obtained from the numerical simulations. The total volume of hyperpolarization increases with the increase in shock strength and is greater for RV− shocks.

It is clear that shocks of opposite polarity yield differences in the volume occupied by shock-induced hyperpolarization at shock end within the 3D ventricles. To investigate how chamber geometry influences the formation of regions of shock-induced hyperpolarization during the shock, simulations in Fig. 5 examine the role of shock polarity on the location of the virtual anodes during the shock. Simulated maps of epicardial V_f and both epicardial and transmural V_m (in an apex-to-base slice through the ventricles) are presented at 1 and 2 ms after shock onset for three different shock strengths. Because V_f (Fig. 5, A–C, left column) represents an average of V_m values transduced from a 3D scattering volume beneath the epicardial recording site, the magnitude of shock-induced VEs in the optical maps is smaller than that in the V_m maps; this is consistent with previous findings (5, 7). The differences between epicardial V_m and V_f decrease with the increase in shock strength for both polarities. The reason is that strong VEs, present mostly on the epicardium for low shock strengths, extend into the transmural direction with the increase in shock strength. Thus, for high shock strengths, the V_m throughout the scattering volume beneath a given epicardial recording site is the same as the potential at the surface site.

Fig. 5.

Simulation results for 5 (A), 15 (B), and 30 V/cm (C) for the first (top, 1) and second (bottom, 2) milliseconds following shock onset. For each shock strength and time, epicardial V_f (left) and both epicardial (middle) and transmural transmembrane potential (V_m; right) are shown for both RV− (top rows) and LV− shocks (bottom rows).

For shocks of 5 V/cm (Fig. 5A), RV− polarity results in hyperpolarization in both the septum and LV free wall (dark blue areas, indicated by the black arrows). Although LV− shocks also result in septal hyperpolarization in the mid-myocardium, shocks of this polarity result in additional hyperpolarization in the RV free wall (black ellipses).

During the shock, a field shock of strength 15 V/cm results in areas of strong negative and positive VEs (Fig. 5B). RV− shocks induce virtual anodes (black arrows) predominantly in the LV free wall, as the septal hyperpolarization that appeared during the 5 V/cm shock (Fig. 5A) has decreased here due to the enlargement of the depolarized regions in the septum. LV− shocks cause hyperpolarization in the RV free wall close to the base and both basal and apical hyperpolarization in the septum (black ellipses).

Although the VE pattern in Fig. 5C (30 V/cm) is similar to that in Fig. 5B, the virtual anodes have increased in area for both polarities, with V_f maps now quite similar to the epicardial V_m maps. Hyperpolarization is predominant in the LV free wall and mid-septum for RV− shocks (black arrows) and present at the RV base and in the apical and basal portions of the septum for LV− shocks (black ellipses).

The asymmetry of right vs. left chamber anatomy results in very distinct epicardial and transmural patterns of shock-induced virtual anodes for RV− and LV− shocks. Clearly, as shown in Fig. 5, RV− shocks induce virtual anodes predominantly in the LV, while LV− shocks result in virtual anodes in the RV/S.

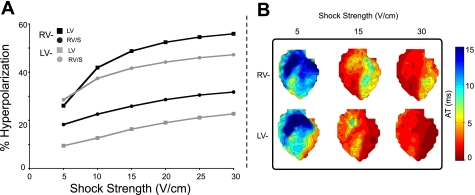
Figure 6A quantifies the tissue volume occupied by hyperpolarization (as a percentage of total regional tissue volume) at shock end for LV and RV/S regions as a function of shock strength. The amount of tissue hyperpolarized at shock end increases with shock strength for both regions and polarities, consistent with results presented in Fig. 4. RV− shocks induce the largest volume of hyperpolarization in the LV (Fig. 6A, solid squares) for all shock strengths except 5 V/cm, while the same quantity is smaller for RV− shocks in the RV/S (solid circles). For an RV− shock of 30 V/cm, ∼56% of the LV is hyperpolarized at shock end, while this amount is only ∼32% in the RV/S; an LV− shock of 30 V/cm results in hyperpolarization of ∼47% of the RV/S region, but only ∼23% of the LV region. For LV− shocks, the largest volume of hyperpolarization is located in the RV/S (shaded circles), while this volume is much smaller in the LV for LV− shocks (Fig. 6A, shaded squares).

Fig. 6.

A: regional tissue volume of hyperpolarization, assessed as a percentage of the total regional tissue volume, as a function of shock strength for the numerical simulations. B: experimental isochrone maps for shock strengths of 5, 15, and 30 V/cm for both RV− (top row) and LV− (bottom row) shocks. RV/S, RV and septum.

Figure 6B presents activation maps (isochrones) from the onset of a diastolic shock to 15 ms postshock, as obtained from one heart for three shock strengths. Following the 5 V/cm shock, for which there is little difference in LV vs. RV/S hyperpolarization for both polarities (Fig. 6A), activation maps are also similar for RV− and LV− shocks. However, for the 15 V/cm shock, the greatest volume of hyperpolarization occurs in the LV for RV− polarity (Fig. 6A, solid squares); the corresponding isochrone map (Fig. 6B, top row) reveals that the longest AT occurs in the LV for an RV− shock. For a 15 V/cm shock of LV− polarity, the greatest volume of hyperpolarization is in the RV/S (Fig. 6A, shaded circles), the region that is associated with the longest AT in the corresponding isochrone map (Fig. 6B, bottom row). Shocks of 30 V/cm induce the largest volume of hyperpolarization in the LV region for RV− shocks, followed by the RV/S region for LV− shocks (Fig. 6A, solid squares and shaded circles, respectively). Isochrones following shocks of 30 V/cm demonstrate that the greatest activation delay is in the LV for RV− polarity (Fig. 6B, top row). The LV is associated with the greatest volume of hyperpolarization for this shock strength and polarity (Fig. 6A, solid circles).

These findings demonstrate, consistent with our hypothesis, that shock-induced virtual anodes are responsible for the decrease in AT following the increase in shock strength in Fig. 2. Furthermore, it is clear that chamber geometry and fiber architecture determine the location of the shock-induced virtual anodes and thus the global time of ventricular activation and the pattern of postshock propagation.

DISCUSSION

This study focuses on the role of ventricular geometry in the response of the myocardium to external, uniform-field shocks delivered in diastole. 3D computer simulations and optical mapping experiments were combined to test the hypothesis that the locations and volumes of the shock-induced regions of hyperpolarization govern the differences in diastolic activation timing and patterns of activation in the ventricles for shocks of reversed polarity.

To test this hypothesis, this study used optical mapping of high temporal resolution, which captured the entire anterior epicardium of the rabbit ventricles and enabled recording of transient shock-induced polarization. Hyperpolarization during diastolic stimulation has been challenging to study previously. The prompt response of F to the shock has been known to reverse when shock polarity is reversed, but early studies were unable to visualize any surface hyperpolarization clearly (16). A number of later experiments have also been unable to detect negative polarizations during diastolic shocks (25, 33, 34). Another investigation (12) observed that transient hyperpolarization appeared at the very beginning of a shock but disappeared within 1 ms. Despite numerous predictions regarding the existence of hyperpolarization during shocks given in diastole, as reviewed by Wikswo and Roth (32), only recently have optical mapping experiments employing global tissue staining (24) demonstrated both positive and negative polarization during diastolic field stimulation. In the present experiments, both epicardial hyperpolarization and depolarization were observed during the application of diastolic shocks.

In this study, computer simulations synthesized optical signals from the results of 3D bidomain simulations to facilitate comparison between experiment and simulation results, taking 3D photon scattering into account (21). Simulation results demonstrated an excellent match to experiments on the anterior epicardium and provided insight regarding the development of VEs within the 3D volume of the ventricles, revealing the role of shock-induced hyperpolarization in activation delays during the shock, consistent with earlier predictions for point stimulation (23). The uniform applied field used in both simulations and experiments facilitated elucidation of the basic contribution of ventricular anatomy to the diastolic shock response, since it eliminated field nonuniformity, shown in itself to result in shock-induced VEs (15). In this case, reversal of shock polarity acted to only reverse the direction of the current flow through the ventricular chambers. Finally, the use of monophasic shocks avoided the additional nonlinear effects associated with biphasic defibrillation shock waveforms (1, 2, 11), allowing us to examine the basic response of the diastolic ventricles to electric shocks.

We found that AT decreases with increasing shock strength, consistent with previous studies using LV wedge preparations (25–27). In the present study, RV− shocks result in significantly longer ATs compared with LV− shocks of the same strength in both simulations and experiments. The increased ATs in RV− shocks are a result of the greater volumes of hyperpolarization induced by RV− shocks compared with shocks of LV− polarity. Because hyperpolarization is associated with the removal of positive charge from the intracellular space, it can stall the propagation of the shock-induced activations for the duration of the shock, as noted in the LV wedge study by Sharifov and Fast (25). The size of the region of shock-induced hyperpolarization is a factor in this activation delay: if the region of effective current sink is small (extent is less than a few length constants), action currents in front of an advancing wave front can bridge this sink region, and the activation can easily traverse the region during the shock without a delay. However, if the region of shock-induced hyperpolarization is of sufficient size, the activation wave front will be unable to traverse the region during the shock, and activation delay will result. For instance, in Fig. 5C, the smaller regions of hyperpolarization existing in RV/S for an LV− shock of 30 V/cm are indicated by the ellipses, while the larger hyperpolarized region in the LV during an RV− shock is indicated by the arrows; the respective ATs for the LV− and RV− shocks are ∼42 and ∼37 ms, indicating dependence of activation delay on the size of the hyperpolarized region.

The location of virtual anodes during uniform-field shocks delivered to a paced activation has been shown to depend on shock polarity (21), indicating the importance of ventricular geometry and fiber orientation in determining the shape and location of shock-induced hyperpolarization within the 3D volume of the ventricles. The location of the virtual anodes in the tissue bulk is of paramount importance to shock outcome, as shown in a recent study by Ashihara et al. (3). In the present study, the main regions of shock-induced hyperpolarization were located in the LV for RV− shocks and in the RV/S for LV− shocks, which is consistent with studies wherein shocks were applied during a paced beat (20, 21). The LV regions of hyperpolarization following RV− shocks were larger compared with those in RV/S for LV− shocks. Thus RV− shocks resulted in significantly longer ATs compared with LV− shocks of the same strength, as observed in both simulations and experiments.

Shock-induced hyperpolarization has been implicated previously as an important factor in postshock propagation dynamics and defibrillation outcome. Studies have demonstrated that an electric shock successfully extinguishes fibrillatory wave fronts without initiating new activations if the shock-induced excitations manage to traverse the postshock excitable areas before the rest of the myocardium recovers from shock-induced depolarization (9, 28). If activation of these excitable areas is delayed, the surrounding myocardium can recover, potentially opening a pathway for reentry. The results of this study suggest an additional role of shock-induced hyperpolarization: creating activation delay during the shock. If the regions of hyperpolarization that develop during the shock are sufficiently large, activation delay may persist until shock end. Clinically relevant defibrillation shocks are of longer duration than used in the present study and could entail significant activation delays during the shock. The results of the present study indicate that a potential paradigm for increasing the probability of a successful defibrillation shock would be to decrease the duration of the shock, while keeping it longer than the time needed for the shock to charge the membrane (the membrane time constant), thus allowing VEs to fully develop. This might also be possible to achieve by adjusting the shock pulse shape, particularly for transthoracic defibrillation (17).

Limitations.

There exist differences in the values of the anterior epicardial ATs between experiment and simulations for low-strength shocks. It is important to note that experimental results average measurements made in several rabbit hearts, whereas simulation results are based on the geometry of a single specimen, and it was not possible to scale the model to the exact geometry of any one of the hearts studied experimentally.

The limitations of the 3D rabbit ventricular model and of experimental techniques used have been described elsewhere (10, 21, 29). These also include the limitations of the membrane model, as well as the lack of small-scale tissue heterogeneities. The excellent match between simulation and experimental results, similar to the agreement demonstrated in Ref. 21, indicates that large-scale geometry and fiber orientation are the most influential determinants of activation delay and the pattern of shock-induced propagation in the present study.

The translation of the findings of the present study to scenarios involving the human heart, particularly in patients with implantable cardioverter-defibrillators, should be performed with caution. The presence of hypertrophy, fibrosis, or scar tissue in the heart could alter shock-induced VEs, including hyperpolarization, and thus the global postshock behavior.

GRANTS

This work was supported by National Heart, Lung, and Blood Institute Grants HL063195 and HL082729 (to N. A. Trayanova) and HL058241 (to J. P. Wikswo), and the Vanderbilt Institute for Integrative Biosystems Research and Education.