Modelling pulmonary blood flow

Abstract

Computational model analysis is a method that has been used widely to understand and interpret complexity of interactions in the pulmonary system. Pulmonary blood transport is a multi-scale phenomenon that involves scale-dependent structure and function, therefore requiring different model assumptions for the microcirculation and the arterial or venous flows. The blood transport systems interact with the surrounding lung tissue, and are dependent on hydrostatic pressure gradients, control of vasoconstriction, and the topology and material composition of the vascular trees. This review focuses on computational models that have been developed to study the different mechanisms contributing to regional perfusion of the lung. Different models for the microcirculation and the pulmonary arteries are considered, including fractal approaches and anatomically-based methods. The studies that are reviewed illustrate the different complementary approaches that can be used to address the same physiological question of flow heterogeneity.

1. Introduction

The pulmonary circulation – also known as the lesser circulation – is the mechanistic conveyor that facilitates exchange of respiratory gases between the body and the environment. It comprises a network of distensible blood vessels, with a reduced muscular population compared with vessels of the systemic circulation. The pulmonary arterial tree distributes deoxygenated blood to the gas exchange surfaces. After emerging from the right ventricle the pulmonary arterial trunk successively bifurcates into increasingly smaller blood vessels that ultimately feed into the dense pulmonary capillary plexus. The pulmonary capillaries wrap over the alveolar surfaces, forming an extremely thin interface between gas and blood. The interface consists of three distinct layers: the alveolar epithelium, the interstitium (accommodating connective tissue fibres and basement membranes), and the capillary endothelium, with a combined thickness of only around 0.1–0.3 µm (Hlastala and Berger, 2001). The oxygenated blood is carried back to the heart through the pulmonary veins which merge into successively larger vessels, normally terminating at four main veins feeding into the left atrium of the heart. The pulmonary trunk receives the entire output from the right heart, but due to the relatively low resistance of the pulmonary circuit a much smaller pressure is required to pump blood through the lung than through the systemic circulation.

The regional distribution of blood in the lung is determined by the effect of gravity on hydrostatic pressure gradients and intrapleural pressure; by the topology of the vascular trees, their material properties, and mechanisms of vasocontrol; and by the physical properties of blood. These factors interact in a dynamically expanding and recoiling organ, with time-varying boundary conditions for blood pressure, and subject to the effect of changes in posture. A further factor is the difference in vascular branching geometry between humans and typical laboratory animals, which complicates interpretation of experimental measurements. The relative contribution of these different factors to the variation in distribution of blood remains under strong debate (Glenny et al., 2008). Early studies of perfusion distribution in the human lung used relatively low resolution external measures averaged over large regions of the lung (e.g. West and Dollery, 1960; Bryan et al., 1964; West et al., 1964; Anthonisen and Milic-Emili, 1966). These studies typically measured a vertical gradient of increasing blood flow from the least (gravitationally) dependent to the most dependent regions of the lung. The well known zonal model (West et al., 1964) was developed on the basis of these observations, concluding that hydrostatic pressure differences are the main determinant of blood flow distribution. Other studies have suggested that gravity is only a minor determinant of pulmonary perfusion. For example, Glenny et al. (1999) demonstrated a persistent flow gradient in the baboon lung, somewhat independent of body posture, yet the zonal model would predict a reversal of the flow gradient with reversal of posture. Other experimental studies of perfusion heterogeneity in different postures support the hypothesis that factors other than gravity are largely responsible for flow distribution. (Musch et al., 2002) used PET (positron emission tomography) imaging to assess the distribution of ventilation and perfusion in prone versus supine humans. They demonstrated that both ventilation and perfusion gradients (favouring caudal lung regions) were maintained in both postures. They also found that flow heterogeneity, as measured by the coefficient of variation squared, was unaffected by posture. (Jones et al., 2001) attained similar results using electron beam computed tomography scans on healthy humans, also comparing the prone and supine postures. Gravity was estimated to contribute only 22–34% of perfusion heterogeneity in the supine posture and 27–41% when subjects were prone.

While gravity certainly contributes to the global distribution of blood, other factors must contribute to the heterogeneity that has been measured within iso-gravitational planes. Agreement between the different schools of thought is complicated by differences in experimental protocols, species differences, and mechanisms that are likely to interact during experiments. Computational models provide a tool that is complementary to experimental studies, and that can be used to study integrated function while controlling complexity and interactions. The mechanisms that would normally interact in the lung and therefore potentially obscure some important function can be controlled in a computational model. For example, the influence of vascular branching asymmetry has been studied using fractal models (Glenny and Robertson, 1991; Parker et al., 1997) and by comparing flow in symmetric and anatomically-based models that represent an individual (Burrowes et al., 2005b). Ideally the influence of a single mechanism can be isolated and quantified, and then the other factors introduced and/or isolated one at a time. Some of these studies have already been completed (e.g. Burrowes et al., 2006), but important studies remain to be done.

2. Heterogeneous structure and function in the pulmonary arteries

2.1 Structure of the pulmonary arterial and venous trees

Cast-based morphological studies of the pulmonary vasculature (Horsfield, 1978; Horsfield and Gordon, 1981) have provided geometric information for vessel length, diameter and number of vessels in each branching generation and order, down to the level of the capillary bed. The ‘accompanying’ or ‘conventional’ pulmonary arteries have a one-to-one correspondence with the conducting airway tree, hence following the airway branching geometry (Weibel, 1963). The pulmonary veins more loosely follow the other two trees, and bifurcate between neighbouring airway and arterial bifurcations. Fung (1991) described the relationship between the pulmonary arteries and veins as “islands in an ocean”, where the arteriolar regions represent the islands, and the venous regions a continuous ocean that fills the space not occupied by airways or arteries.

A characteristic – but often overlooked - feature of the pulmonary vasculature is the extensive system of supernumerary vessels that branch off at approximately right angles from the accompanying arterial (or venous) vessels, and then rapidly bifurcate to supply the closest respiratory tissue (Elliot and Reid, 1965). The functional significance of these vessels remains unclear, however they have potential to provide collateral flow if the conventional vessels are occluded (de Mello and Reid, 1991). Because supernumerary vessels are not visible on angiograms, and due to the presence of a sphincter at their entrance, they have been hypothesised to be unperfused under normal conditions (Elliot and Reid, 1965; Shaw et al., 1999).

2.2 Computational studies

Computational studies of pulmonary flow heterogeneity have employed fractal (Glenny and Robertson, 1991; Krenz et al., 1992; Parker et al., 1997) and anatomically-based (Burrowes et al., 2005b; Burrowes and Tawhai, 2006) models. The following sections are not intended as a comprehensive review of the many modelling studies of the pulmonary circulation. The studies that are reviewed illustrate the different complementary approaches that can be used to address the same physiological question of flow heterogeneity. Other types of model to estimate pulmonary perfusion exist in the literature, however their aim is usually not to understand heterogeneity of perfusion. For example, Spilker et al. (2007) use anatomically-based models to predict patient-specific outcomes from surgery. Proximal pulmonary arteries were constructed from medical imaging, and impedance boundary conditions were derived from linear wave propagation theory applied to morphometrically-based models of the distal vessels. The diameters of the distal vasculature were ‘tuned’ by constricting or dilating vessels uniformly through a whole lung, so that the behaviour of the entire system matched measurements of pressure and flow distribution to the left and right lung. The goal of this type of study is to compare function pre- and post- surgical intervention, and not to differentiate between physiological mechanisms that contribute to perfusion of the normal lung.

2.2.1 Fractal models

In its simplest form, the fractal model specifies the geometric or functional relationship between a parent and child vessel at a bifurcation (for example, the Horsfield Δ model for geometry (Horsfield et al., 1971)), and assumes that this relationship is constant throughout the tree. The division of flow can be a constant, or can include random fluctuations. When the flow division is 0.5, flow is distributed evenly at all bifurcations; when the flow division departs from 0.5 the flow becomes more asymmetric. A convenience of the simplest fractal models is that solutions can be calculated analytically.

Glenny and Robertson (1991) studied the contribution of asymmetric flow division to overall flow heterogeneity using a fractal model with 1) a constant division of flow, and 2) random fluctuations in flow division defined by a fixed standard deviation. They compared predicted results with experimentally measured heterogeneity and found that both models described the heterogeneity of pulmonary blood flow equally well, however the random fluctuation model was felt to be a more realistic representation of the intact arterial tree. This approach to modelling perfusion essentially works in the opposite direction to experiments, to derive an understanding of the system based on simple rules.

Glenny and Robertson (1991) noted that using a flow division estimated for the Horsfield anatomical data (Horsfield and Woldenberg, 1989) would produce a relative flow dispersion much higher than measured in their experimental animals, and surmised that this could be due to the large filling pressure used in Horsfield’s cadaver preparations in comparison to the intact lung in which measurements were made. Indeed by using a large filling pressure, the vascular casts include the supernumerary vessels that are – in theory - usually unperfused (Elliot and Reid, 1965), whereas the measurements from intact animals presumably involve minimal supernumerary recruitment. If supernumerary vessels are dynamically recruited, this will add further complexity to the study of the interactions determining flow heterogeneity. It is even possible that supernumerary recruitment could reduce heterogeneity and/or suggest a more prominent role of gravity. Focussed experimental and modelling studies are therefore needed to examine their functional significance.

Parker et al. (1997) extended the fractal concept to 3D space, using a symmetric bifurcating tree with 3D spatial distribution. The aim was to determine whether heterogeneity in flow would be estimated in iso-gravitational planes in the absence of branching asymmetry. A range of tree geometries was created by varying the branching angle. Flow in the tree structures was estimated by assuming a fractal law: the division of flow at a bifurcation was constant throughout the tree, but variable between simulations. Flow was calculated in 1 cm³ blocks of ‘tissue’, to estimate heterogeneity. Even with equal division of flow at all bifurcations, heterogeneity was predicted in the model. This occurred because the number of vessels in the 1 cm³ blocks was not equal due to the topology of the tree. It could therefore be postulated that one contribution to measurements of heterogeneity in experimental studies is from the same effect, however the distribution of terminal bronchioles and their accompanying small arteries is likely to be more uniform (in a lung expanded to total lung capacity, TLC) than in the artificial topologies generated in this study.

In preference to the discrete generation- or order-dependent summaries provided by morphometric studies, Krenz et al. (1992) used a fractal model to derive continuous functions for the longitudinal distributions of resistance, compliance, and inertance in the pulmonary vascular tree. Their fractal model was designed to represent experimentally measured flow heterogeneity and morphometric parameters. The authors noted that the concise form of their model equations for the pulmonary arterial tree is a counterpart to the classic sheet-flow model of the pulmonary microcirculation, in so much as it provides a concise structural and functional summary of a very complex structure. This is an important feature of this type of model: models with a small number of parameters lend themselves to interrogation by mathematical methods that cannot be directly applied to anatomically-based models such as those of Burrowes et al. (2005a) or Spilker et al. (2007).

One issue with fractal models is that they do not differentiate between conventional and supernumerary vessels. A fractal model must either be all-inclusive or all-exclusive of supernumerary vessels. In the first case the model operates under the assumption that supernumerary vessels are as likely to be perfused as the conventional vessels; in the second case the supernumerary vessels are all unperfused. The current body of literature suggests that the second case is the most likely (Elliot and Reid, 1965; Shaw et al., 1999). The pulmonary vascular trees are often described as having many more vessels than the airway tree; this is represented in Horsfield’s morphometric data for the Strahler branching ratios of the arterial and venous trees, of 3.0 and 3.3, respectively (Horsfield, 1978; Horsfield and Gordon, 1981), each of which are higher than the branching ratio for the bronchial airway tree (2.8). Therefore a fractal model based on Horsfield’s measurements must effectively include the supernumerary vessels. Models that have equivalent number of vessels to the symmetric Weibel model, or to the conducting airway tree, effectively exclude the supernumeraries.

2.2.2 Anatomically-based models

Supernumerary arteries were explicitly included in the models of Onuki and Nitta (1993) and Burrowes et al. (2005a). Onuki and Nitta (1993) modelled the canine pulmonary vasculature and performed preliminary calculations of blood flow. Their primary concern was that prior models did not differentiate between the supernumerary and conventional arteries. Calculation of flow in their initial models showed that flow in perfusion paths with short length can be 1.5 times larger than in long paths.

To model the pulmonary vascular trees in detail, Burrowes et al. (2005a) used an adaptation of an earlier method to model the conducting airway tree (Tawhai et al., 2004). The geometry of the largest pulmonary arterial and venous blood vessels was defined by tracing the centerlines of vessels reconstructed from automated segmentation of multidetector-row computed tomography (MDCT) imaging. The non-segmented conventional arteries that accompany the airways were modelled using a volume-filling branching (VFB) algorithm (Tawhai et al., 2004). In brief, the VFB algorithm generates a tree structure within a volume of arbitrary shape, by successively branching towards the centre of mass of seed points that are contained within the volume. The method incorporates subject-specific anatomical data by incorporating segmented airway or blood vessel centerlines, and the shape of the lung and lobes. The method has been shown to generate morphometrically-consistent tree structures to represent the conducting airways (Tawhai et al., 2004), and the pulmonary arteries and veins (Burrowes et al., 2005a). A model for the pulmonary arterial and venous trees in the left lung is shown in Fig. 1. The right lung in this figure is an iso-surface rendering from the volumetric imaging of the human subject for whom the geometric model was derived. The method generates a representation of the conventional accompanying blood vessels within the geometry of the lobes, but additional steps are required to model the extensive system of supernumerary vessels.

Fig. 1.

Anatomically-based model of the arterial and venous trees. The left lung shows the arteries and veins generated from computed tomography imaging and a volume-filling branching algorithm. The right lung surfaces are rendered from volumetric imaging, illustrating the anatomically-based volume into which the vessels are created.

Burrowes et al. (2005a) modelled the supernumerary arteries and veins by assuming that they would arise from parent branches of diameter less than 1.5 mm (Weibel, 1963) at approximately 90°, and branch rapidly until they terminated at the nearest pulmonary acinus. One criterion that guided the model derivation was that the resulting tree should have Strahler branching ratios close to 3.0 (Horsfield, 1978) and 3.3 (Horsfield and Gordon, 1981) for the arterial and venous trees, respectively. Vessel diameters were defined as 0.3 of the parent diameter, and lengths were calculated using anatomical length to diameter ratios (Horsfield, 1978; Horsfield and Gordon, 1981).

Burrowes et al. (2005b) solved the 1D Navier-Stokes equations in elastic venous and arterial tree models of a human lung from Burrowes et al. (2005a) to study the influence of normal arterial branching, gravity, and posture, on regional perfusion. Boundary conditions were prescribed for pressures at the heart, pressures at the capillary bed, a gravitational acceleration vector, and the transpulmonary pressure. The distribution of flow was compared in a model with spatially distributed symmetric branching, and the anatomically-based model (Burrowes et al., 2005a). With zero gravity (0G) and therefore equal pressure boundary conditions at all vessel outlets, flow to all terminal vessels (the tissue perfusion) in the symmetric model was uniform. When normal gravity (1G) was added, the flow distribution changed to be visually consistent with the zonal model for pulmonary perfusion (see section 3.2, and West (1964)). That is, the tissue perfusion was proportional to the gravitational height of the terminal vessels. For the symmetric model the relationship between tissue perfusion and gravitational height was linear.

In the anatomical model in 0G, tissue perfusion averaged in 50 mm slices with respect to the gravitational axis was relatively constant for regions of lung above the pulmonary artery, but it decreased systematically below the heart. Introducing gravity shifted the averaged regional flow by a similar magnitude to the shift observed in the symmetric model. That is, perfusion was decreased above the heart and increased below the heart with respect to the 0G simulations. However a further feature of the results was that in both the 0G and 1G cases the anatomical model showed a persistent decrease in flow in the most dependent region of the model (see Fig. 2). This decrease was visually consistent with ‘zone 4’, but could not have originated through compression of extra-alveolar vessels or perivascular cuffing, which are mechanisms that have previously been proposed (West, 1999). The arterial model had elastic vessels, but assumed a non-deforming lung at TLC. Relative compression of the vessels in the gravitationally-dependent region therefore cannot be a mechanism in this model. The symmetric and anatomical models differed only in their branching geometry: the governing equations and boundary conditions in each model were identical. The study therefore concluded that the long transit paths in the most apical and basal regions of the anatomical model were the particular feature of the tree structure that caused persistent reduction of flow in these regions (Burrowes et al., 2005b). The model also predicted large heterogeneity in tissue perfusion, even in the absence of gravity. Heterogeneities in the model predictions were consistent with measurements from microsphere deposition studies (Glenny et al., 1999; Hlastala and Glenny, 1999), whereas the 50 mm slice averages were visually consistent with the earlier studies of (West et al., 1964).

Fig. 2.

Tissue perfusion in an anatomically-based human lung model, in the upright and inverted postures, against gravitational height. The upper panel shows mean perfusion calculated in iso-gravitational planes that are 1 mm thick; the lower panel shows results from the same simulation, but averaged in 30 mm thick slices. Figure 2 from Burrowes and Tawhai (2006), with permission.

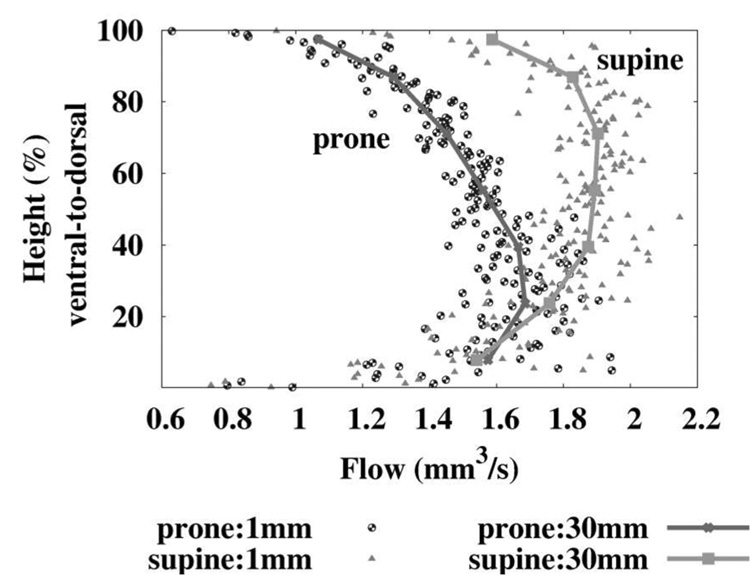
Burrowes and Tawhai (2006) further extended the model to investigate incomplete reversal of flow upon reversal of body posture (Fig. 2 for upright and inverted, and Fig. 3) for prone and supine. Inversion of posture resulted in a clear effect on the gradient of pressure, and therefore radius, at all terminal vessels in the model. However the effect on flow was less significant: while flow in the prone posture was consistently lower than flow supine, the tissue perfusion at any location was similar in either posture. This is consistent with the persistence of dorsal dominance observed in animal experiments, regardless of posture (Beck and Rehder, 1986; Glenny et al., 1999). Because the arterial tree has regionally-dependent path lengths (that is, longer branching paths to the most apical and basal regions) the resistance to flow in these model paths is similar regardless of posture, and therefore there is a persistent (non-gravitational) underlying pattern of flow in the model that is likely to exist to some extent in the real pulmonary arteries.

Fig. 3.

Tissue perfusion in an anatomically-based human lung model, in the prone and supine postures, against gravitational height. Values for mean perfusion are calculated in iso-gravitational slices that are either 1 mm thick, or 30 mm thick. Figure 5 from Burrowes and Tawhai (2006), with permission.

Current limitations of this model analysis include the lack of coupling between the arterial tree and the other vascular components of the pulmonary circulation; there is no interaction between the arteries and the parenchymal tissue; and the model does not include any vasoactive control. The first is the most obvious limiting factor for comparing the theories of gravitational vs. structural influences on regional perfusion. Pressures prescribed as boundary conditions at the terminal vessels of Burrowes et al. (2005b) and Burrowes and Tawhai (2006) varied linearly with gravitational height. Coupling with the pulmonary microcirculation could hypothetically increase the influence of gravity on the simulation results. However, Burrowes (2005) found that there was no difference in the flow distribution when the boundary pressures were equal throughout the tree. This suggests that coupling with the microcirculation may not be critical.

3. The pulmonary microcirculation

3.1 Structure and function

The pulmonary capillary plexus forms an extremely dense network of vessels, with an increased level of complexity and functionality in comparison to the capillaries of the systemic circulation. This strategic design provides a relatively large amount of additional perfusion reserve for conditions of increased flow (e.g. during exercise) and multiple alternate perfusion pathways in the event of pathway blockage at the capillary level. The human lung contains an estimated 480 million alveoli (Ochs et al., 2004) and approximately 280 billion pulmonary capillaries (Weibel, 1963). A single red blood cell (RBC) traveling from an arteriole to a venule via the pulmonary capillaries will pass through around 40–100 capillary segments in the human lung (Hogg, 1991; Huang et al., 2001). Each RBC spends around 1–3 seconds in the capillary network and during this time will traverse around 2–3 alveoli (West, 1979). The resistance to flow in microvessels is determined by the topology of the individual vessels and the resulting network, including vessel diameters, length, number and connectivity of the vessels, and on the apparent viscosity of the blood.

At the microcirculatory level blood must be considered as a two-phase non- Newtonian fluid: particles suspended in blood, particularly RBCs, strongly influence the apparent viscosity and therefore the blood flow in each segment. In blood vessels smaller than about 300 µm in diameter mechanical interactions between RBCs and the tube wall result in the preferential distribution of RBCs near the vessel centre (Pries et al., 1996). This creates a layer of zero hematocrit immediately adjacent to the wall, resulting in a reduction in the apparent viscosity of the blood. This phenomenon is known as the Fahraeus-Lindqvist effect (Fahraeus and Lindqvist, 1931), whereby apparent viscosity decreases with decreasing vessel diameter. Fluid flow velocity varies from zero at the wall of a vessel to a maximum near the centre of the vessel. This means that average RBC velocity is higher than average blood velocity. This leads to a reduction of RBC transit time through a given vessel segment, and hence to a reduction in the hematocrit contained in that segment (the tube hematocrit) relative to the hematocrit of blood entering or leaving it (the discharge hematocrit). This dynamic reduction is known as the Fahraeus effect (Fahraeus, 1929), and results in a decreasing hematocrit as blood traverses the microvasculature. The existence of a RBC-depleted layer adjacent to the tube wall underlies both the Fahraeus and the Fahraeus-Lindqvist effects. Blood viscosity has been found to be strongly hematocrit-dependent (Pries et al., 1996). Another phenomena contributing to RBC distribution is the disproportionate allocation of RBCs and plasma at bifurcations. This phase separation at a junction is proportional to the relative flow rates in the daughter vessels. Combination of the Fahraeus, Fahraeus-Lindqvist, and phase separation effects determines the hematocrit distribution throughout the capillary plexus.

The majority of pulmonary capillaries have diameters similar to or smaller than both red and white blood cells. RBCs are able to deform relatively easily to move through the capillaries, however WBCs (neutrophils in particular) are less deformable and therefore frequently become lodged in a capillary segment for some period of time. This results in an increase in the concentration of neutrophils in the lung to around 40–80 times that in the systemic circulation (Hogg and Doerschuk, 1995); this phenomenon is known as neutrophil margination.

3.2 West’s zonal theory

The different ‘zones’ of flow proposed by West (1964) are due to regional differences in the relationship between the pressures that surround the collapsible capillary vessels: namely the alveolar and capillary blood pressures. While alveolar pressure is likely to have only small regional differences in a healthy, quietly breathing lung, the blood pressure varies significantly due to hydrostatic gradients that result from gravitational forces. The effective pressure around the capillaries is the alveolar pressure. When the alveolar pressure exceeds the capillary blood pressure the capillaries collapse. Where this occurs is classified as ‘zone 1’. If the alveolar pressure only exceeds the blood pressure at the vessel exit (the venule pressure) then the Starling resistor phenomenon occurs, which is also known as the waterfall or sluice gate effect. In this ‘zone 2’ region the capillaries act as a gate to control flow. For collapsible vessels in this state flow is governed by the difference between the vessel inlet pressure (the arteriole pressure) and the alveolar pressure, rather than the difference between inlet and outlet vessel pressures as in ‘zone 3’ flow. The majority of the lung functions under zone 3 conditions where both arteriole and venule pressures exceed alveolar pressure. A further ‘zone 4’ was later added to the model to classify an observed region of reduced flow in the most gravitationally-dependent region of the lung (Hughes et al., 1968).

The zonal model predicts an increase in blood flow in the downwards direction of gravity, and therefore a reversal of the flow gradient with inversion of posture. The zonal model provides a convenient explanation for how gravity – on average - influences perfusion of the microcirculation, but it does not capture the contribution of flow phenomena in the larger blood vessels. The zonal model also describes an averaged behaviour within iso-gravitational planes, and does not seek to quantify variability that may be present at the microcirculatory level.

3.3 Heterogeneity in perfusion of the microcirculation

Under normal conditions some capillary segments are nearly always perfused and form interconnecting pathways across the alveolar wall, while in other regions of the same alveolar wall the blood frequently switches between segments. These fluctuations in perfusion are present even during conditions of constant flow ((Hanger et al., 1997; Wagner et al., 1999).

While the mechanisms remain unknown, it is clear that heterogeneity persists even at the level of the microcirculation, and the degree of heterogeneity has a regional distribution due to hydrostatic pressure gradients (Burrowes et al., 2004).

3.4 Models of the pulmonary microcirculation

The two microcirculatory networks in the body – the systemic and the pulmonary – differ somewhat in structure. Capillaries in the systemic circuit have larger diameters, are longer, and form a much less dense network than the pulmonary capillaries (Weibel, 1984). For this reason different methodologies initially evolved for modelling flow in the two circulations. Flow in the systemic capillaries was modeled within discrete vessels, while flow in the pulmonary capillaries was approximated as a sheet between interconnected posts of tissue: the ‘sheet-flow’ model (Fung and Sobin, 1969).

3.4.1 The sheet-flow model

The sheet-flow model uses parameters to represent an average capillary geometry. The microvascular sheet is characterised by two independent properties: the ratio of the vascular lumen space to the circumscribing tissue space of the network (this quantity has been termed the vascular space tissue ratio, VSTR), and the thickness or height of the microvascular sheet. The theory behind this model provides a means of analysing the pressure, velocity, thickness and streamline distributions in an interalveolar septum. The distribution and transit times of RBCs can also be determined. The model is in general agreement with experimental data for flow and resistance.

Although the sheet-flow model oversimplifies the capillary network’s anatomic structure, it has provided a useful description of the general pattern of blood flow through the alveolar walls. The sheet-flow model enables calculation of flow properties in each alveolar sheet, but the effects of individual segment geometry and the two-phase nature of blood are only accounted for by an increase in the effective resistance to overall flow. Distributions determined in the sheet-flow model are averaged over the entire capillary network; segment-to-segment variability in individual capillaries cannot be predicted. The sheet-flow model also cannot be used to study distributions of cellular transit times from arteriole to venule, because only average times can be determined.

3.4.2 Segmented network models

Because of the limitations of the sheet-flow model, the next generation of pulmonary microcirculatory models used a tube-flow model within a network representation of the pulmonary capillary system. The tube flow model, initially used for the systemic circulation, generally uses an iterative solution technique involving the following steps:

1. An initial Newtonian flow prediction is obtained via solution of Poiseuille-based flow equations;

2. Non-Newtonian dynamics as a result of RBCs are introduced which include the Fahraeus effect (reduction of intravascular hematocrit relative to the inflow hematocrit of a vessel), Fahraeus-Lindqvist effect (dependence of hematocrit on vessel diameter) and phase separation effect (the disproportionate distribution of RBCs and plasma at bifurcations). Conservation of RBCs and plasma flow is applied at every junction. The apparent viscosity of the blood within each blood vessel is then adjusted accordingly.

3. A diameter relationship is then implemented to calculate the adapted diameters based on variable factors, such as the internal blood pressure, response to mechanical and metabolic stimuli, and alveolar and pleural pressures in the case of the pulmonary system.

These steps are repeated until a converged solution is reached.

Dhadwal et al. (1997) first applied the tube-flow method to the pulmonary micro-circulation to obtain more realistic flow and cellular transit time distributions, and to study the effect of capillary geometry on these functional properties.Huang et al. (2001) extended this work by developing a more complex geometric model and incorporating cellular transit calculations. This model consisted of capillary segments randomly generated to fill a 2D square that represented a single alveolar septum. The number of capillary segments, diameters, and level of interconnectedness (the number of segments at a junction) were defined from anatomical data. The square septae were bounded by corner vessels, which are shared by three adjacent intersecting septae. Several of these networks were coupled together to investigate interalveolar flow. Flow entered each septum through a single corner vessel and exited from a single corner vessel on the opposite side of the network. The septae were only lined up one-dimensionally, therefore flow only proceeded from one septum to a single adjacent septum; in reality the capillary network forms a 3D structure and is connected to several adjacent alveolar networks.

A Voronoi mathematical meshing technique was later implemented to construct a more anatomically-realistic geometric representation of the alveolar-capillary structure (Burrowes et al., 2004). The geometry of a single alveolar sac was constructed consisting of 19 alveoli. A capillary mesh – containing approximately 1000 segments – was projected onto the surface of each alveolus, with specific procedures to ensure only a single capillary layer between adjacent alveoli (Fig. 4). The flow model of Huang et al. (2001) was implemented within this geometric structure and used to investigate regional variation in blood flow and cellular transit times in an upright human lung by imposing gravity-dependent transpulmonary and transmural pressure boundary conditions (Burrowes et al., 2004). Solution of the transport model in the microcirculatory structure resulted in predictions of flow, pressure (Fig. 4), radius, and hematocrit in each individual segment in the capillary network. Model analysis demonstrated the sensitivity of predictions to the inlet blood pressure boundary condition, and the allocated capillary diameter distribution. Simulations results illustrated the large amount of reserve perfusion capacity available during normal flow conditions. Preferential flow pathways were seen in various locations, especially at the septal boundaries where adjacent capillary networks converge.

Fig. 4.

Anatomically-based model of the alveolo-capillary network illustrating simulated blood pressures (in Pa). Capillaries are generated over the surface of 19 adjacent alveoli using a Voronoi meshing method, with a single sheet of capillaries between adjacent alveoli. The red-tipped lines indicate the location of inlet arterioles supplying blood inside the alveolar duct; the blue-tipped lines indicate the location of outlet venules draining blood flow the exterior of the network. From Burrowes (2005).

Red and white blood cell transit time distributions were compared in the upper, mid, and lower regions of the lung in the isolated capillary flow model (Burrowes et al., 2004). RBC transit times were calculated using an experimentally estimated factor for the relative velocity of RBCs to whole blood. The transit of WBCs through the pulmonary capillaries is more complex and for these calculations an empirically-derived WBC transit model was used, based on measurements from micropipette aspiration studies. Model results produced experimentally-consistent trends in cellular transit times. Both RBC and WBC transit times were shorter and more homogeneous in the lowest, most gravitationally-dependent regions (within zone 3 flow conditions) due to increased flow rates and more uniform capillary perfusion. The WBC transit model also predicted the incidence of cell stoppage during the transit from arteriole to venule. Around 37% of pathways (of the sampled 50,000) were predicted to result in an averaged sized WBC becoming trapped for at least 1 second.

4. Conclusion and future work

Computational models have provided important insights into the physiological mechanisms of regional pulmonary perfusion. Models are only valuable if they can explain observations, or they are predictive of factors that have not been and/or cannot be measured. The fractal models in section 2.2.1 fall into the first class, whereas the anatomical models in section 2.2.2 are predictive models that are built from anatomical data and have function governed by physical laws. Predictive models can be used to compare between individuals or species, or to evaluate the significance of different interacting functions on a physical outcome. Models can now be constructed that are specific to an individual (Tawhai et al., 2004; Burrowes et al., 2005a) based on medical imaging. Medical imaging is also enabling an increasing range of functional information to be extracted from the in vivo lung (see Glenny (2007) for an introduction). Modalities such as SPECT (single-photon-emission computed tomography), PET (positron emission tomography), MRI (including hyperpolarised MRI imaging) and CT allow a range of regional functional information to be measured in situ. Because functional measurements are typified by heterogeneity, computational models to interpret such measurements will be increasingly important tools.

Recent imaging studies have suggested that a change in posture primarily effects lung tissue deformation with only a minor effect on the distribution of ventilation and perfusion (Petersson et al., 2007). In addition to tissue mechanics affecting perfusion dynamics, pulmonary perfusion is also known to have a significant effect on tissue deformation, particularly in diseases such as hypertension (Scultze-Neick et al., 2000). That is, regional perfusion affects regional tissue deformation. Modelling interaction between the pulmonary circulation and the deformable lung tissue is therefore an important next step.