Models of Ratio Schedule Performance

Abstract

Predictions of P. R. Killeen's (1994) mathematical principles of reinforcement were tested for responding on ratio reinforcement schedules. The type of response key, the number of sessions per condition, and first vs. second half of a session had negligible effects on responding. Longer reinforcer durations and larger grain types engeridered more responding, affecting primarily the parameter a (specific activation). Key pecking was faster than treadle pressing, affecting primarily the parameter δ (response time). Longer intertrial intervals led to higher overall response rates and shorter postreinforcement pauses and higher running rates, and ruled out some competing explanations. The treadle data required a distinction between the energetic requirements and rate-limiting properties of extended responses. The theory was extended to predict pause durations and run rates on ratio schedules.

Killeen (1994) developed a set of principles concerning reinforcement: that incentives excite an organism and elicit responses, there are ceilings on response rates, and organisms are biased toward the particular locations and types of responses that occurred just prior to the incentive. Each of these principles was given substance by providing simple mathematical representations of them. For instance, models of the frst two principles—arousal and constraint—when combined, yield Equation 1:

$$B=\frac{\mathit{aR}∕\delta }{\mathit{aR}+1},\delta >0.$$ (1)

The dependent variable is B, response rate, the dimensions of which are responses per second. The parameter a is the amount of behavior that is evoked by the incentive under the current deprivation conditions. It is called the specific activation, it varies as a function of motivation (Killeen, 1995, in press), and its dimensions are seconds per reinforcer. The variable R is the rate of reinforcement; its dimensions are reinforcers per second. Delta (δ) measures the response time—the time that it takes for an animal to execute a response—and typically takes values between 0.25 and 0.4 s for both pigeon's key pecks and rat's lever presses. It is not the same as the time the key or lever is depressed, as it also includes the time to initiate and terminate the entire action pattern (DeCasper & Zeiler, 1977). Its dimensions are seconds per response.

Equation 1 has the same form as Herrnstein's hyperbola (1970, 1974), but Herrnstein interpreted 1/a as the rate of reinforcement for other (competing) behaviors in the organism's environment. The same form was derived from still other principles by Staddon (1977). It is a robust description of response rates on variable–interval (VI) schedules, but if we take δ literally as response duration, it predicts response rates that are much too high, and it makes incorrect predictions when extended to other schedules (e.g., Pear, 1975). The formulation is incomplete.

The third principle states that responses that precede an incentive will increase in frequency. Most reinforcement schedules require the target response to occur just before the incentive is presented, thus guaranteeing some strengthening of that class. However, an animal usually emits a sequence of responses prior to emitting the target response on which delivery of a reinforcer is contingent; does the last response take sole credit for causing reinforcer delivery or are the other preceding responses also strengthened? Both intuition and data suggest the latter. Some reinforcement schedules (e.g., ratio schedules) are more efficient than others in ensuring that it is sequences of the measured target response alone that precede the incentive and thus receive the credit for reinforcement. On interval schedules, anything that precedes a target response is equally likely to be reinforced; whereas on ratio schedules, a target response preceding the reinforced target response is itself differentially reinforced. This leads to progressive domination of the response repertoire by target responses. Rates on interval schedules would find a lower (and unstable) asymptote. These asymptotic proportions of target and other (unmeasured) responses in the animal's repertoire depend on how tightly the contingencies couple the target response to the incentive. A theory of coupling was provided in Killeen (1994; this article is hereafter referred to as “the theory”), along with predicted coupling coefficients for the major schedules of reinforcement. This article constitutes a test of the models developed for ratio schedules.

The Coupling Coefficient

In the theory, it was shown that the effects of reinforcement extend over a recent sequence of responses, with the weights accorded to the responses decaying progressively as the events become remote. A simple origin for such a decaying trace is the linear or exponentially weighted moving average (Killeen, 1981). If we treat each punctate response as a unit, we may write

$$M_n=\beta y_n+(1-\beta )M_{n-1},0<\beta <1.$$ (2)

Here, M_n represents the contents of an individual's memory immediately after the emission of the nth response; y_n is an index of that response (e.g., 1 if the nth response is a target response and 0 otherwise; it could also be used to index other characteristics, such as force or location), and the currency parameter beta (β) is the weight given to the most recent response. β is a dimensionless weight that ranges between 0 and 1. If β is close to 1, only the last response matters; if it is close to 0, only ancient history matters. Killeen (1994) found that a value of β around 0.25 characterized the rate of decay of memory for a keypeck response.

In an exemplary situation of a fixed-ratio (FR) schedule with a response requirement of four target responses (N = 4), a currency parameter of β = 0.25, M₀ = 0, and an animal that makes primarily target responses, after the first response, M₁ = 0.25. After the second response, Equation 2 gives 0.25 + 0.1875 = 0.4375: The weight of β = 0.25 to the most recent target response, plus the 0.25 that had been attributed to the first response now decayed by (1 − β) (0.75 × 0.25 = 0.1875). After the third response, the weight of target responses in memory is 0.25 + .3281 = .5781; and after the fourth, 0.6836. In general, the sum of n terms of this progression is

$$M_n=1-{(1-\beta )}^n.$$ (3)

An interesting aspect of this model is that reinforcing every response (n = 1; continuous reinforcement, CRF) strengthens the target response by only the value β, here 0.25. If we reinforce every response, we are wasting 75% of the strength of reinforcement. Reinforcing every fourth response strengthens the target response by just over 0.68. On large ratio schedules, a greater fraction of the strengthening effects of reinforcement is focused on the target response than is the case for small ratio schedules. In the limit, as n grows large, we see from Equation 3 that M_n approaches 1.0. As n → 0, M₀ → 0; the consummation of the previous reinforcer can fill memory, erasing the memory of the target responses that led to it (Killeen & Smith, 1984). Closely spaced incentives waste any reinforcing power that overreaches the target responses; it goes to prior consummatory behavior rather than to prior instances of the target response.

Why should target responses dominate the repertoire? Killeen (1994) showed how ratio schedules attract behavior toward exclusive target responding: If we characterize the proportion of target responses in the repertoire as rho (ρ) for large ratio values ρ → 1.0. Rho is lower for other schedules of reinforcement. This analysis is reviewed and qualified in the General Discussion section, but now, for simplicity, we assume that the asymptotic repertoire on ratio schedules tends to consist primarily of target responses—that is, ρ = 1.0. To the extent to which this is incorrect, the recovered value of δ will be inflated by that fraction.

Killeen (1994) preferred the continuous version of Equation 3: M_n = 1 − e^−λn. This is equal to Equation 3 for integer values of n. We may equate the two forms to show that λ = −ln (1 − β). For small values of β, λ ≅ β. The exponential version is a useful form for analyzing responses having a duration that may vary continuously, when examining the relative contributions of time and responses in the decay of memory, and for mathematical analyses of other reinforcement schedules. Those are not central considerations here, however, so we shall use the fundamental model as in Equation 3.

Equation 3 gives the contents of memory after n responses. Is there a way to generalize this equation in characterizing the typical contents of memory on other schedules of reinforcement? The case for FR schedules is the simplest:

$$\zeta =C=M_N=1{(1-\beta )}^N.$$ (4)

This is the coupling coefficient for an FR schedule that requires N responses for reinforcement. It was called zeta (ζ) in the theory. Because ζ is an awkward and unfamiliar symbol, we represent the coupling coefficient with the Roman letter C. It is a function that takes a value between 0 and 1 for a particular schedule. Its value depends on an interaction of the subject's memory parameter β and the nature and particular value of the reinforcement schedule.

On variable-ratio (VR) schedules reinforcement may occur at any time, but on the average, it occurs after N responses have been emitted. To calculate the coupling coefficient, we must integrate the product of the probability of a string lasting for n responses by the weight that each of the responses would receive in memory, over all values of n. In the theory, it was shown that for constant-probability VR schedules, this results in a hyperbolic coupling coefficient:

$$C=\frac{\lambda N}{1+\lambda N},$$ (5)

where, as before, λ = −ln(1 − β).

Both Equations 4 and 5 have the proportion of target responses in the repertoire, ρ, as an implicit multiplier, but that is taken to be equal to 1 for ratio schedules and is omitted. Therefore, in both cases, C approaches 1 as N grows large, but it does so at a faster rate for FR schedules (Equation 4) than for VR schedules (Equation 5).

The coupling coefficient modulates the expression of response rates given by Equation 1:

$$B=\frac{\mathit{CaR}∕\delta }{\mathit{aR}+1},\delta >0.$$ (6)

Equation 6 is the basic equation of prediction, with C given by Equation 4 for FR schedules and by Equation 5 for VR schedules. Its application is, however, trivial because by knowing the rate of reinforcement on ratio schedules, we automatically know what the rate of responding must have been. This is because for ratio schedules,

$$R=\frac{B}{N},N>0.$$ (7)

Equation 7 is the schedule–feedback–function for ratio schedules. Rate of reinforcement equals rate of responding divided by the average ratio requirement. Given the rate of reinforcement, we can accurately predict the rate of responding to be N times as fast, without Equation 6. All is not lost, however; we may insert Equation 7 into Equation 6 to predict response rates as a function of ratio requirement (N):

$$B=\frac{C}{\delta }-\frac{N}{a},a,\delta >0,N\le a∕\delta .$$ (8)

Now we have a true prediction. At small ratio values, coupling (C) is low and response rates low to moderate. As N increases, coupling increases to its maximum, but the lowering rate of reinforcement decreases arousal and, thence, response rates (the subtrahend in Equation 8). Rates approach a linear asymptote with a slope of −1/a and an x intercept of a/δ. The (projected) y intercept is the maximum response rate,1/δ. When the response requirement N exceeds the “extinction ratio,” a/δ, response rate settles at zero (Skinner, 1938).

Equation 8 is similar to one developed by Pear (1975) as a generalization of Herrnstein's (1974) model. It differs because in Equation 8 the coupling coefficient C is not constant, but varies as a function of Schedule type. In his Table 5, Killeen (1994) provided the coupling coefficients for the most common types of reinforcement schedules. When only a few responses are required for reinforcement, C tends to very small values (some of the effects of reinforcement are wasted by not having a long string of responses to act on), and when a large number is required, C tends toward its maximum—on ratio schedules, 1.0. A strong prediction of this model is a downturn in response rates as N → 0, which is not predicted by Pear's version (C constant), and which Pear used as evidence of the failure of Herrnstein's (1974) model to generalize to ratio schedules.

It is the purpose of this article to test Equation 8 in its two realizations (coupling [C] given by Equation 4 for FR schedules and by Equation 5 for VR schedules) against the pattern of data on those schedules. We shall also test the interpretation given to the parameters by the theory. For greater understanding of these functions and of the roles that the three parameters play in them, see Figure 1.

Figure 1.

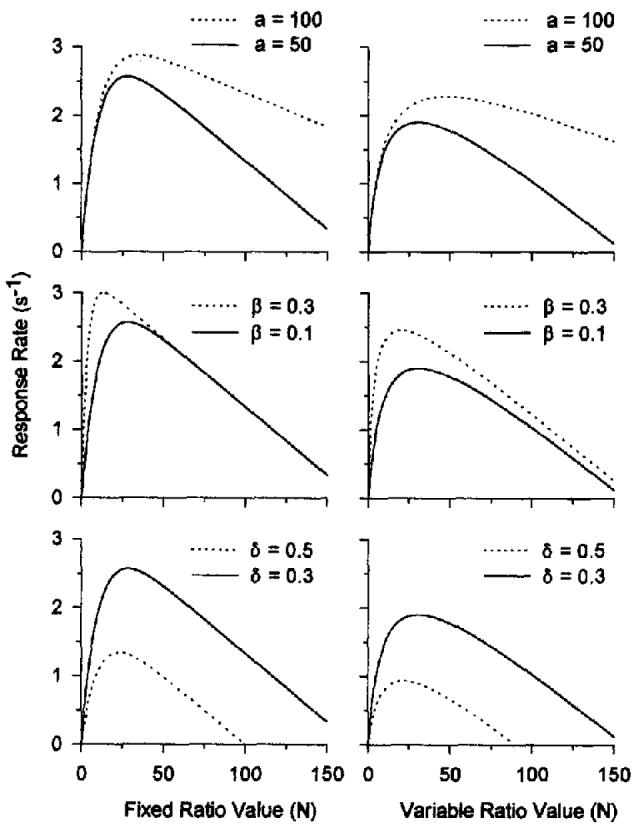
Predicted response rates on ratio schedules given by Equation 8. The solid and dashed lines were derived from Equation 8 for fixed-ratio schedules (left panels, C given by Equation 4) and variable-ratio (VR) schedules (right panels, C given by Equation 5). The parameters of the continuous curves are a = 50, β = 0.1, and δ = 0.3. The dashed lines show the effect of a change in one of the parameters. The top panels show the effect of an increase in the specific activation a, the number of seconds of responding elicited by an incentive. The middle panels illustrate the effect of an increase in the currency parameter β (and an equivalent change in λ for VR schedules). The bottom panels illustrate the effect of an increase in the response duration δ.

The left panels of Figure 1 show the predicted locus of data under FR schedules, and the right panels show the locus under VR schedules. The ascending portions of the functions reflect the increase in coupling with ratio size; the decreasing portion reflects the decrease in activation that is proportional to the decreasing rate of reinforcement under higher ratio values. It should be noted that the predicted locus for FR schedules reaches its maximum faster and falls into a linear trajectory more quickly. Memory is slower to saturate on VR schedules because many of the constituent ratios are less than N, and saturation wiU not occur until the smallest of them attains a sufficienfly large value to offer substantial coupling. The pattern for VR schedules, therefore, rises more slowly and approaches the linear descender more slowly.

The specific activation a is the number of seconds of responding elicited by an incentive. Its value depends on the value of the incentive and the deprivation of the organism. Its role in the function is indicated by the dashed lines in the top panels of Figure 1. Changes in a affect performance as a multiplicative function of ratio size, with −1/a as the slope of the linear portion and N = a/δ as the x intercept.

β is the weight given to the most recent response, causing the earlier memory to be down weighted by (1 − β). Thus, one may think of β as the rate of decay of short-term memory. When β is large, memory for the target response will saturate faster, and this will elevate response rates for smaller ratio requirements. It will have less effect for larger ratios when short-term memory will, in any case, be saturated with target responses. The dashed lines in the middle panels of Figure 1 illustrate the effects of different values of β.

Making the task more difficult will increase response time (δ) leading to lower response rates, as shown by the dashed lines in the bottom panels of Figure 1. Changes in δ move the entire function up and down as though it were simply cut out and repositioned. We begin testing Equations 8 and these interpretations of its parameters by first disposing of some methodological issues.

Experiment 1: Methodological Issues

We examine whether the type of response key influences the response rates; whether within-session changes in rate affect the shape of the data; and how important it is to provide an individual with multiple-session experience on each FR requirement. The conditions reported here as Experiment 1 address these issues. In the first set of conditions, two types of keys were used: a normally open microswitch (Lehigh Valley, Laurel, MD) and a normally closed (Gerbrands, Arlington, MA) key. This was an important comparison because “lab lore” has it that a Gerbrands switch yields cleaner responding than a microswitch, hence the Gerbrands key could potentially affect estimates of the minimum interresponse time δ. It is certainly the case that extreme values of force or displacement parameters will affect rates; we were interested in the more pragmatic question of whether distinctions between the most typically used operanda could be ignored as factors in any future tests of this model. The second issue is a concern because of McSweeney's (e.g., McSweeney, Hatfield, & Allen, 1990; McSweeney & Roll, 1993; McSweeney, Weatherly, & Swindell, 1995) provocative finding that within-session changes in response rates may affect the inferences that we draw from session-average data. The third issue concerns the effect of brief exposure to the contingencies. The amount of exposure to an FR value was reduced from multiple sessions to one session per FR value. This was an important comparison because evaluation of the model requires exposure to a range of ratio values. If response rates were comparable between a single session's exposure versus multiple sessions, it would expedite the collection of data and minimize the effects of aging and motivational drift, both in animals and in experimenters.

Method

Animals

Eight adult, show and homing pigeons (Columba livia), 6 having previous experimental histories with ratio and interval schedules and 2 experimentally naive (Birds 54 and 55), served as subjects. The pigeons were housed individually with free access to water and grit in a room with a 12-hour day/night cycle of illumination with the day cycle starting at 8 a.m. They were maintained at 80% of their ad libitum weights ± 10 g. Supplementary food, consisting of fortified mixed grain, was made available at the end of each day as needed.

Apparatus

An interface panel formed one wall of the experimental area that was 30.5 cm wide, 35 cm deep, and 28 cm high inside a Lehigh Valley (Laurel, MD) sound-attenuating chamber. White noise of 75-dB intensity was presented via a speaker mounted behind the interface panel and from a ventilation fan mounted on the wall opposite the interface panel. A house light mounted on the interface panel 24.5 cm from the chamber floor and 32 cm from the rear wall could be illuminated with a white light. A Plexiglas response key, 2 cm in diameter, was mounted on the interface panel 21 cm above a chamber floor and 17.5 cm from the rear wall. The key could be transilluminated with white light. It required 0.2 N of force to close a microswitch mounted behind the key. In Condition 2, the microswitch key was replaced with a Gerbrands (Arlington, MA) key, 2 cm in diameter, which required 0.2 N force for activation. When the hopper was raised, it provided timed access to grain (milo, millet, or maize, the last in the form of popcorn kernels) and was illuminated by a white light mounted in the top of the hopper opening. Experimental events were controlled and recorded by a PC clone (80386) computer located in the same room as the experimental chamber.

General Procedure

In Experiments 1 and 2, a single response earned the first reinforcer of every session; in the remaining experiments, the first reinforcer was response independent. In all experiments, except the second condition of Experiment 5, there was a 1-s intertrial interval (ITI) in darkness following the delivery of a reinforcer. In all experiments, the first two trials were excluded from the analyses because their response rates were generally not representative of subsequent trials. Response rates for a session were calculated by dividing the number of responses by the time that it took to complete the ratio requirement (N). The postreinforcement pause (PRP; the time to the first response) was included in the time base. Run rates were calculated as (N − 1)/(T − t_P), where T is the average time to complete the ratio, and t_P is the value of the PRP. Only data from ratio values completed by all animals are reported. When more than one session was conducted per condition, the criterion for changing conditions was that three sessions show no monotonic trends. All averages are arithmetic. The level of significance for all statistical tests was set at p < .05, and all t tests were two tailed. For clarity of presentation, some of the conditions are grouped together even though they were collected in a different order.

Key condition

Birds 3, 5, 14, and 15 (Group KC) were reinforced with a 5-s access to millet for pecking an illuminated center key in order to fulfill an FR requirement. The ratio values used were FR 2, 4, 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, 96, 104, 112, 120, 128, and 136. Group KC was given several sessions' exposure (median = 3 sessions) of 50 trials to each FR value, and experienced them in increasing order of magnitude until a bird failed to complete an experimental session within two hours. Group KC was exposed to two progressions through the range of FR values before the response key was changed from a microswitch to a Gerbrands key and was then exposed to the same FR progression once again. The houselight and key light were illuminated at the start of a session and remained illuminated until the end of a session, except during the delivery of a reinforcer while the hopper was activated.

Exposure conditions

Birds 54, 55, 56, and 57 (Group EC) were initially autoshaped to respond to the center key. (Birds 56 and 57 received several sessions of fixed interval [FI] of 30 s and FR 24 schedules before they began the present experiment.) The pigeons were then exposed to multiple sessions of 50 trials on each of the FR values (median = 5 sessions) receiving 5-s access to millet as the reinforcer. We denote this Condition EC1. They were then given a single sessions' exposure, consisting of 50 trials, to each of the following FR values: 2, 4, 6, 8, 16, 24, 32, 40, 56, 72, 88, 104, 120, and 136, first with a 5-s access to milo as the reinforcer (EC2) and then with a 5-s access to millet as the reinforcer (EC3). In this experiment, Condition EC1 will be compared with EC3 (5 sessions of exposure vs. 1 session of exposure). Comparison of EC2 versus EC3 (milo vs. millet) was deferred until Experiment 2.

Results and Discussion

Key Condition

Response rates were averaged within individual animals, (a) over the last two sessions for each FR value, and (b) over both series. The top panel of Figure 2 shows the results. Generally, response rates were high for smaller values of N and decreased as the FR requirement increased, regardless of the type of key. The slopes of regression lines, fitted to the data for the microswitch key (M = −0.019, SD = 0.012) and the Gerbrands key (M = −0.023, SD = 0.015), were not significantly different, t(3) = 1.68. The y intercepts of the regression lines, fitted to the data for the microswitch key (M = 2.686, SD = 0.702) and for the Gerbrands key (M = 2.844, SD = 0.715), were not significantly different, t(3) = 1.02. Although the power of these tests is relatively low, inspection of Figure 2 reaffirms the essential similarity of performance when using these two operanda. A single regression line describes all of the data. We conclude that the type of response key is unimportant.

Figure 2.

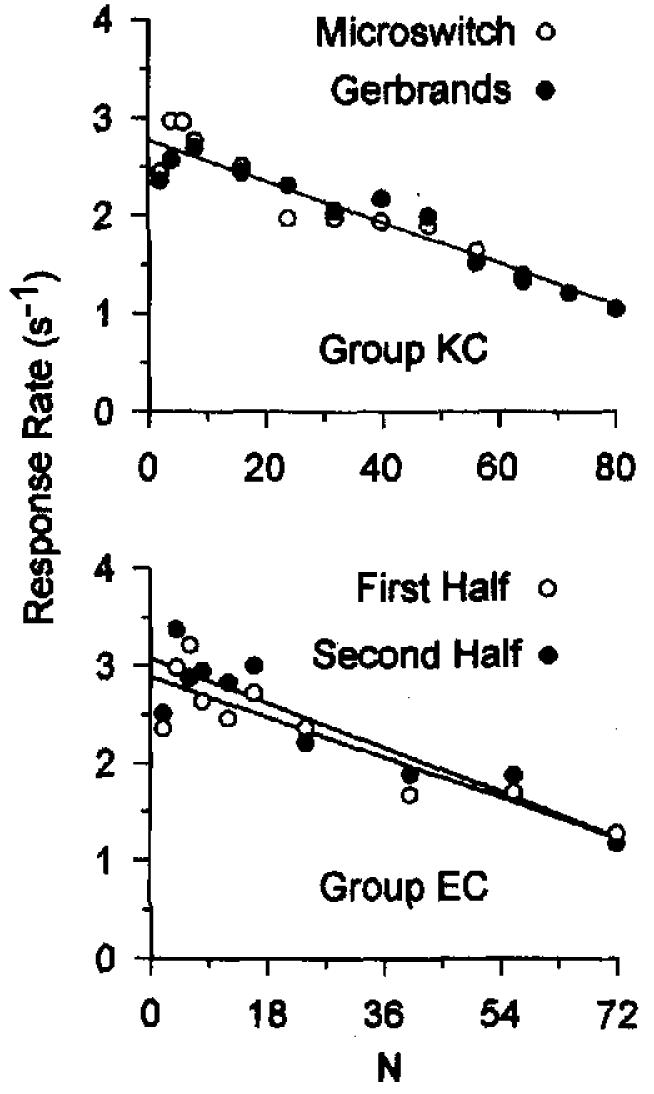
Single-session response rates from Experiment 1, averaged across pigeons and displayed as a function of fixed-ratio value. The top panel shows response rate for Birds 3, 5, 14, and 15 recorded using a microswitch (circles) or a Gerbrands (disks) key. The bottom panel shows the different functions obtained from the first half of a session alone versus the second half of a session alone. The 95% confidence intervals for the regressions within each panel overlap.

Exposure Conditions

We compared response rates from the first 24 trials with response rates from the second 24 trials for each FR value of Condition EC3. The average rates are shown in the bottom panel of Figure 2. There is little difference between average response rates in the first and second half of a session, and the form of the function is the same for both the first and second halves. The slopes of the regression lines for individual animals for the first half (M = −0.021, SD = 0.010) and for the second half (M = −0.020, SD = 0.023) were not significantly different, t(3) = 0.19. The y intercepts of the regression lines fitted to the data for the first half (M = 2.85, SD = 0.85) and for the second half (M = 2.96, SD = 1.14) were also not significantly different, t(3) = 0.68. Within-session changes in response rate that have been shown to be important elsewhere (McSweeney & Roll, 1993) do not affect the relationship between response rate and FR value, even with the 5-s hopper durations used in EC3.

The top left panel of Figure 3 (millet) shows response rates averaged across all pigeons for each day at each FR value for Condition EC1. The later days are denoted by the filled symbols; there is no distinctive difference across sessions. The bottom panel compares the first and last sessions and, with the exception of the data from the FR 2 condition, show no significant differences. If these conditions required many weeks of conditioning to “settle down” to stable performance, we would expert to see the greatest changes over the first few sessions, but no major changes are apparent.

Figure 3.

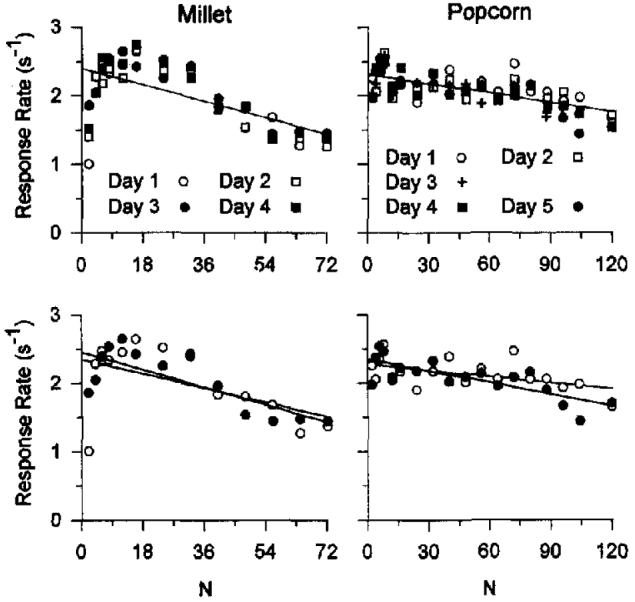
Right column: Response rates for Sessions 1–4 from Experiment 1, averaged across pigeons and displayed as a function of fixed-ratio (FR) values (top panel), with the data from Sessions 1–4 compared directly (bottom panel). Left column: Response rates for the Sessions 1–5 from Experiment 2, averaged across pigeons and displayed as a function of FR values (top panel), with the data from Sessions 1–4 redisplayed in the bottom panel. The 95% confidence intervals for the regressions within each panel overlap.

Because of concerns about stability, we anticipate the results from the next condition and display data from another set of pigeons given five sessions of exposure to each ratio (right column of Figure 3). Once again, there is not much change over sessions. The bottom panel highlights the data from the first and last sessions, where the function for the last session is seen to be slightly, but not significantly, steeper. We conclude that the number of sessions of exposure to an FR did not greatly affect response rates on them, and that there is insufficient information gained from multiple session exposure to each FR value to justify its experimental cost (Killeen, 1978).

Experiment 2: Specific Activation (a)

Experiment 1 provides us with an efficient technique for evaluating the theory's treatment of FR performance. In the following experiment, we begin to test the interpretation of the parameters of Equation 8. The specific activation (a) is predicted to increase with the level of deprivation and with reinforcer quality and quantity. Here, we attempted to change a by varying reinforcer quality and quantity. We manipulated the amount by varying the hopper time. Epstein (1985) showed that with the type of hopper we used, the amount consumed is a linear function of duration of access. We manipulated quality by varying the type of grain. Killeen, Cate, and Tran (1993) showed that pigeons have a strong preference for larger grain types (e.g., popcorn) over smaller grain types (e.g., millet); therefore, we inferred that popcorn would be a more highly valued reinforcer than millet.

Method

Animals

The same 8 pigeons used in Experiment 1 served as subjects here, four each in the different conditions.

Apparatus

The apparatus was the same as that used in Experiment 1. The average weights of the three grains were 101 mg (popcorn), 25 mg (milo), and 6 mg (millet). The key was manufactured by Lehigh Valley.

Procedure

Duration

Reinforcer duration was varied for Birds 3, 5, 14, and 15. The same FR progression as in Experiment 1 was used: 2, 4, 8, 16, 24, 32, 40,48, 56, 64, 72, 80, 88, 96, 104, 112, 120, 128, and 136. The pigeons were exposed to several sessions on each of the FR values (median = 3 sessions). Because Bird 3 extinguished at FR 32, it was given two additional exposures to the progression, where it persevered to FR 48. We took its median response rates and averaged these with the data from the other pigeons. Reinforcer duration was a 5-s access to millet (this Condition 1 replicates Condition EC3 from the previous experiment) versus a 2.5-s access to millet (Condition 2).

Quality

Birds 3, 5, 14, and 15 were then exposed to several sessions on each of the FR values (median = 5 sessions), with a 2.5-s access to popcorn serving as the reinforcer (Condition 3). Birds 54, 55, 56, and 57 were given a single session's exposure to a similar progression of ratio values, In Condition 4, the reinforcer was 5 s of access to milo; and, in Condition 5, the reinforcer was 5 s of access to millet. (The data for Conditions 4 and 5 were collected in Experiment 1.)

There were 50 trials per session for Conditions 1, 2, 4, and 5 and 27 trials per session for Condition 3 (to avoid satiation with the popcorn). When a subject did not complete an experimental session within two hours, both the session and the FR progression were terminated.

Results

Response rates for a session were averaged across individual animals for replications of Condition 1 and across all pigeons for representation in Figure 4. As in the first experiment, the data in Figure 4 show that response rates were generally high at smaller values of N and decreased as the FR requirement increased.

Figure 4.

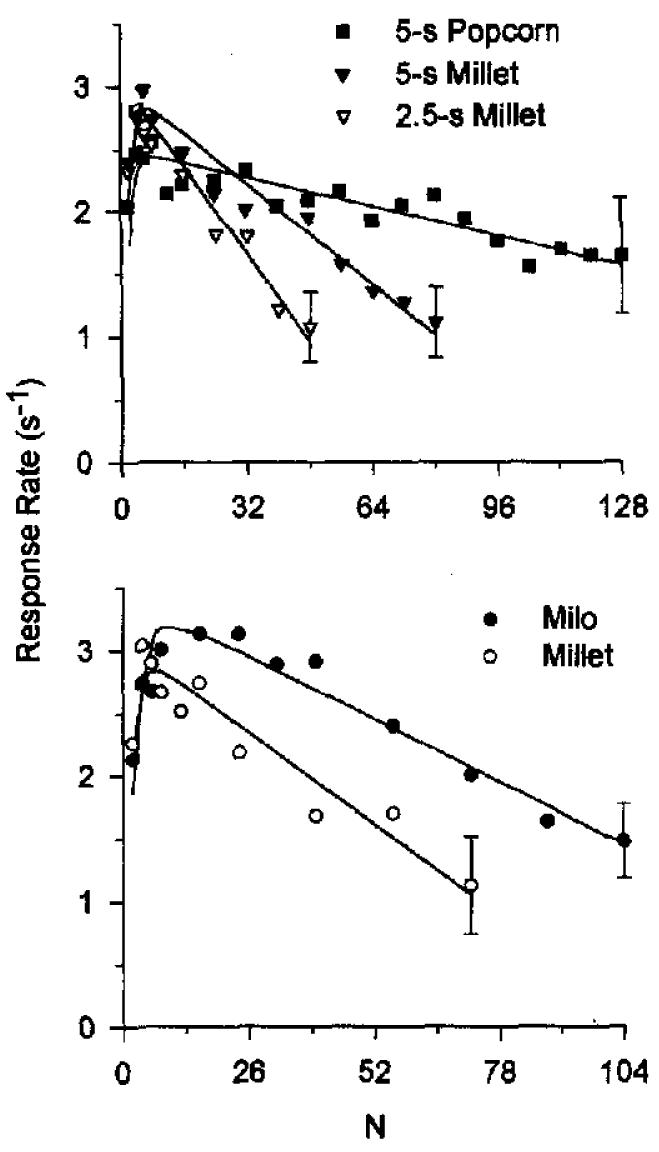
Single-session response rates from Experiment 2, averaged across 4 pigeons (and across replications of Condition 2 for Bird 3). The top panel shows data for Birds 3, 5, 14, and 15. The bottom panel shows data for Birds 54, 55, 56, and 57. The curves are drawn by Equation 8 (parameters are listed in Table 1). The standard error was similar over all fixed-ratio values, and its average is shown by the error bars on the right-most points.

The curves are drawn by Equation 8 with the parameters a and δ allowed to vary freely. The parameter β showed no systematic variation around 0.6 and was set at that value for all conditions except for milo, which required a smaller value. Table 1 gives the parameter values for averaged response rates for each grain condition.

Table 1.

Parameter Estimates Derived by Fitting Equation 8 to the Average Response Rates From Experiments 2 and 3

	Parameter
Condition	a	δ	β	$R_{\mathrm{a}}^2$
Experiment 2
5-s millet	40	0.34	.6	.89
Popcorn	153	0.41	.6	.82
2.5-s millet	25	0.34	.6	.97
5-s milo	53	0.29	.4	.89
5-s millet	39	0.34	.6	.90
Experiment 3
Key peck	64	0.32	.6	.91
Treadle press	196	1.12	.5	.92

Note. $R_{\mathrm{a}}^2$ is the adjusted coefficient of multiple determination.

The accuracy of the model is measured by the adjusted coefficient of multiple determination (Netter, Wasserman, & Whitmore, 1978; $R_{\mathrm{a}}^2$), which is calculated as

$$R_{\mathrm{a}}^2=1-\left(\frac{n-1}{n-p}\right)\left(\frac{\mathrm{SSE}}{\mathrm{SSTO}}\right),p<n.$$ (9)

In this formula, n is the number of observations, p is the number of parameters, SSE is the sum-of-squares error, and SSTO is the sum-of-squares total. If p = 1, this reduces to the simple coefficient of determination (R²), the proportion of variance accounted for by the model. Our criterion for keeping a parameter constant across conditions was that $R_{\mathrm{a}}^2$ not thereby decrease by more than one percentage point. $R_{\mathrm{a}}^2$ is a conservative index of goodness of fit, as it appropriately penalizes a model for its free parameters.

Discussion

As predicted, estimates of a were highest when popcorn was the reinforcer (153), intermediate when a 5-s access to millet was the reinforcer (40), and lowest when a 2.5-s access to millet was the reinforcer (25). This may be seen in the top panel of Figure 4, where the slope is shallowest for popcorn and steepest for the brief millet reinforcer. Estimates of specific activation were higher when milo was the reinforcer (a = 53) than when millet was the reinforcer (a = 39). This may be seen in the bottom panel of Figure 3, where the slope is shallower for milo and steeper for millet. It is clear that preferred grain types and longer reinforcer durations both affect a as predicted.

Pigeons tend to pick up a single seed per peck independently of grain size, so that the weight of the seeds multiplied by the number of seconds of access to the hopper yields a rough approximation of the amount of food obtained under each condition. The product–moment correlation between the amount of food estimated in this manner and the specific activation as given by a across conditions was r = .96.

These predictions and their validation must be viewed in the light of many experimental data that show that behavior is often insensitive to manipulations of amount of reinforcement (e.g., Keesey & Kling, 1961; Neuringer, 1967). These experiments often used interval schedules, where rates in any case might have been near their ceiling. Killeen (1995) developed models for such schedules, which make different predictions than the present model does for ratio schedules. This is because of the positive feedback on ratio schedules, where any demotivation resulting from small magnitudes of reinforcement or to satiation will decrease response rates, which will in turn further decrease the rate of reinforcement (McDowell & Wixted, 1986; McDowell & Wixted, 1988). The change in response rates caused by changes in motivation is found by differentiating Equation 8 with respect to a. The result is Na⁻², which indicates that the effects of changes in a are multiplied by N, the ratio size: Proportionately bigger effects are to be found at larger ratios. This prediction was validated by Powell (1969). It also indicates that the changes will be greatest when motivation is small: Varying the motivation level when it is low will have a large effect; varying the motivation when it is high will have a small effect, one that is attenuated by an inverse square law.

Estimates of δ showed an unsystematic variation around 0.33 s, except for popcorn, where it increased to 0.4 s. This increase is not predicted by the theory. It takes longer to handle the larger grain (Killeen, Cate, & Tran, 1993), and this change in consummatory topography may have been conditioned to the keypeck. Such a classical conditioning of the form of the consummatory response to the operant response was reported by Remy and Zeigler (1993; Ploog & Zeigler, 1996, found that response rates increased with grain size, but that may have been because magnitude of reinforcement [and thus a] also covaried with grain size in their study).

As expected, β remained relatively invariant over these manipulations, with the exception of the milo condition. It is not clear why the value for β was lower in this condition. For FR schedules, only the shortest FR values play any role in determining β, and so its estimation is not highly reliable and it is possible that this deviation merely reflected a sampling error. The value of β plays a larger role in determining VR performance, and it is considered in Experiment 4.

Experiment 3: Response Duration (δ)

In this experiment, we test the assertion of the theory that the parameter δ (delta) reflects differences in response duration. We manipulated δ by requiring pigeons to earn food by depressing a treadle as opposed to pecking a key. We predicted that this change in topography would increase δ, decrease response rates, and lead to extinction at lower ratio values than for key pecking. This prediction follows from the theory, in which the extinction ratio—the largest ratio that can be sustained by the animal—is given as a/δ. In two conditions, pigeons were exposed to a progression of FR values, and the operanda were varied between conditions.

Method

Animals

The same 8 pigeons used previously served as subjects here; they had also experienced the conditions reported in Experiment 4.

Apparatus

The apparatus was the same as that used in Experiments 1 and 2, with the addition of a treadle positioned on the floor of the chamber. The treadle was 7.5 cm long and .5 cm wide. The end of the treadle was 11 cm from the interface panel, 7.5 cm from the rear wall, and 3.5 cm from the chamber floor. A microswitch mounted under the treadle required 0.4 N of force applied to the end of the treadle to be activated. A Plexiglas response key, 2 cm in diameter, that could be illuminated by a green light was mounted on the interface panel 18.5 cm above the chamber floor and 25.5 cm from the rear wall. It required 0.2 N of force to activate the microswitch mounted behind the key.

Procedure

All pigeons were given a single session's exposure to FR values of 2, 4, 6, 8, 16, 24, 32, 40, 56, 72, 88, 104, 120, and 136 with a 3-s access to milo as a reinforcer. In Condition 1, each effective peck of the key caused a 0.14-s offset of the green key light. After completing Condition 1, the treadle was introduced into the experimental chamber. The pigeons were trained to treadle press and were then exposed to the progression of FR values. After completing this initial training, they were exposed to the progression a second time, and it is those data that are reported here. Each effective treadle press caused a 0.14-s offset of the house light.

Results

Response rates for a session were calculated by dividing the number of responses by the time that it took to complete the ratio requirement. Response rates for a session were averaged across individual animals, with the results shown in Figure 5.

Figure 5.

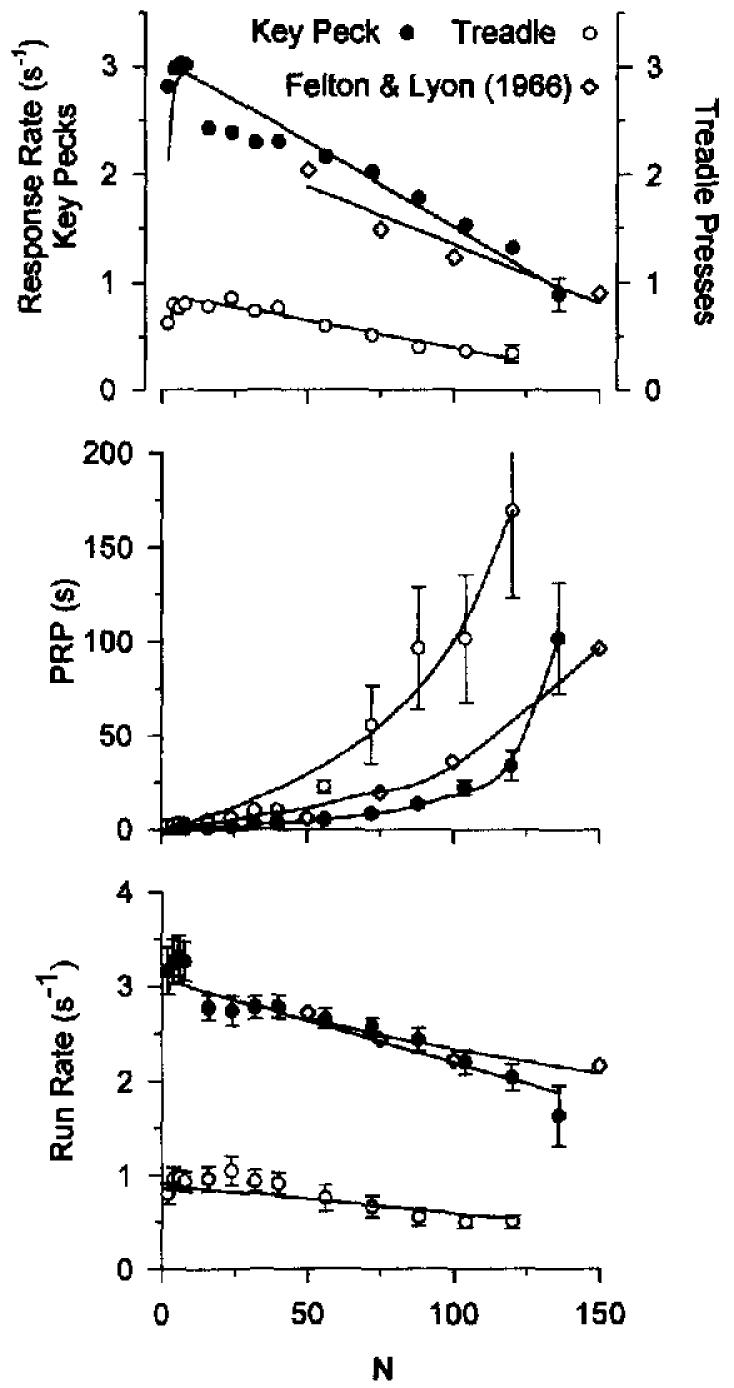
Single-session response rates from Experiment 3, averaged across 8 pigeons. The top panel shows overall response rates for treadle pressing (circles) and key pecking (disks) plotted against fixed-ratio (FR) value. The curves are drawn by Equation 8 (parameters are listed in Table 1). The middle and bottom panels show mean postreinforcement pause (PRP) and mean run rate (excluding PRP) plotted as a function of FR value. The theoretical curves through these data are given by Equations 11 and 12. The mean standard error is shown on the last data point for each condition in the top panel and for all conditions in the other panels.

Pigeons pecked at much higher rates than they pressed the treadle. The curves are drawn by Equation 8, with the parameters a, δ, and β allowed to vary freely and reported in Table 2. The difference in response rates is reflected in differences in the estimated response duration. For key pecking, δ = 0.32 s, close to the modal value noted in Experiment 2. For treadle pressing, δ = 1.12 s.

Table 2.

Parameter Estimates Derived by Fitting Equation 8 to the Average Response Rates From Experiments 4 and 5

	Parameter
Condition	a	δ	β	$R_{\mathrm{a}}^2$
Experiment 4
Key peck	212	0.50	.58	.91
Treadle press	681	2.60	.92	.77
Experiment 5
1-s ITI	165	0.34	.71	.86
20-s ITI	204	0.30	.58	.87

Note. ITI = intertrial interval. β is the value inferred from Equation 5 and the relationship β = 1 − e^−λ. $R_{\mathrm{a}}^2$ is the adjusted coefficient of multiple determination.

The middle panel of Figure 5 shows that the differences in response rates between treadle pressing and key pecking is caused in part by longer PRPs for treadle pressing than for key pecking; however, the bottom panel of Figure 5 shows that the difference is not determined solely by differences in PRP. Response rates after the pause (run rates calculated from the time of the first response until the last response of the FR requirement) were systematically lower for treadle pressing than for key pecking.

As judged by visual goodness-of-fit, β could be fixed at 0.6, but this stabilization did not pass our criterion (no more than a one-point decrease in $R_{\mathrm{a}}^2$). The key-pecking rates showed a discontinuity between FR 8 and FR 16 not found elsewhere in these experiments.

For comparison with a study that conducted many more sessions (a median of 25 per condition), we plot the response rates and pause lengths reported by Felton and Lyon (1966) in Figure 5. The slightly lower slope in the top panel for their data may have been due to their use of a slightly more effective reinforcer. The differences are not great, however, which suggests that our use of a single session per condition has not greatly biased our results. Powell (1968) conducted three sessions per FR value, and his data coincide with ours.

Discussion

As predicted, δ was substantially larger for the treadle-press response. Whereas the theory predicts that the intercept of the function should decrease as δ increases, it also predicts that the slope of the curve should not change (see Equation 8 and the left bottom panel of Figure 1). However, the slope of the curve (1/a) decreased (flattened) threefold, with a going from 64 for key pecking to 196 for treadle pressing. This just compensates for the threefold increase in δ, so that the x intercepts of the two conditions are comparable. These results are inconsistent with the theory, which predicts that the unnormalized curves will be congruent, and thus when normalized by scaling-up the ordinate for treadle pressing, that curve should show a much faster decrease than the key-pecking curve.

Why the failure of this prediction? One of the basic assumptions of the theory—its first principle—is that the strength of responding is directly proportional to the rate of reinforcement and inversely proportional to the duration of the target response. This assumption is built into the equations that lead to Equation 8. If the first principle had posited the dependence on reinforcement rate alone, then the slope of the curve would have been predicted to be not 1/a, but rather 1/(δa). This latter curve is just what was found, namely a deviation from the prediction too close to that of this alternate model to be ignored.

Response duration enters the theory in two ways. According to the first principle, it affects the number of responses that can be elicited by an incentive; and according to the second principle, it determines the ceiling on response rate. In the theory, both effects were represented by δ. It is obvious that a response such as the treadle press, which in this experiment lasted on the average of δ = 1.12 s, cannot be emitted any faster than 1/(δ s); the role of δ in determining the ceiling rate is secure. However, the effort required to make the response was expended at the start and end of the press. While engaged in the response per se, the pigeons were just standing. Response duration does not always capture the energetic requirements of a response, which are of concern for the first principle. Killeen (1994, Footnote 3) anticipated this possibility, but opted to represent both temporal constraints and energetic requirements by δ, as this sufficed for the data under his purview. Clearly, there are cases in which separate representation is necessary, as illustrated by the present data.

Experiment 4: Variable Ratio Schedules

Because of the importance of the differentiation of the two roles for response duration, we felt it important to replicate the results of the previous experiment using a different technique. By collecting the data for each ratio value for treadle pressing and key pecking at the same time, we could minimize the impact of events extraneous to our analysis that might cause variation in the slopes (e.g., the unexplained discontinuity between FR 8 and 16 in the key-peck data from Experiment 3). In Experiment 4, we collect the data for treadle pressing and key pecking in the same session.

Method

Animals and Apparatus

These were the same as those used in Experiment 3. In Experiment 4, the microswitch mounted under the treadle required 0.2 N of force applied to the end of the treadle for activation.

Procedure

All 8 pigeons were given a single session exposure to a progression of VR values; 2, 4, 6, 8, 16, 24, 32, 40, 56, 72, 88, 104, 120, and 136 with a 2-s access to milo as a reinforcer. Separate VR schedules were arranged for key pecking and treadle pressing according to an algorithm by Catania and Reynolds (1968). Sessions began with the houselight on but the keylights off and remained that way for one minute, during which time the pigeons could obtain reinforcement (2-s access to milo) by depressing the treadle. Each effective press of the treadle key caused a 0.14-s offset of the houselight. After one minute, the houselight went off and the green keylight was activated. During the next minute, pigeons could obtain reinforcement by pecking the key. Each effective peck of the key caused a 0.14-s offset of the green key light. Responses that did not earn a reinforcer during the component were credited to the animals when the next component of the same type of response resumed. The mean VR requirement was the same for key and lever, out independent 10-component VR schedules were sampled for each. Each effective treadle press caused a 0.14-s offset of the house light. Sessions terminated after 60 minutes or 90 reinforcers, whichever came flrst.

Results and Discussion

The pattern of data conforms to the predictions of Equation 8, using the coupling cofficint for VR schedules (Equation 5; see Figure 6). As in Experiment 3, most of the differences in the results are accounted for by changes in response duration, with δ increasing from 0.5 s for key pecking to 2.6 s for treadle pressing (see Table 2). Once again, the value of a is signifkantly greater for treadle pressing than for key pecking (the 95% confidence intervals of the regression slopes for VR 16 through VR 136 do not overlap). In Figure 6, the y axis for treadle pressing is enlarged; the inset shows the theoretical curves to scate. These results confirm those of Experiment 3 obtained by using different schedules.

Figure 6.

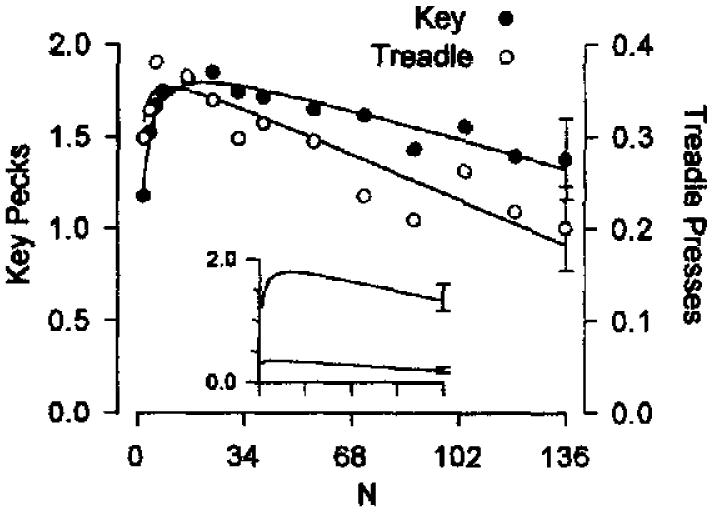
Single-session response rates from Experiment 4, averaged across 8 pigeons. The figure shows overall response rates for treadle pressing (circles) and key pecking (disks) plotted against variable-ratio (VR) value. The curves are drawn by Equation 8 (parameters are listed in Table 2). It should be noted that the axes are normalized; the insert shows the lay of the data on standard coordinates. The standard error was similar over all VR values, and its average is shown by the error bars on the right-most points.

Because motivational variables were controlled in this experiment by measuring rates for key pecking and treadle pressing within the same session, these results reinforce the interpretation of Experiment 3: The simple model used by Killeen (1994) must be generalized to allow for a linear (rather than a proportional) relationship between response duration and energetic requirement.

Experiment 5: Memory Decay (β)

Experiment 2 confirmed the dependence of a on reinforcer value, and Experiments 3 and 4 confirmed the dependence of δ on response topography. Now, we test the interpretation of beta (β) as the rate of decay of short-term memory for the target response. (β is defined as the currency parameter, the weight given to the most recent response; but this also determines the weights remaining available for prior responses, as shown in Equation 3 and its exponential expansion.) Because memory of target responses is assumed to be displaced during the consumption of the reinforcer, instances of target responses must be restocked in memory, and the degree to which this is accomplished is a joint function of β and the number of responses required for reinforcement (N). For β → 1, a single target response would dominate memory; whereas for β = 0.6, Equation 4 indicates that it requires 5 responses on FR schedules to saturate memory (i.e., to drive C > 0.98), and for β = 0.25, 14 responses. For VR schedules, the comparable values of N are given by (−46/ln(1 − β)) to be 12, 50, and 160 for the same decay rates. Therefore, the theory predicts lower response rates for short ratios than for moderate ones and predicts the peak of the inverted U to occur earlier for FR schedules than for VR schedules.

One way of testing this interpretation of β would be to give very brief reinforcers that do not completely displace memory for the prior response. Killeen and Smith (1984) found that animals could report the nature of the response that earned reinforcement, and that accuracy increased from chance at hopper durations of 4 s to 90% for brief hopper flashes. If we attempted to fit Equation 8 to an experiment with a very brief reinforcer, β should take a larger value, but this is not because the rate of memory updating has increased; it is because memory for the target response did not start at zero (also see Killeen, 1994, Section 5.4), and the recovered value of β becomes inflated to reflect this residual information. Examination of very short reinforcer durations would provide an opportunity to extend the model, but this would not be a straight-forward way to manipulate β. Indeed, we do not expect β to be directly manipulable (although it may covary with the duration of the response it weights; Killeen, 1994). It is possible, however, to test alternative rationales for the downturn in rate at low ratio values, the aspect of the data that we believe to be due to weak coupling as governed by β.

Because the rate of reinforcement on ratio schedules is an inverse function of the ratio value, organisms may satiate faster on small ratio requirements than on larger ones. On small ratios, (a) the organisms are fed at a faster rate, and (b) pauses resulting from momentary satiation will constitute a larger portion of their performance than on large ratios. This satiation hypothesis constitutes an alternative explanation for the downturn in response rates at small ratio values (A. Dickinson, personal communication, October 28, 1992). If true, then if we reduce the rate of eating during a session, the inverted U shape should be replaced by a linear function. One way to reduce session eating rates is by manipulating grain size and amount. We did this in Experiment 2 and found no systematic effect on β. Another way to reduce satiation is to increase the ITI, which is what we did in Experiment 5.

Because the role that β plays in FR schedules is rather inconsequential, we introduced a VR schedule as the baseline for this experiment. The theory predicts a more gradual increase in responding with ratio size under VR schedules. This prediction is based on the interpretation of the downturn as being due to truncation of memory by reinforcement; thus, the contrast between the FR curves from the previous experiments and the VR baselines from Experiment 5 and Experiment 4 will provide one test of the memorial prediction. The contrast between the long ITI and short ITI conditions will test the momentary satiation hypothesis. To increase the power of the test of the latter hypothesis, the hopper duration was set to a relatively long value (5 s).

Method

Animals and Apparatus

These were the same as those used in Experiments 1, 2, and 3.

Procedure

In Condition 1, all 8 pigeons were given a single-session exposure to a progression of VR values: 2, 4, 6, 8, 16, 24, 32, 40, 56, 72, 88, 104, 120, and 136 with a 5-s access to milo as a reinforcer. All pigeons experienced each VR value, with 52 trials per session, and a 1-s ITI between trials. The VR was arranged according to the algorithm of Catania and Reynolds (1968). In Condition 2, the ITI was increased from 1 s to 20 s, and all birds experienced the single-session exposure to each of the VR values given above. As before, the chamber was dark during the ITI and any pecks that might have occurred were not recorded. Twenty seconds was chosen for the ITI because it was calculated to reduce the pigeons' eating rate to well below the value at which the downturn was seen in the previous experiments.

Results

Response rates were calculated by dividing the number of responses by the time that it took to complete each VR requirement. The response rates in the top panel of Figure 7 were generally high for smaller values of N and decreased as the VR requirement increased. The curvature is more gradual for the VR schedules than for FR schedules, as seen in the previous figures.

Figure 7.

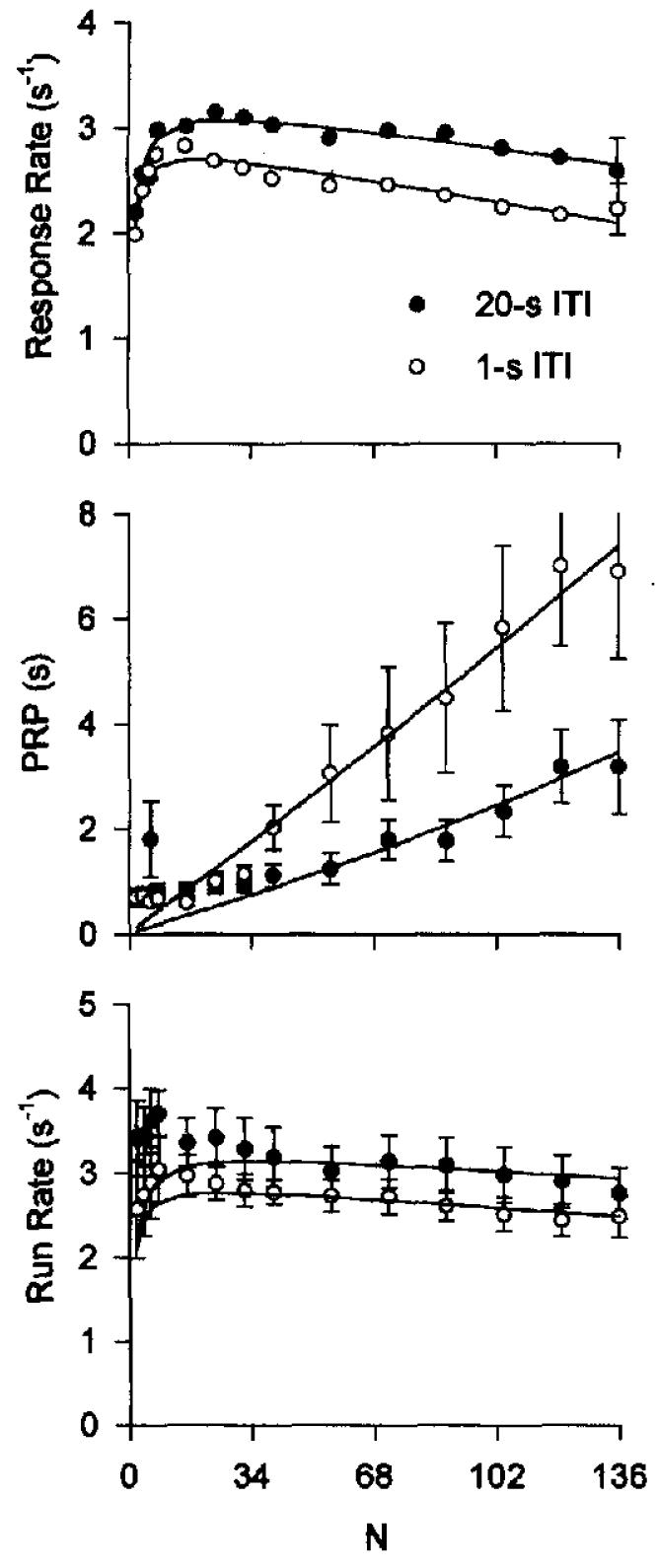
Single-session response rates from Experiment 5, averaged across 8 pigeons. The top panel shows overall response rates for the 1-s intertrial interval (ITI; circles) and for the 20-s ITI (disks) plotted against variable-ratio (VR) value. The curves are drawn by Equation 8 (parameters are listed in Table 2). The middle and bottom panels show mean postreinforcement pause (PRP) and mean running rate (excluding PRP) plotted as a function of VR value. The mean standard error is shown on the last data point for each condition in the top panel and for all conditions in the other panels. The curves through the PRP data are drawn by Equation 11, and those through the run rate data by Equation 12.

Quantitatve estimates of a, δ, and β were derived by fitting Equation 8 to the data presented in the top panel of Figure 7, which draws the curves in that figure. The coupling coefficient for VR schedules is given by Equation 5. Estimates of specific activation a were higher for the 20-s ITI condition (204), than for the 1-s ITT condition (165), and δ was slightly lower (see Table 2). The effect of the ITI on PRP and the running rates are shown in the bottom two panels.

Discussion

Consistent with the interpretation of the theory, there remains a downturn at small ratio values in spite of (a) the lower rate of reinforcement on these schedules, and (b) the provision of a lengthy (20 s) period for the subject to conclude postprandial activities and move past momentary satiation. PRPs were comparable in tiie two conditions until FR 32, when the pauses on the 1-s ITI condition grew longer than those on the 20-s condition.

These results showed that our hypothesis was correct: The initial curvature was not caused by momentary satiation. On the other hand, this manipulation revealed a persistent contrast effect manifested as a systematically higher response rate at all ratio values in the presence of a long ITI. A similar effect was found by Mazur and Hyslop (1982) and also attributed by them to contrast. What causes such contrast? Nevin (1994) suggested that an increased value of a may be the mediator of contrast effects. However, what would cause the increased value of a? Perhaps, here is where satiation enters the picture. The pigeons were repleting at a much lower rate under the long ITI condition, and this might have maintained a higher valuation of the incentive than found on the brief ITI condition, which could explain a larger value for a. (Conversely, the lower overall rate of reinforcement under the long ITI condition would predict lower arousal, unless arousal comes under stimulus control. We have evidence that it does [Beam, Killeen, Bizo, & Fetterman, 1997], but at this point, we leave the increase in a and the correlated decrease in response duration, from 0.34 s to 0.30 s, as topics for future study.)

General Discussion

Quantitative Adequacy of the Model

Equation 8 is not an ad hoc curve fit, such as the power law in psychophysics or the generalized matching law. It is derived from basic principles of reinforcement, and those principles, in turn, are based on the analysis of a large database, some of which is reviewed in Killeen (1994, in press) and Killeen and Bizo (1996). However, there is always room for alternative mathematical representations of the basic principles and for surprises when applying the model to new situations. We have found some here, but primarily in the interpretation of the parameters, not in the adequacy of the quantitative fits between model and data. We moved briskly through the various ratio values on the basis of the results from Experiment 1, and some of the irregularities seen in the data may be due to this restricted database. A picture of the quantitative accuracy of the model at its best is provided by results from Green, Kagel, and Battalio (1982), who took special pains in collecting stable data (also see Baum, 1993). Figure 8 shows their average data from four pigeons over a range of random-ratio VR schedules with at least 30 sessions per condition and with most conditions studied twice. Equation 8 draws the curve.

Figure 8.

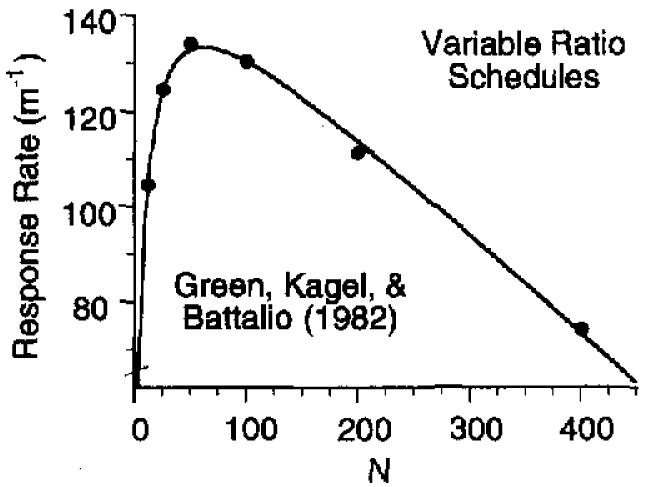
Variable-ratio response rates from 4 pigeons collected by Green, Kagel, & Battalio (1982). The parameters of Equation 8 are λ = 0.44 (β = .36), δ = 0.37, and a = 282.

We may approximate such orderliness by pooling data from similar conditions in our experiment. The top panel of Figure 9 shows the FR key-pecking rates from the two exposures to milo (Experiments 2 and 3) and from the three exposures to millet (Experiment 2). The bottom panel shows the VR key-pecking rates from the three exposures to milo (Experiments 4 and 5). The decency of fit of the model to the data suggests that some of the irregularities in the matches shown earlier were due to the small sample size that constituted the database.

Figure 9.

Top panel: Average fixed-ratio response rates from Experiments 2 and 3. Bottom panel: Average variable-ratio response rates from Experiments 4 and 5. Parameters of Equation 8 are given in Table 3.

Is it valid to average data from such different conditions? The largest portion of the curves is an essentially linear function, and averaging such functions preserves the information about both the shape of the curves and the central tendencies of the parameters that constituted them. Whether in this instance the average curves preserve information about the nonlinear parameter β is an empirical question. Table 3 gives the parameters of the average curves shown in Figure 9, along with the average of the parameters of the data that constitute them in parentheses. (Because the slopes are the reciprocals of a, we use the harmonic mean to calculate the average value of a.) The average curves return parameters, which are good estimates of their constituents. Thus, the average curves are valid representations of the effects of ratio schedules on behavior, and the parameters of the model partition the effects of independent variables orthogonally and additively.

Table 3.

Parameter Estimates Derived by Fitting Equation 8 to the Average Data From Experiments 3, 4, and 5 and the Average of the Constituent Parameters

	Parameter (average parameter)
Condition	a	δ	β	$R_{\mathrm{a}}^2$
Fixed ratio
Milo	65 (60)	0.32 (0.31)	.55 (.54)	.99
Millet	26 (33)	0.33 (0.32)	.56 (.60)	.93
Variable ratio
Milo	191 (191)	0.36 (0.38)	.62 (.62)	.94

Note. For variable-ratio schedules, β is the value inferred from Equation 5 and the relationship β = 1 − e^−λ. $R_{\mathrm{a}}^2$ is the adjusted coefficient of multiple determination.

The VR model provided a better fit to the VR data than did the FR model to those data and conversely. This appropriateness of models to data was also noted by Stephens (1994). This provides a novel and strong test of the predictive validity of the concept of coupling and its instantiation in models such as Equations 4 and 5. However, as the eye can see, either model would provide an acceptable fit to either set of data. An ad hoc approach would not support a distinction between these models on the basis of their goodness of fit to the data; but a principled approach is vindicated by them.

Qualitative Adequacy of the Model

The parameters were responsive to experimental manipulations of the variables that they are believed to represent. When size of and duration of access to grain was varied in Experiment 2, the correlation between reinforcer magnitude and a was r = .96. When the response was changed to the more cumbersome treadle press (Experiments 3 and 4), δ increased accordingly. An alternative satiation explanation of the downturn in rates for small-ratio schedules was tested (Experiment 5) and found to be wanting.

There was some variability in parameters that was unexpected but might entail little more than sampling error: in particular, the smaller value for β for milo in Experiment 2, and the larger value for it in the 1-s ITI condition of Experiment 5.

But there also were some surprises:

1. δ increased substantially for popcorn in Experiment 1; this might have been due to cLassical conditioning of the slower consummatory response for these large grains.

2. In general, response rates were higher with a 20-s ITI than a 1-s ITI in Experiment 5. This is not surprising to anyone familiar with contrast effects, but the model does not predict it. However, it is consistent with both Nevin's (1994) hypothesis concerning the proper representation of contrast in this framework and with a recent treatment of satiation effects on reinforcement schedules (Killeen, 1995) in which the parameter a was expanded to encompass deprivation and repletion.

3. The value of a did not remain invariant with changes in response topography (Experiments 3 and 4), This can be explained by the theory only if response effort is not proportional to response duration. There is some prima facie validity to this possibility, especially in the case of treadle pressing. In other experiments using this treadle, we have observed the pigeons sometimes perching on the lever, although we did not observe that happening in this experiment.

The Fine Structure of Behavior

The Postreinforcement Pause

Perhaps the most obvious omission of the theory is its lack of comment on the radically different within-trial patterns of responding on FR and VR schedules, with the former being characterized as pause-and-run and the latter as being relatively homogenous responding at a high rate. This difference was implicit in the development of the different coupling coefficients, but explicit predictions were never made. On VR schedules, there is always some probability of reinforcement soon after the previous reinforcement; whereas on FR schedules, there never is. Such contingent coupling requires development of the theory.

This is a critical issue. Killeen (1994) addressed the patterning with a diffusion model not unlike that of Staddon and Reid (1990), but the intuitions of that analysis bear development. For the values of β found in Experiments 1 and 2, the effects of an incentive cannot extend backward to encompass more than about a dozen responses; yet, in those same experiments, we demonstrated the ability to maintain behavior at FR requirements of over 100 responses. How can this be? It can be only because the animals are confused about the probability of reinforcement as a function of the times since the previous reinforcement (Killeen & Bizo, 1996)—time perception is imperfect. If one clarifies the situation by requiring the first response to occur on a different key, then, as the theory predicts, it is difficult to sustain performance when more than a dozen consecutive responses to a second key are required for reinforcement.

In spite of this limitation, incentives of the type delivered here can, in theory, maintain many more than a dozen responses: For representative values of a = 65 s and δ = 0.32 s, we predict an extinction ratio (a/δ) of just over 200 responses. How can we use the organisms' ability to sustain this level of nonreinforcement to alleviate their inability to sustain delayed reinforcement? That is exactly the trick performed by VR schedules (and, more precisely, the variant called random ratio schedules), which generate a low but uniform probability of reinforcement for any ordinal response after reinforcement.

The PRP on interval schedules

On fixed schedules—FR and their temporal equivalent FI schedules—the trick is performed by temporal uncertainty. Pigeons and humans both approximate Weber's law in their ability to judge where they are in time (e.g., Fetterman & Killeen, 1992), with the standard deviation of their estimates proportional to the interval timed, σ = wT, (Killeen and Weiss [1987] found the generalized Weber's law, σ = √(wt)² + c², to be more accurate, but for our purposes the simple Weber's law [with c = 0] will suffice.) The constant of proportionality is called Weber's constant, and it is about w = 0.25 for pigeons. If we treat the temporal aspects of ratio schedules as similar to interval schedules (and there is justification for this; see, e.g., Baum, 1993; Killeen, 1969), we may predict that responding will begin when the probability of remforcement at any point in time exceeds the threshold probability given by the reciprocal of the extinction ratio (a/δ)⁻¹. The probability of reinforcement can be considered as being a normal distribution around the mean interreinforcement interval (T). Then, the probability of reinforcement has risen above the threshold when T − t_p = − z(δ/a)σ, a > 0; where z(δ/a) is the z score corresponding to the probability δ/a, and σ is the standard deviation of the temporal discrimination. Solving for the duration of the PRP yields t_p = T + z(δ/a)σ.

This may be written as a fraction of the interreinforcement interval

$$t_{\mathrm{p}}=T[1+z(\delta ∕a)w],a>0.$$ (10)

For a/δ = 200 and w = 0.25, this predicts that the postreinforcement pause will last for 36% of the interval (T*[1 − 2.58* 0.25]), a value in the vicinity of those reported (e.g., Zeiler & Powell, 1994, found a linear function between T and t_p with a slope of around 0.4; Hanson & Killeen, 1981, found a slope of around 0.3).

A small inverse relation predicted between motivation level, represented by a, and pause length is that if the value of a is halved, we expect an increase in the pause duration from 36% to 42% of the interval [1 + z(.01)* 0.25]; whereas if it is doubled, we expect animals to start responding at 30% of the interval. The data on the effects of motivation on PRP are mixed, in part because large reinforcers are (a) better incentives, (b) better satiaters, and (c) better signals of the start of an interval than are small reinforcers. Some of these effects are nicely sorted out by Perone and Courtney (1992). Baron, Mikorski, and Schlund (1992) varied incentive motivation in progressive ratio schedules and found functions similar to those predicted in Equation 11, demonstrating the predicted inverse relation between motivation and pause length.

The PRP on response-initiated delay schedules

If we wait for the animal to start responding before we start timing the FI schedules (a response-initiated delay [RID] schedule), Equation 10 must still be satisfied, and this can be accomplished only by the animal's pausing even longer (Shull, 1970). The obtained interfood interval T now equals the duration of the PRP (t_P) plus the scheduled delay (T_D). We may solve for t_P in terms of the scheduled delay (Equation 10 becomes t_P = [T_D + t_P][1 + z(δ/a)w]) to find that t_P = T_D [1 − z(δ/a)w]/[z(δ/a)w]. For the exemplary parameters (a/δ = 200 and w = 0.25), this is t_P = T_D[0.36/(1 − 0.36)] = 0.55 T_D. The theory thus makes the counterintuitive (or at least counteroptimality) prediction that organisms should pause for a sizeable fraction of the scheduled interval before starting the clock, rather than starting it immediately. Consistent with this analysis, Shull found pauses before initiating the delay of just over half of the scheduled interval, whether or not the beginning of the delay was signalled.

These calculations depend on particular estimates of various parameters, but the prediction of a proportional relationship between pause length before starting the clock and scheduled delay is a general one, both for interval schedules and for schedules in which the characteristic time between reinforcers is a function of when the animal starts responding, as for both RID schedules and ratio schedules. It is a relation that Wynne and Staddon (e.g., 1992; Higa, Wynne, & Staddon, 1991; Innis, Mitchell, & Staddon, 1993; cf. Zeiler & Powell, 1994) called “obligatory linear waiting.” In their various studies, Wynne and Staddon found the pausing to be around 25% of the obtained interfood interval (T), rather than 36%. Manabe (1990), using a variety of procedures and somewhat longer values of delay, found a median slope of 0.32 when regressing pause length against T.

The PRP on ratio schedules

These analyses set the stage for an explicit model of FR pausing. If we accept the phenomenon of linear waiting, then we can predict pause length on FR schedules to be a linear function of T (as shown to be the case by Capehart, Eckerman, Guilkey, & Shull, 1980). But how do we predict T on ratio schedules? We know that rate of reinforcement on ratio schedules equals B/N, where N is the ratio requirement and B is the response rate (see Equation 7). The interreinforcement interval is thus the reciprocal of this, T = N/B. The response rate B is given by Equation 8. Because according to both Equation 10 and the linear-waiting law, the pause length t_p is proportional to T(t_p = kT), we may write

$$t_{\mathrm{p}}=\frac{\mathit{kN}}{\frac{C}{\delta }-\frac{N}{a}},\delta ,a>0,N<a∕\delta .$$ (11)

For small values of N, pause length is predicted to be an approximately linear function of response requirement; but as N grows large, the denominator approaches zero and the pause length grows without bound. This equation reflects the positive feedback nature of these schedules; perturbations that shorten the pause increase the rate and act to shorten the pause even more, whereas perturbations that lengthen the pause can “strain the ratio” and extinguish responding (see, e.g., Baum, 1993).

Figure 10 shows the pause lengths of rats on FR schedules collected by Mazur (1983), with Equation 11 drawing the curve. Because of the multiplicative parameters in the numerator and denominator, this equation is overdetermined. Except for very small ratio values, the role of the coupling coefficient in determining waiting time is minuscule, so we can set C = 1 and can also fix δ at a representative value of 0.4 s. Then, we frnd that values of 0.97 for k and 97 s for a minimize the rms deviation between data and model. (Using the full model and an optimal value of 0.22 for β had no visible effect on the goodness of fit.)

Figure 10.

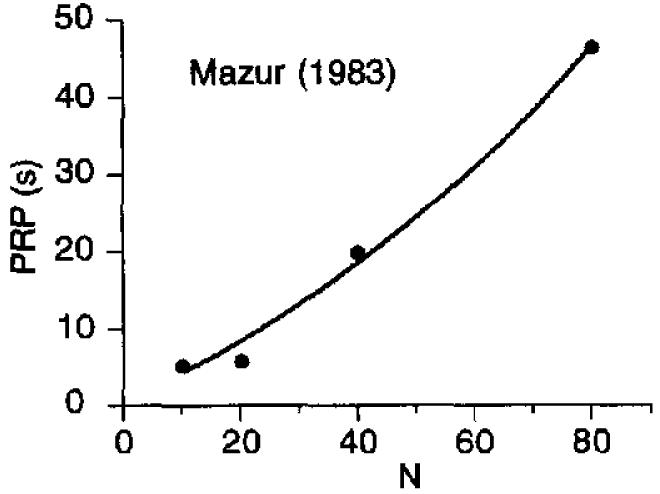
Pause durations of rats exposed to various fixed-ratio schedules. The data are from Mazur (1983); Equation 11 draws the curve. PRP = postreinforcement pause.

To examine the role of the coupling coefficient in pausing requires the use of very small ratio values, along with weak incentives so that there will be adequate pausing for analysis. These conditions were approximated in a study by Keesey and Goldstein (1968), who reported that the PRPs from a single subject reinforced on progressive ratio schedules with brain stimulation of different intensities. On progressive ratio schedules, the response requirement increases after each reinforcer. Figure 11 shows the results, along with the locus of Equation 11. As expected, the value of k decreased monotonically with intensity of stimulation, and a increased monotonically with intensity. However, even here, there was relatively little role played by the coupling coefficient, except for the weakest intensity, the only condition in which there would be a visible difference in the curves. The optimal value for β was 0.20. Therefore, even for this boundary case, we can ignore changes in coupling when predicting PRP length on FR schedules and uniformly set C = 1.

Figure 11.

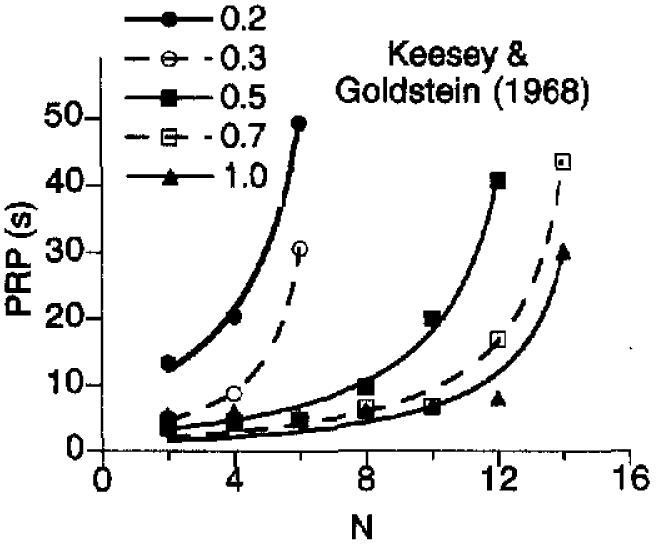
Pause durations of a rat exposed to progressive ratio schedules. The data are averages of 25 trials, collected by Keesey and Goldstein (1968). The reinforcer was 0.5-s stimulation with a pulse train of 50 pulses, each lasting for 0.2 ms. The current in mA is the parameter in the legend. Equation 11 draws the curves. PRP = postreinforcement pause.

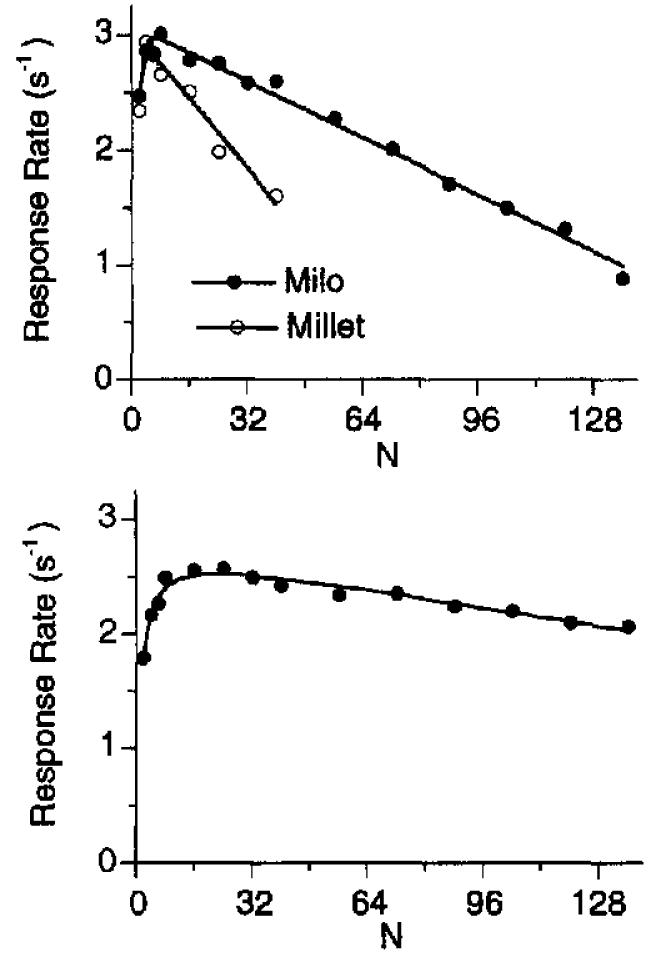
A better test of the predictions of Equation 11 would be in situations in which we could identify the parameter values a priori. We have the benefit of knowing most of the parameters of Equation 11 for the data that we have analyzed in this article. Figure 12 shows the predictions of that equation for the milo and popcorn conditions of Experiment 2, using the parameters from Table 1. In bom cases, k took a value of 0.20. The predictions are not bad, but because there were only 4 pigeons in each condition, the data are noisy.

Figure 12.

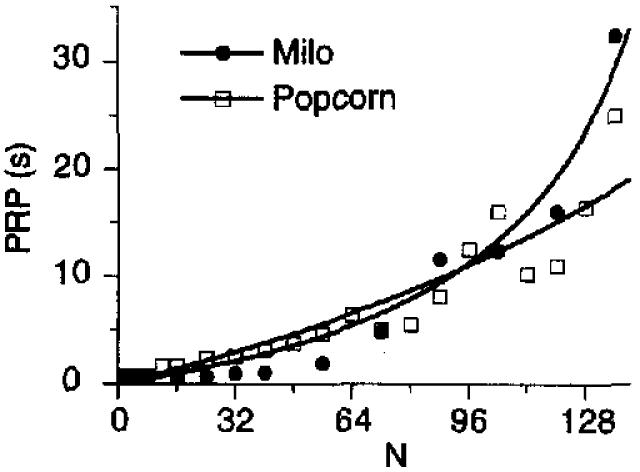
Pause durations of pigeons exposed to various fixed-ratio schedules in which they earned milo or popcorn. Equation 11 draws the curve. The parameters for these curves were taken from Table 1, with the exception of k, which took the value of 0.20 for all curves. PRP = postreinforcement pause.

Figure 5 shows the predictions of Equation 11 for the treadle pressing and key pecking of the 8 pigeons in Experiment 3, using the parameters from Table 1 (dashed unes). The predictions for the treadle-press pausing were very good, but the predictions for key-peck pausing were less successful. If the parameter a is freed, the continuous curves result. The key-pecking data required a smaller value of specifie activation (48) than reported in Table 1 (64), as did the treadle-pressing data (188 rather than 196). Much of this discrepancy may be due to the use of the parameters from the group curve shown in Table 1, which slightly overestimate tiie value of a, as discussed in the analysis of Table 3. For treadle pressing, k took a value of 0.37, and for key pecking, 0.17.

Equation 11 is not limited to FR schedules but should also predict pausing on VR schedules. Since one reinforcer can occur soon after another, we expect pauses to be much shorter on VR schedules, which will be reflected in a smaller value of k. (As expected by this account, Schlinger, Blakely, & Kaczor [1990] found the pausing on VR schedules to vary with the lowest component ratio size.) Using the parameters from Table 2, Equation 11 draws the curves through the PRP data in Figure 7. The values of k were 0.15 for the 1-s ITI condition and 0.07 for the 20-s ITI condition. Coupling and response duration were the same within response type for all three panels but, as before, different values for a were required for adequate fits to the data. The increase in PRP as a function of VR value was noted by Blakely and Schlinger (1988), who also found the predicted covariation in response rate and PRP with changes in reinforcer magnitude.

Run Rates

It is a simple matter of elimination, now with predictions of overall rate and PRP in hand, to predict run rates on ratio schedules. The average time between reinforcers is T = t_P + N/B_R, where B_R is the run rate. The reciprocal of this may be inserted in Equation 6 in place of R. This can be solved for B_R as

$$B_{\mathrm{R}}=\frac{\mathit{aB}}{a+t_{\mathrm{P}}}.$$

Finally, Equation 11 may be used in place of t_P to get the predicted run rate:

$$B_{\mathrm{R}}=\frac{B^2}{B+\mathit{kN}∕a},a>0,$$ (12)

with B given by Equation 8. As t_P (or k) go to zero, as is approximately the case on VR schedules, run rate converges to the predictions for overall rate. Equation 12 draws the curves through the run rate data in Figures 5 and 7. All parameters were held constant with the exception of a, which required different values for an adequate fit to the data.

Summary

We have shown that the theory accounts for overall response rates on fixed- and variable-ratio schedules. Manipulations of variables bearing on the parameters were shown to move them in the expected directions: Increasing reinforcer quality and amount increased a; increasing response requirement increased δ. The downturn in rates at small ratio values is not caused by momentary satiation, leaving the explanation of it in terms of coupling validated. Extensions of the theory to the fine structure of responding during the intervals between reinforcers yielded qualified successes, that is, the resulting models fit the data but required adjusting the value of the activation parameter a. This variation may indicate a limitation of these models, or it may reflect an increase in the animals' arousal during the discriminably different period when they are responding.