Modeling structural adaptation of microcirculation

Abstract

The functional properties of the microcirculation crucially depend on its angioarchitecture, i.e. vessel arrangement and vessel morphology. The microcirculation is subject to continuous dynamic structural adaptation (remodeling) controlled by hemodynamic and metabolic stimuli. Due to the complexity of the interactions among stimuli, reactions and functional properties, adequate understanding of structural adaptation requires mathematical models in addition to experimental investigations. Mathematical models have been developed that allow prediction of realistic vascular properties based on generic patterns of vascular responses. These models can be used to investigate and predict distributions of vessels morphology consistent with certain putative adaptation principles of terminal vascular beds in response to local hemodynamic and metabolic conditions. They have suggested new hypotheses, including the importance of conducted responses in network adaptation, and can explain the mechanisms underlying observed structural and functional network properties. In the future, the value of such models can be enhanced by including the effects of longitudinal stretch and pulsatility, the relationship between acute tone and structural adaptation, and the description of molecular and cellular mechanisms underlying structural responses of microvessels.

Introduction

The basic outline of the vascular system is determined during development by genetic programming, guided by the unique temporal and spatial patterns of structural and molecular features available in the embryo. With establishment of blood flow, control of vascular development is increasingly taken over by feedback signals derived from vascular function including blood flow (shear stress), and blood pressure (circumferential wall stress) in addition to those derived from the metabolic state of the tissue. Mechanical and molecular signals also govern the postnatal structural adaptation of vascular beds with respect to vessel number, diameter, wall thickness and length, in response to functional requirements.

In this process of angioadaptation⁶¹, the properties of vascular beds are determined by the interplay between vascular and cellular reactions to hemodynamic and molecular signals and the functional implications of these reactions, constituting a complex feedback system. Under physiological conditions including development, growth and physical exercise, angioadaptive responses lead to adequate adjustment of the properties of vascular beds.

In pathophysiological situations including inflammation, wound healing and collateralization ⁵, structural adaptation is essential for the regeneration and repair of vessels. However, pathophysiological changes of vascular response characteristics or environmental conditions may lead to vascular mal-adaptation, e.g. inward remodeling and rarefaction in hypertension ^{20; 29; 44} or abnormal vascular properties in tumors.

Structural adaptation can be interpreted as a feedback regulation of vascular morphology in response to available functional stimuli sensed in the vessel or in the tissue. Based on experimental and theoretical considerations, a number of feedback mechanisms in structural adaptation have been proposed. The most prominent example is probably the control of wall shear stress by shear stress dependent change in vessel diameter ^{23; 24; 51}. The parallel action of multiple feedback mechanisms leads to complex cause and effect relations, in which structural and functional characteristics cannot easily be traced back to the underlying mechanisms. Such a system is not easily understood by intuitive or qualitative approaches. Therefore, this review discusses studies aimed at understanding the mechanisms of vascular adaptation and the requirements of stability and functionality by combining experimental approaches with mathematical models. Emphasis is placed on the mechanisms controlling vascular lumen diameter. As a consequence of Poiseuille's law, this structural parameter has critical importance in determining the distribution of blood flow and hence the functional properties of a vascular network.

This concept of structural adaptation implies a high plasticity of the vascular phenotype within microvascular beds (Figure 1). According to this concept, vessel characteristics are not fully determined by differentiation or epigenetic modification, but are continuously controlled by environmental factors. Such characteristics include not only vessel diameter and wall thickness, but also permeability and molecular markers of arterial or venous phenotypes. In principle, a persistent change of the direction of the perfusion ³³ should lead to reversal of the arterio-venous polarity of a given microvascular network. The degree of plasticity may vary with vessel size. Studies with grafted conduit vessels ^{9; 11; 22} show that they adapt according to the situation in which they are placed, although they do not completely attain the phenotype of the original vessel that they replace. A corollary of this plasticity is the fact that there are no inherent bounds or restrictions with respect to the structural and functional results of the adaptive process. The outcome is not calibrated against a ‘blueprint’ of the desired structure or function and depends only on prevailing conditions. Therefore, the response characteristics must be balanced to guarantee adequate structural and functional properties and stability under a range of external conditions. Here, again, the complexity of the mutual interactions requires the use of mathematical models in order to gain quantitative understanding of the system design and the inherent requirements.

Figure 1.

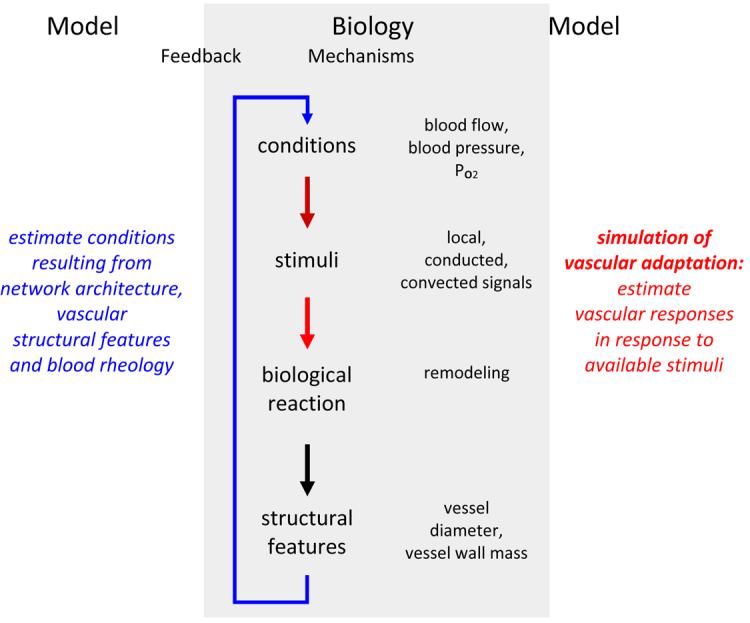
Schematic representation of biological mechanisms of structural vascular adaptation (remodeling). A feedback loop links network structures resulting from adaptation and functional network properties which in turn are the basis for structural adaptation (center). The use of mathematical modeling approaches includes the calculation of functional properties (hemodynamic and metabolic models, left) and the estimation of adaptive vascular responses to these conditions (right).

The process of angioadaptation includes not only the remodeling of existing vessels but also the formation of new vessels. A substantial number of models have been presented that focus on the increase in vessel number by angiogenesis, e.g. during development or tumor growth. This topic is the subject of separate review in this issue ³⁴ and will not be addressed here. Also, the present review focuses on steady state structural adaptation and not on dynamic events ¹⁶ which occur in response to sudden changes of the local conditions.

Development of modeling approaches

For the purposes of predicting blood flow distribution, a vascular network may be regarded as a system of interconnected segments, each having a resistance to blood flow defined by where

$$R=\Delta P∕Q=\left(128L\eta \right)∕\left(\pi D^4\right)$$ (1)

ΔP is the pressure drop along the segment, Q is the flow rate, L is the length, η is the apparent viscosity of blood and D is the luminal diameter ⁵⁵. Given boundary conditions on the segments feeding and draining the network, the flows in all segments may be computed by solving a system of linear equations for the pressures at the junction points ⁵³. The apparent viscosity depends on vessel diameter and hematocrit ^{39; 49}, and hematocrit is generally non-uniformly distributed as a result of unequal phase separation at bifurcations ³⁸, necessitating an iterative solution procedure. The resulting distribution of oxygen levels within microvessels may then be computed, using information about tissue oxygen demand as used in some studies ⁴⁰. When available, detailed information on network geometry can be used as a basis for more precise calculations ^{14; 18; 54}.

In structural adaptation models, each segment diameter D_i(t) (i = 1,…,N) is considered as a function of time t. The adaptive behavior may be represented by a system of differential equations

$$\frac{1}{D_i}\frac{{\mathit{dD}}_i}{\mathit{dt}}=F(S_1,\dots ,S_M)$$ (2)

Here, S₁, …,S_M denote a set of signals or stimuli acting on segment i, and themselves depend on the hemodynamic and metabolic conditions in that segment, and possibly on conditions in other segments and in the surrounding tissue. A key feature of this modeling approach is that the same function F is assumed to apply to all segments. Thus, a set of generic responses or ‘rules’ is assumed to govern the behavior of all segments, when subjected to a given set of signals. The underlying biological assumption is that vessels are completely plastic and are able to change their phenotype without restrictions in response to changing local conditions. This assumption may be violated if a definitive differentiation has led to changes in vascular structure or genetic repertoire which persist irrespective of the prevailing conditions. The assumption of complete plasticity may be justified to a large extent in the microcirculation but less so in larger conduit vessels.

When many adaptive segments are connected together in a normal network, the response ‘rules’ must permit the segments to act cooperatively to generate biologically realistic and functionally adequate behaviors. The development of theoretical models for structural adaptation has involved the sequential identification and incorporation of a number of signals, as discussed in the following sections.

Role of wall shear stress

Early last century, Murray ³² showed theoretically that the overall energy ‘cost’ of maintaining blood vessels and the blood and of pumping blood through the vascular system is minimized if the blood flow in each segment is proportional to the cube of the vessel diameter, a relationship known as Murray's law. The existence of such a relationship has been tested and mostly confirmed in a number of vascular beds ^{15; 28; 58; 62}. From basic principles of hemodynamics, the wall shear stress is given by τ = 32Qη /(πD³), and is therefore approximately constant in a set of vessels satisfying Murray's law. This led to the suggestion ^{23; 24; 51} that such a design would be generated if each vessel could sense wall shear stress and adjust its diameter so as to achieve a uniform level. Vascular reactions to shear stress have been known since Thoma's observation ⁵⁹ of an increase of vessel diameter in vessels carrying a high blood flow and vice versa. Such behavior can be represented mathematically by setting F = k(τ − τ_ref) in eq. (2) where τ = 32Qη/(πD³) and τ_ref is a target or reference value of wall shear stress. If the flow rate Q were to increase, the increase in shear stress would elicit a diameter increase which in turn would bring the shear stress back to the original level.

However, the adaptation rules must yield appropriate behavior not only in a single segment but when segments are interconnected. It is helpful to consider the case of two identical segments connected in parallel, and fed by a fixed total flow rate. The pressure drop in both segments is the same. The hemodynamic relationship τ = ΔPD/(4l) shows that if the diameter of one segment is increased, it will experience a higher shear stress than the other segment and tend to increase further in diameter. The eventual result of this unstable positive feedback is that the diameter of one segment approaches zero and the other carries the entire flow. This defect in the theory of structural adaptation in response to shear stress alone was pointed out in several studies ^{17; 51 19}.

Role of intravascular pressure

The shear stress in the vascular system differs significantly between arterial and venous vessels, with consistently higher levels of shear stress in the arterial system. The transition between the two shear stress domains occurs in the resistance vasculature of the peripheral beds ^{41; 43; 47; 51}. These observations led to the development of the ‘pressure-shear’ hypothesis ⁴⁵ stating that the target value for shear stress is a function of the local intravascular pressure. They show that in addition to shear stress, other stimuli must be included in the control of vascular adaptation, and thus the scope of Murray's law is limited. Structural responses to pressure are well established and have been linked to the development of hypertension ^{10; 30; 31; 43; 60}. If increases in transmural pressure (P) lead to an increase in vessel wall thickness and/or a reduction of vessel diameter, these responses can act to stabilize circumferential wall stress (σ = PD/2w), where w is the vessel wall thickness), similar to the stabilization of shear stress addressed above. Due to the higher pressure level on the arterial side vascular pressure, this leads to smaller, thicker wall vessels on the arterial side and thus contributes to arterio-venous differentiation ⁴⁵. The hypothesis that circumferential stress generated by intravascular pressure stimulates the formation of arcade arterioles from capillaries was tested in a network model by Price and Skalak ^{36; 37}.

Role of metabolic stimuli

It is generally accepted that vascular diameter is also controlled by the metabolic needs of the tissue, as reflected in the local oxygen partial pressure or metabolic signal substances ^{1-4; 43; 45}. The inclusion of responses to metabolic stimuli can resolve the problem of instability resulting from responses to wall shear stress, mentioned above. When the diameter of a given segment drops to a level at which the flow is inadequate to satisfy metabolic demands, for instance causing hypoxia, then a growth signal is generated which inhibits further decrease in diameter. This concept was introduced in the model of Pries et al. ⁴⁶ by including a flow-dependent growth signal that increased with decreasing flow rate in each segment. The mathematical analysis showed that inclusion of such a signal can lead to stable network structures including multiple parallel pathways. In subsequent models ^{40; 43}, this approach was replaced by an explicit simulation of vascular oxygen levels. The responsiveness to oxygen levels is not necessarily direct, but likely occurs through the oxygen-dependent production or uptake of other metabolites or growth factors.

Role of conducted responses

In order to test models for structural adaptation, the authors (Pries et al. 1998, 2001, 2005) used reconstructions of mesenteric microvascular networks with 300-1000 vessel segments in which flow velocities had been measured. This allowed a detailed comparison of the diameter and flow distributions obtained from the simulated adaptation with the measured values. Using this approach, they found that models including only the signals already mentioned (wall shear stress, intravascular pressure, local metabolic stimulus) were not capable of predicting observed distributions of segment diameters and flow velocities. The additional assumption of upstream and downstream information transfer along vessels was needed in order to achieve adequate agreement with observed results.

Integrated model

In further development of the model⁴¹, the upstream information transfer was attributed to conducted responses and the downstream transfer to convection of metabolites (Figure 2). The roles of the individual mechanisms were:

Figure 2.

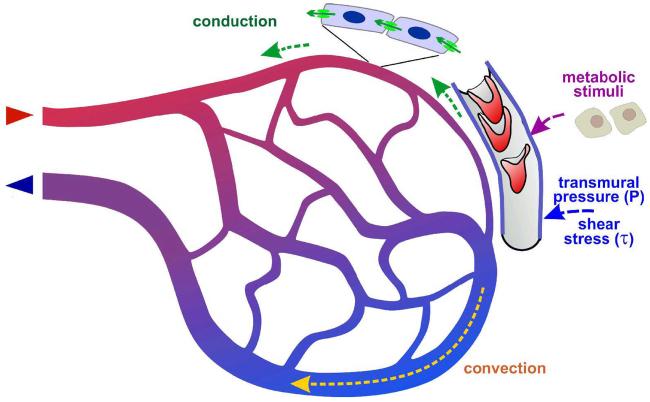
Integration of hemodynamic and metabolic stimuli in microvascular networks. Effects of blood flow, blood pressure and oxygen availability elicit local signals. Adequate adaptation of proximal feeding and draining vessels also requires the transfer of information on these local conditions ⁴⁰; ⁴²; ⁵⁶. In the downstream direction, the most probable mechanism of information transfer is the convection of metabolic signaling substances ⁷; ⁸; ²⁶; ⁵². A possible route for upstream information transfer is the conduction of electrical signals in the vessel wall ⁶; ⁵⁰; ⁵⁷. In order to avoid diameter increase of short proximal arterio-venous connections and consequential shunting of blood flow, it has to be assumed that conduction occurs in the upstream direction only at vascular branch points.

• Shear stress responses homogenize shear stress along flow pathways and thereby reduce energy dissipation;

• Pressure responses establish smaller vessel diameters and higher shear stress on the arterial side of vascular networks ⁴⁵. This arterio-venous asymmetry is of prime functional importance for flow regulation requiring high arterial flow resistance and for fluid balance requiring low capillary pressure.

• Metabolic stimuli couple vessel diameters to the local oxygen demand and prevent the collapse of parallel pathways;

• Information transfer via convection and conduction maintains larger diameters in proximal feeding and draining vessels as compared to short arterio-venous connections, thus preventing the establishment of functional shunts.

Conducted responses influencing the regulation of vascular tone have been observed by Segal and Duling ⁵⁷. The propagation of angioadaptive signals in the vessel wall by conduction of electrical signals through gap junctions between vascular cells (‘conducted response’) has subsequently been described in many animal models (e.g. ^{6; 27; 50}). Interestingly, several molecules implicated in the conducted response, e.g., connexin 37 and connexin 40, are selectively expressed in embryonic arteries, suggesting that these molecules may also play a pivotal role in early flow-controlled angioadaptation.

The model of vascular adaptation was used to investigate the importance of information transfer for structural adaptation, by reducing or abolishing conduction in the upstream direction ^{41; 42; 46}. As shown in Figure 3, this leads to the generation of a short proximal arterio-venous shunt which carries most of the inflow of the network. In the more peripheral regions of the network, the arterial vessels nearly disappeared and hypoxia is observed.

Figure 3.

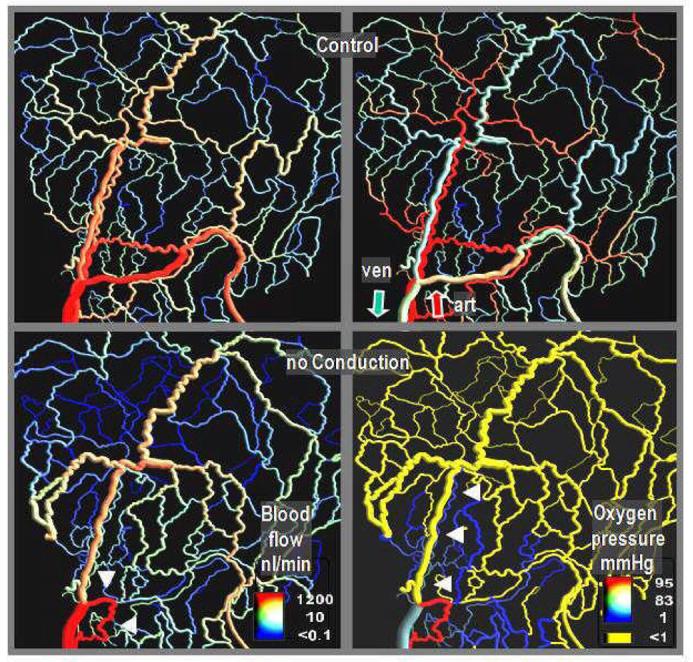
Blood flow distribution (left) and intravascular oxygen partial pressure resulting from simulations of vascular adaptation, with (top row) and without (bottom row) signal propagation along arterial vessel walls via conduction. Calculations were performed for a network in the rat mesentery (546 vessel segments) investigated by intravital microscopy. In the absence of conduction, most arterial vessels (distinguished by the high oxygen partial pressure on the top right panel) shrink to a very narrow diameter (arrow heads on the lower right panel). The blood flow mainly passes through a short arterio-venous shunt (arrow heads on the lower left panel) leading to oxygen depletion in large tissue areas. The results imply that increases in shear stress elicit eutrophic (or slightly hypertrophic/hypotrophic) outward remodeling, while wall stress increases lead to hypertrophic inward remodeling (methods described in ⁴⁰; ⁴²).

Circumferential wall tension and wall mass

In the above model, circumferential wall stress was not explicitly considered. Effects of pressure were implemented by assuming a pressure-dependent set point for shear stress regulation according to experimental data ⁴⁵. Thus, results with respect to arterio-venous asymmetry and capillary pressure were not truly properties of the adaptive system but to some degree imposed on it. Jacobsen and coworkers ²⁰ considered reactions to shear stress and mean wall stress in hexagonal vessel networks. They showed that a typical reaction of vascular structure in hypertension, i.e. eutrophic inward remodeling, required a reduction in vascular sensitivity to shear stress. However, the set points for average wall stress were again fitted to literature data ⁴¹.

In a further development of their model, the authors were able to avoid this limitation ⁴³. Separate reactions of mid-wall vessel diameter (D_m, eutrophic remodeling) and vessel wall area (A_w, growth / involution) to shear stress, transmural pressure and local metabolic state (Figure 4) were considered, including convection and conducted responses. The system of equations (2) was extended to include equations for the evolution of vessel wall area of each segment:

$$(1∕D_m)({\mathit{dD}}_m∕\mathit{dt})=k_{\tau d}\log (\tau ∕{\tau }_{\mathit{ref}}+\epsilon ){(1+k_{w\tau }\log (w∕w_{\mathit{ref}}+\epsilon ))}^{-1}+k_{\mathit{md}}(S_m+k_c{S}_c)-k_{\mathit{sd}}$$ (3)

$$(1∕A_w)({\mathit{dA}}_w∕\mathit{dt})=k_{\sigma g}\log (\sigma ∕{\sigma }_{\mathit{ref}}+\epsilon ){(1+k_{w\sigma }\log (w∕w_{\mathit{ref}}+\epsilon ))}^{-1}+k_{\mathit{mg}}(S_m+k_c{S}_c)-k_{\mathit{sg}}$$ (4)

where w is the wall thickness. The right hand sides in these equations give the integrated stimulus derived from the individual stimuli ⁴³, corresponding to the function F in eq. (2):

• The first terms represent hemodynamic stimuli dependent on τ and σ respectively. Here, τ_ref, and σ_ref are reference levels of τ and σ while ε is a small constant added to avoid singular behavior. k_τd and k_σg represent the respective sensitivities.

• The second terms establish an attenuating effect of wall thickness on the hemodynamic sensitivity which was found to be necessary in order to obtain predictions consistent with experimental data. k_wτ and k_wσ are the respective sensitivities. Logarithmic functions were chosen to give consistent sensitivity to τ, σ and w over a wide range.

• The third terms depends on the metabolic (S_m) and conducted (S_c) signals with the respective sensitivities k_md , k_mg and k_c. S_m is derived from the vascular convective flux (J_m) of a metabolic signal substance⁴⁰: S_m = log(1 + J_m/[Q + Q_R]) where Q_R is a small constant included to avoid singular behavior at low blood flow values. J_m, in turn, is assumed to increase by additional input of each segment with ΔJ_m = L_s (1 − P_O2/R_O2) if the intravascular P_O2 falls below a reference level R_O2. L_s is the length of the segment. The conducted signal is assumed to depend on the value of the conducted signal (J_c): S_c = J_c/(J_c + J₀) where J₀ is again a small constant. In each segment, the mid-segment conducted signal, J_c, is related to that at the downstream end (J_c^down) and the local metabolic signal J_c = (J_c^down + S_m) A exp(−0.5L_s/L₀), where L₀ is the conduction length constant.

• The fourth terms represent the tendency for inward remodeling (k_sd) and involution (k_sg) in the absence of hemodynamic or metabolic stimuli.

Based on the resulting changes in vessel diameter, the distributions of shear stress and wall stress are calculated as described above. Since the results obtained for the steady state are not influenced by a possible direct influence of shear stress on wall area and of wall stress on vessel diameter, they are omitted from the equations for clarity. These steps are iterated until a steady state is achieved in which the sum of all positive and negative stimuli for a given segment approaches zero. In this steady state, all relevant parameters (e.g. shear stress, wall stress, PO₂) exhibit broad distributions with a number of relevant correlations to other parameters ^{40; 43; 46}. Examples are the decline of the shear rate level by about one order of magnitude from the arterial to the venous side of the networks ⁴⁵ and the strong correlation between vessel diameter and circumferential wall stress ⁴³.

Figure 4.

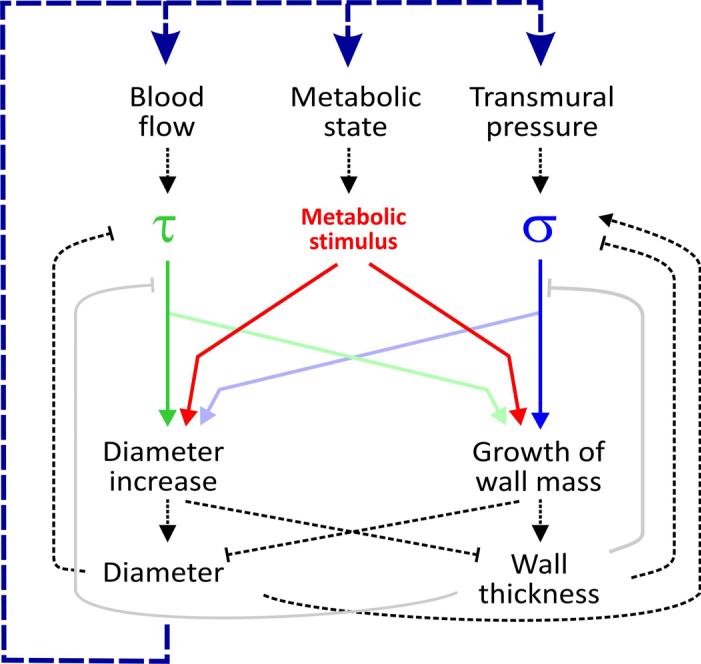
Local hemodynamic and metabolic signals in structural vascular adaptation in an individual vessel segment. The main hemodynamic stimuli are related to the blood flow through the vessel generating wall shear stress at the endothelial surface (τ) and to the transmural pressure difference causing circumferential wall stress (hub stress, σ). A metabolic stimulus is generated by the vessel and/or the tissue cells in response to the local oxygen availability. These stimuli elicit structural vascular responses (remodeling) in vessel diameter and vessel wall mass. The strength and nature of the underlying biological reactions, depicted as colored continuous lines (reactions to τ, σ and the metabolic state) grey continuous lines (effects of vessel wall thickness on sensitivity to τ and σ), critically determines the properties of the vascular bed. The dashed lines indicate physical relations of local nature (black, e.g. according to the law of Laplace) or indirectly via changes in the distribution of flow resistance, blood pressure and oxygen within the vascular network (blue line).

It is of note that this model used only generic mathematical relations between the hemodynamic and metabolic conditions and the related stimuli. No parametric representations of expected biological behavior were included. Therefore, network characteristics obtained by the model according to Figures 2 and 4 and the equations given above are truly emergent properties related to the assumed biological reactions. The comparison of distributions of flow velocity and diameter in individual segments allowed the estimation of the sensitivity parameters (k_τd , k_σg, k_wτ, k_wσ, k_md, k_mg, and k_c). With these values, the model is able to predict distributions of vessel diameter, wall thickness, shear stress, wall stress, pressure and volume flow that are close to those measured in vivo ⁴³.

Model applications and predictions

Based on such a validation, mathematical simulation can be used to quantitatively investigate the impact of changes of systemic conditions and of biological mechanisms. In the context of structural adaptation, this approach has been used to examine changes in blood pressure and perfusion ^{20; 41; 43; 44; 47; 48}, effects of growth factors ³⁵, endothelial function ^{20; 43} and changes in the strength of conducted signals (Figure 4) ^{40; 46}.

Simulation models have the advantage of allowing manipulation of individual biological mechanisms in a graded fashion and without unwanted compensations. Complete elimination of a signal or a response using biological ‘knockout’ approaches in experimental models can provide fundamental insights into biological mechanisms related to molecular function, but leads in some cases to extreme and unspecific reactions that reveal little about the role of the mechanisms involved. In contrast, the graded modifications possible in theoretical model simulations allow more precise interpretation of the sensitivity of the system to a specified intervention. Such findings may in turn stimulate additional experiments.

In figure 5, effects of changes in the shear stress sensitivity of diameter reactions (k_τd in eq. 3) are shown to have biologically desirable as well as problematic effects. Increased shear stress sensitivity leads to more homogenous shear stress distributions and according to Murray's law, to decreased energy requirements for perfusion. Furthermore, shear stress sensitivity was shown to be a central mechanism for the coordination of diameter adaptation in larger feeding vessels in response to changes in metabolic demand in the capillary bed ⁴². However, increased shear stress sensitivity also reduces the decline of shear stress along flow pathways from the arteriolar to the venular portion of the network. According to equation (2), a higher shear stress on the arterial side corresponds to a higher pressure drop and thus to low capillary pressure levels ⁴³, which are crucial for tissue fluid balance. Thus, model analysis shows that vascular reactions must balance the requirements for different physiological requirements and cannot be optimized solely with respect to low energy dissipation. Similar findings have been reported earlier for the effects of the balance between hemodynamic and metabolic sensitivity on energy dissipation, capillary pressure and oxygen deficit within the network ⁴⁰.

Figure 5.

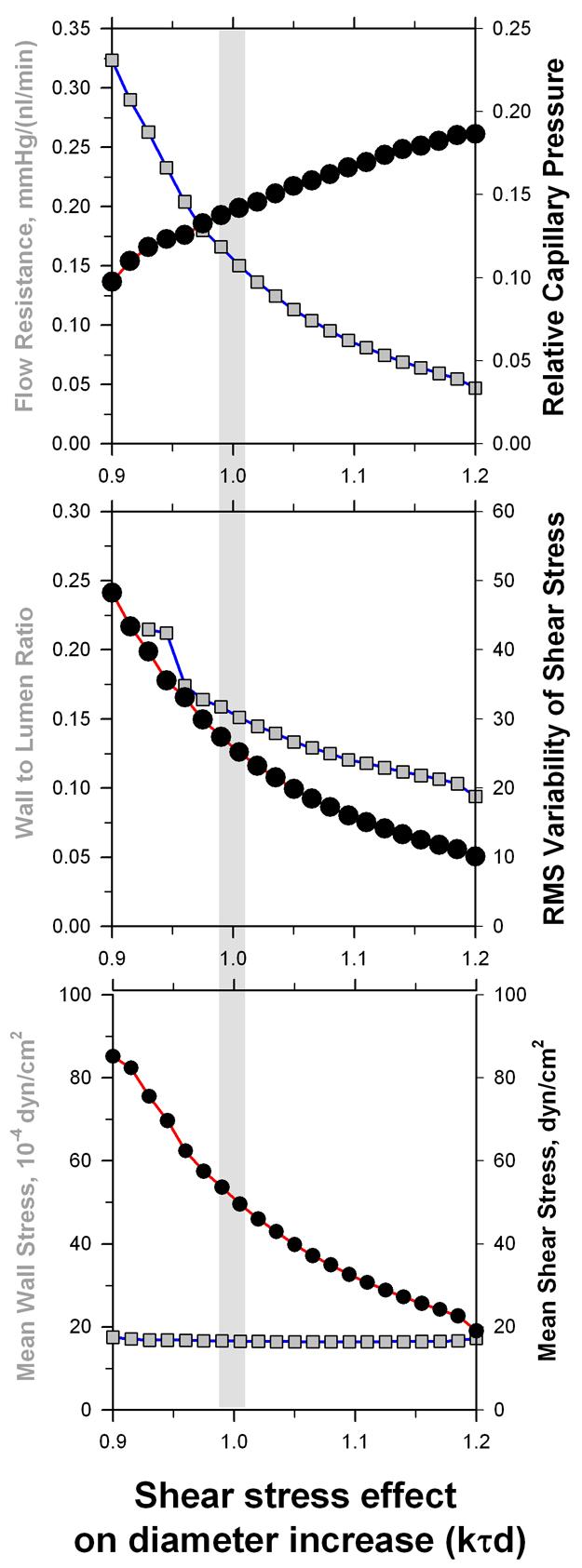
Dependence of structural and functional network parameters for graded changes of the sensitivity of vascular diameter reactions to wall shear stress (k_τd in equation (3), standard reference value 1.0). Mean values for a vascular network with 546 individual vessel segments are given. The effects on mean capillary pressure relative to the difference between arterial input pressure and the venous outflow pressure (upper panel) and the root-mean-square variability of shear stress in individual vessel segments (middle panel) are highlighted. Increased shear stress sensitivity leads to a more homogeneous shear stress distribution, i.e. a closer adherence to the requirements of Murrey's optimization law. However, an increased reactivity to shear stress also reduces the arterio-venous difference in shear stress and pressure drop leading to an increased mean capillary pressure. This would increase net outward filtration from the microvascular bed and thus increase the risk of edema generation.

Another example of the predictive capacity of such models pertains to the role of the conducted response in structural adaptation. According to model results, maintenance of balanced perfusion in topologically heterogeneous microvascular networks requires information transfer upstream from capillaries to feeding arterioles ^{40; 43; 46}, most likely effected by conduction of signals along the vessel wall ⁴² (Figure 3). This important role of conduction was suggested solely based on model simulations, since experimental studies of the conducted response have so far been restricted to the investigation of acute changes of smooth muscle tone. Development of suitable pharmacological and genetic tools should allow critical tests of this hypothesis in vivo in the foreseeable future.

Perspectives

The models described above are focused on the analysis of fundamental mechanisms and minimal requirements for steady-state structural adaptation of vessel diameter and wall mass. Obviously, this leaves a large number of additional dimensions to be explored, probably necessitating the inclusion of additional mechanisms. Such dimensions include pulsatility and external mechanical forces, changes of adaptive properties during development or pathophysiological states (inflammation, wound healing, tumor development), interactions with parenchymal cells in specific tissues, dynamics of vascular adaptation ¹⁶, interaction of vessel adaptation with angiogenesis and pruning ¹³, and interactions between structural adaptation and acute vascular tone ²¹. A major task for future work on these topics is to develop models that (i) include the relevant mechanisms, (ii) do not incorporate parametric descriptions of expected behavior, and (iii) are validated against experimental measurements.

Such models can predict functional behavior on the given level (vessels) and above (vessel networks). However, more detailed levels on smaller scales (cells, molecules) must be treated as black boxes. In the spirit of a ‘middle out’ approach ²⁵, such models should be linked to higher levels to predict of organ behavior, and to lower levels to incorporate establish cellular and molecular models of angioadaptation. For the latter, e.g. the use of cellular automaton models has been introduced ^{12; 35}.

Effects of multiple cooperating and competing stimuli are involved in vascular patterning and adaptation. The complexity of such systems typically requires the development of mathematical models. As discussed above, such models can yield significant insights, including improved understanding of the processes of vascular development, growth, adaptation and regression, and may provide a basis for new therapeutic interventions in diseases including cancer and hypertension that involve abnormal vascular structures.