Theoretical models for regulation of blood flow

Abstract

Blood flow rate in the normal microcirculation is regulated to meet the metabolic demands of the tissues, which vary widely with position and with time, but is relatively unaffected by changes of arterial pressure over a considerable range. The regulation of blood flow is achieved by the combined effects of multiple interacting mechanisms, including sensitivity to pressure, flow rate, metabolite levels and neural signals. The main effectors of flow regulation, the arterioles and small arteries, are located at a distance from the regions of tissue that they supply. Flow regulation requires sensing of metabolic and hemodynamic conditions and transfer of information about tissue metabolic status to upstream vessels. Theoretical approaches can contribute to the understanding of flow regulation by providing quantitative descriptions of the mechanisms involved, by showing how these mechanisms interact in networks of interconnected microvessels supplying metabolically active tissues, and by establishing relationships between regulatory processes occurring at the microvascular level and variations of metabolic activity and perfusion in whole tissues. Here, a review is presented of previous and current theoretical approaches for investigating the regulation of blood flow in the microcirculation.

INTRODUCTION

The control of blood flow has been a topic of central interest to physiologists since the late nineteenth century [27]. Total blood flow to an organ varies according to metabolic requirements, but is relative insensitive to arterial pressure. Local control of blood flow ensures matching of perfusion to spatially varying oxygen demand, thereby achieving efficient oxygen delivery [71]. A number of mechanisms are known to be involved, including autonomic nervous stimuli, circulating substances, mechanical stimulation of vessels, myogenic responses, shear-dependent responses, metabolic responses, conducted responses propagated along vessels, and communication between paired feeding and draining vessels. The consequences of these mechanisms at the whole tissue level, particularly with regard to the metabolic regulation of flow (functional hyperemia) and the autoregulation of flow (maintenance of nearly fixed flow despite changes in perfusion pressure), have been extensively studied. However, the manner in which the various mechanisms combine and interact to produce the observed control of perfusion is not well understood. More than twenty years ago, it was stated that “A significant remaining challenge is that of integrating observations on small and large vessels into a general picture of flow control” [19], and this challenge remains to be met.

Progress has been hampered by the complexity of the problem. The circulatory system consists of a network of many interconnected vessels, and the flow through any segment depends not only on the flow resistance of that segment but also on the resistance of other vessels connected in series and in parallel. The multiple regulatory mechanisms, mentioned above, act to varying extents on segments of different size and type, and depend on variables, including flow rate, pressure and metabolic status, that are themselves dependent on the distribution of flow. Several different modes exist for transfer of information about metabolic and hemodynamic conditions between tissue and vessels and among vessels [64]. In a system with so many interactions and interconnections, it is difficult to unravel cause and effect and to define the role of any individual mechanism in the behavior of the system as a whole.

Theoretical modeling, in combination with experimental studies, has the potential to overcome this difficulty. In a theoretical model, several observed or hypothesized mechanisms can be synthesized into a unified mathematical framework. The model can then be used to predict the overall behavior of the system, taking into account the interactions between different mechanisms occurring at the level of individual cells or segments and the interactions that arise in a network of interconnected segments. The relative roles of various mechanisms can be assessed by selectively removing them from the model (‘mathematical knockouts’), in a way that is difficult or impossible to achieve in an experimental system.

Here, a review is presented of theoretical models for flow regulation in the microcirculation. Key experimental developments and observations that underlie the models are briefly described, and possible directions for future development are indicated.

MODELS FOR MICROVASCULAR HEMODYNAMICS

The volume flow rate Q through a microvessel may be estimated using Poiseuille's law

$$Q=\left(\pi \Delta P{r}^4\right)∕\left(8L\eta \right)$$ (1)

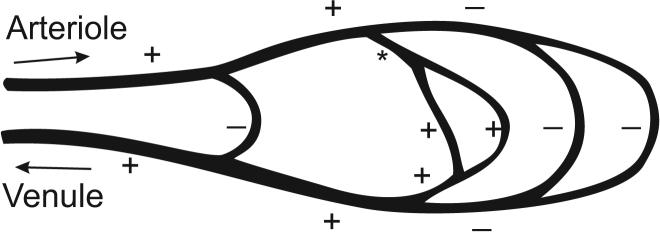
where ΔP is the pressure drop, r is the radius of the segment, L is its length, and η is the apparent viscosity of blood, which is itself a function of vascular diameter and hematocrit, and may also depend on flow rate [58]. The importance of this relationship with regard to flow regulation is well recognized: the proportionality to r⁴ implies a sensitive dependence of flow rate on diameter. For example, a reduction in lumen diameter by 10% would result in a 44% reduction in flow, if all other parameters remained constant. In reality, however, constriction of a single vessel within a network alters the flow, and hence the pressure drop, in other vessels in the network. The actual change in flow is less than predicted by this formula. The effects on network flow of changing the resistance of one segment are shown schematically in Figure 1.

Figure 1.

Schematic depiction of hemodynamic interactions in a microvascular network. Arrows denote flow directions in feeding arteriole (A) and draining venule (V). Dilation of segment (*) causes increased flow in segments in series with the indicated segment (+) and decreased flow in parallel segments (−).

The relationship between vessel diameters and flow distribution in microvascular networks can be understood by considering the vessel segments as forming a network of resistances, analogous to an electrical circuit. The flow resistance R of a segment is defined as the pressure drop along the segment divided by the flow rate, and is, from Poiseuille's law

$$R=\Delta P∕Q=\left(8L\eta \right)∕\left(\pi r^4\right)$$ (2)

If the geometry and topology of the network are specified, along with boundary conditions in the form of pressures or flow rates in the segments feeding or draining the network, then the flow in each segment can be determined. In simple cases, the flows can be computed by using the well-known rules for resistances in series and in parallel, but this is not possible in general. A preferable method [47] is to solve a system of linear equations in which the unknowns are the pressures at each node (connection point of segments). The equations are obtained by imposing the condition that the sum of the flows entering each node is zero, where the flow in each segment depends on the nodal pressures and on the segment resistance.

It is helpful to consider a simple network of vessel segments (Figure 1), supplied by a fixed driving pressure with a single inflow and outflow segment. In such a network, changing the resistance of one segment alters the flow in every segment. In the case of segments in series, decreasing the resistance of one segment causes increased flow along the pathway containing that segment. This draws flow away from other parallel pathways, whose flow decreases. Corresponding changes in the distribution of pressure in the network occur. As discussed below, vascular segments sense and respond to the levels of flow and pressure that they experience. An alteration in the distribution of flows and pressures within the network can lead to active diameter changes in other segments of the network.

Many theoretical models for microvascular blood flow and regulation have been based on simplified network topologies, in which the vasculature is considered as a chain of elements in series, each one representative of a specific class of vessels. While such an approach may be appropriate, it should be kept in mind that actual microvascular networks are heterogeneous in structure [56], with large variations in the lengths and numbers of segments forming complete flow pathways, and with wide dispersion in the distributions of hemodynamic parameters such as pressure, velocity and wall shear stress among vessels belonging to a given category. Such heterogeneity can have important effects on functional behavior of networks [18] and should be considered in development of models for regulation.

MODELS FOR CELLULAR RESPONSES

Arteriolar diameter is controlled by contraction or relaxation of vascular smooth muscle (VSM). The level of tone generated by a vascular smooth muscle cell (SMC) depends on several factors, including its length and tension, local levels of metabolites and signaling molecules, communications with other cells via gap junctions, and neural inputs. Ideally, theoretical simulations of flow regulation should be based on an integrated model for the responses of an individual VSM to all these stimuli. Such a model is not available, but some aspects of cellular responses have been considered theoretically.

A model for the electrophysiology and mechanics of SMCs was developed by Gonzalez-Fernandez and Ermentrout [28], with the goal of understanding the origin and dynamics of vasomotion (spontaneous oscillations in diameter) of small arteries. The dynamics of membrane potential, potassium and calcium ion conductances and intracellular calcium binding were explicitly considered. Mechanical properties of the cells were represented by a three-element model, consisting of an active tension-generating component in series with a nonlinear passive spring, both in parallel with a second nonlinear spring. The active and passive length-tension relationships of smooth muscle were included. As typical for muscle cells, the maximum active tension that can be generated increases and then decreases with increasing length of the active element. This behavior was represented by a modified Gaussian function. The actual active tension was assumed to be equal to the maximal tension multiplied by a factor between zero and one that depends dynamically on intracellular calcium level. A strongly nonlinear form was assumed for the parallel passive component, with tension increasing rapidly near a critical maximum length. A force-velocity relationship was introduced to allow simulation of time-dependent behavior. Myogenic effects were simulated by assuming that one of the parameters in the model, defining the voltage dependent variation in calcium conductance, is a function of intravascular pressure. The model predicted a myogenic response, i.e., a decrease in vessel diameter with increasing pressure above 50 mmHg. This study introduced a number of useful concepts, particularly with regard to the representation of vessel wall mechanics. Limitations were a lack of quantitative comparisons with experimental data, and the assumption that myogenic effects depended directly on pressure rather than on wall stress or tension (see next section).

Yang et al. [72] developed a model for SMCs incorporating both electrochemical and chemomechanical subsystems. Their approach was similar in some respects to the work just described [28] but apparently independent. A Hodgkin-Huxley type model was used to describe membrane electrochemistry, and a multi-state model was used for calcium-induced calcium release. The mechanical model for the cell was as described above, with the addition of a viscoelastic element in series with the active contractile element. Several aspects of the model were tested by quantitative comparisons with experimental data. The SMC model was then used in a vessel-level model of the myogenic response [73]. Results were presented for one case predicting myogenic constriction similar to that observed in cerebral vessels. In this analysis, it was assumed that the increased stress in the vessel wall is transmitted to the SMC membrane, increasing the conductivity of stretch-sensitive ion channels in the membrane and leading to muscle contraction. A limitation of this model is that the relationship between circumferential wall stress and membrane strain is over simplified. Under circumstances where vessel diameter decreases in response to increased pressure, circumferential tension typically increases but cell membrane strain decreases. If stretch-sensitive ion channels in the cell plasma membrane do indeed play a central role in the myogenic response, it must be via a more complex mechanical interaction.

In subsequent work, Yang et al. [74] developed a model for the nitric oxide/cGMP pathway in SMCs. Nitric oxide (NO) is an important vasodilator substance. Effects of NO on activation of soluble guanylate cyclase (sGC), cGMP production and degradation, cGMP-mediated regulation of Ca²⁺-activated K⁺ channels, and the myosin contractile system were simulated. The generation of NO by endothelial cells has also been addressed theoretically [9]. Predicted rates of NO production by endothelial nitric oxide synthase were found to be lower than would be needed to activate the sGC pathway in SMCs, based on a simulation of periarteriolar NO transport [39]. These studies suggest that more than one mechanism may be involved in both the production of NO by endothelial cells and its vasoactive effects on SMCs. Furthermore, other endogenous mediators such as endothelium-derived hyperpolarizing factor (EDHF) can communicate between endothelial cells and SMCs.

Cellular-level modeling of the mechanisms involved in blood flow regulation is a logical approach for understanding the processes involved, and will be especially useful for understanding effects of pharmacological mediators. As the above examples illustrate, this work is at a relatively early stage, and the multiplicity of biochemical and biophysical mechanisms involved remains a major challenge. Phenomenological models describing responses at the vessel level, as described next, therefore provide a more practical basis for describing flow regulation in networks and tissues, at least for the present.

MODELS FOR VASCULAR RESPONSES

Myogenic response

The myogenic response has been the subject of many experimental studies [37], particularly with regard to its role in the autoregulation of blood flow. The biophysical mechanism by which stretching of SMCs stimulates contraction has not been established. One point of debate has been whether stress (tension) or strain (elongation) is actually sensed. In a basic sense, this question is easily answered. Overall elongation of the SMC cannot be the signal for myogenic contraction, since the signal would then go to zero once the cell contracted to its original length, and constriction to less than the initial diameter (as frequently observed) would not occur. This does not, however, rule out the possibility that some component of the cell (a 'sensor element'), connected in series with the contractile elements, experiences elongation under increased tension, even when the cell as a whole is shortened. The behavior of a model of this type was discussed by Johnson [37] and considered to be consistent with observed myogenic behavior.

Johnson and Intaglietta [38] developed a model for the myogenic response in which the level of tension generated depended on the relative change in intravascular pressure according to a gain parameter. Such a model can generate a range of responses, ranging from passive dilation to strong constriction with increasing intravascular pressure. Direct dependence of diameter or tension generation on intravascular pressure was assumed in a number of subsequent theoretical studies [12, 22, 26, 28, 45]. According to the Law of Laplace, the average circumferential stress in the vessel wall is given by

$$\sigma =PD∕2w$$ (3)

where P is the transmural pressure difference, D is the diameter and w is the wall thickness. (This relationship assumes thin-walled vessels, where w << D.) The ratio D/2w generally ranges from 2 to 10 in the arterioles and small arteries [57]. Therefore, the dominant stress acting on smooth muscle cells is circumferential stress and this, rather than pressure, is the mechanical stimulus more likely to drive the myogenic response. The model of Borgström and Grände [5] took such an approach. The active tension in the wall was assumed to be the sum of two terms, one proportional to the circumferential stress and one proportional to the rate of change of circumferential stress with time. Model predictions were consistent with observed dynamic responses to changes in intravascular pressure.

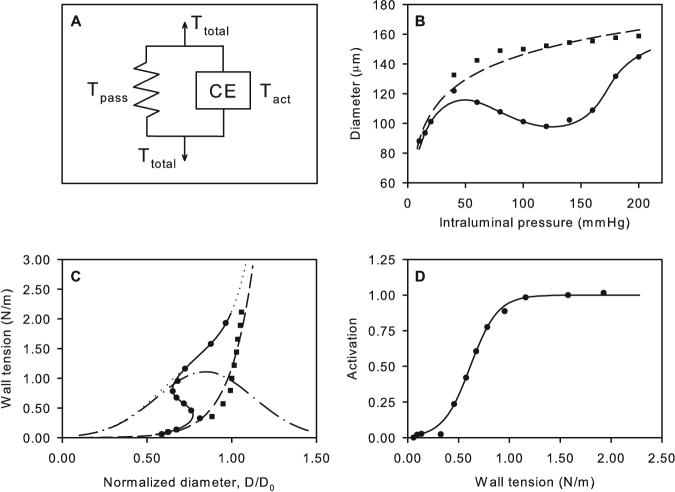
Using experimental data of Kuo et al. [41, 43], Fung [25] deduced a length-tension relationship for VSM in the form of an inverted parabola. This model did not include variation in the level of VSM tone. A model for the myogenic response based on the length-tension characteristics of VSM, and including variable tone, was developed by Carlson and Secomb [8]. This model includes features of several of the models described above. As in the model of Gonzalez-Fernandez and Ermentrout [28], the vessel wall is represented mechanically as a nonlinear spring in parallel with a contractile unit (Figure 2A). The wall tension is:

$$T_{\mathit{total}}=\mathit{PD}∕2=T_{\mathit{pass}}+A_{\mathit{act}}^{\mathit{max}}$$ (4)

where T_pass is the passive component, T_act^max is the maximal active component, and A, the activation, represents the level of VSM tone (0 ≤ A ≤ 1). The passive component is approximated by an exponential function of diameter:

$$T_{\mathit{pass}}=C_{\mathit{pass}}\exp \left[{C^{\prime }}_{\mathit{pass}}(D∕D_0-1)\right]$$ (5)

The constant C′_pass represents the wall tension at a reference diameter D₀, and C′_pass describes the steepness of the diameter-tension relationship. The active component is a Gaussian function [28]:

$$T_{\mathit{act}}^{\mathit{max}}=C_{\mathit{act}}\exp \left[-{\left(\frac{D∕D_0-{C^{\prime }}_{\mathit{act}}}{{C^{″}}_{\mathit{act}}}\right)}^2\right]$$ (6)

where C′_act gives the maximum active tension, C′_act determines the diameter at which maximal active tension is generated, and C″_act determines the width of the Gaussian function. Activation is given by a sigmoidal function of wall tension:

$$A=\frac{1}{1+\exp \left[-S_{\mathit{tone}}\right]}\text{where}{S}_{\mathit{tone}}=C_{\mathit{myo}}{T}_{\mathit{total}}-C_{\mathit{tone}}$$ (7)

and C_myo and C_tone are unknown parameters. With fitted parameter values, this model gives a close approximation to experimentally observed pressure-diameter curves from a number of studies [8]. An example is shown in Figure 2.

Figure 2.

Model for myogenic response based on length tension relationships of vascular smooth muscle. A. Spring and contractile element representation of vessel wall response. B. Pressure-diameter relationships. C. Length-tension relationships. D. Dependence of activation on wall tension. Symbols: Experimental data for rat mesenteric arterioles [6] (■ passive, ● active). Curves: model results (– – passive, — active). In C, predicted maximally active VSM tension (– . –) and total tension (…) are also shown. Modified from [8].

Shear-dependent response

Vasodilation of blood vessels in response to increased wall shear stress has been shown in many experimental studies [23, 40, 42, 55, 59, 61]. Changes in blood flow alter the wall shear stress (τ) acting on the inner endothelial surface of the vessel:

$$\tau =\Delta \mathit{Pr}∕\left(2L\right)=4Q\eta ∕\left(\pi r^3\right)$$ (8)

Shear stress is transmitted to endothelial cells mainly by the endothelial surface layer [62]. The response of endothelial cells to increased shear stress includes increased release of NO. Although the intracellular signaling processes have been extensively studied, the cellular mechanism responsible for mechanotransduction of shear stress remains elusive.

Liao and Kuo [46] obtained experimental data on myogenic contraction without flow and with a controlled level of wall shear stress, and developed empirical relationships to describe the observed variation of diameter. In the model of Fung [25], the data [43] could be fitted by assuming a length-tension curve whose shape depends on wall shear stress. In the model of Cornelissen et al. [12], the level of tone generated in each segment of the coronary arterial tree was assumed to depend on the concentration of NO generated by endothelial cells, which was taken as a sigmoidal function of wall shear stress.

The model described in eqs. (4) - (7) can be extended in a natural way to include effects of wall shear stress [7], by including an additional term in the quantity S_tone:

$$S_{\mathit{tone}}=C_{\mathit{myo}}{T}_{\mathit{total}}-C_{\mathit{shear}}\tau +{C^{″}}_{\mathit{tone}}$$ (9)

Here, C_myo and C_shear are coefficients reflecting the sensitivity of vascular tone to the wall tension and wall shear stress, and C″_tone is a constant. The fact that the summation is carried out before the sigmoidal function is applied ensures that the activation is within the available range 0 ≤ A ≤ 1 under all conditions. The resulting fit to experimental data [66] is shown in Figure 3.

Figure 3.

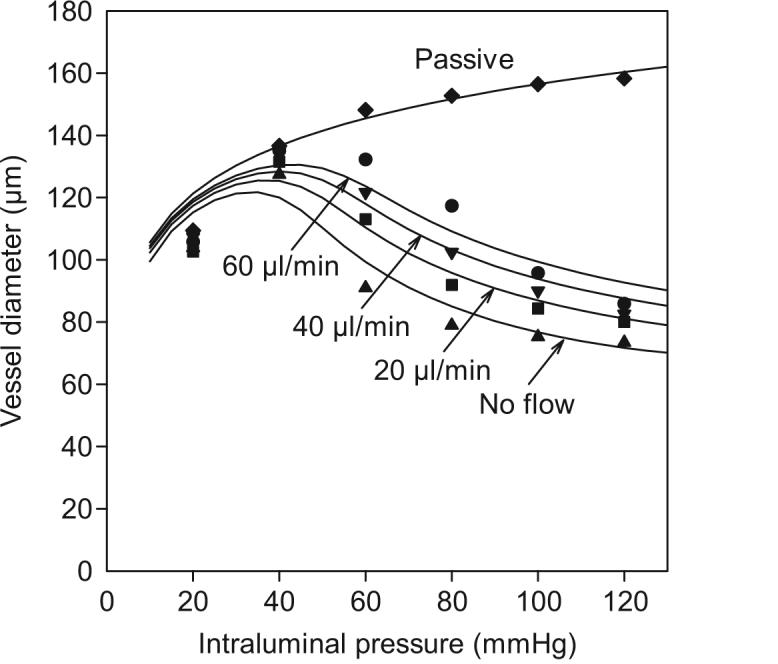
Pressure-diameter relationships predicted by model including both myogenic and shear dependent responses. Symbols: Experimental data for rat cremaster arterioles [66]▲ no flow; ■ 20 ml/min; ▼ 40 ml/min; ● 60 ml/min. Curves: corresponding model predictions. Modified from [7].

Metabolic response

Vascular responses to metabolic conditions are clearly necessary for metabolic regulation of blood flow and the development of functional hyperemia. Oxygen is a crucial metabolite, and arterioles in vivo react to oxygen levels, constricting as surrounding oxygen levels are increased [16]. Duling and Berne [17] observed that oxygen levels decline along arterioles and hypothesized that sensitivity of arteriolar smooth muscle to oxygen might provide a mechanism for blood flow regulation. However, Jackson [35] showed that arterioles are insensitive to changes in local oxygen level within a normal physiological range. This suggested that the sensing of oxygen levels occurs in downstream vessels or in the parenchyma and initiates responses that are conducted to the arteriole. Subsequent work has supported this hypothesis, as discussed below.

Several theoretical models have included metabolic responses. Borgström and Gestrelius [4] assumed that a vasodilator substance is generated by metabolic activity and that its concentration affects the dependence of VSM activation on calcium concentration. Iida [34] assumed that the vessel wall acts as a linear spring with a variable elastic modulus that depends on both the VSM strain (myogenic effect) and on the blood flow rate (metabolic effect). Ursino et al. [70] assumed that a decrease of blood flow rate below a set point, dependent on metabolic needs, causes dilation. Groebe [30] assumed that tissue metabolic status is sensed by the venules, which then actively constrict or dilate. According to this concept, arteriolar constriction or dilation occur by myogenic and shear-dependent responses to the alterations in hemodynamics caused by altered venular resistance. While the concept of metabolic sensing at the venules is logical, this model requires a level of vasoactive response in venules that does not correspond to observation.

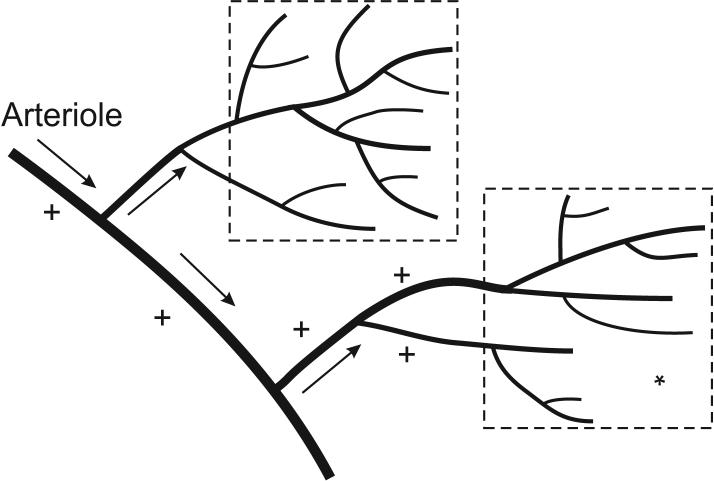
Given that arterioles are the main effectors of blood flow regulation, a crucial aspect of the metabolic response is the need for arterioles to receive information about the metabolic status of the tissue that they supply (Figure 4). Oxygen demand and oxygen levels are often spatially heterogeneous in tissue. For instance, in a partially activated skeletal muscle, active and inactive fibers are interspersed. Theoretical simulations [48] show that if arterioles respond only to local oxygen levels, effective oxygenation of active fibers is not achieved. Upstream communication to the arteriole from the bundle of capillaries that it supplies is required.

Figure 4.

Schematic illustration of the need for communication between tissue sites and upstream arterioles supplying those regions. Increased metabolic demand in a tissue region (*) requires dilation of vessels feeding that region (+) to provide increased perfusion.

Mechanisms of information transfer in the microcirculation were reviewed by Secomb [64]. Of particular importance is the existence of conducted responses, propagated from cell to cell along the vessel walls via gap junctions, which involve changes in membrane potential and ionic concentrations. As discussed in previous reviews [10, 31, 64], conducted responses occur via both endothelial and smooth muscle cells. This phenomenon has most often been studied in arterioles, but capillaries and venules also participate in conducted responses [2, 11, 13, 15, 68].

A series of studies by Ellsworth and colleagues [11, 14, 20, 21] has examined the hypothesis that ATP release by red blood cells in venules is involved in metabolic flow regulation. The rate of ATP release increases with decreasing oxyhemoglobin saturation [3]. Application of ATP to venules stimulates upstream conducted responses via the capillaries leading to arteriolar vasodilation [11]. The combination of saturation-dependent ATP release and conducted responses initiated by ATP represents a highly plausible mechanism for metabolic regulation.

In recent work, Arciero et al. [1] have developed a theoretical model for metabolic flow regulation based on this mechanism. Flow along a pathway consisting of seven representative segments is considered, of which two (large and small arterioles) are vasoactive. The variations of oxyhemoglobin saturation and intravascular ATP level along the flow pathway depend on the rate of oxygen consumption in the surrounding tissue. In particular, the rate of release of ATP in the venules depends on the decline of red blood cell saturation occurring in the arterioles and capillaries. The conducted response is defined by integrating in the upstream direction a signal proportional to the ATP concentration. The integration is performed starting at the venule and taking into account exponential decay of the signal with distance along the vessel. The resulting signal at the arterioles is introduced as an additional term in the quantity S_tone in eq. (8), and arteriolar diameters are calculated using eqs. (3) - (6). The model predicts that the ATP-dependent mechanisms can account for variation of perfusion with oxygen consumption rates in the low to moderate range, in good agreement with experimental observations. An unexpected finding was that the myogenic and shear-dependent mechanisms do not contribute significantly to the metabolic response.

In further studies using this approach [7], autoregulation of blood flow was simulated. In response to increased arterial pressure, the myogenic response tends to decrease arteriolar diameters, while the shear-dependent response has the opposite tendency. With these two responses combined, predicted autoregulation was weak. However, the addition of the metabolic mechanism as described above led to a predicted variation of flow rate with arterial pressure that is consistent with observed autoregulatory behavior.

Arterioles with diameters 30-40 μm and above are frequently paired with corresponding venules in skeletal muscle. This paired countercurrent arrangement allows the diffusive exchange of metabolites between venules to arterioles. Several studies have provided evidence that this mechanism of information transfer participates in control of blood flow [33, 60, 67]. This mechanism has not yet been investigated theoretically.

MODELS FOR VASOMOTION

In many tissues, spontaneous oscillations in the diameter and blood flow of arterioles is observed, with typical frequencies in the range 3-20 cycles per minute. This phenomenon has been much studied, but its physiological significance is still not clear [53, 63]. Its occurrence is sensitive to the physiological status of the tissue. In some preparations, it is normally present but inhibited by reductions in arterial pressure [51], while in others it is normally absent but can be stimulated by histamine [29].

A number of theoretical models for vasomotion have been developed, based on differing hypotheses regarding its origin. The model of Gonzalez-Fernandez and Ermentrout [28], mentioned earlier, includes effects of both membrane ion transport and vascular wall mechanics. It predicts the occurrence of vasomotion over a wide range of pressures, but not at very low or very high pressures, in agreement with experimental observations of the pressure dependence of vasomotion. Ursino et al. [69, 70] developed a model in which the oscillations arise from the interactions between several active segments, each with static and rate-dependent components of myogenic activation, as previously assumed by Borgstrom et al. [5]. Parthimos et al. [54] considered that the oscillations were generated by intrinsic cellular mechanisms, including the coupled activity of intracellular and membrane Ca²⁺ oscillators. This model led to behavior with chaotic dynamics. Incorporating some aspects of that work, Jacobsen et al. [36] developed a model for the spatial distribution of calcium levels within an individual SMC and proposed that a shift from wave-like fluctuations to synchronized oscillations of Ca²⁺ may underlie the appearance of vasomotion.

From these studies, two main possibilities emerge. One is the existence of cells or groups of cells in the vessel wall with intrinsic oscillatory behavior, acting as ‘pacemakers’ to drive vasomotion in several nearby segments, as earlier hypothesized [52]. The other is that vasomotion results from interactions between the dynamics of cellular responses and the mechanics of the vessel wall and blood flowing. In reality, both types of mechanisms may be involved.

Flow autoregulation and oscillatory behavior in the renal circulation have received much attention. An additional mechanism of flow regulation is present in the kidney, tubuloglomerular feedback (TGF). The combined effects of TGF and myogenic responses lead to complex dynamics including chaotic behavior [44, 50]. Autoregulation in response to changes in arterial pressure shows strong frequency dependence and may be important in protecting the glomerulus from fluctuations in blood pressure [49]. The above recent citations represent only a small sample of the literature on this topic.

CONCLUSIONS

Development of theoretical models for local regulation of blood flow dates back at least to the 1960s [32]. In the intervening years, more has been learned about several mechanisms that contribute to blood flow regulation. Experimental studies have systematically explored the effects on vascular tone of two or more simultaneous stimuli [24, 66]. The essential role of conducted responses has been increasingly recognized [65]. These experimental developments provide a basis for increasingly detailed and realistic models.

In future work, several trends can be anticipated. The effects of multiple interacting mechanisms will be incorporated in models, so that their contributions to metabolic regulation, autoregulation and other aspects of flow control can be assessed. Models will more fully reflect the multiple scales of the system, including molecular, cellular, vessel, network and tissue-level phenomena. This may be best achieved by developing models on a given level in the context of smaller and/or larger scale phenomena, rather than by attempting to describe processes at all these scales within a single model. In the biological research community, it is now widely recognized that mathematical and computational approaches are needed to help understand complex phenomena. This certainly applies to flow regulation in the microcirculation.