Statistical and computational models of the visual world paradigm: Growth curves and individual differences

Abstract

Time course estimates from eye tracking during spoken language processing (the “visual world paradigm”, or VWP) have enabled progress on debates regarding fine-grained details of activation and competition over time. There are, however, three gaps in current analyses of VWP data: consideration of time in a statistically rigorous manner, quantification of individual differences, and distinguishing linguistic effects from non-linguistic effects. To address these gaps, we have developed an approach combining statistical and computational modeling. The statistical approach (growth curve analysis, a technique explicitly designed to assess change over time at group and individual levels) provides a rigorous means of analyzing time course data. We introduce the method and its application to VWP data. We also demonstrate the potential for assessing whether differences in group or individual data are best explained by linguistic processing or decisional aspects of VWP tasks through comparison of growth curve analyses and computational modeling, and discuss the potential benefits for studying typical and atypical language processing.

Introduction

In the decade since the (re)discovery that eye movements provide an exquisitely sensitive online measure of spoken language processing (Tanenhaus, Spivey-Knowlton, Eberhard, & Sedivy, 1995; cf. Cooper, 1974), the “visual world paradigm” (VWP) has been applied to time course questions at the level of sentences (Altmann & Kamide, 1999; Tanenhaus et al., 1995), phonologically based lexical competition (Allopenna, Magnuson, & Tanenhaus, 1998), semantically based lexical competition (Huettig & Altmann, 2005; Yee & Sedivy, 2006), and even subphonemic details of word recognition (Dahan, Magnuson, Tanenhaus, & Hogan, 2001b; McMurray, Tanenhaus, & Aslin, 2002; Salverda, Dahan, & McQueen, 2003).¹ Typically, participants are presented with a set of objects (on a tabletop or computer display) and they follow spoken instructions to interact with the display (touching, clicking, or moving objects) or answer spoken questions about the display. In contrast to conventional psycholinguistic techniques like lexical decision or naming, one typically obtains multiple data points during processing for each trial.

For example, in a display containing beaker, beetle, speaker, and carriage, as a participant hears an instruction like click on the beaker, he might generate an eye movement to beetle when only the first two segments have been heard, and then look to the beaker 100 ms later. This leads to trial-level data schematized in the upper row of Fig. 1. At any moment on a single trial, a participant can either fixate an object or not, so trial level proportions are 0 or 1 for each item of interest at any point in time. Trial data are averaged over items and participants in order to arrive at a time course estimate like that shown in the bottom of Fig. 1. From the data of Allopenna et al. (1998), for example, we learn that fixation proportions map onto phonetic similarity over time; by the time listeners are hearing the/i/in a word like beaker, they are equally likely to be fixating the target or a cohort (like beetle), while rhymes (like speaker) are fixated less and later (but more than unrelated items, like carriage). VWP data stand in stark contrast to data from tasks like lexical decision, where the data points represent single, post-perceptual measures. As a result, the VWP provides fine-grained data in the context of a natural task. However, there are three important gaps in current analyses of this paradigm. We describe each briefly, and then describe our approach to filling these gaps.

Fig. 1.

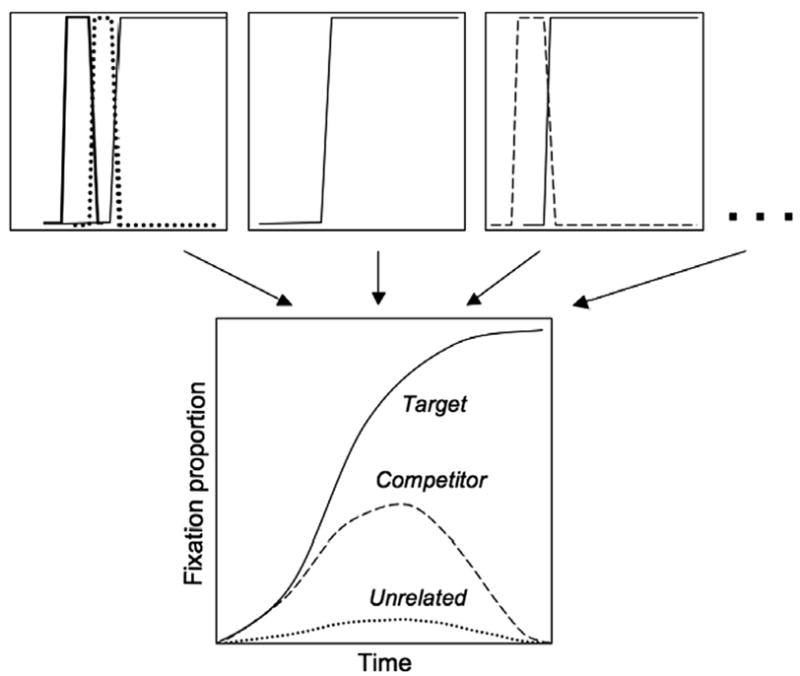
Schematic of typical eye movement averaging for the visual world paradigm. For individual trials (top), a participant can only fixate one object at a time, giving a time series of 0.0 and 1.0 proportions for each possible fixation target. Trials are averaged (typically across items and participants) to yield continuous time-course estimates of, e.g., lexical activation and competition.

First gap: appropriate analysis of time

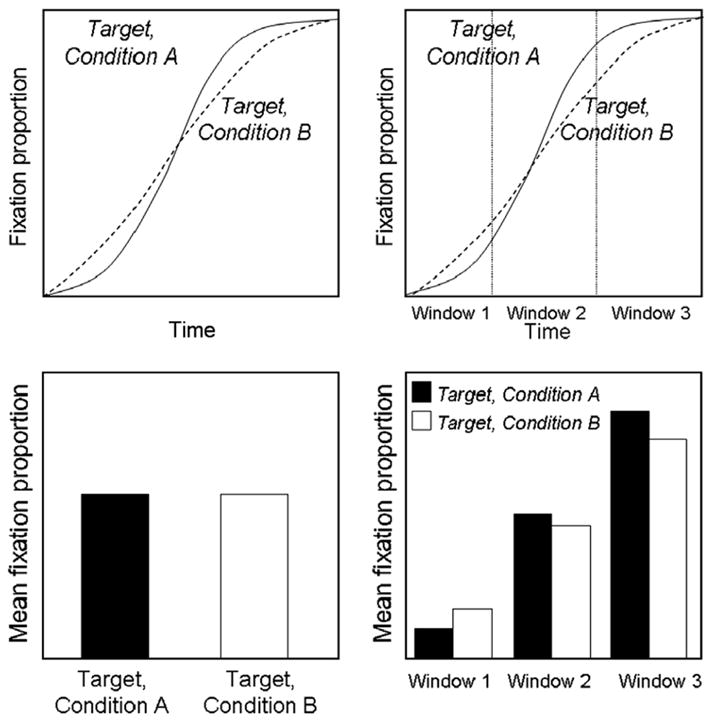
Although the paradigm’s most powerful contribution is the ability to estimate the fine-grained time course of activation and competition among linguistic representations, when the data are analyzed statistically, time is usually ignored or treated inappropriately. Figs. 2–4 illustrate typical approaches. In the simplest strategy, standard general linear model (GLM) analyses, such as analysis of variance or t-tests, are applied to a greatly compressed representation of the time course data. Fig. 2 and the left columns of Figs. 3 and 4 schematize this approach; mean fixation proportion to each item is computed for a single window of analysis on the time course data (top in each figure), resulting in data like that schematized in the lower panels of each figure. While this approach minimizes the number of GLM assumptions violated (cf. Chambers, Tanenhaus, & Magnuson, 2004; Magnuson, Tanenhaus, Aslin, & Dahan, 2003), it expressly discards the precious fine-grained detail the VWP provides. The data are presented graphically in continuous time course form, but statistical analyses are applied to the radically reduced mean proportions. Aside from the loss of grain, this approach works well for data where relations among items of interest are stable across the analysis window (as in Fig. 3). For cases where, however, there is a change in the rank order of fixation proportions over time (e.g., where one competitor type dominates early in the time course, but another does later, or, as in Fig. 4, there is an interaction with time in a comparison of targets from different conditions), this approach is obviously inappropriate, as it does not retain any detail about time course.

Fig. 2.

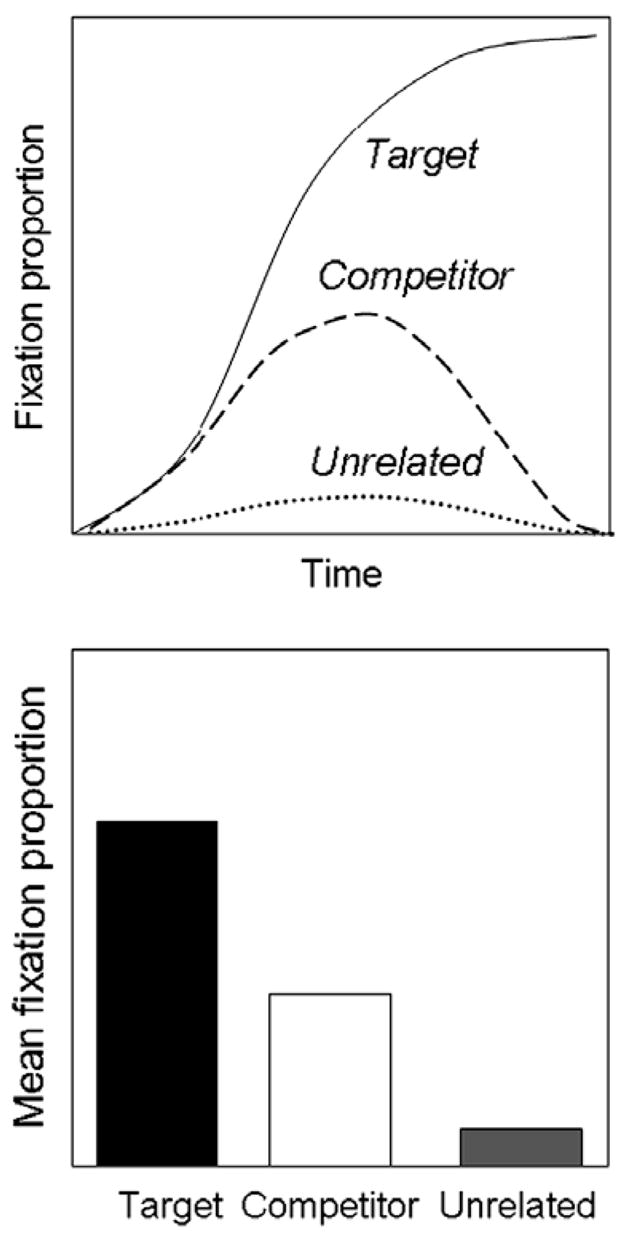
Schematic of “area” analyses. Proportions over time for a target, competitor, and unrelated item (top) are converted to single numbers—average fixation proportion over the entire time window (or some smaller window).

Fig. 4.

An example of a case where multiple windows are required to capture change over time; in this case, target proportion interacts with time. Two or more windows are required to capture this interaction, but window selection is problematic (see text).

Fig. 3.

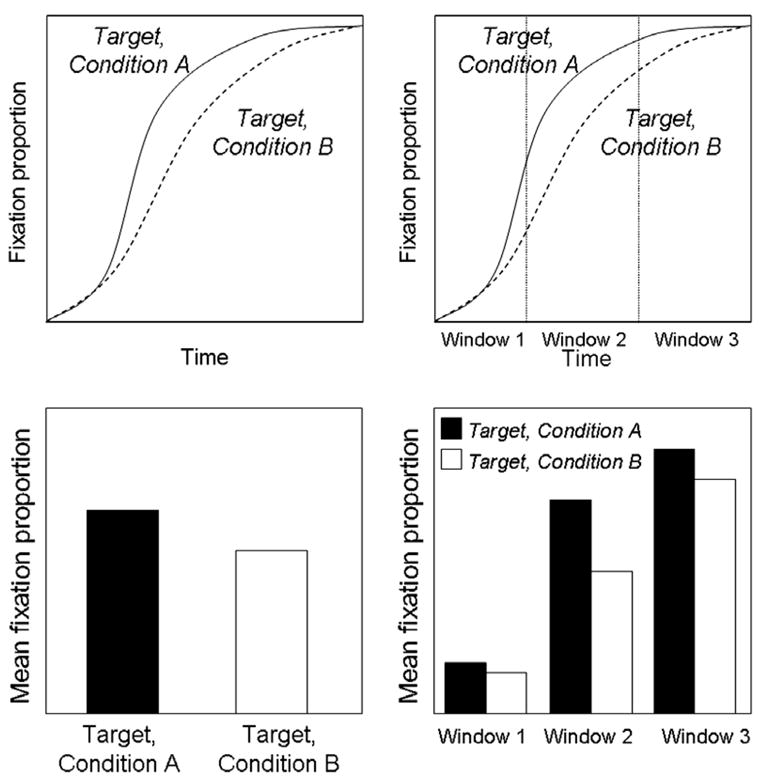
Area analyses comparing target proportions in different conditions with a single time window (left) and three successive time windows (right). A common approach is to define a series of time windows (often many more than three) and to include “window” in a repeated measures ANOVA (violating independence assumptions, since successive windows are strongly related).

Another common approach is to calculate mean fixation proportions in successive windows of analysis (right columns of Figs. 3 and 4), and to perform a repeated measures analysis on mean fixation proportions across windows (Allopenna et al., 1998). This preserves more of the time course, but there are typically no independent principles for determining the “correct” time windows and different size windows can produce very different results. More importantly, this approach treats time as a factor with levels corresponding to individual time windows. This analysis naturally focuses on whether the patterns of data in some time windows differ from patterns in other windows, not on the trajectory of change over time (i.e., the estimate of the time course of cognitive processing), which is the unique insight provided by the VWP.

We describe a statistical approach, growth curve analysis (GCA), which builds on techniques explicitly designed to assess change over time (Singer & Willett, 2003). These techniques have been applied primarily to longitudinal behavioral data in the developmental literature. To apply it to VWP data, eye tracking data are treated as longitudinal data collected on a fast time scale. The approach provides a formal model of the impact of differences between conditions and/or individuals on parameters (such as intercept and slope) of individual × condition curves of fixation proportions over time. We will introduce the method in detail and then by example after discussing the other gaps in current approaches to VWP data.

Second gap: characterizing individual differences

Researchers who have examined trial-by-trial data from the VWP know that there is substantial between-participant variability; to the best of our knowledge there have been no attempts to assess this variability, and so its implications are unknown. Simply describing these differences is an important step—how well do measures of central tendency describe the range of performance observed, and how is performance distributed over that range? Under growth curve analysis, parameters are estimated that characterize individual differences. The mere characterization of variability across individuals provides a starting point for analyzing individual differences. Our approach goes further, with the aim of unpacking whether individual differences stem from differences in language processing or other processes, such as motor-decision processes controlling eye movements.

Third gap: interpreting individual differences

Going beyond description and unpacking individual differences requires that we grapple with some vexing methodological questions about the VWP. There are compelling arguments that fixation probabilities over time provide an exquisitely sensitive estimate of linguistic processing (given, for example, that fixations map onto phonetic similarity over time down to a subphonemic level; Dahan et al., 2001b). However, eye movement behavior in the VWP is influenced by the contents of the display (Dahan, Magnuson, & Tanenhaus, 2001a), and we expect individual differences in motor-decisional thresholds for saccades. We will present a strategy for grappling with these issues by comparing growth curve analysis with simulations of the TRACE model of speech perception (McClelland & Elman, 1986) coupled with a simple decision model that converts TRACE activations to predicted fixation proportions over time (Allopenna et al., 1998; Dahan et al., 2001a). Specifically, we test combinations of TRACE and decision parameters for simulating individual and individual × condition data. It may be possible to fit the same data by changing TRACE parameters or decision model parameters. To the degree that individual data can be fit by TRACE but cannot be fit by the decision model, we can provisionally attribute individual differences to variation in linguistic processing. With a model like TRACE, we can further explore the range of model parameters that provide good individual × condition fits to generate causal hypotheses regarding differences in linguistic processing. When applied at the individual or group level, this approach has promise for illuminating characteristics of language impairments.

In the next section, we provide a brief, fairly informal introduction to growth curve analysis. Then we turn to practical examples, analyzing some recent VWP spoken word recognition results. We begin with examples at the group level, and then demonstrate assessment of individual differences using growth curve and TRACE models. We close with a brief discussion of implications and alternative approaches. Readers interested in applying growth curve modeling should see Singer and Willett (2003). The book is refreshingly accessible, and there is an accompanying web site with sample code for SAS, SPSS, and S+/R. In addition, we provide general step-by-step instructions for GCA in the Appendix A, and SAS and R code and raw data for the analyses presented here are available at http://magnuson.psy.uconn.edu/GCA (we have run the analyses in SAS and R, though many statistical packages have multi-level modeling capabilities and any of them should be able to conduct growth curve analyses).

Growth curve analysis

The growth curve modeling approach to analyzing data from the VWP rests on the assumption that the properties of the task (the characteristics of the selected words, the visual display, etc.) create an underlying probability distribution of fixation locations (i.e., targets, competitors, distractors, etc.) over time. The observed fixation proportions reflect this underlying distribution. The goal of the analytic approach is to describe the functional form of the probability distribution. It is not a model of the underlying processes (just as ANOVA would not be). Rather, the method quantifies the major aspects of the distribution that result from the underlying processes. This statistical approach provides appropriate and rigorous quantification of observed data, including significance tests.

Growth curve modeling was developed for classical longitudinal designs, in which data collection is typically done over months or years. However, the key structural issues are the same whether measurements are made over a few seconds or over multiple years. We will outline the basic architecture of the model and then show how it can be easily adapted to the VWP.

Growth curve modeling, and its close cousin, hierarchical linear modeling (Raudenbush & Bryk, 2002), are part of a family of techniques that represent a generalization of standard regression approaches, such as ordinary-least-squares (OLS). The major innovation is that, conceptually, growth curve models contain two (or more) hierarchically related submodels, rather than a single model that applies to the entire sample. The first submodel, usually called level-1, captures the effect of time. To introduce this concept, consider an experiment in which each individual participated in only one condition. This makes individuals the smallest grain of analysis in the model hierarchy and the following model gives a value for the dependent measure, Y, for an individual participant, i, at a particular measurement occasion, j.

$$Y_{ij}={\alpha }_{0i}+{\beta }_{1i}\ast {\text{Time}}_{ij}+{\epsilon }_{ij}$$ (1)

The i subscript here indexes individuals and j indexes measurement occasions. As in OLS regression models, we have an intercept, α_0i, a slope, β_1i, and an error term, ε_ij. However, unlike standard models, the intercept and the slope are allowed to vary across individuals, hence the i subscripts. This variation is captured in the second set of models, called level-2 models. That is, there is potentially a level-2 model for each parameter of the level-1 model, which describes that level-1 parameter in terms of population means, fixed effects, and random effects.

When we move to the level-2 models, the equations become a bit more complex. In particular, as we break the intercept and slope down into structural and stochastic components, we will refer to them using one variable to represent structural components (gamma: γ) and another to represent stochastic components (zeta: ζ). Subscripts will indicate whether we are referring to intercept or slope. For example, terms at level-2 where the first subscript is 0 refer to intercept components and a first subscript of 1 indexes slope components (as will become clear shortly). This notational complexity has two benefits. First, it is consistent with the conventions of Singer and Willett (2003). Second, this notation facilitates working with the polynomials. As we move to fitting more complex curves, we will add further polynomial terms. These terms will continue to be referred to by the same variables (γ, ζ) with the first index indicating the polynomial order (0 = intercept, 1 = slope [linear], 2 = quadratic, 3 = cubic, etc.).

The level-2 model for the intercept is: α_0i = γ₀₀ + ζ_0i, where γ₀₀ is the population average value for the intercept and ζ_0i is the deviation of an individual’s intercept from the average intercept. The residual term, ζ_0i, allows each individual’s intercept in the first model, α_0i, to vary around the population average intercept, γ₀₀. The analogous model for the slope is: β_1i = γ₁₀ + ζ_1i, where γ₁₀ is the population average value for the slope and ζ_1i is the deviation of an individual’s slope from the average slope. The residual term, ζ_1i, allows the slope parameter in the first model, β_1i, to vary around the population average slope, γ₁₀.

If we substitute the models just specified for the intercept and slope into the first equation, we get:

$$Y_{ij}=({\gamma }_{00}+{\zeta }_{0i})+({\gamma }_{10}+{\zeta }_{1i})\ast {\text{Time}}_{ij}+{\epsilon }_{ij}$$ (2)

To facilitate an analogy to standard OLS regression, it is useful to reorganize the model into its structural and stochastic portions:

$$Y_{ij}={\gamma }_{00}+{\gamma }_{10}\ast {\text{Time}}_{ij}+({\epsilon }_{ij}+{\zeta }_{0i}+{\zeta }_{1i}\ast {\text{Time}}_{ij})$$ (3)

Considered this way, the current model is closely analogous to an OLS regression model (γ₀₀ is analogous to the intercept, γ₁₀ to the slope), but the error term is now the sum of three components. The terms in the parentheses (i.e., ε_ij + ζ_0i + ζ_1i * Time_ij) collectively represent error in this model. For current purposes, we adopt this standard error covariance structure, but we note that many other structures can also be specified within this framework.

The residual term, ε_ij, retains its usual meaning and assumptions; it is drawn from a normal distribution with a mean of zero and its values are independent across persons and measurement occasions. Each individual also has a constant added to each measurement occasion, the residual term ζ_0i, and another residual, ζ_1i, that interacts with Time. These latter two terms allow error to be correlated across measurement occasions, as one might expect when measurements are repeated for each individual. The product term, ζ_1i * Time_ij, allows error to be heteroscedastic within each individual. That is, the effect of this residual depends on the magnitude of Time_ij. These latter two residual terms, ζ_0i and ζ_1i, are also assumed to have means of zero and to be drawn from a bivariate normal distribution, with unknown variances and covariance. These terms are homoscedastic across individuals and constant across an individual’s measurement occasions (see Singer & Willett, 2003, pp. 243–265, for a more complete discussion of the composite error term).

The level-2 models can also include structural terms that capture the effects of different experimental conditions. For example, the model for the intercept (α_0i in Eq. (1)) can be expanded to include an effect of some condition, C:

$${\alpha }_{0i}={\gamma }_{00}+{\gamma }_{0c}\ast C+{\zeta }_{0i}$$ (4)

The potential effect of condition that could be captured here would be on the intercept itself, the value at which all other level-1 predictors are zero. A similar model would be used to capture the effect of condition on the slope (β_1i in Eq. (1)):

$${\beta }_{1i}={\gamma }_{10}+{\gamma }_{1c}\ast C+{\zeta }_{1i}$$ (5)

Here condition affects the rate of change over time. Much of the power of the growth curve approach lies in its ability to describe these over-time curves using simple linear equations at level-1 and model the effects of different conditions through the parameters within those equations at level-2. A level-2 model can be specified for each of the polynomial terms. The first term in each level-2 model can be considered the population average for the polynomial term, γ_n0, where n indicates the order of the level-1 term (i.e., γ₀₀, γ₁₀, γ₂₀, γ₃₀, γ₄₀, for the intercept, linear, quadratic, cubic, and quartic, respectively). This parameter estimates the value of the polynomial term when all other terms in its particular level-2 model are zero. The second term, γ_nc, indexes the effect of condition, C, on the polynomial term. If there are more than two conditions and they are categorically distinct (e.g., three or more word types or three or more training types), it may be necessary to include multiple condition terms. That is, the model would set one of the conditions as a baseline and estimate parameters for each of the other conditions relative to the baseline.

The final term, ζ_ni, is an error term that allows for individual (or individual × condition) variation around these effects. In theory, all level-2 models can have error terms. However, in practice, it would be unusual to include all of them in the model. The error terms, also called random effects, are quite “expensive” in terms of the amount of data needed to estimate them. A hidden cost is that the model must estimate not only the variance of the random effect, but also a covariance parameter with all other random effects in the model. Thus, the number of variance/covariance parameters required grows geometrically with the addition of random effects. These random effect error terms capture the structure in the data not explained by the fixed effects, thus, they play two important related roles: statistically, they make the model describe the data more accurately; theoretically, they describe relationships in the data not captured by fixed effects. Which random effects should be included in a particular analysis depends on the expected error structure and the research questions under investigation. In typical VWP data, participants are likely to differ in the rate of activation of lexical representations; thus, linear and quadratic random effects are likely to be the most important both for capturing the error structure and for quantifying individual differences for further analysis, as we shall see later.

Thus far, we have considered the level-1 model as representing the trajectory of an individual’s performance over time. However, in many experiments, we have individuals in more than one condition, thus making the combination of individual and condition the smallest grain of analysis. The model is completely indifferent to whether the level-1 trajectories come from individuals or individuals × conditions. Likewise, the effect of being in a condition and the effect of being a particular person can both be represented in the level-2 models. That is, the model can tease apart differences in curve parameters (intercept, slope, etc.) that are attributable to conditions from those that are attributable to individuals. To make this point more concrete, the following model includes both an effect of condition, C, and of person, P, on the slope:

$${\beta }_{1k}={\gamma }_{10}+{\gamma }_{1c}\ast C+{\gamma }_{1p}\ast P+{\zeta }_{1k}$$ (6)

where k indexes individuals × conditions (in practice, P would naturally be a set of dummy-coded variables, rather than a single scalar). This is an extension of Eq. (5), which only had an effect of condition.

Fig. 5 schematically demonstrates the relationship between level-1 and level-2 models. In the top left panel a level-1 linear model is represented. In the bottom left panel the intercept term is replaced by a level-2 model that includes an effect of the difference between two conditions (as in Eq. (4)), where the solid line is the data from one condition and the dashed line is the data from the other condition; in the top right panel a similar substitution is made for a level-2 model that includes an effect of the difference between two participants, where the circles are data from one participant and the triangles are data from the other participant. In the bottom right panel the intercept term is replaced by the full level-2 model including effects of condition and participant (analogous to Eq. (6)). The condition term captures the effect of condition C on the intercept and the participant term captures the effect of individual participant P on the intercept. A separate parameter estimated for each participant and variation across these parameters characterizes the variation in intercepts between participants. By extending this approach to the other terms in the level-1 model, we can evaluate the effect of condition and participant on other terms (slope, quadratic, etc.).₂

Fig. 5.

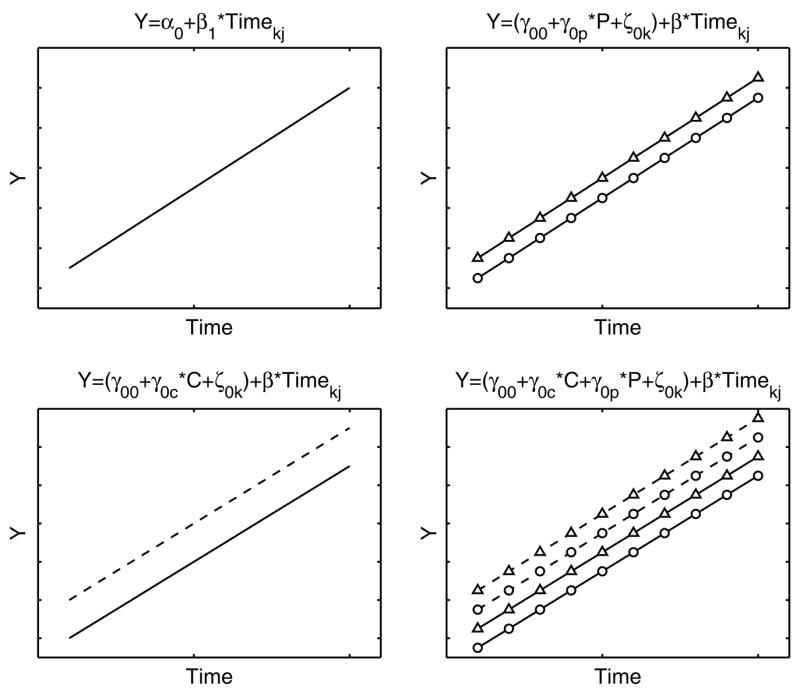
Schematic of multilevel linear model approach. The top left panel shows the level-1 model. The top right panel adds a level-2 model that includes an effect of participant P, triangles and circles correspond to two different participants. The bottom left panel adds a level-2 model that includes an effect of condition C, solid and dashed lines correspond to two different conditions. The bottom right panel combines these level-2 models so that both condition and participant effects are represented.]

In introducing the level-1 model, we have initially included only two terms, the intercept and slope, to describe the curve. This would limit the model to representing straight lines. However, the model is easily expanded to capture more complex forms. One way to accomplish this is through the use of power polynomials (an alternative approach is to use other non-linear functions, such as the logistic; while this approach is very much in the same spirit, we believe power polynomials afford important advantages for many research applications, as we discuss in more detail below). Power polynomials are capable of representing the curvilinear relationship between fixation proportion and time. A standard way to create the power polynomials is to simply raise Time to a particular power. For example, a quadratic curve (i.e., a curve with a single inflection) can be represented by introducing Time²; a cubic curve (two inflections) by further including Time³. One issue with creating the polynomials in this way is that the terms (e.g., Time, Time², Time³) are highly collinear. Therefore, introducing a higher order term (e.g., Time³) changes the estimated effects of lower order terms (e.g., Time²). This is particularly problematic when one wishes to model effects on those lower order terms. For example, one might wish to test an effect of condition on the first-order (linear) time term, but also wish to capture the curvilinear nature of the relationship by adding the squared term, Time². In this circumstance, it is inconvenient for the squared term to influence the linear term, as the experimental effect is hypothesized to be on the linear term.

One strategy to avoid this issue is to employ orthogonal power polynomials. The orthogonal polynomials are linear transformations of the non-orthogonal polynomial terms just described, but they are uncorrelated with one another. Specifically, they are the orthonormal basis vectors for the space defined by natural polynomials of a given order and given number of time steps (many statistical software packages, including R and SAS, have built-in functions for computing orthogonal polynomials). Because the time vectors are orthogonal, they are mutually independent (perpendicular); thus, including a higher-order term does not change the value of the estimated lower-order terms. Higher-order models could also contain higher-order residual error terms (i.e., ζ_2i, ζ_3i, etc.), which would capture heteroscedasticity of residuals over time. The second-order term (ζ_2i * Time²) is of particular importance because variance in VWP data tends to be low at the tails (the asymptotic portions of the curve) and high in the middle.

To illustrate the ability of power polynomials to represent fairly complex functional form, we generated a data set using a fourth-order polynomial. This allows us to demonstrate how the terms (intercept, linear, quadratic, cubic, and quartic) independently affect the form of the curve. Each panel of Fig. 6 shows data from the fourth-order model with three different values for one of the terms, with remaining terms held constant. The top row shows hypothetical target fixation curves (roughly monotonically increasing functions) and the bottom row shows hypothetical competitor fixation curves (rise and fall trajectories indicating transient activation). Fig. 6 shows how the various terms contribute to creating the curvilinear form: the intercept term reflects an overall vertical shift in the curve (note that the orthogonal polynomials change the interpretation of the intercept: the intercept term now indexes the average height of the curve, making it analogous to area under the curve), the slope term reflects the overall angle of the curve, the quadratic term reflects the symmetric rise and fall rate around a central inflection point, and the cubic and quartic terms similarly reffect the steepness of the curve around inflection points. To emphasize the effects of 3rd and 4th order terms (which are usually low) the solid lines in Fig. 6 reflect changes of sign (positive vs. negative) for these parameters.

Fig. 6.

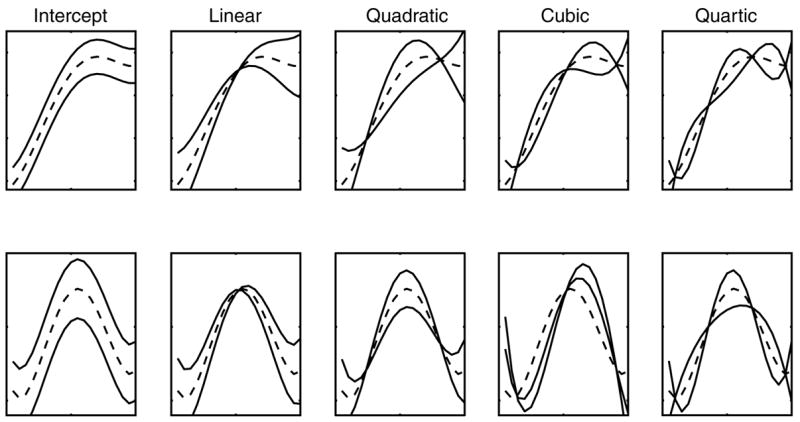
Effects of manipulating individual model parameters on the shape of VWP fixation proportion curves. The top row shows schematic target fixation curves (roughly monotonic rising indicating increasing activation), the bottom row shows schematic competitor fixation curves (rise and fall trajectory indicating transient activation). Each panel shows three levels for a single parameter, the middle value is shown as a dashed line for ease of interpretation.

Interpreting the lower-order terms is fairly straightforward, but significant effects on terms higher than the quadratic can be dificult to interpret. A general rule-of-thumb is that the order of the terms reflects the number of changes of focus of fixation: the intercept (0th order) is a constant difference, the linear (1st order) term is a single change of focus (i.e., from neutral start to target), the quadratic (2nd order) term is two changes in focus (i.e., from neutral start to competitor, from competitor to target), the cubic (3rd order) term is three changes in focus (i.e., from neutral start to target, to competitor, back to target), etc. However, in the context of typical VWP studies, 3rd and 4th order terms may also reflect asymmetries around curvature captured primarily by the quadratic term and tend to be very sensitive to the asymptotic tails of fixation proportion curves. As a result 3rd and 4th order terms may not have clear cognitive interpretations. Typical VWP experiment design and fixation pre-processing assumes activation of a particular target lexical representation or activation and then decay or deactivation of a competitor lexical representation. In the target case, there is a monotonic increase in fixation proportion, so only intercept and linear terms will relate meaningfully to cognitive processing. In the competitor case, there is a single peak of fixation proportion with roughly symmetric activation and deactivation time course, thus the intercept, linear, and quadratic terms will relate meaningfully to cognitive processing. Note that for target fixation data, if fixations that occur after target selection are included in the analyses (e.g., returns from the target to the central fixation cross), the data will contain a second change of fixation focus, thus, the quadratic term will capture important aspects of the time course of target fixation. This approach to handling target fixation data provides more time course data for analysis, making possible differences in time course easier to detect statistically using GCA (see discussion below). The cubic term would gain a meaningful cognitive interpretation in a VWP design that would lead participants to tend to look to an object, then away, and then come back to it.

Fig. 6 also assists in understanding the effects of the level-2 models. As we discuss below, the level-2 models affect the curves through the polynomial terms themselves. Therefore, the figure provides a graphical representation of what an effect on each polynomial term means for the curve. That is, the variations shown in Fig. 6 can be thought of as level-2 effects (such as effects of experimental condition or individual) on level-1 parameters that determine the shape of the curve.

Practical examples of growth curve analysis

Analysis of target fixations

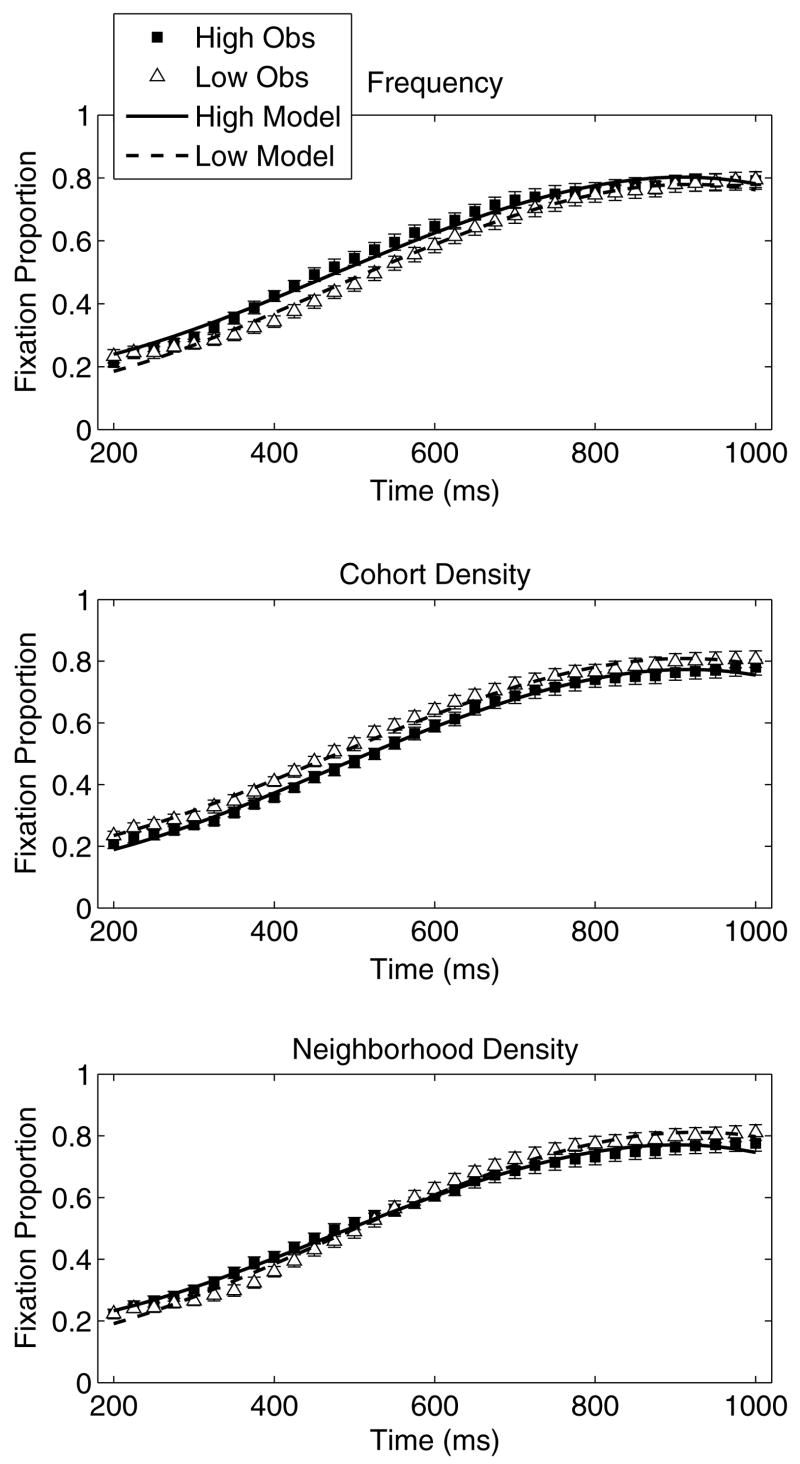
As an example of the growth curve approach applied to the visual world paradigm, we present results from a VWP investigation of effects of frequency, cohort density (sum of frequencies of words overlapping with a target at onset), and lexical neighborhood density (sum of frequencies of words differing from the target by no more than one phoneme) on spoken word recognition (see Magnuson, Dixon, Tanenhaus, & Aslin, 2007, for details). As in typical VWP experiments, on each trial, four simple pictures were presented on a computer screen and participants were given a spoken instruction to click on one of the four presented pictures (e.g., “Click on the bed”). The frequency of occurrence, cohort density, and neighborhood density of the target words were manipulated (high vs. low) in a fully crossed design yielding 8 cells with 16 words in each cell (128 total trials). The level-1 model contained 4 terms (intercept, linear, quadratic, and cubic) and described the over-time fixation proportion at the individual × condition level; the quartic term was unnecessary here, because the curve only had two bends (the curve shape is consistent in this regard across participants and conditions). The analysis requires a discrete representation of time, but the time scale resolution can be as fine as the experimenter chooses. Indeed, unlike separate time bin analyses, which increase the likelihood of false positives due to multiple comparisons, greater temporal resolution generally improves GCA performance. The effect of each of the independent variables (frequency, neighborhood density, and cohort density) was introduced in the level-2 model for the intercept and linear terms. The model also included a dummy-coded effect for each individual at level-2.

The target fixation model fits (lines) are shown in Fig. 7 along with the data (symbols). As can be seen in the figure, the model reproduces the major aspects of the average over-time distribution quite well. The analysis also provides tests of the parameters. One standard significance test for adding a parameter to a model involves the deviance statistic, often called –2LL (minus 2 times the log-likelihood). Change in deviance, ΔD, is distributed as chi-square, with degrees of freedom equal to the number of parameters added. The change in deviance allows us to test whether including the parameter increases the fit of the model, much as a change in R² does in OLS regression. Table 1 shows the model parameters, deviance statistics, and significance levels.

Fig. 7.

Observed data (symbols) and model fits (lines) for frequency (top panel), cohort density (middle panel), and neighborhood density (bottom panel) effects. Reprinted with permission from Magnuson et al. (2007).

Table 1.

Results of target fixation analyses of frequency, cohort density and neighborhood density effects

Model	–2LL	ΔD	p<
Base	44481.99	—	—
Frequency
Intercept	44475.99	6.0	.05
Linear	44474.01	1.99	n.s.
Cohort density
Intercept	44474.69	7.30	.05
Linear	44474.49	0.20	n.s.
Neighborhood density
Intercept	44481.73	0.26	n.s.
Linear	44467.40	14.33	.01

Frequency and cohort both had significant effects on the intercept (α_0i in Eqs. (1) and (4)), but not the slope (β_1i in Eqs. (1) and (5)). These effects reflect constant advantages for items with high frequency (due to greater familiarity) and for items with low cohort density (due to fewer competitors) across the window of analysis. Neighborhood density did not affect the intercept, but did have a reliable effect on the slope; items with a lower neighborhood density had a steeper slope. Magnuson et al. (2007) explain the cross-over in the neighborhood time course from a high- to a low-density advantage as a result of differences in the proportion of neighbors that are also cohorts. The model predictions match the average data quite well, recreating the major form of the curves and the condition effects on the curves.

The model also has individual-level parameters that allow it to represent differences between individuals. These individual differences reside within the level-2 models in two different types of parameters. In the previous section we described level-2 fixed effect parameters that allow each individual to have a different average trajectory. The model also captures individual differences through the random effects. The model, as we have specified it here, estimates two residual terms for each individual × condition trajectory, one for the intercept and one for the slope. These residuals capture the individual- level differences in the condition effects. That is, they are estimates of how much adjustment should be made to the intercept and slope terms to fit the individual × condition trajectory, given the effects of condition and individual already in the model. Thus, the residuals are akin to an individual × condition interaction term.

In summary, the model captures both individual differences in average performance, via the structural or fixed terms in the level-2 model, and individual differences in the effect of conditions via the level-2 residuals. We consider individual differences in more detail after presenting a second example.

Analysis of competitor fixations

The growth curve analysis method can capture both “target”-type and “competitor”-type curve shapes (typical differences are illustrated in the bottom of Fig. 1 and in Fig. 6). In this section we apply GCA to data from a word learning (artificial lexicon) study in order to examine cohort and rhyme competition in spoken word recognition and the development of these effects (see Magnuson et al., 2003, for full description of the behavioral methods; similar results were found by Allopenna et al., 1998, using real words and no training). The behavioral data were collected from participants learning novel names for novel geometric objects. The set of names contained onset cohort competitors (e.g., pibo–pibu), rhyme competitors (e.g., pibo–dibo), and unrelated pairs (e.g., pibo–tupa). Participants were trained in two 2-h sessions on consecutive days. Each session concluded with a set of test trials. On each test trial, a target item appeared with three distractor items; the distractors contained either one cohort competitor and two unrelated items (“cohort” condition), one rhyme competitor and two unrelated items (“rhyme” condition), or three items unrelated to the target (“unrelated” condition).

Magnuson et al. (2003) used the single average proportion approach and ANOVA to address three critical questions, which we revisit here using growth curve models: (1) does phonological similarity influence lexical activation (measured by fixation behavior)? To answer this question we compare fixation proportions to phonological competitors (cohort and rhyme) and unrelated items. (2) Does the time course of phonological similarity (onset vs. offset) influence the time course of lexical activation? To answer this question we compare fixation of onset (cohort) and offset (rhyme) competitors. (3) Do the patterns of lexical activation change over the course of learning? To answer this question we compare results from the first test session (after 1 day of training) to results from the second test session (after 2 days of training).

The data were fit using the same approach as the target fixation data (a 4th-order term was added because there are now three bends in the curve). The effects of condition were evaluated in the level-2 models. The symmetric rise-and-fall shape of competitor-type fixation proportion curves suggests that differences in amount of competition should primarily impact the intercept and quadratic terms, since orthogonal polynomial intercept effects correspond to differences in average height of the curve³ and quadratic effects correspond to differences in rise/fall rate (note that the quadratic term captures symmetric differences in rise and fall rate and asymmetric differences would be captured by linear and/or cubic terms). For the three-condition comparison, the unrelated condition was used as a baseline (via dummy-coding) and separate parameters were estimated for the cohort and rhyme conditions for each time term.

Table 2 shows the results of this analysis for day 1 and day 2 data and the behavioral data and model fits are plotted in Fig. 8.⁴ The model fit data reflect the impact of adding both cohort and rhyme effects on each time term. Except for the cubic term, condition effects on all time terms improved model fit and, as predicted, the largest effect was on the quadratic term. That is, the difference between phonological competitors (cohort and rhyme) and unrelated controls was primarily in the rise and fall of the fixation probability curves.

Table 2.

Results of three condition competitor fixation analyses

Model	Model fit			Parameter estimates
				Cohort			Rhyme
	–2LL	ΔD	p<	Est.	t	p<	Est.	t	p<
Day 1
Base	5966.7	—	—	—	—	—	—	—	—
Intercept	5978.3	11.6	0.01	0.05884	3.87	0.001	0.05681	3.73	.001
Linear	5985.3	7	0.05	0.1676	2.47	0.05	0.1461	2.15	.05
Quadratic	6061.0	75.7	0.00001	−0.2284	7.83	0.0001	−0.2122	7.27	.0001
Cubic	6063.2	2.2	n.s.	−0.03925	1.34	n.s.	−0.03629	1.24	n.s.
Quartic	6073.1	9.9	0.01	0.09065	3.11	0.01	0.03501	1.20	n.s.
Day 2
Base	12251.7	—	—	—	—	—	—	—	—
Intercept	12279.4	27.7	0.0001	0.08762	6.40	0.0001	0.04608	3.37	.001
Linear	12289.3	9.9	0.01	0.1862	3.04	0.01	0.1476	2.41	.05
Quadratic	12431.4	142.1	0.00001	−0.2264	11.75	0.0001	−0.07479	3.88	.0001
Cubic	12431.8	0.4	n.s.	0.00410	0.21	n.s.	0.01194	0.62	n.s.
Quartic	12436.9	5.1	0.05	0.03972	2.06	0.05	0.03575	1.86	.1

Fig. 8.

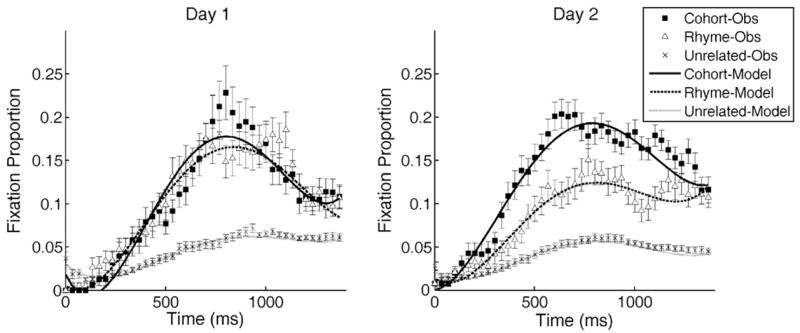
Observed (symbols) data for cohort competitors (squares), rhyme competitors (triangles) and unrelated distractors (x’s) and model fits (lines). Error bars indicate ±1SE. On day 1, there is equivalent cohort and rhyme competition (higher fixation proportion for competitors than unrelated items); on day 2 the time course of cohort and rhyme competition is significantly different (see text for details).

We can further examine whether each parameter estimate was reliably different from the baseline condition (dummy-coding requires a baseline for comparison), which in this case was the unrelated distractor condition. Table 2 shows the level-2 parameter estimates for cohort and rhyme relative to the unrelated baseline—the effects were highly consistent, showing very strong effects on intercept and quadratic terms and weaker effects on slope for both conditions. These results indicate that both cohort and rhyme competitor fixation were reliably different from unrelated fixation on both days of testing.

To compare cohort and rhyme competitors directly we restricted the analysis to just those two conditions. With only two conditions, the ΔD significance directly indexes the difference between the two conditions, so tests of significance on parameter estimates are generally redundant. The results (Table 3) indicate that on day 1 there was no difference between cohort and rhyme competition (only the 4th order term marginally improved model fit), but on day 2 there was a significant effect of condition (cohort vs. rhyme) on intercept and quadratic terms. That is, differences in the time course of phonological similarity produced differences in mean fixation proportion and in rise/fall rates of fixation probability. These results are completely consistent with the analyses used by Magnuson et al. (2003), but stem from an analysis paradigm expressly designed to characterize change over time and provide the opportunity for analysis of individual differences, which is the focus of the next section.

Table 3.

Results of cohort–rhyme competitor fixation analysis

Model	–2LL	ΔD	p<
Day 1
Base	2388.2	—	—
Intercept	2388.2	0.0	n.s.
Linear	2388.3	0.1	n.s.
Quadratic	2388.5	0.2	n.s.
Cubic	2388.5	0.0	n.s.
Quartic	2391.1	2.6	.1
Day 2
Base	6215.0	—	—
Intercept	6221.3	6.3	.01
Linear	6221.6	0.3	n.s.
Quadratic	6264.2	42.6	.0001
Cubic	6264.3	0.1	n.s.
Quartic	6264.4	0.1	n.s.

Individual differences in VWP data

The previous sections demonstrate that growth curve analysis provides a robust and powerful statistical tool for understanding the time course of effects of experimenter- manipulated variables such as word frequency and phonological similarity. In addition, this analytic method can quantify individual participant effects for a variety of within-participant designs. For within-participant designs, the level-2 models carry information about individual differences averaged over conditions (i.e., does a particular individual tend to look more quickly to the target?) and individual × condition effects (i.e., is the effect of this factor different for this individual relative to the effect of this factor for other individuals?). Thus, the analyses reveal quite a bit about individual differences, in addition to the usual information about the effects of experimental manipulations.

To demonstrate how GCA allows us to address individual differences, we return to the data from Magnuson et al. (2007). Recall that the level-1 model described the over-time trajectory using a third-order polynomial. We allowed individual effects to enter the model through each of the four terms (i.e., intercept, linear, quadratic, and cubic). This allows individual participants to have level-1 models with different values for each of these terms. The model estimates these individual-level parameters. Table 4 shows the correlations among these estimated individual effects. Individual differences in how participants look to the target (averaged over conditions) are interrelated. A theory of looking behavior should be able to account for such individual differences, in addition to manipulated effects.

Table 4.

Correlations among individual participant effects on intercept, linear, quadratic, and cubic parameters

	Intercept	Linear	Quadratic	Cubic
Intercept	1.0	0.66*	−0.60	−0.32
Linear	0.66	1.0	−0.35	−0.58
Quadratic	−0.60	−0.35	1.0	0.11
Cubic	−0.32	−0.58	0.11	1.0

Bold = p < .05

^*p < .01.

The Magnuson et al. (2007) experiment compared three key lexical characteristics (frequency, cohort, and neighborhood), and so individual differences in the effects of the manipulations are of particular interest. We can ask, for example, whether the effects of each manipulation are stable across participants, or whether there are individual differences in the relation of each manipulation to the others. To simplify the exposition, we focus on the frequency and cohort effects. In this case, GCA tells us how participants differ from each other in their response to the frequency and cohort manipulations. Recall that there was an effect of frequency on the intercept, such that the curve for higher frequency words was shifted up relative to lower frequency words. There was also an effect of cohort density on the intercept; the curve was shifted upwards for words with low cohort density compared to those with high cohort density. The level-2 models include a residual term for each individual × condition combination. The residual terms carry information about the degree to which this individual × condition trajectory differs from the average trajectories for both this condition and this individual.

To obtain the estimated individual × condition effects for the frequency and cohort density manipulations, we averaged the residuals over the levels of the other variable. This gives us four residual values for each individual for both the intercept and the slope (see Appendix A for a more detailed explanation of how these residual values are computed). The bivariate correlations among these individual × condition effects are shown in Table 5. The individual × condition effects on the intercept are moderately related to one another. This means that, in terms of the height of the curve, individual differences in the effect of frequency are related to individual differences in the effect of cohort density. Consider the implications of this relationship for the condition effects presented in Fig. 7. Note that the effects are in opposite directions, and hence have parameter estimates with opposite sign. Positive residuals amplify the positively signed effects, but reduce negatively signed ones, and vice versa. Therefore, the positive relationship between the residuals implies that participants with strong cohort density effects have weak frequency effects. That is, a positive relationship between residuals is a negative relationship between frequency and cohort effect sizes because the effects are in opposite directions.

Table 5.

Correlations among individual × condition intercept and linear term residuals

	Intercept-Cohort	Linear-Cohort	Intercept-Frequency	Linear-Frequency
Intercept-Cohort	1.0	−0.19	0.55*	−0.15
Linear-Cohort	−0.19	1.0	−0.28	0.14
Intercept-Frequency	0.55*	−0.28	1.0	−0.094
Linear-Frequency	−0.15	0.14	−0.094	1.0

Bold = p < .05

^*p < .01.

These individual difference patterns (negative relationship between individual participant frequency and cohort effects and lack of relationship between condition effects and overall curve shape) provide relatively strong constraints on cognitive theories of individual variation among healthy college-age adults. As a first step towards understanding these patterns in cognitive terms we examined whether changes in the dynamics of processing in the TRACE model would produce the behaviorally observed pattern. In the case of spoken word recognition, the TRACE model (McClelland & Elman, 1986) has proved a particularly fruitful means of modeling VWP data, providing a concrete testbed for mechanistic hypotheses regarding the time course of word recognition (e.g., Allopenna et al., 1998; Dahan et al., 2001a, 2001b). The TRACE model is composed of three processing levels (features, phonemes, and words) with bidirectional information flow between levels, and several parameters governing processing within and between levels (e.g., feedforward and feedback gain, decay rates, etc.). Hypotheses regarding individual differences can be tested by examining whether manipulation of the corresponding parameters produces the behaviorally observed pattern of variability across individuals. Of particular interest were the following two questions: (1) is the observed variability more likely to be due to decision-level differences or linguistic processing differences? (2) Is the observed variability more likely to be due to lexical processing differences or phonological processing differences?

Simulations were carried out using jTRACE (Strauss, Harris, & Magnuson, 2007). We began with the standard TRACE parameter values, and then modified a small subset to model individual differences, as we describe below. jTRACE includes the three frequency implementations (resting level, post-perceptual, and bottom- up connection strength) described by Dahan et al. (2001a). We used the bottom-up connection strength implementation, in which connections from phonemes to words are proportional to word frequency. A 270- word lexicon was specially designed to manipulate cohort size and word frequency independently. To that end, the lexicon contained cohorts that were large (more than 20 words) or small (less than 5 words). One to three words were selected from each cohort to be target words (1 for small cohorts, 2–3 for large cohorts). Half of these target words were randomly assigned to the high frequency condition by setting their frequency to 10, and all other word frequencies were set to 1. This set of materials was designed to create a relatively simple context for testing the effects of different parameters on cohort and word frequency effects. A natural lexicon would be expected to produce the same results, though the limitations of the TRACE model’s phonetic inventory make it difficult to create strong independent manipulations of cohort density and frequency.

With the standard TRACE parameters, the target words showed robust frequency and cohort size effects. We tested the effects of manipulating six parameters (described below). For each parameter tested, 15 “individual” simulations were carried out holding all parameters constant except the test parameter, which was manipulated in equal steps from very low to very high (specific values depended on the parameter tested). Model fixation probabilities were computed from activations using Luce (1959) choice rule and the four-alternative- forced-choice linking hypothesis (the simpler version of Allopenna et al., 1998, method described by Dahan et al., 2001a). The decision model we used to convert TRACE activations to response probabilities contains only one free parameter (k, in the Luce choice rule), which we manipulated to test the hypothesis that the behavioral individual differences were due to decision- level differences. Five other parameters governing lexical- and phoneme-level dynamics were also tested. Only the phoneme-to-word frequency weight scaling parameter (s; see Dahan et al., 2001a for details) produced the behaviorally observed pattern of a negative relationship between individual participant frequency and cohort effects and a lack of relationship between condition effects and overall curve shape (Table 6 summarizes the general patterns of variability for each parameter tested).

Table 6.

TRACE parameters with default (standard) values, value range tested in individual difference simulations, and the general pattern of results

Parameter	Computational function	Default value	Value range	General pattern
k	Response competition	7	2–12	Primary variability in curve shape with positively correlated cohort and frequency effects
αpw	Phoneme-to-word weights	0.05	.01–.09	Positive correlation between frequency and cohort effects (frequency effects more variable)
δp	Phonological decay rate (working memory)	0.03	.01–.05	Variability in cohort effects but not in frequency effects
δw	Lexical decay rate (working memory)	0.05	.01–.09	Variability in cohort effects but not in frequency effects
γw	Lexical layer competition	0.03	.01–.05	Positive correlation between frequency and cohort effects (cohort effects more variable)
s	Frequency sensitivity	0.13	.03–.23	Negative correlation between frequency and cohort effects

Fig. 9 shows cohort and frequency effects for three values (low, medium/default, and high) of k and s. Variation of the decision-level k parameter (top two rows of Fig. 9) produced large variability in curve shape (smaller values of k produced much less sharp curves) and this difference was related to both cohort (top row) and frequency (second row) effect sizes, which were highly positively correlated (i.e., as k varied, frequency and cohort effect sizes increased and decreased together). This pattern is not consistent with the observed behavioral data, suggesting that the behaviorally observed individual differences were not due to decision-level differences (with the caveat that one might be able to model these differences with a different decision model). positively correlated (i.e., as k varied, frequency and cohort effect sizes increased and decreased together). This pattern is not consistent with the observed behavioral data, suggesting that the behaviorally observed individual differences were not due to decision-level differences (with the caveat that one might be able to model these differences with a different decision model).

Fig. 9.

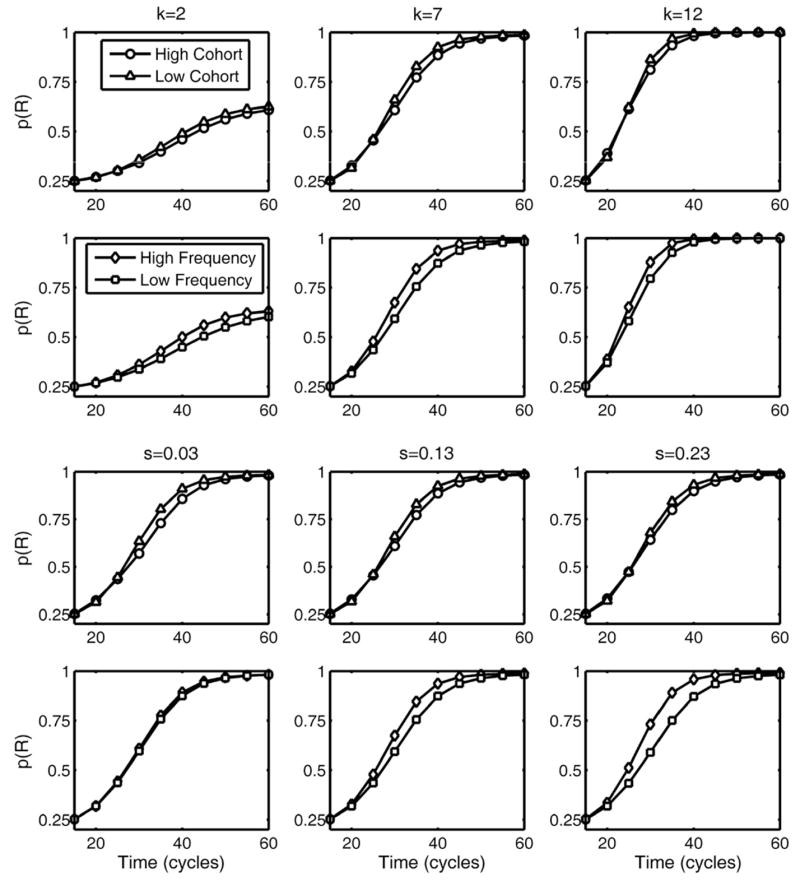
TRACE “individual difference” plots of cohort (first and third row) and frequency (second and fourth row) effects under manipulation of k (top two rows) and s (bottom two rows). Manipulation of k primarily affects curve shape and cohort and frequency effects tend to increase together. Manipulation of s has small impact on curve shape and opposite effects on frequency and cohort effects.

In contrast, variation of s (bottom two rows of Fig. 9) had very little impact on overall curve shape and increasing values increased frequency effects (Fig. 9, bottom row) and decreased cohort effects (Fig. 9, third row). It is trivial that increasing the frequency scaling parameter would increase frequency effect size, but the decreasing of cohort effect size requires some analysis. We found that the decrease in cohort effect size was driven by high frequency items because their low frequency cohort competitors could not keep up with the high frequency targets. That is, as frequency differences become exaggerated, the effect of competition from low frequency cohort competitors was reduced for high frequency target words. There was virtually no effect of s on the cohort effect for low frequency items because the difference between average cohort competitor frequency and target frequency was much smaller for low frequency targets than for high frequency targets. Although this pattern is not a necessity (higher frequency words could have higher frequency cohorts), it is reasonable that high frequency words would be more likely to “stand out” above their cohort more than low frequency words. Indeed, even though cohort density (summed cohort frequencies) was controlled, this pattern was true of the words used in the behavioral experiment (Magnuson et al., 2007) as well: for low frequency items, mean target log frequency was 2.4 and mean cohort log frequency was 1.7; for high frequency items, mean target log frequency was 4.7 and mean cohort log frequency was 1.6.

This examination of the model makes a strong prediction for the behavioral data: the between-participant variability in cohort effect size should be larger for high frequency items than for low frequency. That is, the individual participant random effects for the cohort term should be larger for high frequency words than low frequency words. A simple test of this prediction is to examine the variance in the intercept term for low and high frequency conditions separately; the high frequency conditions should have greater variability in the intercept term. The behavioral data were consistent with this prediction: the estimated variance for low frequency conditions was 3841.54, and for high conditions it was 5687.00, F(59, 59) = 1.48, p < .07. This post-hoc analysis is consistent with the TRACE model prediction that individual differences in cohort effect size occur more for high frequency words and lends further support to the claim that TRACE model frequency scaling parameter s captures differences among the college-age adult participants. We leave for future research the additional behavioral testing required to test this prediction fully. As our goal was simply to demonstrate the approach, we have not attempted to address these patterns at a theoretical level by considering, for example, why there should be individual differences in frequency gain; future research will address this question.

This section described how growth curve analyses can be used to quantify and investigate patterns of individual differences. This is an important strength of the growth curve method: condition, individual, and individual × condition effects can all be examined in a single set of analyses and the technique is powerful enough to pull out patterns of variability in a relatively small number of participants (15) drawn from a relatively homogenous group (healthy, college-age adults). As a result, this statistical technique is a very promising tool for applying eye-tracking methods to studying larger individual differences such as changes due to development and aging and acquired and developmental language disorders. We have demonstrated some first steps in using growth curve analyses and computational modeling to address individual differences. We used growth curve analysis to quantify and describe individual differences. We then examined whether variation in different parameters in the TRACE model would lead to analogous differences, with a particular focus on distinguishing linguistic from decisional bases of individual differences (e.g., the pattern of individual differences we just analyzed was captured by manipulating a parameter governing phonological–lexical dynamics but not by manipulating a decision-level parameter). At this point, we simply wish to emphasize the power of the statistical and computational modeling approach: growth curve statistical modeling revealed aspects of the behavioral data that were not accessible using previous approaches to VWP data analysis, and computational modeling using the TRACE model helped to evaluate possible cognitive interpretations of the results and made further predictions for behavioral testing.⁵

General discussion

The visual world paradigm has proven to be a powerful technique for investigating spoken language processing from subphonemic details to sentence processing, though the paradigm lacks standard and appropriate statistical tools for analyzing time course data. In this report we have described a statistical technique based on multilevel polynomial regression that is specifically developed for analyzing change over time. We have shown how this technique can be used to analyze typical visual world paradigm data and how it can be used to examine individual differences. Combined with computational modeling using the TRACE model of speech perception, we have taken a first step towards understanding individual differences in spoken word recognition in cognitive terms.

One possible criticism of using orthogonal polynomials is that they are not well-suited to capturing the asymptotic details in both tails of VWP fixation probability curves and that an alternative function would be a better starting point. Scheepers, Keller, and Lapata (2007), for example, advocate using the logistic function. The logistic curve-fitting approach is very much in the same spirit as our approach since it also aims to capture the full time course of fixation probability. Both approaches have strengths and weaknesses. As with all statistical models, researchers will need to make an informed decision about the appropriateness of the model for their situation. One major advantage of the growth curve approach is that the model of the average is the average of the individual participant models. Put differently, there are easily defined mathematical relations between the average data pattern and the underlying probability distribution from which individual data patterns are (presumed to be) drawn. This property may seem unremarkable to researchers who work primarily with linear models; it is a core property of linear models. But non-linear models, like the logistic, do not share this property. Given a non-linear model, the average data pattern is not indicative of the underlying probability distribution, regardless of whether one is averaging across participants or trials. Paradoxically, this implies that to the degree that the average data pattern is fit by a logistic curve, the greater the assurance that the individual data patterns were not logistic in form themselves. Therefore, if one aggregates data by averaging, some deep and awkward questions arise about what the estimated parameters mean—what are they estimating, if not the underlying probability distribution that generated the individual data patterns? Of course, there is no rule that mandates averaging, but the types of models at issue require aggregated data, and averaging is a standard aggregation method. In general, one needs to be able to specify the linkages among the underlying distribution, the individual (or finest grained data), and the aggregated data.

The process of averaging, even in linear models, can raise some legitimate concerns: what about a case where two different patterns of individual data that give rise to the same average data (e.g., one dataset with several “slow” participants and several “fast” participants vs. one with much less variability between participants)? GCA would distinguish these cases based on distributional differences in the level-2 individual participant parameters. In contrast, on the logistic approach, it is necessary to address individual and group levels separately (e.g., Scheepers et al., 2007, fit full and subset group average data, but not individual participant data) because for logistic curves the model of the average data is typically not the average of individual participant models (i.e., logistic curves are not dynamically consistent; Keats, 1983).

On the other hand, the logistic approach may provide better fits at the asymptotes of VWP data. The polynomials in GCA do a good job of capturing the general form of the curve within the analyzed time window, but may produce strange behavior outside of that range (e.g., an extended period with fixation proportions at static levels). We suggest that the asymptotes in these data are generally not where the action is: often the asymptotes are artifacts of the task. For example, curves start flat because participants are not looking at any objects before the trial begins and it takes about 200 ms to plan and execute an initial saccade. Since VWP trials are self-terminating and last different durations, an asymptotic right tail can arise due to padding short trials to be the same duration as long trials. In either case, since the experimental focus is on time course bracketed by the asymptotic ends of fixation curves, the asymptotes themselves are of comparatively less interest than the transitions.

Nonetheless, there may be cases where the tails are important. For example, consider the schematic data patterns shown in Fig. 10: the left panel shows a constant advantage for one condition (vertical shift), the right panel shows a faster time course of activation for one condition (horizontal shift). Orthogonal polynomial GCA would describe both of these patterns as differences in the intercept term and fail to distinguish between them (because the orthogonal polynomial intercept corresponds to the average curve height). It is important to note that in practice, such ambiguity would be rare, as it requires an equal shift at both ends of the curve (asymmetric shifts would affect the linear term) of modest magnitude (due to the necessarily asymptotic shape of the curves, large shifts change trajectory curvature and would affect the quadratic term); nonetheless, this is a weakness of GCA using orthogonal polynomials. There are a number of ways to overcome this weakness. Perhaps the simplest is to include fixations after target selection (e.g., fixations back to a central cross), which would allow the quadratic term to capture the crucial time course differences. In the resulting curves, a constant advantage for one condition would still result in an effect on the intercept, but a faster activation and decay profile would be captured by the quadratic term. Another approach would be to use natural polynomials, in which case the vertical shift would still predict an intercept difference and the horizontal shift would predict effects on higher-order terms, though (as discussed above) at the cost of losing independence of the coefficients. Another solution would be to use a logistic function, as advocated by Scheepers et al. (2007), in which case the vertical shift would predict an effect on the y-intercept term and the horizontal shift would predict an effect on the x-axis location of the central infection point (see Scheepers et al. for model details and parameter interpretation). However, the logistic approach also has weaknesses as described above (lack of independence of terms and the need to model group average data and individual participant data separately). In general, model selection should be informed by the hypotheses under investigation. GCA using orthogonal polynomials is a robust and powerful statistical tool that has many advantages, but it is not going to be perfect for every analysis and researchers should consider the strengths and weaknesses of different models in planning analyses of their data.

Fig. 10.

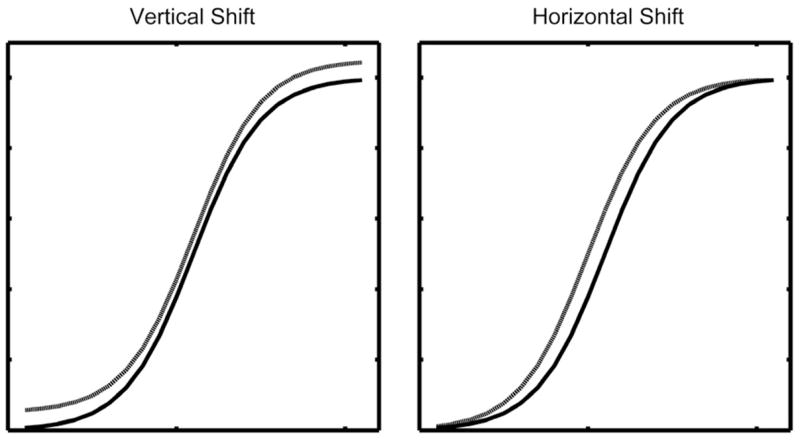
Schematic demonstration of data from two conditions that differ by a constant advantage (vertical shift, left panel) or by time course of activation (horizontal shift, right panel).

In summary, our approach makes two contributions to understanding the time course of spoken language processing tapped in the VWP. First, the statistical approach provides sorely needed tools appropriate for evaluating changes in fixation proportions over time. Second, it provides a foundation for evaluating between-participant variability in the visual world paradigm. By combining a robust statistical approach to change over time with systematic computational modeling, we provide an important step towards understanding individual differences in a naturalistic task with low memory and task demands, which may provide a powerful means of investigating theoretical questions and language impairments.

Appendix A

Step-by-step instructions for GCA

1. Read in data.

2. Create orthogonal time vectors of appropriate size and add them to the data structure.

3. Fit base model that contains all effects except those under investigation.

4. Gradually (individually) add critical effects, noting the change in model fit (–2LL) when each term is added.

5. Evaluate significance of changes in –2LL and differences in parameter estimates as appropriate.

Table A1.

Example condition coding and residual values for participant 1

Participant	Condition			Residual
	Frequency	Cohort density	Neighborhood density	Intercept (ζ01)	Linear (ζ11)
1	1	1	1	Z01	Z11
1	1	1	0	Z02	Z12
1	1	0	1	Z03	Z13
1	1	0	0	Z04	Z14
1	0	1	1	Z05	Z15
1	0	1	0	Z06	Z16
1	0	0	1	Z07	Z17
1	0	0	0	Z08	Z18

Each condition is represented as 1 (high) or 0 (low).

Averaging residuals for individual by condition effects

To illustrate how we calculated the average residuals for the individual by condition effects, we present Table A1. The table shows the eight records [2 (Frequency) × 2 (Cohort density) × 2 (Neighborhood density)] for a single hypothetical individual. Consider as an example of the computations, the cohort density effects on the intercept. To obtain these values, we averaged over the levels of frequency using neighborhood density as a repeating factor. The four resulting terms were thus computed as: M(Z₀₁, Z₀₂), M(Z₀₃, Z₀₄), M(Z₀₅, Z₀₆), M(Z₀₇, Z₀₈). The resulting means capture the magnitude of the residual terms for this individual for high and low cohort density (separately for levels of frequency). The frequency residuals were calculated analogously (i.e., by averaging over levels of cohort density): M(Z₀₁, Z₀₃), M(Z₀₂, Z₀₄), M(Z₀₅, Z₀₇), M(Z₀₆, Z₀₈).