Large negative linear compressibility of Ag₃[Co(CN)₆]

Abstract

Silver(I) hexacyanocobaltate(III), Ag₃[Co(CN)₆], shows a large negative linear compressibility (NLC, linear expansion under hydrostatic pressure) at ambient temperature at all pressures up to our experimental limit of 7.65(2) GPa. This behavior is qualitatively unaffected by a transition at 0.19 GPa to a new phase Ag₃[Co(CN)₆]-II, whose structure is reported here. The high-pressure phase also shows anisotropic thermal expansion with large uniaxial negative thermal expansion (NTE, expansion on cooling). In both phases, the NLC/NTE effect arises as the rapid compression/contraction of layers of silver atoms—weakly bound via argentophilic interactions—is translated via flexing of the covalent network lattice into an expansion along a perpendicular direction. It is proposed that framework materials that contract along a specific direction on heating while expanding macroscopically will, in general, also expand along the same direction under hydrostatic pressure while contracting macroscopically.

Negative linear compressibility (NLC), whereby a material expands along a specific direction on increasing hydrostatic pressure, is a very unusual effect. Indeed in a study of elastic constant data from 500 noncubic crystal phases, only 13 displayed NLC, and of those, 11 structures were of monoclinic or lower symmetry (1). Despite its rarity, NLC is a highly attractive mechanical property, with a key application being the development of effectively incompressible optical materials (1, 2). Such materials could be used in high-pressure environments, such as in optical telecommunications devices that must function at deep-sea pressures >1,000 atm. NLC also offers a means of producing ultrasensitive pressure detectors, such as interferometric optical sensors for sonar and aircraft altitude measurements. The effect is also often coupled to so-called “auxetic” behavior, which is itself being used to improve shock resistance in, e.g., body armor (3).

Of the few known examples among inorganic materials, the most pronounced NLC effects have been reported for LaNbO₄ (4), elemental Se (5), the BXO₄ (X = P, As) family (6), and the spin-Peierls compound α′-NaV₂O₅ (7). In some other cases, transient NLC behavior may occur only at pressures just above a strain-induced phase transition to a structure of lower symmetry (e.g., refs. 8 and 9), or as a result of an uptake of additional interstitial molecules (10, 11).

One fundamental barrier to the practical application of NLC is that its magnitude is generally much smaller than the “normal” (positive) compressibilities of standard materials.* By convention, linear compressibility is defined as the relative rate at which a given dimension ℓ decreases with pressure (at constant temperature): K_ℓ = −(∂lnℓ/∂p)_T. Typical values for crystalline materials lie in the range K_ℓ ≃ 5–20 TPa⁻¹ (12) (i.e., their linear dimensions decrease by ≈1% for each GPa increase in pressure). In contrast, a NLC coefficient K_c ≃ −2 TPa⁻¹ has been reported for α-cristobalite structured BAsO₄ (6); in trigonal Se, one finds K_c ≃ −1.2 TPa⁻¹ (5), whereas in monoclinic LaNbO₄, NLC appears either to be negligible [K_[210] ≃ −0.2 TPa⁻¹ (4)] or similar to that in Se (13).

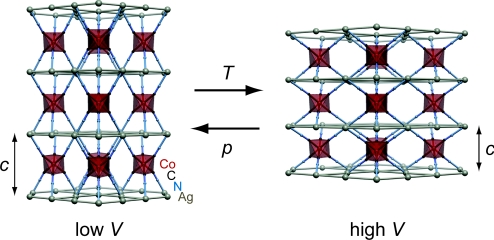
Here, we use high-pressure neutron powder diffraction to show that substantially stronger NLC behavior is to be found in the framework material Ag₃[Co(CN)₆], for which we obtain K_c ≃ −75 TPa⁻¹. The structural changes are so rapid that a first-order transition is found to occur at 0.19 GPa to a previously unidentified phase, whose structure is 16% more dense. Remarkably, this new phase also shows a strong NLC effect, with K_c ≃ −5 TPa⁻¹ up to our experimental limit of 7.65 GPa. We chose to study Ag₃[Co(CN)₆] because, upon heating, its framework structure contracts remarkably strongly along 1 direction as the overall volume increases (14). Should the same geometric mechanism operate under changes in pressure, we reasoned that, by flexing to reduce its volume, the lattice would be forced to expand along the negative thermal expansion (NTE) axis (Fig. 1). Moreover, because NTE is so strong in this material (its linear coefficients of thermal expansion, α ≃ ±130 MK⁻¹, are ≈10 times larger than those of typical materials), we expected the magnitude of any NLC effect to be similarly pronounced.

Fig. 1.

Compression mechanism in Ag₃[Co(CN)₆], exaggerated for illustrative purposes: In order for the framework to reduce its volume (either in response to a decrease in temperature or an increase in pressure), it must expand along the trigonal axis (c).

The concept of looking for unusual pressure-dependent behavior in NTE materials has a sound physical basis. These materials often have low-density structures and, importantly, possess phonon modes with negative Grüneisen parameters (i.e., some vibrational energies decrease under applied pressure). By way of an example, the isotropic NTE material ZrW₂O₈ exhibits both a low-pressure phase transition (15) and pressure-induced amorphization (16), the latter attributed to increased bonding as the energies of many rigid unit modes fall to zero (17). Another NTE material, Zn(CN)₂, actually becomes softer at higher pressures, reflecting an anomalous decrease in vibrational energies driven by changes to the underlying potential surface (18). Furthermore, in elemental Se the mechanism responsible for NTE along the Se spiral axis (19) probably accounts for NLC along the same direction (5); indeed the concept of a more general link between NTE and NLC is developed as part of the present study.

We begin by reporting the compressibility of the ambient phase Ag₃[Co(CN)₆]-I. We then report the structure of the previously undescribed high-pressure phase formed at 0.19 GPa, followed by a description of its pressure- and temperature-dependent behavior. We conclude with a discussion concerning the general relationship between NTE and NLC in framework materials.

Results and Discussion

Compressibility of Ambient Pressure Phase I.

The structure of Ag₃[Co(CN)₆]-I consists of 3 interpenetrating distorted cubic networks, each with CoC₆ octahedra at the cube apices and with edges formed by approximately linear CNAgNC bridges (20). This topology gives rise to a trigonal structure (in space group P3̄1m) in which layers of CoC₆ octahedra alternate with layers of Ag atoms, stacked parallel to the crystal c axis at intervals of c/2 (Fig. 1). Within individual layers, the [Co(CN)₆] octahedra are arranged on a triangular lattice, and their separation corresponds directly to the lattice parameter a. The Ag atoms, which are separated by the distance a/2, are arranged on a related Kagome lattice. These layers are connected via flexible CoCNAgNCCo covalent linkages, oriented approximately parallel to the 〈101〉 directions. This particular arrangement means the covalent bonding interactions do not determine the absolute crystal dimensions but act only to couple any expansion within the (001) plane to a contraction along c (and vice versa). Instead, the lattice dimensions appear to reflect the equilibrium separation of weak dispersion-like Ag–Ag “argentophilic” interactions (21). Indeed, the crystal thermal expansion resembles that of van der Waals solids (e.g., Xe) more strongly than typical framework materials (14).

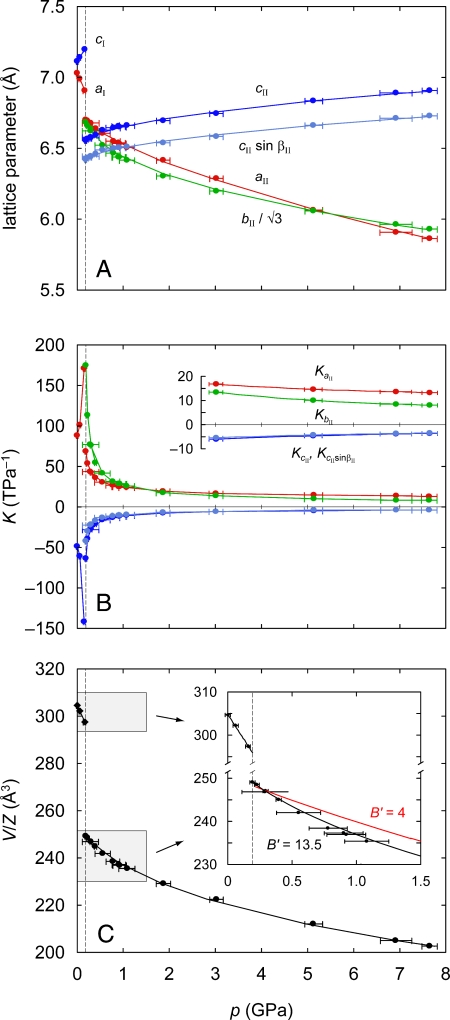
We collected neutron diffraction patterns for Ag₃[Co(CN)₆]-I at 3 pressure values before the material transformed into a new phase at a transition pressure of 0.19 GPa. We discuss this transition in more detail below but consider first the compressibility of the ambient phase, for which lattice parameters are shown in Fig. 2. We see in Fig. 2A that trigonal Ag₃[Co(CN)₆]-I does indeed show NLC with a significant expansion along the c axis as pressure increases. This is accompanied by an even larger contraction along a. Numerical values for the compressibilites were obtained by linear fits to the data, giving K_a = +115(8) TPa⁻¹ and K_c = −76(9) TPa⁻¹. This NLC effect along c is more than an order of magnitude greater than that observed in (e.g.) BAsO₄ (6). Indeed, we believe that Ag₃[Co(CN)₆]-I exhibits the strongest NLC effect yet reported for any inorganic material. We note also that the compressibility along a is also remarkable for its magnitude and similar to that of solid Xe, for which K_a = +130(12) TPa⁻¹ at 100 K (22).

Fig. 2.

Pressure dependence of various structural parameters: lattice parameters (A), linear compressibilities extracted from parameterized fits to the lattice parameter data (B), and volume per formula unit V/Z (C). The Inset in C shows linear (Phase I) and third-order Birch–Murnaghan (Phase II) fits to the V/Z data near the phase transition.

Considering, in turn, the effect of pressure on unit cell volume, we calculate a bulk modulus of B = 6.5(3) GPa from a linear fit to the data in Fig. 2C. We note that this value is small, and not dissimilar to the estimate B_calc = 9.9 GPa obtained by using ab initio calculations (23). Unfortunately, the paucity of data does not allow us to determine the pressure derivative B′ with any certainty.

Phase Transition and Structure of Phase II.

Further compression precipitates a transition at 0.19 GPa to a new phase, Ag₃[Co(CN)₆]-II, accompanied by a volume change ΔV/V = 16.25(4)% that is much larger than that observed over the whole temperature range at ambient pressure (14). This volume change includes compression in all directions, but the compression is most significant along a direction parallel to the c axis of phase I, with a relative change in length of Δℓ/ℓ = 10.78(9)% compared with values of between 3.01(3)% and 3.21(3)% for the basal plane directions.

The Ag₃[Co(CN)₆]-II diffraction patterns could be indexed according to a unit cell in the monoclinic space group C2/m, a maximal subgroup of P3̄1m. These 2 groups are related by loss of the threefold inversion axis in P3̄1m, and give a_II ≈ a_I, b_II ≈ $\sqrt{3}$b_I, and c_II ≈ c_I (where II and I refer to monoclinic phase II and trigonal ambient pressure phase I, respectively; see Fig. 3A). The absence of a 3̄ axis parallel to c allows a shear of the unit cell along a perpendicular direction (parallel to a_II); the extent of this shear is related to the monoclinic angle β_II, which we found to be ≈100° over the pressure range studied (90° ≡ no shear). Unit cell dimensions at the low- and high-pressure extremes of our data were as follows (Z = 2 in both cases): [0.226(10) GPa] a = 6.6934(13) Å, b = 11.5391(18) Å, c = 6.5661(13) Å, β = 101.479(13)°, V = 496.99(9) ų; [7.65(17) GPa] a = 5.8657(23) Å, b = 10.270(3) Å, c = 6.908(3) Å, β = 103.079(29)°, V = 405.36(19) ų.

Fig. 3.

Representations of the pressure-induced structural transition in Ag₃[Co(CN)₆]. (A) In both the ambient trigonal phase I (Left; shown with the outline of its monoclinic supercell for ease of comparison) and high-pressure monoclinic phase II (Center and Right), [Co(CN)₆] octahedra (shown in polyhedral representation) are connected via Ag atoms (large spheres). (B) The framework topology differs between phases because the shear parallel to a_I/a_II is coupled to a shift of 2/3 of the Ag atoms by 1/4 of a unit cell in the same direction. This transforms the argentophilic Kagome layers of phase I into a reentrant honeycomb (“bow-tie”) arrangement in phase II. (C) Subsequent compression increases the extent of “puckering” in this 2-dimensional lattice, approaching a triangular network.

Our first structural model for this phase simply incorporated a shear into the network connectivity of phase I. One-third of the approximately linear CoCNAgNCCo linkages of phase I (those roughly parallel to [101]_II, and whose central Ag atom we denote by Ag1) are then stretched taut, whereas the other 2/3 (now distinct by symmetry, with central atoms Ag2) are very strongly buckled. Structural refinement against our data at 0.23(2) GPa produced acceptable fits with this model, but gave very short Ag2N bond lengths of 1.81 Å within the “buckled” CoCNAg2NCCo chains (note an AgN distance of 2.02 Å in phase I). In addition, it was not possible to refine sensible atomic displacement parameters for the Ag2 atoms [located in this model at ($\frac{1}{4}$, $\frac{1}{4}$, $\frac{1}{2}$)]. Instead, from among a number of different ordered and disordered models, our data showed a preference for the Ag2 atom to be located at (0, y, $\frac{1}{2}$) with y ≈ $\frac{1}{4}$. This model gave a good fit to the data [see supporting information (SI)], produced a stable refinement and gave sensible atom positions, [Co(CN)₆] octahedral geometries, bond lengths, and thermal displacement parameters; refined atom coordinates and isotropic displacement parameters are given in Table 1, and the model itself is illustrated in Fig. 3A.

Table 1.

Refined atomic coordinates and isotropic displacement parameters for Ag₃[Co(CN)₆]-II from data measured at 0.226(10) GPa

Atom	x	y	z	Biso, Å2
Co	0	0	0	0.4(7)
	0	0	0	0.65(10)
Ag1	0.5	0	0.5	4.4(8)
	0.5	0	0.5	0.65(10)
C1	0.8252(22)	0	0.1818(21)	0.24(19)
	0.842(6)	0	0.201(4)	0.65(10)
N1	0.7150(17)	0	0.3020(17)	0.74(18)
	0.757(4)	0	0.3306(28)	0.65(10)
Ag2	0	0.2404(13)	0.5	2.1(3)
	0	0.1904(28)	0.5	0.65(10)
C2	0.1634(17)	0.1190(8)	0.1574(15)	1.15(17)
	0.2108(29)	0.1227(15)	0.1448(29)	0.65(10)
N2	0.2582(14)	0.1854(6)	0.2592(19)	1.13(13)
	0.324(3)	0.1984(13)	0.2415(22)	0.65(10)

Corresponding values at 7.65(17) GPa are shown in italics. For the higher-pressure data, thermal displacements were modeled by using a common parameter, whereas the low-pressure data were of sufficient quality to allow refinement of individual displacement parameters.

The Ag2 shift of ≈$\frac{1}{4}$ a_II converts the argentophilic Kagome lattice into a “reentrant honeycomb” or “bow-tie” arrangement (Fig. 3 B and C). An important consequence is that the original CoCNAg2NCCo linkages, which connect Co atoms of neighboring (010)_I planes in phase I, are replaced by bent linkages that join Co atoms of the same (010)_II plane in phase II. This means that there is actually no covalent connectivity between adjacent (010) planes in the high-pressure structure. Instead, neighboring planes “interdigitate” as the CNAg2NC “hoops” of each layer project into cavities of the next (see Fig. 3A Upper Center). Consequently, one might expect the structure to be reasonably soft along the b_II axis because the interlayer separation will be dictated primarily by weak Ag–Ag interactions.

We note that, in principle, the Ag2 displacements need not be coupled to the shear; that the 2 events occur simultaneously suggests that Ag–Ag interactions may help drive the transition. Intriguingly, the lattice parameters of phase I just below p_c are significantly less extreme than those obtained by cooling at ambient pressure, and so the material would be capable of further volume reduction in this phase than that observed under increasing pressure. We considered the possibility that phase I may be a metastable form, but we found that the phase was quantitatively recoverable upon pressure release. The extent of Ag displacements is strongly temperature dependent, and it may be that thermal motion of the Ag atoms encourages a transition at a greater volume than that obtainable upon cooling. We note also the multipolar interactions between neighboring Ag atoms will be frustrated in the Kagome layers of phase I, but this frustration will be ameliorated in the bow-tie network of phase II. Whether frustration plays an additional role in the thermodynamics of this compound is an interesting possibility that we leave as an open question for further study.

Compressibility of High-Pressure Phase II and Pressure-Dependent Changes to Structure.

The decrease from trigonal to monoclinic symmetry complicates the compressibility behavior of Ag₃[Co(CN)₆]-II. The a_II and c_II axes are no longer principal axes, but in practice, we find that the principal axes [in the (010) plane] coincide with the unit cell axes to within 5°. So the values K_aII, K_bII, and K_cII give quite good approximations to the principal components of the compressibility tensor. The related parameter K_cII sin β_II corresponds to the compressibility perpendicular to Ag- and [Co(CN)₆]-containing layers.

We refined values of the phase II lattice parameters at 15 points over the pressure range 0.19–7.65 GPa; our results are shown in Fig. 2A, and the corresponding lattice parameter values and fits to data are given in SI. What is immediately clear is that Ag₃[Co(CN)₆]-II also shows NLC, because the terms c_II and c_II sin β_II increase with increasing pressure. The lattice parameter variation was fitted according to a set of empirical expressions x(p) = x₀ + λ(p − p_c)^ν, where in this case, p_c = 0.19 GPa. This enabled calculation of a smooth compressibility curve for each direction in the lattice; the corresponding K values are shown in Fig. 2B. Although values approach those of phase I just above the phase transition, average values from linear fits to lattice parameter data >3 GPa give principal components of the compressibility tensor of +15.2(9), +9.6(5), and −5.3(3) TPa⁻¹ along axes approximately parallel to a, exactly parallel to b, and approximately parallel to c, respectively. Although NLC is much less extreme in this phase than in phase I, the behavior is still significantly stronger than that observed in all previous studies. The pressure dependence of the unit-cell volume for this phase can be fitted well by a third-order Birch–Murnaghan equation of state (24), giving B_pc = 11.8(7) GPa and B′ = 13.5(12) (Fig. 2C). These values show that phase II is also initially very soft but becomes significantly harder with increasing pressure (i.e., B′ ≫ 4). A second-order Birch–Murnaghan fit, for which B′ is constrained to equal 4, gives a substantially lower R² value (0.9705 vs. 0.9987) and clearly does not represent the data well (see Fig. 2C Inset). Consequently, Ag₃[Co(CN)₆]-II shows very strong third-order behavior, of a degree normally found only for low-dimensional materials, e.g., graphite-like BC (B′ = 8.0) (25) and layered GeSe₂ (B′ = 9.1) (26)]. Such a large value of B′ in a fully 3-dimensional framework suggests that the elastic constants exhibit anomalous pressure dependencies, a finding that we hope will stimulate further investigation elsewhere.

So how does the structure itself vary under pressure? We found that the [CoC₆] coordination geometries were essentially unaffected by lattice compression and that the original connectivity of this phase was maintained throughout the entire pressure range (see Table 1 for atom coordinates at 2 representative pressure values). Where the variation is most noticeable is in the magnitude of the “interdigitation” effect described above. This can be quantified by the Ag2 y coordinate, which decreases from an initial value of 0.2404(13) at 0.226(10) GPa to 0.1904(28) at 7.65(17) GPa as the extent of interdigitation increases. This has very little effect on any covalent bonding interactions in the framework, but it does vary the geometry of Ag–Ag interactions in the Ag-containing layers: The “knot” of the bow-tie lattice is increasingly “pinched” as y_Ag2 becomes progressively smaller than $\frac{1}{4}$ (Fig. 3C). As a result, all Ag...Ag neighbor distances become more similar with increasing pressure, with the overall arrangement approaching that of a triangular lattice (which would occur for y_Ag2 = $\frac{1}{6}$, but would not increase the lattice symmetry). We believe the mechanism responsible for NLC to be strongly related to this change in Ag environment. The [Co(CN)₆] octahedra sit above and below the knots of the Ag-containing bow-tie lattice; as these knots tighten, the octahedra are forced to move in a direction perpendicular to the Ag sheets, resulting in the corresponding lattice parameter increase. The relatively large positional changes involved are permitted by the flexibility of the lattice: both in terms of the weak argentophilic forces between neighboring (010)_II layers and in terms of the geometric underconstraint of CoCNAg linkages.

We note in passing that the reentrant honeycomb lattice is an example of a 2-dimensional structure with a negative Poisson's ratio (27, 28). Such materials (also known as auxetics) have important mechanical properties; see, for example, refs. 3 and 29 and references therein. In the present context, we note that this property is responsible for coupling the compressibility along b to behavior of a similar sign and magnitude along a.

Thermal Expansion of Phase II.

Our original motivation for studying NLC in Ag₃[Co(CN)₆] was that—although thermodynamics allows for different compression mechanisms under pressure increase and temperature reduction—we reasoned that NLC and NTE may be linked in many cases. Having found both effects to occur in phase I, we were interested to determine whether phase II also shows NTE.

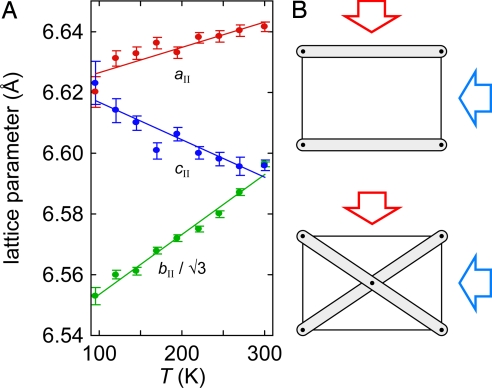
The temperature dependence of the lattice constants, measured at an applied pressure of 0.395(10) GPa, is illustrated in Fig. 4A. Again, the coefficients of thermal expansion α_a and α_c need not correspond to principal components of the thermal expansion tensor, but in practice, we find that there is little difference between the two. What is obvious from our measurements is that Ag₃[Co(CN)₆]-II shows large PTE along a and b, but there is a similarly strong NTE effect along c. From linear fits to the data, we obtain principal thermal expansivities of α = +13.3(25), +30.0(16) and −23(3) MK⁻¹ along axes approximately parallel to a, exactly parallel to b, and approximately parallel to c, respectively; the volume coefficient of thermal expansion is α_V = +20.5(25) MK⁻¹. The NTE effect approximately parallel to c is approximately twice that of ZrW₂O₈ at ambient pressure (30) and comparable with that in other cyanides such as Zn(CN)₂ and Cd(CN)₂ (31). It is also 6–7 times smaller than in phase I; so, perhaps fortuitously, both the compressibilities and the thermal expansivities of the 2 phases differ by what is essentially an order of magnitude in each case. For additional information see Figs. S1 and S2.

Fig. 4.

High pressure thermal expansion and Grüneisen isotropy in Ag₃[Co(CN)₆]. (A) Temperature dependence of phase II lattice parameters measured at p = 0.395(10) GPa. (B) Uniaxial compression in layered materials is strongly direction dependent (Upper), whereas that in connected frameworks produces similar internal strains (here, compression of the same framework “struts”) for very different applied directions (Lower).

Concluding Remarks

The observation of NLC within 2 phases of Ag₃[Co(CN)₆] is remarkable and indicates that significant flexibility is retained within Phase II despite the large increase in density at the phase transition. Furthermore, the orientations of the principal axes are similar in both phases, being substantially parallel and perpendicular to the 2 distinct Ag lattices, respectively. This suggests that a similar mechanism is responsible for NLC in both phases: The framework structures are strongly compressible in directions parallel to the weakly bound argentophilic layers, and this compression is geared via the flexible network to an expansion along a perpendicular axis.

The similarity in compression mechanisms under cooling and under compression led us to consider the existence of a more general link between anisotropic NTE and NLC in framework materials. Clearly, materials that expand with decreasing temperature along a specific direction while contracting overall would, in principle, be able to reduce their volume under increasing hydrostatic pressure while expanding along the same direction that exhibits NTE. This is seen in (for example) Se (5, 19), α′-NaV₂O₅ along the orthorhombic a and b directions (7, 32), Pb_0.7Ca_0.3TiO₃ (33), monoclinic NbOPO₄ (34, 35), and now in Ag₃[Co(CN)₆]-I and Ag₃[Co(CN)₆]-II.

The thermodynamic formalisms that relate thermal expansion to compressibility in anisotropic materials are well-understood (36). Omitting shear terms, we have

where C_T is the isothermal specific heat, V the unit cell volume, S_ij the elastic compliances, and γ_j the components of the anisotropic Grüneisen function (weighted sums over the anisotropic mode Grüneisen parameters). Because the S_ij often have negative values for anisotropic materials, it is quite common for uniaxial NTE to be observed even if the γ_j are all positive (36). Eq. 1 is commonly recast by substituting K_i = Σ_jS_ij to give

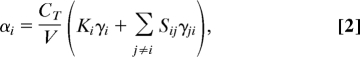where γ_ji = γ_j − γ _i. The summation term on the right-hand side of Eq. 2 is a cross-linking term that describes how thermal expansion along each axis is affected by expansion along the other 2 axes. Because the γ_i may have different signs, and because the cross-linking term can become significant for large γ_ji, there is no thermodynamic requirement that NLC and NTE must coexist. Our argument here, as developed below, is that for flexible framework materials, the Grüneisen function is relatively isotropic (i.e., γ_ji ≪ γ_i). This means that the cross-linking term of Eq. 2 becomes a second-order correction, so that negative α_i values are likely to correspond to negative K_i values whenever the material as a whole exhibits positive thermal expansion (i.e., γ > 0).

That the Grüneisen function should be nearly isotropic is perhaps not immediately obvious, and we believe that the key here is to consider the effect of network connectivity on the mechanical properties of these materials: namely, that stresses applied in perpendicular directions affect the same bonds in similar ways (Fig. 4B). Considering the framework of Ag₃[Co(CN)₆]-I as a specific example, a decrease in either a or c (holding c or a constant, respectively) will compress the CoCNAgNCCo linkages in essentially the same manner. Hence, the directional Grüneisen functions, which are isothermal strain derivatives of the vibrational entropy S, are likely to reflect a common change in phonon frequencies:

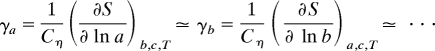(here C_η is the heat capacity under constant strain).

Grüneisen isotropy in framework materials can only be a first-order approximation at best. However, it is encouraging that in β-quartz—one of the few anisotropic frameworks for which directional γ_j values are known—one finds γ_ji/γ_j < 10% (37). The opposite behavior is seen in layered anisotropic materials, such as graphite, where a compression perpendicular to the carbon layers produces a very different microscopic strain to a parallel compression (Fig. 4B); indeed, the γ_i even have different signs in this case (38).

Working within an isotropic Grüneisen approximation, we can now replace the γ_j in Eq. 1 by an isotropic function γ^ to give

and hence the suggested proportionality. So, although it is not possible to say that NTE and NLC are thermodynamically required to coexist, it does seem likely that a general correspondence will be observed for framework materials. Moreover, because NTE can be very strong for some of these compounds, we expect that the same materials may yet be found to exhibit equally strong NLC behavior. If the phenomenon does indeed prove more commonplace than once thought, an increasingly diverse selection of NLC materials will facilitate technological exploitation of their unusual compressibilities. For example, optical sensors used in altitude measurements rely on pressure-induced changes to optical path lengths. The sensitivity of these devices, which depends on the difference between the change in refractive index (usually positive on increasing density) and the linear compressibility is maximized when the latter is negative (1). Optically transparent NTE/NLC framework materials—such as Ag₃[Co(CN)₆]—would present the first realistic candidates for such applications.

In summary, there are 2 key results contained in this article. The first is the identification and subsequent rationalization of NLC in Ag₃[Co(CN)₆], an effect that is many times larger even than the typical (positive) compressibilities of “normal” solids. We have discovered and characterized its trigonal–monoclinic phase transition at 0.19 GPa, and have shown that the high-pressure form also exhibits both NLC and NTE. The second key outcome is to show that Grüneisen isotropy allows a more general expectation that anisotropic NTE framework materials will also show NLC (and vice versa). Thermal expansion is more readily measured than compressibility, presenting a useful method for screening likely NLC candidates.

Materials and Methods

The polycrystalline Ag₃[Co(CN)₆] sample was prepared as in ref. 14 and loaded into either a TiZr helium-gas pressure cell mounted on a closed cycle helium refrigerator (0 < p < 0.6 GPa, 20 < T < 300 K, sample volume ≈1.5 cm³) or an encapsulated TiZr gasket arrangement within a Paris–Edinburgh (P–E) press (0 < p < 9 GPa, sample volume ≈90 mm³) (39). TiZr, alloyed in the correct proportions, has an average neutron scattering length of zero and so does not produce background Bragg scattering. Included in the sample space within the gasket of the P–E press was a lead sphere, for use as a pressure marker, and a deuterated methanol–ethanol mixture, as a pressure transmitting fluid. Sample pressures in the gas pressure cell were determined directly from the He pressure (variance, dp ≃ 100 bar, 0.01 GPa); those in the P–E press were obtained by fitting the measured Pb lattice parameter to the known equation of state for Pb (as described in ref. 40; dp ≃ 0.15–0.2 GPa). Data were collected as a function of neutron time-of-flight at the ISIS Spallation Neutron Source, Rutherford Appleton Laboratory, U.K. by using the Polaris (41) and Pearl (42, 43) diffractometers for measurements within the gas cell and P–E press, respectively. Typical data collection times were ≈4 hours per pressure. Standard routines were used for data focusing and normalization and to account for pressure cell absorption. The resulting normalized powder diffraction patterns were then analyzed by using the GSAS Rietveld refinement package (44) using data from detectors centered around 2θ = 35° and 2θ = 90° (Polaris) or 2θ = 90° only (Pearl), the latter a multiphase refinement including the sample, Pb (pressure marker) and weak contributions from Ni and WC (anvil components).