Abstract
Inter-domain motion in proteins plays an important role in biomolecular interaction. Its presence also complicates interpretation of many spectroscopy measurements. Nuclear Magnetic Resonance (NMR) study of domain dynamics relies on knowledge of its rotational correlation function. The Extended Model Free (EMF) approach has been implemented to analyze coupled domain and overall motions for calmodulin, a dual-domain protein; however, the validity of EMF treatment in coupled motion has not been tested. We performed stochastic simulations on a dual-vector system employing two simple restraints to drive hydrodynamics and domain coupling: 1. both unitary vectors diffuse randomly on the surface of a sphere, 2. vectors are correlated through user-defined inter-vector potential. The resulting correlation curve can be adequately fit with either a single- or double-exponential decay function. The latter is consistent with the EMF treatment. The derived order parameters S2 range from about 0.4 to 1, while the motion separation, the ratio of overall and domain motion time scales (τm/τs), ranges from 1 to 4. A complete overlap between time scales occurs when S2 is less than 0.4, and the correlation function effectively behaves as a single-exponential. The S2 values are consistent with theoretical predictions from the given potential function, differing by no more than 0.03, suggesting EMF to be a generally valid approach. In addition, from the dependence of S2 on τm/τs obtained from simulation, we found out a cosine potential, favoring extended conformers, as opposed to the normally assumed cone potential, reached a better agreement to experimental data.
Introduction
A multi-domain protein can possess inter-domain motion, i.e. domain swinging, twisting and stretching etc. Proteins rely on this domain motion to explore their conformational space1,2 and the process is essential for numerous biological functions.3,4 The time scale of domain motion, ranging from ns to ms, depends on the magnitude of the energy barrier separating its conformational states. In theory with a sufficiently accurate force field, the domain motion could be studied using molecular dynamics (MD) simulations. However currently this is not practical due to the length of simulation needed to sample this motion properly.5 Experimental approaches for studying domain motion include time-resolved spectroscopy6 and NMR spin relaxation.7 The domain rotational correlation function plays crucial role in data interpretation, however, it is challenging to derive its functional form analytically.
NMR spin relaxation rates are functions of spectral densities. They correspond to data points on the curve of the rotational correlation function of the vector bearing an interacting spin pair, usually a bond vector. In the absence of domain motion, the correlation function for individual bond vectors can be factored into a double-exponential decay function with correlation times on the scale of ns and ps, respectively. This approach is known as Model Free (MF).8,9 The slower ns motion corresponds to the overall hydrodynamics of a rigid protein body, while the local libration motion of individual bonds occurs on a ps time scale. The square of the generalized order parameter S2 defines the amplitude of the ps motion. This measures the spatial restriction of a bond vector within the overall diffusion frame. When domain motion exists, both its time scale and amplitude could be close to the overall diffusion, therefore the correlation function on the short ns time scale, or motion coupling, is not well defined. We exclude extremely slow domain motions on μs–ms time scale, as their effect on correlation function would be the ensemble average for all conformers with distinct geometry.10
Currently two treatments of NMR data have been proposed to analyze the domain motion on a ns time scale. Both employ the backbone 15N spin relaxation data of model proteins to derive characteristic domain motion parameters. One approach is the Interconversion between Two distinct States (ITS) model, which has been applied to di-Ubiquitin (di-Ubi).11,12 Di-Ubi has been known to assume both open and closed domain conformations and the equilibrium is pH sensitive. In Ryabov and Fushman's ITS model11,12 the overall diffusion frame of di-Ubi was conserved for both states; the domain motion was taken into account by explicitly formulating the exchange equilibrium between “open” and “closed” geometries into the total correlation function.
The other is the Extended Model Free (EMF) approach. The original EMF method, which introduces an additional exponential term in the correlation function of the MF type, yielding three exponentials, was proposed to account for slow motion of loop residues on the order of 1−3 ns.13 Within the EMF treatment the domain motion is separated from the overall diffusion and characterized by a slow motion order parameter (Ss2), and its correlation time (τs) on a short ns time scale, faster than the overall motion. This type of analysis was applied to a dual-domain protein, calmodulin. For calmodulin an Ss2 value of 0.7 and τs value of 3 ns were derived, while its effective overall correlation time is 9 ns.14 Higher temperature leads to a reduction of the order parameter and less separation between the time scales of the domain and overall motions.15
Here, we evaluate whether the EMF treatment is sufficient to characterize the correlation function of ns domain motion in general, and in particular, which criteria can be used to confirm that such a treatment is valid. Since our focus is on the domain motion, in order to simplify the analysis, the correlation function term corresponding to the fast (ps) motion will be omitted from here on. We use S2 instead of Ss2 since only one order parameter is present. We carried out in silico stochastic simulations on a dual-vector system coupled with various inter-vector potentials. From the trajectory a rotational correlation function was numerically calculated which can be fit with exponential decay functions. At the outset it might seem that the employment of diffusing vectors as a model for domain motion is not realistic. However it is a good model to evaluate the validity of the Model Free treatment. A similar simplification was made in a string-bead model employed for Brownian dynamics simulation on Pin1 protein.16 Here, our vector model remains a simple enough model to analyze, allows the evaluation of various interaction potentials, and still captures the essentials of the relatively complex coupled dynamics.
For all potentials used in the simulations, the obtained order parameters are consistent with theoretical values when an appropriate overall diffusion frame is chosen. This affirms the EMF approach as a good approximation for dynamic analysis of coupled-motions involving inter-domain mobility. Finally, we discuss some experimental aspects related to the EMF approach and its range of validity.
Methods and Theory
Brownian Rotational Simulation and Model Potentials
A system composed of two unitary vectors sharing the same origin, A and B (Figure 1), was subjected to a stochastic simulation. Each vector was assigned an identical rotational diffusion constant Do, 16×106 s−1. The characteristic correlation time τo is around 10 ns (τo = 1/6Do). Both vectors diffuse randomly on the surface of the unitary sphere, but their motions are also modulated through an inter-vector potential. Eq. [1] below, adopted from Zhou's algorithms,17 was applied to calculate the propagation of Brownian dynamics trajectory,
| [1] |
where a and b are time dependent coordinates of unitary vectors A and B, respectively, θ is the inter-vector angle, U is the potential function, R is a Gaussian random number with mean of 0 and variance of 1, the time-step Δt is 1 ps. Each trajectory consists of 5×108 steps. The full time course of the simulation corresponds to 500 μs.
Figure 1.
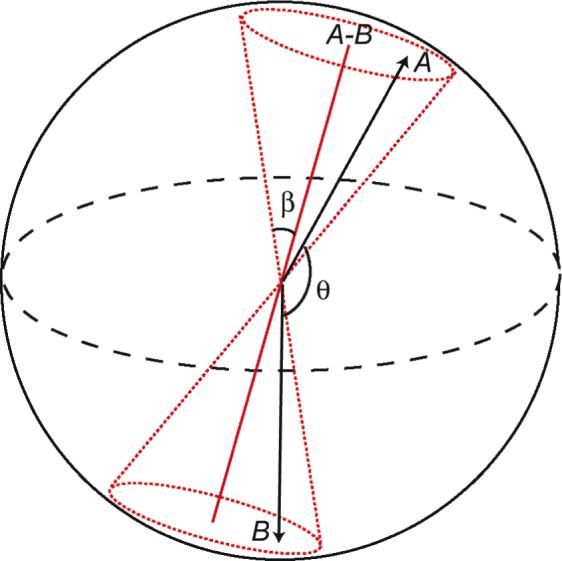
Schematic representation of the dual-vector system. Angle θ is the inter-vector angle. Dotted lines in red define the space of the cone with semi-cone angle β. The symmetry axis of the cone lies along vector A-B.
Simulations were carried out with various types of inter-vector potential, and within each potential a range of coupling strength was also tested. The simplest potential model is diffusion within the cone, and the vector A-B (Figure 1), serves as the cone symmetry axis. Specifically, during a simulation the angle between vectors A (or B) and A-B, (180°-θ)/2, must be less than the given semi-cone angle β. There is no potential gradient (dU/dcosθ = 0) within the cone. A set of cone simulations was performed with β ranging from 5° to 90° at 5° increments.
Other model potentials are cosine functions of θ defined in Eq. [2], where i is the exponential order and the scaling factor k is varied from 1 to 10 to adjust the potential strength. The cosine potentials favor the fully extended conformer with θ being 180°. The θ value is restricted to be greater than 90°.
| [2] |
EMF and its Correlation Function
The EMF treatment inherits the concept of motion separation, the overall and the internal, from the classic MF approach.8 In addition to fast internal motion characterized by Sf2 and τf in MF, for EMF one more internal motion occurs on a slower correlation time τs with the order parameter SS2.13 Here since the fast internal motion (Sf2 and τf) is not simulated, only one order parameter S2, in place of SS2, is present. The final correlation function (C) of vector A or B in the treatment of EMF is the product of overall (Co) and internal correlation (Ci) functions (Eq. [3-6]). The overall motion is assumed to be isotropic with a single correlation time τm and the reason for this will be described later in the text.
| [3] |
| [4] |
| [5] |
| [6] |
Curve Fitting and F-test
The correlation decay curve for the vectors was calculated numerically according to Eq. [7], where a is the time dependent trajectory of the vector A, P2 operator stands for the second order Legendre Polynomial, τ samples all time points ranging from 0 to T-t within the trajectory with T being the full time course, and the angular bracket indicates the average over all available τ values. For each correlation curve a total of 1000 data points were calculated at the time resolution of 100 ps. Correlation curves for vectors B and A-B were calculated similarly.
| [7] |
The first step towards dynamics analysis is to establish EMF type motions, whose correlation function should follow a double-exponential decay. The initial single- and double-exponential curve fittings for correlation curve CA were performed using non-linear minimization routine within Grace (Grace Development Team). In order to avoid over-fitting and biased sampling a total of 50 data points were extracted randomly from each 0.02 interval in the full correlation decay curve CA. For fitting the single-exponential curve, the correlation time τm is the only variable (Eq. [5] with S2 = 1). S2 and τ' are the two additional variables for the double-exponential fitting (Eq. [5]). S2 was set to vary in the range of 0−1. The correlations times τm and τ' were set in the range of 0−2 τo. Theoretically 2 τo is the slowest time scale possible. This occurs when vectors A and B form one rigid body.
The F-test was performed to justify the necessity of approximating the curve with a double-exponential decaying function. F value was calculated according to Eq. [8],
| [8] |
where χ12 and χ22 are the chi-square of residuals out of single- and double-exponential fitting, respectively, p1 and p2 are the number of variables used in single- and double-exponential fitting, and N is the number of data points used in the fitting. The rejection probability function Pf was calculated from the values of F, p2-p1 and N-p2.18 A threshold of 1% was used. A similar F-test is carried out to check for the suitability between the double- and triple-exponential decays. The exponential fittings of correlation curves for vector A-B (CA-B) were also subjected to the F-test.
Order Parameters from Simultaneous Minimization
When the correlation curve CA was determined by F-test to be double-exponential and CA-B being single-exponential, the order parameter S2 and the correlation times τm and τs were extracted from simultaneous minimization of CA and CA-B curves. Both share the same value of τm. A three-dimensional grid search (S2, τm and τs) was performed to locate the minimum using MATLAB 2007b (The Mathworks, MA). The same minimization was repeated on CB and CA-B. The results for τm were identical from both fits. The reported values of S2 and τm/τs were the average of the two and the error ranges were taken from the difference between them.
Theoretical Order Parameters
It is straightforward to solve the closed formula for order parameter as long as the potential function is available and the overall motion frame is defined. For the cone potential the order parameter of vector A or B with respect to the vector A-B is given by Eq. [9]. For the three cosine potentials (U1−3) the energy term needs to be included as a Boltzmann factor (Eq. [10]). Integrations were carried out using Mathematica 6.0.1 (Wolfram Research Inc., IL).
| [9] |
| [10] |
Results
Potential Models
First we need to make sure that our Brownian simulations conform to the assigned potential. Examples of conformer distribution are plotted along the inter-vector angle θ (Figure 2). For the cone potential the population scales with sinθ. All cosine potentials (U1−3) tend to push the conformer to be extended. The potential minima of U1−3 can approach, but cannot be equal to, the completely extended conformer with θ being 180°, since the energy at the polar point, ln(1/sinθ), is infinitely high.
Figure 2.
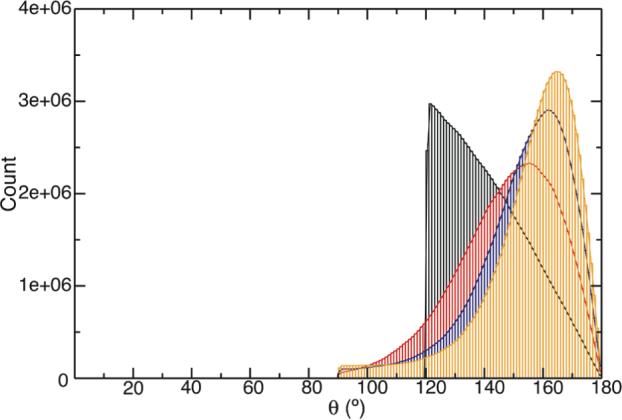
Representative histogram plots of the inter-vector angle θ distribution under the 30° cone potential (black) and cosine potentials U1 (red), U2 (black) and U3 (orange) with potential scaling factor k = 5.
Establishing EMF Type of Motions
We evaluated single-, double- and triple-exponential curve fittings to the correlation curve of vector A. For all simulations the triple-exponential function did not improve the fitting quality since the amplitude of the third exponential decay was on the order of 10−5 or less and there was no further decrease in chi-square (data not shown). The preference for individual curve being single- or double-exponential decay was chosen based on the F-test (Table S1-4). For the cone potential with semi-cone angle β ranging from 10° to 45° EMF motion is established because the probability that the double-exponential fitting was unnecessary, as determined by the F-test, was below 1%, the chosen cut-off for Pf value (Table S1). When β is either 5° or over 50°, the single-exponential fitting is preferred over double, as judged by the larger Pf values (> 1%) and the negative F value (Table S1). Examples of the curve fitting are shown in Figure S1. The same F-test was applied to the fitting of the correlation curves obtained using the cosine potentials U1−3. All motions simulated under cosine potentials with scaling factor k covering 1 to 10 fall in the double-exponential, thus EMF regime (Table S2-4).
Establishing the Overall Motion
The presence of a double-exponential decay in a correlation curve indicates the presence of two motions with distinct time scales. It is important to point out that in a complex coupled system, one can not assume that there will be an overall motion. Adopting the EMF treatment intrinsically imposes an overall motion in the analysis relative to which the order parameter is defined. If this assumption is valid, however, then there should be an overall motion envelope in the correlation function. In the case where a proper reference vector exists, it can be used to separate the overall motion from the total correlation function. To locate the overall diffusion frame an ad hoc approach is described below, while in reality the presence of more bond vectors will help.
The motion under a cone potential with cone-size of 5° results in a single-exponential decay correlation function for both vectors A and B. The correlation time is 2.0 τo, the same as for rigid diffusion of the two vectors. In fact the correlation curve of vector A-B, CA-B, is indistinguishable from CA or CB in this case. The system has not deviated significantly from a rigid diffusion and the amplitude of internal motion is minute. It is tempting to suggest from this finding that the motion of the vector A-B represents the overall motion.
When the cone-size increases to 30°, the correlation function CA out of the grid search of vector A alone is 0.57e-t/2.00τo + 0.43e-t/0.76τo with a minimum chi-square value of 0.0183 (red curves in Figure 3). The EMF parameters from the above fit are 0.57 for S2 and 2.00 τo for τm. The τm value is close to the correlation time of vector A-B, 1.90 τo, which was obtained from an independent fit for curve CA-B. If vector A-B represents the overall motion, both A-B and A should share the same τm. A simultaneous fit of correlation curves CA and CA-B results in the functional form of 0.63e-t/1.90τo + 0.37e-t/0.71τo with a minimum chi-square value of 0.0206 for curve CA (blue curves in Figure 3). The co-fitting results in a higher S2, 0.63, and a shorter τm, 1.90 τo. Based on the surface plot of chi-square along the dimension of order parameter S2, the two fits are within the same minimum (Figure 3B). In addition there is virtually no difference between the two fits on the correlation curve (Figure 3A). The S2 value of 0.63 is consistent, vide infra, with the theoretically calculated order parameter. Thus the vector A-B can be a reasonable reference for the overall motion.
Figure 3.
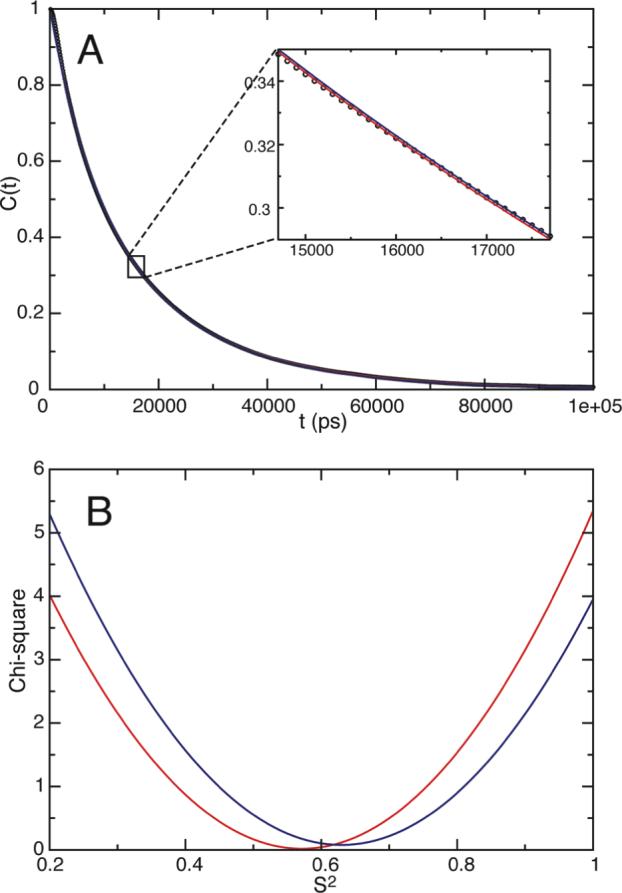
Examples of exponential curve fittings for vector A under a 30° cone potential (A) and the chi-square surface plot along the order parameter dimension (B). Red and blue lines in both panels (A and B) correspond to best fit to correlation function CA only and both CA as well as CA-B, respectively. The numerically calculated correlation curve for vector A is shown in dots (A). The fitted curves in (A) are not clearly visible due to their close agreement, thus strong overlap, to the correlation function.
If we choose vector A-B as the overall diffusion frame, then the internal motion is the local diffusion of vectors A or B with respect to A-B. One question arises, why should the correlation function of A-B be a single exponential decay characterized by τm? Obviously the overall diffusion frame cannot be isotropic for a real dual-domain protein like calmodulin, but it is still reasonable for us to treat the overall motion (Co) with a single correlation time τm. The coupled dual-vector system is axially symmetric and the vector A-B is its long principal axis. According to Woessner's anisotropic diffusion formula,19 the long axis of the overall diffusion frame has only one time scale, free of any other motions on the perpendicular plane (Eq. [11]). In fact the F-test on the curve fitting of the correlation curve CA-B confirms its single-exponential character.
| [11] |
Order Parameter S2
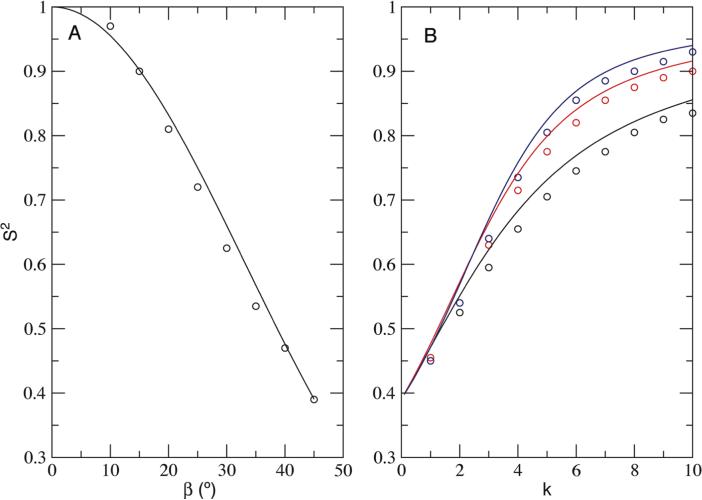
The concept of order parameter imposes a certain reference frame. In the classical MF treatment the reference would be the overall diffusion frame of a protein itself. Here the vector A-B, the symmetry axis of ensemble conformers, serves as the overall diffusion vector. We are able to predict the theoretical order parameters from the potential function alone (see Methods and Theory for detail). As stated before, the current simulated order parameters were obtained from co-fitting of CA (or CB) and CA-B curves (Table S5-8), and they agree well with the theoretical values with a maximum difference of 0.03 (Figure 4). For the cone potential most of the obtained order parameters S2 are slightly lower than the theoretical values (Figure 4A). Similar observations are seen for all cosine potentials (Figure 4B).
Figure 4.
Order parameter S2 obtained from EMF analysis. (A) Cone potentials with different semi-cone angle β and (B) Cosine potentials with different potential scaling factor k. Theoretical S2 values are plotted as solid lines. Order parameters from the analysis are shown as circles for the cone potential (black), potential U1 (black), U2 (red) and U3 (blue).
The differences in the order parameter, ΔS2, could result from several possibilities. First of all, the length of simulation matters, e.g. S2 obtained using just one fifth of the length of the trajectory can differ by as much as 0.05 from the theoretical value. The discrepancy can also rise from the smaller separation between the overall and internal time scales. Generally ΔS2 increases when S2 decreases. However this trend is reversed when S2 is lower than 0.5∼0.6. This complication comes from the incompleteness in conformer sampling when the coupling is weak: for instance the 30° cone potential did not sample enough conformers at the edge of the cone (Figure 2), which will lead to a slight increase in S2.
Nevertheless, the fact the observed S2 from simulation is consistent with theoretical prediction, and the single exponential character of its correlation function indicates the choice of vector A-B to represent the overall motion is accurate. The EMF treatment is a valid tool to extract true order parameters.
Time Scale Separation τm/τs
MF theory was developed for cases where the overall motion occurs on time scales typically 2−3 orders slower than internal motion. When EMF theory was initially introduced to account for the loop dynamics, the time scale separation was only about 10 fold.13 It has been assumed traditionally that the order parameter, or more accurately, the generalized order parameter, and the internal motion are independent of each other. Here, a strong correlation between order parameter and the time scale separation exists (Figure 5). When S2 is higher than 0.85, the motion separation τm/τs levels off at nearly 3−4 fold for all potentials. When the separation is 1, S2 reaches its minimum detectable value, ∼0.4.
Figure 5.
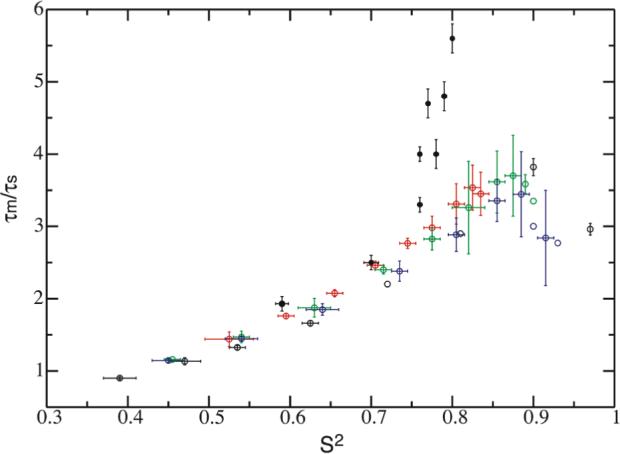
The correlation between S2 and time scale separation τm/τs. Experimental data from Table 1 are marked as solid circles in black. Dynamic parameters from simulations are shown as open circles for the cone potential (black), potential U1 (red), U2 (green) and U3 (blue). Error bars that are not displayed are within the circles.
The overlap of time scales leads to the collapse of a double-exponential function to a single-exponential one. When the coupling is weak and the order parameter is less than a certain value (∼0.4), the domain motion correlation time approaches that of the overall motion. For example when the cone size is larger than 45°, the correlation curve is always single-exponential, though the theoretical order parameters still possess significant values. In the case of this weak coupling one cannot extract a true order parameter. The only manifestation of the domain coupling would be the increase in apparent τm value compared to the one under independent diffusion (τo), e.g. the correlation curve of 60° cone potential follows a single exponential decay with its correlation time as 1.1 τo (Figure S1).
Experimental S2 and τm/τs
When interpreted in the context of the dynamic study of calmodulin using NMR, the vectors used in the simulation correspond to the “parallel” N-H bond vectors that are aligned along the long-axis of the diffusion frame.14 We further compared our simulation results to the experimentally characterized S2 and τm/τs values on the N- and C-terminal domains of calmodulin obtained at four different temperatures (Table 1).15 Order parameters S2 from the “parallel residues” were used. The overall motion τm was re-calculated to correspond to the motion of the long-axis (Table 1). The S2 and τm/τs values are superimposed in Figure 5. The parameters of the calmodulin domain dynamics at 43°C are close to the ones simulated from the cosine potential U1. Motions at lower temperatures do not follow the results calculated from either cone or cosine potentials. This is not surprising since the real domain potential within calmodulin is expected to be much more complicated and temperature dependent.
Table 1.
Experimental Results on Domain Motion of Calmodulina
| 21 °C | 27 °C | 35 °C | 43 °C | |||||
|---|---|---|---|---|---|---|---|---|
| N | C | N | C | N | C | N | C | |
| τc (ns)b | 11.55 | 9.87 | 8.12 | 6.88 | ||||
| ηc | 1.62 | 1.62 | 1.62 | 1.62 | ||||
| τm (ns)d | 13.94 ± 0.04 | 11.91 ± 0.04 | 9.80 ± 0.04 | 8.30 ± 0.04 | ||||
| τm/τse | 5.6 ± 0.2 | 4.7 ± 0.2 | 4.8 ± 0.2 | 4.0 ± 0.1 | 4.0 ± 0.2 | 3.3 ± 0.1 | 2.5 ± 0.1 | 1.9 ± 0.1 |
| S2f | 0.80 ± 0.002 | 0.77 ± 0.002 | 0.79 ± 0.003 | 0.76 ± 0.002 | 0.78 ± 0.003 | 0.76 ± 0.003 | 0.70 ± 0.009 | 0.59 ± 0.008 |
Experimental data were reproduced from measurements on “parallel residues” of calmodulin in the ref.15
τc = 1/(2Dzz+4Dxx,yy)
η = Dzz/Dxx,yy
τm (1/6Dxx,yy) was recalculated from τm = τc(4+2η)/6. The error range of τm was propagated from experimental errors on τc and η adopted from the ref.15
The error range of τs was adopted from the ref.15
The error range of S2 was adopted from the ref.15
Summary and Discussion
We carried out stochastic simulations and employed the EMF approach to analyze the correlation function of domain motions that are coupled. No theoretical approach to derive this correlation function has been developed, and MD simulation for the required time scale is impractical. To this end, we chose a simulation model of two randomly diffusing vectors A and B that are correlated through an interacting potential. This conceptually is similar to the two-body Slowly Relaxing Local Structure (SRLS) method20 for analysis of 15N spin relaxation data.21 In the SRLS model the dynamic coupling was between the overall and local diffusion tensors, the latter of which defines local motion of the N-H bond. In our model the coupling is between two “local” vectors, and there is no explicit overall diffusion tensor. The apparent overall motion from subsequent EMF analysis of the correlation curve is a result of the strong inter-vector potential. The simple potentials we employed are one-state potentials so that the internal domain motion is always faster than or equal to the overall motion. This is different from di-Ubi model where τex is longer than τm11 or other corrections to MF where the internal motion correlation time τe is longer than τm.22 We also emphasize that the concept of motion coupling implies a situation where the domain motion time scale is close to the ns time scale of hydrodynamic diffusion. We now discuss some experimental aspects, considerations, and range of validity related to EMF analysis.
Overall Diffusion Frame
Intrinsically, the EMF approach imposes a context of overall motion. Since this is not explicitly well defined in our model system or for real multi-domain proteins in general, we must show that one can choose a reference that can be used to reliably separate the overall motion envelope from the full correlation function. Here, we have shown that the connecting vector A-B in the limit of very small spatial restriction mimics the rigid tumbling of the two vectors. When there is some spatial restriction, the diffusion of vector A-B has a correlation time close to that of the slower component found for either vector A or B. In addition the calculated order parameter from the simulated trajectory agrees well with the theoretical values. All of these taken together indicate that the A-B vector effectively represents the overall motion in our simulation. Furthermore we found the S2 value to be highly dependent on the accuracy of the overall motion τm, thus necessitating simultaneous fitting of the domain and the overall correlation function. In practice there is no a priori overall reference frame in real multi-domain proteins. Fortunately, relaxation data from a list of interaction (bond) vectors pointing to different directions in each domain can be used in lieu of the A-B vector to allow determination of the reference frame for the overall motion. For RNA molecules where bond vectors have limited spatial distribution, a molecular elongation approach has been employed to separate the overall motion from the domain motion.23
Domain Motion Parameters
The domain motion order parameter from the EMF treatment of our simulations ranges from 0.4 to 1, and is consistent with the theoretical values derived from the interaction potential with a maximum deviation of 0.03. Domain motions with their order parameter lower than 0.4 will not yield a double-exponential decay correlation function. Instead their correlation curve will collapse to a single-exponential decay function due to the complete overlap between τm and τs. We propose an S2 value of 0.4 as a divider for strong and weak coupling regimes. For cases where the order parameter for the domain motion is undefined (S2 < 0.4), weak domain motion coupling may be manifested as an increase in the overall correlation time τm. In fact a close look at published results on protein domain motion reveals all extractable domain motion S2 values fall in the range of 0.6−0.9,14,15,24,25 which indicates the EMF treatment is both the necessary and a natural choice when strong coupling exists.
The overall motion correlation time τm is always larger than τo, the assigned correlation time for individual domain. Both correlation times are defined in Cartesian space. In our simulation τm ranged from 1.7 to 2.0 τo (Table S5-8) for all EMF type of motions. The motion coupling slows down the domain sampling in Cartesian space. In contrast the domain motion correlation time τs can be either larger or smaller than τo (Table S5-8). It seems counter-intuitive at the first sight that a motion with τs less than τo could ever exist in the system. The domain correlation time τs is defined within the reference (overall) motion frame. The τs can be interpreted as the time it takes to sample the domain conformer space, which will be faster than its Cartesian diffusion when the conformer space is small. This is usually associated with higher S2 (> 0.6−0.7, Table S5-8).
An insightful physical meaning of domain motion correlation time τs is not readily apparent, as it should carry collectively all types of domain motions. Its counterpart in MF analysis is the effective internal correlation time τe, which is the area underneath the internal correlation curve and cannot be treated as a quantity descriptive of a single mode motion.8,9 Previously we have employed experimental τs along with Ss2, in the context of wobbling-in-the-cone model, to derive the cone diffusion coefficient Dw, which is more physically meaningful.15,26 Clearly a model dependent analysis for τs is necessary when a physically accurate domain motion time scale interpretation is required. We can however use the derived τs and S2 to set a boundary for validity of the EMF treatment. Based on our current simulation the value of τs may have an upper limit that is close to 1.1 τm when order parameter S2 is in the weak-coupling limit of 0.4 for EMF approach to still be valid (Figure 5).
Domain Sizes
Although vectors A and B in our model were assigned identical diffusion constants, implying A and B are similar in size, the main conclusion is expected to be valid for multi-domain protein with different domain size. However the overall diffusion vector will experience a shift toward the slower tumbling vector. A trial simulation was carried out with vector A tumbling 10 times faster than vector B under potential U2. The proper overall diffusion frame is the slower vector B now, the correlation function of which behaves as a single-exponential decay as expected (S2 = 1). The extractable order parameter for A has a difference of 0.05−0.06 from theoretical values, and the larger ΔS2 may result from a coarse resolution on the numerically calculated correlation curve.
NMR Experimental Considerations
Experimentally more data points from correlation curve will help to locate the proper dynamic parameters. We previously derived experimental S2 and τm/τs from relaxation measurements at 3 different fields, 8.5, 14.1 and 18.8 T, the largest field range available.15 The use of data obtained at the 8.5 T has proven to be important.14 Future study on slow motion may need to cover even larger field ranges, and may include 13C relaxation, so that more frequency components of spectral density, or correlation function, can be better defined.
With our simple model we have shown through simulations that the EMF approach is generally applicable for correlation function of coupled motions. Since the result is on correlation function, the EMF treatment should be applicable to the field of NMR as well as other spectroscopies. From our study it is also clear that to characterize these types of motions, one would need very long dynamic trajectories. Our simulations, which cover eight orders of magnitude in time, still do not capture all the features of the correlation functions perfectly. At the same time more proteins are being discovered with multiple domains as well as with large unstructured fragments, where this type of simulation is also applicable with proper modification. Further studies will clearly be needed with more sophisticated and appropriate models to better interpret and derive diffusion parameters from spectroscopy analysis, which, in turn, will help in understanding functionally relevant coupled motions in proteins.
Supplementary Material
Acknowledgement
We thank Attila Szabo for many helpful discussions and James Gruschus for careful reading of the manuscript. This work was supported by the Intramural Research Program of the NIH, National Heart, Lung, and Blood Institute.
Footnotes
Supporting Information Available Curve fitting examples are provided for several trajectories under cone potential (Figure S1). F-test results are shown in Table S1-4. 3D grid search results are shown in Table S5-8. This material is available free of charge via the Internet at http://pubs.acs.org.
References
- 1.Bertini I, Del Bianco C, Gelis I, Katsaros N, Luchinat C, Parigi G, Peana M, Provenzani A, Zoroddu MA. Proc. Natl. Acad. Sci. USA. 2004;101:6841–6846. doi: 10.1073/pnas.0308641101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Frederick KK, Marlow MS, Valentine KG, Wand AJ. Nature. 2007;448:325–329. doi: 10.1038/nature05959. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.McCammon JA. Rep. Prog. Phys. 1984;47:1–46. [Google Scholar]
- 4.Berg OG, von Hippel PH. Annu. Rev. Biophys. Biophys. Chem. 1985;14:131–160. doi: 10.1146/annurev.bb.14.060185.001023. [DOI] [PubMed] [Google Scholar]
- 5.Wong V, Case DA. J. Phys. Chem. B. 2008;112:6013–6024. doi: 10.1021/jp0761564. [DOI] [PubMed] [Google Scholar]
- 6.Slaughter BD, Allen MW, Unruh JR, Urbauer RJB, Johnson CK. J. Phys. Chem. B. 2004;108:10388–10397. [Google Scholar]
- 7.Bruschweiler R. Curr. Opin. Struct. Biol. 2003;13:175–183. doi: 10.1016/s0959-440x(03)00036-8. [DOI] [PubMed] [Google Scholar]
- 8.Lipari G, Szabo A. J. Am. Chem. Soc. 1982;104:4546–4559. [Google Scholar]
- 9.Lipari G, Szabo A. J. Am. Chem. Soc. 1982;104:4559–4570. [Google Scholar]
- 10.Wallach D. J. Chem. Phys. 1967;47:5258–5268. [Google Scholar]
- 11.Ryabov Y, Fushman D. Proteins. 2006;63:787–796. doi: 10.1002/prot.20917. [DOI] [PubMed] [Google Scholar]
- 12.Ryabov YE, Fushman D. J. Am. Chem. Soc. 2007;129:3315–3327. doi: 10.1021/ja067667r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Clore GM, Szabo A, Bax A, Kay LE, Driscoll PC, Gronenborn AM. J. Am. Chem. Soc. 1990;112:4989–4991. [Google Scholar]
- 14.Baber JL, Szabo A, Tjandra N. J. Am. Chem. Soc. 2001;123:3953–3959. doi: 10.1021/ja0041876. [DOI] [PubMed] [Google Scholar]
- 15.Chang SL, Szabo A, Tjandra N. J. Am. Chem. Soc. 2003;125:11379–11384. doi: 10.1021/ja034064w. [DOI] [PubMed] [Google Scholar]
- 16.Bernado P, Fernandes MX, Jacobs DM, Fiebig K, Garcia de la Torre J, Pons M. J. Biomol. NMR. 2004;29:21–35. doi: 10.1023/B:JNMR.0000019499.60777.6e. [DOI] [PubMed] [Google Scholar]
- 17.Zhou HX. Biophys. J. 1993;64:1711–1726. doi: 10.1016/S0006-3495(93)81543-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Bevington PR, Robinson DK. Data reduction and error analysis for the physical sciences. 2nd ed. McGraw-Hill; New York: 1992. [Google Scholar]
- 19.Woessner DE. J. Chem. Phys. 1962;36:1–4. [Google Scholar]
- 20.Polimeno A, Freed JH. J. Phys. Chem. 1995;99:10995–11006. [Google Scholar]
- 21.Tugarinov V, Liang Z, Shapiro YE, Freed JH, Meirovitch E. J. Am. Chem. Soc. 2001;123:3055–3063. doi: 10.1021/ja003803v. [DOI] [PubMed] [Google Scholar]
- 22.Vugmeyster L, Raleigh DP, Palmer AG, 3rd, Vugmeister BE. J. Am. Chem. Soc. 2003;125:8400–8404. doi: 10.1021/ja029480f. [DOI] [PubMed] [Google Scholar]
- 23.Zhang Q, Sun X, Watt ED, Al-Hashimi HM. Science. 2006;311:653–656. doi: 10.1126/science.1119488. [DOI] [PubMed] [Google Scholar]
- 24.Braddock DT, Louis JM, Baber JL, Levens D, Clore GM. Nature. 2002;415:1051–1056. doi: 10.1038/4151051a. [DOI] [PubMed] [Google Scholar]
- 25.Yoshida T, Oka S, Uchiyama S, Nakano H, Kawasaki T, Ohkubo T, Kobayashi Y. Biochemistry. 2003;42:4101–4107. doi: 10.1021/bi027191y. [DOI] [PubMed] [Google Scholar]
- 26.Chang SL, Tjandra N. J. Am. Chem. Soc. 2001;123:11484–11485. doi: 10.1021/ja016862x. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.