Objective assessment of image quality. IV. Application to adaptive optics

Abstract

The methodology of objective assessment, which defines image quality in terms of the performance of specific observers on specific tasks of interest, is extended to temporal sequences of images with random point spread functions and applied to adaptive imaging in astronomy. The tasks considered include both detection and estimation, and the observers are the optimal linear discriminant (Hotelling observer) and the optimal linear estimator (Wiener). A general theory of first- and second-order spatiotemporal statistics in adaptive optics is developed. It is shown that the covariance matrix can be rigorously decomposed into three terms representing the effect of measurement noise, random point spread function, and random nature of the astronomical scene. Figures of merit are developed, and computational methods are discussed.

1. INTRODUCTION

Scientific and medical images are acquired for specific purposes, and the quality of an imaging system is ultimately determined by how well the images fulfill those purposes. In broad terms the purpose, or task, of the imaging system is to learn something about the object that produced the image. More specifically, the tasks of interest can be divided generically into classification and estimation. In a classification task, the goal is to label the object, or to say to which of two or more classes it belongs. Estimation tasks are concerned with extraction of numerical information from the images.

How well the task can be performed depends not only on the task and imaging system but also on the means by which the task is performed, or the observer. For classification tasks, the observer is often a human, such as a radiologist or photointerpreter, and some measure of classification accuracy can be used as a figure of merit for the combined performance of the imaging system and the observer. Alternatively, images can be classified by computer algorithms or mathematical models. It is possible in many cases to construct ideal observers that achieve the best possible performance on a given task with images from a given imaging system; performance of an ideal observer can be regarded as a figure of merit for the imaging system alone, since it does not depend on the capabilities of humans, ad hoc feature-extraction schemes, or other suboptimal classification methods.

Estimation tasks can also be performed by humans, but it is more common to use a computer algorithm to analyze the image and report numerical values for one or more parameters of interest. Again, estimation algorithms that are optimal in some statistical sense can be used to obtain figures of merit for the imaging system itself, but as with classification tasks, this metric will depend on the specific estimation task chosen.

This task-based approach to image quality, often called objective assessment, is now well established in radiological imaging, and in fact virtually mandatory in that field, but it is widely applicable to other areas of imaging as well. For a comprehensive review and discussion of both medical and nonmedical applications, see Barrett and Myers.¹

In the first paper of this series,² it was emphasized that task performance is inherently statistical and that calculation or measurement of objective performance has to account for all sources of image randomness, including the randomness of the objects themselves or the background on which they are superimposed. This paper examined a variety of estimation and classification tasks with both optimal and suboptimal observers, and it derived relationships between the objective figures of merit for estimation and classification tasks. An important conclusion of this paper is that not only the absolute level of image noise, but also its correlation structure, is important for both kinds of task. Image correlations can be introduced by the image detector or subsequent image processing or reconstruction, but they are also inherent in the objects being imaged.

The second paper in the series³ examined Fourier methods for quantifying task performance. Though familiar Fourier techniques are rigorously applicable only for linear, shift-invariant imaging systems with stationary noise, this paper considered a more general descriptor called the Fourier crosstalk matrix, which is applicable to any linear imaging system. The crosstalk matrix was related to the Fisher information matrix for estimation of Fourier coefficients and used to discuss classification and estimation tasks.

The third paper in the series⁴ looked specifically at classification tasks with the ideal observer. It developed the theory of the ideal observer and set the stage for practical computation of its performance in radiological imaging.^1,5–7

The goal of the present paper is to show how the methodology of objective assessment of image quality can be applied to an important nonradiological imaging area, namely astronomical adaptive optics (AO). It should serve as a case study of how the various sources of randomness in a complex imaging system can be systematically enumerated and analyzed and how they affect task performance. In addition, this paper adds to the methodology of objective assessment in two respects: It considers the effect of a random system operator, and it analyzes task performance on sequences of correlated images.

Section 2 is a background section, containing little that is new but introducing the viewpoint and notation used in the remainder of the paper. In particular, the critical concept of multiply stochastic images is introduced and integrated into specific figures of merit for task performance.

Section 3 is a detailed statistical analysis of a generic AO system, and Section 4 applies the results of the analysis to task-based assessment of image quality. The goal of Section 5 is to show that the resulting figures of merit can actually be computed in practice. Section 6 summarizes the results and conclusions of the analysis.

2. BACKGROUND

A. Descriptions of Digital Imaging Systems

A digital imaging system is one that delivers a discrete set of data, {g_m,m=1, … ,M}, or equivalently an M × 1 data vector g. For a single static image, M is the number of pixels in the image, but multiple image frames indexed by time, wavelength, or viewing angle can also be included in the data vector.

The object itself is not discrete, even though we often model it as such; instead, a real-world object is a function of some number of continuous variables. We shall write this function as f(r) with the understanding that the vector r includes all independent variables needed to describe the object, including time if the object is not static. In general, r has q components, where q=2 for a two-dimensional (2D) static object. When we do not wish to be specific about the independent variables, we shall denote the object as f, with the boldface indicating a vector in a Hilbert space.¹

The components of g are random variables because the object being viewed is randomly chosen from some ensemble of objects, because of measurement noise and possibly because the imaging system itself is random. Object randomness is discussed in Subsection 2.B below, and consideration of random systems is postponed to Subsection 3.B. For now, we define an average data vector $\overline{\mathbf{g}}\left(\mathbf{f}\right)$, where the overbar indicates an ensemble average over the measurement noise for a given object and imaging system.

A system is said to be linear if each component of $\overline{\mathbf{g}}\left(\mathbf{f}\right)$ is a linear functional of f. The most general form of this linear functional is

$${\overline{g}}_m\left(\mathbf{f}\right)={\int }_{\infty }\mathrm{d}\mathfrak{r}{h}_m\left(\mathfrak{r}\right)f\left(\mathfrak{r}\right),m=1,\dots ,M,$$ (2.1)

where the index ∞ indicates that the integral runs over the complete range of all q variables that make up r. In abstract operator form, Eq. (2.1) can also be written as

$$\overline{\mathbf{g}}\left(\mathbf{f}\right)=\mathcal{H}\mathbf{f},$$ (2.2)

where the linear operator H is defined by the M integrals in Eq. (2.1). Since H maps a function of continuous variables to a discrete vector, it is referred to as a continuous-to-discrete, or CD, operator.¹ The kernel h_m(r) in Eq. (2.1) is called the sensitivity function of the linear imaging system. It is also a point response function in the sense that h_m(r₀) is the mean response of the mth measurement when the object is a point, δ(r—r₀), but of course the integral in Eq. (2.1) is not a convolution.

Since the data vector has a finite dimension and the object is a vector in an infinite-dimensional Hilbert space, CD operators necessarily have null functions. The only components of f that can be captured by, even in the absence of noise, are linear combinations H of the sensitivity functions.

B. Random Objects and Doubly Stochastic Images

For a single object f, the conditional probability density function (PDF) of the image, denoted pr(g|f), describes the randomness of the measurement noise only. This PDF (or probability mass function in the case of discrete random variables) usually has a simple and well-understood form, for example a multivariate Gaussian for electronic readout noise or a Poisson in the case of photon-counting statistics.

To fully characterize random objects, we would need a PDF on f; if we had such a thing, we could write the final PDF on the data as

$$\mathrm{pr}\left(\mathbf{g}\right)=\int \mathrm{d}\mathbf{f}\mathrm{pr}(\mathbf{g}\mid \mathbf{f})\mathrm{pr}\left(\mathbf{f}\right),$$ (2.3)

where in principle the integral is over all parameters needed to specify the object. An alternative notation that means the same thing is

$$\mathrm{pr}\left(\mathbf{g}\right)=\langle \mathrm{pr}(\mathbf{g}\mid \mathbf{f}){\rangle }_{\mathbf{f}},$$ (2.4)

where the angle brackets denote an average over the quantities indicated by the subscript, in this case over an ensemble of objects.

There are many situations where the average in Eq. (2.4) can be performed analytically or approximated numerically without an explicit PDF for the object ensemble. Numerically, Monte Carlo sampling methods make it possible to do the averaging whenever we can simulate the objects, though the computational requirements are likely to be severe. Analytically, multivariate normal and log-normal models are tractable even when the dimensionality of the object description is very large, and there are mathematical models known as lumpy and clustered lumpy backgrounds^8,9 that accurately represent tissue distributions encountered in medical imaging yet remain mathematically tractable even in the limit of an infinite-dimensional Hilbert space for the object. Also, there is a large literature on constructing lower-dimensional representations that capture the essential features of interesting objects by the use of wavelets^10,11 or independent-components analysis.^12,13

A survey of the state of the art in object statistics is given in Barrett and Myers,¹ and some examples relevant to astronomy will be given in Section 4 and Appendix A.

The conditional mean image $\overline{\mathbf{g}}\left(\mathbf{f}\right)$ is defined as the average of g with respect to pr(g|f). If we also average over random objects, the overall mean image, denoted $\overline{\overline{\mathbf{g}}}$, is given in component form by

$${\overline{\overline{g}}}_m=\langle g_m{\rangle }_{\mathbf{g},\mathbf{f}}=\langle \langle g_m{\rangle }_{\mathbf{g}\mid \mathbf{f}}{\rangle }_{\mathbf{f}}=\int \mathrm{d}\mathbf{f}\int \mathrm{d}\mathbf{g}{g}_m\mathrm{pr}(\mathbf{g}\mid \mathbf{f})\mathrm{pr}\left(\mathbf{f}\right).$$ (2.5)

For a linear imaging system,

$${\overline{\overline{g}}}_m=\langle {\overline{g}}_m{\rangle }_{\mathbf{f}}={\int }_{\infty }\mathrm{d}\mathbf{r}{h}_m\left(\mathbf{r}\right)\overline{f}\left(\mathbf{r}\right).$$ (2.6)

Conditional and overall covariance matrices can be defined similarly. The conditional covariance matrix, which describes the measurement noise, is given in component form as

$$[{\mathbf{K}}_{\mathbf{g}\mid \mathbf{f}}{]}_{\mathit{mm}\prime }=\langle [g_m-{\overline{g}}_m\left]\right[g_{m\prime }-{\overline{g}}_{m\prime }]{\rangle }_{\mathbf{g}\mid \mathbf{f}}$$ (2.7)

or in outer-product form as

$${\mathbf{K}}_{\mathbf{g}\mid \mathbf{f}}=\langle [\mathbf{g}-\overline{\mathbf{g}}][\mathbf{g}-\overline{\mathbf{g}}{]}^{\mathrm{t}}{\rangle }_{\mathbf{g}\mid \mathbf{f}}.$$ (2.8)

For Poisson noise, $[{\mathbf{K}}_{\mathbf{g}\mid \mathbf{f}}{]}_{\mathit{mm}\prime }={\overline{\mathtt{g}}}_m{\delta }_{\mathit{mm}\prime }$.

The overall covariance matrix is defined by

$${\mathbf{K}}_{\mathbf{g}}\equiv \langle [\mathbf{g}-\overline{\overline{\mathbf{g}}}][\mathbf{g}-\overline{\overline{\mathbf{g}}}{]}^{\mathrm{t}}{\rangle }_{\mathbf{g},\mathbf{f}}={\langle \langle [\mathbf{g}-\overline{\overline{\mathbf{g}}}][\mathbf{g}-\overline{\overline{\mathbf{g}}}{]}^{\mathrm{t}}{\rangle }_{\mathbf{g}\mid \mathbf{f}}\rangle }_{\mathbf{f}}.$$ (2.9)

Now add and subtract $\overline{\mathbf{g}}$ in each factor:

$$\begin{array}{cc}\hfill {\mathbf{K}}_{\mathbf{g}}& ={\langle \langle [\mathbf{g}-\overline{\mathbf{g}}+\overline{\mathbf{g}}-\overline{\overline{\mathbf{g}}}][\mathbf{g}-\overline{\mathbf{g}}+\overline{\mathbf{g}}-\overline{\overline{\mathbf{g}}}{]}^{\mathrm{t}}{\rangle }_{\mathbf{g}\mid \mathbf{f}}\rangle }_{\mathbf{f}}\hfill \\ \hfill & ={\langle \langle [\mathbf{g}-\overline{\mathbf{g}}][\mathbf{g}-\overline{\mathbf{g}}{]}^{\mathrm{t}}{\rangle }_{\mathbf{g}\mid \mathbf{f}}\rangle }_{\mathbf{f}}+\langle [\overline{\mathbf{g}}-\overline{\overline{\mathbf{g}}}][\overline{\mathbf{g}}-\overline{\overline{\mathbf{g}}}{]}^{\mathrm{t}}{\rangle }_{\mathbf{f}}.\hfill \end{array}$$ (2.10)

Note that the cross term has vanished identically, since

$$\begin{array}{cc}\hfill {\langle \langle [\mathbf{g}-\overline{\mathbf{g}}][\overline{\mathbf{g}}-\overline{\overline{\mathbf{g}}}{]}^{\mathrm{t}}{\rangle }_{\mathbf{g}\mid \mathbf{f}}\rangle }_{\mathbf{f}}& =\langle \langle [\mathbf{g}-\overline{\mathbf{g}}]{\rangle }_{\mathbf{g}\mid \mathbf{f}}[\overline{\mathbf{g}}-\overline{\overline{\mathbf{g}}}{]}^{\mathrm{t}}{\rangle }_{\mathbf{f}}\hfill \\ \hfill & =\langle [\overline{\mathbf{g}}-\overline{\mathbf{g}}][\overline{\mathbf{g}}-\overline{\overline{\mathbf{g}}}{]}^{\mathrm{t}}{\rangle }_{\mathbf{f}}=0.\hfill \end{array}$$ (2.11)

Thus, with no assumptions about independence of g and f, we can write

$${\mathbf{K}}_{\mathbf{g}}={\overline{\mathbf{K}}}_{\mathbf{g}}^{\text{noise}}+{\mathbf{K}}_{\overline{\mathbf{g}}}^{\mathrm{obj}},$$ (2.12)

where the first term describes the measurement noise and the second term arises from object variability. For most kinds of noise, including Poisson noise in photon-counting detectors and electronic readout noise in detector arrays, ${\overline{\mathbf{K}}}_{\mathbf{g}}^{\text{noise}}$ is diagonal.

The second term in Eq. (2.12) is not diagonal. Recall that the object is a random process f(r) and hence described by an autocovariance function:

$$K_{\mathbf{f}}(\mathbf{r},\mathbf{r}\prime )=\langle \left[f\right(\mathbf{r})-\overline{f}(\mathbf{r}\left)\right]\left[f\right(\mathbf{r}\prime )-\overline{f}(\mathbf{r}\prime \left)\right]\rangle .$$ (2.13)

The autocovariance function can be regarded as the kernel of an integral operator ${\mathcal{K}}_{\mathbf{f}}$, and for a linear imaging system, the second term in the decomposition can be written formally as

$${\mathbf{K}}_{\overline{\mathbf{g}}}^{\mathrm{obj}}=\mathcal{H}{\mathcal{K}}_{\mathbf{f}}{\mathcal{H}}^{†},$$ (2.14)

where ${\mathcal{H}}^{†}$ is the adjoint¹ of the operator $\mathcal{H}$.

C. Tasks and Observers

This subsection provides a brief survey of key concepts from statistical decision theory. A more complete discussion can be found in many sources.^1,14,15

1. Classification Tasks

In a classification task, the goal is to assign the object that produced an image to one of two or more classes. If the hypothesis that f belongs to the kth class is denoted H_k, then the probability law for the data when hypothesis H_k is true is pr(g|H_k). In terms of the PDFs discussed above,

$$\mathrm{pr}(\mathbf{g}\mid H_k)=\int \mathrm{d}\mathbf{f}\mathrm{pr}(\mathbf{g}\mid \mathbf{f})\mathrm{pr}(\mathbf{f}\mid H_k).$$ (2.15)

When regarded as a function of H_k for a fixed (observed) g, pr(g|H_k) is referred to as the likelihood of the hypothesis for that data set.

A binary classification task is one where there are only two classes or hypotheses. In a signal-detection task, for example, the hypotheses are signal-absent and signal-present. If we assume that each image must be assigned without equivocation either to hypothesis H₀ (e.g., signal-absent) or to H₁, the decision on a binary task can be made in complete generality by computing some scalar test statistic t(g) from the data; the observer then decides on H₁ if the test statistic is greater than a decision threshold and decides on H₀ otherwise. The value of the threshold controls the trade-off between true positive decisions (correctly choosing H₁) and false positive decisions (choosing H₁ when H₀ is true). In signal-detection problems, the true-positive fraction (TPF) is called the probability of detection, and the false-positive fraction (FPF) is called the false-alarm rate.

A plot of TPF versus FPF as the threshold is varied is called a receiver operating characteristic (ROC) curve. Meaningful figures of merit for binary classification include the TPF at a specified FPF (the Neyman—Pearson criterion), the area under the ROC curve (AUC), and certain detectability indices derived from the ROC curve. The probability of detection alone is not a meaningful metric since it can always be made large, even unity, simply by choosing a low threshold.

Another common figure of merit for binary classification tasks is the signal-to-noise ratio (SNR) on the test statistic. Not to be confused with the more common pixel SNR, the SNR for a specific test statistic t(g) is defined as

$${\mathrm{SNR}}_t^2=\frac{{[\langle t(\mathbf{g})\mid H_1\rangle -\langle t(\mathbf{g})\mid H_0\rangle ]}^2}{\frac{1}{2}\mathrm{Var}\left\{t\right(\mathbf{g})\mid H_1\}+\frac{1}{2}\mathrm{Var}\left\{t\right(\mathbf{g})\mid H_0\}},$$ (2.16)

where ⟨t(g)|H_k⟩ is the expected value of the test statistic when hypothesis H_k is true and Var{t(g)|H_k} is the corresponding variance. If the test statistic is normally distributed under both hypotheses, the AUC is uniquely determined by SNR_t.

2. Optimal Observers for Binary Classification

The ideal observer on a binary task is defined variously as one that maximizes the AUC, maximizes the TPF at all specified FPFs, or minimizes a cost function defined in terms of TPF and FPF. By any of these criteria, the test statistic used by the ideal observer is the likelihood ratio $\Lambda \left(\mathbf{g}\right)\equiv \mathrm{pr}\left(\mathbf{g}\mid H_1)∕\mathrm{pr}(\mathbf{g}\mid H_0\right)$, so the ideal observer for a binary problem is one that calculates either the likelihood ratio or its logarithm $\lambda \left(\mathbf{g}\right)\equiv \text{ln}\Lambda \left(\mathbf{g}\right)$. There are several examples where this computation is feasible,^5–7,16,17 but in many problems $\lambda \left(\mathbf{g}\right)$ and $\Lambda \left(\mathbf{g}\right)$ are complicated nonlinear functions of the data for which no closed form is possible, and in any case their computation requires knowledge of the data PDF under both hypotheses.

A more tractable alternative to the ideal observer is the ideal linear observer, often called the Hotelling observer^1,2,18,19 in the literature on objective assessment of image quality. Linear observers compute linear discriminants, so the test statistic has the form t(g)=w^tg, where w is an M × 1 vector called the template, and w^tg denotes its scalar product with the M × 1 data vector. The Hotelling discriminant uses a template that maximizes a certain class separability measure,²⁰ and if the classes are equally probable it also maximizes the SNR defined in Eq. (2.16). Linear test statistics are usually normally distributed by virtue of the central limit theorem, and in this case maximizing this SNR is equivalent to maximizing the AUC among linear observers. It can also be shown that the Hotelling test statistic is equal to the log-likelihood ratio if the raw data are normally distributed with the same covariance under both hypotheses, so the Hotelling observer is identical to the ideal observer in this case and thus maximizes the AUC among all observers, not just linear ones.

Computation of the Hotelling test statistic requires only the overall mean vectors and the covariance matrices of the data under the two hypotheses. The test statistic is given by

$$t_{\mathrm{Hot}}\left(\mathbf{g}\right)={\mathbf{w}}^{\mathrm{t}}\mathbf{g}=[{\overline{\overline{\mathbf{g}}}}_1-{\overline{\overline{\mathbf{g}}}}_0{]}^{\mathrm{t}}{\mathbf{K}}_{\mathrm{av}}^{-1}\mathbf{g},{\mathbf{K}}_{\mathrm{av}}\equiv \frac{1}{2}[{\mathbf{K}}_{\mathbf{g}\mid H_1}+{\mathbf{K}}_{\mathbf{g}\mid H_0}].$$ (2.17)

The inverse of the average covariance matrix is related to the familiar signal-processing operation of prewhitening, and for this reason, the Hotelling observer is sometimes called a prewhitening matched filter; unless the noise is stationary, however, the prewhitening and matched filtering cannot be carried out in the Fourier domain.

The Hotelling discriminant (2.17) should not be confused with the Fisher discriminant. Basically the difference is that the Hotelling discriminant uses ensemble means and covariances and the Fisher discriminant uses sample means and covariances. In fact, the Fisher discriminant is almost never applicable to raw pixel values in images, since the dimension of the covariance matrix is M×M, where M is the number of pixels, and a sample covariance of this size would be invertible only if the number of sample images were greater than M — 1, which is very difficult to achieve. As we shall see in detail in Section 5, however, it is indeed possible to estimate and invert the ensemble covariance used by the Hotelling observer.

A figure of merit for the Hotelling observer is the Hotelling SNR, sometimes called the Hotelling trace; it is given by

$$\begin{array}{cc}\hfill {\mathrm{SNR}}_{\mathrm{Hot}}^2& \equiv [{\overline{\overline{\mathbf{g}}}}_1-{\overline{\overline{\mathbf{g}}}}_0{]}^{\mathrm{t}}{\mathbf{K}}_{\mathrm{av}}^{-1}[{\overline{\overline{\mathbf{g}}}}_1-{\overline{\overline{\mathbf{g}}}}_0]\hfill \\ \hfill & =\mathrm{tr}\left\{{\mathbf{K}}_{\mathrm{av}}^{-1}\right[{\overline{\overline{\mathbf{g}}}}_1-{\overline{\overline{\mathbf{g}}}}_0\left]\right[{\overline{\overline{\mathbf{g}}}}_1-{\overline{\overline{\mathbf{g}}}}_0{]}^{\mathrm{t}}\},\hfill \end{array}$$ (2.18)

where tr{·} denotes the trace (sum of the diagonal elements) of the matrix.

Often the Hotelling observer is applied not to the raw data but to a data set of reduced dimensionality obtained by passing g through a set of linear filters; in this case it is referred to as the channelized Hotelling observer (CHO). The channels can be chosen to preserve the class separability or to construct an observer that accurately predicts the performance of human observers as measured by psychophysical studies. For a thorough review of the CHO and its many successful applications in medical imaging, see Barrett and Myers.¹

3. Detection of Signals at Random Locations

When the signal location is random, the ideal decision strategy in Gaussian measurement noise is to subtract the mean background contribution at each pixel (assumed known), perform a prewhitening matched filter operation for each possible signal location, and exponentiate.^21,22 The output of these operations is averaged over all possible locations of the signal to determine the ideal observer’s decision variable. A comparison with a threshold is then done to render a decision as to whether or not the signal is present in the scene. No location information is provided by this observer when the decision is made.

The Hotelling formalism allows signals to be random but runs into difficulty when the signal can be at a random location. If all locations in the field of view are equally probable, the mean difference image ${\overline{\overline{\mathbf{g}}}}_1-{\overline{\overline{\mathbf{g}}}}_0$ is a constant and the linear test statistic (2.17) conveys little information. In fact, no linear observer will perform well in this situation. Nevertheless, as we shall see, the Hotelling framework can still be quite useful in the presence of signal-location uncertainty.

If the only randomness in the signal is its location, it is natural to consider a linear detection strategy that applies a prewhitening matched filter to each of the possible signal locations. Typically, the location that gives the largest Hotelling test statistic is chosen as the tentative location of a signal, and that test statistic is compared with a threshold to decide between signal-present and signal-absent at that location. The operation of finding the maximum is nonlinear, so the overall operation is nonlinear.

If the inverse covariance is the same for each signal location, it can be precomputed and used for each location. Moreover, if the signal is large relative to a pixel, so that its image is approximately shift-invariant, there is no need to recompute the mean data vector for each possible location either. Then, for a signal with uniform location uncertainty, the ideal linear approach becomes one of scanning the prewhitening matched filter over the field of view, and the observer is referred to as a scanning Hotelling observer.²³

When the image of the signal is location-dependent, the Hotelling framework can be further generalized to incorporate this information into the observer’s template at each signal location under test. This will be the case, for example, when the pixel size is large relative to the signal. Samson et al.¹⁶ investigated the problem of point-target detection when the image is comparable in size with a pixel and randomly located with respect to the pixel. Of course, other forms of signal randomness can be incorporated into the Hotelling formalism by the requisite adjustment in the expected data at each location.

There are several advantages to the Hotelling formalism over computation of the ideal observer’s test statistic in the location-uncertain task. The addition of a scanning mechanism to the Hotelling formalism yields a test statistic that is easily computed. Moreover, it was shown by Nolte and Jaarsma²¹ that the scanning Hotelling observer achieves a performance level that is nearly ideal in certain regimes, specifically ones in which the signal is equally likely at all locations and the noise variance is small. In addition, the scanning operation results in a determination of the signal’s location along with a test statistic for the detection task.

A useful way to characterize the performance on the joint detection—localization problem is with a localization ROC (LROC) curve,²⁴ which is a plot of the probability of detection and correct localization versus the false-alarm rate; the figure of merit for this task is the area under the LROC curve. If only the probability of detection is of interest, area under the conventional ROC curve (AUC) can be used, even with the scanning strategy. In many cases the area under the LROC correlates well with the AUC for a signal at a fixed location as various system parameters are varied.²⁵ For a discussion of observer strategies that maximize the area under the LROC curve, see Khurd and Gindi.²⁶

4. Estimation Tasks

In a pure estimation task, an object of interest is known to be present, but we wish to determine numerical values for parameters that describe the object. We assemble these parameters into a vector θ(f), and the relevant likelihood is denoted pr(g|θ). An estimate of θ is denoted $\widehat{\theta }$. The bias and variance of $\widehat{\theta }$, often combined into a mean square error (MSE), are conventional figures of merit for the estimation task.

There is a well-known lower bound, called the Cramér—Rao bound, on the variance of any estimator.^14,15 An unbiased estimator that achieves the bound is said to be efficient. An efficient estimator can be regarded as the ideal observer for an estimation problem, but in many problems no efficient estimator exists. A practical alternative is the maximum-likelihood (ML) estimator, which chooses the value of θ(f) that maximizes pr(g|θ) for the observed g. An ML estimator is efficient if an efficient estimator exists, and it is asymptotically efficient as more or better data are acquired.

Another alternative is an ideal linear estimator, which computes a linear (or affine) functional of the data. A linear estimator is ideal if the bias is zero and the variance is as small as possible. Different forms of the ideal linear estimator use different degrees of prior information and different ways of computing the variance, but a useful one to highlight for this discussion is the generalized Wiener estimator. This estimator is unbiased in a global sense (the average of $\widehat{\theta }$ over all data g and over a prior distribution of θ is equal to the prior mean $\overline{\theta }$), and it minimizes the ensemble mean square error (EMSE) defined in the same global sense. For doubly stochastic data, this estimator is given by²⁷

$$\widehat{\theta }=\overline{\theta }+{\mathbf{K}}_{\theta ,\mathbf{g}}{\mathbf{K}}_{\mathbf{g}}^{-1}[\mathbf{g}-\overline{\overline{\mathbf{g}}}],$$ (2.19)

where K_g is the overall (doubly stochastic) covariance matrix of g and K_θ,g is the cross-covariance of θ and the data. The optimal EMSE that results from this estimator is given by

$$\mathrm{EMSE}=\mathrm{tr}{\mathbf{K}}_{\theta }-\mathrm{tr}{\mathbf{K}}_{\theta ,\mathbf{g}}{\mathbf{K}}_{\mathbf{g}}^{-1}{\mathbf{K}}_{\theta ,\mathbf{g}}^{\mathrm{t}}.$$ (2.20)

The generalized Wiener estimator is the counterpart of the Hotelling observer in two respects: Both use prior knowledge of an ensemble of objects, and both form their output by a linear operation on prewhitened data [cf. Eqs. (2.17) and (2.19)]. For both, it is necessary to determine the overall data covariance and to be able to invert it.

3. STATISTICAL ANALYSIS OF ADAPTIVE OPTICS SYSTEMS

A generic AO system viewing an astronomical scene through a turbulent atmosphere is shown in Fig. 1. The astronomical scene consists of the object being studied (the science object), a reference object, which may consist of one or more natural or laser guide stars, and a background, defined as everything else in the field of view of the science camera. In some cases the reference object may be part of the science object, as when the task is to detect a faint companion around a known star, which then also functions as the guide star.

Fig. 1.

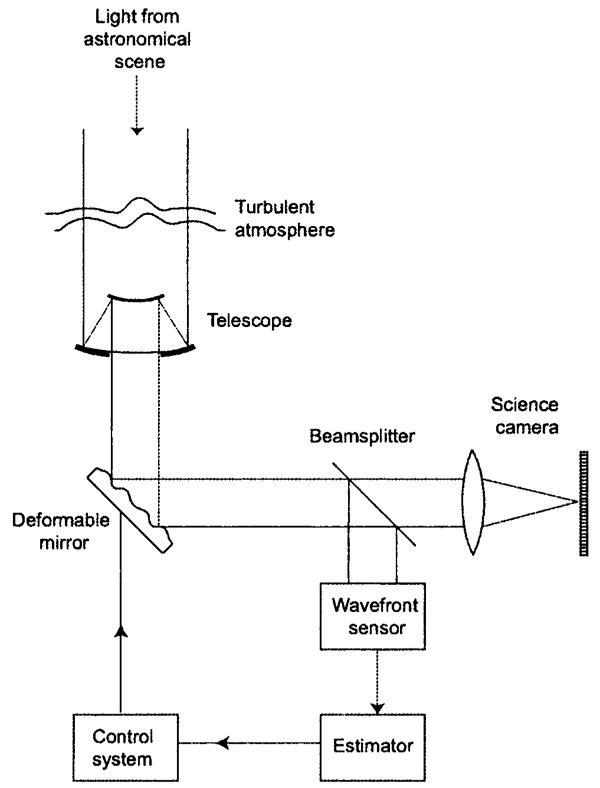
Illustration of an adaptive optics system.

Light passing through the telescope is reflected from a deformable mirror before being relayed to the science camera, which records the final image (or images) of the scene. Part of the light emerging from the deformable mirror is diverted by a beam splitter to a wavefront sensor in order to acquire information about the distorted wavefront. An estimator converts the output of the wavefront sensor to estimates of wavefront parameters, and a control system converts these estimates into control signals to be applied to the deformable mirror. Ideally, the control signals would produce a mirror deformation equal and opposite to the wavefront distortions produced by the atmosphere, and an uncorrupted image would be passed on to the science camera.

The wavefront sensor and estimator are often treated as a single element in the literature; a wavefront sensor in that view is a subsystem that delivers estimates of parameters such as local wavefront tilts. We shall find it convenient, however, to separate these two boxes as in Fig. 1. The wavefront sensor box might, for example, include a lenslet array and an image detector in a Shack—Hartmann configuration, and the estimator box could include computation of image centroids to get the tilts for each lenslet aperture. One reason for showing the estimator box separately is that sophisticated ML methods can also be used for going from the detector output in the sensor to estimates of wavefront parameters.²⁸ These methods are based on accurate statistical models, and they permit estimation of parameters other than simple tilts.

The control system uses the estimated wavefront parameters, sometimes for several consecutive frames of data, to derive the signals to be applied to the actuators in the deformable mirror. The control system is often referred to as a wavefront reconstructor since it is conceptualized as a two-step process, first reconstructing (estimating) the entire wavefront from tilts or other sensor data, then deriving the control signals from the reconstruction. As a black box, however, it just transforms the wavefront parameter estimates to control signals. Usually the transformation is implemented as a matrix multiplication.

Various random processes affect the statistics of the data from the science camera. The most obvious source of randomness is the photon or electronic noise associated with detection of the image by the science camera. The atmosphere would not be a source of randomness if the AO system were perfect, but it is not for several reasons. First, a deformable mirror with a finite number of actuators cannot exactly match a continuous wavefront even if the latter is known perfectly; second, the wavefront sensor itself measures only a finite number of parameters of the wavefront; and third, this measurement is degraded by photon or electronic noise in the sensor. Finally, there is always a temporal delay between measuring the wavefront and applying the correction. For all of these reasons, the corrected wavefront is imperfect and noisy, and the point spread function (PSF) in the main imaging path between the astronomical scene and the science camera is random.

Moreover, as discussed in Section 2, objects being imaged are themselves random. The astronomical scene will usually include some unknown background that has to be treated as a random process, and a laser guide star is random because of laser fluctuations and variable characteristics of the atmospheric layer from which the laser light is scattered. Even the science object can have random parameters; a faint companion, for example, can be at an unknown location and have unknown brightness.

The goal of this section is to analyze the statistical properties of this AO system without saying much about specific implementations and without making very many restrictive assumptions. Emphasis will be on determining the covariance properties of the images, since, as we saw in Subsections 2.C and 2.D, several important figures of merit for task performance can be computed from covariance matrices without knowledge of the full PDF. The results from this section will be related to task performance in Section 4.

A. Notation and Assumptions

1. Science Data

Because our goal is to characterize the statistics of the data from the science camera, we begin by establishing the notation for those data. Suppose that a sequence of J discrete frames of data is acquired, and each frame consists of the outputs of M detector pixels. An individual measurement (one pixel in one frame) can be denoted $g_m^{\left(j\right)}$, where j = 1, … ,J and m = 1, … ,M. The set {gm(j), m=1, ,M} for fixed j is the M × 1 vector g^(j), and the set {g^(j), j=1, … ,J} is the complete data set from the science camera, denoted G.

The object being imaged is denoted as f(r,t), where r is a 2D vector of x—y coordinates in the telescope focal plane; angular coordinates of the astronomical object are found by dividing x and y by the focal length of the telescope.

The relation between object and mean image is assumed to be linear as in Eq. (2.1). With the extra index for frame number and with r=(x,y,t) and r=(x,y), Eq. (2.1) becomes

$${\overline{g}}_m^{\left(j\right)}={\int }_{\infty }{\mathrm{d}}^{2}r{\int }_{-\infty }^{\infty }\mathrm{d}t{h}_m^{\left(j\right)}(\mathbf{r},t)f(\mathbf{r},t),m=1,\dots ,M,j=1,\dots ,J,$$ (3.1)

where the overbar in this case denotes an average with respect to the conditional PDF $\mathrm{pr}[g_m^{\left(j\right)}\mid h_m^{\left(j\right)}(\mathbf{r},t),f(\mathbf{r},t\left)\right]$. Note that linearity in this sense holds even if the PSF is derived from the object, since the average implied by the overbar is conditional on a specified PSF.

Both the object f(r,t) and the kernel $h_m^{\left(j\right)}(\mathbf{r},t)$ are spatiotemporal random processes. The kernel is related to the incoherent PSF of the main imaging path (atmosphere, telescope, deformable mirror, science camera) by

$$h_m^{\left(j\right)}(\mathbf{r},t)=\mathrm{rect}\left[\frac{t-t_j-\frac{1}{2}T}{T}\right]\int {\mathrm{d}}^2{r}_d{d}_m\left({\mathbf{r}}_d\right)p({\mathbf{r}}_d,\mathbf{r},t),$$ (3.2)

where the jth frame extends from time t_j to t_j+T, d_m(r) describes the response of the mth detector pixel, and p(r_d,r,t) is the time-dependent incoherent PSF of the main path, with the variable r_d denoting position in the detector plane. Note that the PSF is not assumed to be shift-invariant (isoplanatic).

With Eq. (3.2), the linear imaging relation in Eq. (3.1) can be written in detail as

$${\overline{g}}_m^{\left(j\right)}=\int {\mathrm{d}}^2{r}_d{d}_m\left({\mathbf{r}}_d\right){\int }_{t_j}^{t_j+T}\mathrm{d}t\int {\mathrm{d}}^{2}rp({\mathbf{r}}_d,\mathbf{r},t)f(\mathbf{r},t).$$ (3.3)

In words, the noiseless incoherent image of a particular object through a particular PSF is integrated over the frame time and the pixel area to get ${\overline{\mathtt{g}}}_m^{\left(j\right)}$.

We shall assume that the object is a slowly varying function of time, essentially constant over one frame of the science camera, in which case Eq. (3.3) becomes

$${\overline{g}}_m^{\left(j\right)}={\int }_{\infty }{\mathrm{d}}^{2}r{h}_m^{\left(j\right)}\left(\mathbf{r}\right)f^{\left(j\right)}\left(\mathbf{r}\right),m=1,\dots ,M,j=1,\dots ,J,$$ (3.4)

where f^(j)(r)=f(r,t_j

$$h_m^{\left(j\right)}\left(\mathbf{r}\right)=\int {\mathrm{d}}^2{r}_d{d}_m\left({\mathbf{r}}_d\right)p^{\left(j\right)}({\mathbf{r}}_d,\mathbf{r}),$$ (3.5)

$$p^{\left(j\right)}({\mathbf{r}}_d,\mathbf{r})={\int }_{t_j}^{t_j+T}\mathrm{d}tp({\mathbf{r}}_d,\mathbf{r},t).$$ (3.6)

A useful abstract notation analogous to Eq. (2.2) is

$$\overline{\mathbf{G}}={\mathcal{H}}_s\mathbf{F},$$ (3.7)

where ${\mathcal{H}}_s$ is a linear operator mapping the object sequence F, which is the set of all f^(j)(r), to a sequence of digital images, with the jth image in the sequence determined by the kernel $h_m^{\left(j\right)}\left(\mathbf{r}\right)$. The operator ${\mathcal{H}}_s$ is random, since the PSF p(r_d, r,t) and hence the kernel $h_m^{\left(j\right)}\left(\mathbf{r}\right)$ is random.

To summarize the notation for the main imaging path, the science camera produces an image sequence G, where $\overline{\mathbf{G}}$ (the average of G over only the measurement noise in the science camera) is related to the object F by a random operator ${\mathcal{H}}_s$, the properties of which are determined by the set P of random incoherent PSFs, each of which has been temporally averaged over a frame.

2. Control Loop

The control loop comprises the wavefront sensor, estimator, control system, and deformable mirror. The detector on the wavefront sensor consists of L pixels, and it observes the wavefront for a time T’, not necessarily the same as the frame time for the science camera. After the kth frame, the detector on the wavefront sensor produces a set of signals, $\{v_l^{\left(k\right)},l=1,\dots ,L\}$, or equivalently an L × 1 data vector v^(k); the whole set of $\{{\mathbf{v}}^{\left(k\right)},k=1,\dots ,K\}$ is denoted V. The total time duration for wavefront sensing is the same as for data acquisition with the science camera, so KT’=JT.

The estimator uses the vector of sensor signals for one frame, v^(k), and produces estimates of wavefront parameters for that frame, ${\widehat{\tau }}^{\left(k\right)}$, which might, for example, be tilts over the subapertures in a Shack—Hartmann sensor. The control system takes estimates of wavefront parameters for previous frames, ${\widehat{\tau }}^{(k-1)},{\widehat{\tau }}^{(k-2)},\dots$, and computes drive voltages to apply to the N actuators of the deformable mirror on the current frame; for reasons that will become clear, we denote these signals as ${\widehat{\alpha }}_n^{\left(k\right)}$ or as the N × 1 vector ${\widehat{\alpha }}^{\left(k\right)}$

We assume that the control system is linear and that it makes use of the output of the estimator for the K₀ frames preceding the current one. Thus its input—output relation can be written in matrix—vector form as

$${\widehat{\alpha }}^{\left(k\right)}=\sum _{k\prime =1}^{K_0}{\mathbf{M}}^{(k\prime )}{\widehat{\tau }}^{(k-k\prime )},$$ (3.8)

where ${\mathbf{M}}^{(k\prime )}$ is the control matrix for a lag of k′ frames. This matrix might be derived by considering some algorithm for wavefront reconstruction and then estimating ${\widehat{\alpha }}^{\left(k\right)}$ from the reconstruction, but if these steps are linear, their effect can be included in the control matrix.

3. Mirror and Atmosphere

The wavefront perturbation produced by the deformable mirror is assumed to be a linear combination of influence functions $\left\{\psi \right(\mathbf{r}),n=1,\dots ,N\}$, where N is the number of actuators. If the deformable mirror is in a plane conjugate to the telescope pupil and the voltage ${\widehat{\alpha }}_n^{\left(k\right)}$ is applied to the nth actuator during frame k of the control loop, then the effect of the mirror on the wavefront is represented as

$$W_{\mathrm{DM}}^{\left(k\right)}(\mathbf{r}\prime )=\sum _{n=1}^N{\widehat{\alpha }}_n^{\left(k\right)}{\psi }_n(\mathbf{r}\prime ),$$ (3.9)

where r’ denotes a point in the pupil.

To use the same representation for the mirror and the atmosphere, we expand the atmospheric wavefront as a sum of influence functions plus a residual. For a monochromatic point source that would image to point r₀ in the image plane in the absence of aberrations, we express the actual wavefront in the pupil as

$$W_{\mathrm{atm}}(\mathbf{r}\prime ,t;{\mathbf{r}}_0)=\sum _{n=1}^N{\alpha }_n(t;{\mathbf{r}}_0){\psi }_n(\mathbf{r}\prime )+\Delta W_{\mathrm{atm}}(\mathbf{r}\prime ,t;{\mathbf{r}}_0),$$ (3.10)

where the sum is the least-squares fit of $W_{\mathrm{atm}}(\mathbf{r}\prime ,t;{\mathbf{r}}_0)$ by the set of influence functions, and the residual $\Delta W_{atm}(\mathbf{r}\prime ,t;{\mathbf{r}}_0)$ is the portion of the wavefront that cannot be corrected by the deformable mirror.

The corrected wavefront emerging from the mirror is thus given by

$$\begin{array}{cc}\hfill W(\mathbf{r}\prime ,t;{\mathbf{r}}_0)& =W_{\mathrm{atm}}(\mathbf{r}\prime ,t;{\mathbf{r}}_0)-W_{\mathit{DM}}^{\left(k\right)}(\mathbf{r}\prime )\hfill \\ \hfill & =\sum _{n=1}^N[{\alpha }_n(t;{\mathbf{r}}_0)-{\widehat{\alpha }}_n^{\left(k\right)}]{\psi }_n(\mathbf{r}\prime )+\Delta W_{atm}(\mathbf{r}\prime ,t;{\mathbf{r}}_0),\hfill \\ \hfill & kT\prime \le t<(k+1)T\prime .\hfill \end{array}$$ (3.11)

If α_n(t;r₀) is approximately constant over the frame period and well approximated by ${\widehat{\alpha }}_n^{\left(k\right)}$, then the wavefront is compensated as closely as it can be with the given mirror; hence the notation ${\widehat{\alpha }}_n^{\left(k\right)}$ for the mirror drive voltages. Note, however, that the actual α_n(t;r₀) is a function of the continuous time variable while ${\widehat{\alpha }}_n^{\left(k\right)}$ is a constant during one frame of the control loop.

4. Random Point Spread Functions

The relation of the PSF to the pupil function of the imaging system is well-known. For quasimonochromatic light of wavelength λ and a point object at r₀ (in image-plane coordinates), we can define an effective pupil function by

$$a_{\mathrm{pup}}(\mathbf{r}\prime ,t;{\mathbf{r}}_0)=a_{\mathrm{ap}}(\mathbf{r}\prime )\exp \left[\mathrm{i}\frac{2\pi }{\lambda }W(\mathbf{r}\prime ,t;{\mathbf{r}}_0)\right],$$ (3.12)

where again r’ specifies location in the pupil, a_ap(r’) is a binary (0–1) function describing the clear aperture of the pupil, and $(2\pi ∕\lambda )W(\mathbf{r}\prime ,t;{\mathbf{r}}_0)$ is the phase distortion for an object at r₀ (in image-plane coordinates).

The anisoplanatic coherent PSF is a scaled Fourier transform of the pupil function, given by

$$\begin{array}{cc}\hfill p_{\mathrm{coh}}({\mathbf{r}}_d,{\mathbf{r}}_0,t)\propto & {\int }_{\infty }{\mathrm{d}}^{2}r\prime a_{\mathrm{ap}}(\mathbf{r}\prime )\exp \left[\mathrm{i}\frac{2\pi }{\lambda }W(\mathbf{r}\prime ,t;{\mathbf{r}}_0)\right]\hfill \\ \hfill & \times \exp \left[\mathrm{i}\frac{2\pi }{\lambda f}({\mathbf{r}}_d-{\mathbf{r}}_0)\cdot \mathbf{r}\prime \right],\hfill \end{array}$$ (3.13)

where f is the back focal length of the science camera. The incoherent PSF is proportional to the squared modulus of the coherent one, and the effective PSF for the jth frame is given from Eq. (3.6) as

$$p^{\left(j\right)}({\mathbf{r}}_d,{\mathbf{r}}_0)=C{\int }_{t_j}^{t_j+T}\mathrm{d}t\mid p_{\mathrm{coh}}({\mathbf{r}}_d,{\mathbf{r}}_0,t){\mid }^2,$$ (3.14)

where the constant C and the units of f(r₀) are chosen so that ${\overline{\mathtt{g}}}_m^{\left(j\right)}$ is the mean number of photons detected by pixel m during frame j. If the atmosphere and deformable mirror could be modeled jointly as a thin phase screen in the pupil, $W(\mathbf{r}\prime ,t;{\mathbf{r}}_0)$ would be independent of the object coordinate r₀ and the system would be isoplanatic.

For simplicity we drop the subscript on r₀ in what follows. Moreover, the PSF p^(j)(r_d,r) will be denoted as p^(j) for short, and the set of all p^(j) for j=1, … ,J will be denoted by P.

5. Speckle

We can usually assume that the control loop works well enough that the corrected phase excursions are small, so that relation (3.13) can be approximated as

$$\begin{array}{cc}\hfill p_{\mathrm{coh}}({\mathbf{r}}_d,\mathbf{r},t)\propto & {\int }_{\infty }{\mathrm{d}}^{2}r\prime a_{\mathrm{ap}}(\mathbf{r}\prime )[1+\mathrm{i}\varphi (\mathbf{r}\prime ,t;\mathbf{r})-\frac{1}{2}{\varphi }^2(\mathbf{r}\prime ,t;\mathbf{r}\left)\right]\hfill \\ \hfill & \times \exp \left[\mathrm{i}\frac{2\varphi }{\lambda f}({\mathbf{r}}_d-\mathbf{r})\cdot \mathbf{r}\prime \right],\hfill \end{array}$$ (3.15)

where $\varphi (\mathbf{r}\prime ,t;\mathbf{r})\equiv (2\lambda ∕\gamma )W(\mathbf{r}\prime ,t;\mathbf{r})$. The form in relation (3.15) is general enough to describe weak atmospheric scintillation if $\varphi (\mathbf{r}\prime ,t;\mathbf{r})$ is allowed to be complex.

The Fourier integral in relation (3.15) can be written as

$$\begin{array}{cc}\hfill {\int }_{\infty }& {\mathrm{d}}^{2}r\prime a_{\mathrm{ap}}(\mathbf{r}\prime )[1+\mathrm{i}\varphi (\mathbf{r}\prime ,t;\mathbf{r})-\frac{1}{2}{\varphi }^2(\mathbf{r}\prime ,t;\mathbf{r}\left)\right]\exp (2\pi \mathrm{i}\rho \cdot \mathbf{r}\prime )\hfill \\ \hfill & =A_{\mathrm{ap}}\left(\rho \right)+\mathrm{i}[A_{\mathrm{ap}}\ast \Phi ]\left(\rho \right)-\frac{1}{2}[A_{\mathrm{ap}}\ast \Phi \ast \Phi ]\left(\rho \right),\hfill \end{array}$$ (3.16)

where $\rho \equiv ({\mathbf{r}}_d-\mathbf{r})∕\lambda f$ is a 2D spatial frequency (measured in cycles per unit length in the focal plane of the science camera), $A_{\mathrm{ap}}\left(\rho \right)$ and $\Phi (\rho ,t;\mathbf{r})$ are, respectively, the 2D Fourier transforms of $a_{\mathrm{ap}}(\mathbf{r}\prime )$ and $\varphi (\mathbf{r}\prime ,t;\mathbf{r})$ with respect to the pupil coordinate r’, and the asterisk denotes convolution.

From Eq. (3.14), the effective incoherent PSF for the jth frame is given to second order in $\Phi (\rho ,t;\mathbf{r})$ by

$$\begin{array}{cc}\hfill p^{\left(j\right)}({\mathbf{r}}_d,\mathbf{r})& =C{\int }_{t_j}^{t_j+T}\mathrm{d}t\mid p_{\mathrm{coh}}({\mathbf{r}}_d,\mathbf{r},t){\mid }^2\hfill \\ \hfill & =C{\int }_{t_j}^{t_j+T}\mathrm{d}t\{\mid A_{\mathrm{ap}}{\mid }^2+\mid [A_{\mathrm{ap}}\ast \Phi ]{\mid }^2\hfill \\ \hfill & -\mathrm{Re}\left[A_{\mathrm{ap}}^{\ast }\right(A_{\mathrm{ap}}\ast \Phi \ast \Phi \left)\right]\hfill \\ \hfill & -2\mathrm{Im}\left[A_{\mathrm{ap}}^{\ast }\right(A_{\mathrm{ap}}\ast \Phi \left)\right]{\}}_{\rho =({\mathbf{r}}_d-\mathbf{r})∕\lambda f,}\hfill \end{array}$$ (3.17)

where the arguments in the integrand have been omitted for clarity.

The randomness in this PSF stems from the three random processes evident in Eq. (3.11), namely the atmospheric coefficients α_n(t;r), the control signals ${\widehat{\alpha }}_n^{\left(k\right)}$, and the uncorrectable part of the atmospheric turbulence, $\Delta W_{\mathrm{atm}}(\mathbf{r}\prime ,t;\mathbf{r})$. The resulting PSF can be regarded as a speckle pattern produced by the weak residual phase variations across the pupil. The last two terms in Eq. (3.17) show that this speckle pattern is modulated or “pinned” by the Airy rings of the ideal PSF (proportional to A_ap). Pinned speckle in AO has been studied by several authors,^29–32 but usually in the context of univariate statistics such as variance and PDF at a single point. In Section 5 we shall see how to obtain the covariance properties needed for objective assessment of image quality with linear observers.

6. Random Objects

We have already denoted the temporal sequence of astronomical scenes as F, and it will also be useful to decompose an astronomical scene into science object, guide star, and background (everything else), so that

$$\mathbf{F}={\mathbf{F}}_{\mathrm{sci}}+{\mathbf{F}}_{\mathrm{gs}}+{\mathbf{F}}_{\mathrm{bg}}.$$ (3.18)

The three components are random for different reasons and require different stochastic descriptions. If the task is detection of a faint star, the science object can be modeled as a point source of unknown location and brightness, so it is described fully by a three-dimensional PDF on these parameters. A natural guide star is at a known location and its brightness can be measured independently, so it is not random at all. A laser guide star is random because of variations in laser intensity and fluctuations in the distribution of atmospheric molecules being excited.

The background term could describe a complicated star field, modeled as a random point process,¹ or it could refer to the thermal sky background in the far infrared, which bears a striking similarity to the lumpy backgrounds used to model medical images. Even if the background is spatially uniform, it has to be treated as a random process since the background brightness is unknown and possibly time-varying.

B. Triply Stochastic Averaging

In this subsection we generalize the doubly stochastic averaging process introduced in Subsection 2.B in two ways: We add a third source of randomness (the random PSF), and we consider a sequence of correlated images. We begin by developing a general formalism of nested averages over the three main sources of randomness, and then we apply it to calculation of the mean vectors and covariance matrices of the science-camera data. As we know from Section 2, these quantities are important determinants of image quality for both classification and estimation tasks.

1. Nested Probability Density Functions

Let T(G) denote an arbitrary (possibly vector-valued) function of the image sequence G. An overall average of this function is given formally by

$$\begin{array}{cc}\hfill \overline{\overline{\overline{\mathbf{T}\left(\mathbf{G}\right)}}}& ={\langle {\langle \langle \mathbf{T}\left(\mathbf{G}\right){\rangle }_{\mathbf{G}\mid \mathbf{P},\mathbf{F}}\rangle }_{\mathbf{P}\mid \mathbf{F}}\rangle }_{\mathbf{F}}\hfill \\ \hfill & =\int \mathrm{d}\mathbf{F}\int \mathrm{d}\mathbf{P}\int \mathrm{d}\mathbf{G}\mathbf{T}\left(\mathbf{G}\right)\mathrm{pr}(\mathbf{G}\mid \mathbf{P},\mathbf{F})\mathrm{pr}(\mathbf{P}\mid \mathbf{F})\mathrm{pr}\left(\mathbf{F}\right).\hfill \end{array}$$ (3.19)

Consider first the inner average, over G given P and F. Since the PSF and the object are fixed by the conditional PDF, the only remaining randomness in this average is the measurement noise of the science camera. Since different photons are detected in different frames and the frame time is far larger than any electronic correlation time, we can write

$$\mathrm{pr}(\mathbf{G}\mid \mathbf{P},\mathbf{f})=\prod _{j=1}^J\mathrm{pr}({\mathbf{g}}^{\left(j\right)}\mid {\mathbf{P}}^{\left(j\right)},{\mathbf{f}}^{\left(j\right)}).$$ (3.20)

Moreover, the measurement noise components in different detector pixels in the same frame are usually statistically independent (an exception sometimes occurs in detectors with built-in gain²⁸), in which case

$$\mathrm{pr}({\mathbf{g}}^{\left(j\right)}\mid {\mathbf{P}}^{\left(j\right)},{\mathbf{f}}^{\left(j\right)})=\prod _{m=1}^M\mathrm{pr}(g_m^{\left(j\right)}\mid {\mathbf{P}}^{\left(j\right)},{\mathbf{f}}^{\left(j\right)}).$$ (3.21)

Finally, for pure electronic noise (but not for Poisson noise), we can assume that $\mathrm{pr}({\mathtt{g}}_m^{\left(j\right)}\mid {\mathbf{p}}^{\left(j\right)},{\mathbf{f}}^{\left(j\right)})=\mathrm{pr}\left({\mathtt{g}}_m^{\left(j\right)}\right)$, independent of the random PSF and the object. For Poisson noise, the statistics are determined by the mean, so $\mathrm{pr}({\mathtt{g}}_m^{\left(j\right)}\mid \mathbf{p},{\mathbf{f}}^{\left(j\right)})=\mathrm{pr}\left[{\overline{\mathtt{g}}}_m^{\left(j\right)}\right(\mathbf{p},{\mathbf{f}}^{\left(j\right)}\left)\right]$.

With the object decomposition (3.18), the second average, over the random PSFs P given the object sequence F, really involves pr(P|F_sci,F_bg,F_gs); different circumstances will permit different assumptions about this density. The greatest simplification is when the background and science object make a negligible contribution to the output of the wavefront sensor and when the guide star is nonrandom; in that case, pr(P|F)=pr(P). An intermediate case is that where the randomness of the guide star cannot be neglected, and then pr(P|F)=pr(P|F_gs). Finally, if the wavefront data are derived from the science object itself, we have to use pr(P|F) without simplification. We shall carry along the two extremes, a general pr(P|F) and an independent model, pr(P|F)=pr(P), in what follows.

Even if we assume that P is independent of F, however, it is generally not correct to assume that the PSFs for different science-camera frames, p^(j) and p^(j′) with j≠j′, are independent; temporal correlations are present because of the atmospheric correlation time and because the control system uses outputs of the wavefront sensor for multiple previous sensor frames to determine the drive signals to the mirror on the current sensor frame.

The final average in Eq. (3.19) is over the object variability, and in principle it requires a huge-dimensional PDF pr(F), or even several such PDFs for different hypotheses if we consider a classification task. In practice, however, the decomposition (3.18) suggests several simpler stochastic descriptions. It will often be valid, for example, to assume that the science object, background, and guide star are statistically independent, so pr(F) =pr(F_sci)pr(F_bg)pr(F_gs), and further assumptions can be applied to each factor. If the science object is independent of time, for example, pr(F_sci) reduces to pr(f_sci), where f denotes a single object rather than a sequence. Moreover, as discussed at the end of Subsection 3.B, pr(f_sci) might be a low-dimensional PDF on a few parameters of scientific interest. The background PDF pr(F_bg) is more difficult in general, but the figures of merit discussed here require only the mean object and a spatiotemporal autocovariance function. The guide-star PDF pr(F_gs) is trivial for a nonrandom natural guide star but more complicated for a laser guide star.

2. Means

To see how triply stochastic averaging works in a relatively simple case, let T(G) be a single datum $g_m^{\left(j\right)}$, the output of one detector pixel for one frame of data from the science camera. The statistics of $g_m^{\left(j\right)}$ depend on the incoherent PSF p^(j) and noise realization for frame j, and the noise can depend on the object for that frame in the case of Poisson noise. The PSF for frame j can, however, depend on the object (especially the guide star) for previous frames. The overall (triple-bar) average of this datum can thus be written most generally as

$${\overline{\overline{\overline{g}}}}_m^{\left(j\right)}={\langle {\langle \langle g_m^{\left(j\right)}{\rangle }_{{\mathtt{g}}_m^{\left(j\right)}\mid {\mathbf{p}}^{\left(j\right)},{\mathbf{f}}^{\left(j\right)}}\rangle }_{{\mathbf{p}}^{\left(j\right)}\mid \mathbf{F}}\rangle }_{\mathbf{F}}.$$ (3.22)

If we average over detector noise alone, then the single-bar average is given in component form directly from our assumption of conditional linearity, Eq. (3.7), by

$${\overline{g}}_m^{\left(j\right)}={\overline{g}}_m^{\left(j\right)}({\mathbf{p}}^{\left(j\right)},{\mathbf{f}}^{\left(j\right)})=\int {\mathrm{d}}^{2}r{h}_m^{\left(j\right)}\left(\mathbf{r}\right)f^{\left(j\right)}\left(\mathbf{r}\right),$$ (3.23)

where the PSF and object for frames other than the jth are irrelevant for this conditional average, conditioned on PSF and object.

The next average is over the random PSFs P given F. Since averaging is a linear operation that can be interchanged with integration under broad conditions (loosely speaking, so long as all integrals converge), it follows that

$${\overline{\overline{g}}}_m^{\left(j\right)}={\overline{\overline{g}}}_m^{\left(j\right)}\left({\mathbf{f}}^{\left(j\right)}\right)=\int {\mathrm{d}}^{2}r{\overline{h}}_m^{\left(j\right)}\left(\mathbf{r}\right)f^{\left(j\right)}\left(\mathbf{r}\right),$$ (3.24)

where the average kernel is related to the average incoherent PSF by [cf. Eq. (3.5)]

$${\overline{h}}_m^{\left(j\right)}\left(\mathbf{r}\right)=\int {\mathrm{d}}^2{r}_d{d}_m\left({\mathbf{r}}_d\right){\overline{p}}^{\left(j\right)}({\mathbf{r}}_d,\mathbf{r}).$$ (3.25)

If we assume that the PSF is temporally stationary and ergodic, the index j on ${\overline{p}}^{\left(j\right)}({\mathbf{r}}_d,\mathbf{r})$ and hence on ${\overline{h}}_m^{\left(j\right)}\left(\mathbf{r}\right)$ can be omitted. On the other hand, though the notation does not show it, ${\overline{p}}^{\left(j\right)}({\mathbf{r}}_d,\mathbf{r})$ can depend on the object sequence F and in particular on the guide star over multiple frames.

The final average, over the object variability, yields

$${\overline{\overline{\overline{g}}}}_m^{\left(j\right)}=\int {\mathrm{d}}^{2}r\langle {\overline{h}}_m^{\left(j\right)}\left(\mathbf{r}\right)f^{\left(j\right)}\left(\mathbf{r}\right){\rangle }_{\mathbf{F}}=\int {\mathrm{d}}^{2}r{\overline{h}}_m^{\left(j\right)}\left(\mathbf{r}\right){\overline{f}}^{\left(j\right)}\left(\mathbf{r}\right),$$ (3.26)

where the second form holds if p^(j) is independent of F.

Each of these component averages is the mth component of a corresponding M × 1 average vector; for example, ${\overline{\overline{g}}}^{\left(j\right)}$ is the mth component of ${\overline{\overline{\mathbf{G}}}}^{\left(j\right)}$. We shall also use overbars on the whole set G in a similar fashion. For example, $\overline{\overline{\mathbf{G}}}$ can be regarded as an MJ × 1 vector with the (m, j)th component given by ${\overline{\overline{g}}}_m^{\left(j\right)}$.

3. Covariance Matrices

By analogy to Eq. (2.9), the overall covariance matrix of a triply stochastic image sequence is defined as

$$\begin{array}{cc}\hfill {\mathbf{K}}_{\mathbf{G}}& \equiv {\langle \left[\mathbf{G}-\overline{\overline{\overline{\mathbf{G}}}}\right]{\left[\mathbf{G}-\overline{\overline{\overline{\mathbf{G}}}}\right]}^{\mathrm{t}}\rangle }_{\mathbf{G},\mathbf{P},\mathbf{F}}\hfill \\ \hfill & \equiv {\langle {\langle {\langle \left[\mathbf{G}-\overline{\overline{\overline{\mathbf{G}}}}\right]{\left[\mathbf{G}-\overline{\overline{\overline{\mathbf{G}}}}\right]}^{\mathrm{t}}\rangle }_{\mathbf{G}\mid \mathbf{P},\mathbf{F}}\rangle }_{\mathbf{P}\mid \mathbf{F}}\rangle }_{\mathbf{F}}.\hfill \end{array}$$ (3.27)

To be explicit, K_G is an MJ × MJ matrix with components given by [cf. Eq. (2.7)]

$$[{\mathbf{K}}_{\mathbf{G}}{]}_{\mathit{mm}\prime }^{(\mathit{jj}\prime )}={\langle {\langle {\langle \left[g_m^{\left(j\right)}-{\underset{g}{\equiv }}_m^{\left(j\right)}\right]\left[g_m^{(j\prime )}-{\underset{g}{\equiv }}_m^{(j\prime )}\right]\rangle }_{\mathbf{G}\mid \mathbf{P},\mathbf{F}}\rangle }_{\mathbf{P}\mid \mathbf{F}}\rangle }_{\mathbf{F}}.$$ (3.28)

Now, as in Eq. (2.10), add and subtract terms in each factor of Eq. (3.27):

$$\begin{array}{cc}\hfill {\mathbf{K}}_{\mathbf{G}}& =\langle \langle \langle [\mathbf{G}-\overline{\mathbf{G}}+\overline{\mathbf{G}}-\overline{\overline{\mathbf{G}}}+\overline{\overline{\mathbf{G}}}-\overline{\overline{\overline{\mathbf{G}}}}]\hfill \\ \hfill & \times [\mathbf{G}-\overline{\mathbf{G}}+\overline{\mathbf{G}}-\overline{\overline{\mathbf{G}}}+\overline{\overline{\mathbf{G}}}-\overline{\overline{\overline{\mathbf{G}}}}{]}^{\mathrm{t}}{\rangle }_{\mathbf{G}\mid \mathbf{P},\mathbf{F}}{\rangle }_{\mathbf{P}\mid \mathbf{F}}{\rangle }_{\mathbf{F}}.\hfill \end{array}$$ (3.29)

Even without any assumptions of independence, the cross covariance $\langle \langle \langle [\mathbf{G}-\overline{\mathbf{G}}][\overline{\mathbf{G}}-\overline{\overline{\mathbf{G}}}{]}^{\mathrm{t}}\rangle \rangle \rangle$ vanishes identically, just as it did in Eq. (2.10). A similar argument shows that $\langle \langle \langle [\overline{\mathbf{G}}-\overline{\overline{\mathbf{G}}}][\overline{\overline{\mathbf{G}}}-\overline{\overline{\overline{\mathbf{G}}}}{]}^{\mathrm{t}}\rangle \rangle \rangle$ also vanishes, and we can write

$${\mathbf{K}}_{\mathbf{G}}={\overline{\overline{\mathbf{K}}}}_{\mathbf{G}}^{\text{noise}}+{\overline{\mathbf{K}}}_{\overline{\mathbf{G}}}^{\mathrm{PSF}}+{\mathbf{K}}_{\overline{\overline{\mathbf{G}}}}^{\mathrm{obj}},$$ (3.30)

where

$${\overline{\overline{\mathbf{K}}}}_{\mathbf{G}}^{\text{noise}}\equiv {\langle {\langle {\langle \left[\mathbf{G}-\overline{\mathbf{G}}\right][\mathbf{G}-\overline{\mathbf{G}}{]}^{\mathrm{t}}\rangle }_{\mathbf{G}\mid \mathbf{P},\mathbf{F}}\rangle }_{\mathbf{P}\mid \mathbf{F}}\rangle }_{\mathbf{F}},$$ (3.31)

$${\overline{\mathbf{K}}}_{\overline{\mathbf{G}}}^{\mathrm{PSF}}\equiv {\langle {\langle \left[\overline{\mathbf{G}}-\overline{\overline{\mathbf{G}}}\right]{\left[\overline{\mathbf{G}}-\overline{\overline{\mathbf{G}}}\right]}^{\mathrm{t}}\rangle }_{\mathbf{P}\mid \mathbf{F}}\rangle }_{\mathbf{F}},$$ (3.32)

$${\mathbf{K}}_{\overline{\overline{\mathbf{G}}}}^{\mathrm{obj}}\equiv {\langle \left[\overline{\overline{\mathbf{G}}}-\overline{\overline{\overline{\mathbf{G}}}}\right]{\left[\overline{\overline{\mathbf{G}}}-\overline{\overline{\overline{\mathbf{G}}}}\right]}^{\mathrm{t}}\rangle }_{\mathbf{F}}.$$ (3.33)

Thus the overall covariance matrix for a triply stochastic image sequence can be rigorously decomposed into three terms representing, respectively, the contributions from measurement noise, from the random PSF, and from randomness in the object being imaged.

The first term, ${\overline{\overline{\mathbf{K}}}}_{\mathbf{G}}^{\text{noise}}$, comes from readout and Poisson noise, with at least the Poisson component averaged over P and F. With the noise modeled as in Eq. (3.21), we can write

$$[{\overline{\overline{\mathbf{K}}}}_{\mathbf{G}}^{\text{noise}}{]}_{\mathrm{mm}\prime }^{(\mathit{jj}\prime )}=[{\sigma }_m^2+{\underset{g}{\equiv }}_m^{\left(j\right)}]{\delta }_{\mathit{mm}\prime }{\delta }_{\mathit{jj}\prime }.$$ (3.34)

The second term, ${\overline{\mathbf{K}}}_{\overline{\mathbf{G}}}^{\mathrm{PSF}}$, is the contribution from the random PSF, averaged over the object class. If the AO system worked perfectly, this term would vanish since the PSF would not be random. Also, if the integration time of the science camera goes to infinity and the atmospheric statistics are ergodic, so that infinite time averages are the same as ensemble averages, then again the PSF term vanishes. With a real system and a finite integration time, this term describes the residual speckle pattern from the uncorrected part of the random atmospheric phase. In the most general case, it is given in component form by

$$\begin{array}{cc}\hfill [{\overline{\mathbf{K}}}_{\overline{\mathbf{G}}}^{\mathrm{PSF}}{]}_{\mathit{mm}\prime }^{(\mathit{jj}\prime )}& =\int {\mathrm{d}}^{2}r\int {\mathrm{d}}^{2}r\prime \langle \langle f^{\left(j\right)}\left(\mathbf{r}\right)f^{(j\prime )}(\mathbf{r}\prime )\left[h_m^{\left(j\right)}\left(\mathbf{r}\right)-{\overline{h}}_m^{\left(j\right)}\left(\mathbf{r}\right)\right]\hfill \\ \hfill & \times \left[h_{m\prime }^{(j\prime )}\right(\mathbf{r}\prime )-{\overline{h}}_{m\prime }^{(j\prime )}(\mathbf{r}\prime \left)\right]{\rangle }_{\mathbf{P}\mid \mathbf{F}}{\rangle }_{\mathbf{F}}.\hfill \end{array}$$ (3.35)

If P is independent of F, we obtain

$$\begin{array}{cc}\hfill [{\overline{\mathbf{K}}}_{\overline{\mathbf{G}}}^{\mathrm{PSF}}{]}_{\mathit{mm}\prime }^{(\mathit{jj}\prime )}& =\int {\mathrm{d}}^{2}r\int {\mathrm{d}}^{2}r\prime \langle f^{\left(j\right)}\left(\mathbf{r}\right)f^{(j\prime )}(\mathbf{r}\prime ){\rangle }_{\mathbf{F}}\langle \left[h_m^{\left(j\right)}\left(\mathbf{r}\right)-{\overline{h}}_m^{\left(j\right)}\left(\mathbf{r}\right)\right]\hfill \\ \hfill & \times \left[h_{m\prime }^{(j\prime )}(\mathbf{r}\prime )-{\overline{h}}_{m\prime }^{(j\prime )}(\mathbf{r}\prime )\right]{\rangle }_{\mathbf{P}}.\hfill \end{array}$$ (3.36)

One way to interpret Eq. (3.36) is to move the average over F outside the integral. The integral then represents the covariance of the sensitivity function as manifest in the data for a particular spatiotemporal object, and the result is averaged over objects.

The final term, ${\mathbf{K}}_{\overline{\overline{\mathbf{G}}}}^{\mathrm{obj}}$, is the contribution from object randomness. In the general case, it is given by

$$\begin{array}{cc}\hfill [{\mathbf{K}}_{\overline{\overline{\mathbf{G}}}}^{\mathrm{obj}}{]}_{\mathit{mm}\prime }^{(\mathit{jj}\prime )}& =\int {\mathrm{d}}^{2}r\int {\mathrm{d}}^{2}r\prime \langle \left[{\overline{h}}_m^{\left(j\right)}\right(\mathbf{r}\left)f^{\left(j\right)}\right(\mathbf{r})-\langle {\overline{h}}_m^{\left(j\right)}(\mathbf{r}\left)f^{\left(j\right)}\right(\mathbf{r}{\rangle }_{\mathbf{F}}]\hfill \\ \hfill & \times \left[{\overline{h}}_{m\prime }^{(j\prime )}(\mathbf{r}\prime )f^{(j\prime )}(\mathbf{r}\prime )-\langle {\overline{h}}_{m\prime }^{(j\prime )}(\mathbf{r}\prime )f^{(j\prime )}(\mathbf{r}\prime ){\rangle }_{\mathbf{F}}\right]{\rangle }_{\mathbf{F}}.\hfill \end{array}$$ (3.37)

If P is independent of F,we get

$$\begin{array}{cc}\hfill {\left[{\mathbf{K}}_{\overline{\overline{\mathbf{G}}}}^{\mathrm{obj}}\right]}_{\mathit{mm}\prime }^{(j,j\prime )}& =\int {\mathrm{d}}^{2}r\int {\mathrm{d}}^{2}r\prime {\overline{h}}_m^{\left(j\right)}\left(\mathbf{r}\right){\overline{h}}_{m\prime }^{(j\prime )}(\mathbf{r}\prime )\langle \left[f^{\left(j\right)}\right(\mathbf{r})-{\overline{f}}^{\left(j\right)}(\mathbf{r}\left)\right]\hfill \\ \hfill & \times \left[f^{(j\prime )}(\mathbf{r}\prime )-{\overline{f}}^{(j\prime )}(\mathbf{r}\prime )\right]{\rangle }_{\mathbf{F}}\hfill \\ \hfill & =\int {\mathrm{d}}^{2}r\int {\mathrm{d}}^{2}r\prime {\overline{h}}_m^{\left(j\right)}\left(\mathbf{r}\right){\overline{h}}_{m\prime }^{(j\prime )}(\mathbf{r}\prime )K_{\mathrm{f}}^{(j,j\prime )}(\mathbf{r},\mathbf{r}\prime ),\hfill \end{array}$$ (3.38)

where $K_{\mathbf{f}}^{(j,j\prime )}(\mathbf{r},\mathbf{r}\prime )$ is the spatiotemporal autocovariance function of the object, sampled at discrete time points:

$$\begin{array}{cc}\hfill {\mathit{K}}_{\mathbf{f}}^{(j,j\prime )}(\mathbf{r},\mathbf{r}\prime )& \equiv {\mathit{K}}_{\mathbf{f}}(\mathbf{r},\mathbf{r}\prime ,t,t\prime ){\mid }_{t=t_j,t\prime =t_{j\prime }}\hfill \\ \hfill & =\langle \left[f^{\left(j\right)}\left(\mathbf{r}\right)-{\overline{f}}^{\left(j\right)}\left(\mathbf{r}\right)\right]\left[f^{(j\prime )}(\mathbf{r}\prime )-{\overline{f}}^{(j\prime )}(\mathbf{r}\prime )\right]\rangle .\hfill \end{array}$$ (3.39)

The interpretation of Eq. (3.38) is that ${\mathbf{K}}_{\overline{\overline{\mathbf{G}}}}^{\mathrm{obj}}$ is the object autocovariance function mapped through the ensemble-average CD imaging system to the final image sequence from the science camera. Some useful analytic forms for the autocovariance function are given in Appendix A.

When P is independent of F, the object and PSF terms can usefully be combined. Adding Eqs. (3.36) and (3.38) and doing some algebra, we get

$$\begin{array}{cc}\hfill {\left[{\overline{\mathbf{K}}}_{\overline{\mathbf{G}}}^{\mathrm{PSF}}+{\mathbf{K}}_{\overline{\overline{\mathbf{G}}}}^{\mathrm{obj}}\right]}_{\mathit{mm}\prime }^{(j,j\prime )}& =\int {\mathrm{d}}^{2}r\int {\mathrm{d}}^{2}r\prime \left\{{\overline{f}}^{\left(j\right)}\right(\mathbf{r}\left){\overline{f}}^{(j\prime )}\right(\mathbf{r}\prime \left)\right[{\mathbf{K}}_{\mathbf{h}}{]}_{\mathit{mm}\prime }^{(j,j\prime )}(\mathbf{r},\mathbf{r}\prime )\hfill \\ \hfill & +{\overline{h}}_m^{\left(j\right)}\left(\mathbf{r}\right){\overline{h}}_{m\prime }^{(j\prime )}(\mathbf{r}\prime )K_{\mathrm{f}}^{(j,j\prime )}(\mathbf{r},\mathbf{r}\prime )\hfill \\ \hfill & +\left[{\mathbf{K}}_{\mathbf{h}}{]}_{\mathit{mm}\prime }^{(j,j\prime )}\right(\mathbf{r},\mathbf{r}\prime \left)K_{\mathrm{f}}^{(j,j\prime )}\right(\mathbf{r},\mathbf{r}\prime \left)\right\},\hfill \end{array}$$ (3.40)

where

$$\left[{\mathbf{K}}_{\mathbf{h}}{]}_{\mathit{mm}\prime }^{(j,j\prime )}\right(\mathbf{r},\mathbf{r}\prime )\equiv \langle [h_m^{\left(j\right)}\left(\mathbf{r}\right)-{\overline{h}}_m^{\left(j\right)}\left(\mathbf{r}\right)\left]\right[h_{m\prime }^{(j\prime )}(\mathbf{r}\prime )-{\overline{h}}_{m\prime }^{(j\prime )}(\mathbf{r}\prime )]{\rangle }_{\mathbf{P}}.$$ (3.41)

Now the PSF and object enter symmetrically into the overall covariance, reflecting the fact that we can do the averages over P and F in either order if they are independent. Note, however, that the autocovariance of the discretized PSF is more complicated than the object autocovariance since $h_m^{\left(j\right)}(\mathbf{r}$ depends on a pixel index m in addition to the spatial variable r and the discretized time index j.

Various special cases of Eqs. (3.36), (3.38), and (3.40) can be given. If the object is independent of time, as it often is in astronomy, the superscripts j and j’ can be omitted on $f(\cdot )$ everywhere and on K_f. On the other hand, if the object is temporally stationary, then $K_{\mathbf{f}}^{(j,j\prime )}(\mathbf{r},\mathbf{r}\prime )=K_{\mathbf{f}}^{(j-j\prime )}(\mathbf{r},\mathbf{r}\prime )$. Similarly, if the atmospheric statistics are temporally stationary, we can omit the superscript on ${\overline{h}}_m(\mathbf{r}$ and regard the average over P in Eq. (3.36) as a function of j—j’. To combine these cases, if the atmospheric statistics are temporally stationary and the object is either nonrandom, time-independent (but spatially random), or temporally stationary, then both the object and PSF terms depend on j—j’.

An important practical situation is that when the image detector in the science camera does not introduce pixel-to-pixel correlations, the object is independent of time, the atmospheric statistics are temporally stationary, and the PSF is independent of the object; if all of these conditions are satisfied, the overall covariance can be written in component form as

$${\left[{\mathbf{K}}_{\mathbf{G}}\right]}_{\mathit{mm}\prime }^{(j,j)}=\left[{\sigma }_m^2+{\overline{\overline{\overline{\mathbf{g}}}}}_m\right]{\delta }_{\mathit{mm}\prime }{\delta }_{\mathit{jj}\prime }+{\left[{\overline{\mathbf{K}}}_{\overline{\mathbf{G}}}^{\mathrm{PSF}}\right]}_{\mathit{mm}\prime }^{(j-j\prime )}+{\left[{\mathbf{K}}_{\overline{\overline{\mathbf{G}}}}^{\mathrm{obj}}\right]}_{\mathit{mm}\prime }.$$ (3.42)

4. TASK PERFORMANCE IN ASTRONOMICAL ADAPTIVE OPTICS

In this section we consider three important tasks that arise in astronomical imaging: detection of point objects on a random background, detection of faint companions such as exoplanets, and photometry. For each task, we briefly discuss how it is performed in current practice, and then we discuss statistically optimal approaches that make use of the formalism developed above. For each task, two distinct outcomes are obtained: expressions for task-based figures of merit for assessment of image quality and methods that might be useful for actually performing the tasks. Computational aspects are treated in Section 5.

A. Detection of Point Objects on a Random Background

The detection of point sources is an essential task in observational astronomy.³³ Increasing sensitivity to point sources permits detection of fainter objects up to a given distance or the detection of objects of a given luminosity at larger distances. Applications inside the solar system include the early detection of near-earth asteroids, as well as Kuiper-belt and other trans-Neptunian objects. In stellar astronomy, it is of interest to detect free-floating brown dwarfs and planets, which may make up a substantial fraction of the missing dark matter. Point-source detection is also relevant to the detection of extragalactic objects such as quasars or active galactic nuclei, which are unresolved even with the largest available apertures.

Point-source detection is strongly influenced by the background. A spatially uniform diffuse background creates Poisson noise that interferes with the ability of any observer to perform the detection, and spatial inhomogeneities as in galactic cirrus or dense unresolved star fields can cause spurious peaks that lead to false alarms in the detection task. Even isolated nearby stars can cause false alarms if their PSFs overlap the site of a potential detection; the effect of the PSF is random because the luminosity and precise location of the interfering star are random (or at least unknown to the observer) and the PSF itself is random because of noise in the wavefront sensor and uncorrected atmospheric effects.

1. Current Practice

The standard imaging practice in observational astronomy consists of obtaining one or several images of the object of interest, together with other images that are needed for the image processing. These include dark images, which are obtained with the shutter closed, and flat fields, which are obtained with uniform illumination on the sky or of a screen inside the telescope dome. The dark images reveal structure in the detector readout noise and are subtracted from the object frames. The flat fields are used to determine the detection sensitivity across the field of view. The dark image is subtracted from the flat field, and the object images are divided by the result. Median filters may be applied to sequences of dark images and flat fields to obtain smoother estimates.

The mean and variance of the sky background are usually estimated before source detection is attempted. This information may be obtained either from an image or sequence of images of a source-free field or by median filtering the actual image of the object. Variations of the sky background over the image may be estimated by dividing the image into regions called tiles and estimating the sky background in each tile by median filtering.

For observation at near-infrared wavelengths (as is the case for most current AO systems), the sky background is strong and variable. For broadband observations at wavelengths shorter than 2 μm, an important component of the background is dominated by emission from hydroxyl radicals in the ionosphere, which vary due to the passage of gravity waves.³⁴ Longward of 2 μm, the background is dominated by thermal emission from the sky and telescope. In the far infrared, background due to thermal emission from galactic dust clouds has a fractal-like spatial structure.³⁵

The thermal background from the telescope and sky is usually removed by chopping and nodding; chopping refers to rapidly interchanging the field of view on and off the object, usually by rocking the telescope secondary mirror at several hertz. However, the telescope background estimated from the off-object measurements will not be identical to the background at the object, so the telescope is moved periodically (nodded) so that the new off-object position corresponds to the previous on-object position. This process will introduce artifacts if there are objects present in the regions of interest or if the object is larger than the chop throw. Bertero et al.³⁶ describe a Fourier-based algorithm to restore nodded and chopped images that can remove these artifacts.

After the noise in the image is estimated, objects are usually detected by searching for pixels that are higher than the background by some amount, say three standard deviations. Extended objects are then detected by finding connected pixels that are significantly higher than the noise.³⁷ A more sophisticated approach involving wavelet transforms has been proposed³⁸ but does not seem to be standard practice.

2. Spatiotemporal Hotelling Observer

Though the current practice in astronomy certainly recognizes the importance of background in point-source detection, little attention has been given to optimal detection algorithms that incorporate information about the spatial and temporal correlations of the background or knowledge of the statistics of the random PSF. The Hotelling observer provides a rigorous framework for doing so.

In contrast to the purely spatial Hotelling observer described in Subsection 2.C, however, the Hotelling observer for astronomy should be spatiotemporal. The raw data in most astronomical observations are a sequence of frames from a CCD camera or other electronic detector, but these frames are almost always summed, after various corrections as described above, to get a single image that is used for the science task. There is no reason in principle to believe that this summation preserves the information content of the data, defined in terms of ability of an ideal observer to perform the task. If the task will be performed by a human observer, however, a long sequence of individual frames is of little use, so some form of summation is required. In what follows we discuss the optimal spatiotemporal Hotelling observer applied to an image sequence and show how it can be used to provide a single summed image for direct observation, without loss of information. Suboptimal summation methods are also discussed for comparison.

By analogy to Eq. (2.17), the Hotelling test statistic for a triply stochastic image sequence is

$$\begin{array}{cc}\hfill t_{\mathrm{Hot}}\left(\mathbf{G}\right)& ={\mathbf{W}}^t\mathbf{G}={\left[{\underset{\mathbf{G}}{\equiv }}_1-{\underset{\mathbf{G}}{\equiv }}_0\right]}^t{\mathbf{K}}_{\mathrm{av}}^{-1}\mathbf{G},\hfill \\ \hfill {\mathbf{K}}_{\mathrm{av}}& \equiv \frac{1}{2}[{\mathbf{K}}_{\mathrm{G}\mid H_1}+{\mathbf{K}}_{\mathrm{G}\mid H_0}]\cdot \hfill \end{array}$$ (4.1)

Note that the template W is itself an image sequence.

An important special case is where the signal is weak, so that the spatiotemporal covariance matrix is the same under both hypotheses (signal-present and signal-absent) and given in general by Eq. (3.30). Since the noise term in the covariance matrix is diagonal, as shown by Eq. (3.34), the inverse needed to compute t_Hot(G) exists. Practical ways of finding (or avoiding) the inverse are discussed in Section 5; for now, we simply proceed as if the inverse were known.

The Hotelling test statistic for a weak spatiotemporal signal is

$$t_{\mathrm{Hot}}\left(\mathbf{G}\right)=\sum _{m=1}^M\sum _{m\prime =1}^M\sum _{j=1}^J\sum _{j\prime =1}^J{\overline{\overline{S}}}_m^{\left(j\right)}{\left[{\mathbf{K}}_G^{-1}\right]}_{\mathit{mm}\prime }^{(j,j\prime )}{g}_{m\prime }^{(j\prime )},$$ (4.2)

where ${\overline{\overline{s}}}_m^{\left(j\right)}$ is the mean signal at pixel m in frame j. The averaging implied by the double overbar here is over measurement noise and an ensemble of PSFs. Often we will want to consider the signal that we want to detect as random, and in those cases a third overbar can be added to accord with Eq. (4.1).

We see from Eq. (4.2) that the ideal linear detection strategy is to do a spatiotemporal prewhitening operation followed by a matched filter with the mean signal. The corresponding Hotelling detectability is given by [cf. Eq. (2.18)]

$${\mathrm{SNR}}_{\mathrm{Hot}}^2=\sum _{m=1}^M\sum _{m\prime =1}^M\sum _{j=1}^J\sum _{j\prime =1}^J{\overline{\overline{S}}}_m^{\left(j\right)}[{\mathbf{K}}_{\mathrm{G}}^{-1}{]}_{\mathit{mm}\prime }^{(j,j\prime )}{\overline{\overline{S}}}_{m\prime }^{(j\prime )}.$$ (4.3)

If we assume that the object to be detected is independent of time and that the PSF statistics are temporally stationary, the mean difference signal is independent of j, and we can write its value at the mth pixel simply as ${\overline{\overline{s}}}_m$. The interpretation is that ${\overline{\overline{s}}}_m$ is the image of the signal object blurred by the long-term average of the partially corrected PSF and with measurement noise averaged out. Note that this signal can be random, so long as its ensemble mean is independent of time. In that case, we can rewrite Eq. (4.2) as

$$\begin{array}{cc}\hfill & t_{\mathrm{Hot}}\left(\mathbf{G}\right)=\sum _{m=1}^M{\overline{\overline{S}}}_m{g}_m^{\left(\mathrm{pw}\right)},\hfill \\ \hfill g_m^{\left(\mathrm{pw}\right)}& \equiv \sum _{m\prime =1}^M\sum _{j=1}^J\sum _{j\prime =1}^J{\left[{\mathbf{K}}_{\mathrm{G}}^{-1}\right]}_{\mathit{mm}\prime }^{(j,j\prime )}{g}_{m\prime }^{(j\prime )}.\hfill \end{array}$$ (4.4)

The set $\left\{{\mathtt{g}}_m^{\left(\mathrm{pw}\right)}\right\}$ or the vector g^(pw) represents a single frame of prewhitened data; after the spatiotemporal prewhitening, it is easy to form the Hotelling test statistic for many different signals that one might seek to detect. In fact, the single image g^(pw) can also be presented to a human observer as an optimally preprocessed summary of the raw image sequence.

An alternative strategy, routinely used in astronomy, is simply to sum the frames without the prewhitening step. The test statistic for such a nonprewhitening (NPW) observer is given by

$$t_{\mathrm{npw}}\left(\mathbf{G}\right)=\sum _{m=1}^M{\overline{\overline{S}}}_m{g}_m^{\left(\mathrm{npw}\right)},g_m^{\left(\mathrm{npw}\right)}\equiv \sum _{j=1}^J{g}_m^{\left(j\right)}.$$ (4.5)

The Hotelling and NPW observers are equivalent (their test statistics differ by an irrelevant constant factor) if and only if the data are independent and identically distributed both spatially and temporally. Correlations in either the pixel index m or the frame index j necessarily reduce the detection performance of the NPW observer relative to that of the Hotelling observer; such correlations can arise from either the PSF term or the object term in the data covariance.

3. Signal-Known-Exactly Detection on a Uniform Background

To illustrate the spatiotemporal Hotelling observer, consider the detection of a nonrandom point object on a sky background that is spatially constant over the field of view but can vary randomly with time over the duration of the observation. The autocovariance function for the object in this case is discussed in Appendix A.

The PSF term in the covariance can usually be neglected in this problem. To see this point, we assume that the background is spatially constant at the random time-varying value C(t) and rewrite Eq. (3.36) as

$$\begin{array}{cc}\hfill & {\left[{\overline{\mathbf{K}}}_{\overline{G}}^{\mathrm{PSF}}\right]}_{\mathit{mm}\prime }^{(j,j\prime )}=[{\overline{C}}^2+{\mathbf{K}}_C(t_j,t_{j\prime })]\int d^{2}r\int d^{2}r\prime \langle [h_m^{\left(j\right)}\left(\mathbf{r}\right)-{\overline{h}}_m^{\left(j\right)}\left(\mathbf{r}\right)]\hfill \\ \hfill & \times [h_{m\prime }^{(j\prime )}(\mathbf{r}\prime )-{\overline{h}}_{m\prime }^{(j\prime )}(\mathbf{r}\prime )]{\rangle }_{\mathbf{P}}\hfill \\ \hfill & =[{\overline{C}}^2+K_C(t_j,t_{j\prime })]\langle \left[\int d^{2}r{h}_m^{\left(j\right)}\left(\mathbf{r}\right)-\int d^{2}r{\overline{h}}_m^{\left(j\right)}\left(\mathbf{r}\right)\right]\phantom{\rangle }\hfill \\ \hfill & \times {[\left[\int d^{2}r\prime h_{m\prime }^{(j\prime }(\mathbf{r}\prime )-\int d^{2}r\prime {\overline{h}}_{m\prime }^{(j\prime )}(\mathbf{r}\prime )\right]\rangle }_{\mathbf{P}}.\hfill \end{array}$$ (4.6)

We note from Eq. (3.5), however, that $\int {\mathrm{d}}^{2}r{h}_m^{\left(j\right)}\left(\mathbf{r}\right)$ is a non-random constant so long as $\int {\mathrm{d}}^{2}r{p}^{\left(j\right)}({\mathbf{r}}_d,\mathbf{r})$ is a constant, which it is whenever the underlying continuous PSF is isoplanatic. Thus, if the atmosphere can be modeled as a thin phase plate in the pupil, the PSF term in the data covariance for a spatially constant background vanishes. If there is substantial anisoplanatism, the PSF term is not identically zero, but it should be small since the image of a constant background should be nearly constant in any practical case.

The mean PSF is still important, however, since it determines the signal to be detected. For a time-independent point object of known luminosity at a known location [the so-called signal-known-exactly (SKE) task], the signal part of the object distribution is f_s(r)=A_sδ(r—r_s). In general the corresponding mean signal in the data will depend on j through ${\overline{h}}_m^{\left(j\right)}\left(\mathbf{r}\right)$, but if the atmosphere is temporally stationary, the mean signal at the mth detector pixel is

$${\overline{\overline{S}}}_m={\mathbf{A}}_s{\overline{h}}_m\left({\mathbf{r}}_s\right).$$ (4.7)

We also assume that all detector elements are identical, so that the variances of the electronic noise and the Poisson noise from the uniform background are independent of m. With Eqs. (3.42), (A10), and (3.38), the overall covariance matrix is

$${\left[K_G\right]}_{\mathit{mm}\prime }^{(j,j\prime )}=({\sigma }^2+{\eta }^{\overline{\mathbf{C}}}){\delta }_{\mathit{mm}\prime }{\delta }_{j,j\prime }+{\eta }^2{\mathbf{K}}_C(t_j,t_{j\prime }),$$ (4.8)

where $\eta \equiv \int {\mathrm{d}}^{2}r{\overline{h}}_m\left(\mathbf{r}\right)$ which can be interpreted as the flatfield image; η is independent of m if the system is isoplanatic and the detector elements are identical.

It is shown in Subsection 5.B that the inverse covariance has the form

$${\left[K_G^{-1}\right]}_{\mathit{mm}\prime }^{(j,j\prime )}={({\sigma }^2+{\eta }^{\overline{\mathbf{C}}})}^{-1}{\delta }_{\mathit{mm}\prime }{\delta }_{j,j\prime }-{\mathbf{Q}}^{(j,j\prime }),$$ (4.9)

where Q^(j,j’) is defined by Eq. (5.16). With Eqs. (4.2), (4.7), and (4.9), the Hotelling test statistic can be written as

$$t_{\mathrm{Hot}}\left(\mathbf{G}\right)=\frac{A_s}{{\sigma }^2+\eta \overline{C}}\sum _{m=1}^m\sum _{j=1}^J{\overline{h}}_m\left({\mathbf{r}}_s\right)[g_m^{\left(j\right)}-\eta {\widehat{C}}^{\left(j\right)}],$$ (4.10)

where

$$\eta {\widehat{C}}^{\left(j\right)}\equiv ({\sigma }^2+\eta \overline{C})\sum _{m\prime =1}^M\sum _{j\prime =1}^J{\mathbf{Q}}^{(j,j\prime )}{g}_{m\prime }^{(j\prime )}.$$ (4.11)

The interpretation of Eq. (4.10) is that the data are first preprocessed by subtracting the estimate ηĈ^(j) of the background in each frame and then passed through a matched filter. The background estimate is found, according to Eq. (4.11), by summing over all pixels in each frame and also doing a weighted sum over correlated frames, with the weighting specified by Q^(j,j’). The resulting test statistic is optimal in terms of task performance; for detection of a nonrandom point object on a time-varying but spatially uniform background by a linear observer, the test statistic defined in Eq. (4.10) gives the largest Hotelling detectability and, to a good approximation, the largest area under the ROC curve.

From Eqs. (4.3), (4.7), and (4.9), the Hotelling detectability for this task is given by

$$\begin{array}{cc}\hfill & {\mathrm{SNR}}_{\mathrm{Hot}}^2=A_s^2\sum _{m=1}^M\sum _{m\prime =1}^M\sum _{j=1}^J\sum _{j\prime =1}^J{\overline{h}}_m\left({\mathbf{r}}_s\right){\left[{\mathbf{K}}_G^{-1}\right]}_{\mathit{mm}\prime }^{(j,j\prime )}{\overline{h}}_{m\prime }\left({\mathbf{r}}_s\right)\hfill \\ \hfill & =\frac{J{A}_s^2}{{\sigma }^2+\eta \overline{C}}\sum _{m=1}^M{\left[{\overline{h}}_m\left({\mathbf{r}}_s\right)\right]}^2\hfill \\ \hfill & -A_s^2{\left[\sum _{m=1}^M{\overline{h}}_m\left({\mathbf{r}}_s\right)\right]}^2\sum _{j=1}^J\sum _{j\prime =1}^J{\mathbf{Q}}^{(j,\prime j)}.\hfill \end{array}$$ (4.12)

The last line represents the reduction in detectability from having to estimate the background, even when that estimation is done optimally. It can be shown, however, that this term varies asymptotically as M^-1, where M is the number of pixels in a frame and hence, in this problem, the number of pixels that can be averaged to get an estimate of the background. Thus

$${\mathrm{SNR}}_{\mathrm{Hot}}^2\approx \frac{J{A}_s^2}{{\sigma }^2+\eta \overline{C}}\sum _{m=1}^M{\left[{\overline{h}}_m\left({\mathbf{r}}_s\right)\right]}^2\left(M\text{large}\right),$$ (4.13)

which is exactly the expression that would be obtained if the background were nonrandom and known to the observer.

Several important conclusions can be drawn from relation (4.13). Obvious ones are that the detectability is larger for stronger sources, more frames, and less electronic noise. We see also that the detectability is proportional to the sum of the squares of the discretized mean PSF values; since this sum increases with the Strehl ratio of the system, it can be used to quantify the effect of uncorrected atmospheric blur on the flat-background SKE detectability.

Another consequence of the sum over m is that the detectability can be high even if no single pixel exceeds the noise level; detection by a Hotelling observer is determined by the noise in the test statistic t_Hot(G), and it is only the SNR of that quantity that matters, not the pixel SNR. The Hotelling SNR can be much better than the pixel SNR because of the optimal summation across pixels. Indeed, the human observer also does a very good job of summing over pixels, a fact that was known already to Albert Rose in 1950 and has been very well verified in the decades since then.³⁹

Since data from multiple pixels are used by both human and Hotelling observers, it follows that there is no disadvantage in detection performance to using small detector pixels; if more pixels fit within the mean PSF, more of them are used in forming the test statistic and the performance cannot decrease (at least for pure Poisson noise). This contradicts the common view⁴⁰ that oversampling is bad because it decreases the SNR; it decreases only the irrelevant single-pixel SNR. There might be engineering or economic arguments for using larger pixels, but they cannot be justified on grounds of detectability.

4. Random, Nonuniform Backgrounds

SKE detection tasks with random, spatially nonuniform backgrounds (so-called lumpy backgrounds) have played an important role in developing realistic task-based figures of merit in medical imaging,^1,6–9 and they should prove equally useful in astronomy. The important difference, however, is that the PSF term varies randomly with time in astronomy; therefore, as we shall see, the correlations are spatiotemporal even for a temporally constant background.

When the PSF is independent of the object, the PSF term in the data covariance is given by Eq. (3.36). An important special case is when the time-independent background is spatially stationary (or at least approximately so over the field of view), so that $\langle f\left(\mathbf{r}\right)f(\mathbf{r}\prime )\rangle ={\overline{f}}^2+K_f(\mathbf{r},\mathbf{r}\prime )$. By the same argument as that used in Eq. (4.6), the term proportional to ${\overline{f}}^2$ in Eq. (3.36) vanishes identically if the continuous PSF is isoplanatic, and it should be small in most practical cases. If the PSF is also temporally stationary, Eq. (3.36) becomes

$$\begin{array}{cc}\hfill & {\left[{\mathbf{K}}_{\overline{G}}^{\mathrm{PSF}}\right]}_{mm\prime }^{(j-j\prime )}\approx \int d^{2}r\int dr\prime K_f(\mathbf{r}-\mathbf{r}\prime )\langle \left[h_m^j\left(\mathbf{r}\right)-{\overline{h}}_m\left(\mathbf{r}\right)\right]\hfill \\ \hfill & \times [h_{m\prime }^{(j\prime )}(\mathbf{r}\prime )-{\overline{h}}_{m\prime }(\mathbf{r}\prime )]{\rangle }_{\mathbf{P}}.\hfill \end{array}$$ (4.14)

This expression is zero if the PSF is nonrandom (perfect AO system), and it is often small by the argument below Eq. (4.6) if the background is spatially uniform but of random level. More generally, spatiotemporal correlations result from an interaction of spatial background structure and a spatiotemporal PSF.

If we combine the object term with the PSF term as in Eq. (3.40) and use the noise term from Eq. (3.34), we get

$$\begin{array}{cc}\hfill & {\left[K_G\right]}_{mm\prime }^{(j-j\prime )}=\left[{\sigma }^2+\overline{\overline{\overline{g}}}\right]{\delta }_{mm\prime }{\delta }_{jj\prime }+\int d^{2}r\int d^{2}r\prime K_f(\mathbf{r}-\mathbf{r}\prime )\hfill \\ \hfill & \times \langle h_m^{\left(j\right)}\left(\mathbf{r}\right)h_{m\prime }^{(j\prime )}(\mathbf{r}\prime ){\rangle }_{\mathbf{P}}.\hfill \end{array}$$ (4.15)

We have dropped the indices on $\underset{g}{\equiv }$ to be consistent with the assumptions of spatial and temporal stationarity, and we have dropped the index on the electronic noise variance σ² on the assumption that all detectors are identical.

In most practical applications in astronomy, the spatial correlation length of the background is large compared with the field of view of the telescope, and any particular realization of the background might be well described by a constant plus a linear variation in brightness. In that case, the integral in Eq. (4.15) can be evaluated if the means and variances of the constant and linear terms are known.

Once the integral is performed, the evaluation of the Hotelling test statistic and SNR requires a matrix inversion. Common practice in image analysis is to approximate covariance matrices as block-circulant matrices when they arise from digital representations of stationary random processes. This approximation, which is reasonable if the correlation length of the random process is small compared with the image size, permits diagonalization and inversion of the covariance by use of the discrete Fourier transform (DFT). Unfortunately the circulant approximation would rarely be applicable in the present problem because the correlation length is usually long. In that case the matrix in Eq. (4.15) is block-Toeplitz rather than block-circulant, and the inverse can be performed with the help of methods discussed in Subsection 5.B. The method of preconditioned conjugate gradients, in which the circulant approximation to the Toeplitz is used only in the preconditioner, may also be useful.⁴¹

However the inverse is performed, the resulting spatiotemporal prewhitening operation will, by definition, perform an optimal linear compensation for the background nonuniformity, consistent with the statistical information built into it. No other linear operation, such as local background estimation, can achieve better performance.

B. Detection of Faint Companions

Over 160 extrasolar planets have been detected in the decade since the detection of a planet orbiting the star 51 Peg.⁴² Most of these planets have been detected by spectroscopic monitoring of radial velocity variations of the parent stars. Some planets have also been detected by the observation of transits of the planet behind the parent star⁴³ and “anomalous” microlensing events.⁴⁴

Recently, direct images of what appear to be substellar objects have been obtained by using the adaptive optics system on the Very Large Telescope. In both of these detections, the companion object was approximately 0.7 arcsec from the central star, which was about ten times the diffraction limit, and approximately 6 mag fainter than the central star (in the K band). The central star in the detection by Neuhauser et al.⁴⁵ is a young T Tauri star, and the companion mass is not tightly constrained [1–42 Jupiter masses (MJup)]. This companion may therefore be a brown dwarf rather than an exoplanet. The detection of Chauvin et al.⁴⁶ does seem to be an exoplanet, as they constrain the mass to 5±2 MJup (the boundary mass between brown dwarf and exoplanet is controversial but is in the region of 12 MJup). The central star in this detection is itself a brown dwarf, which greatly reduces the magnitude difference with the exoplanet. Direct detection of exoplanets nearer to the diffraction limit around main-sequence stars is much more difficult, as the ratio of the intensities will be ∼ 10⁹ at visible wavelengths and ∼ 10⁶ in the near infrared.

1. Current Practice

The limitation on direct detection of faint companions is noise from the central star, but it is speckle noise associated with the random PSF rather than photon noise that dominates.^47,48 These speckles arise from uncorrected atmospheric aberrations and slowly varying telescope or instrumental aberrations. There is a lot of work going on in the development of techniques to suppress the speckles by using coronography and pupil masks.⁴⁹

A promising approach to removing the speckles is simultaneous differential imaging (SDI). Images are acquired simultaneously in at least two adjacent passbands, in one of which the companion is expected to be dim or absent. If the images are subtracted, then the speckle structure should be practically identical and the detection of any companions is limited by photon noise. A suitable wavelength is 1.6 μm, which corresponds to the methane absorption band found only in cold atmospheres. A critical issue with this technique is the minimization of non-common-path errors between the different wavelength channels.⁵⁰

2. Covariance Terms

As the discussion above indicates, the dominant covariance term limiting the detection of faint companions is likely to be the PSF term, since it is this term that describes the speckle pattern. We know from Eqs. (3.35) and (3.36) that the PSF term involves an average over random objects, where the object in this problem includes the companion (under the signal-present hypothesis), the host star, light from the host star scattered by a circumstellar dust cloud, and any other background that might be present. For the purpose of the PSF term, however, we can assume that the host star is far brighter than any other light source in the field of view. If we also assume that the host star is nonrandom, with a known luminosity and position, then no averaging over random objects is needed to construct the PSF term. To be specific, if the host star is described by $f_{\ast }\left(\mathbf{r}\right)=A_{\ast }\delta (\mathbf{r}-{\mathbf{r}}_{\ast })$, with A_* and r_* fixed and known to the observer, then the PSF term is given from Eq. (3.35) as

$$\begin{array}{cc}\hfill & {\left[{\overline{\mathbf{K}}}_{\overline{G}}^{\mathrm{PSF}}\right]}_{mm\prime }^{(jj\prime )}=A_{\ast }^2\langle [h_m^{\left(j\right)}\left(r_{\ast }\right)-{\overline{h}}_m^{\left(j\right)}\left(r_{\ast }\right)][h_{m\prime }^{(j\prime )}\left(r_{\ast }\right)-{\overline{h}}_{m\prime }^{(j\prime )}\left(r_{\ast }\right)]{\rangle }_{\mathbf{P}}\hfill \\ \hfill & =A_{\ast }^2{\left[K_h\right]}_{\mathit{mm}\prime }^{(j,j\prime )}(r_{\ast },r_{\ast }).\hfill \end{array}$$ (4.16)

The noise term, though likely to be weak in this application, should be included for a complete theory. The noise is uncorrelated, as shown in Eq. (3.34), but nevertheless the form of the average PSF plays a role since the noise in the mth pixel includes Poisson fluctuations from light originating from the star and coupled into that pixel by the average PSF. In addition, there are noise contributions arising from other background light and from electronic noise. If the electronic noise variance and the mean number of detected background photons are independent of m and j,we get

$${\left[{\overline{\overline{\mathbf{K}}}}_{\mathbf{G}}^{\text{noise}}\right]}_{\mathit{mm}\prime }^{(j,j\prime )}=[{\sigma }^2+{\underset{g}{\equiv }}_{\mathrm{bg}}+A_{\ast }{\overline{h}}_m^{\left(j\right)}\left(r_{\ast }\right)]{\delta }_{mm\prime }{\delta }_{jj\prime }.$$ (4.17)

The object term in the data covariance does not include the effects of the direct light from the host star, which is assumed to be nonrandom and known, but it does include light from random dust clouds and general sky background. The background considerations are the same as those in Subsection 4.A, and dust clouds can be included by simulation methods described in Subsection 5.A.

3. Hotelling Observer

For a specified position r_c where a companion might or might not be present, the mean signal in the Hotelling formulas is given by ${\overline{A}}_c{\overline{h}}_m^{\left(j\right)}\left({\mathbf{r}}_c\right)$, where ${\overline{A}}_c$ is the mean brightness of possible companions. This mean brightness enters into the final expressions for detectability but is just an irrelevant constant in the template.

Of course r_c is not known a priori, so the Hotelling test statistic can be evaluated for a range of possible locations and the maximum chosen as the final test statistic to be used for the detection decision. If other data suggest possible locations, then the search over locations can be constrained accordingly.

If the observations cover a sufficient time that significant movement of the companion might be expected, a fully spatiotemporal Hotelling observer can be constructed. For a particular assumed orbit, the function r_c(t) will be known and the corresponding mean signal will be ${\overline{\overline{s}}}_m^{\left(j\right)}={\overline{A}}_c{\overline{h}}_m^{\left(j\right)}\left[{\mathbf{r}}_c\right(t_j\left)\right]$. For faint companions the covariance matrix is independent of the orbit chosen, so it is straightforward to compute the Hotelling test statistic for a set of possible orbits consistent with other data such as radial velocity measurements.

4. Simultaneous Differential Imaging

To adapt the Hotelling theory to SDI, we need one more index on the data to indicate the spectral band. We denote an observation at pixel m in frame j for band b as ${\mathtt{g}}_{\mathit{bm}}^{\left(j\right)}$, where b=1,2 if there are just two spectral bands. The first step in processing SDI data is to form the difference image, with components given by

$$\delta {\mathtt{g}}_m^{\left(j\right)}\equiv {\mathtt{g}}_{2m}^{\left(j\right)}-{\mathtt{g}}_{1m}^{\left(j\right)},$$ (4.18)

and the problem is to detect a companion from this new data set.

To simplify the analysis, we assume that the contributions to the data covariance from sky background, dust clouds, and any possible companion are negligible and that the brightness and position of the host are nonrandom and known to the observer. With these assumptions the object term in the covariance is zero.

The noise is assumed to be independent in the two bands, so the noise variances add. With no background, the same readout noise in all pixels of both detectors, and temporally stationary atmospheric statistics, Eq. (4.17) becomes

$${\left[{\overline{\mathbf{K}}}_{\delta \mathrm{G}}^{\text{noise}}\right]}_{\mathit{mm}\prime }^{(j,j\prime )}=[2{\sigma }^2+{A_1}_{\ast }{\overline{h}}_{1m}\left(r_{\ast }\right)+{A_2}_{\ast }{\overline{h}}_{2m}\left(r_{\ast }\right)]{\delta }_{mm\prime }{\delta }_{jj\prime },$$ (4.19)

where ${\overline{h}}_{\mathit{bm}}\left(\mathbf{r}\right)$ is the mean sensitivity function and A_b* is the brightness of the host star for band b. One overbar on K has been deleted, since averaging over random objects is not needed.

The PSF term for the difference data is defined by

$${\left[{\mathbf{K}}_{\delta \overline{\mathrm{G}}}^{\mathrm{PSF}}\right]}_{\mathit{mm}\prime }^{(j,j\prime )}\equiv \langle {[\delta \overline{\mathbf{g}}-\langle \delta \overline{\mathbf{g}}{\rangle }_{\mathbf{P}}]}_m^{\left(j\right)}{[\delta \overline{\mathbf{g}}-\langle \delta \overline{\mathbf{g}}{\rangle }_{\mathbf{P}}]}_{m\prime }^{(j\prime )}{\rangle }_{\mathbf{P}}.$$ (4.20)

For a nonrandom point object and a wavelength-dependent PSF,

$$\begin{array}{c}{[\delta \overline{\mathbf{g}}-\langle \delta \overline{\mathbf{g}}{\rangle }_{\mathbf{P}}]}_m^{\left(j\right)}=A_{2\ast }[h_{2m}^{\left(j\right)}\left(r_{\ast }\right)-{\overline{h}}_{2m}\left(r_{\ast }\right)]\hfill \\ \hfill -A_{1\ast }[h_{1m}^{\left(j\right)}\left(r_{\ast }\right)-{\overline{h}}_{1m}\left(r_{\ast }\right)],\end{array}$$ (4.21)

but the usual assumption in SDI is that the PSF is independent of wavelength. In that case, we find that

$${\left[{\mathbf{K}}_{\delta \overline{\mathrm{G}}}^{\mathrm{PSF}}\right]}_{mm\prime }^{(jj\prime }={(A_{2\ast }-A_{1\ast })}^2{\left[{\mathbf{K}}_{\mathrm{h}}\right]}_{\mathit{mm}\prime }^{(j,j\prime )}(r_{\ast },r_{\ast }).$$ (4.22)

Comparing this result with Eq. (4.16), we see that the PSF term has the same form but is reduced in magnitude by (A_2*—A_1*)²/A_*².

The signal from the faint companion is also reduced. If we denote the object function for the companion in band b as f_bs(r), then

$$\delta {\overline{\overline{s}}}_m=\int d^{2}r{\overline{h}}_m\left(\mathbf{r}\right)[{\overline{f}}_{2s}\left(\mathbf{r}\right)-{\overline{f}}_{1s}\left(\mathbf{r}\right)].$$ (4.23)

Thus the noise is doubled in forming the difference image (compared with a single image with the same mean number of photons), the PSF term in the covariance is reduced by a potentially large factor, and the mean signal is also reduced. The signal and both terms in the covariance are reduced further by the need to use narrowband filters in SDI. The net gain or loss in detectability can be determined by comparing the Hotelling SNR² values for the two data sets G and δG and comparing both with the SNR² for data obtained over a broader spectral range.

C. Photometry

Astronomers are interested not only in detecting objects but also in determining the flux coming from them. By estimating flux, and in particular estimating the flux in different wavelength ranges (i.e., the color), they can determine physical properties (temperature, age, mass, etc.) of the object in question.

1. Current Practice

The estimation of flux from images, which is referred to as photometry, is usually carried out in one of two ways: aperture photometry or PSF fitting. In aperture photometry the flux in an area including the object is summed, and an estimate of the background is subtracted. The background estimate is obtained simply by summing the flux inside an aperture where no objects are believed to be present. The aperture used to estimate the background is usually an annulus around the object.

Aperture photometry will not work in crowded fields, and in this case it is usual to employ PSF fitting. In this approach a model of the objects in the field is fitted to the data. This requires accurate knowledge of the PSF and is complicated if the PSF varies over the field. Esslinger and Edmunds⁵¹ simulated crowded fields with PSFs from a real AO system and used a standard photometry package, DAOPHOT, to estimate stellar magnitudes by PSF fitting. They found that even when using the correct PSF in fitting, the rms error in magnitude determination was as high as 0.1 mag for densities lower than a few stars per square arcsecond, and they concluded that they cannot get good photometric precision in crowded fields. They also tested the photometry of simulated faint companions by means of deconvolution and found that deconvolution gave worse results than PSF fitting.

2. Spatiotemporal Wiener Estimator

Since aperture photometry makes questionable assumptions about the background, and PSF fitting breaks down in crowded star fields, it is reasonable to investigate linear methods like the Wiener estimator that incorporate statistical models of the background.

The Wiener estimator for a doubly stochastic spatial problem was given in Eq. (2.19), and the associated ensemble mean square error (EMSE) was given in Eq. (2.20). For estimation of a parameter θ(F) from triply stochastic spatiotemporal data, these equations generalize to

$$\widehat{\theta }=\overline{\theta }+{\mathbf{K}}_{\theta ,\mathbf{G}}{\mathbf{K}}_{\mathbf{G}}^{-1}\left[\mathbf{G}-\underset{\mathbf{G}}{\equiv }\right],$$ (4.24)

$$\text{EMSE}=\mathrm{tr}{\mathbf{K}}_{\theta }-\mathrm{tr}{\mathbf{K}}_{\theta ,\mathrm{G}}{\mathbf{K}}_{\mathrm{G}}^{-1}{\mathbf{K}}_{\theta ,\mathrm{G}}^{\mathrm{t}}.$$ (4.25)

Calculation of the grand mean $\underset{\mathbf{G}}{\equiv }$ and the two covariances K_G and K_θ,_G must now include the fact that θ is random. Since θ is a function of F, we can write

$$\langle \cdots {\rangle }_{\mathbf{F}}=\langle \langle \cdots {\rangle }_{\mathbf{F}\mid \theta }{{\rangle }_{\theta }}^{,}$$ (4.26)

and the grand mean is

$$\underset{\mathbf{G}}{\equiv }={\langle \langle \langle \langle \mathbf{G}{\rangle }_{\mathbf{G}\mid \mathbf{P},\mathbf{F}}{\rangle }_{\mathbf{P}\mid \mathbf{F}}{\rangle }_{\mathbf{F}\mid \theta }\rangle }_{\theta }\equiv {\langle {\overline{\overline{\mathbf{G}}}}_{\theta }\rangle }_{\theta }.$$ (4.27)

We do not add a fourth overbar, since there are still fundamentally just three sources of randomness: measurement noise, PSF, and object.

If θ is an N × 1 vector and G is MJ × 1, then the cross-covariance K_θ,G is an N × MJ matrix given by

$$\begin{array}{cc}\hfill {\mathbf{K}}_{\theta ,\mathrm{G}}& ={\langle {\langle {\langle {\langle \left[\theta -\overline{\theta }\right]{\left[\mathbf{G}-\underset{\mathbf{G}}{\equiv }\right]}^{\mathrm{t}}\rangle }_{\mathbf{G}\mid \mathbf{P},\mathbf{F}}\rangle }_{\mathbf{P}\mid \mathbf{F}}\rangle }_{\mathbf{F}\mid \theta }\rangle }_{\theta }\hfill \\ \hfill & ={\langle [\theta -\overline{\theta }]{\left[{\underset{\mathbf{G}}{\equiv }}_{\theta }-\underset{\mathbf{G}}{\equiv }\right]}^{\mathrm{t}}\rangle }_{\theta }.\hfill \end{array}$$ (4.28)

A useful form of the overall covariance K_G is obtained if we add and subtract ${\underset{\mathbf{G}}{\equiv }}_{\theta }$ in definition (4.27) and then use Eq. (4.26):

$$\begin{array}{cc}\hfill {\mathbf{K}}_{\mathbf{G}}& ={\langle {\langle {\langle \langle \left[\mathbf{G}-\underset{\mathbf{G}}{\equiv }\right]{\left[\mathbf{G}-\underset{\mathbf{G}}{\equiv }\right]}^{\mathrm{t}}{\rangle }_{\mathrm{G}\mid \mathbf{P},\mathbf{F}}\rangle }_{\mathbf{P}\mid \mathbf{F}}\rangle }_{\mathbf{F}\mid \theta }\rangle }_{\theta }\hfill \\ \hfill & =\langle {\mathbf{K}}_{\mathbf{G}\mid \theta }{\rangle }_{\theta }+{\langle \left[{\underset{\mathbf{G}}{\equiv }}_{\theta }-\underset{\mathbf{G}}{\equiv }\right]{\left[{\underset{\mathbf{G}}{\equiv }}_{\theta }-\underset{\mathbf{G}}{\equiv }\right]}^{\mathrm{t}}\rangle }_{\theta },\hfill \end{array}$$ (4.29)

where

$${\mathbf{K}}_{\mathbf{G}\mid \theta }\equiv {\langle {\langle {\langle \left[\mathbf{G}-{\underset{\mathbf{G}}{\equiv }}_{\theta }\right]{\left[\mathbf{G}-{\underset{\mathbf{G}}{\equiv }}_{\theta }\right]}^{\mathrm{t}}\rangle }_{\mathbf{G}\mid \mathbf{P},\mathbf{F}}\rangle }_{\mathbf{P}\mid \mathbf{F}}\rangle }_{\mathbf{F}\mid \theta }.$$ (4.30)

3. Estimating the Luminosity of a Star at a Known Location

To illustrate the use of the Wiener estimator, consider the problem of estimating the luminosity of a star at a known location on a time-independent random background f_bg(r). The star of interest will be described by $f_{\ast }\left(\mathbf{r}\right)=\theta \delta (\mathbf{r}-{\mathbf{r}}_{\ast })$ where the scalar θ is the parameter to be estimated.

For this problem, the conditional mean in component form is

$$\begin{array}{cc}\hfill {\left[{\underset{\mathbf{G}}{\equiv }}_{\theta }\right]}_m^{\left(j\right)}& =\int d^{2}r{\overline{h}}_m^{\left(j\right)}\left(\mathbf{r}\right)\left[{\overline{f}}_{bg}\left(\mathbf{r}\right)+\theta \delta (\mathbf{r}-r_{\ast })\right]\hfill \\ \hfill & =\int d^{2}r{\overline{h}}_m^{\left(j\right)}\left(\mathbf{r}\right){\overline{f}}_{bg}\left(\mathbf{r}\right)+\theta {\overline{h}}_m^{\left(j\right)}\left(r_{\ast }\right),\hfill \end{array}$$ (4.31)

and the grand mean is

$${\left[\underset{\mathbf{G}}{\equiv }\right]}_m^{\left(j\right)}=\int d^{2}r{\overline{h}}_m^{\left(j\right)}\left(\mathbf{r}\right){\overline{f}}_{bg}\left(\mathbf{r}\right)+\overline{\theta }{\overline{h}}_m^{\left(j\right)}\left(r_{\ast }\right).$$ (4.32)

From these results and Eq. (4.28), the cross-covariance becomes simply

$${\left[{\mathbf{K}}_{\theta ,\mathbf{G}}\right]}_m^{\left(j\right)}={\sigma }_{\theta }^2{\overline{h}}_m^{\left(j\right)}\left(r_{\ast }\right),$$ (4.33)

where the terms involving ${\overline{f}}_{\mathrm{bg}}$ have canceled and the cross-covariance has only a single pair of indices (m,j) since θ is a scalar.

The last term in Eq. (4.29) is given by

$${\left[{\langle \left[{\underset{\mathbf{G}}{\equiv }}_{\theta }-\underset{\mathbf{G}}{\equiv }\right]{\left[{\underset{\mathbf{G}}{\equiv }}_{\theta }-\underset{\mathbf{G}}{\equiv }\right]}^{\mathrm{t}}\rangle }_{\theta }\right]}_{\mathit{mm}\prime }^{(j,j\prime )}={\sigma }_{\theta }^2{\overline{h}}_m^{\left(j\right)}\left(r_{\ast }\right){\overline{h}}_{m\prime }^{(j\prime )}\left(r_{\ast }\right),$$ (4.34)

and the overall covariance is

$${\left[{\mathbf{K}}_{\mathrm{G}}\right]}_{\mathit{mm}\prime }^{(j,j\prime )}={\left[\langle {\mathbf{K}}_{\mathrm{G}\mid \theta }\rangle \right]}_{\mathit{mm}\prime }^{(j,j\prime )}+{\sigma }_{\theta }^2{\overline{h}}_m^{\left(j\right)}\left(r_{\ast }\right){\overline{h}}_{m\prime }^{(j\prime )}\left(r_{\ast }\right).$$ (4.35)

The details of the first term depend on the background model chosen.

If the atmospheric statistics are stationary, we can drop the superscript on ${\overline{h}}_m^{\left(j\right)}$ and write Eq. (4.24) as

$$\widehat{\theta }=\overline{\theta }+{\sigma }_{\theta }^2\sum _{m=1}^M{\overline{h}}_m\left(r_{\ast }\right)\left[g_m^{\left(\mathrm{pw}\right)}-{\overline{\overline{\overline{g}}}}_m^{\left(\mathrm{pw}\right)}\right],$$ (4.36)

where $g_m^{\left(j\right)}$ is defined in Eq. (4.4) and, from Eq. (4.32),

$$\begin{array}{cc}\hfill {\underset{g}{\equiv }}_m^{\left(\mathrm{pw}\right)}& \equiv \sum _{m\prime =1}^M\sum _{j=1}^J\sum _{j\prime =1}^J{\left[{\mathbf{K}}_{\mathrm{G}}^{-1}\right]}_{\mathit{mm}\prime }^{(j,j\prime )}[\int d^{2}r{\overline{h}}_m,\left(\mathbf{r}\right){\overline{f}}_{bg}\left(\mathbf{r}\right)\phantom{]}\hfill \\ \hfill & \phantom{[}+{\overline{\theta h}}_{m\prime }\left(r_{\ast }\right)].\hfill \end{array}$$ (4.37)

Use of Eq. (4.36) requires prior knowledge of the mean and variance of θ as well as knowledge of the mean and covariance of the data. If the prior variance ${\sigma }_{\theta }^2\to 0$, Eq. (4.36) shows that $\widehat{\theta }\to \overline{\theta }$; if we have no prior uncertainty, the best estimate is the prior mean. In more realistic cases, ${\sigma }_{\theta }^2$ controls the relative weights placed on the prior mean and a correction term computed by a prewhitening matched filter. One way to choose $\overline{\theta }$ and ${\sigma }_{\theta }^2$ is to first estimate θ by a conventional algorithm and to assign a realistic error to the result.

The EMSE that results from the optimal estimator (4.36) is

$$\text{EMSE}={\sigma }_{\theta }^2-{\sigma }_{\theta }^4\sum _{m=1}^M\sum _{m\prime =1}^M\sum _{j=1}^J\sum _{j\prime =1}^J{\overline{h}}_m\left({\mathbf{r}}_{\ast }\right){\left[{\mathbf{K}}_G^{-1}\right]}_{mm\prime }^{(jj\prime )}{\overline{h}}_{m\prime }\left({\mathbf{r}}_{\ast }\right).$$ (4.38)

The second term here is very similar to the expression in Eq. (4.12) for detection of a point object; both are quadratic forms in the mean signal, and both involve the inverse of the overall covariance matrix K_G (though this matrix is different in the two problems because of the randomness of θ). Increasing such a quadratic form increases the SNR of the optimal linear discriminant and decreases the EMSE of the optimal linear estimator. For more on the connection between detection and estimation problems, see the first paper in this series.²

5. COMPUTATIONAL METHODS

In this section we discuss the practical issues involved in applying the formalism developed above. In keeping with the title of this paper, the primary goal is to develop methods of estimating task-based figures of merit for image quality, but in fact the approaches used will also lead to ways of actually performing the tasks.

The major practical difficulties for both the Hotelling observer and the generalized Wiener estimator fall into two categories: (1) determining various averages of the data (G with different numbers of overbars) and the three components in a covariance decomposition like Eq. (3.30) or Eq. (3.42); (2) actually computing figures of merit involving matrix inverses as in Eq. (4.3) or Eq. (4.38). These two aspects are treated in Subsections 5.A and 5.B, respectively.

A. Finding the Means and Covariance Components

In categorizing the possible approaches to finding the means and covariance components for purposes of assessment of image quality, we should first ask if the assessment is to be carried out on a real imaging system, on a simulated system, or purely theoretically. A simulated system is advantageous since there we have the luxury of simulating the various random effects separately, and in particular we can simulate noise-free images. Fortunately, numerous highly developed simulation codes are now available for AO,^52–54 and much of the discussion below will assume that such code is available.

In a sense, a real imaging system is the ultimate simulation; it is more realistic and far faster than any software approach to producing similar images. Though we cannot “turn off” noise or atmospheric degradations, we can accumulate large numbers of images rapidly and therefore get good statistical quality in covariance estimates. The main drawback to using real systems, however, is that we must build them first; often we would like to use objective figures of merit to evaluate and optimize systems that do not yet exist.

1. Means

Single, double, and triple averages of the data are defined in Eqs. (3.23), (3.24), and (3.26), respectively. In general, each of these averages depends on the hypothesis for a classification task or on the parameter value for an estimation task. In a sense, only the final triple-bar average is important in task performance, since that is the only average that appears in the final figures of merit, but the two others are needed to compute covariance components; as the notation implies, ${\overline{\mathbf{K}}}_{\overline{\mathbf{G}}}^{\mathrm{PSF}}$ is the average conditional covariance of the single-bar mean data (conditional on a fixed F and then averaged over F), while ${\mathbf{K}}_{\overline{\overline{\mathbf{G}}}}^{\mathrm{obj}}$ is the covariance of the double-bar mean.

Key to computing both the double-bar and triple-bar averages is the mean CD kernel ${\overline{h}}_m^{\left(j\right)}\left(\mathbf{r}\right)$ [see Eqs. (3.24) and (3.26)]. As noted several times above, this mean kernel is independent of j if the atmosphere is temporally stationary, but it depends on the seeing, as specified for example by the Fried parameter r₀, and of course it depends on the details of the AO system.

In principle, ${\overline{h}}_m^{\left(j\right)}\left(\mathbf{r}\right)$ could be computed directly from the mean continuous PSF by Eq. (3.25), and the mean PSF itself could be found by averaging Eq. (3.17). This would require modeling the atmosphere, the noise on the output of the detector in the wavefront sensor, the propagation of the noise through the estimator and control system of Fig. 1, the effect of the noisy control signals on the pupil wavefront, and finally the nonlinear relation between wavefront and incoherent PSF. A more practical approach is to run one of the simulation codes mentioned above and compute a sample average. Alternatively, for an existing imaging system, the kernel can be obtained by imaging an isolated bright star.

Finally, various analytical approximations to ${\overline{h}}_m^{\left(j\right)}\left(\mathbf{r}\right)$ can be found in the literature. Usually the approach is to assume that the partially corrected mean PSF can be represented as a diffraction-limited core and a more or less uniform halo of size determined by r₀, with the relative amount of light in each component determined by the Strehl ratio achieved by the closed-loop AO system. Such one-parameter descriptions risk oversimplification of a very complex system, but they may be adequate for computing the triple-bar mean signal and the object term in the covariance. The Strehl ratio provides almost no information about the PSF term in the covariance (except that it vanishes as the Strehl ratio approaches unity).

2. From Object Autocovariance Function to Data Covariance Matrix

When the PSF is independent of the object, the object term in the covariance can be computed in two steps: First calculate or estimate the autocovariance function of the object, $K_{\mathbf{f}}^{(j,j\prime )}(\mathbf{r},\mathbf{r}\prime )$ as defined by Eq. (3.39), then use the average response function of the system to transfer it to the discrete data domain as in Eq. (3.38), thereby obtaining the contribution of the object randomness to the covariance matrix of the data. Note carefully the distinction between the autocovariance of the object (a function) and the contribution of the object variability to the covariance of the data (a matrix). Note also that only the ensemble average of the CD response function enters into Eq. (3.38); we do not need knowledge of individual, random PSFs or response functions to compute the object term in the covariance.

There are numerous situations where the autocovariance function of the object can be stated analytically. Appendix A provides such expressions for three important cases: a collection of independent stars or other point objects, a diffuse sky background modeled as a spatially stationary random process, and a spatially uniform sky background that varies randomly with time. In all of these cases, it is straightforward to transfer the object variability through the imaging system by Eq. (3.38) and to store the result for later use.

Similar advantages accrue if we consider either spatially stationary backgrounds as in relation (A8) or temporally stationary ones as in Eq. (A10). For example, if the background is spatially stationary and time-independent and the atmosphere is temporally stationary, then Eq. (3.38) becomes

$${\left[{\mathbf{K}}_{\underset{\mathbf{G}}{=}}^{\mathrm{obj}}\right]}_{\mathit{mm}\prime }^{(j,j\prime )}={\int }_{\infty }{d}^{2}r{\int }_{\infty }{d}^{2}r\prime {\overline{h}}_m\left(\mathbf{r}\right){\overline{h}}_{m\prime }(\mathbf{r}\prime )K_f(\mathbf{r}-\mathbf{r}\prime ).$$ (5.1)

If the PSF is isoplanatic over the portion of the detector needed for performing the task and all detector elements are identical, then ${\overline{h}}_m\left(\mathbf{r}\right)=\overline{h}(\mathbf{r}-{\mathbf{a}}_m)$, where the mth pixel is centered at r=a_m and the function $\overline{h}(\cdot )$ is the same for all pixels. In that case standard Fourier manipulations yield

$$\begin{array}{cc}\hfill {\left[{\mathbf{K}}_{\underset{\mathbf{G}}{=}}^{\mathrm{obj}}\right]}_{\mathit{mm}\prime }^{(j,j\prime )}& ={\int }_{\infty }{d}^{2}r{\int }_{\infty }{d}^{2}r\prime \overline{h}(\mathbf{r}-{\mathbf{a}}_m)\overline{h}(\mathbf{r}\prime -{\mathbf{a}}_{m\prime })K_{\mathrm{f}}(\mathbf{r}-\mathbf{r}\prime )\hfill \\ \hfill & ={\int }_{\infty }{d}^2\rho S_f\left(\rho \right)\mid \overline{H}\left(\rho \right){\mid }^2\exp [2\pi i\rho \cdot ({\mathbf{a}}_{m\prime }-{\mathbf{a}}_m)],\hfill \end{array}$$ (5.2)

where $\overline{H}\left(\rho \right)$ is the 2D Fourier transform of $\overline{h}\left(\mathbf{r}\right)$ and, by the Wiener—Khinchin theorem, the power spectral density $S_{\mathbf{f}}\left(\rho \right)$ is the Fourier transform of $K_{\mathbf{f}}\left(\mathbf{r}\right)$. Thus the covariance matrix with these assumptions is a function of only the single 2D vector a_m′-a_m, and it can be stored and displayed as an image with just M pixels.

3. Object Term: Sample Methods

Often no analytic autocovariance function will be available but good simulation code will exist for generating realistic objects. For example, Refregier⁵⁵ discusses efficient ways of representing galaxies in terms of Hermite—Gauss functions.

Suppose that L sample objects are generated, with each object being a spatiotemporal sequence in general. Let the lth such object at time t=t_j be denoted as $f_l^{\left(j\right)}\left(\mathbf{r}\right)$. The simulated noise-free image of this object through the ensemble-average imaging system is given in component form by [cf. Eq. (3.24)]

$${\overline{\overline{g}}}_{lm}^{\left(j\right)}={\int }_{\infty }{d}^{2}r{\overline{h}}_m^{\left(j\right)}\left(\mathbf{r}\right)f_l^{\left(j\right)}\left(\mathbf{r}\right).$$ (5.3)

In a high-quality simulation, the integral in this expression will be approximated by sampling r on a discrete grid with a grid spacing that is small compared with the resolution of the imaging system.

After L images have been simulated, the sample covariance matrix, denoted ${\widehat{\mathbf{K}}}_{\overline{\overline{\mathbf{G}}}}^{\mathrm{obj}}$, is computed from

$${\left[{\widehat{\mathbf{K}}}_{\underset{\mathbf{G}}{=}}^{\mathrm{obj}}\right]}_{\mathit{mm}\prime }^{(j,j\prime )}=\frac{1}{L-1}\sum _{l=1}^L\Delta {\underset{g}{=}}_{lm}^{\left(j\right)}\Delta {\underset{g}{=}}_{lm\prime }^{(j\prime )},$$

$$\Delta {\underset{g}{=}}_{lm}^{\left(j\right)}\equiv {\underset{g}{=}}_{lm}^{\left(j\right)}-\frac{1}{L}\sum _{l=1}^L{\underset{g}{=}}_{lm}^{\left(j\right)}.$$ (5.4)

Since the images used here are generated by passing noise-free sample objects through the ensemble-average PSF, this sample covariance is an estimate of the object term in the ensemble covariance, with no contribution from measurement noise or randomness in the PSF.

The sample covariance defined in Eq. (5.4) is an unbiased estimate of ${\mathbf{K}}_{\overline{\overline{\mathbf{G}}}}^{\mathrm{obj}}$, but it is not invertible since its rank is at most L-1. The ensemble matrix in general has J²M² elements, but the sample matrix is fully specified by LMJ pixel values; it can be stored as L separate images (or image sequences), where in practice L can be a few hundred or a few thousand. If the object is independent of time and the atmospheric statistics are stationary, the object term is independent of j and j′, so we can take J = 1 and reduce the storage and computation still further.

4. Point Spread Function Term in the Covariance

Given the complexity of the random mechanisms involved, a full theoretical treatment of the PSF term may not be possible. The only realistic approach may be simulation, but even here theory will provide some simplification in special cases.

Consider, for example, the problem of detecting faint companions, where it can be argued that the object (mainly the host star) is nonrandom and the PSF term is given by Eq. (4.16). That expression can be estimated by a sample covariance analogous to Eq. (5.4):

$${\left[{\widehat{\overline{\mathbf{K}}}}_{\overline{\mathbf{G}}}^{\mathrm{PSF}}\right]}_{\mathit{mm}\prime }^{(j,j\prime )}=\frac{A_{\ast }^2}{L-1}\sum _{l=1}^L\Delta h_{lm}^{\left(j\right)}\left(r_{\ast }\right)\Delta h_{lm\prime }^{(j\prime )}\left(r_{\ast }\right),$$

$$\Delta h_{lm}^{\left(j\right)}\left(r_{\ast }\right)\equiv h_{lm}^{\left(j\right)}\left(r_{\ast }\right)-\frac{1}{L}\sum _{l=1}^L{h}_{lm}^{\left(j\right)}\left(r_{\ast }\right).$$ (5.5)

The result needs to be stored only for m and m′ such that the corresponding pixel locations are within the width of the PSF from the host star and, if the atmosphere is temporally stationary, only for a few values of j-j′, so the storage requirements are modest.

For random objects with independent P and F, we need the second moment of the object in order to compute the PSF term in the data covariance by Eq. (3.36), and we have two simulation options. First, if an analytic form for the second moment $\langle f^{\left(j\right)}\left(\mathbf{r}\right)f^{(j\prime )}(\mathbf{r}\prime )\rangle$ is known, it can be used to generate Monte Carlo samples of r and r’, for example by the rejection method.¹ If we generate I such coordinate pairs, with the ith denoted (r_i,r_i’), then

$${\left[{\widehat{\overline{\mathbf{K}}}}_{\overline{\mathbf{G}}}^{\mathrm{PSF}}\right]}_{\mathit{mm}\prime }^{(j,j\prime )}=\frac{\mathcal{N}}{I}\sum _{i=1}^I\left[\frac{1}{L-1}\sum _{l=1}^L\Delta h_{lm}^{\left(j\right)}\left({\mathbf{r}}_i\right)\Delta h_{lm\prime }^{(j\prime )}\left({\mathbf{r}}_i^{\prime }\right)\right],$$ (5.6)

where the normalizing constant, defined by $\mathcal{N}\equiv \int {\mathrm{d}}^{2}r\int {\mathrm{d}}^{2}r\prime \langle f^{\left(j\right)}\left(\mathbf{r}\right)f^{(j\prime )}(\mathbf{r}\prime )\rangle$, can often be computed analytically if the second moment is known. Storage of the result may be more onerous in this case than in Eq. (5.5), since pixels m and m′ could be rather far apart and still coupled by the second moment; in that case, however, the PSF term would describe long-range, slowly varying correlations, so it could be smoothed and sampled coarsely for storage.

If we do not have an analytic expression for the second moment but do have good object simulation code, we can still use simulation methods to estimate the PSF term. We can simulate L’ objects, each a discretized version of some $f_{l\prime }^{\left(j\right)}\left(\mathbf{r}\right),l\prime =1,\dots ,L^{\prime }$. We can also generate L sample PSFs $p_l^{\left(j\right)}({\mathbf{r}}_d,\mathbf{r}),l=1,\dots ,L$, each of which is then discretized by some approximation to Eq. (3.5) to generate a sample kernel $h_{\mathit{lm}}^{\left(j\right)}\left({\mathbf{r}}_n\right)$ and a noise-free sample image. Now, however, the sample image is denoted ${\overline{\mathtt{g}}}_{{\mathit{ll}}^{\prime }m}^{\left(j\right)}$ instead of ${\overline{\overline{g}}}_{\mathit{lm}}^{\left(j\right)}$ as in Eq. (5.3) because only the measurement noise has been averaged out and the result still depends on the particular object l′. The PSF term is then estimated by approximating Eq. (3.36) as

$${\left[{\widehat{\overline{\mathbf{K}}}}_{\overline{\mathbf{G}}}^{\mathrm{PSF}}\right]}_{\mathit{mm}\prime }^{(j,j\prime )}=\frac{a_{\mathrm{pix}}^2}{L\prime }\sum _{l\prime =1}^{L\prime }\left[\frac{1}{L-1}\sum _{l=1}^L\Delta {\overline{\mathtt{g}}}_{ll\prime m}^{\left(j\right)}\Delta {\overline{\mathtt{g}}}_{ll\prime m\prime }^{(j\prime )}\right],$$ (5.7)

$$\Delta {\overline{\mathtt{g}}}_{ll\prime m}^{\left(j\right)}\equiv {\overline{\mathtt{g}}}_{ll\prime m}^{\left(j\right)}-\frac{1}{L\prime }\sum _{l\prime =1}^{L\prime }{\overline{\mathtt{g}}}_{ll\prime m}^{\left(j\right)},$$

where a_pix is the area of the pixel used in the simulation of the object (preferably much smaller than the pixel in the science camera).

A similar procedure can be used if P and F are not independent. In that case the simulated object must be used as input to the simulation code for the PSF, and a more complicated average consistent with Eq. (3.35) must be used.

As a final comment on the PSF term, note that it depends on the atmospheric statistics as specified by the Fried parameter r₀; to be realistic, the value used should be specific to the observing conditions. In fact, if the covariances are to be used actually to perform the task instead of just for objective assessment of image quality, a measured value of r₀ for the particular data being analyzed could be used. Moreover, if r₀ is monitored as a function of time during the data run, it can be used to construct a temporally nonstationary covariance, which can then be used with a Hotelling observer or Wiener estimator; this observer would have knowledge of seeing as a function of frame index j and would, by definition, use that information in a statistically optimal way.

5. Noise Covariance

Unless we want to consider detectors with a built-in gain mechanism, such as intensified CCDs, the noise term in the covariance is easy to evaluate. We see from Eq. (3.34) that the noise term is diagonal and that the diagonal elements are determined by the electronic noise variance ${\sigma }_m^2$ and the triple-bar average image.

The electronic noise variance is a characteristic of the science camera and can be determined as a function of pixel index m by analyzing dark frames. We frequently assumed above for simplicity that the result was independent of m; this assumption may be adequate for assessment of image quality but should be avoided for actual data analysis. Moreover, if any flat-fielding corrections are to be used with real data, they should be applied before ${\sigma }_m^2$ is measured; uniform average response does not guarantee uniform noise.

The contribution of Poisson noise to Eq. (3.34) is determined by the overall (triple-bar) mean image; the formalism tells us that there is no need to know the Poisson noise in an individual image. The requisite overall mean can be determined by the same simulation methods mentioned above. An important point that will be used below is that the resulting estimate of the noise term is full rank even if the number of samples is far less than M.

For analysis of real data, the Poisson contribution must also be modified to account for flat-fielding corrections. For example, if the output of pixel m is multiplied by an experimental factor α_m, then the Poisson part of the noise term becomes

$${\left[{\overline{\overline{\mathbf{K}}}}_{\mathbf{G}}^{\mathrm{Pois}}\right]}_{\mathit{mm}\prime }^{(j,j\prime )}={\alpha }_m^2{\overline{\overline{\overline{g}}}}_m^{\left(j\right)}{\delta }_{mm\prime }{\delta }_{jj\prime }.$$ (5.8)

B. Computing Figures of Merit

We turn next to the problem of evaluating or estimating objective figures of merit that involve inverses of very large covariance matrices. The possible approaches include (1) iterative computation of the Hotelling template, (2) Neumann-series matrix inversion, (3) use of the Woodbury matrix-inversion lemma, and (4) reduction of the dimensionality of the problem by various methods, including channels and principal-components analysis (PCA). All of these methods make use of the decomposition of the covariance matrix and the fact that the noise term is full rank and usually diagonal, therefore easy to invert. The methods have all have been used extensively in medical applications, and all of them are described in detail in Chap. 14 of Barrett and Myers¹ for purely spatial data; here we provide only a short summary and a discussion of ways of extending the methods to spatiotemporal data.

1. Iterative Computation of the Hotelling Template

From Eq. (4.1), the spatiotemporal Hotelling template for a weak, nonrandom signal can be expressed symbolically as

$$\mathbf{W}={\mathbf{K}}^{-1}\overline{\overline{\mathbf{S}}},\overline{\overline{\mathbf{S}}}\equiv {\underset{\mathbf{G}}{\equiv }}_1-{\underset{\mathbf{G}}{\equiv }}_0,$$ (5.9)

with another overbar to be added to S for random signals. An iterative algorithm that solves for the template in the purely spatial case has been used in medical imaging,^1,19 and its spatiotemporal generalization is

$${\widehat{\mathbf{W}}}_{n+1}={\widehat{\mathbf{W}}}_n+\alpha {\left[{\overline{\overline{\mathbf{K}}}}_{\mathbf{G}}^{\text{noise}}\right]}^{-1}\left[\overline{\overline{\mathbf{S}}}-{\mathbf{K}}_{\mathbf{G}}{\widehat{\mathbf{W}}}_n\right].$$ (5.10)

where ${\widehat{\mathbf{W}}}_n$ is the estimate of the template at the nth iteration and α is a constant that controls the convergence rate. Note that if convergence is achieved, the steady-state solution satisfies Eq. (5.9).

After N iterations, the estimated template is ${\widehat{\mathbf{W}}}_N$, and the corresponding estimate of the Hotelling detectability is just the scalar product:

$${\widehat{\mathrm{SNR}}}_{\mathrm{Hot}}^2={\overline{\overline{\mathbf{S}}}}^{\mathrm{t}}{\widehat{\mathbf{W}}}_N.$$ (5.11)

Alternatively, the template can be applied to two sets of simulated image sequences, with and without the signal of interest, to generate two corresponding sets of test statistics from which an ROC curve can be constructed. In either case, the errors in the final detectability estimates need to be assessed; methods of doing so are described in Barrett and Myers.¹

2. Neumann Series

The Neumann series is the matrix counterpart of the familiar rule for summing a geometric series. From the Neumann formula we can write

$$\begin{array}{cc}\hfill {[\mathbf{D}+\mathbf{B}]}^{-1}& ={[\mathbf{I}+{\mathbf{D}}^{-1}\mathbf{B}]}^{-1}{\mathbf{D}}^{-1}=\left[\sum _{j=0}^{\infty }{[-{\mathbf{D}}^{-1}\mathbf{B}]}^j\right]{\mathbf{D}}^{-1}\hfill \\ \hfill & ={\mathbf{D}}^{-1}-{\mathbf{D}}^{-1}{\mathbf{BD}}^{-1}+{\mathbf{D}}^{-1}{\mathbf{BD}}^{-1}{\mathbf{BD}}^{-1}+\cdots ,\hfill \end{array}$$ (5.12)

provided that D^-1 exists and the series converges uniformly. If D^-1 is known analytically, the inverse of [D+B] can thus be written as a sum of matrix products with no inversion at all required.

To apply Eq. (5.12) to the problems considered in this paper, we take D as the noise term in the data covariance and B as the sum of the object and PSF terms. Thus, from. Eq. (3.34),

$${\left[{\mathbf{D}}^{-1}\right]}_{\mathit{mm}\prime }^{(j,j\prime )}=\frac{1}{{\sigma }_m^2+{\overline{\overline{\overline{g}}}}_m^{\left(j\right)}}{\delta }_{mm\prime }{\delta }_{jj\prime },$$ (5.13)

and formulas for the Hotelling template, the Hotelling detectability, and the EMSE of the Wiener estimator follow readily. For example, the detectability for a weak time-dependent signal is

$$\begin{array}{cc}\hfill {\mathrm{SNR}}_{\mathrm{Hot}}^2& =\sum _{m=1}^M\sum _{j=1}^J\frac{{\left({\overline{\overline{S}}}_m^{\left(j\right)}\right)}^2}{{\sigma }_m^2+{\overline{\overline{\overline{g}}}}_m^{\left(j\right)}}\hfill \\ \hfill & -\sum _{m=1}^M\sum _{m\prime }^M\sum _{j=1}^J\sum _{j\prime =1}^J\frac{{\overline{\overline{s}}}_m^{\left(j\right)}{\left[{\overline{\mathbf{K}}}_{\overline{\mathbf{G}}}^{\mathrm{PSF}}+{\mathbf{K}}_{\overline{\overline{\mathbf{G}}}}^{\mathrm{obj}}\right]}_{\mathit{mm}\prime }^{(j,j\prime )}{\overline{\overline{s}}}_{m\prime }^{(j\prime )}}{({\sigma }_m^2+{\overline{\overline{\overline{g}}}}_m^{\left(j\right)})({\sigma }_{m\prime }^2+{\overline{\overline{\overline{g}}}}_{m\prime }^{(j\prime )})}+\cdots .\hfill \end{array}$$ (5.14)

The first term is just what we would get for detection on a nonrandom background [cf. Eq. (4.12)], and the second term is a first-order estimate of the decrease in detectability (note the minus sign) arising from the spatiotemporal covariance of the object and PSF. Higher-order terms, not shown, refine the estimate of object and PSF effects, and the series will converge quickly if these effects are weak. Thus the Neumann approach is most applicable in the low-light situations often encountered in astronomy.

In spite of the quadruple sum, the second term of Eq. (5.14) might be relatively easy to compute. The sums over pixel indices m and m′ need to cover only those pixels where the signal to be detected is nonzero, an area determined by the width of the uncorrected PSF. For example, if the task is detection of a point object and the science camera has 1000×1000 pixels, then M = 10⁶ and the double sum in principle contains 10¹² terms, but if an uncorrected PSF covers only 1000 pixels, then there are only 10⁶ nonzero terms in the double sum, a million-fold reduction in computation. Moreover, the double sum over j and j′ reduces to a single sum if the signal, PSF, and background are all temporally stationary random processes.

3. Matrix-Inversion Lemma

The Woodbury matrix-inversion lemma states that

$$\begin{array}{cc}\hfill {[\mathbf{A}-\mathbf{UBV}]}^{-1}& ={\mathbf{A}}^{-1}+{\mathbf{A}}^{-1}\mathbf{UB}{\left[{I-\mathrm{VA}}^{-1}\mathbf{UB}\right]}^{-1}{\mathbf{VA}}^{-1}\hfill \\ \hfill & ={\mathbf{A}}^{-1}+{\mathbf{A}}^{-1}\mathbf{U}{[\mathbf{I}-{\mathbf{BVA}}^{-1}\mathbf{U}]}^{-1}{\mathbf{BVA}}^{-1}.\hfill \end{array}$$ (5.15)

This lemma is most useful when the perturbation term UBV has low rank, and we shall see two examples below where this is the case. For other forms of the lemma and a good discussion, see Tylavsky and Sohie.⁵⁶

One application of the matrix-inversion lemma is to the problem of detection of a known signal on a spatially uniform background of random, time-varying level. The covariance matrix for this problem, given in Eq. (4.8), is MJ × MJ (where M is the number of detector pixels and J is the number of frames). To find its inverse, we use the lemma with U chosen as an M × 1 array of blocks, each block being a J × J unit matrix (hence U is MJ × J), and V = U^t. Thus, for any J × J matrix T, UTV is an MJ × MJ matrix with elements $[\mathrm{UTV}{]}_{\mathit{mm}\prime }^{(j,j\prime )}=T^{(j,j\prime )}$. Note also that VU = MI_J, where I_J is the J × J unit matrix. It then follows from Eq. (4.8) and the second form of Eq. (5.15) that

$$\begin{array}{cc}\hfill {\left[{\mathbf{K}}_{\mathbf{G}}^{-1}\right]}_{\mathit{mm}\prime }^{(j,j\prime )}& ={({\sigma }^2+\eta \overline{C})}^{-1}{\delta }_{mm\prime },{\delta }_{jj\prime }-\frac{{\eta }^2}{{({\sigma }^2+\eta \overline{C})}^2}\hfill \\ \hfill & \times {\left[{\left({\mathbf{I}}_J+\frac{\mathbf{M}{\eta }^2}{{\sigma }^2+\eta \overline{C}}{\mathbf{K}}_J\right)}^{-1}{\mathrm{K}}_j\right]}^{(jj\prime )}\hfill \\ \hfill & \equiv {({\sigma }^2+\eta \overline{C})}^{-1}{\delta }_{mm\prime }{\delta }_{jj\prime }-{\mathbf{Q}}^{(jj\prime )},\hfill \end{array}$$ (5.16)

where K_J is a J × J matrix with elements $[\mathrm{UTV}{]}_{\mathit{mm}\prime }^{(j,j\prime )}=T^{(j,j\prime )}$. The matrix to be inverted in Eq. (5.16) is only J × J, so it is feasible to perform the inverse with standard linear-algebra packages. One might be tempted to assume stationarity and use a DFT for the inversion, but even with stationarity K_J is Toeplitz and not circulant, so the DFT does not exactly diagonalize the matrix.

Another important application of the matrix-inversion lemma arises when we have approximated the PSF term and/or the object term in the covariance with sample covariance matrices as in Eqs. (5.5)-(5.7). To illustrate the approach, consider the faint-companion problem where the PSF term is estimated from L samples as in Eq. (5.5). We also assume for simplicity that the object term is negligible. Then, in a method suggested by Brandon Gallas,¹ we can write the sample estimate of the PSF term, Eq. (5.5), as

$${\widehat{\overline{\mathbf{K}}}}_{\overline{\mathbf{G}}}^{\mathrm{PSF}}={\mathbf{RR}}^{\mathrm{t}},$$ (5.17)

where R is an MJ × L matrix with elements

$${\mathbf{R}}_{lm}^{\left(j\right)}=\frac{A_{\ast }}{\sqrt{\mathbf{L}-1}}\Delta h_{lm}^{\left(j\right)}\left(r_{\ast }\right).$$ (5.18)

From the matrix-inversion lemma,

$$\begin{array}{cc}\hfill {[{\overline{\overline{\mathbf{K}}}}_{\mathbf{G}}^{\text{noise}}+{\mathbf{RR}}^{\mathrm{t}}]}^{-1}& ={\left[{\overline{\overline{\mathbf{K}}}}_{\mathbf{G}}^{\text{noise}}\right]}^{-1}-{\left[{\overline{\overline{\mathbf{K}}}}_{\mathbf{G}}^{\text{noise}}\right]}^{-1}\hfill \\ \hfill \times \mathbf{R}& {[{\mathbf{I}}_L+{\mathbf{R}}^{\mathrm{t}}{\left[{\overline{\overline{\mathbf{K}}}}_{\mathbf{G}}^{\text{noise}}\right]}^{-1}\mathbf{R}]}^{-1}{\mathbf{R}}^{\mathrm{t}}{\left[{\overline{\overline{\mathbf{K}}}}_{\mathbf{G}}^{\text{noise}}\right]}^{-1}.\hfill \end{array}$$ (5.19)

The advantage of this form is that only an L × L matrix needs to be inverted, where L is a few hundred or a few thousand in practice, rather than an MJ × MJ matrix, where M may be 10⁶. This inverse can then be used to estimate the Hotelling discriminant or the corresponding detectability. Even though we are using sample covariance matrices here, we are not reducing the Hotelling discriminant to a Fisher discriminant; instead we are estimating the Hotelling discriminant in a problem where the Fisher discriminant does not exist.

4. Dimensionality Reduction

A common way of dealing with large covariance matrices in automated signal detection and pattern recognition is to combine the original measurements (MJ of them in our context) into some much smaller set of numbers, often called features. If the features are linear combinations of the data, then the feature extractor is a linear operator called a channel.

If N features are used, the Hotelling test statistic and detectability can be computed by inverting an N × N matrix. Though this method is very valuable in many practical settings, it is not recommended for assessment of image quality since there is no way of knowing how much information has been lost in the dimensionality reduction. At best, the resulting detectability is a figure of merit for the combination of the feature-selection algorithm and the imaging system, while the interest in objective assessment is only in the latter.

Sometimes, however, it is possible to construct channels such that the Hotelling detectability calculated for the linear features is essentially the same as for the raw data; in this case the channels are said to be efficient. Efficient channels for use in image-quality assessment can often be constructed by using strong prior knowledge that one would not necessarily have in actual signal-detection problems. For example, if we consider the task of detecting a rotationally symmetric signal at a known location in a spatially isotropic random background, the templates that define the channels can be taken as rotationally symmetric functions. Moreover, if we know a priori that the correlation length of the background is relatively long, the channel functions can be broad and smooth. Such considerations led to the use of a small set of Laguerre—Gauss functions as potentially efficient channels⁵⁷ in medical problems, and a detailed simulation study⁵⁸ showed that they could indeed be efficient. Alternatively, inefficient channels that accurately predict the performance of human observers can be used.^59–61

Another way of reducing the dimensionality of a covariance matrix is PCA. In essence, PCA amounts to performing an eigenanalysis of a sample covariance matrix and discarding all eigenvectors except those corresponding to the N largest eigenvalues. Thus, if we consider an M′ × M′ sample covariance matrix $\widehat{\mathbf{K}}$ formed from L samples, it has an approximate spectral representation of

$$\widehat{\mathbf{K}}\approx \sum _{n=1}^N{\lambda }_n{\varphi }_n{\varphi }_n^{\mathrm{t}}\equiv \Phi \wedge {\Phi }^{\mathrm{t}}(N\le L-1),$$ (5.20)

where, in the first form, $\widehat{\mathbf{K}}{\varphi }_n={\lambda }_n{\varphi }_n$, the λ_n are ordered by decreasing values, and the eigenvectors {ϕ_n,n = 1, …,N} are orthonormal and have dimension M′ × 1. In the second form, Φ is an M′ × N matrix with ϕ_n as its nth column and Λ is an N × N matrix with the values of λ_n along the diagonal. In practice PCA is most useful if we can take $N⪡L-1$.

To apply PCA to AO, we interpret $\widehat{\mathbf{K}}$ as the sum of sample estimates of the object and PSF terms in the covariance decomposition and hence take M′ = MJ. As discussed in Subsection 5.A, these sample estimates can be computed by noise-free simulation, and we can let the simulation code run long enough to get the desired accuracy in the estimate. Then, for some L that is large but still $⪡MJ$, we can use standard algorithms to solve for the N eigenvectors with largest eigenvalues and use them to simplify any of our formulas for objective figures of merit.

6. SUMMARY AND CONCLUSIONS

One goal of this paper was to show in detail how the principles of objective or task-based assessment of image quality could be applied to the important practical problem of adaptive optics (AO), especially in astronomy. A second goal was to use this application to extend the methodology of objective assessment itself by considering spatiotemporal systems with random point spread functions (PSFs).

A continuous-to-discrete (CD) model of the imaging system was used throughout. In CD models, the object to be imaged is treated as a function of continuous variables, but the image is a discrete set of numbers or a finite-dimensional vector. The objects considered here were spatiotemporal functions of two spatial variables and the time, and the data were indexed by a pixel index m and a frame number j. An immediate consequence is that a data vector is huge, with MJ elements, where M is the number of pixels in the image detectors (∼10⁶) and J is the number of frames (often thousands in astronomy).

Since task performance must be measured in statistical terms, the statistical properties of objects and images are crucial. We therefore performed a general statistical analysis of a generic AO system. Though formal expressions for the full multivariate probability density function of the data were given, they were used mainly to compute the mean vectors and covariance matrices needed to compute performance on detection and estimation tasks with linear observers. In particular, it was shown that the MJ × MJ covariance matrix could be written rigorously as a sum of three terms, referred to as the noise, PSF, and object terms. The noise term was so called since it would vanish if there were no Poisson or readout noise in the data. Similarly, the PSF term would vanish if the PSF were nonrandom, as with a perfect AO system, and the object term would vanish if there were no random spatial or temporal structure in the astronomical scene. In spite of these designations, all three terms were affected by all three sources of randomness, especially in the case where the guide star or other reference source for the AO system was considered to be random and part of the object. Formulas were derived for each of the three terms in the covariance expansion.

To illustrate various aspects of the theory, three specific tasks of astronomical interest were analyzed: detection of a weak pointlike object on a random background, detection of a faint companion, and photometry. The primary observer considered for the two detection tasks was the ideal linear discriminant, known in the objective-assessment literature as the Hotelling observer. The observer considered for the photometric estimation task was the Wiener estimator, which is ideal in the sense that it minimizes the ensemble mean square error among all linear and globally unbiased estimators. Like the Hotelling discriminant, the Wiener estimator requires knowledge of the ensemble covariance matrix and the ability to invert it.

Several methods were presented for estimating each of the three terms in the covariance matrix. The noise term is the easiest to handle since in almost all practical circumstances the noise is uncorrelated from pixel to pixel or frame to frame. Thus the noise covariance is at least diagonal and often simply a multiple of the MJ × MJ identity matrix. The random object and PSF, on the other hand, introduce complicated spatiotemporal correlations. Some cases where the object term could be expressed analytically were discussed, and sample methods for approximating that term in other cases were presented. At the present state of our understanding of AO systems, no analytic model for the PSF term in the covariance is available, but sample methods are straightforward.

Because of the presence of the diagonal noise term, the overall covariance is invertible in principle, even when sample methods are used for the object and PSF terms. Several practical algorithms for dealing with the inverse and computing figures of merit for task performance were presented. Since the viability of all of these algorithms has been established with purely spatial data in the medical-imaging literature, there is little doubt of their practicality for spatiotemporal data from AO systems.

The main conclusion of this paper, therefore, is that a rigorous statistical, task-based assessment of image quality in AO is possible and that the time is ripe for its application.

APPENDIX A: ANALYTIC AUTOCOVARIANCE FUNCTIONS FOR RANDOM OBJECTS

As we saw in Eq. (3.38), the object term in the spatiotemporal covariance matrix can be interpreted as a transformation of the autocovariance function of the object random process through the ensemble-average imaging system. In this appendix we provide analytic expressions for the object autocovariance function for three situations of practical interest in astronomy.

1. Star Fields

Consider a collection of time-independent point objects described by

$$f\left(\mathbf{r}\right)=\sum _{n=1}^N{A}_n\delta (\mathbf{r}-{\mathbf{X}}_n),$$ (A1)

which is a random process specified by 2N+1 random quantities: the N amplitudes A_n, the N position vectors x_n, and N itself. We assume that the positions are drawn independently from some known PDF pr_x(x_n), that the number of points in some finite region of space is statistically independent of the number in any nonoverlapping region, and that the probability of two or more points lying in some small area Δa goes to zero as Δa → 0; these assumptions would make f(r) a Poisson random process were it not for the random amplitudes A_n. We assume that the amplitudes are drawn independently from pr_A(A_n) and that A_n is independent of x_n. The ensemble mean object is given by

$$\overline{f}\left(\mathbf{r}\right)={\langle {\langle \sum _{n=1}^N{A}_n\delta (\mathbf{r}-{\mathbf{x}}_n)\rangle }_{\left\{A_n\right\},\left\{{\mathbf{X}}_n\right\}\mid N}\rangle }_N,$$ (A2)

where the inner expectation is over the sets {A_n,n = 1, … ,N} and {x_n,n = 1, … ,N}, while the outer expectation is over N. With the independence assumptions stated above,

$$\begin{array}{cc}\hfill \overline{f}\left(\mathbf{r}\right)& ={\langle N{\int }_0^{\infty }d{A}_n{\mathrm{pr}}_A\left(A_n\right)A_n{\int }_{\infty }{d}^2{x}_n{\mathrm{pr}}_{\mathbf{x}}\left({\mathbf{x}}_n\right)\delta (\mathbf{r}-{\mathbf{x}}_n)\rangle }_N\hfill \\ \hfill & =\overline{N}\langle A_n\rangle {\mathrm{pr}}_{\mathbf{x}}\left(\mathbf{r}\right)=\langle A_n\rangle b\left(\mathbf{r}\right),\hfill \end{array}$$ (A3)

where $\overline{N}\equiv \langle N\rangle$ and b(r), defined by

$$b\left(\mathbf{r}\right)\equiv \overline{N}p{r}_{\mathbf{x}}\left(\mathbf{r}\right),$$ (A4)

can be interpreted as the mean number of point objects per unit area at location r. For example, in a globular cluster it is common to assume that b(r)∝|r-r₀|^-β for some positive number β and some range of distances from the cluster center r₀.

The autocorrelation function of f(r) is defined by

$$\begin{array}{cc}\hfill & \langle f\left(\mathbf{r}\right)f\left(r\prime \right)\rangle \hfill \\ \hfill & ={\langle {\langle \sum _{n=1}^N\sum _{n\prime =1}^N{A}_n{A}_{n\prime }\delta (\mathbf{r}-{\mathbf{x}}_n)(\mathbf{r}={\mathbf{x}}_{n\prime })\rangle }_{\left\{A_n\right\}\left\{{\mathbf{x}}_n\right\}\mid N}\rangle }_N.\hfill \end{array}$$ (A5)

In the double sum, there are N terms for which n=n′ and N²-N terms for which n≠n′. With the independence assumptions we find that

$$\begin{array}{cc}\hfill \langle f\left(\mathbf{r}\right)f\left(r\prime \right)\rangle =& \langle N^2-N\rangle \langle A_n{\rangle }^{2}p{r}_{\mathbf{x}}\left(\mathbf{r}\right)p{r}_{\mathbf{x}}\left(r\prime \right)\hfill \\ \hfill & +\langle N\rangle \langle A_n^2\rangle \int d^2{x}_{n}p{r}_{\mathbf{x}}\left({\mathbf{x}}_n\right)\delta (\mathbf{r}={\mathbf{x}}_n)\delta (r\prime -{\mathbf{x}}_n)\hfill \\ \hfill =& ({\sigma }_N^2+{\overline{N}}^2-\overline{N})\langle A_n{\rangle }^{2}p{r}_{\mathbf{x}}\left(\mathbf{r}\right)p{r}_{\mathbf{x}}\left(r\prime \right)\hfill \\ \hfill & +\overline{N}\langle A_n^2\rangle p{r}_{\mathbf{x}}\left(\mathbf{r}\right)\delta (\mathbf{r}-r\prime ),\hfill \end{array}$$ (A6)

where σ²_N is the variance of N. In spite of the random amplitudes, the independence assumptions imply that N is Poisson,¹ so ${\sigma }_N^2=\overline{N}$.

The final autocovariance function is given by

$$K_{\mathbf{f}}(\mathbf{r},r\prime )\equiv \langle f\left(\mathbf{r}\right)f\left(r\prime \right)\rangle -\overline{f}\left(\mathbf{r}\right)\overline{f}\left(r\prime \right)=\langle A_n^2\rangle b\left(\mathbf{r}\right)\delta (\mathbf{r}-r\prime ).$$ (A7)

Thus f(r) is uncorrelated with f(r′) for r≠r′; the data produced by an imaging system will, however, be correlated, with the correlation length determined by the system resolution. Neither the object nor the image data will be spatially stationary unless the point density b(r) is a constant.

This analysis can be extended to the case where b(r) is itself a random process,¹ representing for example an ensemble of globular clusters.

2. Spatially Stationary Background Models

The autocovariance of the object can often be expressed analytically for a diffuse sky background with some random spatial structure. An example would be the light scattered from galactic dust distributions, often referred to as galactic cirrus.

If the random diffuse background is a wide-sense stationary random process, or at least approximately so over the field of view in some astronomical study, it can be specified by its power spectral density S_f(ρ), where ρ is a 2D spatial-frequency vector (in image-plane coordinates). If a functional form for S_f(ρ) is known or can be estimated from observations, then the needed autocovariance function is readily obtained by a 2D Fourier transform (Wiener—Khinchin theorem). In the special case where the background is isotropic, S_f(ρ) depends only on the magnitude of ρ, denoted ρ, and the autocovariance is obtained by a Hankel transform.

As an example, it is found³⁵ that galactic cirrus in the far infrared has a power spectrum given approximately by S_f(ρ)∝ρ^-γ over about a two-decade range in ρ; the experimental value found for γ is about 3. This power-law spectral density indicates a scale-invariant or fractal structure, but the experimental power spectra seem to approach a constant value rather than diverging as ρ → 0. If we avoid the divergence by taking S_f(ρ)∝(ρ+ρ₀)^-γ, the autocovariance function needed in Eq. (3.39) is purely spatial and given by

$$K_{\mathbf{f}}(\mathbf{r},\mathbf{r}\prime ,t,t\prime )\propto 2\pi {\int }_0^{\infty }\rho d\rho (\rho +{\rho }_0{)}^{-\gamma }{J}_0(2\pi \rho \mid \mathbf{r}-\mathbf{r}\prime \mid ),$$ (A8)

where J₀(·) is the zero-order Bessel function of the first kind. The parameters γ and ρ₀ can be estimated from actual data, and the integral can be performed numerically.

3. Random Background Level

Above we considered a diffuse background with spatial structure but no time dependence; the opposite situation—no spatial variation but a time-dependent background level—also occurs frequently in astronomy.

The background model in this case is simply

$$f(\mathbf{r},t)=C\left(t\right),$$ (A9)

where C(t) is a temporal random process specifying the fluctuating background level. The spatiotemporal autoco-variance function of f(r,t) is the same as the temporal autocovariance of C(t), denoted K_C(t,t′). If C(t) is stationary, its ensemble mean $\langle C\left(t\right)\rangle$ is independent of time and can be denoted $\overline{C}$, and the autocovariance is a function only of the time difference, so that K_C(t,t′)=K_C(t-t′).

Two limits are of interest. If C(t) is stationary and sufficiently slowly varying that it is constant over one frame of the science camera, Eq. (3.39) becomes

$$,K_{\mathrm{f}}^{(jj\prime )}(\mathbf{r},\mathbf{r}\prime )=K_C(t_j-t_{j\prime }),$$ (A10)

and if it varies so slowly that it is constant over the entire study, then

$$K_{\mathrm{f}}^{(jj\prime )}(\mathbf{r},\mathbf{r}\prime )={\sigma }_{C,}^2,$$ (A11)

where σ²_C is the variance of C. Even though this latter autocovariance function is independent of both spatial and temporal variables, it can have an important impact on task performance (see Subsections 4.A and 4.C).