Determination of the Transition-State Entropy for Aggregation Suggests How the Growth of Sickle Cell Hemoglobin Polymers can be Slowed

Abstract

Sickle cell anemia is associated with the mutant hemoglobin HbS, which forms polymers in red blood cells of patients. The growth rate of the polymers is several micrometers per second, ensuring that a polymer fiber reaches the walls of an erythrocyte (which has a 7-μm diameter) within a few seconds after its nucleation. To understand the factors that determine this unusually fast rate, we analyze data on the growth rate of the polymer fibers. We show that the fiber growth follows a first-order Kramers-type kinetics model. The entropy of the transition state for incorporation into a fiber is 95 J mol⁻¹ K⁻¹, very close to the known entropy of polymerization. This agrees with a recent theoretical estimate for the hydrophobic interaction and suggests that the gain of entropy in the transition state is due to the release of the last layer of water molecules structured around contact sites on the surface of the HbS molecules. As a result of this entropy gain, the free-energy barrier for incorporation of HbS molecules into a fiber is negligible and fiber growth is unprecedentedly fast. This finding suggests that fiber growth can be slowed by components of the red cell cytosol, native or intentionally introduced, which restructure the hydration layer around the HbS molecules and thus lower the transition state entropy for incorporation of an incoming molecule into the growing fiber.

Introduction

Polymerization of sickle cell hemoglobin, HbS, is one of the basic events in the pathophysiology of sickle cell anemia.^1,2 It occurs in the venous circulation,³ when HbS is in deoxy state and in its R conformation. HbS polymerization is a first-order phase transformation,⁴ and it follows a pathway common for all such transformations: after discrete events of nucleation of polymer fibers, they grow by incorporating single molecules from solution.^5–8 The typical growth rates of an HbS polymer fiber are of the order of several micrometers per sec ond,^9,10 so that a polymer fiber reaches the cell walls within a few seconds after nucleation.^8,10 The resulting deformation and damage of the cell membrane are among the major events in the disease pathophysiology.^11,12 Slower growth would allow cells with nucleated polymers to reach the arterial circulation undamaged, where hemoglobin is in its T state and does not polymerize, while the polymers formed in the venous circulation dissolve. In this article, we analyze the mechanisms of incorporation of HbS molecules into growing polymer fibers and suggest potential means to slow the fiber growth.

Results and Discussion

Kinetic model of HbS polymer fiber growth

The growth kinetics of HbS can be quantified by direct monitoring of a supersaturated solution of HbS in a way that allows detection of individual, nucleated, growing fibers. The solution composition mimics the composition of the red cell cytosol: the solution contains only 0.15 M phosphate buffer at pH 7.35, 0.05 M sodium dithionite to facilitate deoxygenation,⁹ and hemoglobin S with concentration from 200 to 230 mg ml⁻¹. These HbS concentrations are lower than those in the red cells, where they are around 350 mg ml⁻¹; on the other hand, we carry out the experiments in completely deoxygenated conditions, while there is significant oxygen pressure in the venous circulation. With these caveats, we view the growth rates measured in our setup as representative for the HbS fiber growth rates in the red cells. The solution is held in a thin slide, and individual fibers as short as 0.5–1 μm are detected at the times of their appearance. Their length can be determined in subsequent times. The procedure for determination of the fiber growth rate, R, from sequences of images of the evolution of HbS polymerization and other experimental details are discussed in Ref. 13. In the same article, it was shown that due to the slow diffusive supply of HbS molecules from the solution to the growing end of a fiber, the average growth rate of the HbS fibers is reduced,¹⁴ in comparison to the case of oversupply of material, by a factor κ ≈ 3.

The fiber growth rates R in Fig. 1a are 2–4 μm s⁻¹. Since human red cells have a diameter of about 7 μm, if similar rates are found in the red cells of patients with sickle cell anemia, the fibers would reach the cell walls and stretch the cells within 2–3 s. These rates are faster by at least a factor of 10× than the fastest rate recorded for the growth of any protein ordered structure and 100× and 1000× faster than the typical values of these rates.¹⁵ To a certain extent, this fast kinetics is due to the high concentration of HbS. To identify the additional factors that contribute to the fast growth rate and those that could help control and slow the growth, we need to understand the mechanism of incorporation of the HbS molecules into the fibers and the nature and magnitude of the respective free-energy barriers. For this, we develop a testable model of the incorporation.

Fig. 1.

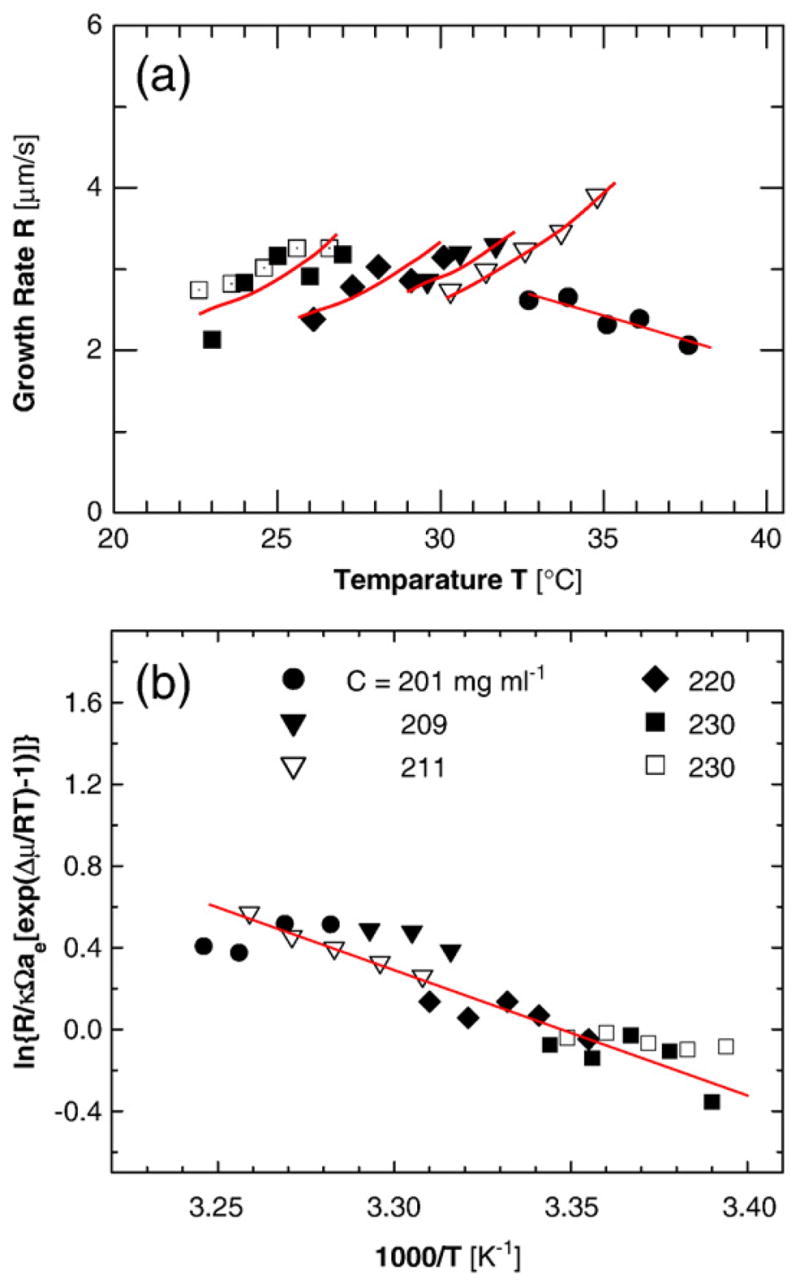
The kinetics of growth of the HbS fibers. (a) Growth rate R as a function of temperature at five HbS concentrations as indicated in (b), two independent data sets at C=230 mg ml⁻¹ are shown (from Ref. 9). Lines for each HbS concentration are merely guides for the eyes. (b) Plot of data in (a) in Arrhenius coordinates, according to Eq. (5).

The growth rate R is proportional to the net number of molecules that join a growth site at the growing end of a fiber per unit time

$$R=b(j_{+}-j_{-}),$$ (1)

where b=5.5 nm is the effective diameter of an HbS molecule, j₊ is the number of molecules entering a growth site, and j₋ is the number of molecules departing from a growth site per unit time. A growth site is a location at which an incoming molecule has half of the number of neighbors inside the polymer.^16,17Equation (1) assumes that the density of growth sites is high, equal to 1, and that their creation is not a kinetic obstacle. In view of the HbS polymer structure, where the 14 molecules in a cross section are at different heights¹⁸ (Fig. 2a), this is a natural assumption.

Fig. 2.

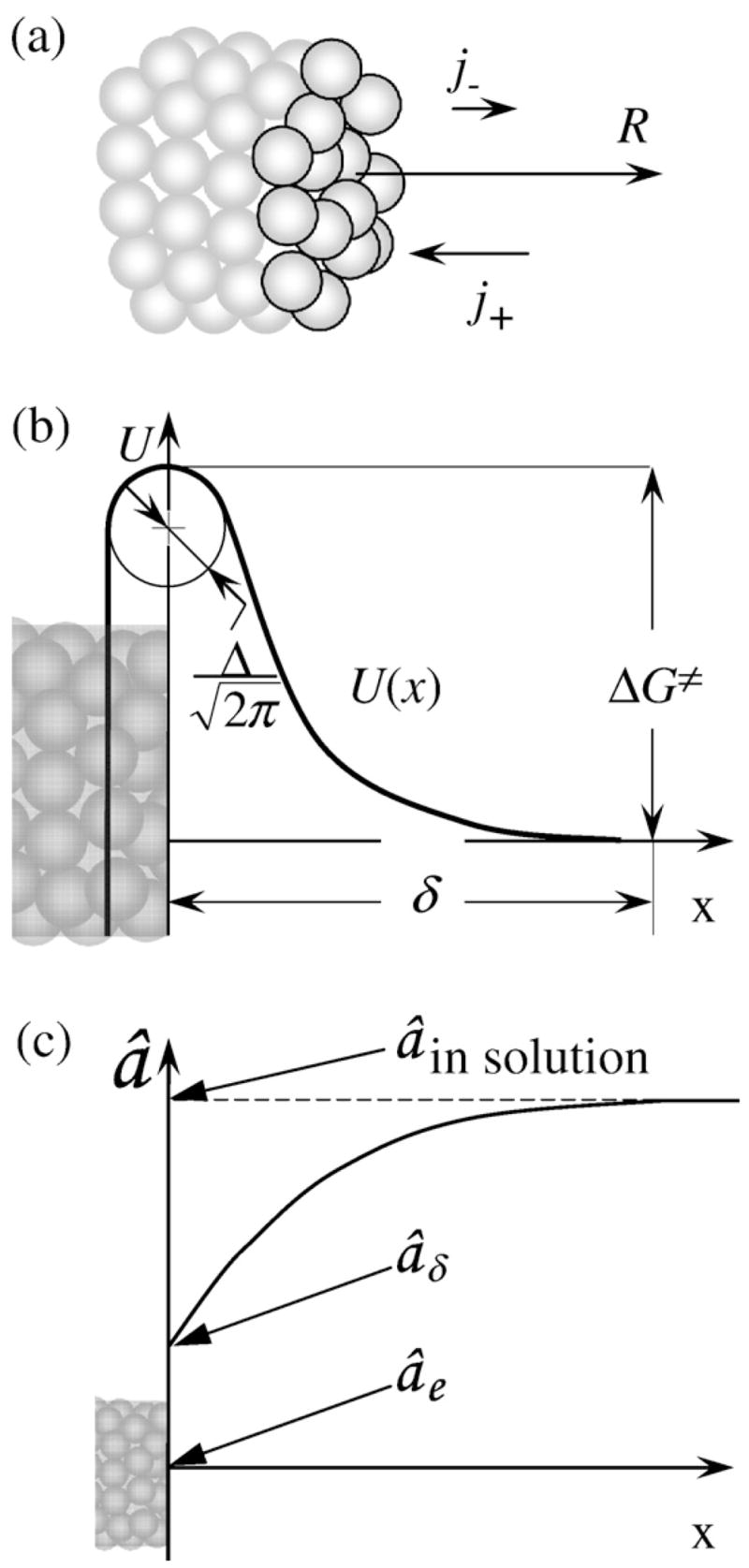
(a) Schematic representation of a growing fiber. HbS molecules at the growing edge are highlighted. (b) Schematic illustration of the free-energy relief U(x) in front of the growing fiber; for the meaning of the symbols, see the text. Growth rate R, incoming flux j₊, and departing flux j₋ of molecules in (a) and x-axis in (b) are directed along the fiber axis (c). Schematic representation of the distribution of HbS activity in front of a growing HbS polymer fiber. The x-scale in (c) is much coarser than that in (b).

The incoming flux into a site is j₊ =ĴΔS_site ≈ Ĵb², where ΔS_site is the area of the cross section of the fiber per growth site. Thus, we evaluate the flux Ĵ of molecules with concentration n that, driven by a concentration gradient, overcome a barrier to reach the surface. The barrier is due to the interaction of an incoming HbS molecule with the HbS molecules at the surface of the fiber. We denote with U(x) the potential of the mean force of this interaction. U(x) has a repulsive part, as discussed below, and an attractive part due to the hydrophobic forces that keep the HbS molecules in the fiber together. These hydrophobic contacts are formed between valine of one HbS molecule (the mutation from glutamate, an acidic amino acid residue in normal adult hemoglobin, to valine in HbS is the crucial mutation underlying sickle cell anemia) and alanine, phenylalanine, and leucine from an adjacent HbS molecule.^19–22 In Fig. 2b, the resulting free-energy relief U(x) is schematically depicted as a function of the distance x from the fiber-growing surface. The potential of the mean force reaches its maximum value ΔG^≠ at the crossing of the increasing and receding branches. This ΔG^≠ = ΔH^≠−TΔS^≠, and it represents the free energy of the transition state, that is, the barrier for incorporation, whose enthalpy, ΔH^≠, and entropy, ΔS^≠, components are discussed below.

To evaluate Ĵ, we use the generalized Fick’s law, Ĵ =(âD/k_BT)dμ/dx, with μ(T,x)=μ₀(T)+ k_BTln[â(x)]+ U(x), where â is the HbS activity. This transforms to:^23,24

$$\widehat{J}=D\left[\frac{\text{d}\widehat{a}(x)}{\text{d}x}+\widehat{a}(x)\frac{\text{d}(U(x)/k_{\text{B}}T)}{\text{d}x}\right],x>0.$$ (2)

Equation (2) is often referred to as the Smoluchowski equation.²⁵

We represent U(x) around its maximum with a symmetric function and introduce the parameter Λ as the radius of curvature of U(x)/k_BT at this maximum:²⁶

$$\mathrm{\Lambda }={(1/2\pi \parallel {\partial }^2(U/k_{\text{B}}T)/\partial x^2{\parallel }_{max})}^{-1/2}.$$ (3)

The end of a single 14-member growing fiber can be considered as a point sink for HbS molecules, supplied by the entire three-dimensional space around it. The integration of Eq. (2) for this case should be carried out in three dimensions. However, the data in Fig. 1a were collected with fiber bundles, which were several micrometers thick. Thus, each individual fiber inside this bundle is only supplied from the solution space immediately in its front, and a one-dimensional integration of Eq. (2) is appropriate.

We position the x-axis along the fiber axis (Fig. 2b) and place its beginning, x=0, at the location of the U(x) maximum. In search of a steady Ĵ =const, we integrate Eq. (2) with two sets of boundary conditions:

1. At a distance δ from the surface, x≥δ and U=0, and the HbS activity is â_δ. If there were no constraints due to the diffusion of HbS toward the growing end of a fiber, â_δ would be equal to â in the solution bulk (Fig. 2c). However, because of the slow diffusion, (â_δ−â_e) = κ⁻¹(â−â_e).⁹ The distance δ is chosen such that it is longer than the range of interaction of the solute molecules with the surface, which can be a few solvent molecular sizes, that is, 1 nm, and is shorter than the distances between the HbS molecules in the solution, n^−1/3 ≈ 8 nm. Since the rate of diffusion over a sharp barrier only depends on the curvature around the maximum,^24,27 the choice of δ does not affect the result.

2. In the fiber, that is, at x≤0, â =0.

With these two boundary conditions, the integration yields

$$\widehat{J}=D/\mathrm{\Lambda }exp(-\mathrm{\Delta }{G}^{\ne }/k_{\text{B}}T){\widehat{a}}_{\delta }.$$ (4)

In equilibrium, both â and â_δ equal the solubility â_e, and j₊ = j₋. Since j₋ does not depend on â, and with b³ =Omega;, the volume that one HbS molecule occupies in the fiber, the growth rate R is

$$\begin{array}{l}R=b(j_{+}-j_{-})=\mathrm{\Omega }\frac{D}{\mathrm{\Lambda }}exp\left(-\frac{\mathrm{\Delta }{G}^{\ne }}{k_{\text{B}}T}\right)\left({\widehat{a}}_{\delta }-{\widehat{a}}_e\right)\\ =\frac{\mathrm{\Omega }{\widehat{a}}_{e}D}{\mathrm{\Lambda }}exp\left(\frac{\mathrm{\Delta }{S}^{\ne }}{k_{\text{B}}}\right)exp\left(-\frac{\mathrm{\Delta }{H}^{\ne }}{k_{\text{B}}T}\right)[exp(\mathrm{\Delta }{\mu }_{\delta }/k_{\text{B}}T)-1]\\ ={\kappa }^{-1}\frac{\mathrm{\Omega }{\widehat{a}}_{e}D}{\mathrm{\Lambda }}exp\left(\frac{\mathrm{\Delta }{S}^{\ne }}{k_{\text{B}}}\right)exp\left(-\frac{\mathrm{\Delta }{H}^{\ne }}{k_{\text{B}}T}\right)[exp(\mathrm{\Delta }\mu /k_{\text{B}}T)-1].\end{array}$$ (5)

In Eq. (5), [exp(Δμ_δ/k_BT) −1]= â_δ/â_e −1=κ⁻¹ [â/â_e −1]=κ⁻¹ [exp(Δμδ/k_BT) −1] is the driving force for polymerization. With this, Eq. (5) has the typical form for a first-order chemical rate law.28 According to the Stokes–Einstein expression, D=k_BT/3πηb, where η is the solution viscosity.29,30 The reciprocal dependence between R and η makes Eq. (5) similar to a Kramers-type kinetics law,31,32 as should be expected for a reaction in solution. The product Ωâ_e accounts for the change in molecular concentration of HbS between the solution and the fiber.

Does the model apply to HbS fiber growth?

The parameters ΔG^≠, ΔH^≠, ΔS^≠, and Δ characterize the potential of interaction U(x) between an incoming molecule and the fiber edge. Since a hemoglobin molecule carries around 0.5 to 1 elementary charge at the pH of the HbS polymerization experiments (pH 7.35), adjusted to that of the blood, U(x) is likely of nonelectrostatic origin. Numerous recent experimental^33–37 and theoretical^38–41 works have shown that a several-angstrom-thick solvent layer exists around protein molecules. Within this hydration layer,^37,42 the water molecules are in either of two states, between which a dynamic equilibrium exists: directly attached to the protein surface and “free.” Another equilibrium exists between the hydration layer and the bulk solution water.³⁷ This layer determines the thermodynamics and kinetics of enzyme–substrate and DNA–drug binding.^43,44 It has been demonstrated that enthalpy and entropy contributions from the solvent layer largely determine the thermodynamics of crystallization of several proteins.^45–49 It has also been shown that the dynamics of the water molecules within the hydration layer and of exchange between the layer and the bulk water determine the kinetics of incorporation into crystals.^26,50,51 In view of the hydrophobic contacts between the mutated β6 valine and the alanine, phenylalanine, and leucine from an adjacent HbS molecule,^19–22 it is natural to assume that the water structure dynamics will also constitute the main component of the barriers for incorporation of HbS molecules into fibers.

For molecules whose aggregation is hampered by a hydration layer, ΔH^≠ mostly represents the energy of the interactions (hydrogen bonds and van der Waals) inside this hydration layer, which are broken when the hydration water is pushed out of the contact site between two adjacent molecules.^52–56 Remarkably, ΔH^≠ for about 10 diverse substances, ranging from inorganic salts, to organic molecular compounds, to proteins and viruses, was found to be within a narrow range centered on 30 kJ mol^≠1.⁵⁷ This consistency of ΔH^≠ suggests that the barrier is determined by the removal of a small number of water molecules at the contact site, even for molecules as large as viruses. Correspondingly, the width Λ was found to be of the order of several water molecules, that is, from 0.6 to 1 nm.^{34,37,47,55,58,59} If the barrier for incorporation of HbS molecules into HbS fibers is of similar origin, we expect similar values for ΔH^≠ and Λ.

To test if Eq. (5) and the assumptions behind it apply to the growth of HbS polymer fibers, in Fig. 1b, we replotted the data from Fig. 1a in Arrhenius coordinates, corresponding to the rate law in Eq. (5). The chemical potential difference Δμ and the activity â were calculated for each HbS concentration and temperature using six virial coefficients B_i for HbS as in Ref. 60. Using temperature-dependent â_e = γC_e and Δμ accounts for the dependence of HbS solubility on temperature.18 The factor κ⁻¹ in Eq. (5) accounts for the depletion of HbS concentration near the fiber edge. The data in Fig. 1b fit a straight line, which supports the applicability of Eq. (5).

To additionally test the validity of the model behind Eq. (5), we evaluate the parameters of this model from the slope and intercept of the straight line in Fig. 1b. Since the viscosity η decreases with increasing temperature, D in Eq. (5) is a function of temperature, D=D_oexp(−E_η/k_BT), where E_η is the effective Arrhenius activation energy for η. For water and low-concentration buffers, E_η is ~ 15 kJ mol⁻¹.⁶¹ With this E_η, D₀ =1.4×10⁻⁴ cm² s⁻¹. In view of the temperature dependence of D, the slope of the straight line in Fig. 1b corresponds to ΔH^≠+E_η. From the data in Fig. 1b, ΔH^≠+E_η =43 kJ mol⁻¹, so that ΔH^≠=28 kJ mol⁻¹. This value is within the range found for other species forming ordered solid phases from solution. This correspondence supports the applicability of Eq. (5) to the growth of HbS polymers, and the suggestion that the activation barrier for incorporation of HbS molecules into a growing fiber characterizes the rearrangement of the water shell at the contact surfaces of the HbS molecules.

The transition-state entropy and the free-energy barrier for incorporation

The intercept of the straight line in Fig. 1b is equal to ln(D₀/Λ)+ ΔS^≠/k_B. Prompted by the agreement between the value of ΔH^≠ for HbS polymerization and the expectations from a hydration model, we take Λ=1 nm. With the above value for D₀, we obtain ΔS^≠=95 J mol⁻¹ K⁻¹.

The transition-state entropy ΔS^≠ contains two contributions: from the loss of rotational and translational degrees of freedom of the incoming molecule and from the loss or gain of rotational and translational degrees of freedom of water molecules. The HbS contribution is always negative. The loss of rotational degrees of freedom in the transition state is equivalent to selecting a molecular orientation suitable for incorporation into the fiber. This entropy has been estimated and found to be of the order −50 J mol⁻¹ K⁻¹ for protein molecules.⁶² The water molecule contribution may be negative or positive, depending on whether additional water molecules are trapped between the incoming HbS molecule and the fiber edge or some of those associated to the HbS molecules in the solution and to the fiber edge are released.^45,46 Estimates are that the release of one water molecule contributes ~ 20 J mol⁻¹ K^{−145,48,63,64} to the total entropy of the transition state. In general, depending on the sign and magnitude of the water contribution, the total ΔS^≠ may be either positive or negative.

The positive sign of the total ΔS^≠ determined from the data in Fig. 1b indicates that the entropy gain stemming from the release of associated water is greater in magnitude than the entropy loss of the HbS molecule. The entropy contribution to the free-energy barrier for incorporation into the HbS polymer fiber lowers this barrier and accelerates the growth of the polymer. Furthermore, the obtained value for ΔS^≠ is close to the value of the standard entropy for HbS polymerization, ΔS^o, which, at 25°C, is 103 J mol⁻¹ K⁻¹.¹⁸ Both of these facts agree with an evaluation, using molecular dynamics, of the thermodynamic parameters, ΔG, ΔH, and ΔS, of the hydrophobic interaction between two flat graphene sheets of 60 carbon atoms each, or an interface of ~ 130 Ų, approaching each other in water (Fig. 3).^55,65,66 The agreement indicates that the positive value of ΔS^≠ reflects the gain of degrees of freedom of the water molecules, which are associated to the HbS molecules in the solution and are set free upon the formation of the transition state and the subsequent incorporation.^54,56,67 Such gain is expected for the hydrophobic contacts that form between the valine at the β6 site and the alanine, phenylalanine, and leucine from the adjacent HbS molecules.^19–22 The magnitude of ΔS^≠ resulting from the simulations, obtained from the value of TΔS ≈ 7.5 kJ mol⁻¹ in Fig. 3 at 298 K, is ~ 25 J mol⁻¹ K⁻¹ per C–C pair.⁵⁵ This is lower in magnitude than the value of ΔS^≠ for incorporation of HbS molecules into a growing fiber, indicating the participation of several atoms from the two adjacent HbS molecules in the hydrophobic contact in the fiber. The similarity between ΔS^≠ and ΔS^o cannot be used to judge for or against a drying transition as the gap between the contact sites on the incoming HbS molecules and resident HbS molecules in the fiber shrinks: in the case of a drying, ΔS^≠ would be associated with the last layer of water removed from the gap. However, since the hydrophobic contact sites on the HbS molecules have relatively small area,^19–22 it is unlikely that drying out occurs.

Fig. 3.

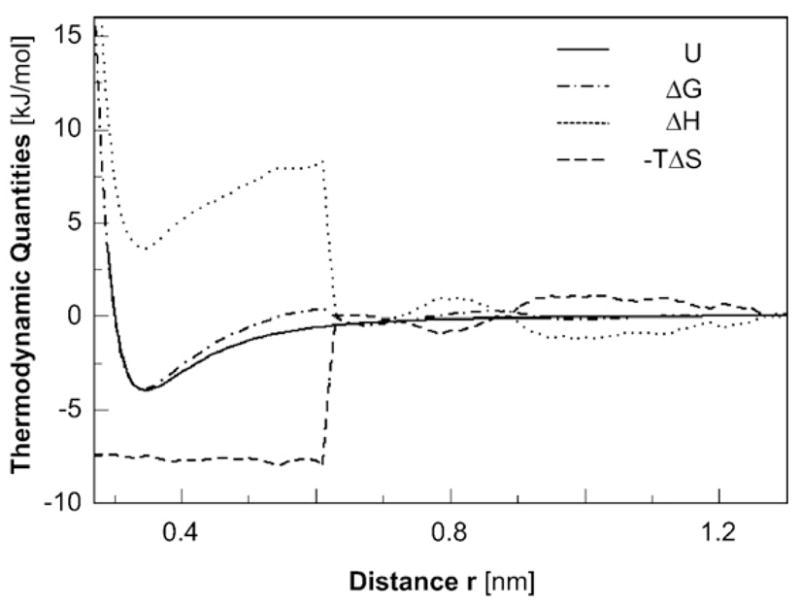
Interactions between idealized hydrophobic surfaces. Two graphene carbon surfaces of 60 atoms each are brought together in water via free-energy simulations.⁵⁵ Plotted as a function of the plate-to-plate separation r and normalized to represent the contribution per atom in the surfaces are the changes in energy U, the free energy ΔG, the enthalpy ΔH, and the entropic contribution −TΔS.

From the values of ΔH^≠ and ΔS^≠, the transition-state free energy ΔG^≠ is negligible; that is, the entropy and enthalpy contributions to the incorporation barrier cancel out and incorporation is effectively barrier free. Note that ΔH^≠ and ΔS^≠ are never negligible. This value of ΔG^≠ indicates that the fast growth of the HbS polymer fibers is due to the strong structuring of the water molecules around the HbS in solution, yielding a high value for the transition-state entropy ΔS^≠ when they are released during incorporation into the fibers.

There is very limited data on ΔS^≠ for other aggregating systems. Results on the kinetics of adsorption of the ions of NH₄H₂PO₄ on the surface of a crystal of this material indicate that the rate of adsorption is well modeled by (D/Λ) exp(ΔS^≠/k_B)exp(−H^≠/k_BT).59,68 Arrhenius plots of the data yielded ΔH^≠=28 kJ mol⁻¹. Using independently determined D yielded Λ=13 Å,⁵⁹ very close to expectations from the water shell model. This suggests that ΔS^≠ ~ 0, likely as a result of the compensation of its two components.

Clinical implications and open questions

The large positive value of the transition-state entropy for the incorporation of HbS molecules into fibers suggests that if ΔS^≠ could be lowered, this could slow the rate of fiber growth and, in this way, prevent the disastrous consequences of HbS polymerization. Indeed, bringing down ΔS^≠ to 50 J mol⁻¹ K⁻¹ would slow the rate of fiber growth by a factor of ~ 5000×, from a few micrometers per second to a few micrometers per hour. The consequences for the disease pathophysiology would be that even if HbS polymers nucleate in the erythrocyte cytosol, the fibers would not grow to a size comparable to that of the cell, ~7 μm, for the ~10 s that red blood cells spend in the low-oxygen environment in the venous circulation. The caveat is that growth regulation via rearrangement of water structures has been accomplished for just two systems.^51,69 In the case of insulin crystallization,⁷⁰ regulation required significant amounts of the active additive⁶⁹; in the case of calcite growth, nanomolar amounts of additives were used, but they only led to effects of less than 2× on the growth rate. Still, the structuring of water around protein molecules in solution is an area of active research, and it is likely that insights will be produced, which may lead to suggestions for suppression of the growth of the HbS polymers.³⁷

A tantalizing hypothesis is that hydroxyurea is active in such rearrangement. Hydroxyurea is used in patients with sickle cell anemia and in those with thrombocytosis. Its chemical similarity to a known osmolyte, urea, could explain the beneficial effects of hydroxyurea, evident in patients before fetal hemoglobin expression is enhanced.⁷¹ (Expression of fetal hemoglobin and the resulting dilution of HbS in the red cell are viewed as the greatest benefits of the hydroxyurea treatment for sickle cell anemia^72,73). Urea denatures proteins by rearranging the water involved in the hydrophobic attraction;^74,75 thus, the hypothesis that hydroxyurea may have similar effects is not unfounded. One could imagine that other osmolytes could similarly change the rate of attachment to an HbS fiber by changing the free-energy barrier for association.

Abbreviation used

HbS

sickle cell hemoglobin