Balancing Solvation and Intramolecular Interactions

Abstract

The efficient and accurate characterization of solvent effects is a key element in the theoretical and computational study of biological problems. Implicit solvent models, particularly generalized Born (GB) continuum electrostatics, have emerged as an attractive tool to study the structure and dynamics of biomolecules in various environments. Despite recent advances in this methodology, there remain limitations in the parameterization of many of these models. In the present work, we demonstrate that it is possible to achieve a balanced implicit solvent force field by further optimizing the input atomic radii in combination with adjusting the protein backbone torsional energetics. This parameter optimization is guided by the potentials of mean force (PMFs) between amino acid polar groups, calculated from explicit solvent free energy simulations, and by conformational equilibria of short peptides, obtained from extensive folding and unfolding replica exchange molecular dynamics (REX-MD) simulations. Through the application of this protocol, the delicate balance between the competing solvation forces and intramolecular forces appears to be better captured, and correct conformational equilibria for a range of both helical and β-hairpin peptides are obtained. The same optimized force field also successfully folds both beta-hairpin trpzip2 and mini-protein Trp-Cage, indicating that it is quite robust. Such a balanced, physics-based force field will be highly applicable to a range of biological problems including protein folding and protein structural dynamics.

Introduction

Successful applications of molecular dynamics (MD) simulations to studying the structure and function of biomolecules hinge on the quality of the underlying molecular force field and the sampling efficacy of the simulation protocol. In particular, the solvent environment plays a critical role in the structure, dynamics and function of biomolecules. However, efficient and accurate treatment of solvation has been a perpetual problem in molecular modeling, despite its prime importance.^1,2 Explicit inclusion of all solvent molecules arguably provides the most accurate and detailed description, but it significantly increases the computational cost and severely limits the simulation timescale and amount of sampling that are practically achievable. Furthermore, interesting quantities such as solvation energies converge very slowly because all solvent degrees of freedom need to be averaged out. Therefore, it is often desirable to describe the mean influence of solvent molecules around the solute without having to treat the solvent explicitly.This has motivated continual efforts in the development of various implicit solvent models.^2-4 Implicit solvent models may yield considerable disagreement with explicit water simulations due to the absence of the granularity of solvent molecules, especially in short-range effects when the detailed interplay of a few water molecules (which are significantly distinct from the bulk water) is important.^4,5 However, there are many biological problems for which implicit solvent models can provide insights that are very difficult to gain from explicit solvent models, such as protein-protein or protein-ligand binding thermodynamics, scoring of protein conformations in structure prediction, protein conformational changes upon binding and pH changes, and peptide and protein folding and unfolding studies.^2,6-8

In the popular continuum electrostatics treatment of solvent, the solute interior and solvent region are described as featureless ”low” (solute) and ”high” (solvent) dielectric regions respectively.³ The electrostatic solvation energy of a solute with an arbitrary shape, including the solvent-screened charge-charge interactions, can be rigorously calculated from numerical solutions of the Poisson-Boltzmann (PB) equation using finite-difference methods.^9-12 While particular successes in applications to complex biomolecular systems are evident,^13,14 the computational cost of solving the PB equation remains a bottleneck to its application to protein folding and routine dynamics simulations of biomolecules, despite progress in fast PB computational methodologies.^15,16

Based on the same underlying continuum representation, the generalized Born (GB) formalism approximates the PB electrostatic solvation energy as an efficient pairwise summation that allows analytical force calculations,^17,18

$$\Delta G_{\mathrm{elec}}=-\frac{1}{2}\left(1-\frac{1}{\epsilon }\right)\sum _{ij}\frac{q_i{q}_j}{\sqrt{r_{ij}^2+R_i^{\mathrm{GB}}{R}_j^{\mathrm{GB}}\exp (-r_{ij}^2∕F{R}_i^{\mathrm{GB}}{R}_j^{\mathrm{GB}})}},$$ (1)

where r_ij is the distance between atoms i and j, q_i is the atomic charge, $R_i^{\mathrm{GB}}$ is the so-called “effective Born radius” of atom i and ε is the solvent (high) dielectric constant. F is an empirical factor whose value may range from 2 to 10, with 4 being the most common value. Note that the (low) dielectric constant of the solute interior is assumed to be 1 (same as vacuum). ΔG_elec then corresponds to the electrostatic free energy of transferring the solute from vacuum to a medium of dielectric constant ε. The effective Born radius, $R_i^{\mathrm{GB}}$, is a key quantity in the GB formalism. It corresponds to the distance between a particular atom and its hypothetical spherical dielectric boundary, chosen such that the self (or atomic) electrostatic solvation energy, ΔG_elec,i, satisfies the Born equation,¹⁹

$$\Delta G_{\mathrm{elec},\mathrm{i}}=-\frac{1}{2}\left(1-\frac{1}{\epsilon }\right)\frac{q_i^2}{R_i^{\mathrm{GB}}}.$$ (2)

In principle, the “exact” effective Born radii can be calculated from Eqn. (2) using the self electrostatic solvation energy obtained through the PB theory. The principal assumption in the GB method is that the solvent-shielded charge-charge interactions can be reproduced by the cross-term summation in Eqn. (1) with the effective Born radii. Indeed, Eqn. (1) has been shown to closely reproduce the PB electrostatic solvation energy, provided that the effective Born radii are accurate.^20,21 As such, most of the extensive literature on extensions of the GB theory has been focused on efficient and accurate evaluation of the Born radii, and ΔG_elec,i or $R_i^{\mathrm{GB}}$ from PB calculations serve as standard benchmarks for assessing various GB approximates. Many modifications, extensions and improvements have been made over the last several years^22-37 and various implementation are now available in virtually all major molecular modeling software packages. At present, the GB formalisms have reached a mature stage and the achievable accuracy can be essentially identical to the PB method.²¹ Successful applications to various biological problems have demonstrated the great potential of the GB implicit solvent models for studies of biomolecular structure and function.^2,8 The main limitation of GB at present lies in its parameterization, manifested as several limitations observed previously indicating over-stabilized salt-bridges and distorted peptide and protein conformational equilibria.^7,8

The successes and failures of various solvent models arise in principle from their ability to balance delicate energetics between sets of competing interactions, i.e., the solvation preference of sidechains and backbones in solution versus the strength of solvent-mediated interactions between these moieties in a complex protein environment. The intra-molecular Coulombic interaction energy in the protein is known to be strongly anti-correlated with the electrostatic solvation energy. Similarly, the intra-molecular van der Waals (vdW) dispersion interaction energy in the protein also strongly anti-correlates with the nonpolar solvation energy.⁸ These competing, opposing forces mostly cancel each other, and a shift in the balance, depending upon the extent of specific interactions in a given protein conformation and environment, can lead to a bias in conformational equilibria. To what extent a GB implicit solvent force field can capture this delicate balance is a key in the success of its applications. For example, as mentioned above, it has been noticed previously that many existing continuum electrostatics solvation models (GB as well as PB) over-stabilize salt-bridges,^38-42 which can partially account for the observed discrepancies in the conformational equilibria and free energy surfaces for several peptides.^40,43,44 This over-stabilization might be amplified even more in the low dielectric protein interior, which appears to be particularly problematic in applications such as protein design.⁴⁵ Unfortunately, achieving sufficient balance of the competing interactions in a force field for complex heterogeneous systems is a challenging task. In addition to the general difficulty that force fields optimized with high-level quantum mechanics are not directly transferable to solvent environments, there is a severe lack of direct experimental data on solvation energies of proteins as well as the pairwise interactions between polar groups in solvent environments. As such, it appears that one has to resort to explicit water simulations and available (indirect) experimental observables (e.g., thermodynamic stability and conformation equilibria of peptides and proteins) in the implicit solvent force field optimization efforts.⁸

Toward this end, we first examine the solvent-mediated interactions between polar groups present in proteins and optimize the implicit solvent force field based on potentials of mean force (PMF) obtained from explicit solvent simulations. In continuum electrostatics, the extent of solvent exposure of each atom at the dielectric boundary dictates all of the electrostatic and most of nonpolar solvation energetics. Thus, it is physically appropriate to optimize the input radii, by which the low dielectric region and the high dielectric region are divided, not only based on total solvation free energy of individual sidechains but also in consideration of solvent-mediated interactions. We have demonstrated previously that by adjusting the GB input radii for the peptide backbone, it is possible to reproduce the solvent mediated backbone H-bond strength given by TIP3P explicit water model⁴⁶ and thus improve the agreement with experimentally measured conformational equilibria of small helical peptides.⁸ In principle, the partial charges, Lennard-Jones parameters, and torsional energetics in the underlying molecular mechanics force field may also need to be adjusted for a specific implicit solvent model to achieve sufficient balance. However, given that current force fields have been extensively calibrated over the past decades to achieve proper solvent-solute and solute-solute interactions in explicit solvent,⁴⁷ at this stage, it is reasonable to focus primarily on optimizing the input radii in the GB implicit solvent. Furthermore, analogous to previous efforts to improve the treatment of the peptide backbone in the context of the TIP3P explicit solvent,⁴⁸ we also empirically adjust backbone dihedral energetics self-consistently with the GB input radii optimization to achieve proper conformation equilibria. Note that adjustment of backbone torsion energetics has also been previously applied to fine tune the Amber force fields.⁴⁹

The atomic input radii for continuum electrostatics have been previously optimized based on the radial solvent charge distribution to reproduce the electrostatic solvation energy obtained from explicit solvent charging free energy calculations for both proteins^50,51 (hereinafter referred to as the Nina’s radii) and nucleic acids.⁵² The Nina’s radii set has been shown to work well in several applications including peptide folding⁵³ and protein NMR structure refinement.^54,55 Therefore it offers a good starting point for further optimization. The input radii are further optimized here to explicitly balance the interactions between amino acid polar groups in a GB implicit solvent, guided by PMFs obtained from explicit solvent free energy simulations. The optimized radii are then assessed by extensive folding and unfolding simulations of a range of peptides and mini-proteins. Correct prediction of conformational equilibria for both helical peptides and β-hairpins has been considered as an important aspect of a molecular force field. It has been the focus of many force field development and parameterization efforts.^37,49,56-60 The simulated conformational equilibria also provide a key feedback for the parameterization of both the input radii and backbone dihedral energetics. An important limitation of such a recursive approach is the slow convergence of conformational equilibria even for small peptides. In this study, an advanced sampling technique, namely, the replica exchange molecular dynamics (REX-MD) method^61-64 has been used extensively to speed up the conformational sampling.

Methods

Force Field

The CHARMM22/CMAP all-atom force field^65-67 with a GBSW implicit solvent model³³ is optimized in this work. GBSW employs a vdW-based surface with a smooth dielectric boundary. Born radii are calculated by a rapid volume integration scheme that includes a higher-order correction term to the Coulomb field approximation, as introduced previously for a closely related GBMV implementation.³¹ Default GBSW parameters were used with a 0.6 Å smoothing length (i.e., w=0.3 Å) along with 50 Lebedev angular integration points and 24 radial integration points up to 20 Å for each atom.³³ The nonpolar solvation energy was estimated from the solvent-exposed surface area (SA) using a phenomenological surface tension coefficient of 0.005 kcal/mol/Ų.

Model Peptides and Proteins

A primary focus of the current optimization efforts is to achieve proper balance of secondary structure preferences. As such, we have chosen a range of α and β peptides and a designed mini-protein. The systems are listed in Table 1, with a summary of representative folding simulations previously reported in the literature. Note that there is not yet a single force field that can provide proper conformational equilibria for all these peptides, while some of these force fields did successfully fold subsets of both α and β peptides as well as other sequences not listed. A similar deficiency of the current protein force fields in balancing the secondary structure preferences was also recently observed using C-peptide of RNase A and GB1p β-hairpin.⁶⁸ Consistent with the experimental conditions, both termini of (AAQAA)₃ peptide were blocked with Ace and NH₂ respectively; the C-terminal of trpzip2 was blocked with NH₂; and all the other peptides were simulated with unblocked termini. The sequences of the β-hairpins are as following: GEWTYDDATKTFTVTE (GB1p); GEWTYDDATKTATVTE (GB1m1); KKYTWNPATGKATVQE (HP5A); KKWTYNPATGKFTVQE (GB1m3); SWTWENGKWTWK-NH₂ (trpzip2). Note that GB1m1, HP5A and GB1m3 are derived from the native sequence of the C-terminal β-hairpin (residues 41-56) of the B1 domain of protein G (GB1p) but display reduced or enhanced stability: (unfolded) GB1m1 < HP5A < GB1p < GB1m3 (most folded).⁶⁹ Therefore, these peptide sequences provide a particularly useful control for the optimization.

Table 1.

Representative successful ab initio folding simulations using all-atom or united-atom (explicit polar hydrogens) physics-based models

Peptide	PDB ID	Structure	Length	Force Fields	References
(AAQAA)3	N/A	α (50%a)	15	CHARMM19/SAS CHARMM22/SCP-ISM Amber84/m-GBSAd	56 70 71
GB1p	3gb1 (41-56)	β (30-80%b)	16	OPLS/GBSA OPLS-AA/SGB OPLS-AA/AGBNP CHARMM19/cGBSTILL	72 73 57 74
GB1m1	N/A	β (6%c)	16	Irbäck and Mohanty	60
HP5A	N/A	β (21%c)	16	N/A	N/A
GB1m3	N/A	β (86%c)	16	Irbäck and Mohanty	60
trpzip2	1le1	β (90%d)	12	Amber99-m1e/GBSA OPLS-AA/GBSA Amber96/GBSA	49 58 75
Trp-cage	1l2y	α/coil	20	Amber99-m2f/GBSA Amber94/GBSA Amber-m3g/GBSA CHARMM19/(ACE,EEF1,SASA) CHARMM22/ACE CHARMM22/CMAP/ACE PFF01 Irbäck and Mohanty	76 77,78 79 80 80 80 81 60

^ahelicity measured by NMR chemical shifts at 270K.⁸²

^bpopulation estimated from multiple NMR chemical shift probes (∼30% at 298 K⁶⁹ or 42% at 278 K⁸³) and from the tryptophan fluorescence experiment (∼80% at 273 K).⁸⁴

^cfolded population estimated by NMR chemical shifts at 298K;⁶⁹

^dpopulation estimated from thermal unfolding analysis.⁸⁵

^ewith modified backbone dihedral energetics.

^fwith modified backbone dihedral energetics.

^gwith a new but unreferenced Amber force field.

Interaction Models and PMF Calculations

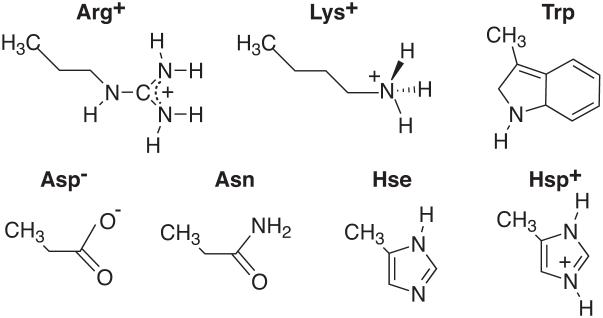
Figure 1 shows a list of the polar amino acid sidechain models for which pair-wise interactions were examined. A alanine dipeptide (Ace-Ala-Nme) was used to model the peptide backbone. A modified alanine dipeptide dimer was used to mimic backbone hydrogen bonding interaction, which was described elsewhere.⁸ All molecules were described by the CHARMM22 all atom force field. A total of 23 hydrogen bonding pairs between the sidechains as well as between the sidechains and backbone in various configurations (side, head-to-head, or stacking approaches) were studied. Some examples of the dimer configurations are given in Figure 2 and the rest is shown in the Supporting Material.

Figure 1.

Models of polar amino acid sidechains.

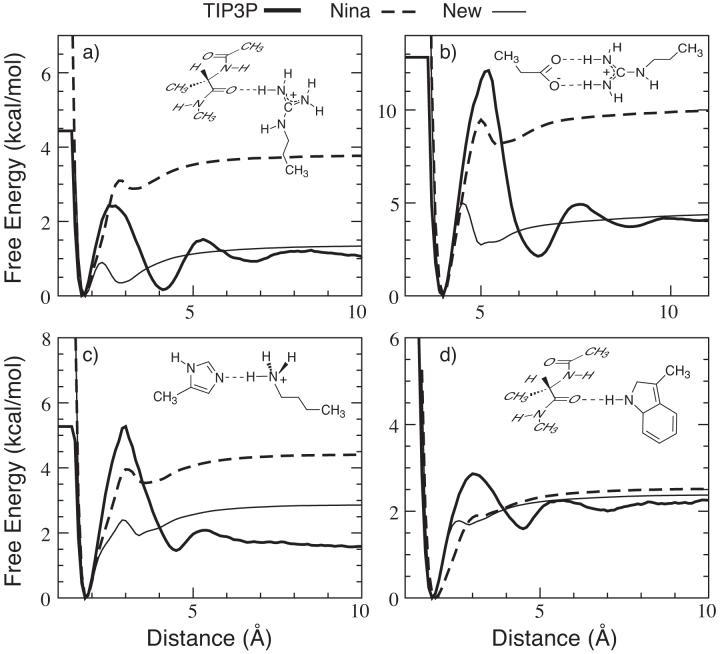
Figure 2.

Free energy profiles of four dimers in TIP3P water (thick lines) and GBSW implicit solvent with the Nina’s radii (dashed lines) and re-optimized radii (thin lines). The dimer configurations are shown in the inserts. The reaction coordinates plotted in the x-coordinates are (a) r(O...H), (b) r(CZ...CD), (c) r(NE2...H) and (d) r(O...H). Note that the heavy atoms were constrained in two orthogonal planes for the dimers shown in panels a and d.

In the explicit solvent simulations the dimers were constrained to move along a reaction coordinate, i.e., a straight line in specific dimer orientations (see Figure 2) using the MMFP module in CHARMM.⁸⁶ The system was solvated by about 750 TIP3P⁴⁶ water molecules in a rectangular box with periodic boundary conditions. To remove the artifacts associated with truncation of electrostatic forces, the Particle-Mesh Ewald method (PME)⁸⁷ was used to calculate the long-range electrostatic interactions. The vdW energy was smoothly switched off over the range of 10-12 Å by use of a switching function.^88,89 Biased sampling along the reaction coordinate was carried out using the umbrella sampling technique⁹⁰ and the final PMF was calculated using the weighted histogram analysis method (WHAM).^91,92 For each window, equilibration simulations of 60 picoseconds (ps) at constant pressure and temperature (NPT) were followed by 1.0 nanosecond (ns) of production sampling at constant volume and temperature (NVT). The SHAKE algorithm⁹³ was applied to fix lengths of all bonds involving hydrogen atoms and a time-step of 2 femtoseconds (fs) was used. Corresponding PMFs in implicit solvent were computed directly by translating the molecules away from each other along the reaction coordinate. Note that the resulting PMFs do not include the contribution of solute conformational entropy. However, this contribution is assumed to be similar in both explicit and implicit solvent models and thus omitting it in both cases should not affect the optimization results.

Backbone Dihedral Energetics

Modification of the backbone dihedral energetics was made possible by the ϕ/ψ CMAP torsion crossterm recently introduced in CHARMM.^48,66,67 As proper balance of secondary structure preference is one of the primary goals, the modifications were focused on the extended (β) and helical regions of the ϕ/ψ space. Stabilization (or de-stabilization) of particular conformations was achieved by adding cosine shaped “valleys” (or “humps”) centered at the appropriate ϕ/ψ coordinates. For example, stabilization of the extended (β) conformation was achieved by the following modification,

$$\Delta E(\varphi ,\psi )=-0.5k_{\max }[2+\cos (d_1\pi ∕r)+\cos (d_2\pi ∕r)],$$ (3)

with $d_l=\min [r,\sqrt{{(\varphi -{\varphi }_l)}^2+{(\psi -{\psi }_l)}^2}]$, l = 1, 2, where the radius r = 45° and the centers (ϕ₁, ψ₁) = (-120°1, 125°) and (ϕ₂, ψ₂) = (-150°, 160°).

The input radii were first systematically optimized to reproduce the pairwise interaction strengths between the polar groups, as shown in Fig. 2. An iterative procedure was adopted to empirically tune the radii as well as the backbone dihedral energetics, guided and judged by extensive folding and unfolding simulations. The basic strategy is as follows. Whenever the backbone energetics is changed, the backbone input radii are adjusted such that helicity of (AAQAA)₃ is close to the experimental value (∼ 50% at 270 K). Folding and unfolding simulations of the GB1p series β-hairpins (GB1m1, GB1p, HP5A, GB1m3) are followed to examine whether the correct folding thermodynamics is obtained. The final parameters are then further examined by folding simulations of trpzip2 and Trp-cage as well as control simulations of a range of other proteins (see Results and Discussion). Note that due to the large parameter space and slow convergence of simulations, popular semi-automatic optimizations procedures such as the z-score optimization^59,94-96 are too expensive to be used here.

Folding and Unfolding Simulations

The folding (starting from fully extended structures) and unfolding/control (starting from the native structures) were carried out using the REX-MD facility available in the MMTSB Tool Set^63,64 (available from http://mmtsb.scripps.edu) together with the CHARMM program.⁸⁶ Briefly, multiple copies (replicas) of the system are simulated at different temperatures independently and simultaneously. Exchanges of simulation temperatures are periodically attempted according to a Metropolis type algorithm. In the course of an REX-MD simulation, replicas can travel up and down the temperature space automatically in a self-regularized fashion, which, in turn, induces a nontrivial walk in temperature space and reduces the probability of being trapped in states of local energy minima. 16 replicas in a temperature range of 270 K to 550 K were used in all simulations unless otherwise noted. The temperatures were distributed exponentially within the specified ranges. SHAKE was applied to fix the lengths of all bonds with hydrogen atoms and a time-step of 2 femtoseconds (fs) was used. Exchanges of simulation temperatures were attempted every 2.0 picoseconds (ps) of MD. The total simulation lengths range from 20 nanoseconds (ns) for (AAQAA)₃ to 50 ns for the β-hairpins. The overall exchange ratios of these simulations range from 0.3 to 0.5.

Structural Analysis

The post-analysis was done largely with CHARMM and the MMTSB Tool Set. The helicity was computed from the average 1-4 hydrogen bond frequency defined by the criteria d_Oi··HNi+4 ≤ 2.6 Å, where d_Oi··HNi+4 is the distance between the carbonyl oxygen of residue i, O_i, and the amide hydrogen of residue i + 4, HN_i+4. Note that using backbone dihedral criteria resulted in similar but shifted helicity curves for the (AAQAA)₃ peptide (data not shown). Similar distance criteria were used to count the backbone hydrogen bonds in the β-hairpins. Sidechains are considered to be in contact if the shortest distance among heavy atoms is no greater than 4.2 Å.

Results and Discussion

Input Radii Optimization

The backbone input radii were optimized first to reproduce the backbone hydrogen bonding strength (using a modified alanine dipeptide dimer⁸) in TIP3P explicit solvent and the experimental helicity of (AAQAA)₃. It turned out that only the amide nitrogen (CHARMM atom type: NH1) needed to be adjusted in the original Nina’s set. Note that adjustment of backbone input radii is strongly coupled with the backbone dihedral modification (described in the next section). Once the backbone input radii were chosen, input radii of polar sidechains were optimized to maximally reproduce the strengths of pair-wise interactions between the polar groups. The final modifications to the Nina’s radii set are summarized in Table 2. Only a few atom types need to be adjusted and the modifications mainly involve heavily charged nitrogen atoms. Even though most changes are small, they often dramatically improve the agreement of interaction strength with explicit solvent results. For example, Figure 2 compares the PMFs of several dimers in the GBSW implicit solvent before and after optimization with the explicit solvent interaction curves. It shows that many interactions are indeed significantly over-stabilized with the original Nina’s radii and such over-stabilization can be effectively eliminated or reduced by the input radii optimization. Note that the solvation peaks (oscillations in the TIP3P PMFs) are mostly absent in the GBSW implicit solvent, which is due to the lack of solvent granularity and adoption of a vdW-like surface. The first solvation peak can be effectively reproduced by incorporating the solvent reentrant surface in the dielectric boundary such as in the GBMV model,³¹ without having to include any explicit water molecules in the implicit solvent. However, it is not clear whether there is any significant consequence in capturing such fine details in the interactions. While the folding kinetics might be altered, the absence of large solvation peaks might actually speed up the conformational sampling without introducing any thermodynamic bias.

Table 2.

Modifications to the Nina’s input radii that are self-consistent with a CHARMM22/CMAP^GBSW (see next section) force field with the GBSW implicit solvent

Residue	Atom	Nina (Å)	New (Å)
backbone	NH1	2.30	2.03
Lys	NZ	2.13	1.80
Arg	N*	2.13	1.70
	CZ	2.80	2.20
Gln/Asn	O*	1.42	1.60
	N	2.15	2.00
Hse	ND	1.80	1.90
Hsp	N*	2.30	1.90
Trp	NE	2.40	1.85
	C*	1.78	2.00

^*refers to a wild card character.

Backbone Dihedral Crossterm Modifications

While modifications to both helical and extended regions in the ϕ/ψ space were explored during the iterative empirical optimization, the final adjustment only involves stabilization of the extended region. The analytical expression of Eqn. 3 was used with k_max = 1.5 kcal/mol. Figure 3 shows a contour plot of the final adjustment to the original CMAP based on high-level quantum mechanical (QM) calculations.⁶⁶ It is interesting to note that stabilization of the extended (β) region with respect to the helical region (∼ 1.5 kcal/mol) happens to agree well with that in the latest empirically adjusted CMAP for the TIP3P water based on explicit solvent simulations of several proteins in both crystal and aqueous environments.⁴⁸ However, changes to the QM CMAP surface are more extensive in the CMAP for the TIP3P water and both helical and extended ϕ/ψ regions are further stablized. A stabilization of extended conformations is also in line with observations that helical conformations seem to be over-stabilized in the CHARMM22/QM CMAP force field with the TIP3P water. For example, it predicts (AAQAA)₃ to be over 90% helical at 270 K, in contrast to an experimental value of about 50%.⁸²

Figure 3.

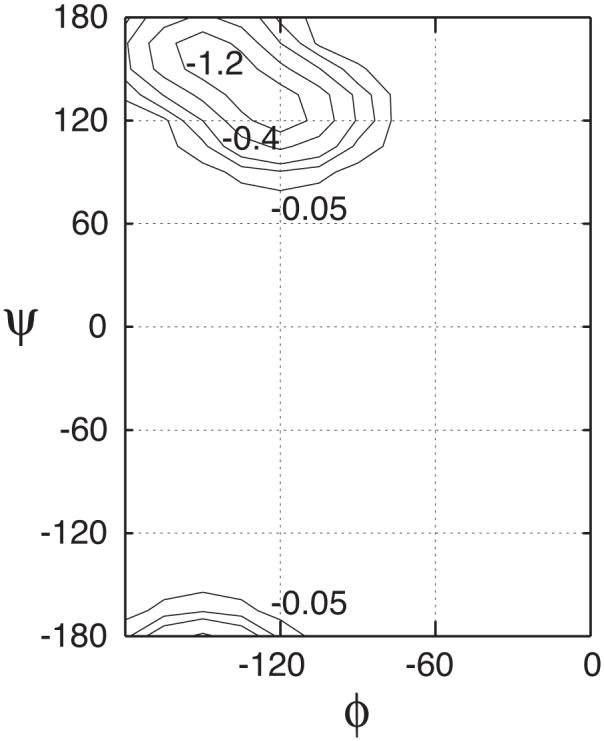
Modifications to the original QM CMAP.⁶⁶ The analytical expression of Eqn. 3 was used with k_max = 1.5 kcal/mol. The contour levels are -0.05, -0.2, -0.4, -0.8 and -1.2 (in kcal/mol).

Conformational Equilibria of (AAQAA)₃ and GB1p Series Peptides

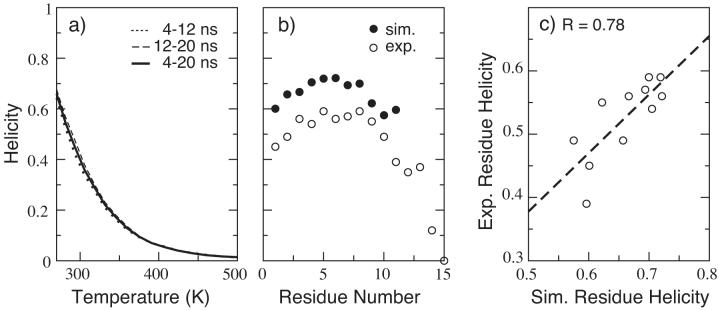
Here we only present the results of simulations using the final optimized implicit solvent force field, i.e., CHARMM22 with the modified implicit solvent CMAP (denoted CMAP^GBSW) plus the GBSW implicit solvent with the optimized input radii as described above. Figure 4 shows the simulated helicity of(AAQAA)₃ computed from a 20 ns REX-MD folding simulation in comparison with the experimental results.⁸² Many folding and unfolding events were observed during the course of the simulation. The values of overall helicity computed using different time intervals indicate that the simulation converges well (see Figure 4 a). The computed helicity of ∼65% at 270 K is in reasonable agreement with the experimental value of ∼ 50%. Furthermore, the simulated and experimental distributions of residue helicity also agree well with a high correlation coefficient of R = 0.78.

Figure 4.

Simulated and experimental helicity of (AAQAA)₃. (a) Simulated helicity as a function of temperature; (b) Simulated and experimental residue helicity at 270 K; (c) Correlation of simulated and experimental residue helicity at 270 K for residues 1-11. The simulated residue helicity was computed using snapshots from 4-20 ns of the simulation. The experimental values was adopted from Table 3 of Ref.82 Note that the simulated helicity for residues 12-15 were not computed as the distance criteria d_Oi··HNi+4 ≤ 2.6Å was used.

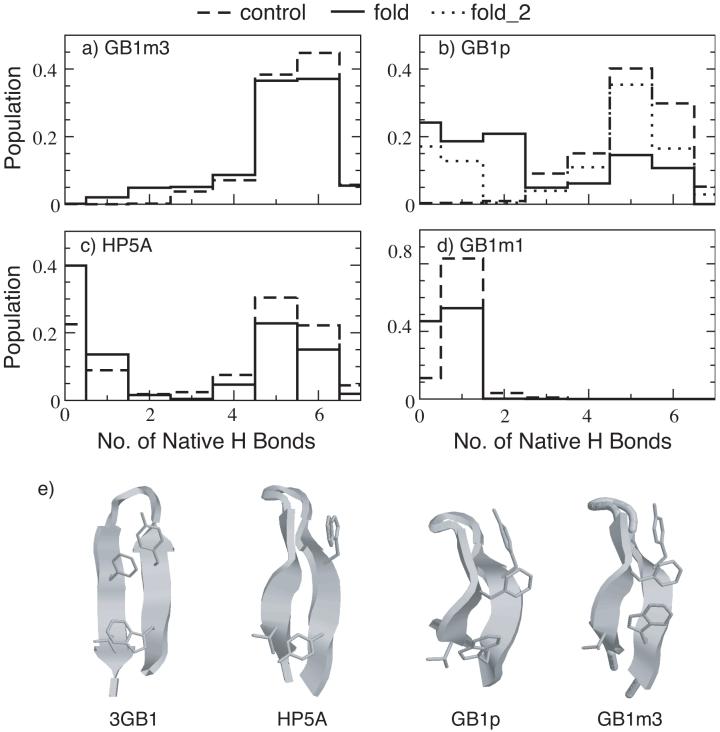
In Figure 5, we compare the probability distributions of the number of native hydrogen bonds $\left(N_{\mathrm{hb}}^{\mathrm{nat}}\right)$ at 270 K for the β-hairpin series derived from residues 41-56 in the fragment of the protein G B1 domain. Since the folding timescale of β-hairpins is significantly longer than that of helix-coil transition, convergence of simulations of limited total length (tens of ns) is not guaranteed even if certain properties converge to some plateau values. As such, the REX-MD simulations were initiated from both fully extended conformations (folding) and folded hairpin conformations (control) to further examine the degree of convergence. The folded hairpin conformations were built from an NMR structure of protein G B1 domain (PDB ID: 3gb1).⁹⁷ The total simulation lengths ranged from 30 ns for the control simulations up to 50 ns for the folding simulations. Multiple folding and unfolding events were observed in most simulations. Conformations during the last 10 ns were used to computed the probability distributions shown in Figure 5. The distributions for GB1m3 and GB1m1 appear to converge more readily, reflected by the good agreement between results from the control and folding simulations. However, convergence was not achieved for GB1p even with 50-ns REX-MD simulations. This might be related to the possible difference in the folding/unfolding rates of the three sequences. A recent study demonstrates that a stronger turn-promoting sequence (such as the D47P mutation in GB1m3) increases the hairpin stability primarily by increasing the folding rate, whereas a stronger hydrophobic cluster stabilizes the hairpin by decreasing the unfolding rate.⁹⁸ Furthermore, the poor convergence for GB1p folding simulation might be related to the fact that the REX setup is suboptimal for GB1p. The melting temperature of GB1p was shown to be T_m ∼ 300 K, compared to T_m ∼ 330 K for Gb1m3.⁶⁹ With only 16 replicas spanning 270 K to 550 K, only three replicas are actually simulated under the T_m of GB1p. An additional REX-MD simulation with the temperature range reduced to 270-400 K (with 6 temperature windows below T_m ∼ 300 K) appears to converge faster, yielding a native hydrogen bond probability distribution very similar to that of the control simulation (see Figure 5 b). Note that both folding and control simulations of HP5A were carried out with 16 replicas spanning 270-400 K based on the same reasoning. These folding and unfolding simulations seem to correctly reproduce the experimental results that GB1m3 is the most folded and GB1m1 is largely unfolded. Furthermore, assuming conformations with $N_{\mathrm{hb}}^{\mathrm{nat}}\ge 4$ as native, the native populations turn out to be about 88% for GB1m3, 61% (fold_2) for GB1p, 43% for HP5A and 0% for GB1m1 from the folding simulations, which are also in very good agreement with the experimental data (see Table 1). Representative structures from the folded structures of HP5A, GB1p and GB1m3 are shown in Figure 5 e, in comparison with the fragment structure from the protein G B1 domain. All stand-alone hairpins show a characteristic twist observed in other stable hairpins such as the trpzip series.⁸⁵ Close packing of hydrophobic sidechains are present in most folded structures. In particular, residue Phe52 in GB1m3 packs with both Tyr45 and Trp43 and thus contributes significantly to the observed stability. Mutation of Phe52 to alanine thus dramatically destabilizes the hairpin (such as in GB1m1).

Figure 5.

Probability distributions of the number of native hydrogen bonds for (a) GB1m3, (b) GB1p, (c) HP5A and (d) GB1m3 at 270 K, and (e) representative folded hairpin structures of HP5A, GB1p and GB1m3 in comparison with the experimental fragment structure (PDB ID: 3gb1). The distributions were computed from the last 10 ns of REX-MD simulations of 30 to 50 ns in total length. The hydrogen bonds taken as native are the same for all peptides. They are (in protein G B1 residue numbering): E42(N)-T55(O), E42(O)-T55(N), T44(N)-T53(O), T44(O)-T53(N), D46(N)-T51(O), D46(O)-T51(N) and D47(O)-K50(N). fold_2 is an additional REX-MD folding simulation for GB1p using 16 replicas at 270-400 K, carried out to improve the convergence. Both folding and control simulations of HP5A used 16 replicas spanning 270-400K.

Folding of Trpzip2 and Trp-Cage

To further examine the quality of the optimized implicit solvent force field, both control and folding REX-MD simulations of a range of proteins of various size and topology were carried out. REX control simulations of 5 to 10 ns in length were performed for: a designed ββα motif FSD-1 (PDB:1FSV); helical bundle proteins, the villin headpiece (PDB:1VII) and B domain of protein A (PDB:1BDC); two β sheet motifs, betanova and a WW domain (PDB:1E0L); and two α/β proteins, protein G B1 domain (PDB:3GB1) and a dihydrofolate reductase complex (PDB:1RX7). The results demonstrate that most proteins are stable with native secondary structures and tertiary packing well conserved. The only two exceptions are betanova and FSD-1, where the tertiary structure and part of secondary structures are lost at the end of the simulations. However, these results seem to agree with experimental measurements For example, the folded population in aqueous solution was estimated to be about 8% for betanova⁹⁹ and the beta-hairpin in FSD-1 appears to be less stable than the helix.¹⁰⁰ Thus we conclude that the consistent GBSW implicit solvent optimized force field well produces the conformations of natively folded proteins.

Folding proteins using a first-principles approach is much more costly and is typically limited to small proteins. Here we present the results of folding two sequences, trpzip2 and Trp-cage. Trpzip2, a 12-residue tryptophan zipper, is a designed β-hairpin with a type I’ turn and contains a characteristic structural motif of tryptophan-tryptophan cross-strand pairs .⁸⁵ It is the smallest peptide to adopt an unique tertiary β-fold with exceptional stability. Trp-cage is a 20-residue designed mini-protein with a stable compact folded state.¹⁰¹ The native structure contains a short α-helix, a single turn of 3₁₀-helix and a rigidified poly-proline C-terminal tail. The well-structured hydrophobic core consists of the indole sidechain of Trp6 buried between rings of Pro12 and Pro18. The structure is further stabilized by two tertiary hydrogen bonds, one between the sidechain of Trp6 (N^ε1H) and the backbone of Arg16 (CO) and the other one between the backbone groups of Trp6 (CO) and Gly11 (NH). The small sizes and extraordinary stabilities of these two peptides make them ideal for computer simulation studies of protein folding (e.g., see Table 1). Here we are mainly interested in examining the ability of the optimized implicit solvent force field to fold these peptides correctly. Accurate estimate of thermodynamic properties requires even more extensive simulations and therefore was not attempted here.

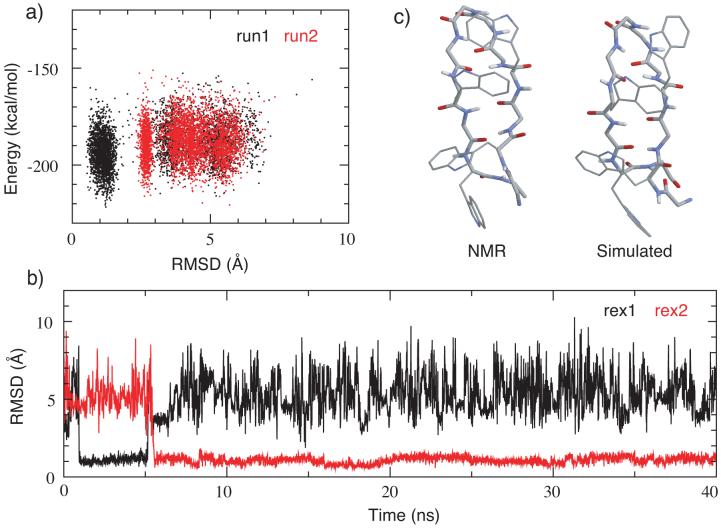
Two 40-ns REX-MD simulations were carried out to fold trpzip2 from a fully extended conformation. Two folding events were observed in one of the simulations while none was observed in the other. Figure 6a shows the correlation of C_α RMSD to the NMR structure (PDB ID: 1le1) with the total potential energy at the the lowest temperature (270K) from both simulations. Clearly, the folded conformations (with RMSD∼ 1.0Å) have lower average energies. The fact that no folding event was observed in one of the REX-MD simulation probably reflects a sampling limitation, constrained by the total simulation length as well as the sampling protocol. Note that trpzip2 is mainly stabilized by reducing the unfolding rate through the hydrophobic sidechain contacts. Forming the type I’ turn requires the backbone of Asn6 to adopt an α_L conformation, possibly further limiting the folding rate of trpzip2 (compared to the GB1p series hairpins described above). The predicted folded structure, obtained by clustering the last 10 ns of the successful folding simulation (run1 of Figure 6 a), contains all native structure characteristics, including the type I’ turn, two tryptophan sidechain contacts and all five native backbone hydrogen bonds. However, the configuration of the tryptophan sidechains appears to be versatile and the most populated packing, particularly, Trp4 and Trp11, is slightly different from the NMR structures.

Figure 6.

(a) Potential energy versus C_α RMSD from two REX-MD folding simulations of trpzip2. Snapshots were taken every 5 REX steps from both lowest temperature ensembles (270 K). (b) C_α RMSD versus time for the two replicas from REX-MD run1 that successfully folded. (c) A representative folded structure in comparison with the average NMR structure. The structure is the centroid of the largest cluster (538 of 1000 structures) from the last 10 ns of simulation run1. The RMSD values from the NMR structure are 1.0 Å for the backbone atoms and 2.1 Å for all heavy atoms.

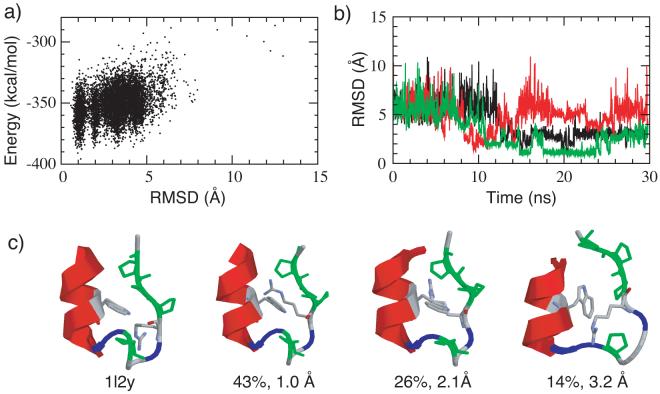
The results of the Trp-cage folding simulation are shown in Figure 7. The energy versus RMSD plot of the lowest temperature ensemble (see Figure 7 a) shows a strong correlation and the native states (low RMSD values) are significantly stabilized with respect to other conformations. Multiple folding and unfolding events were observed during a total of 30 ns REX-MD simulation, three of which are shown in Figure 7 b. Detailed structural analysis reveals that all secondary structure elements and the major tertiary contacts (see above) are correctly formed in the dominant clusters, with two representative structures shown in Figure 7 c. The indole sidechain of Trp6 forms native contacts with the proline rings as well as the backbone of Arg6 in most low RMSD (low energy) structures. Near native conformations (e.g., with RMSD values around 2 Å) often contain a less compact hydrophobic core and distorted 3₁₀ helical turn. Consequently, the poly-proline tail is less ordered with respect the N-terminal helix. Most misfolded structures observed involve the Trp6 sidechain either trapped in wrong orientation in the cage or completely blocked outside of the cage. One of the frequently observed misfolded structures is shown in Figure 7 c.

Figure 7.

(a) Potential energy versus C_α RMSD plot from a REX-MD folding simulations of mini-protein Trp-cage. All snapshots from the lowest temperature ensembles at 270 K are included. (b) C_α RMSD versus time for three of the replicas from that successfully folded. Note that one of the replica unfolded later during the simulation. (c) Representative folded and misfolded structures in comparison with the average NMR structure (PDB ID: 1l2y). Proline residues are colored green and glycine residues are colored blue. The structures shown are the centroids of the largest clusters from the last 10 ns of the simulation. The occupancies and backbone RMSD values are shown in the figure. The heavy atom RMSD values (backbone plus the hydrophobic sidechains from tryptophan and proline residues) from the NMR structure are 0.98 Å, 2.08 Å and 3.78 Å respectively (left to right).

Conclusion

An implicit solvent force field has been optimized in the context of the GBSW model³³ in CHARMM. The input radii, by which the solute-solvent boundary is defined, can be further optimized by directly examining the underlying pair-wise interaction between amino acid polar groups. Due to a paucity in direct experimental data, such an optimization is guided by explicit solvent free energy simulations and by the conformational equilibria of several short peptides. The peptide backbone torsion energetics also needed to be adjusted self-consistently with the GB input radii optimization. Advanced sampling techniques such as the REX-MD method can be effectively used to speed up the convergence of equilibrium thermodynamic properties, facilitating direct comparison with the experimental results. The final optimized implicit solvent force field appears to be properly balanced, correctly reproducing the conformational equilibria of both the helical (AAQAA)₃ peptide and the GB1p series β-hairpins. In particular, the force field successfully predicts changes in stability of several sequentially similar hairpins, GB1m1, HP5A, GB1p and GBm3, that were revealed by NMR experiments.⁶⁹ Successful folding simulations of several nontrivial stable peptides and proteins including trpzip2 and Trp-cage further demonstrate that the optimized force field is quite robust and might be applicable to study the folding of proteins in general. Such a first-principle approach can be a very powerful tool for structural biology as it is based on basic physical principles and free of empirical assumptions. However, it may also often be limited by the extensive sampling required for convergence. For example, difficulties in sufficient sampling and convergence were encountered even with short peptides such as GB1p and trpzip2. As such, continued efforts should be invested in developing more efficient sampling schemes, such as our recent investigation on using torsion angle molecular dynamics to speed up sampling of protein conformations.¹⁰² Together with the ever increasing computational power, one might be able to fold more complex proteins, especially those with significant β contents, using an all-atom first-principles approach in the near future.