Old men running: mechanical work and elastic bounce

Abstract

It is known that muscular force is reduced in old age. We investigate what are the effects of this phenomenon on the mechanics of running. We hypothesized that the deficit in force would result in a lower push, causing reduced amplitude of the vertical oscillation, with smaller elastic energy storage and increased step frequency. To test this hypothesis, we measured the mechanical energy of the centre of mass of the body during running in old and young subjects. The amplitude of the oscillation is indeed reduced in the old subjects, resulting in an approximately 20% smaller elastic recovery and a greater step frequency (3.7 versus 2.8 Hz, p=1.9×10⁻⁵, at 15–17 km h⁻¹). Interestingly, the greater step frequency is due to a lower aerial time, and not to a greater natural frequency of the system, which is similar in old and young subjects (3.6 versus 3.4 Hz, p=0.2). Moreover, we find that in the old subjects, the step frequency is always similar to the natural frequency, even at the highest speeds. This is at variance with young subjects who adopt a step frequency lower than the natural frequency at high speeds, to contain the aerobic energy expenditure. Finally, the external work to maintain the motion of the centre of mass is reduced in the old subjects (0.9 versus 1.2 J kg⁻¹ m⁻¹, p=5.1×10⁻⁶) due to the lower work done against gravity, but the higher step frequency involves a greater internal work to reset the limbs at each step. The net result is that the total work increases with speed more steeply in the old subjects than in young subjects.

1. Introduction

In the old age, muscular force is reduced (Doherty 2003). This has been attributed mainly to atrophy of muscle mass with reduction of its cross-sectional area (Frontera et al. 2000; Trappe et al. 2003), but also to a deficit in force production at the level of the interaction between actin and myosin (Phillips et al. 1991; Frontera et al. 2000; Lowe et al. 2001; Morse et al. 2005).

The effect of the reduced muscular force on the mechanical work done during locomotion is not known. The mechanical work done during walking has been found to be not significantly greater in old subjects in spite of a greater metabolic energy expenditure, which was ascribed to co-contractions of antagonistic muscles (Mian et al. 2006). The mechanical work done during running in the old subjects has not been measured.

The bouncing mechanism of running, contrary to the pendular mechanism of walking (Cavagna et al. 1976), requires a much larger muscular intervention to maintain the motion of the centre of mass. A stretch-shorten cycle of the muscle–tendon units takes place at each running step with a large input and output of mechanical energy during the vertical oscillation of the bouncing system. We hypothesized that the reduced muscular force in the old subjects would cause a lower amplitude of the vertical oscillation, with a smaller amount of elastic energy stored, a shorter aerial time and a greater step frequency. All these factors are likely to modify the mechanical work done during running and the metabolic energy expenditure.

To test this hypothesis, we measured (i) the external mechanical work done to maintain the motion of the centre of mass of the body and (ii) the natural frequency of the bouncing system, in old and young subjects running on the level at different speeds. In addition, we calculated, for the same subjects, internal and total mechanical work.

2. Material and methods

(a) Subjects and experimental procedure

The experiments were made on eight old subjects free of orthopaedic, neurological and cardiovascular diseases (men, age 73.6±5.5 years, height 1.72±0.06 m, weight 71.1±9.2 kg, mean±s.d. throughout the study) and eight healthy young subjects (six men and two women, age 20.8±1.6 years, height 1.76±0.08 m, weight 63.4±10.0 kg). Three subjects in each group were trained (running several kilometres at least once a week) while five were sedentary. The results reported in this study are an average of the data obtained in all subjects of each group regardless of their training. In agreement with the finding that the age-related effect on muscle–tendon units are similar in runners and non-active subjects (Karamanidis & Arampatzis 2005), similar results were obtained here by comparing the three old subjects trained with the three male young subjects untrained (data not shown). The average body mass index (body mass per height²) was 24.0±3.2 kg m⁻² in the old and 20.5±1.9 kg m⁻² in the young subjects. Informed written consent was obtained from each subject.

Subjects ran back and forth along a 50 m runway that had built into it, at the level of the floor, a 4×0.5 m force platform sensitive to the force exerted by feet in the forward and vertical directions. Analysis was made on a total of 124 runs in the old subjects at a speed of 3 to 13–17 km h⁻¹, and 229 runs in the young subjects at a speed of 3 to 17–21 km h⁻¹. In the old subjects, the number of runs was limited to avoid fatigue effects during the tests.

(b) Vertical oscillation of the centre of mass

According to the spring–mass model of running (Blickhan 1989), the step period τ and the vertical oscillation of the centre of mass S_v have been divided into two parts: a lower part taking place when the vertical force is greater than the body weight (t_ce and S_ce), and an upper part taking place when the vertical force is smaller than body weight (t_ae and S_ae; Cavagna et al. 1988). These two parts take place, respectively, below and above the equilibrium position of the spring–mass system, where the vertical force equals body's weight. Alternatively, the step period and the vertical displacement were also divided, according to tradition, into their fractions taking place during the ground contact time (t_c and S_c) and during the aerial time (t_a and S_a). However, this division does not apply to the spring–mass model, particularly at low running speeds when most of the oscillation (sometimes the whole of it) occurs in contact with the ground. Note that t_ce<t_c because during contact the vertical force may be less than the body weight, whereas t_ae>t_a for the same reason. A diagram showing the relationship between the total contact time t_c, the contact time during which the vertical force is greater than body weight (‘effective’ contact time t_ce), and the time, both in contact and on the air, during which the vertical force is less than body weight (effective aerial time t_ae) is given in fig. 1 of Cavagna et al. (2005). The total step period is τ=t_ce+t_ae=t_c+t_a and similarly the total vertical displacement is S_v=S_ce+S_ae=S_c+S_a. All of the above divisions of τ and S_v have been determined in this study from the platform records as described in detail in the electronic supplementary material I.

In a harmonic oscillator, the rebound is symmetric, i.e. the duration and the amplitude of the lower part of the vertical oscillation are equal to those of the upper part (i.e. t_ce=t_ae and S_ce=S_ae). The vertical momentum lost and gained during t_ce must equal the vertical momentum lost and gained during t_ae, i.e.

$${\overline{a}}_{\text{v},\text{ce}}{t}_{\text{ce}}={\overline{a}}_{\text{v},\text{ae}}{t}_{\text{ae}},$$ (2.1)

where, ${\overline{a}}_{\text{v},\text{ce}}$ and ${\overline{a}}_{\text{v},\text{ae}}$ are the average vertical accelerations of the centre of mass during the effective contact time t_ce and the effective aerial time t_ae, respectively. A symmetric rebound (i.e. t_ce=t_ae) implies the same average vertical acceleration during the lower and upper parts of the rebound (i.e. ${\overline{a}}_{\text{v},\text{ce}}={\overline{a}}_{\text{v},\text{ae}}$). In running, the average vertical acceleration during the lower part of the rebound ${\overline{a}}_{\text{v},\text{ce}}$ increases continuously with speed (Schepens et al. 1998), whereas a limit is set to the average vertical acceleration during the upper part of the rebound ${\overline{a}}_{\text{v},\text{ae}}$, which cannot exceed 1g (it is 1g when t_ae=t_a). It follows that in running the rebound becomes asymmetric (i.e. t_ce<t_ae) at the speed (approx. 11 km h⁻¹) where the average vertical acceleration during t_ce exceeds 1g (Cavagna et al. 1988; Schepens et al. 1998).

(c) Vertical stiffness

The mass-specific vertical stiffness, k/M_b, is given by the slope of the relationship between vertical acceleration a_v and vertical displacement S_v in the range corresponding to the amplitude of the oscillation of the spring–mass system, i.e. from its equilibrium position (a_v=1g) to its maximal deformation (a_v,mx; Cavagna et al. 1988). The mass-specific vertical stiffness was therefore measured as k/M_b=a_v,mx/S_ce, where S_ce is the amplitude of the oscillation, i.e. the vertical displacement of the centre of mass of the body from a_v=1g to a_v,mx. Correspondingly, the natural frequency of the spring–mass system was calculated as f_s=(a_v,mx/S_ce)^0.5/(2π).

Note that vertical stiffness, as defined above, is not necessarily a measure of elastic properties. The lengthening of a muscle–tendon unit as force increases, and shortening as force decreases, must in part be attributable to stretch and recoil of elastic elements, but may also be due in part to relative sliding of actin and myosin filaments (i.e. to the contractile elements doing negative followed by positive work). Vertical stiffness therefore gives an unambiguous measure of elastic energy storage only on the assumption that the muscle is kept isometric and the whole of the length change is taken by elastic elements. This condition may be approached at high running speeds (Cavagna 2006).

(d) External work measurement

The procedure used (Cavagna 1975) is described in detail in the electronic supplementary material I.

(e) Internal work estimation

The mass-specific positive work done per unit distance to accelerate the limbs relative to the centre of mass of the body, W_int/M_bL, has been calculated for each run from the experimental values of step length L (m), average running speed $\overline{V}$_f(m s⁻¹), step frequency f (Hz) and mass of the body M_b (kg) according to the equation (Cavagna et al. 1997)

$$W_{\text{int}}/M_{\text{b}}L(\text{J}{\text{kg}}^{-1}{\text{m}}^{-1})=0.140\times {10}^{-0.200L}\times {\overline{V}}_{\text{f}}\times f.$$ (2.2)

The data calculated from equation (2.2) in the young subject group are in good agreement with experimental data measured assuming a transfer of energy between the segments of each limb (Willems et al. 1995).

The calculated values of W_int/M_bL as a function of speed in km h⁻¹ were interpolated by a second-order polynomial fit yielding (R=0.935)

$$W_{\text{int},\text{young}}/M_{\text{b}}L(\text{J}{\text{kg}}^{-1}{\text{m}}^{-1})=0.1754+0.036841{\overline{V}}_{\text{f}}+0.00041132{\overline{V}}_{\text{f}}^{\text{2}},$$ (2.3)

for the young subjects group and (R=0.952)

$$W_{\text{int},\text{old}}/M_{\text{b}}L(\text{J}{\text{kg}}^{-1}{\text{m}}^{-1})=0.2056+0.019227{\overline{V}}_{\text{f}}+0.0030675{\overline{V}}_{\text{f}}^{\text{2}},$$ (2.4)

for the old subjects group.

(f) Statistics

The data collected as a function of running speed were grouped into classes of 1 km h⁻¹ intervals as follows: 3 to less than 4 km h⁻¹, 4 to less than 5 km h⁻¹…, 20 to less than 21 km h⁻¹. The data points in figures 1–3 represent the mean±s.d. in each of the above speed intervals and the values near the symbols in figure 1 give the number of items in the mean. When comparing the means of different variables within a subject group, with the same number of items at a given running speed, a paired samples t-test was used (table 1 in the electronic supplementary material II) to determine when the means are significantly different. Asterisks in figures 1 and 2 denote statistically significant difference at p<0.05 between variables within each subject group. When comparing the means of different variables between the two subject groups having different numbers of items at a given running speed, an independent-samples t-test was used (table 2 in electronic supplementary material II). This comparison was made over a speed range (more than 3 km h⁻¹ to less than 17 km h⁻¹) sustained by all young subjects and a number of old subjects decreasing with the increasing speed. The t-tests were performed using SPSS for Windows v. 11.0.1 (SPSS, Chicago, USA).

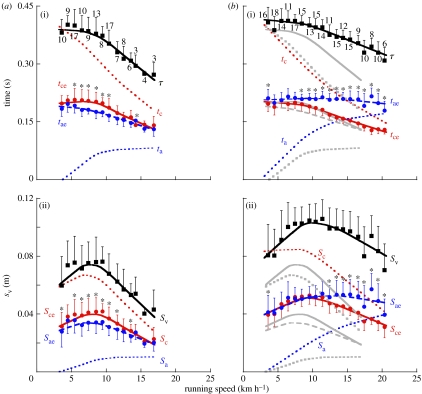
Figure 1.

(a) Old subjects. (b) Young subjects, with superposed old subject lines (grey lines) for comparison. (a(i),b(i) indicate the step period (τ, black filled squares) and its fractions). (a(ii), b(ii) indicate the total vertical displacement during the step (S_v, black filled squares) and its fractions). The red circles indicate the duration of the effective contact phase when the vertical force is greater than body weight (t_ce), and the vertical displacement during this phase (S_ce, which represents the amplitude of the oscillation in the spring–mass model of running, Cavagna et al. (1988)). The blue circles indicate the duration of the effective aerial phase when the vertical force is lower than body weight (t_ae) and the vertical displacement during this phase (S_ae). The red dotted line indicates the contact time (t_c) and the vertical displacement (S_c) during it. The blue dotted line indicates the aerial time (t_a) and the vertical displacement (S_a) during it. The vertical bars indicate the s.d.±mean; the values near the symbols in (a(i),b(i)) indicate the number of items in the mean. Asterisks denote statistically significant difference at p<0.05 between variables within each subject group. Lines represent the weighted mean of all the data (KaleidaGraph v. 4.0.3), their only purpose is to be a guide for the eye: they do not describe the underlying physical mechanism. Note that both the step period τ and the amplitude of the oscillation S_ce are smaller in the old than in the young subjects, whereas the time of contact t_c and the effective contact time t_ce are about the same. This indicates that the fraction of the step during which the vertical force exceeds body weight is greater in the old subjects. The similar effective contact time t_ce in old and young subjects indicates a bouncing system having the same natural frequency (figure 2), with lower amplitude of the oscillation S_ce in the old subjects.

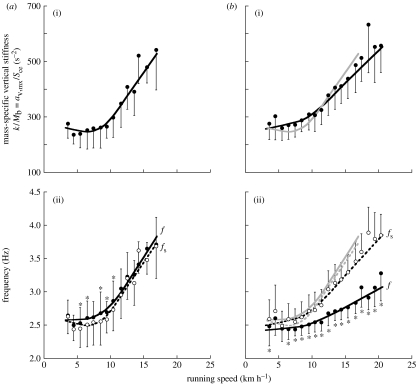
Figure 2.

(a) Old subjects. (b) Young subjects. (a(i),b(i)) The mass-specific vertical stiffness, which is similar in old and young subjects. (a(ii),b(ii)) Shows that the step frequency (f, continuous line) is greater in the old than in the young subjects. In addition, over most of the speed range, the step frequency is similar to the natural frequency of the system (f_s, dashed line) in the old subjects, whereas it is less than the frequency of the system in the young subjects. Statistics and other indications are the same as in figure 1.

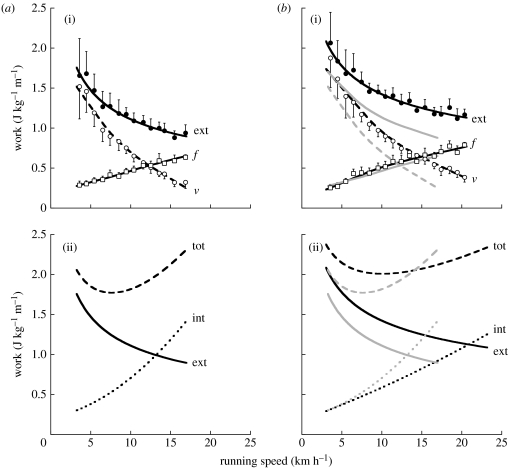
Figure 3.

(a) Old subjects. (b) Young subjects. (a(i),b(i)) The external work done per unit distance (filled circles) is plotted with its two components: the work done against gravity (open circles) and to sustain the forward velocity changes (open squares). Note that the external work is lower in old than in the young subjects due to a lower work done against gravity with a similar work to sustain the forward velocity changes. (a(ii),b(ii)) The total mechanical work done per unit distance (dashed line) is given as the sum of the external work (solid line) and the internal work to accelerate the limbs relative to the centre of mass (dotted line). Note the sharp increase with speed of the total work done by the old subjects due to a greater internal work resulting from their greater step frequency (figure 2). Statistics and other indications are the same as in figure 1.

3. Results

(a) Lower and upper part of the rebound

The step period (τ; figure 1a(i),b(i)) and the vertical displacement of the centre of gravity during each step (S_v, figure 1a(ii),b(ii)) are given as a function of the running speed in figure 1 (black squares) with their fractions corresponding to the lower (t_ce and S_ce, red circles) and upper (t_ae and S_ae, blue circles) parts of the rebound. The fractions taking place during the ground contact phase (t_c and S_c, red dotted lines) and during the aerial phase (t_a and S_a, blue dotted lines) are also given for comparison.

The results on the young subject group are roughly consistent with those reported in the literature (Cavagna et al. 1988; Schepens et al. 1998), i.e. the rebound tends to be symmetric at low speeds (t_ce=t_ae and S_ce=S_ae) and asymmetric at high speeds (t_ce<t_ae and S_ce<S_ae). Indeed, in young subjects, asymmetry seems to occur at a speed (8–10 km h⁻¹) lower than that reported in the literature (11 km h⁻¹). In contrast, the results obtained in the old subjects show two significant differences: (i) the rebound is symmetric at the highest speeds attained (t_ce=t_ae and S_ce=S_ae) and (ii) the asymmetry when present, at intermediate speeds, is reversed (i.e. t_ce>t_ae and S_ce>S_ae), i.e. the lower part of the oscillation lasts more and has a greater amplitude than the upper part. According to equation (2.1), a reversed asymmetry indicates that the muscular push exerted by the old subjects during the effective contact time (lower part of the vertical oscillation) results in an average acceleration upwards, which is smaller than the average acceleration downwards due to gravity during the effective aerial time (upper part of the vertical oscillation). The physiological significance of this finding will be discussed below.

(b) Amplitude of the vertical displacement

The vertical displacement of the centre of mass of the body at each running step, S_v, attains a maximum at intermediate speeds, which is lower in the old than in the young subjects: approximately 7.5 cm at approximately 7.5 km h⁻¹ in the old subjects group, and approximately 10 cm at approximately 10 km h⁻¹ in the young subjects. Similar values of S_v were measured with a different experimental procedure in old and young adults running at approximately 10 km h⁻¹ (Karamanidis & Arampatzis 2005).

The reduction of S_v in the old subjects is due to a reduction of all its components (S_ce, S_ae, S_c and S_a), but it is particularly relevant to consider here the reduction of S_ce, which represents the amplitude of the oscillation of spring–mass system from its equilibrium position (vertical force equal body weight) to its maximum compression (maximal vertical force). The amplitude of the oscillation is lower in the old than in the young subjects (figure 1). As expected, this is accompanied by a lower upward acceleration attained at the end of compression, a_v,mx and a lower maximal upward velocity, V_v,mx, attained when a_v=0. The lower vertical velocity results, in turn, into a shorter effective aerial time t_ae (figure 1).

(c) Frequency of the spring–mass system and the steps

Figure 1a(i),b(i) shows that the step period (τ=t_ae+t_ce) is shorter in the old than in the young subjects. This is due to the shorter effective aerial time t_ae, whereas the effective contact time t_ce is equal in the old and in the young subjects.

According to the spring–mass model of running, the effective contact time t_ce represents a half-period of the oscillation of the elastic system. A similar half-period suggests a similar resonant frequency f_s=1/(2t_ce)=(k/M_b)^0.5/(2π) of the apparent elastic system over which the body bounces each step, i.e. a similar mass-specific vertical stiffness (k/M_b). Figure 2 shows that the mass-specific vertical stiffness (k/M_b=a_v,mx/S_ce) in the old subjects is in fact similar to that of the young subjects (see table 2 in the electronic supplementary material II). In both groups, k/M_b tends to be about constant up to approximately 10 km h⁻¹ and then increases with speed.

Figure 2a(ii),b(ii) shows the step frequency f plotted together with the resonant frequency of the system f_s. At most running speeds: (i) f is greater in the old than in the young subjects, (ii) in the old subjects f is similar to f_s, whereas (iii) in the young subjects f is lower than f_s.

(d) Work

The mass-specific external work W_ext done per unit distance to sustain the motion of the centre of mass of the body in a sagittal plane is plotted in figure 3 as a function of the running speed. It can be seen that whereas the work done to sustain the forward speed changes W_f increases similarly with speed in old and young subjects, the work done against gravity W_v is appreciably lower in the old subjects. Correspondingly lower is the external work W_ext≈W_f+W_v, particularly at the highest speeds attained.

Figure 3a(ii),b(ii) gives the total mechanical work done per unit distance W_tot=W_ext+W_int, where W_ext is the positive work done to maintain the motion relative to the surroundings, whereas W_int is the work done to accelerate the limbs relative to the centre of mass.

4. Discussion

The results support our working hypothesis that the impaired muscle function in the old subjects results in a smaller amplitude of the vertical oscillation of the centre of mass, with a lower upward acceleration and a reduced duration of the aerial phase. These in turn imply: (i) less elastic energy stored, (ii) a higher step frequency, (iii) a lower external work to maintain the motion of the centre of mass of the body relative to the surroundings, and (iv) a greater internal work to accelerate the limbs relative to the centre of mass.

(a) Elastic energy

Length changes of muscle–tendon units result from the length change of muscle and of tendons in a proportion depending on muscle activation, which increases with increasing running speed. Evidence has been provided suggesting that above 13–14 km h⁻¹ the muscle is kept quasi-isometric with the consequence that the length change of the muscle–tendon unit is mostly sustained by tendons (Cavagna 2006). Stiffness of ‘elastic’ elements and elastic energy storage and recovery are therefore more reasonably measured in the high-speed range.

The maximal upward acceleration attained by four of the old subjects in their high-speed range (15–17 km h⁻¹) is 10.77±1.97 m s⁻² (average of seven runs) whereas that attained at the same speeds by all the young subjects is 18.86±2.74 m s⁻² (average of 24 runs). These figures translate into a maximal vertical force of 1.515 and 1.836 kN, respectively. The lower force attained during the bounce by the old subjects may be explained in part by the well-documented loss of muscular strength (e.g. Doherty 2003), and in part by a strategy aimed to increase the safety of their muscular–skeletal system (Karamanidis & Arampatzis 2005).

The vertical stiffness k at 15–17 km h⁻¹ is 37.32±8.85 kN m⁻¹ (n=7) in the old subjects and 28.69±6.50 kN m⁻¹ (n=24) in the young subjects. Assuming a linear force–length curve of the elastic elements, their maximum elongation (from zero to the maximal vertical force attained) would be: (1.515/37.32)=0.041 m in the old subjects and (1.836/28.69)=0.064 m in the young subjects.

Since the gravitational potential energy and the kinetic energy of the centre of mass are very nearly in phase during running, the elastic system undergoes its maximum strain when the vertical component of the ground reaction force is at a maximum and the horizontal component is nil. The elastic energy stored at each step can therefore be computed using the vertical force only, as (1515×0.041)/2=30.75 J and (1836×0.064)/2=58.75 J for the old and young subjects, respectively.

The external work done at each step is 81.15 J in the old subjects and 123.84 J in the young subjects. It follows that the elastic contribution to the external work done at each step would be 30.75/81.15=0.38 and 58.75/123.84=0.47, respectively.

These rough calculations indicate an approximately 20% less elastic bounce of the body in the old subjects. A relatively lower amount of elastic energy, stored during the previous deceleration of the centre of mass, is available during the push to lift and reaccelerate the centre of mass in the forward direction. As a consequence, a relatively greater amount of this work has to be replaced anew at each step to account for the losses at the expense of greater metabolic energy expenditure. The same amount of mechanical work is therefore likely to request larger energy expenditure in the old subjects than in the young subjects.

(b) Frequency of the spring–mass system and the steps

The mass-specific vertical stiffness is similar in old and young subjects, resulting in a similar natural frequency of the bouncing system (figure 2). A lower stiffness of the tendons of calf muscle and quadriceps femoris (Karamanidis & Arampatzis 2005; Onambele et al. 2006) was measured in the old subjects during maximal voluntary contractions. On the other hand, an increase with age of the stiffness of the series elastic elements within both tendons and muscle has been reported for the elbow flexor muscles (Valour & Pousson 2003). An increased leg stiffness was found during downward stepping (Hortobágyi & DeVita 2000). It should be pointed out that in the complex deformation of the whole body bouncing off the ground, the apparent vertical stiffness is the result of a number of muscle–tendon units in series whose elastic properties depend primarily on the level of muscle activation. The similar value of the mass-specific vertical stiffness found in old and young subjects is therefore not necessarily an indication of the stiffness of their tendons or muscle–tendon units measured during maximal voluntary contractions. It is interesting that all the factors affecting the mass-specific vertical stiffness during running result in a similar value in old and young subjects. To our knowledge, this is the first study to compare vertical stiffness on running in old and young subjects.

Does the natural frequency of the system affect the frequency of the steps? In the old subjects, the lower effective aerial time, t_ae, causes an increase in step frequency f=1/(t_ce+t_ae) to values, which are equal to, sometimes greater than, the frequency of the system f_s=1/(2t_ce) (figure 2). This is in contrast with the young subjects' choice to adopt, for a large speed range, a step frequency lower than that of the system by increasing t_ae relative to t_ce (figures 1 and 2).

Factors that determine the choice of the step frequency at a given running speed are: (i) tuning the step frequency f to the natural frequency of the system f_s (Cavagna et al. 1997) and (ii) choosing a step frequency that minimize the total (external plus internal) aerobic-limited step-average power, within the limits set by the anaerobic-limited push-average power (Cavagna et al. 1991). The first strategy is usually adopted at low running speeds and abandoned for the second strategy at high running speeds. This is done by increasing the average upward acceleration ${\overline{a}}_{\text{v},\text{ce}}$ above 1g, with the consequence that t_ae exceeds t_ce (equation (2.1)), and the step frequency, f=1/(t_ce+t_ae), becomes lower than the frequency of the system, f_s=1/(2t_ce). In this way, the increment of the aerobic step-average power is contained. In other words, running with high, long leaps is a convenient strategy to adopt to decrease the request in oxygen consumption, provided that enough anaerobic push-average power is at disposal to allow these leaps.

The old subjects never adopt the second strategy. The average upward acceleration never exceeds 1g even in their high-speed range, 15–17 km h⁻¹, where ${\overline{a}}_{\text{v},\text{ce}}=7.42\pm 1.23\text{m}{\text{s}}^{-2}$ (n=7): it follows that f≈f_s at all speeds (figure 2). Actually in some cases the symmetry of the rebound is reversed, with the duration of the lower part of the oscillation greater than that of the upper part. In these cases the step frequency adopted is greater than the frequency of the system (figure 2). This allows development of a lower force during the push, requires a push-average power approximately 60% that of the young subjects (791.9±167.6 versus 1331.9±290.3 W, p=7.1×10⁻⁶), but the increase in step frequency results in a greater W_int (see below). In contrast, the second strategy is followed by the young subjects, where ${\overline{a}}_{\text{v},\text{ce}}=12.48\pm 1.8\text{m}{\text{s}}^{-2}$ (n=24) in the same speed range (15–17 km h⁻¹), resulting in a step frequency lower than the frequency of the system (f<f_s), which limits the increase of W_int at high running speeds (see below). In addition, the greater deformation of the elastic system allows a greater usage of elastic energy (see calculation above).

(c) Work

It is known that a change of the step frequency at a given speed has opposite effects on the external power, which decreases with increasing step frequency, and the internal power to reset the limbs at each step, which increases with frequency (Cavagna et al. 1991). To what extent the lower step-average external power, due to the lower force during the push in the old subjects, is counterbalanced by a greater step-average internal power due to their increased step frequency?

The total work done per unit distance (total power divided by the average forward speed) was measured by summing W_int/M_bL, calculated from equations (2.3) and (2.4) for the young and old subjects, respectively, to the following empirical equations obtained by interpolation of all the experimental data of W_ext/M_bL as a function of speed in km h⁻¹: (R=0.831)

$$W_{\text{ext},\text{young}}/M_{\text{b}}L(\text{J}{\text{kg}}^{-1}{\text{m}}^{-1})=2.9738{\overline{V}}_{\text{f}}^{-0.32017},$$ (4.1)

for the young subjects group and (R=0.762)

$$W_{\text{ext},\text{old}}/M_{\text{b}}L(\text{J}{\text{kg}}^{-1}{\text{m}}^{-1})=2.8445{\overline{V}}_{\text{f}}^{-0.40856},$$ (4.2)

for the old subjects group.

The resulting total work done per unit distance, W_tot/M_bL, shows that the lower external work per unit distance in the old subjects is progressively accounted for, with increasing speed, by greater internal work due to their increased step frequency: the difference is reversed above approximately 14 km h⁻¹ (figure 3). W_tot/M_bL reaches a sharper minimum at about approximately 7.5 km h⁻¹ in the old subjects and a blunt minimum at approximately 8–12 km h⁻¹ in the young subjects.

Kram & Taylor (1990) suggested that the metabolic energy expenditure in running is primarily due to the cost of generating and maintaining force during the contact time, t_c. Figure 1 shows that both t_c and the fraction of the step where force exceeds body weight t_ce are similar in old and young subjects, but represent a larger fraction of the step period in the old subjects. In other words, force must be generated more frequently and maintained relatively longer in the old subjects: this per se may increase their energy expenditure, even if the lower activated muscle mass may have the opposite effect. The lower usage of the elastic energy in the old subjects may increase their metabolic energy expenditure for the same mechanical work output. The oxygen consumption during running at 10 km h⁻¹ was found to increase with age in trained female runners (Evans et al. 1995).

In conclusion, the reduction of muscular force in old age results in lower elastic energy storage and in a modification of the mechanical work done per unit distance during running according to the following succession of events. The lower force causes a lower vertical acceleration, a smaller vertical displacement and a lower effective aerial time resulting in a greater step frequency. The smaller vertical displacement causes a reduction of the work against gravity resulting in a reduction of the external work, since the work to sustain the forward speed changes is unaltered. The greater step frequency, however, causes greater internal work to reset the limbs at each step resulting in a total mechanical work, external plus internal, which becomes relevant at high running speeds.

Supplementary Material

Platform Records Analysis

This section explains how the measurements performed with the force platform are used in order to work out the various mechanical quantities used throughout the paper

Statistical Tables

This section contains two tables showing the statistical confidence of the results presented in the paper as a function of the running speed