Robustness of linkage maps in natural populations: a simulation study

Abstract

In a number of long-term individual-based studies of vertebrate populations, the genealogical relationships between individuals have been established with molecular markers. As a result, it is possible to construct genetic linkage maps of these study populations by examining the co-segregation of markers through the pedigree. There are now four free-living vertebrate study populations for whom linkage maps have been built. In this study, simulation was used to investigate whether these linkage maps are likely to be accurate. In all four populations, the probability of assigning markers to the correct chromosome is high and framework maps are generally inferred correctly. However, genotyping error can result in incorrect maps being built with very strong statistical support over the correct order. Future applications of linkage maps of natural populations are discussed.

1. Introduction

The last decade has witnessed a dramatic advance in evolutionary genetic studies of pedigreed natural populations of vertebrates. The principal reasons for this development are (i) the maturation of individual-based long-term study systems such that datasets are sufficiently large to undertake complex statistical analyses, (ii) the relative ease with which pedigrees can be inferred using molecular markers (Garant & Kruuk 2005; Pemberton 2008), and (iii) the uptake of the animal model approach to quantitative genetic studies (Kruuk 2004). Despite the logistical and analytical difficulties involved with inferring quantitative genetic parameters in natural populations, considerable success has been achieved in this area (Boag & Grant 1978), particularly since the animal model was first used to estimate the heritability of fitness traits in the wild (Reale et al. 1999; Kruuk et al. 2000). These pioneering studies paved the way to sophisticated examinations of the processes that determine (or constrain) microevolutionary changes (Kruuk et al. 2002), including investigations into gene by environmental variation (Merilä et al. 2001; Charmantier & Garant 2005; Nussey et al. 2005; Wilson et al. 2006) and the role of genetic correlations between the traits (Sheldon et al. 2003) and sexes (Foerster et al. 2007). There is no doubt that pedigree-based studies of natural populations have contributed enormously to current understanding of the evolutionary process. However, quantitative genetic studies cannot pinpoint the loci responsible for phenotypic variation.

One way in which loci of adaptive significance in natural populations can be identified is through linkage mapping studies (Slate 2005). Here, a suite of mapped markers that span the genome at roughly evenly spaced intervals are typed in a panel of related individuals, and the presence of a quantitative trait locus (QTL) is inferred by co-segregation between marker alleles and phenotypic trait values. Map construction is possible only if large numbers of markers and a well-resolved pedigree comprising at least several hundred individuals are available, otherwise it is difficult to infer the correct marker order of closely linked markers. Mapping in natural populations is further complicated by the fact that marker phase can be difficult to infer when only one parent is known or when sibships are small. Therefore, most linkage maps have been constructed from specially created crosses in model (Lister & Dean 1993) or agriculturally important (Kappes et al. 1997; Groenen et al. 2000) organisms or from human pedigrees (Dib et al. 1996). More recently, linkage maps have now been constructed in four populations for which long-term individual-based datasets are available (table 1), and where natural pedigrees (rather than experimental breeding programmes) have been used to follow the co-segregation of marker alleles. Two of these mapping populations are in ungulate species (Slate et al. 2002b; Beraldi et al. 2006) and two are in passerine birds (Hansson et al. 2005; Backström et al. 2006a).

Table 1.

Natural populations with linkage maps.

	Great reed warblers Acrocephalus arundinaceus	Collared flycatchers Ficedula albicollis	Soay sheep Ovis aries	Red deer Cervus elaphus
location	Lake Kvismaren, Sweden	Gotland, Sweden	St Kilda, Scotland	Rum, Scotland
N	812a	365	585	361
generations	6	2	6	5
marker type	microsatellelites & AFLPs	SNPs	microsatellites	microsatellites
number of markers	58Mb; 142 (59Mb/83Ab); 103 (53Mb/50Ab)	53c	255d	93d
reference	Hansson et al. (2005); Åkesson et al. (2007); Dawson et al. (2007)	Backström et al. (2006a)	Beraldi et al. (2006)	Slate et al. (2002b)

^aCurrent mapping panel comprises 1024 birds (value used in simulations).

^bM denotes microsatellites and A denotes AFLPs.

^c53 SNPs typed across 23 genes. Intragenic SNPs scored as single locus haplotypes for linkage mapping such that 23 loci were mapped.

^dA small number of typed markers were allozymes (four in Soay sheep and three in red deer).

There are several motivations for developing linkage maps in natural populations, but these can be categorized into addressing two types of broad question. First, there are questions relating to the evolution of genomes, karyotypes or recombination rates. For example, maps of related organisms can be compared to infer how genomes or karyotypes differ and the evolutionary explanations for such differences (Backström et al. 2006a; Dawson et al. 2007). Similarly, one might construct sex-specific linkage maps in order to detect and understand sex differences in recombination rate (heterochiasmy; Hansson et al. 2005). These questions directly consider map features such as gene order and chromosome lengths, both of which are properties of the population under study rather than of individuals.

The second broad application of maps is to identify genomic regions that explain phenotypic variation between individuals. Most obviously, linkage mapping can be used to identify loci responsible for variation at simple Mendelian (Beraldi et al. 2006; Gratten et al. 2007) or polygenic (Slate et al. 2002b; Beraldi et al. 2007a,b) traits. There are alternative approaches to identifying loci that explain trait variation. For example, association (or linkage disequilibrium) mapping does not (usually) require a pedigree to identify loci responsible for phenotypic variation, while heterozygosity–fitness correlation studies may detect genomic regions where heterozygote advantage or associative overdominance is present (Hansson & Westerberg 2002). However, the inferences that can be made from these approaches are greatly limited without a map; indeed, linkage maps are useful tools to establish whether levels of linkage disequilibrium are sufficient to attempt association mapping in a natural population (Backström et al. 2006b; Slate & Pemberton 2007). In this second category of map-based analysis, the map is simply a tool to aid detection of loci affecting individual variation; importantly, the map features per se are not the characters under study.

Given the recent development of linkage mapping in pedigreed natural populations, it is timely to consider whether these maps are likely to be accurate and to investigate what factors should be considered when building them. The factor most likely to cause incorrect map construction is genotyping error, which can lead to the inference of spurious recombination events, resulting in inflated maps or incorrectly assigned marker locations. The factor that is most likely to result in unassigned markers is insufficient power to detect linkage. Power is likely to be defined by pedigree size (and structure), marker informativeness and marker density. This paper describes an analysis of simulated markers in pedigrees identical to those used in mapping studies of natural populations to consider the following points: What is the probability of assigning markers to the correct (or an incorrect) chromosome? How often is the inferred marker order likely to be correct? How accurate are estimated map lengths? What is the effect of genotyping error on map construction? How amenable are different types of molecular marker to linkage mapping? Both microsatellite and SNP markers are simulated and comparisons between error-free and erroneous genotype datasets are made. It is expected that map construction will be easier with microsatellites than SNPs as they are typically more variable and therefore better able to resolve whether inherited chromosomes are recombinant or non-recombinant. In addition to exploring the robustness of linkage maps from natural populations, I highlight some new research questions that could be addressed with them.

2. Material and methods

(a) Mapping populations

The mapping populations used in the simulations were all based on real pedigreed populations of free-living vertebrates (see table 1 for details). Mapping panel pedigree structures were obtained from the relevant literature or were supplied by the lead authors of the relevant paper. Pedigrees were assumed to be correct because, in practice, any mistakes in a pedigree are readily identifiable once a large number of markers have been typed in the mapping panel (Slate et al. 2002b; Beraldi et al. 2006). The flycatcher pedigree provides an interesting counterpoint to the other pedigrees in this study. Birds chosen for the mapping pedigree were all members of paternal half- or full-sibships, or were their parents. Birds that provided pedigree links between the sibships were not included and so the mapping panel can be regarded as a series of unrelated two-generation families. This mapping panel has a very similar structure to domestic livestock mapping pedigrees such as those used to map the cattle (Barendse et al. 1997) and chicken (Groenen et al. 1998) genomes. The great reed warbler pedigree also relies on half- and full-sibships to maximize power to map markers, but these families are interlinked and span several generations. The sheep and red deer mapping panels are more complex: although they contain some large half-sibships, they span several (overlapping) generations, include some inbreeding and rely on singletons and small sibships to link the larger families. The structures of the red deer and Soay sheep pedigrees are more directly analogous to human pedigrees than to domestic livestock.

(b) Simulation details

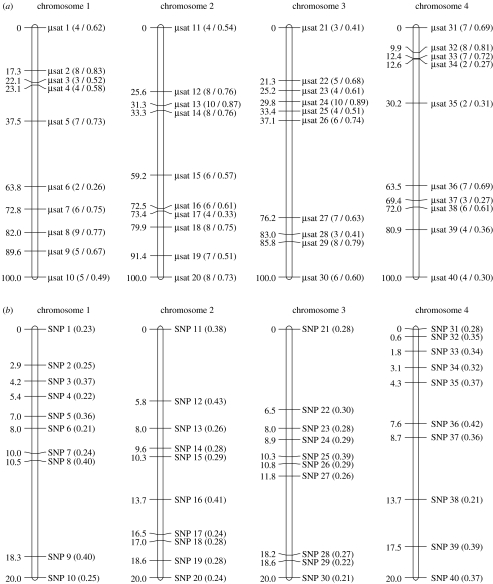
Three different scenarios were analysed by simulation. Scenario 1 involved four chromosomes, each 100 cM long and typed at 10 microsatellite markers. Markers were assigned to random locations but with the end markers constrained to be at positions 0 and 100 cM. The number of alleles and expected heterozygosity (assuming Hardy–Weinberg equilibrium) were sampled from a distribution based on data reported in previous mapping studies (Slate et al. 2002b; Beraldi et al. 2006) such that across the 40 markers the number of alleles ranged from 2 to 10 (mean=5.70) and expected heterozygosity ranged from 0.26 to 0.89 (mean=0.60). Marker locations and variability are shown in figure 1a. Scenario 2 also used 40 simulated markers, located on four different chromosomes. However, the chromosomes were shorter (20 cM long) and the markers were less variable. Here, they were all assumed to be biallelic single-nucleotide polymorphisms (SNPs), with minor allele frequency (MAF) sampled from a uniform distribution ranging from 0.20 to 0.45 such that mean (s.e.) MAF was 0.31 (0.01) and mean expected heterozygosity was 0.42 (0.01). Scenario 2 was designed to mimic SNP genotyping, which has become a tractable method of creating high-density maps of natural populations as a result of developments in pyrosequencing (Margulies et al. 2005) and high-throughput SNP genotyping (Murray et al. 2004). Scenario 3 was identical to scenario 1, except that a 5% genotyping error was introduced at each locus.

Figure 1.

Maps of the simulated chromosomes under (a) scenarios 1 and 3 and (b) scenario 2. Values in parentheses refer to the number of alleles and expected heterozygosity of microsatellites (figure 1a) or the minor allele frequency of each SNP (figure 1b).

Genotypes were assigned to individuals in the mapping population using the SimPed software (Leal et al. 2005). SimPed uses Monte Carlo simulation to assign genotypes to founder individuals based on user-defined allele frequencies. Genotypes at linked markers are then converted to haplotypes for each founder. Next, the offspring are allocated an allele at the first marker on a haplotype by randomly sampling from the parental haplotype. Offspring alleles at subsequent linked markers are determined by the haplotype allele inherited at the first marker and a user-supplied recombination fraction between adjacent markers. The process is repeated until all non-founder individuals are assigned genotypes based on their parental haplotypes. Markers were assumed to be in linkage equilibrium within the founder individuals in each simulated population. Fifteen independent replicates of each scenario were simulated in each of the four populations (i.e. a total of 4 populations×3 scenarios×15 replicates=180 sets of four chromosomes were simulated).

(c) Linkage mapping analyses

Linkage mapping was performed using a version of the CriMap software (Green et al. 1990) that has been modified by Xuelu Liu (Animal Genomics and Breeding group, Monsanto Corporation) to better handle large or complicated pedigree structures, such as those typically encountered in natural populations. Complex pedigrees were first split into subfamilies using the CRIGEN command. Subsequent CriMap analyses then followed similar guidelines to those used in the original mapping pedigrees on which these simulations were based. First, linked markers were identified using the TWOPOINT command, with all pairs of markers producing LOD scores in excess of 3.0 being regarded as linked. A note was made of any unlinked marker pairs that produced LOD scores in excess of 2.0 and in excess of 3.0. In total, there were 600 pairs of unlinked markers per replicate. Markers were assigned to linkage groups on the basis of two-point LOD scores. For each linkage group, the most parsimonious marker order was determined using the BUILD, FLIPS, FLIPS3 and FLIPS5 commands. Log likelihoods were compared between the simulated marker order and the most parsimonious marker order if the two orders did not match. If the most parsimonious marker order differed from the simulated marker order, then the inconsistency was categorized into one of the following five classes: (i) a two-marker inversion; (ii) a three-marker inversion; (iii) a more than three-marker inversion; (iv) rearrangement that could not be explained by a simple inversion; and (v) a ‘fission’ (whereby the markers on the simulated chromosome were inferred to be spread across two separate linkage groups). The estimated length of each inferred linkage group was compared to the simulated lengths (100 cM for scenarios 1 and 3, and 20 cM for scenario 2).

3. Results

(a) Scenario 1: microsatellites

Under scenario 1, the probability of successfully assigning markers to the correct linkage group was high, ranging from 0.95 (red deer) to 1.0 (great reed warblers; table 2). The proportion of unlinked marker pairs that were spuriously inferred to be linked was very low, and in all cases where this occurred each marker had much greater two-point LOD scores with a marker on the correct chromosome. Consequently, no markers were assigned to an incorrect chromosome. In all populations, the simulated marker order was often the most parsimonious marker order (values ranged from frequency 0.67 in red deer to frequency 0.97 in great reed warblers). Where there was a discrepancy between simulated marker order and inferred marker order, it was usually due to an inversion involving two tightly linked markers (e.g. microsatellites 3 and 4, 16 and 17, 33 and 34 or 37 and 38; figure 1a) and the log likelihoods of the two alternative orders were always similar (LOD<2.0). Estimated map length was usually very close to simulated map length, although in red deer it was slightly underestimated.

Table 2.

Summary of inferred maps under the 3 simulation scenarios. (The proportion of markers that were assigned to the correct or an incorrect chromosome are reported in the first two rows. These values do not always sum to 1.0, as some markers remained unassigned. Among unlinked marker pairs the proportion of pairwise combinations that gave spurious evidence of linkage with LOD > 2.0 or 3.0 are reported. Mean (s.e.) estimates of map length should be compared to simulated lengths of 100 cM (scenarios 1 and 3) or 20 cM (scenario 2). The proportion of replicates where the most parsimonious marker order was the simulated order is reported. Discrepancies between the inferred marker order and the actual marker order were classified into the listed categories and their frequencies are reported.)

	great reed warblers	collared flycatchers	Soay sheep	red deer
scenario 1—microsatellites
proportion correctly assigned	1.00	0.99	0.99	0.95
prop wrongly assigned	0	0	0	0
prop spurious twopoint LOD>2	1.0×10−3	2.2×10−4	2.2×10−3	2.0×10−3
prop spurious twopoint LOD>3	0	0	1.1×10−4	3.3×10−4
mean (s.e.) length (cM)	99.8 (0.6)	101.5 (1.6)	99.2 (0.8)	95.9 (1.4)
real order most parsimonious	0.97	0.92	0.80	0.67
inversions (2 markers)	0.03	0.03	0.13	0.20
inversions (3 markers)	0	0.02	0.02	0.02
inversions (>3 markers)	0	0.03	0	0.02
rearrangement	0	0	0.05	0.10
scenario 2—SNPs
proportion correctly assigned	1.00	1.00	1.00	0.95
prop wrongly assigned	0	0	0	0
prop spurious twopoint LOD>2	1.1×10−3	1.6×10−3	8.9×10−4	3.4×10−3
prop spurious twopoint LOD>3	2.2×10−4	1.1×10−4	0	1.2×10−3
mean (s.e.) length (cM)	20.2 (0.3)	19.8 (0.4)	19.9 (0.4)	20.7 (0.7)
real order most parsimonious	0.97	0.75	0.52	0.28
inversions (2 markers)	0.03	0.20	0.22	0.28
inversions (3 markers)	0	0	0.02	0.02
inversions (>3 markers)	0	0	0	0
rearrangement	0	0.050	0.25	0.42
scenario 3—microsatellites with 5% error
proportion correctly assigned	1.00	0.97	0.94	0.84
prop wrongly assigned	0	0	0.002	0.002
prop spurious twopoint LOD>2	1.1×10−3	7.8×10−4	2.0×10−3	2.6×10−3
prop spurious twopoint LOD>3	0	4.4×10−4	3.3×10−4	5.6×10−4
mean (s.e.) length (cM)	162.7 (2.0)	128.3 (1.4)	150.6 (2.7)	154.0 (3.6)
real order most parsimonious	0.45	0.48	0.27	0.13
inversions (2 markers)	0.40	0.20	0.28	0.13
inversions (3 markers)	0.07	0	0.05	0.08
inversions (>3 markers)	0	0.02	0	0.03
rearrangement	0.07	0.02	0.23	0.38
fission	0	0.30	0.17	0.23

(b) Scenario 2: SNPs

Scenario 2 produced similar results to scenario 1, with a high proportion of markers assigned to the correct group, no markers assigned to an incorrect linkage group and accurate estimates of map length (table 2). The most parsimonious marker order was less likely to be the correct order than under scenario 1, although the most frequent discrepancy between inferred and simulated marker order remained a two-locus inversion with the two orders producing very similar log likelihoods (LOD typically less than 1.0).

(c) Scenario 3: microsatellites with genotyping error

When genotyping error occurred, map inference was notably less accurate. Markers were still typically assigned to the correct chromosome, although rare exceptions were identified in Soay sheep and red deer. More strikingly, the estimated map length was inflated (mean chromosome length varied from 128.3 in flycatchers to 162.7 cM in great reed warblers). The most parsimonious map order matched the simulated marker order in less than 50% of cases in all four populations, with complex rearrangements frequently observed in red deer. Incorrect marker orders were often observed to have strong statistical support over the correct order (e.g. LOD=26.8 for an inversion between markers 32 and 33 in great reed warblers, LOD=5.9 for an inversion between markers 16 and 17 in flycatchers, LOD=13.0 for a rearrangement involving markers 28–30 in Soay sheep and LOD=27.8 for a rearrangement involving markers 31–34 in red deer). In collared flycatchers, Soay sheep and red deer, it was relatively common (frequency 0.17–0.30) for individual chromosomes to be erroneously treated as two discrete linkage groups. Typically, this occurred when linkage between distantly linked adjacent markers was not detected (e.g. a failure to detect linkage between markers 35 and 36 would result in markers 31–35 being treated as one linkage group and markers 36–40 a second linkage group; figure 1a).

4. Discussion

The main objective of this paper was to assess whether linkage maps constructed in pedigreed natural populations are likely to be accurate. Simulations show that under certain conditions the assumption that linkage maps are correct is robust. In all pedigrees chromosomal assignments, marker order and map length tend to be reliable when highly polymorphic microsatellites spaced at approximately 10 cM intervals are typed with a low error rate (scenario 1). The observation that the most parsimonious marker order may be incorrect is, at face value, worrying. However, it is a common practice to build so-called framework maps, whereby markers are only included on the map if the most likely marker order is deemed significantly better (typically supported by a LOD score of 3.0 or more) than any alternative marker order (e.g. Backström et al. 2006a; Beraldi et al. 2006). Here, the difference in log likelihoods between the most parsimonious order and the correct order never exceeded 2.0 in any population and once markers of ambiguous position were omitted the framework maps were always correct.

Scenario 2 simulations indicate that robust linkage map construction from high-density screens of low variability SNPs will also be feasible. A high proportion of markers (0.95–1.00) were assigned to the correct chromosome and estimated chromosome lengths were unbiased. The probability of the most parsimonious marker order being the correct order was lower than with microsatellites (especially in red deer and Soay sheep) but as with scenario 1, framework maps were usually correct. In one instance, an inaccurate framework map of chromosome 2 in red deer was better supported than the actual map order.

Under scenario 3, where genotyping error was incorporated, an effect on correct inference of marker order was observed. In all four populations, the probability of the most parsimonious map being correct was lower than 0.5 and inaccurate framework maps with strong statistical support were also reported. The simulated genotyping error rate was relatively high (0.05), but not unprecedented in mapping studies. For example, in Soay sheep, 22 out of 255 markers had error rates in excess of this value (Beraldi et al. 2006), while in red deer an error rate of approximately 4% has been reported (Slate et al. 2000). In great reed warblers, the microsatellite error rate has not been reported. In collared flycatchers, the SNP genotype error rate was estimated at just 0.06%, which possibly reflects the accuracy of new high-throughput SNP-typing platforms. Although error rates tend to be lower with SNPs, an important caveat is that typing errors are more readily detectable with microsatellites than SNPs because parent–offspring inconsistencies are more likely to arise with highly variable markers. These errors can then be removed or corrected prior to linkage analysis. Conversely, typing errors with SNPs rarely cause parent–offspring mismatches and so will be retained in linkage analysis where they can wrongly provide evidence for recombination events resulting in erroneous marker order or inflated maps. Even when microsatellites with reasonably high variability (mean expected heterozygosity of 0.60) were simulated, over 50% of genotyping errors did not result in parent–offspring mismatches. These undetected errors resulted in an approximately 40% overestimate of the number of recombination events.

Given the problems caused by typing error, it is worth considering what impact, if any, it has had on recent empirical studies. Fortunately, this does appear to be minimal. For example, McRae & Beraldi (2006) reported a subtle difference in marker order between Soay sheep and the domestic sheep International Mapping Flock (IMF) on chromosome 1. The best Soay sheep marker order was significantly more likely than the order reported in the IMF (LOD=3.15). Although the simulations suggest erroneous rearrangements with this degree of support could arise in the presence of typing error, the loci in question had an estimated error rate of 0 in the Soay mapping population (Beraldi et al. 2006). Furthermore, another independent mapping population of Charollais sheep also provided evidence of a rearrangement relative to the IMF in the same genomic region (McRae & Beraldi 2006). In great reed warblers, there is evidence of heterochiasmy–-recombination rates being lower in males (Hansson et al. 2005; Åkesson et al. 2007), but there is no reason to suspect that typing errors should cause sex biases in map length. Both the great reed warbler and the collared flycatcher maps revealed low recombination rates and some rearrangements relative to chicken (Backström et al. 2006a; Dawson et al. 2007). However, if typing error was present then map length would be overestimated and therefore the reported differences in map length between chickens and passerines would be conservative. The chromosomal rearrangements between both species and chickens are present whether maps with all markers or framework markers are used and therefore they are also likely to be robust. Finally, a comparison between the Rum red deer linkage map and a map constructed from a cross between red deer and Père David's deer (Elaphurus davidianus; Slate et al. 2002a) provides no evidence that the Rum map is inflated or incorrect. In summary, there is no compelling reason to doubt the marker order of the maps described above, even in regions that purport to show evidence of chromosomal rearrangements relative to model organisms.

A related point to consider is the accuracy of those papers that have used linkage maps to identify QTL in natural populations. Typically, the most parsimonious marker order is used in mapping studies, so what effect will errors in marker order have on the ability to identify and fine map QTL? It is probable that simple map errors such as a juxtaposition of two closely linked markers will not greatly affect the probability of type I (falsely declaring linkage) or type II (the failure to detect linkage) error in QTL mapping. However, attempts to refine the location of a QTL may be compromised if marker order or recombination fractions are wrongly assumed in fine mapping projects. Of course, if additional markers are added to a region containing a QTL (to refine QTL position), map errors might be identified and corrected. The effect of map errors on QTL detection is an area worthy of further study, but is beyond the scope of this paper.

It could be argued that running just 15 replicates (60 chromosomes) of each scenario/population combination inevitably results in crude estimates of map accuracy. However, qualitative differences between the different populations and scenarios are readily apparent, even with this limited number. Because the construction of each chromosomal map involves several manual processes and is time consuming, it would have been logistically impossible to perform a much larger number of replicates. Similarly, only four chromosomes were simulated in each replicate, whereas in reality each species has more chromosomes (sheep: 2n=54; red deer: 2n=68; passerines: 2n=76–82). Simulating extra chromosomes would have resulted in a greater amount of manual processing/interpretation of CriMap files without qualitatively changing the conclusions. Extrapolating from table 2, the proportion of markers assigned to incorrect chromosomes would have been lower than 2%, even in the worse case scenario of 5% typing error rate in the Rum red deer mapping pedigree.

It is notable that the collared flycatcher pedigree produced more accurate maps than either the Soay sheep or red deer pedigrees, despite containing fewer individuals than the former and a similar number to the latter. The flycatcher pedigree is only two generations deep, but every offspring is a part of a large full- or half-sibship (or both) and for all progeny both parents were typed. Therefore, the number of informative meioses (i.e. the ability to determine if gametes are recombinant or non-recombinant) is greater in the flycatchers than the two ungulate populations. Many passerine birds produce large broods, sometimes more than once in a season, such that mapping pedigrees with relatively high power can be obtained in just a few field seasons. In longer-lived vertebrates, the accumulation of sufficient data to build maps can take much longer (the red deer mapping panel includes animals born 30 years apart).

One potential use of linkage maps that has not been exploited is as a tool to understand the adaptive significance of individual variation in recombination rates (Otto & Lenormand 2002). The degree to which an individual's chromosomes are recombinant or non-recombinant provides information about recombination rates during gametogenesis in their parents. In other words, each offspring provides an independent estimate of recombination rate in the parent. In principle, it should be possible to address a number of exciting evolutionary questions about recombination rates in natural populations including the effects of environmental conditions on recombination rate (is recombination rate phenotypically plastic?), the evidence for selection on recombination rate and the heritability of recombination rate. In a sense, this type of investigation brings together the two broad categories of linkage map-based research outlined in §1. The frequencies of recombination events are the focus of such a study, yet it is individual variation in recombination rate that is under scrutiny rather than population-wide summary statistics.

In conclusion, simulations show that linkage maps constructed from natural populations are probably robust, although great care must be taken to identify (and in some cases remove) loci with reasonably high error rates. Studies that aim to compare marker order between populations are particularly prone to misinterpretation unless framework maps with reliable markers are used. As high-throughput SNP genotyping becomes more commonplace, maps will be constructed in other populations and more loci underlying variation in polygenic and simple Mendelian traits will be identified. Studies that examine selection and evolution of these loci will complement and build on the highly successful quantitative genetic studies that have been conducted in pedigreed natural populations over the last decade.