Exploring plasticity in the wild: laying date–temperature reaction norms in the common gull Larus canus

Abstract

Exploration of causal components of plasticity is important for insight into evolutionary dynamics and an organism's ability to respond to climate change. Among individuals, variation in plasticity can be due to genotype–environment interaction (G×E) or a result from environmental effects associated with an individual. We investigated plasticity for laying date in the common gulls Larus canus, using data collected in Estonia during 37 years (n=11 624 records on 2262 females, with 472 relatives). We used a sliding window approach to find the period in spring during which mean temperature best explained the annual mean laying date. Then, considering the spring temperature as a quantitative description of the environment, we used pedigree information and a random regression animal model to determine the variation in plasticity for the laying date–temperature relationship. We found that individuals differ in the plasticity of laying date (such that there is increased variation among individuals for the laying date in warmer springs), and that approximately 11% of variation in the laying date is heritable, but we found no statistical support for G×E. Plasticity in this species is not constrained by warmer springs.

1. Introduction

Temperature has a profound impact on the seasonal timing of many life-history events in iteroparous organisms, including migration (Jonzen et al. 2006) and reproduction (Réale et al. 2003; Both et al. 2004; Nussey et al. 2005). Temperatures have increased and are projected to increase in the coming decades (IPCC 2007). In response to this global warming, the phenology of an overwhelming number of animals and plants has changed in the recent decades (Walther et al. 2002; Parmesan 2006), primarily through the mechanism of phenotypic plasticity (Walther et al. 2002). However, for a proper understanding of how populations will respond to climate change, we need to understand the mechanisms and limitations of such plasticity. For example, can we expect continued advances in phenology if the climate change continues indefinitely? This question is especially relevant for life-history traits, such as the seasonal timing of reproduction, which are clearly related to individual fitness (Visser et al. 2004). For example, reduced capacity to adjust laying date to a changing environment has been shown to have population-level consequences in the pied flycatcher Ficedula hypoleuca (Both et al. 2006).

Long-term studies where repeated measures are made on individuals across multiple years often reveal heterogeneity in the individual-specific response to climate, with certain individuals being more plastic in their phenology than others. This variation has been termed I×E (individual–environment interaction; Nussey et al. 2007). Although each individual is a unique genotype, I×E in itself cannot be interpreted equivalent to genotype–environment interaction (G×E), because any environmental effects experienced by an individual during its life will be fully confounded with the effects of its genes. Such individual-specific environmental effects are termed permanent environmental effects in quantitative genetics (Lynch & Walsh 1998). Importantly, longitudinal individual-based data allow studying the consequences of plasticity for an individual's fitness, and the causes of plasticity can be studied under natural environmental conditions (Brommer et al. 2003; Nussey et al. 2007). Of particular interest is whether variation in plasticity has a genetic basis (i.e. due to a genotype–environment interaction G×E). If so, then plasticity is heritable, and selection has the potential to maintain, or even increase, the capacity of individuals to adjust their phenology to climatic conditions. For example, the climate change has increased selection on plasticity in Dutch great tits (Parus major) that adjust their laying date in response to temperature (Nussey et al. 2005). While G×E has been shown in this case (Nussey et al. 2005), similar plastic responses in collared flycatchers Ficedula albicollis show no heritable variation (Brommer et al. 2005). When springs get warmer, this species' phenotypic adjustment of laying date to temperature levels off (plasticity decreases) and continued climate warming is thus predicted to constrain plasticity, possibly to such a degree that it can have population-level consequences.

Provided a pedigree is available, I×E can be partitioned into genetic and permanent environmental effects. This can be achieved by comparing plasticity across relatives in the population using a particular form of quantitative genetic analysis based on random regressions (Meyer & Hill 1997; Meyer 1998; Schaeffer 2004; Nussey et al. 2007). A random regression animal model (RRAM) is an implementation of the concept of infinite-dimensional reaction norms (Kirkpatrick & Heckman 1989; Gomulkiewicz & Kirkpatrick 1992; Kirkpatrick et al. 1994) within the context of an animal model. Instead of modelling covariances across separate environments (Via & Lande 1985), an infinite-dimensional reaction norm allows values for additive genetic and other effects to vary as continuous functions of an environmental covariable. Pedigree information can be used to partition the variance in the parameters describing these functions, and this information can be used to describe the (co)variances across environments (e.g. Meyer & Kirkpatrick 2005).

Here, we apply an RRAM approach to explore plasticity using data from a long-term study of laying date in the common gulls (Larus canus) breeding in Estonia. Common gulls are long-lived migratory birds that breed in colonies. Laying early is an important life-history decision, and has been shown to be under consistent directional selection in this population (Rattiste 2006). Because we study a natural population, the environment is not controlled, and hence we consider, as a description of the annual environment, the average temperature during a time window that shows the highest correlation with the annual mean laying date. We then use pedigree information to apply a RRAM framework in which a series of models are compared in order to test whether (i) plasticity in the laying date–temperature relationship occurs, (ii) individuals differ in this relationship, and (iii) variation in plasticity across individuals also occurs on the genetic level.

2. Material and methods

(a) Study population and methods

Data comprise 11 624 laying date records made on 2262 females over a period of 37 years. The main material of the present study was collected during 1968–1983 and 1986–2004 on three offshore islets, Kakrarahu (3.7 ha), Paljarahu (2.5 ha) and Hoorahu (0.5 ha), situated in Matsalu National Park, Estonia (58°46′ N 23°26′ E). Each islet forms a geographically different breeding colony of common gulls. Routinely, through daily checks of the nests in the colonies throughout the breeding season, the laying date of each egg was recorded. We assumed that the laying date in the common gull is a female trait, and defined it as the date when a female laid her first egg in the season (relaying was discarded). Laying date was expressed in ‘April days’, where 1st of April is 1, and 1st of May is 31. Nestlings were ringed directly after hatching. Adult birds were sexed and individually marked at their first breeding event, and were identified in the later years by direct observations from a hide without catching them. At least 94% of nest owners (both males and females) were identified each year.

(b) Quantifying the environment

Local temperature was used to describe the climatic conditions and test for plastic responses. In order to make a non-arbitrary choice of the appropriate climatic time window, we searched for the period that provided the best correlation between the average temperature and the annual mean laying date. Daily temperature measures were obtained from Virtsu (1968–1972, 1976–2006) and were complemented with the measures from Heltermaa (1973–1975) from the Estonian Meteorological and Hydrological Institute. Both these weather stations are approximately 24 km from the study area and are adjacent to the Baltic Sea. We calculated Pearson's correlations between the mean annual laying dates and the mean daily temperature determined using a sliding window, where the window size was varied from 5 to 52 days and all possible windows in a year were considered. The time period during which the mean temperature provided the highest correlation with the mean laying date was taken to represent the best description of local environmental conditions. In addition to local temperature, we also considered the North Atlantic Oscillation (NAO) index as a possible larger scale measure of climatic overwintering conditions that could influence laying dates. However, multiple regression of mean laying date on NAO and local temperature indicated that the former had no effect (results not shown).

(c) Modelling laying date as a function of the environment

The laying date d of individual i in each annual environment was modelled as a continuous function of the year-specific temperature T. We first considered the phenotypic effects only in the random regression phenotypic model (RRPM)

$$d_{iT}={\mu }_{\text{F}}+bT+y+f({\text{ind}}_{oi},T)+{ϵ}_{iT}.$$ (2.1)

Equation (2.1) specifies a mixed model with the fixed effects μ_F and bT, the random effects y and f(ind_oi, T), and residuals ε_iT on the r.h.s. The overall fixed-effect mean μ_F encompasses fixed effects for a number of factors that were found to influence the laying date (Rattiste 2006). We corrected for colony, breeding status of the individual (new partner or the pair bred together previously or unknown) and the individual's and her partner's breeding experience. Breeding experience (in years since the individual first bred) was treated as a factorial variable and is effectively a proxy of age (see Rattiste 2004). T is the year-specific temperature (measured in the period that best explained laying date; see above) standardized to zero mean and unit standard deviation, and b is the fixed-effect regression coefficient of the mean laying date changes with T. Year (y) was included as a random-effect term in order to model variation across years, which is not explained by annual temperature. Differences across individuals were described by the function f(ind_oi, T). Polynomial functions of order o were used to allow the exploration of constant (o=0), linear (o=1) and nonlinear (o>1) relationships. The function f(ind_oi, T) thus allows estimation of symmetric variance–covariance matrix (of dimension o+1), for random regression coefficients. For example, a zero-order polynomial results in a single variance being estimated for differences in the laying date at the mean temperature across individuals, while a first-order polynomial function (ind_0i+ ind_1i T) applies a linear reaction norm model for individual-specific values across T such that variances in elevation (ind_0i) and slope (ind_1i) are estimated, as well as the covariance between them.

The residual error ε_iT was assumed to come from temporary environmental effects and to be uncorrelated across records. Residual variances were allowed to be specific for each environment T (i.e. heterogeneous error variance structure). Since phenotypic variance in a reproductive trait often increases as the environment gets more favourable (warmer), assuming a constant (homogeneous) residual variance with T could cause upward bias in the estimates of I×E (and/or G×E). In fact, while fitting a single homogeneous residual variance did lead to a much poorer model fit (based on log likelihood, results not shown), it did not qualitatively change the estimates of the causal variance components.

Starting from the basic model with only the above-described fixed effects and residuals (model 1), random effects were sequentially entered in a specific order and their significance was statistically tested using a likelihood ratio test (LRT). An LRT is a test between nested models where −2 times the difference in log likelihood provides a chi-squared distributed test statistic with the difference in the number of estimated (co)variance terms as the associated degrees of freedom. We first allowed for variation across years (y, model 2). We then modelled individual-specific variation in elevation (I, f(ind_0i, T), model 3) and elevation and slope (I+I×E, f(ind_0i, ind_1i, T), model 4). We also tested for higher-order terms.

(d) Modelling the genetics of plasticity

An RRPM (equation (2.1)) can be expanded by splitting up the phenotypic variance associated with the reaction norms across individuals f(ind_oi, T) into additive genetic and permanent environment effects, denoted by the functions f(a_oi, T) and f(pe_oi, T), respectively, to obtain the RRAM

$$d_{iT}={\mu }_{\text{F}}+bT+y+f({\text{pe}}_{oi},T)+f({\text{a}}_{oi},T)+{ϵ}_{iT}.$$ (2.2)

Statistical significance of partitioning the phenotypic variance across individuals into additive genetic and permanent environmental effects on elevation (G (f[a_0i, T])+ PE (f[pe_0i, T]), model 5) and elevation and slope (G+G×E (f[a_0i, a_1i, T])+PE+PE×E(f[pe_0i, pe_1i, T]), model 6) can then be evaluated with an LRT, as described above. We calculated the narrow-sense heritability of laying date as the ratio of additive genetic variance over the sum of all variance components included in the most parsimonious model.

A pedigree allows determination of relatedness (coefficient of co-ancestry) among individuals in a population, such that the term f(a_oi, T) in equation (2.2) can be solved using a restricted maximum-likelihood (REML) linear mixed model (Meyer & Hill 1997; Schaeffer 2004). The pedigree used to estimate the additive genetic effects consisted of offspring that recruited into the breeding population and their parents, as well as individuals of unknown parentage. In total, 1142 offspring recruited (1130 recruits with both parents known, 8 with only their father and 4 with only their mother known). The natal dispersal of female common gulls is larger than that of males, and approximately 80% of recruits are males. There were 204 females whose mother was known. Most of the parents (90.6% (588/649) of mothers and 68.0% (444/653) of fathers) had themselves unknown parents, and were assumed to be base individuals, and 21% of females (472/2262) had at least one female relative with one or more laying dates in the pedigree.

Parents providing care for offspring were assumed to be the genetic parents, which is correct for females, but may introduce pedigree error in the presence of extra-pair paternity (EPP). EPP has been shown to be low (3.6%) in a Polish population of common gulls (Bukacińska et al. 1998), and such a rate is unlikely to seriously bias estimates of additive genetic (co)variance components (Charmantier & Réale 2005). Furthermore, EPP is particularly unlikely to bias additive genetic estimates for a female trait such as the laying date, because most information stems from the comparisons between mothers and daughters, whose relatedness is not affected by EPP.

We did not consider common environmental effects due to relatives sharing the same nest environment, because only 7.6 and 0.4% of the nests had two and three recruits (of both sexes), respectively (Rattiste 2004). However, we did test for shared temporal environmental effects in the groups of individuals that started to breed in the same year. This effect was not significant and is therefore not included in the models presented herein. We also tested for the maternal effects on the laying date that might inflate our estimate of additive genetic variance. Of the 204 females whose mothers were known, 58 individuals had one maternal sister and 12 individuals had two maternal sisters. We assumed that females with unknown mothers all had a different mother. We also contrasted the variance across maternal groups by combining all females whose mother was unknown in the same group, but this did not show any variance across mothers (0%).

All models were fitted in ASReml v. 2 (VSN International) and fully converged, without constraining any of the (co)variance components. Estimates and means are reported with their associated standard error, unless mentioned otherwise. Approximate standard errors (ASE) for random regression variance components as a function of environmental values were calculated according to Fischer et al. (2004), and the approximate 95% CI was estimated as double the ASE. Environment-specific heritabilities were estimated as the ratio of the additive genetic variance over the sum of all estimated variance components for each year.

3. Results

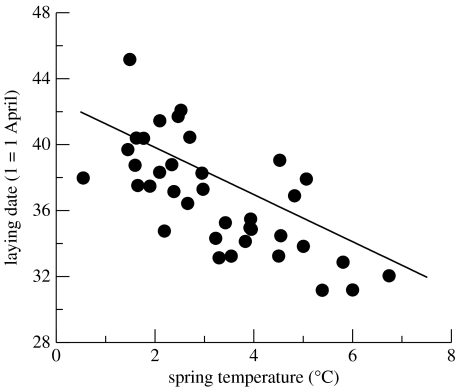
The sliding window approach showed that a time period of 28 days from Julian days 81 to 107 (31 March to 26 April in non-leap years) provided the highest correlation between the average temperature and the annual mean common gull laying dates (r=−0.71; figure 1). We refer to the average temperature during this period as spring temperature. Spring temperature increased during the study period (linear regression against year, b=0.052±0.02, t₃₅=2.6, p=0.014), although the mean laying date did not change (linear regression b=0.016±0.048, t₃₅=0.3, p=0.73).

Figure 1.

Annual mean laying dates for 1968–2006 (except 1984 and 1985) plotted against the annual mean temperature during the period that showed the highest correlation with the mean laying date. Laying date is expressed in April days (1 April=1, 1 May=31). The plotted line shows the fixed-effect elevation (laying date at mean temperature of 3.27 °C) and slope (−1.43 d °C⁻¹) fitted using a REML mixed modelling procedure described in table 1 and the text.

We used average spring temperature (standardized as described earlier) as our measure of environmental conditions. Mixed model analysis showed that laying date advanced with 2.12±0.41 days per standard deviation in spring temperature (=1.43 d °C⁻¹; figure 1). Statistical comparison of mixed models showed clear improvements in the model fit up to and including the specification of individual-specific elevations (I) and slopes (I×E) in the laying date–temperature relationship (model 4; table 1). Thus, individuals not only differ in average laying date but also differ in their plastic responses to local spring temperature (I×E). Partitioning the variation across individuals in their elevation (I) into a genetic (G) and permanent environmental (PE) component further proved to be a significant improvement of model fit (model 5; table 1). The significant genetic component shows that laying date is heritable. Furthermore, there is evidence for a significant permanent environment effect component of variance. However, partitioning variance in phenotypic plasticity across individuals (I×E) into a genetic (G×E) and permanent environmental component (PE×E) did not result in a significantly better fit (table 1). The estimated variance associated with G×E was about four times higher than that attributed to PE×E (model 6; table 1). However, the associated standard errors are large, and it is clear that these components of the observed I×E cannot be reliably separated.

Table 1.

Hierarchical models describing 11 624 laying dates of 2262 common gull females over 37 years as a function of the annual spring temperature. (Qualitatively, the same results were obtained when the females that bred only once were excluded (see §3). The estimated variance with standard error in parentheses is given for terms (as specified in equations (2.1) and (2.2)) that were included in the model, with ‘—’ indicating terms that were not included. Models are nested with increasingly higher-order terms, where the significance of each higher-order term is based on the increase in log likelihood (log L), starting with the model with environment-specific residuals only (model 1) and ending with model 6 which includes all terms in equation (2.2). Terms are year (y) or a function of either the phenotypic variance across individuals (ind) or its components, the additive genetic effect (a) and permanent environmental effect (pe) as a polynomial function with the order (0 or 1) indicated by subscript. For all the models, the number of estimated (co)variance terms are provided with the likelihood ratio test (Χ² statistic with associated d.f.) between the given model and the model that is one hierarchical step higher (i.e. 2 versus 1, 3 versus 2, etc.). The statistics of the most parsimonious model is indicated in italics.)

	random regression model terms							test
model	I (ind0)	I×E (ind1)	G (a0)	G×E (a1)	PE (pe0)	PE×E (pe1)	y	log L	Χ2	d.f.	p
model 1	—	—	—	—	—	—	—	−24351.64
model 2	—	—	—	—	—	—	6.08 (1.48)	−23201.36	2300.6	1	≪0.001
model 3	7.32 (0.341)	—	—	—	—	—	5.84 (1.41)	−22259.64	116.6	1	≪0.001
model 4	7.38 (0.347)	1.25 (0.313)	—	—	—	—	5.80 (1.40)	−22220.55	78.2	2	<0.001
model 5	—	1.24 (0.313)	3.00 (1.20)	—	4.36 (1.20)	—	5.85 (1.42)	−22217.47	6.2	1	0.013
model 6	—	—	3.98 (1.24)	0.987 (1.21)	3.98 (1.24)	0.235 (1.22)	5.86 (1.42)	−22216.47	2.0	2	0.37

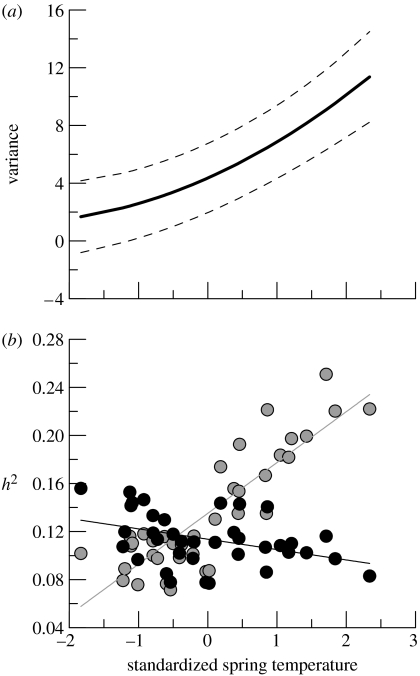
Most of the variance in the laying date was due to year-specific residual variance, which was on average 13.87±0.86 (range 6.04–26.41), and showed, as expected, no trend across temperatures (t₃₅=0.5, p=0.62). In the most parsimonious model (model 5), the individual-specific elevations and slopes were highly correlated (0.85±0.16). Because warmer temperatures lead to earlier laying, this positive correlation indicates that individuals that lay late (i.e. have a high elevation) tend to have a shallower (more positive) slope in their laying date–temperature relationship. Consequently, model 5 implies that there was little non-genetic variation across individuals in years with a cold spring, whereas this variance component rapidly increased during warmer springs (figure 2a). Under the assumption of constant additive genetic variance (model 5; table 1), estimated heritabilities were modest (approx. 11% in the average environment) and declined somewhat in warmer springs (black circles and black line in figure 2b). For comparison, we also calculated the year-specific heritabilities for the parameters estimated under the non-supported model 6 including G×E; these showed a clear increase in the heritability of laying date in warmer springs (grey circles and grey line in figure 2b).

Figure 2.

(a) Variance in laying date and its approximate 95% confidence due to presumably non-genetic individual-specific causes (sum of permanent environmental component and I×E) estimated under model 5 (table 1) as a function of standardized (zero mean, unit standard deviation) spring temperature. (b) Narrow-sense heritabilities h² (ratio of additive genetic variance over the sum of all variance components) for all 37 years as a function of standardized spring temperature. Plotted are the heritabilities under parameters estimated by model 5 (black circles and fitted regression line with a=0.11±0.0034 (t₃₅=33.8, p<0.001) and b=−0.0086±0.0034 (t₃₅=−2.5, p=0.016)) and model 6 (grey circles and fitted regression line with a=0.14±0.004 (t₃₅=32.7, p<0.001) and b=0.042±0.0042 (t₃₅=10.1, p<0.001)), as shown in table 1.

The functional form of the relationship between the laying date and temperature was assumed to be linear (first-order polynomial), because higher-order polynomials did not improve model fit (results not shown). We repeated the analysis using data on females that bred more than once (n=1813). Qualitatively, the same result was obtained, with the RRAM allowing for additive genetic, permanent environmental component and I×E as the best model (model 5 versus model 4: Χ₁²=6.8, p=0.009; model 6 versus model 5: Χ₂²=2.1, p=0.35).

There was little evidence of a maternal effect, explaining a low and insignificant proportion of variance (0.04±0.06 (s.e.)), although the power of this approach was low given that few mothers were known (see §2).

4. Discussion

Common gulls lay earlier in warmer springs. Here, we show that individuals differ in the slope of their relationship of laying date to temperature; not all individuals are able to advance laying in warmer springs to the same degree. We further show that laying date is a heritable trait in the common gull females, but do not find statistical support for an interaction between genotype and spring temperature. The high correlation between elevation and slope indicates that late-laying birds are less plastic than early-laying birds. Consequently, warmer springs lead to early-laying birds getting disproportionally earlier than late-laying birds (the variation in the laying date increases).

Modelling G×E in a natural pedigreed population using an RRAM on repeated measures requires a suitable description of the environment to be identified. The ‘quality’ of the annual environment can be described with respect to the focal trait. For example, Larsson et al. (1997) explored G×E in the head length of the common gulls, and defined the quality of the annual environment according to the year-specific head growth of the offspring. Alternatively, a measure of population productivity can be used to describe the environment (e.g. Wilson et al. 2006). Ideally, however, the environmental covariate is a truly extrinsic variable. We find that laying date correlates well with the temperatures from 31 March to 26 April, which is just after the common gulls arrive in Estonia (overall average of 26 March, data from Rootsmäe & Rootsmäe 1981; Rootsmäe 1991, 1998), but before most of them start to breed. In addition to the effect of temperature, we still find highly significant variation across years indicating that local temperature, as expected, is an incomplete description of all relevant environmental conditions. Importantly, however, the environment in a natural population cannot be controlled, and unidentified factors will therefore always possibly be involved in determining the environmental conditions that are relevant to the common gulls in deciding when to lay.

The breeding phenology of migratory seabirds is often thought to be determined more by large-scale climatic effects (e.g. NAO), with local conditions of greater importance for resident species (Frederiksen et al. 2004). By contrast, here we found that local climatic conditions are important for phenology despite the fact that common gulls are migratory. The sea and the islands in the western Estonian archipelago are still frozen and covered by snow around the time common gulls arrive at the breeding site, and local weather conditions are important in determining when the sea ice melts (Jaagus 2006). This in turn determines when the study area becomes available for nest building. In addition, local temperature affects the availability of fish (herring and sprat) through local sea surface temperature (Brunel & Boucher 2007), and is likely to affect the availability of terrestrial invertebrates (mainly earthworms) that the common gulls feed on.

(a) Variation in plasticity across individuals

Previous studies exploring the genetics of plasticity in a natural population (Brommer et al. 2005; Nussey et al. 2005) were based on an initial evaluation of I×E using linear mixed models, after which best linear unbiased predictor (BLUP) values for an individual's elevation (i.e. phenotype in the average environment) and slope (i.e. plasticity) were extracted. These predicted values were then analysed in a second step using an animal model. Instead of this two-step approach, we have used random regression directly within an animal model context RRAM (Meyer 1998; Schaeffer 2004; Nussey et al. 2007). An RRAM is a more powerful approach because it directly models the additive genetic effect on the phenotypic data, instead of the first generating BLUPs that describe these data. The use of BLUPs in a two-step approach ignores the uncertainity involved in generating BLUPs, and using such BLUPs in an animal model falsifies the assumption of independence across individuals needed to generate them in the first place. An RRAM has been used to study G×E in the wild (Wilson et al. 2005, 2006), and is a commonly used method in animal breeding (Lynch & Walsh 1998; Schaeffer 2004; Meyer & Kirkpatrick 2005). In the absence of pedigree information, this framework can also be used if one is interested in modelling phenotypic plasticity (I×E) only (equation (2.1), a random regression phenotypic model, Nussey et al. (2007)).

We found no statistical support for splitting up the phenotypic variation across individuals in their laying date–temperature relationships (I×E) into a genetic and permanent environmental component. This probably reflects a lack of power. Common gulls are long-lived birds, and there are sufficient repeated observations on individuals to describe I×E. However, splitting up the rather small I×E variance into a genetic and non-genetic component is statistically challenging in this species, because laying date is a female-linked trait while dispersal out of the study area is female biased in this case, consequently only 21% of females have at least one (measured) female relative in the population. Nevertheless, the available pedigree information has sufficient power to separate genetic versus permanent environmental effects on the elevation of the laying date–temperature relationship. Because female-biased dispersal is common in birds, analyses of plasticity in an avian reproductive trait might be generally hampered by pedigrees containing relatively less information on the relevant sex. In the case of the common gull, our limited power to separate the genetic and non-genetic components of I×E hampers a complete understanding of the evolutionary implications of plasticity under a climate change scenario. The statistically best supported model (model 5) shows a slight decline in the heritability of laying date in warmer springs, suggesting that climate warming may constrain the evolution of this trait (depending on the annual selection gradients; cf. Wilson et al. 2006). However, this model assumes that all variation in the laying date–spring temperature slopes across individuals have non-genetic causes. A radically different prediction of increasing heritability with warmer springs emerges when allowing for the possibility that part of the variation in the laying date–spring temperature slopes is genetic (i.e. G×E is included, model 6). Although this latter model is not statistically supported, the predicted relationship between heritability and spring temperature is sufficiently different as to caution against making strong inferences on how heritability of the common gull laying date depends on spring temperature.

The study of plasticity of life-history traits in response to climate in the wild can provide important evolutionary and ecological insights. By focusing on how individuals (rather than population averages) respond to climate, we can gain understanding in the causes (and consequences) of plasticity (Nussey et al. 2007). Variation in plasticity (I×E) is not ubiquitous; Reed et al. (2006) found that laying date in the common guillemot shows a plastic response to NAO, but that individuals do not vary in their plasticity. Furthermore, variation in plasticity (I×E) need not reflect genetic variance for plasticity (G×E). In the collared flycatcher (Brommer et al. 2005), I×E is apparently environmentally driven, and a conservative (with respect to genetic effects) interpretation of the current results suggests that this is also true in the common gulls. However, plasticity in the laying date remains unaffected by warmer temperatures in the common gulls, whereas it gets increasingly constrained in the collared flycatcher, illustrating that the climate change may—through individual responses—have quite different impacts on a reproductive trait in different species. Long-term individual-based studies in wild populations combined with animal model methodology have the potential to make important contributions to our understanding of plasticity, and may allow us to predict how climate change affects the potential for evolution in natural populations.