Abstract
Reproduction is thought to entail costs, but assessing survival costs associated with maturation as organisms express reproductive genes for the first time is problematic because many will die prior to expressing a phenotype. We quantified selection acting on this invisible fraction by measuring selection on predicted breeding values for clutch size estimated from a multigenerational pedigree of side-blotched lizards in which clutch size was heritable (h2=0.25±0.04). The survival effects of predicted breeding values for clutch size during maturation, however, differed between males and females indicating ontogenetic conflict. Increased mortality during maturation was associated with lower predicted breeding values for clutch size for females, but higher predicted breeding values for males who do not produce a clutch. Genetic correlations between clutch size and male and female survival were consistent with calculated selection differentials. Experimental yolk removal did not affect progeny survival during maturation, indicating that selection on maturing progeny was not due to confounding yolk-volume maternal effects, and hormone manipulations confirmed clutch size as the target of viability selection during maturation. Such episodes of selection prior to phenotypic expression of the trait will have important consequences for the evolution of reproductive investment.
Keywords: ontogenetic conflict, clutch size, cryptic selection, trade-offs, Uta stansburiana
1. Introduction
Post-laying or post-parturition costs of reproduction are thought to constrain adaptation. Increased reproductive output in current reproductive effort should reduce survival or fecundity during future reproductive episodes (Williams 1966) due to pleiotropic action of genes across fitness components (Reznick et al. 2000), which are referred to as life-history trade-offs. Most studies of the cost of reproduction have focused on post-laying costs of reproduction such as female survival for subsequent reproductive episodes. However, many individuals may be selectively eliminated from the population during the maturation process, when the reproductive endocrine system is activated for the first time. While male progeny do not produce a clutch of eggs, nevertheless the same endocrine genes that are likely to contribute to additive genetic effects of clutch size in females, such as follicle-stimulating hormone (FSH), are also used in males to initiate sperm production (reviewed in Sinervo & Calsbeek 2003; Mills et al. in press). However, quantifying the survival consequences of the initial expression of reproductive traits such as clutch size prior to the phenotypic expression of the trait is highly problematic and impossible to assess at the phenotypic level in males, which do not produce clutches. The proportion of individuals that do not survive long enough to express a phenotype has been referred to as the invisible fraction (Grafen 1988), and selection acting during this phase can lead to biased estimates of selection (Hadfield 2008). The term cryptic natural selection has been used to describe the phenomenon (Sinervo 1999), but here we adopt Grafen's term, invisible fraction.
An alternative to measuring selection on phenotypes is to quantify selection directly on breeding values. Breeding values are a statistical measure of the underlying genetic merit of a particular individual for a trait and represent the sum of all additive genetic effects across all loci for that particular individual (Lynch & Walsh 1998). Despite being expressed only in females, alleles for female reproductive traits such as clutch size are inherited from both the father and the mother. As a result, it is possible to not only estimate the additive genetic basis to clutch-size variation but also to generate predicted breeding values for clutch size for both males and females (e.g. Postma & van Noordwijk 2005) by analysing mutigenerational pedigrees using a restricted maximum-likelihood ‘animal model’ approach (Kruuk 2004). Selection differentials can, therefore, be calculated based on predicted breeding values (Postma 2006) from an episode of selection prior to the phenotypic expression of reproductive traits such as clutch size. This approach is similar to quantifying maternal selection gradients (sensu Kirkpatrick & Lande 1989). The potential bias associated with non-random mortality in the invisible fraction (e.g. Bennington & McGraw 1995) can also be addressed by explicitly modelling the genetic correlation between viability and the trait of interest (Hadfield 2008). For example, Kruuk et al. (2002) used the genetic correlation between antler mass and male breeding success to examine selection on antler mass; however, this approach has not yet been used to examine viability selection on the invisible fraction.
Survival effects of the initial expression of clutch-size variation, however, might also be confounded with maternal effects linked to offspring quality or clutch size itself (Sinervo et al. 1992; Schluter & Gustafsson 1993). Mothers that produce large clutches also lay small eggs and mothers that produce small clutches lay large eggs (Sinervo & Licht 1991). Female or male progeny might die owing to maternal effects of yolk provisioning that are correlated with clutch size, but not causally related to clutch-size genes that progeny express at maturity. As a result, complementary experimental manipulations (Sinervo & DeNardo 1996) are needed to assess the importance of maternal effects for offspring survival. Manipulations of clutch size resolve costs of reproduction (Gustafsson & Sutherland 1988) that have otherwise proven difficult to measure in natural phenotypic variation. However, the applicability of manipulations to elucidate costs of reproduction has been questioned. Reznick (1985, 1992) and others (Chippindale et al. 1993; Leroi et al. 1994) argue that assessing genetically based life-history trade-offs is the only effective method to assess costs.
In this study, we quantified the selective trade-offs (Van Tierderen & de Jong 1994; Pischedda & Chippindale 2006; Foerster et al. 2007) between clutch size and survival during maturation (prior to the expression of clutch size) in side-blotched lizards, Uta stansburiana, a small 4–10 g phrynosomatid lizard that initiates maturation within 1 year. Selection was quantified by predicting clutch-size breeding values (Postma 2006) from a multigenerational field pedigree for both male and female lizards that survived or died during maturation, based on field pedigree analysis (Kruuk 2004). We further tested whether survival of progeny during maturation was due to yolk-volume maternal effects by manipulating yolk volume of individual eggs and tested whether clutch size was the target of selection during maturation by experimentally ablating ovarian follicles during maturation to decrease clutch size and manipulating exogenous hormones to induce females to lay a larger clutch or larger total clutch mass (Sinervo & DeNardo 1996). Survival of offspring from treated females was censused over the same interval (e.g. maturation) as those cohorts used in our genetic assessment of clutch-size breeding values. Thus, we could validate the magnitude of maturational costs detected in selection analysis of genetic variation compared to the induced variation in clutch size.
2. Material and methods
Side-blotched lizards emerge from winter hibernacula at the end of February. At this time, males begin feeding, their testis rapidly enlarges and they begin defending territories. Females begin feeding, and defending territories, but do not begin to develop follicles and yolk up ova until the middle of March. Average survival probability of progeny that emerge from winter hibernacula oscillates between 0.1 and 0.5 for females and 0.08 and 0.28 for males, of those progeny that hatched the previous year (see Sinervo et al. 2000b). The first eggs are ovulated at the beginning of April and the first clutch is laid around the middle of April. Subsequent clutches are laid every month, if females survive. Surviving females typically lay eggs throughout the summer until September (up to six clutches). All progeny mature within 1 year, and because most females do not survive their first year of reproduction Uta is nearly an annual species.
Side-blotched lizards have been captured at the same study site in the Central Valley of California (36.99620° N, −121.05068° W) since 1989. Near-term female side-blotched lizards (dams) have consistently been captured with oviducal eggs prior to oviposition and set up in ovipositoria (Sinervo & DeNardo 1996). Eggs were incubated in a laboratory environment (−200 kPa and 28°C). Presence of two enlarged post-anal scales in males, but not females, allows progeny to be sexed at hatching. Hatchlings were permanently marked with a unique number, released into the wild within 1–3 days of hatching at nest sites that were randomized with respect to territories of sires and dams (Sinervo et al. 2006). Free-ranging progeny were captured the next year and clutch size was measured as per methods described previously.
Paternity was determined for offspring in some years with nine microsatellite loci (Zamudio & Sinervo 2000). We genotyped progeny (N=458, 160, 212, 78, 103, 284), dams (N=68, 96, 40, 35, 48, 100) and sires (N=124, 56, 44, 40, 43, 147), and assigned paternity (with a significant p<0.05 paternity assignment and/or with exclusionary criteria) to 71, 75, 86, 57, 73 and 81% of progeny collected in 1992, 1996, 1998, 1999, 2001 and 2002, respectively. Paternity in each year was assigned with Kinship v. 1.3 (Goodnight, K. F., Quellar, D. C.& Poznansky, T. 1998 Kinship, http://www.bioc.rice.edu/∼kfg), which combines maximum likelihood and exclusionary criteria. Previous analyses have found that the results from Kinship are comparable to the results from Cervus (Marshall et al. 1998). Detailed methods on paternity analyses are described in Zamudio & Sinervo (2000), Sinervo & Clobert (2003) and Sinervo et al. (2006). Our sample of progeny from sires (N=1295 genotyped) across the pedigree was not as complete as the sample of progeny from dams (N=6889 total: 313, 565, 834, 1205, 570, 653, 489, 444, 290, 475, 337, 189, 364, 105, 56 hatchlings produced from 1989 to 2003, respectively). However, we sampled sires from several years across the entire female pedigree (see above).
(a) Pedigree analysis
Maternal linkages from oviposition in captivity and paternal linkages determined by paternity analysis were used to generate a multigenerational pedigree for this population. The pedigree consisted of a total of 7247 individuals born between 1989 and 2002, including 1411 base animals and 1395 individuals with great-grand parents in the pedigree. The analysis of clutch size included a total of 1751 clutches from 1150 animals (range of one to six observations per female), which corresponded to 747 dam-offspring pairs, 1866 maternal half-sib pairs, 160 paternal half-sib pairs, and 50 sires, 149 grand dams and 20 grand sires with offspring and grand offspring with phenotypic data. Note that because progeny were randomized with respect to dam and sire territory, the likelihood of inbreeding in the pedigree is minimized, and in fact only a single close consanguineous mating (e.g. sib–sib) has been observed across all years with both maternal and paternal pedigrees. However, side-blotched lizards have a large dispersal distance (Sinervo et al. 2006) and inbreeding is a rare event even in those studies where progeny have been released at the dam's territory (Sinervo et al. 2006).
The heritability of clutch size was estimated from a restricted maximum-likelihood animal model analysis (Kruuk 2004) of the multigenerational pedigree using the program DFREML (Meyer 1989). The fixed effect structure of the model was determined prior to the animal model analysis using general linear models in R (R Development Core Team 2007). Mean values were used for 26 missing observations for female mass after laying. Lay date (F1,1711=193.5, p<0.0001; b=− 0.025±0.006), year (F12,1711=18.8, p<0.0001) and the mass of the female after laying (F1,1711=9.4, p=0.002; b=1.88±0.50) were all found to be significant predictors of a female's clutch size. In addition, there was a significant nonlinear effect of female's mass after laying (quadratic effect: F1,1711=14.1, p=0.0002; b=− 0.21±0.05) and significant interactions between lay date and year (F12,1711=3.7, p<0.0001) and post-lay mass and year (F12,1711=3.6, p<0.0001). There were no other nonlinearities and diagnostic plots indicated the appropriateness of the model, including the normality of the residuals. A mixed-effect model in which the female's identity was included as a random effect (female variance=0.67; CIs: 0.58–0.77) significantly improved the fit to the data when compared with the model containing only fixed effects (likelihood-ratio test: Χ12=60.5, p<0.0001) indicating consistent differences among females in their clutch sizes.
The animal model analysis for clutch size, therefore, included a fixed effect for the year, and two covariates. Lay date was included as a linear covariate, while both linear and quadratic terms were fitted for female post-lay mass. These covariates were also nested within the year to account for the interactions with year, such that separate fixed-effect parameters were fitted for each year. A random effect linked to the pedigree was used to estimate the heritability of clutch size. A more complex model in which an additional random effect was fitted for the identity of the female's dam was used to test for maternal effects on clutch size. In all animal models, clutch size was analysed as an attribute of the dam and not of her offspring, so these maternal effects represent variation among females in their effects on the clutch size of their daughters. Maternal effects were estimated to be small in the analysis with the two maternal covariates (see §3). We also tested whether results were dependent on inclusion of the lay date and post-lay mass covariates, by rerunning the analysis without these maternal covariates. The results of these models were extremely similar (see below). The addition of a permanent environmental effect associated with the repeated clutch-size records per female did not significantly improve the fit to the data (Χ12=2.47, p=0.12), so this effect was not considered further. Heritabilities (h2) are, therefore, reported as the ratio of additive genetic variance (VA) to total phenotypic variance (VP), where VP is the sum of VA, environmental variance unique to each female or clutch-size observation (VE) and environmental variance due to the identity of her dam (i.e. variance among dams in the clutch size of their daughters: VM), where applicable. Maternal effects are reported as the proportion of VP that was due to VM (m2).
(b) Predicted breeding values
Predicted breeding values were generated from the animal model analysis without the maternal covariates using DFREML (Meyer 1989). The accuracy of these predicted breeding values calculated as the correlation between true and predicted breeding values (following Postma 2006) was 0.32, which was quite low. This corresponds to a reliability (i.e. squared correlation between true and predicted breeding values; Postma 2006) of 0.10. The low accuracy of our predicted breeding values probably occurred owing to the relatively small number of lizards in the pedigree for which clutch-size data were available (1150 out of 7247 animals). Clutch size of males is not known and many animals die before maturation (Sinervo et al. 1992). We rarely miss female progeny that mature (e.g. catchability below is greater than 0.97, for one capture, three captures are staged) and we measure the clutch size of a very large fraction of reproductive females in the population (93% of N=1150). The selection differentials based on predicted breeding values that we used to quantify ontogenetic conflict, however, are not biased by low reliability (Postma 2006).
(c) Selection on predicted breeding values
For lizards born between 1989 and 1998, we quantified selection acting prior to clutch formation from selection differentials based on predicted breeding values for clutch size and survival between emergence from hibernacula to production of the first clutch. This time period reflects the stage in the life cycle of both sexes when the reproductive system is activated for the first time (e.g. a primiparous females). Data on survival of progeny after overwintering (e.g. first month of the breeding season) were based on 782 maturing female and 392 maturing male progeny. Of this total, we had detailed survival records (three recaptures stage each month; Sinervo et al. 2006) for progeny (N=769 female and N=217 male progeny) in the core area of the study plot (1 km in diameter), not in the peripheral areas where progeny might disperse (3 km in diameter), therefore analyses of cryptic selection during the maturational period from emergence until females produced a first clutch (e.g. primiparous episode) were based on 491 females born in the first clutch of the previous season (i.e. first-clutch progeny), 278 females born in later clutches from the previous year (i.e. later clutch progeny), 128 first-clutch male progeny and 89 later clutch male progeny. Probability of recovery of progeny in the spring is high (97–98%) owing to natal philopatry and because our census spans a large meta-population (6 km in diameter, Sinervo et al. 2006). We partitioned analyses by clutch (first versus later clutches) owing to the differences in survival selection (Sinervo et al. 1992), even though all progeny mature within 1 year. Survival censuses in the current study are from a time frame in the reproductive cycle, the one-month maturation period, which has not been previously analysed in this species. Previous studies (Sinervo et al. 1992, 2000b) have assessed survival from hatching to emergence from winter hibernacula at the start of maturation. We also compared the results from ordinary ANCOVA (clutch, sex are factors, breeding values for clutch size is a covariate) with ANCOVA based on logistic regression, which can deal with the non-normality of the errors for survival probabilities. In addition, we tested our results based on predicted breeding values from a model that considered year as the only fixed effect to ensure that the inclusion of the maternal covariates did not have an important impact on our results. The results of breeding values on progeny survival were essentially identical in both analyses so that these analyses were performed with these terms deleted.
(d) Genetic correlations with survival
We corroborated these selection differentials by examining genetic correlations between clutch size and survival during maturation in both female and male first-clutch progeny using a multivariate animal model (Kruuk et al. 2002; Hadfield 2008). Year was included as a fixed effect for both male and female survival and clutch size was fitted with year as a fixed effect as well as with post-lay mass and lay date as covariates described previously. A significant maternal effect was fitted for female survival (m2=0.12±0.05; Χ12=7.19, p=0.007), but there were no apparent maternal effects on male survival. The trivariate model, which included clutch size, female survival and male survival, did not converge, but each of the bivariate models converged on similar values. The binary nature of the male and female survival traits violate the assumption of normality of errors in the restricted maximum-likelihood animal model approach, but do not affect the estimates of the genetic correlation (see also Kruuk et al. 2000). We, therefore, provide estimates of the genetic correlations between clutch size, female survival and male survival, but interpret the significance of these with caution.
(e) Experimental manipulation of maternal effects
We manipulated the yolk volume of approximately half the eggs from most clutches (approx. 97% of all clutches) in each year of the study to examine effects of egg size and yolk-volume maternal effects on offspring survival during maturation. Approximately 20% of the yolk by mass was aspirated from half of the freshly laid eggs in each manipulated clutch with a 25 Gauge syringe (Sinervo & Huey 1990). Eggs were weighed before and after manipulation. Remaining eggs (controls) were poked with a syringe to control for effects of needle insertion. We also controlled maternal effects associated with female oviposition and egg incubation (eggs incubated individually in cups with vermiculite: chamber temperature=28°C; hydric conditions =−200 kPa of vermiculate) that might confound heritability estimates in the wild (Calsbeek & Sinervo 2007). The effects of the manipulation were tested by including the volume/mass of yolk removed (units) as a covariate in a model of offspring survival during the period from overwintering emergence to production of their first clutch. Egg size (g) was also included as a covariate in this model. Controls received a covariate for yolk removal of zero.
(f) Experimental manipulation of clutch size and costs of reproduction
In 3 years of strong natural selection on clutch size (1991–1993), we tested whether clutch was in fact the target of selection during maturation by experimentally adjusting clutch size in females prior to maturation. Note that this differs from the maternal effect manipulation above. Here, we manipulated the clutch size of a subset of females just prior to maturation as opposed to manipulating the yolk volume of the eggs that they came from (maternal effect). We reduced clutch size and total mass by ablating follicles on the surface of the left ovary (Sinervo & Licht 1991). Follicles on the surface of the right ovary were left intact (1992, N=41; 1993, N=45). Females undergoing follicle ablation produce two fewer eggs compared with a mean clutch size of five eggs for control females (range 3–9 eggs on the first clutch, 2.4 g clutch mass). We increased clutch size and mass by implanting Elvax pellets (Dow Corning) in which we had embedded ovine FSH (Sinervo & DeNardo 1996). Hormone release from implants was designed to increase clutch size by two eggs (1993, N=30), as previously assessed in laboratory trials (Sinervo & Licht 1991). Clutch mass was also increased with corticosterone implants (1991, N=18; 1992, N=60; 1993, N=42) that were designed to increase clutch mass by 0.6 g (Sinervo & DeNardo 1996). Induced effects of corticosterone implants on clutch mass are comparable to that of FSH implants. Details on anaesthesia and surgical protocols are found in Sinervo & DeNardo (1996). Survival was studied from treatment (early March) to production of the first clutch (mid-April). One-month survival of treated females was compared with control females undergoing sham manipulation (surgery with empty implant) and to control females that were not manipulated. Each manipulation along with associated sham-manipulated controls was performed on a set of study plots located next to the pedigree study plots. Females on plots were randomly assigned to either treated (N above), sham manipulated (N=20, 61 and 55 for 1991–1993, respectively) or unmanipulated groups (N=111, 109 for 1992, 1993). Analogous experimental manipulations of clutch size could not be performed for males since they do not produce a clutch.
In this comparison we used only the phenotypic values for dam's clutch for the female progeny, rather than breeding values, because this allowed us to directly compare the magnitude of selection on clutch size (as passed on by dams) with the magnitude of experimental manipulations in clutch size. The breeding values for clutch size in female progeny and the raw dam values for clutch size are of course significantly correlated (r2 =0.18, F1,739=133.23, restricted to female progeny), given that raw dam values were used to estimate breeding values. Statistical tests were based on methods described for genetic analyses (above) and computation of selection differentials from experimental variation followed Sinervo (2000). A 500 m buffer zone surrounded each study plot and daily censuses continued for two months after the first-clutch census to ensure that females were not missed (e.g. a total of three recapture periods).
3. Results
(a) Heritability of clutch size
The heritability of clutch size from the animal model analysis was 0.25±0.04. The inclusion of an additional random maternal effect term did not significantly improve the fit of the model (Χ12=2.74, p=0.098), the maternal effect term was small and not significantly different from zero (m2=0.011±0.020) and the estimate of heritability was not affected by the inclusion or exclusion of the maternal effect term (h2=0.24±0.05 with maternal effect included). The exclusion of laying date and post-laying mass as maternal covariates resulted in significant but small maternal effects (m2=0.022±0.021; Χ12=6.16, p=0.013) but did not have a large effect on the estimate of clutch-size heritability (0.19±0.04). Breeding values were predicted from the model that excluded the maternal covariates but included the maternal random effect.
(b) Selection differentials on clutch-size breeding values
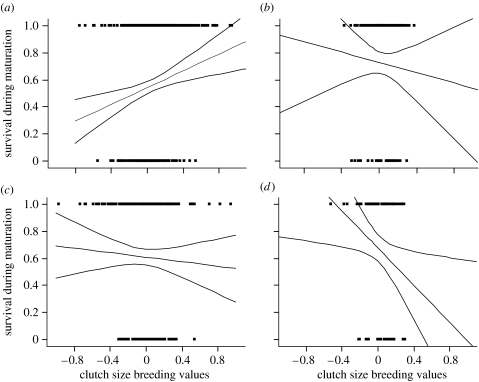
Mean breeding values for female progeny surviving from emergence to first reproduction were higher than that for all females alive at the start of spring. However, selection differentials on breeding values for clutch size varied by clutch and were strong for first-clutch female progeny and weak (near zero) for later clutch female progeny (table 1; figure 1). In contrast, the reverse pattern was observed for male progeny. Mean breeding values for male progeny surviving from winter emergence to first reproduction were lower than that for all male progeny alive at the start of spring (table 1; figure 1). Selection against male progeny with high breeding values was more intense on later clutch male progeny compared with first-clutch progeny (table 1). In addition, yolk removal (Χ2=1.24, p=0.27) and natural variation in egg mass (Χ2=0.08, p=0.76) did not affect survival from winter emergence to first reproduction, and these terms were removed from the final model. Moreover, none of the two-way interactions of yolk removal and egg mass with sex and clutch were significant and were dropped from the final model. The effects of breeding values and interaction terms sex and clutch (table 1) remained significant in all models.
Table 1.
Selection on breeding values expressed as selection differentials (s±s.e.) computed from the distribution of animals that survived compared with those prior to the episode of selection, which was the period from winter emergence to the time of first-clutch production (primiparous event). (Lizards begin the maturation process at this time, which is culminated by the production of the first clutch. Reported differentials represent a significant two-way interaction for breeding values for clutch size and progeny gender (logistic regression Χ2=6.30, p=0.01), a significant interaction for clutch-size breeding values and first versus later clutch progeny (Χ2=7.56, p=0.006), and a non-significant interaction for gender and first versus later clutch (Χ2=1.29, p>0.26). The three-way interaction was not significant and was deleted (Χ2=0.14, p>0.7), but a significant year effect on survival was retained (Χ2=6.53, p=0.01). The experimental and natural maternal effects (i.e. yolk-volume removed, experimental clutch-size reduction or egg mass) were not significant (see text).)
| female progeny | male progeny | |
|---|---|---|
| first-clutch cohort | s=0.073±0.022 | s=−0.029±0.040 |
| F1,490=10.68 | F1,276=0.52 | |
| p=0.001 | p=0.47 | |
| later clutch cohort | s=−0.020±0.029 | s=−0.122±0.008 |
| F1,127=0.48 | F1,87=5.22 | |
| p=0.47 | p=0.02 |
Figure 1.
Effects of breeding values for clutch size on survival of female and male progeny partitioned by the first versus later clutch progeny. (a) First-clutch female progeny, (b) first-clutch male progeny, (c) later clutch female progeny, (d) later clutch male progeny. The linear relationship between survival and breeding values are shown (e.g. selection gradient) along with the confidence limits. However, statistical tests are based on the univariate selection differential, s, which is computed from the difference between the distribution of breeding values of survivors after the process of maturation (e.g. production of the first clutch) and distribution for breeding values (pooling distributions from the top, survival=1 and bottom, survival=0) when progeny emerge from winter hibernacula and begin to mature (table 1). See table 1 for selection differentials (s) and selection gradients (β) and p-values for individual tests, as well as ANCOVA (ordinary and logistic regression) of clutch and sex and interactions with breeding values for clutch size.
The estimate of the genetic correlation between clutch size and female survival was 1.0 (rg=1.0±1.1), whereas the genetic correlation between clutch size and male survival was −1.0 (rg=− 1.0±2.2). There was also a negative genetic correlation between male and female survival (rg=− 0.4±1.5), but in all cases CIs overlapped with both −1 and 1.
(c) Experimentally induced clutch size and clutch mass and maturational survival
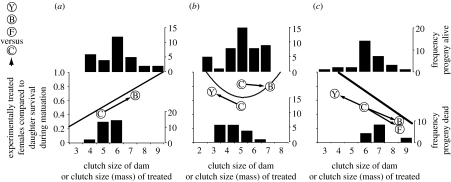
Selection on clutch-size breeding values was corroborated with results from manipulations of ovarian development. Across all years, survival selection acting on female progeny, for these phenotypic values for a dam's clutch size, varied significantly by year×clutch parity (first versus later)×dam's clutch size in their effects on maturational survival (F9,612=2.05, p=0.04). Inspection of individual year effects indicated that the years 1991–1993 contributed most strongly to this interaction. We directly compared the survival effects of dam's clutch size, which are genetically correlated with daughter's clutch size, with the experimentally induced effects of clutch size on maturing females in each of these 3 years (table 2). In 1991, corticosterone implants induced a large clutch mass in maturing females and these implants also increased maturational survival compared with control females (figure 2a, F1,36=4.21, p=0.05). In 1992, ablating follicles reduced clutch size and enhanced maturational survival compared with controls (figure 2b, F1,142=5.28, p=0.02). However, inducing large clutch mass with corticosterone implants in the same year did not affect maturational survival (figure 2b, F1,155=1.27, p=0.26). In 1993, follicle ablation reduced clutch size and enhanced maturational survival compared with controls (figure 2b, F1,139=3.79, p=0.05). Inducing large clutch size via exogenous FSH decreased maturational survival (figure 2c, F1,141=8.84, p=0.003), and inducing higher clutch mass via exogenous corticosterone decreased maturational survival (figure 2c, F1,153=7.68, p=0.006). Survival of sham-manipulated and unmanipulated females did not differ (1992: F1,220=0.18, p=0.67), and thus surgery does not affect survival.
Table 2.
Selection gradients (±s.e.) computed from survival of female progeny during maturation as a function of clutch-size variation of mothers (figure 2). (Selection gradients were also computed for three manipulations of ovarian development: follicle ablation reduced clutch size; FSH implants increased clutch size; and corticosterone implants increased clutch mass. Significance of selection surfaces is given by: *p=0.05; **p<0.05; ***p<0.01. Significant directional selection gradients (β) that acted on genetic variation were detected in all 3 years, and a disruptive selection gradient (γ) was observed in 1992. Genetic selection gradients are comparable in magnitude and direction to experimentally induced selection gradients in all but one case (e.g. no quadratic selection was detected in 1992 using corticosterone implants, see figure 2).)
| selection differential form experimental manipulations (β) | ||||
|---|---|---|---|---|
| selection on genetic variation (β and γ) | corticosterone | follicle ablation | FSH | |
| 1991 | β=0.304±0.145** | 0.403±0.196** | ||
| 1992 | β=−0.622±0.310** | −0.045±0.040n.s. | −0.101±0.044** | |
| γ=0.067±0.032** | ||||
| 1993 | β=−0.170±0.084** | −0.136±0.070* | −0.313±0.105*** | −0.258±0.093*** |
Figure 2.
Comparison of survival selection on clutch size as detected with manipulations (arrows) and genetic correlations (regression lines). Arrows indicate change in probability of maturational survival (left axis) as a function of mean change in clutch size (number of eggs, x-axis) for experimental compared with control groups (Y, yolkectomy of follicle (i.e. ablation); B, Corticosterone implant; F, FSH implant; C, sham-manipulated control; in 1992 two control groups are shown: follicle ablation controls and corticosterone implant controls). The thick regression lines indicate the relationship between maturational survival probability of daughters (abscissa) as a function of dam's clutch size (ordinate), which is indicative of an underlying genetic correlation between the fitness traits clutch size and survival. Histograms depict the frequency distribution of daughters that survived (fitness=1, top histograms) or died (fitness=0, bottom histograms) during maturation as a function of the mother's clutch size. Based on these changes in frequency distribution, significant directional selection (p<0.05, solid line) favoured survival of female offspring in (a) 1991 whose mother produced large clutches the previous year. Significant disruptive selection on female offspring in (b) 1992 favoured female offspring whose mother produced either large or small clutches and selectively eliminated those female offspring whose mother produced intermediate-sized clutches the previous year. Significant directional selection (solid line) favoured survival of female offspring in (c) 1993 whose mother laid a small clutch the previous year.
It is not possible to test the direct effect of clutch-size manipulations on maturing male progeny, as we did for maturing female progeny (above). The tests of clutch-size manipulations on maturing females (above) indicate that they experience dramatic costs of reproduction during the pre-laying period, which parallel the genetic contribution from the dam (figure 2). This group of treated females gives rise to both male and female progeny in the pedigree, and we can analyse the maternal effects of the clutch-size reduction on survival of progeny during maturation. For male progeny, we can test whether experimental clutch-size manipulation of mothers affected the survival of male progeny during the maturational period (i.e. a maternal effect on survival), given the follicle ablation procedure described for the pedigree. There was no effect of experimental clutch-size treatment that was applied to dams on son's maturational survival (Χ2=1.2, p=0.27). We also tested whether maturational survival of both male and female progeny was due to clutch-size treatment, but neither the effects of the manipulation were significant (Χ2=2.07, p=0.15) nor were the interactions for clutch-size treatment with sex, clutch or breeding values, but all of the terms for clutch-size breeding values (table 1) remained significant. Therefore, the survival selection reported in table 1 and figure 2 arise from the additive effects of genes for clutch size that progeny express when they mature, not from induced yolk-volume (see above) or induced clutch-size maternal effects.
4. Discussion
(a) Genetic and experimental measures of natural selection
Concordant results from genetic and experimental assays of natural selection during 3 years, when selection on clutch size was strongest, indicate that maturing side-blotched lizards incur substantial selective costs during maturation, even before they lay their first clutch (figures 1 and 2; table 1). Maturational costs of reproduction acting on this invisible fraction are impossible to detect using traditional studies of phenotypic selection. A traditional estimate of phenotypic selection on current reproduction entails measuring clutch size, which can then be used only to assess consequences for future reproductive success, such as the effects on post-laying survival.
Natural history observations suggest that changes in pattern of selection across 1991–1993 were driven by a fivefold increase in predatory coachwhip snakes, Masticophis flagellum (Sinervo & DeNardo 1996). Large clutches in lizards increase pre-laying reproductive burden of the clutch mass in females, decrease sprint speed in lizards, which we have linked directly to the increases in mortality risk (Miles et al. 2000). It would not be surprising that such effects may operate on survival during maturation. Before the rise in predatory snakes, females that matured with a large clutch were favoured (i.e. 1991). After the rise in snake prevalence, those females maturing with a large clutch were selected against (i.e. 1993). Since 1993, coachwhip snakes have resulted in an elevated mortality rate of lizards (Sinervo & DeNardo 1996). Pre-laying mortality ranged from 15 to 25% in 1990–1992 and doubled to 50% in the years immediate after 1993 (e.g. 1994–1995, Sinervo & DeNardo 1996).
Transient low survival of females laying large clutches in high predation years (1993) is intuitively appealing and consistent with life-history theory. However, why should females laying large clutches (i.e. either induced by hormones or as a consequence of genes) in other years (e.g. 1991) enjoy high survival? In addition, in the evolutionary long term, the pedigree study (1989–2002) indicates that first-clutch female progeny with large breeding values for clutch size had significantly higher survival, while breeding values for later clutch progeny appeared to be nearly neutral in their effects on survival (figure 1). Our finding presents a paradox for life-history theory, which would predict that females producing fewer eggs (e.g. small breeding values for clutch size) should have higher maturational survival.
The expectation of costs of reproduction associated with high energetic investment is an overly simplifying assumption of life-history theory (Williams 1966) that focuses on costs from physiological processes rather than ecologically or socially mediated costs of reproduction. Expression of genes for large clutches in females may have generated a hormone profile that is conducive to high survival because it elevates plasma levels of other hormones, such as the stress hormone corticosterone known to enhance female survival (Comendant et al. 2003). Indeed, in low predation years, exogenous corticosterone elevated survival (figure 2, 1991). The form of natural selection that gives rise to selective costs of reproduction depends on the degree to which ecological causes (predation), physiological causes (i.e. hormones and reproductive energetics), social causes (density-dependent selection) or the interaction among all three agents of selection result in differential survival, and how each agent targets specific reproductive traits like clutch size. Fluctuations in the direction and intensity of natural selection, such as observed in the side-blotched lizard (Sinervo et al. 2000a,b), are likely to be common in nature (Gibbs & Grant 1987). Nevertheless the long-term action of selection on female breeding represents a paradox for life-history theory, which predicts the existence of trade-offs between current effort (e.g. clutch size and total clutch mass) that impacts future reproductive success.
(b) Differences in selection on clutch-size genes in males and females
The paradox presented by the positive relationship between clutch size and female progeny survival is resolved through a consideration of selection on males. Antagonistic patterns of selection in males (figure 1) have favoured a clutch size in females that is below the point where the female survival/reproduction trade-off should occur. Thus, we observed genetic evidence of ontogenetic conflict in clutch size. We also observed a genetically based ontogenetic trade-off between progeny produced on the first clutch and those from later clutches. Later clutch progeny tend to express the expected trade-off between clutch size and survival, while first-clutch progeny deviate strongly from this expectation based on life-history theory. Genetic trade-offs related to functional design of the sexes or between juvenile and adult phases are referred to as intersexual ontogenetic conflict or simply ontogenetic conflict (Rice & Chippindale 2001). Many alleles that are favoured under sexual selection on male morphology and physiology are of limited value during natural selection on female or juvenile morphology and physiology and vice versa. Several studies have documented evidence of ontogenetic conflict (Calsbeek & Sinervo 2004; Pischedda & Chippindale 2006; Foerster et al. 2007). Here, we identify a specific trait under ontogenetic conflict (clutch size), which differentially affect survival in the sexes. Elsewhere, we have identified that male body size is another trait that exhibits ontogenetic conflict on progeny survival (Calsbeek & Sinervo 2004).
We resolved 25% of the variation in clutch size that was heritable and suggest that adaptive plasticity (owing to selection that favours female modulation of clutch size and egg mass; Sinervo et al. 1992) will probably contribute to additional unexplained variation in clutch size. Such variation would be due to a genotype×environment interaction with density, the salient cue that induces variation in other female life-history traits. Previous studies on side-blotched lizards (Sinervo & Licht 1991; Sinervo 2000) and the manipulations of clutch size used in our study indicate that levels of FSH regulate clutch size. In males, FSH regulates other reproductive activities besides gonadal function and sperm production, such as territorial behaviour and mate attraction (Mills et al. in press). Our study indicates that expression of these genes affecting clutch size during female reproduction can have beneficial survival effects, but the positive effects are balanced in the evolutionary long term by negative survival effects on males during maturation.
Natural selection during maturation should be prevalent in costly to produce traits, such as the ova of females or sexually selected traits of males. Experimental paradigms used in this study to document life-history trade-offs in females could be extended to mortality costs of sexual ornaments and testosterone (Marler & Moore 1988, 1991; Ketterson & Nolan 1992; Sinervo et al. 2000a; Mills et al. in press), particularly since models of sexual selection assume that pre-reproductive male mortality are related to development of male ornaments (Pomiankowski 1988). Development of male ornaments during maturation should be sensitive to reproductive hormones (Marler & Moore 1988, 1991; Ketterson et al. 1991) as is the case for development of ova in females (Sinervo & Svensson 1998). Therefore, it is probable that endocrine system genes of males in other vertebrates, which are under strong sexual selection and pre-maturational survival selection, may likewise have correlated effects on female life-history traits, given that endocrine pathways of reproduction are shared between the sexes (Sinervo & Calsbeek 2003).
(c) Measurement of phenotypic selection versus genetic or experimental approaches
Strong natural selection acting during maturation could not have been detected with traditional measures of phenotypic selection (e.g. Arnold 1983; Lande & Arnold 1983; Arnold & Wade 1984). Progeny had not yet laid their clutch before they were selectively eliminated from the population. Moreover, male progeny appear to use the same genes for clutch size in other functions that increase pre-maturational risk of mortality. We quantified selection on breeding values and performed manipulative experiments to detect such cryptic natural selection. Cryptic natural selection may be common if physiology or morphology changes with time and these ontogenetic changes also elevate the selective risk of mortality. Current models in which phenotypic measurements of selection are partitioned from the measurement of genetic variance and covariance (Arnold 1983; Lande & Arnold 1983; Arnold & Wade 1984) may be inadequate for detecting natural selection on many traits (Endler 1986), given the likelihood of an invisible fraction. Genotypic selection analysis (Van Tierderen & de Jong 1994; Kruuk 2004; Pischedda & Chippindale 2006; Foerster et al. 2007) as used in this study can circumvent many of the pitfalls of phenotypic selection analysis. Moreover, endocrine manipulations provide causal links between natural selection and physiological processes underlying ovarian regulation.
Results from our study may also explain why selective costs are rarely detected in natural phenotypic variation, while experiments often reveal costs of reproduction. Natural selection that acts on females during maturation may selectively eliminate a large fraction of females before reproductive traits can be measured. Once strong natural selection has exerted its influence during maturation, natural phenotypic variation in the cohort may be so depleted that additional selection will not lead to measurable post-laying costs of reproduction. Experiments increase variation and inflate the representation in the tails of frequency distribution for traits (Sinervo et al. 1992), thereby enhancing the power to detect selection acting on traits such as pre- or post-laying costs of reproduction (Gustafsson & Sutherland 1988; Sinervo & DeNardo 1996).
Results of our study provide strong support for the usage of phenotypic manipulations in detecting costs of reproduction in the wild contrary to the negative opinions expressed by many (Reznick 1985, 1992; Reznick et al. 2000; Chippindale et al. 1993; Leroi et al. 1994) regarding the usage of phenotypic manipulations. We agree with these authors' claims that phenotypic manipulations achieved by altering environment (e.g. food) do not assess costs that are related to genetically based life-history trade-offs (Sinervo & Svensson 1998). In contrast, mechanistic manipulations of the ovary (or testes) should perturb allocation by physiological pathways similar to those governed by the genes regulating gonadal development (Sinervo & Svensson 1998; Sinervo 1999; Sinervo & Clobert in press). Ovarian manipulations and complementary manipulations of male endocrine function (Mills et al. in press) hold promise for revealing costs expressed during all phases of reproduction, including the maturational processes that are under natural and sexual selection. Referencing manipulations to genetical analysis of selective life-history trade-offs validates that experimentally induced costs are not merely pharmacological effects of hormones. Conversely, referencing results from long-term pedigree data confirm that no hidden bias confounds the quantitative genetic methods (e.g. unmeasured maternal effects). Given conserved mechanisms underlying vertebrate hormones, it is probable that manipulations of the gonad could also be applied to other vertebrate taxa like birds or mammals (Oksanen et al. 2002) to test the generality of maturational costs of reproduction in other species and expose the action of selection on this invisible fraction, which includes both the progeny that die before traits can be measured as well as male progeny that do not express female traits (and vice versa).
Acknowledgments
All protocols have been approved by Chancellor's Committee on Animal Research, UCSC, in accord with IACUC.
Research was supported by NSF grants BSR 89-19600, DEB 93-07999, IBN 96-31757, DEB 0108577, and IBN 0213179 awarded to B.S. Pedigree assembly and synthesis was funded by NSF grant LTREB DEB 051597 awarded to B.S. and A.G.M. We wish to thank Phil Stadler, R. Schrimp, the Hultgren family, and especially the Arbielbeidee family for giving permission to work on their land. Jen Graff, Dale DeNardo and Kelly Zamudio assisted with capture of gravid females in the experiments. Bill Hill, Loeske Kruuk, Bruce Lyon, Erik Svensson, Ryan Calsbeek, Tosha Comendant and two anonymous referees improved the quality of earlier drafts of the manuscript. Ellen Ketterson, Curt Lively and David Reznick provided many stimulating discussions on the topic of costs of reproduction over the years.
Footnotes
One contribution of 18 to a Special Issue ‘Evolutionary dynamics of wild populations’.
References
- Arnold S.J. Morphology, performance and fitness. Am. Zool. 1983;23:347–361. [Google Scholar]
- Arnold S.J, Wade M.J. On the measurement of natural and sexual selection: theory. Evolution. 1984;38:709–719. doi: 10.1111/j.1558-5646.1984.tb00344.x. doi:10.2307/2408383 [DOI] [PubMed] [Google Scholar]
- Bennington C.C, McGraw J.B. Phenotypic selection in an artificial population of Impatiens pallida: the importance of the invisible fraction. Evolution. 1995;49:317–324. doi: 10.1111/j.1558-5646.1995.tb02244.x. doi:10.2307/2410342 [DOI] [PubMed] [Google Scholar]
- Calsbeek R, Sinervo B. Within-clutch variation in offspring sex determined by differences in sire body size: cryptic mate choice in the wild. J. Evol. Biol. 2004;17:464–470. doi: 10.1046/j.1420-9101.2003.00665.x. doi:10.1046/j.1420-9101.2003.00665.x [DOI] [PubMed] [Google Scholar]
- Calsbeek R, Sinervo B. Correlational selection on lay date and life-history traits: experimental manipulations of territory and nest site quality. Evolution. 2007;61:1071–1083. doi: 10.1111/j.1558-5646.2007.00098.x. doi:10.1111/j.1558-5646.2007.00098.x [DOI] [PubMed] [Google Scholar]
- Chippindale A.K, Leroi A.M, Kim S.B, Rose M.R. Phenotypic plasticity and selection in Drosophila life-history evolution. I. Nutrition and costs of reproduction. J. Evol. Biol. 1993;6:171–193. doi:10.1046/j.1420-9101.1993.6020171.x [Google Scholar]
- Comendant T, Sinervo B, Svensson E, Wingfield J. Social competition, corticosterone and survival in female lizard morphs. J. Evol. Biol. 2003;16:948–955. doi: 10.1046/j.1420-9101.2003.00598.x. doi:10.1046/j.1420-9101.2003.00598.x [DOI] [PubMed] [Google Scholar]
- Endler J.A. Princeton University Press; Princeton, NJ: 1986. Natural selection in the wild. [Google Scholar]
- Foerster K, Coulson T, Sheldon B, Pemberton J.M, Clutton-Brock T.H, Kruuk L.E.B. Sexually antagonistic genetic variation in the red deer. Nature. 2007;447:1107–1111. doi: 10.1038/nature05912. doi:10.1038/nature05912 [DOI] [PubMed] [Google Scholar]
- Gibbs H.L, Grant P.R. Oscillating selection on Darwin's Finches. Nature. 1987;327:511–513. doi:10.1038/327511a0 [Google Scholar]
- Grafen A. On the use of data on lifetime reproductive success. In: Clutton-Brock T.H, editor. Reproductive success. The University of Chicago Press; Chicago, IL: 1988. [Google Scholar]
- Gustafsson L, Sutherland W.J. The costs of reproduction in collared flycatcher Ficedula albicollis. Nature. 1988;335:813–815. doi:10.1038/335813a0 [Google Scholar]
- Hadfield J.D. Estimating evolutionary parameters when viability selection is operating. Proc. R. Soc. B. 2008;275:723–734. doi: 10.1098/rspb.2007.1013. doi:10.1098/rspb.2007.1013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ketterson E, Nolan V., Jr Hormones and avian life histories: an integrative approach. Am. Nat. 1992;140:S33–S62. doi: 10.1086/285396. doi:10.1086/285396 [DOI] [PubMed] [Google Scholar]
- Ketterson E.D, Nolan V, Jr, Wolf L, Ziegenfus C, Dofty A.M, Jr, Ball G.F, Johnsen T.S. Testosterone and avian life histories: the effect of experimentally elevated testosterone on corticosterone and body mass in dark-eyed juncos. Horm. Behav. 1991;25:489–503. doi: 10.1016/0018-506x(91)90016-b. doi:10.1016/0018-506X(91)90016-B [DOI] [PubMed] [Google Scholar]
- Kirkpatrick M, Lande R. The evolution of maternal characters. Evolution. 1989;43:485–503. doi: 10.1111/j.1558-5646.1989.tb04247.x. doi:10.2307/2409054 [DOI] [PubMed] [Google Scholar]
- Kruuk L. Estimating genetic parameters in natural populations using the ‘animal model’. Phil. Trans. R. Soc. B. 2004;359:873–890. doi: 10.1098/rstb.2003.1437. doi:10.1098/rstb.2003.1437 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kruuk L.E.B, Clutton-Brock T.H, Slate J, Pemberton J.M, Brotherstone S, Guinness F.E. Heritability of fitness in a wild mammal population. Proc. Natl Acad. Sci. USA. 2000;97:698–703. doi: 10.1073/pnas.97.2.698. doi:10.1073/pnas.97.2.698 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kruuk L.E.B, Slate J, Pemberton J.M, Brotherstone S, Guinness F, Clutton-Brock T.H. Antler size in red deer: heritability and selection but no evolution. Evolution. 2002;56:1683–1695. doi: 10.1111/j.0014-3820.2002.tb01480.x. [DOI] [PubMed] [Google Scholar]
- Lande R, Arnold J. The measurement of selection on correlated characters. Evolution. 1983;37:1210–1226. doi: 10.1111/j.1558-5646.1983.tb00236.x. doi:10.2307/2408842 [DOI] [PubMed] [Google Scholar]
- Leroi A.M, Kim S.B, Rose M.R. The evolution of phenotypic life-history trade-offs: an experimental study using Drosphila melanogaster. Am. Nat. 1994;144:661–676. doi:10.1086/285699 [Google Scholar]
- Lynch M, Walsh B. Sinauer Associates; Sunderland, MA: 1998. Genetics and analysis of quantitative traits. [Google Scholar]
- Marler C.A, Moore M.C. Evolutionary costs of aggression revealed by testosterone manipulations in free-living male lizards. Behav. Ecol. Sociobiol. 1988;23:21–26. doi:10.1007/BF00303053 [Google Scholar]
- Marler C.A, Moore M.C. Supplementary feeding compensates for testosterone-induced costs of aggression in male mountain spiny lizards, Sceloporus jarrovi. Anim. Behav. 1991;42:209–219. doi:10.1016/S0003-3472(05)80552-4 [Google Scholar]
- Marshall T.C, Slate J, Kruuk L.E.B, Pemberton J.M. Statistical confidence for likelihood-based paternity inference in natural populations. Mol. Ecol. 1998;7:639–655. doi: 10.1046/j.1365-294x.1998.00374.x. doi:10.1046/j.1365-294x.1998.00374.x [DOI] [PubMed] [Google Scholar]
- Meyer K. Restricted maximum likelihood to estimate variance components for animal models with several random effects using derivative-free algorithm. Gen. Select. Evol. 1989;21:317–340. doi:10.1051/gse:19890308 [Google Scholar]
- Miles D.B, Sinervo B, Frankino W.A. Reproductive burden, locomotor performance, and the costs of reproduction in free ranging lizards. Evolution. 2000;54:1386–1395. doi: 10.1111/j.0014-3820.2000.tb00570.x. [DOI] [PubMed] [Google Scholar]
- Mills, S., Hazard, L., Lancaster, L., Mappes, T., Miles, D. B., Oksanen, T. & Sinervo, B. In press. Gonadotropin hormone modulation of testosterone, immune function, performance and behavioral trade-offs among male morphs of the lizard, Uta stansburiana. Am. Nat [DOI] [PubMed]
- Oksanen T, Koskela E, Mappes T. Hormonal manipulation of offspring number: maternal effort and reproductive costs. Evolution. 2002;56:1530–1537. doi: 10.1111/j.0014-3820.2002.tb01463.x. [DOI] [PubMed] [Google Scholar]
- Pischedda A, Chippindale K.A. Intralocus sexual conflict diminishes the benefits of sexual selection. PLoS Biol. 2006;4:e356. doi: 10.1371/journal.pbio.0040356. doi:10.1371/journal.pbio.0040356 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pomiankowski A. The evolution of female mate preference for male genetic quality. In: Harvey P, Partridge L, editors. Oxford surveys in evolutionary biology. Oxford University Press; New York, NY: 1988. pp. 136–184. [Google Scholar]
- Postma E. Implications of the difference between true and predicted breeding values for the study of natural selection and micro-evolution. J. Evol. Biol. 2006;19:309–320. doi: 10.1111/j.1420-9101.2005.01007.x. doi:10.1111/j.1420-9101.2005.01007.x [DOI] [PubMed] [Google Scholar]
- Postma E, van Noordwijk A.J. Gene flow maintains a large genetic difference in clutch size at a small spatial scale. Nature. 2005;433:65–68. doi: 10.1038/nature03083. doi:10.1038/nature03083 [DOI] [PubMed] [Google Scholar]
- R Development Core Team. Vienna, Austria; R Foundation for Statistical Computing: 2007. R: a language and environment for statistical computing. See http://www.R-project.org. [Google Scholar]
- Reznick D. Costs of reproduction: an evaluation of the empirical evidence. Oikos. 1985;44:257–267. doi:10.2307/3544698 [Google Scholar]
- Reznick D. Measuring costs of reproduction. Trends Ecol. Evol. 1992;7:42–45. doi: 10.1016/0169-5347(92)90104-J. doi:10.1016/0169-5347(92)90150-A [DOI] [PubMed] [Google Scholar]
- Reznick D, Nunny L, Tessier A. Big houses, big cars, superfleas, and the cost of reproduction. Trends Ecol. Evol. 2000;15:421–425. doi: 10.1016/s0169-5347(00)01941-8. doi:10.1016/S0169-5347(00)01941-8 [DOI] [PubMed] [Google Scholar]
- Rice W.R, Chippindale A.K. Intersexual ontogenetic conflict. J. Evol. Biol. 2001;14:685–693. doi:10.1046/j.1420-9101.2001.00319.x [Google Scholar]
- Schluter D, Gustafsson L. Maternal inheritance of condition and clutch size in the collared flycatcher. Evolution. 1993;47:658–667. doi: 10.1111/j.1558-5646.1993.tb02119.x. doi:10.2307/2410077 [DOI] [PubMed] [Google Scholar]
- Sinervo B. Mechanistic analysis of natural selection and a refinement of lack's and William's principles. Am. Nat. 1999;154:S26–S42. doi: 10.1086/303281. doi:10.1086/303281 [DOI] [PubMed] [Google Scholar]
- Sinervo B. Adaptation, natural selection, and optimal life history allocation. In: Mousseau T.A, Sinervo B, Endler J.A, editors. Adaptive genetic variation in the wild. Oxford University Press; New York, NY: 2000. pp. 41–64. [Google Scholar]
- Sinervo, B. & Calsbeek, R. 2003 Ontogenetic conflict and morphotypic selection on physiology, life history, and adaptive sex allocation. In Symposium volume: selection and evolution of performance in nature, vol. 43 (eds J. Kingsolver & R. B. Huey), pp. 419–430. Integrative and comparative biology. Oxford, UK: Society for Integrative Biology, Oxford University Press. [DOI] [PubMed]
- Sinervo B, Clobert J. Morphs, dispersal behavior, genetic similarity and the evolution of cooperation. Science. 2003;300:1949–1951. doi: 10.1126/science.1083109. doi:10.1126/science.1083109 [DOI] [PubMed] [Google Scholar]
- Sinervo, B. & Clobert, J. In press. Life history strategies, multidimensional trade-offs and behavioural syndromes. In Behavioral ecology: an evolutionary perspective on behaviour (eds E. Danchin, L.-A. Giraldeau & F. Cézilly). Oxford, UK: Oxford University Press.
- Sinervo B, DeNardo D.F. Costs of reproduction in the wild: path analysis of natural selection and experimental tests of causation. Evolution. 1996;50:1299–1313. doi: 10.1111/j.1558-5646.1996.tb02370.x. doi:10.2307/2410670 [DOI] [PubMed] [Google Scholar]
- Sinervo B, Huey R.B. Allometric engineering: an experimental test of the causes of interpopulational differences in locomotor performance. Science. 1990;248:1106–1109. doi: 10.1126/science.248.4959.1106. doi:10.1126/science.248.4959.1106 [DOI] [PubMed] [Google Scholar]
- Sinervo B, Licht P. The physiological and hormonal control of clutch size, egg size, and egg shape in Uta stansburiana: constraints on the evolution of lizard life histories. J. Exp. Zool. 1991;257:252–264. doi:10.1002/jez.1402570216 [Google Scholar]
- Sinervo B, Svensson E. Mechanistic and selective causes of life history. Oikos. 1998;83:432–442. doi:10.2307/3546671 [Google Scholar]
- Sinervo B, Doughty P, Huey R.B, Zamudio K. Allometric engineering: a causal analysis of natural selection on offspring size. Science. 1992;258:1927–1930. doi: 10.1126/science.258.5090.1927. doi:10.1126/science.258.5090.1927 [DOI] [PubMed] [Google Scholar]
- Sinervo B, Miles D.B, DeNardo D.F, Frankino W.A, Klukowski M. Testosterone, endurance, Darwinian fitness: proximate bases of the rock-paper–scissors game of alternative male strategies. Horm. Behav. 2000a;38:222–233. doi: 10.1006/hbeh.2000.1622. doi:10.1006/hbeh.2000.1622 [DOI] [PubMed] [Google Scholar]
- Sinervo B, Svensson E, Comendant T. Density cycles and an offspring quantity and quality game driven by natural selection. Nature. 2000b;406:985–988. doi: 10.1038/35023149. doi:10.1038/35023149 [DOI] [PubMed] [Google Scholar]
- Sinervo B, Calsbeek R, Comendant T, Both C, Adamopoulou C, Clobert J. Genetic and maternal determinants of effective dispersal: the effect of sire genotype and size at birth in side-blotched lizards. Am. Nat. 2006;168:88–99. doi: 10.1086/505765. doi:10.1086/505765 [DOI] [PubMed] [Google Scholar]
- Van Tierderen P.H, de Jong G.H. A general model of the relation between phenotypic selection and genetic response. J. Evol. Biol. 1994;7:1–12. doi:10.1046/j.1420-9101.1994.7010001.x [Google Scholar]
- Williams G.C. Natural selection, the costs of reproduction, and a refinement of Lack's principle. Am. Nat. 1966;100:687–690. doi:10.1086/282461 [Google Scholar]
- Zamudio K, Sinervo B. Polygyny, mate-guarding, and posthumous fertilizations as alternative male strategies. Proc. Natl Acad. Sci. USA. 2000;97:14 427–14 432. doi: 10.1073/pnas.011544998. doi:10.1073/pnas.011544998 [DOI] [PMC free article] [PubMed] [Google Scholar]