Abstract
Laser diodes (LD) are commonly used for optical neural recordings in chronically recorded animals and humans, primarily due to their brightness and small size. However, noise introduced by LDs may counteract the benefits of brightness when compared to low−noise light emitting diodes (LEDs). To understand noise sources in optical recordings, we systematically compared instrument and physiological noise profiles in two recording paradigms. A better understanding of noise sources will help improve optical recordings and make them more practical with fewer averages. We stimulated lobster nerves and rat cortex, then compared the root mean square (RMS) noise and signal−to−noise ratios (SNRs) of data obtained with LED, superluminescent diode (SLD) and LD illumination for different numbers of averages. The LED data exhibited significantly higher SNRs in fewer averages than LD data in all recordings. In the absence of tissue, LED noise increased linearly with intensity, while LD noise increased sharply in the transition to lasing and settled to noise levels significantly higher than the LED’s, suggesting that speckle noise contributed to the LD’s higher noise and lower SNRs. Our data recommend low coherence and portable light sources for in−vivo chronic neural recording applications.
Keywords: Invertebrate, Imaging, Evoked response, Mayer waves, Photodiode, Coherent
Introduction
Intrinsic optical signals have the potential to revolutionize the way neuroscientists record and image neuronal function, but low signal−to−noise ratios currently limit their usefulness. Neural activation initiates both fast and slow optical changes. Cellular swelling and molecular conformational changes elicit rapid changes in light scattering and birefringence concomitant with membrane depolarization (Cohen et al., 1968; Tasaki et al., 1968; Rector et al., 2005). Neural activity also increases metabolism and elicits slower cascades of hemodynamic events that can be monitored through light absorption by oxy− and deoxy−hemoglobin. Investigators have non−invasively monitored changes in blood flow and the oxy−/deoxy−hemoglobin ratio using near−infrared spectroscopy and diffuse optical tomography (for review see Villringer and Chance, 1997; Boas, 2002). In−vitro studies have shown that scattering and birefringence signals result from a combination of mechanisms including changes in refractive index, protein conformation, and other processes associated with changes in membrane potential (Foust and Rector, 2007). Several studies support cellular swelling as the primary mechanism underlying the scattered light change (Cohen, 1973; Tasaki and Byrne, 1992; Yao et al., 2003), and some studies also point to swelling as a contributor to the birefringence signal (Yao et al., 2005). These changes might also be detected with near−infrared light in adult humans (Steinbrink et al. 2000; Franceschini and Boas, 2004; Maclin et al., 2004). However, the small signal−to−noise ratio hinders their advancement as a functional imaging modality.
A better understanding of noise sources will help us improve optical recordings and make them more practical with fewer averages. Some noise components are common to all optical neural recording systems. A detailed discussion of electrical and optical noise sources can be found in Horowitz and Hill (1989) and Zochowski et al. (2000). Briefly, light sources, photodiodes and amplifiers introduce several types of noise including Johnson (thermal) noise and shot noise. Shot noise, a white noise source caused by quantum fluctuation of emitted and detected photons, dominates at low intensities. Both Johnson noise and shot noise are independent of frequency. Pink noise, or 1/f noise, occurs naturally in biological systems and as electronic flicker noise. Due to the inverse relation, 1/f noise dominates the low frequencies, but is overshadowed by white noise sources above a cornerstone frequency characteristic of the system. The generation and recombination of electrons within semiconductor−based photon detectors also introduce noise.
Illumination noise sources represent some of the most difficult issues to address. While variations in light intensity due to mechanisms such as arc wander and power supply fluctuations can be accounted for by direct detection of the output light with a reference photodiode, other illumination noise sources, such as shot noise, are much more difficult to control. Speckle noise from coherent laser diode (LD) and partially−coherent superluminescent diode (SLD) sources may contribute to the system noise as random interference patterns cross the edge of the detector. While speckle noise has been a long known problem in microscopy and imaging, it remains a problem and contributes to noise in optical recordings (Rigden and Gordon, 1962; Considine, 1966; Schmitt et al., 1999). Since speckle interference patterns from coherent light sources, such as lasers, are extremely bright, slight movements that cause the speckle to cross the boundary of a detector will fluctuate the optical signal significantly. In fact, several groups use speckle to image changes in cerebral blood flow (i.e., Dunn et al., 2001).
The presence of living tissue in an optical system also introduces noise through physiological activity on molecular, cellular, and whole organism scales. Respiratory, cardiac, and vascular oscillations, along with other skeletal muscle activity, contribute to optical noise in multiple frequency ranges. Although instrument noise is generally considered to be lower than contributions of physiological noise sources (i.e., circulation and respiration), both physiological and instrument noise sources are still significantly larger than the fast optical signals to be recorded in−vivo directly corresponding to electrical events, especially for single−pass measurements.
Few studies have systematically characterized the sources of signal noise in light source/detection instrumentation, and such measurements could influence the methods used to detect fast intrinsic optical changes in−vivo. Thus, the purpose of these experiments was to systematically compare the noise profiles of LDs, SLDs and LEDs in two neural recording paradigms. These studies also provide a procedure to assess the number of averages required to adequately record optical signals.
Methods
Light sources
We compared three light sources (LED, SLD, and LD) in−vitro and two sources (LED, LD) in−vivo. The LED (660nm, rated at 3.5mcd or 1.6mW, B5b−436−30, Roithner Lasertechnik GmbH, Vienna, Austria) and SLD (833 nm, 9 mW, Superlum Diodes Ltd., Moscow, Russia) were operated in free space. The LD (660 nm, 5mW, D660−5, US−Lasers, Inc., Baldwin Park, CA) was coupled to a 1 mm diameter fiber optic. The LD and SLD were temperature regulated by feedback−controlled thermoelectric coolers. The LED and LD were driven with batteries at constant voltage, and the SLD was powered with a current regulated power supply (Superlum Pilot 4, Superlum Diodes Ltd., Moscow, Russia). While current regulated supplies are generally preferred for both LEDs and LDs due to very slow temperature and drift effects, we found no difference between the two methods in our RMS noise levels.
In−vitro: crustacean nerve
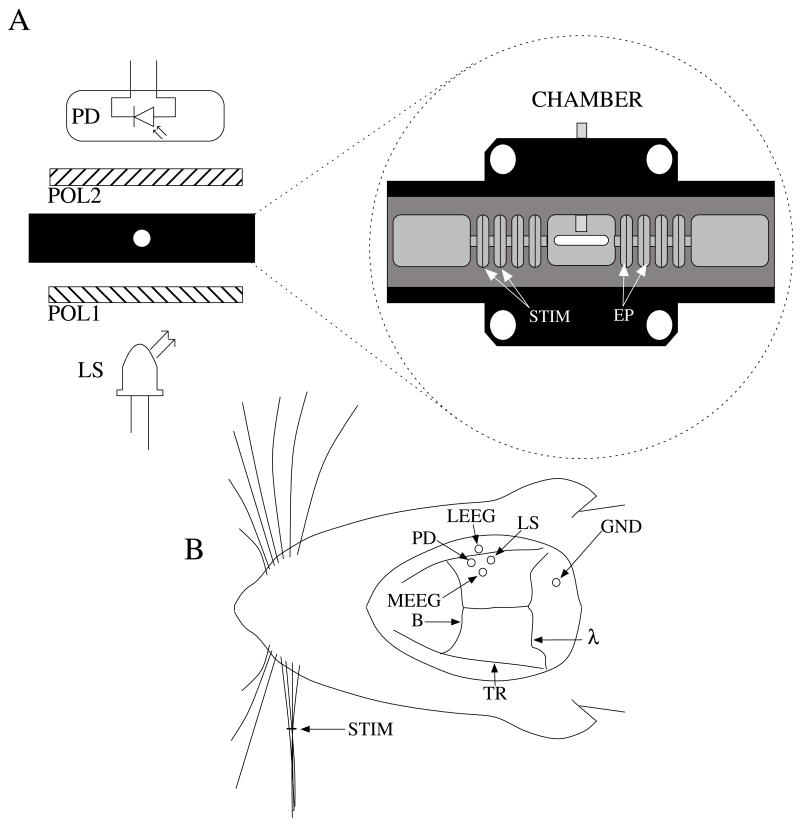
We extracted nerves from the first two most rostral walking legs of lobsters (Homarus americanus), using the Furusawa “pulling out” method (Furusawa, 1929), and tied the ends with silk sutures to prevent axoplasmic leakage. Our invertebrate recording technique has been reported earlier (Carter et al., 2004). Briefly, we placed each isolated nerve in a recording chamber flooded with marine crustacean solution (in mM: 525 NaCl, 13.3 KCl, 12.4 CaCl2, 24.8 MgCl2, 5.0 dextrose, to pH 7.0 with NaHCO3). The chamber featured a central, rectangular well with four smaller wells on either side. Each well was fitted with a silver electrode and isolated with petroleum jelly. A set of electrodes on one side of the imaging window delivered current pulse stimuli (Fig 1A, STIM), and a second set of electrodes (EP) recorded the electrical response after the population action potentials passed through the center optical well. The bottom of the central well contained a narrow slit covered with a microscope slide through which the light was transmitted during optical recordings. Light from an LED, SLD, or LD light source (Fig. 1A, LS) passed through a polarizer (POL1; for LED and LD: VIS 4 K, Linos Photonics, Milford, MA; for SLD: Polarcor 05P109AR.16, Newport Corp., Irvine, CA) oriented at 45 degrees with respect to the long axis of the nerve bundle. Transmitted light passed through a second polarizer (POL2) crossed 90 degrees with respect to the first. The birefringent light intensity was recorded with a photodiode (PD) positioned over the second polarizer. The apparatus was constructed on an anti−vibration floating table (Minus K, Inglewood, CA) to minimize mechanical noise contributions. During neural tissue measurements, all light sources were driven to produce an initial output power between 1 and 3 mW.
Figure 1.
Schematic of in−vitro (A) and in−vivo (B) optical recording paradigms. For the in−vitro paradigm (A), we stimulated lobster nerves with short current pulses (STIM), and the resulting field potential was recorded on the other side of the window (EP). Light from an LED, SLD, or LD (LS) transmitted through the recording chamber between crossed polarizers (POL1, POL2). The transmitted intensity was recorded with a photodiode (PD). For the in−vivo paradigm (B), epidural electrodes (LEEG, MEEG) recorded the electrical evoked responses after whisker twitch stimuli, and an LED or LD (LS), and a photodiode (PD) implanted over the barrel cortex recorded optical responses.
Each nerve was stimulated with 0.2 ms current pulses (~2 mA) at random intervals between one and two seconds (0.67 Hz average stimulation rate), using a direct current isolated stimulator (Model A365R, World Precision Instruments, Inc., Sarasota, FL). Electrical responses were recorded with a differential amplifier (Linear Technology LT1167) and filtered between 0.1 Hz and 3.2 kHz, with x1000 gain. Optical signals were filtered (0.1 Hz – 3.2 kHz), amplified with a x1000 gain, and digitized simultaneously with the electrical signals, at 20 kHz per channel. We averaged data across 1000 stimuli using three nerves for each light source.
In−vivo: rat barrel cortex
Sprague−Dawley and Long−Evans female rats (250–300 g, Taconic, n=3) were anesthetized with 100 mg/kg ketamine and 10 mg/kg xylazine and placed in a stereotaxic frame. All animal procedures were approved by the Washington State University Animal Care and Use Committee. We continuously monitored electrocardiogram signals from subcutaneous pin electrodes. Stainless steel screw electroencephalogram (EEG) electrodes entered holes drilled 4 mm posterior to bregma (Fig. 1B, B), 3 mm medial (MEEG) and 1 mm lateral (LEEG) of the right temporal ridge (TR). The EEG ground reference hole (GND) was drilled 2 mm caudal to lambda and 3 mm to the right of the midline. The photodiode was coupled to a 1 mm diameter, 8 mm long piece of plastic fiber optic. The free end of the photodiode fiber was inserted into a 1.5 mm diameter hole (PD) positioned 2 mm caudal to bregma medial to the right temporal ridge, applying light pressure to the dura to reduce the cardiac artifact. LED and LD illumination was directed into another 1.5 mm diameter hole (LS) placed 2 mm caudal of the photodiode hole. The dura was left intact beneath all holes.
We twitched a group of whiskers (C0, C1, C2, D0, and D1) on the side contralateral to the EEG and optical detectors with a burst (5 twitches at 10 Hz) of 2 ms, 1 mm upward deflections. Stimuli, auditory controls, and sham controls were randomly interleaved at 7.5 second intervals. Optical (AC photodiode ×500, DC photodiode ×1), LEEG, MEEG, and EKG signals were filtered (0.1 Hz to 3.2 kHz) and digitized at 20 kHz. We averaged across 200 stimuli (plus equal numbers of auditory and sham trials) with LED and LD light sources and then euthanized the rat with a lethal dose of sodium pentabarbitol. We filtered the cardiac artifact off−line by finding the average optical response per heart beat and subtracting the average cardiac waveform from the optical data at every cardiac trigger point in the data set (Gratton and Corballis, 1995; Franceschini and Boas, 2004).
Instrument noise measurement
We assessed the noise contributions from the light sources and photodiodes by illuminating the photodiode with each light source (LED, LD and SLD) in turn, and calculating the RMS of signals collected at 20 kHz for 200 seconds, varying the intensity of the light sources in steps. We plotted the root mean square (RMS, eq. 1) noise at each intensity against the radiant flux through the photodiode (68 mm2, UDT−555UV/LN, UDT Sensors, Hawthorne, CA).
For a collection of n samples {x1, x2, …, xn}:
| (1) |
Noise contributions from the photodiode and amplifier were calculated to be 5.67 μV, which included photodiode dark current noise, amplifier input noise, and Johnson noise in the resistors. Table 1 outlines the contributions of the photodiode, amplifiers, and resistors for a 500 Hz bandwidth; the complete photodiode/amplifier circuit is described in Carter et al. (2004). Since these noises are uncorrelated, their contributions add in quadrature to form the total instrument noise. Thus, we expect the measured RMS of the dark signal noise to fall close to the anticipated value, 5.67 μV calculated from the component specifications.
Table 1.
Noise contributions of the photodiode dark current, the integrated op−amp input noise, the free op−amp input noise, and Johnson noise from feedback resistors. The addition of the noises in quadrature predicts the total instrument noise, 5.67 μV. After instrument noise, the RMS noise contributions of illumination and physiological sources are tabulated in−vitro (lobster) and in−vivo (rat) and compared to the peak amplitudes of the stimulus−evoked optical changes. The standard errors for these measurements are large due to variability of signal strength and illumination intensity from trial to trial, but values give the reader a general idea of each source’s noise generation.
| Noise source | RMS Contribution (Δf = 500Hz), μV | Quantity in Circuit | ||
|---|---|---|---|---|
| PD Op amp (UDT−555UV), Input Noise Voltage | 0.45 | 1 | ||
| PD (UDT−555UV/LN), Dark Current Noise | 0.91 | 1 | ||
| Op amp (TL074), Input Noise Voltage | 4.00 | 2 | ||
| 1 Mohm Resistor Johnson Noise | 2.88 | 4 | ||
| Total Expected Instrument Noise in Quadrature | 5.67 μV | |||
| Measured Instrument Noise | 4.53 μV | |||
| Noise Source | LED | LD | ||
| Lobster, In−vitro | μV | dI/I × 10−4 | μV | dI/I × 10−4 |
| Emitter (shot, speckle) RMS Noise | 114.1 | 0.70 | 190.0 | 9.55 |
| Peak Signal Size In−vitro | 128.6 ± 34.2 | 1.15 ± 0.34 | 48.1 ± 12.7 | 1.83 ± 0.46 |
| Rat, In−vivo | μV | dI/I × 10−4 | μV | dI/I × 10−4 |
| Emitter (shot, speckle) RMS Noise | 77.4 ± 22.0 | 0.64 ± 0.17 | 225.5 ± 111.5 | 3.51 ± 0.91 |
| Cardiac RMS Noise (3Hz) | 215.0 ± 72.2 | 1.82 ± 0.60 | 106.6 ± 48.5 | 1.72 ± 0.64 |
| Respiration RMS Noise (1Hz) | 182.1 ± 3.6 | 1.55 ± 0.02 | 56.5 ± 6.0 | 1.08 ± 0.08 |
| Mayer Waves RMS Noise (0.0 to 0.4Hz) | 616.8 ± 401.0 | 5.22 ± 3.37 | 550.3 ± 482.2 | 8.26 ± 7.19 |
| Total Noise Measured In−vivo | 824.0 ± 325.8 | 6.98 ± 2.72 | 680.7 ± 446.0 | 10.7 ± 6.2 |
| Peak Signal Size In−vivo | 381.7 ± 262.1 | 3.35 ± 2.19 | 162.3 ± 64.7 | 2.97 ± 0.66 |
The photodiode readings were calibrated and compared with an optical power meter (OPM, console PM100, head S130A, Thorlabs GmbH, Karlsfeld, Germany). We correlated the amplifier output (Vout, volts) with radiant flux (e, watts) measured with the OPM, and found the following linear fit:
| (2) |
Radiant flux is a measure of radiant energy per unit time across the entire electromagnetic spectrum. Radiometric measures were chosen instead of photometric measures such as luminous flux (lumens) because photometric quantities are wavelength dependent and limited to the visible spectrum. Thus, the SLD emitted near−infrared light and could not be analyzed using photometric units.
Physiological noise assessment
For each experiment, in−vitro and in−vivo, 450 seconds of optical data were recorded in the absence of stimulation. We partitioned each data set into 150 second epochs, applied a 2nd order Butterworth filter from 0.05 to 20 Hz, and subsampled down from 20 kHz to 100 Hz. A Fast−Fourier transform (FFT) of the 100 Hz data was used to assess the frequency characteristics of slow physiological noise sources. The FFTs were compared across light sources, and living and dead tissue.
Stimulus evoked signal−to−noise
For both in−vitro and in−vivo paradigms, we compared the RMS noise and SNRs (Eq. 4) of the optical signal across light sources,
| (3) |
| (4) |
where Irms is the RMS noise from the optical recording. Because RMS deviation is proportional to the inverse square root of the number of trials (N), we expected that the SNR would grow proportionally with square root N, assuming constant signal amplitude (dI/I). Unfortunately, due to degradation of the lobster nerve over time, the signal does not remain constant. While in−vitro paradigm signals can be discerned from single pass measurements, in−vivo trials often require 10–100 averages for the signal amplitude to rise above the noise. Thus, for in−vitro measurements, we sequentially plotted the RMS and SNR across number of averages, but this method was inappropriate for the in−vivo data in which signals were not discernible in single passes. For our in−vivo data, we plotted mean SNR across number of averages per bin, using 200 combinations of the data for each set of averages. Since cardiac pulsation contributed a large systematic noise source which could be removed, we applied the EKG filter to signals before averaging and calculating the amplitude, RMS, and SNR values.
Results
Source−detector noise
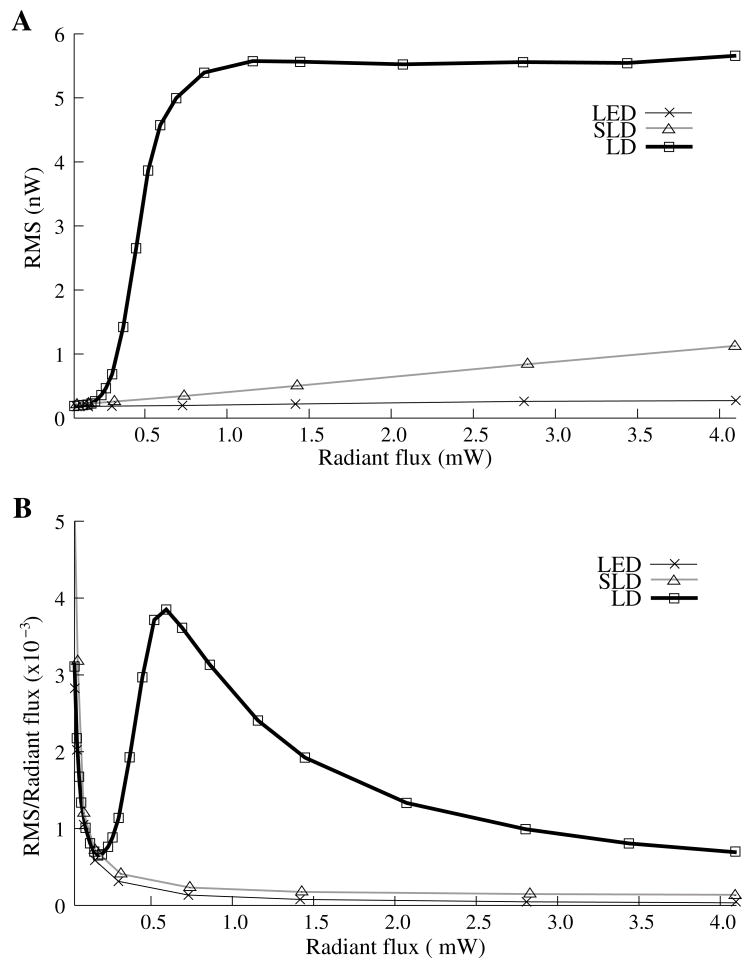
RMS noise increased linearly with intensity for the LED and SLD (Fig. 2A). The LD noise increased with the LED and SLD noise at low intensities, but increased sharply at 0.5 mW to a noise level exceeding those of the LED and SLD by a factor of 5 or greater (Fig. 2A).
Figure 2.
The relationship between noise (RMS) and radiant flux (RF). Panel A shows RMS against radiant flux for three sources: LED, SLD and LD. Upper limits for LED, SLD, and LD RMS in the illustrated range are 0.27, 1.14, and 5.67 nW, respectively. Panel B shows RMS normalized to the radiant intensity. The laser’s sharp increase in RMS at 0.5 mW reflects noise introduced as the LD transitioned from LED mode to lasing.
We divided RMS noise by radiant flux to account for the effects of differing intensities on RMS. Figure 2B shows the data from Figure 2A normalized to the radiant flux (RF) measured using the 68 mm2 photodiode. All three sources showed a rapid decrease in RMS/RF between 0 and 0.25 mW. At 0.5 mW, the LD RMS/RF increased sharply in the transition to lasing. Above 0.75 mW of radiant flux, the RMS/RF of all three light sources decreased (Fig. 2B).
Instrument dark noise
In the absence of light, we measured a total of 4.53 μV RMS noise from the photodiode and amplifier (Fig. 3A), slightly lower than the predicted value, 5.67 μV (Table 1).
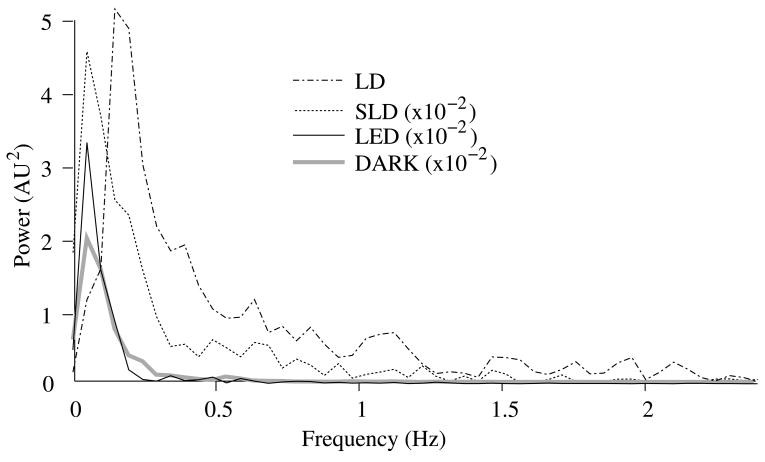
Figure 3.
Power spectra of optical signals (450s) in−vitro from the unstimulated lobster nerves. The thick gray line shows the spectra of the dark noise with superimposed traces showing the spectra of the LD, LED, and SLD signals transmitted through lobster nerve. LD, LED and SLD signals were normalized to their DC intensities prior to FFT analysis. Note that the spectral power scale for the LD data is two orders of magnitude greater than the DARK, LED or SLD power across all frequencies.
Physiological noise
The FFTs of the in−vitro signals recorded in the presence of a healthy nerve yielded no significant peaks different from trials recorded with a dead nerve (data not shown). Figure 3 shows FFTs of in−vitro data for the live nerve under LED, SLD, and LD illumination. Before taking the FFT, each data set was divided by the baseline intensity to control for intensity variations. The FFT data illustrates 1/f noise present, and LD noise power was two orders of magnitude greater than the SLD and LED spectra across all frequencies.
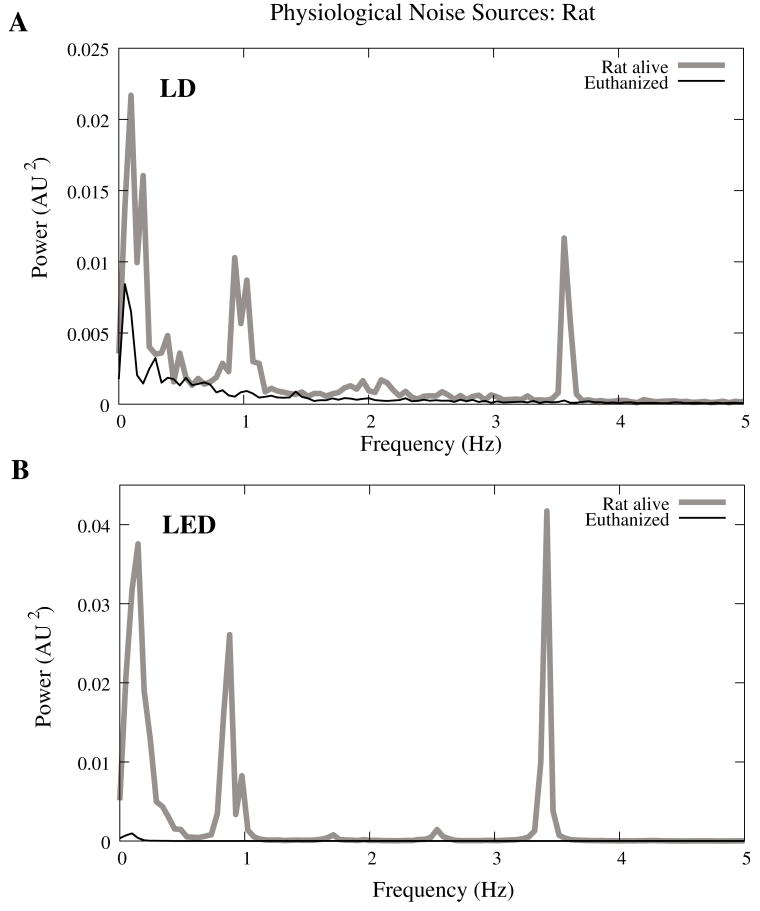
Rat optical noise spectra featured peaks at 3.36±0.42 Hz and 1.37±0.47 Hz during anesthesia. These peaks were absent from data collected after the rat was euthanized (Fig. 4A,B). The low frequency power was also reduced in dead tissue. The 1/f, cardiac, and respiratory peaks in the LED FFT (Fig. 4B) were equivalent in amplitude to the LD FFT (Fig. 4A).
Figure 4.
Power spectra of optical signals in−vivo with an LED (A) and LD (B) source. Both spectra feature peaks that correspond to 1/f, respiratory (0.9 Hz), and cardiac signatures (3.5 Hz). Since low frequency components below 0.5 Hz are greater in the live rat, we assume slow vascular oscillations (Mayer waves) may contribute to noise in this frequency range.
Table 1 shows the RMS noise contributions in the cardiac (~3 Hz), respiratory (~1 Hz) and slow vascular (0–0.4 Hz) frequencies. The euthanized rat optical RMS was subtracted from the live rat optical RMS in quadrature to find physiological noise RMS in each characteristic frequency band.
In−vitro paradigm
The illumination intensity for the laser was limited by the dynamic range of the photodiode amplifiers. LED and SLD sources were driven at maximum intensity without approaching the rails of the photodiode amplifier. Baseline measured radiant power for the transmission birefringence data was 0.57–0.74 μW for the LD, 0.36–0.51 μW for the SLD, and 3.1–3.3 μW for the LED.
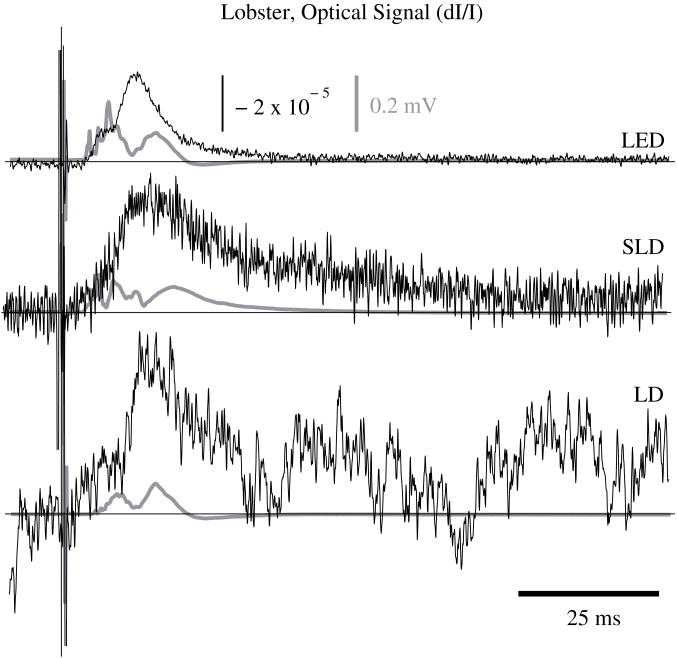
We defined signal amplitude as the difference between the monophasic optical peak and baseline. Signal amplitudes ranged from −1.4 to −8.0 × 10−5 dI/I (Fig. 5) or 4.4 to 54 μV after 1000 averages. The optical changes were rapid (5–15 ms from stimulus to peak) and short in duration (< 30 ms). The highest amplitude optical changes occurred at the beginning of each experiment (−0.6 to −2.9 × 10−4 dI/I or 14 to 186 μV, after 100 averages) and then degraded over the 17− to 33−minute recording periods (1000 stimuli at 1–2s random inter−stimulus intervals). As shown in Table 1, SNRs for single pass measurements in lobster nerves with LED illumination were approximately 1:1. Additional filtering (1 to 100 Hz) improved SNRs to about 10:1. More than 150 averaged trials were required to discern the birefringence signal in LD data, even after bandpass filtering. For LD lobster data, the illumination intensity was about 2 times dimmer due to the high peak−to−peak noise from the LD. Since the eventual size of the signal appeared to depend on the illumination intensity, raw signals measured with the LD were lower. However, after dividing the absolute signal size by illumination intensity, the dI/I values were comparable between LED and LD sources (Fig. 5).
Figure 5.
In−vitro optical data for LED, SLD, and LD from stimulated lobster nerves. Black traces show the optical signals (dI/I) and gray traces show the stimulus evoked field potential. The vertical line indicates the time of stimulus. Each trace represents the average of 1000 trials.
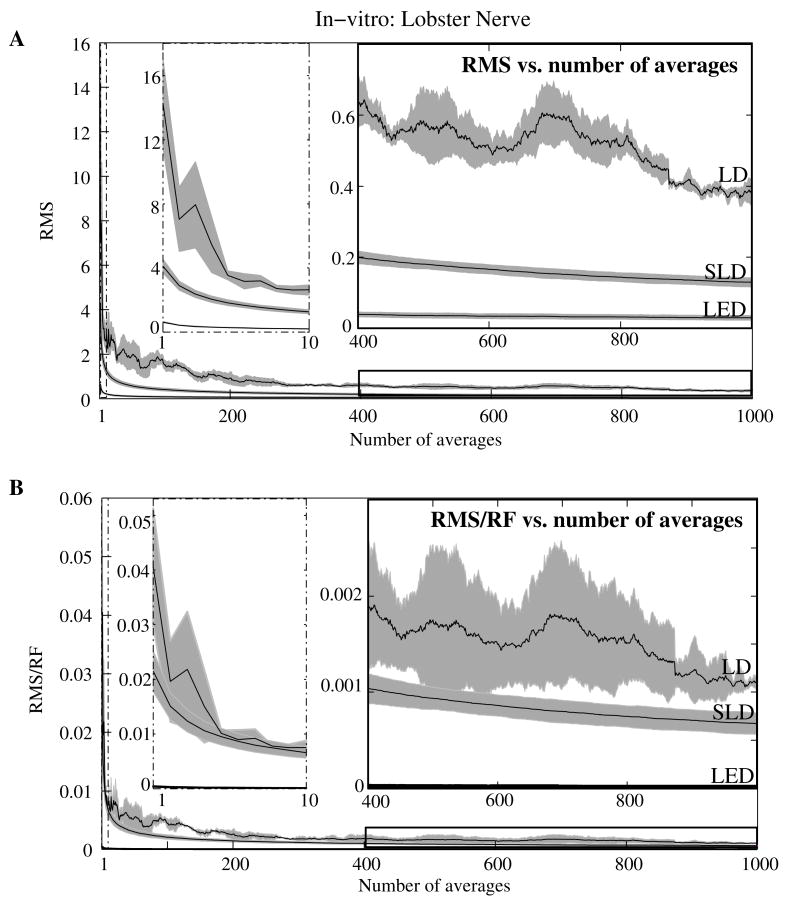
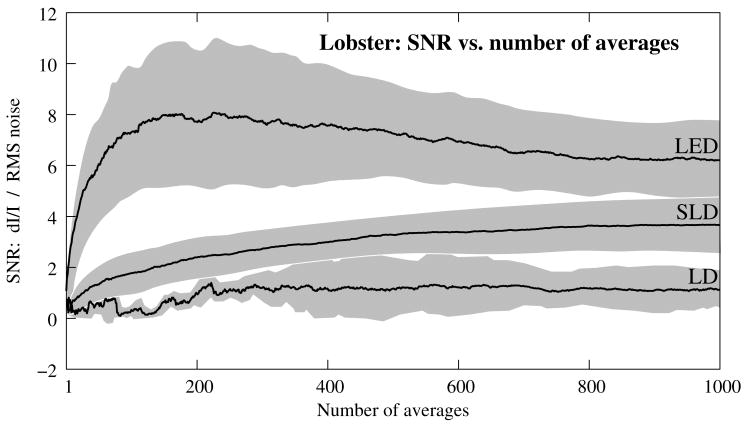
Figure 6A shows the mean and standard error of RMS noise calculated for each source across 1000 averages. RMS fell steeply in the first 100 averages, and then continued to decrease gradually from 200 to 1000 averages. RMS levels were greatest for LD, SLD, and LED data respectively (Fig. 6A); these differences were further exaggerated when the RMS levels were normalized to the intensity of each source (Fig. 6B). Figure 7 compares the mean signal−to−noise−ratio (SNR) for optical signals collected with the three sources across 1000 averages. The LED average SNRs increased proportional to the square root of the number of averages, peaked near 150 averages, and then gradually decreased with the degradation of the nerve over time. The SLD data had significantly lower SNRs than the LED data, and SNRs for LD data were significantly smaller than LED or SLD SNRs across 1000 averages. The LD SNRs was highly variable in the first 200 trials because the signal was significantly below the noise for the LD light source.
Figure 6.
RMS noise and RMS/RF across averages in−vitro from the stimulated lobster nerves. Panel A shows the mean and standard error for RMS noise in transmission birefringence signals for the LED, SLD, and LD across 1000 averages. LED RMS values are 0.62 for single pass and 0.029 at 1000 averages. The same in shown in panel B, except that the RMS has been normalized to the radiant flux (RF) of each source. LED RMS/RF values are 4.2 × 10−4 for single pass and 1.9 × 10−5 at 1000 averages. Each line represents n=3 nerves. The measured baseline radiant power in−vitro was 0.57–0.74 μW for the LD, 0.36–0.51 μW for the SLD, and 3.1–3.3 μW for the LED.
Figure 7.
The mean and standard error of SNRs (dI/I divided by RMS) of the in−vitro transmission birefringence changes from the stimulated lobster nerves for three light sources across 1000 averages. Each line represents the average of n=3 nerves. The black line is the mean, and the grey background illustrates standard error. The gradual decrease of the LED SNRs after the peak at 150 averages reflects the degradation of the nerve over time.
In−vivo paradigm
Unlike the in−vitro optical data, the in−vivo optical dI/I amplitude varied greatly from rat to rat depending on illumination and photodiode placement relative to the activated area (Fig. 8). Therefore, we have chosen to separately display mean SNR data from three rats rather than the mean and standard error across the three rats, to illustrate the variability in signals we observed between rats. Figure 8 displays the FFT analysis of rat optical data (no stimuli) before and after applying the cardiac filter. As was demonstrated by others (Gratton and Corballis, 1995; Franceschini and Boas, 2004), the cardiac filter reduced the cardiac peak at 2.9 Hz by a factor of 90. Similar to the in−vitro paradigm, the LD illumination intensity was limited by the dynamic range of the amplifier while the LED was driven to maximum intensity. The measured baseline radiant power for the rat scattered light data was 0.84 – 1.27 μW for the LD and 0.81 – 2.07 μW for the LED.
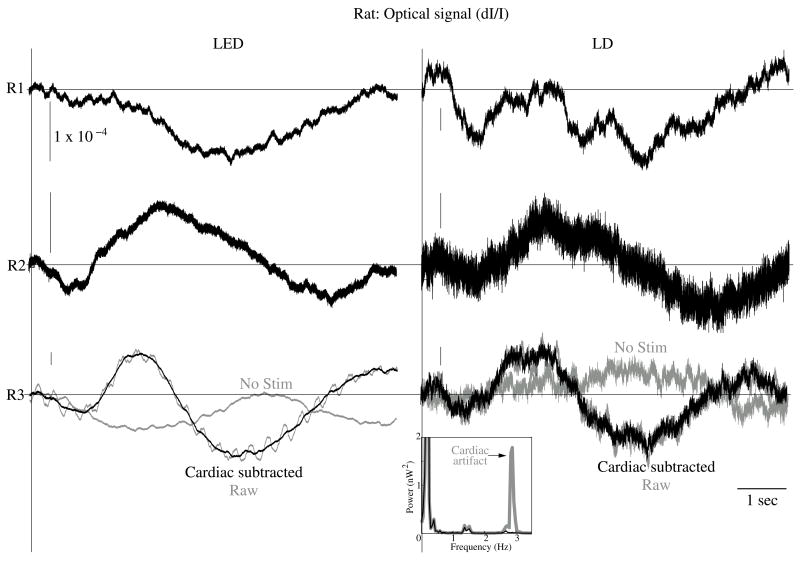
Figure 8.
In−vivo optical data during rat whisker twitches. Black traces show cardiac subtracted hemodynamic optical changes during and after whisker twitch stimulation (5 twitch burst at 10 Hz, 7.5s inter−stimulus intervals, 200 averages). Vertical lines indicate the beginning of the burst. Data is displayed for three rats: R1, R2, and R3 with LED (left column) and LD (right column) illumination. The gray traces for rat R3 show the pre−cardiac filtered signal (Raw), and without stimulation (No Stim). An inset FFT of the R3 data pre− (gray trace) and post− (black trace) cardiac filtering shows removal of the 2.8 Hz peak.
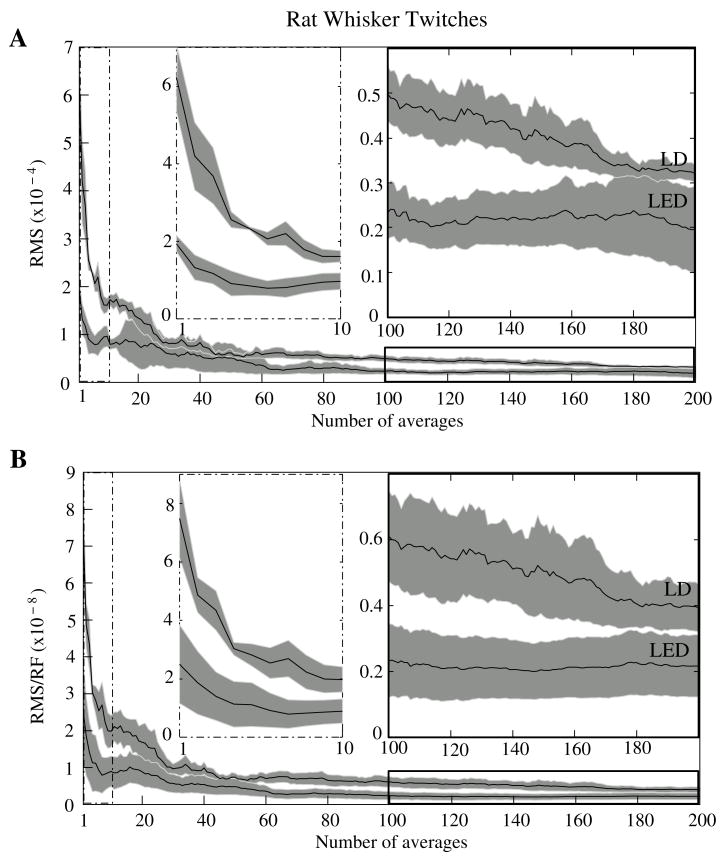
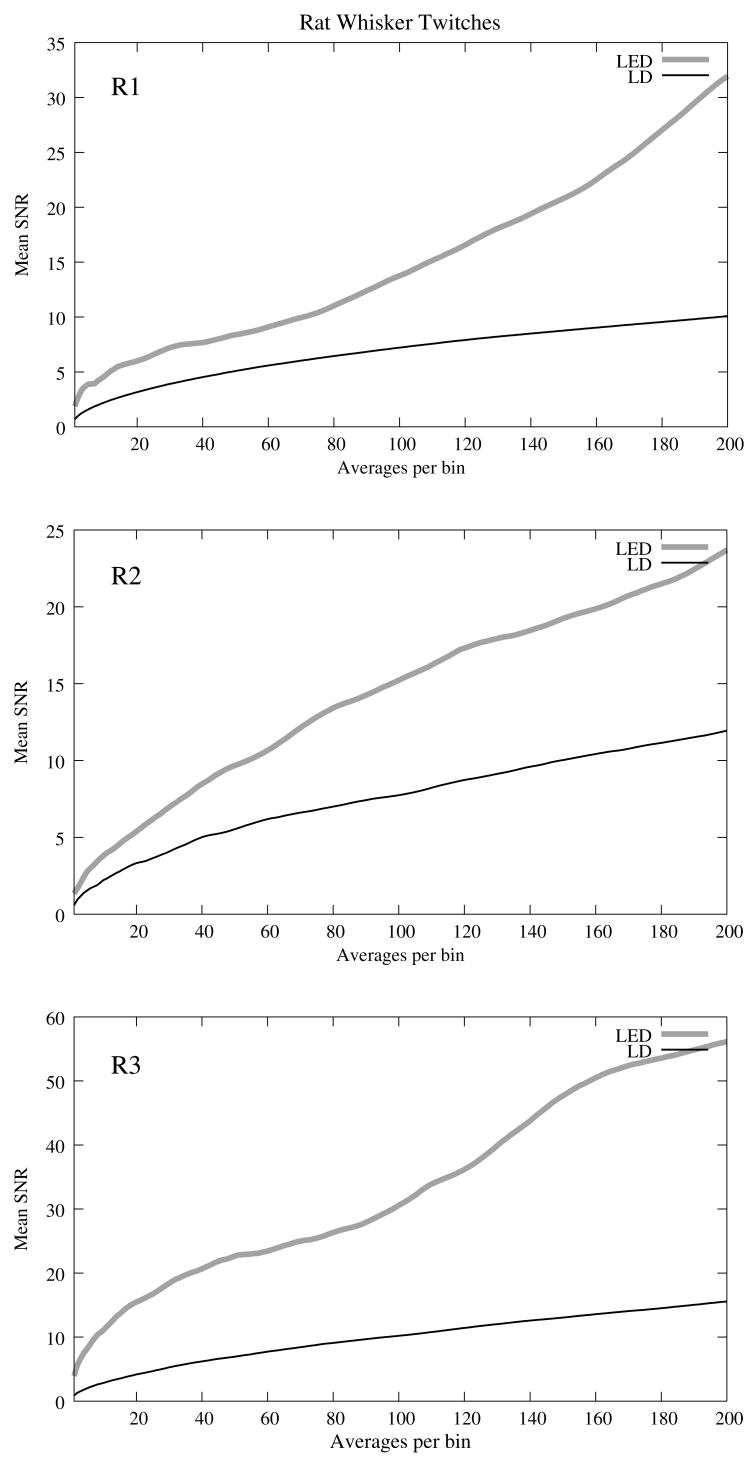
The optical signals featured a tri−phasic, hemodynamic response described in detail by several studies (i.e., Rector et al., 2001; Chen−Bee et al., 2007). Defining the signal amplitude as the difference between the first peak at ~3s and subsequent trough at ~5s, dI/I amplitude ranged from 0.9 to 7.7 × 10−4, or 60 to 900 μV. The lower left waveform in Figure 8 displays the optical data before and after cardiac subtraction. Figure 9A shows the average and standard error of RMS noise calculated across 200 averages. We divided each RMS value by the baseline light intensity to control for varied illumination intensities (Fig. 9B). RMS and RMS/RF for the LD were three times greater than LED RMS or RMS/RF in single pass trials, and LD noise continued to be significantly higher than LED noise across 200 averages. Figure 10 separately plots mean SNRs across number of averages per bin for three rats. In all cases, the mean SNRs obtained under LED illumination increased in fewer averages than LD SNRs (Figure 10).
Figure 9.
RMS noise across averages in−vivo during rat whisker twitches. Panel A shows the mean (black line) and standard error (gray background) for RMS noise in cardiac−subtracted hemodynamic signals for the LED and LD from 1 to 200 averages. The same is shown in Panel B, except that the RMS has been normalized to the radiant flux of each source. Measured baseline radiant power in−vivo was 0.84 – 1.27 μW for the LD and 0.81 – 2.07 μW for the LED.
Figure 10.
The SNRs for in−vivo optical data using LED and LD light sources during rat whisker twitches across number of averages per bin for rats R1, R2, and R3.
Discussion
The LED data had significantly higher SNRs in fewer averages than LD data for both the in−vitro and in−vivo recordings. Since instrument noise approached the signal size, it was important to reduce the noise sources as much as possible; but, the biggest gains in SNR were obtained by using LEDs (Table 1). In−vitro, the peak signal size was greater than the LED and photodiode noise contributions, yielding clear signals in few or no averages. The high noise of the LD necessitated slightly lower intensity illumination to stay within the dynamic range of the photodiode amplifier, and thus the signal size was smaller; however, the SNR was much smaller, requiring 100 or more averages to see the signal. Similarly in−vivo, signal size was smaller than total noise for both LED and LD trials, but SNRs for LED trials were higher because of lower noise.
Source−detector noise
At low intensities, the RMS/RF curves for all sources looked identical, rapidly decreasing with increasing radiant flux, which was expected as the relative contributions of shot noise and photodiode dark current decreased relative to other noise sources at higher intensities. When plotting RMS noise against radiant power, the laser’s sharp increase in RMS at 0.5 mW reflects noise introduced as the LD transitioned from LED mode to lasing. After the transition to lasing, the LD’s RMS remained significantly higher than LED or SLD RMS, implicating speckle as a possible disadvantage of coherent light sources. Although speckle interference patterns were not directly characterized in these experiments, the sharp increase in RMS noise concomitant with the laser’s transition from LED mode to lasing suggests that speckle arising from self interference of coherent light may have contributed significantly to the LD instrument noise. Additionally, our previous studies using CCD imaging technology (Rector et al., 2001) use LEDs specifically because we observed a significant speckle pattern in the images obtained with LDs.
Similar to the non−coherent LED, the noise profile of the semi−coherent SLD increased linearly with increasing radiant flux, indicating the absence of a transition point in this source. Above intensities dominated by shot noise, SLD RMS increased at a faster rate than LED RMS (Fig. 2A), suggesting that speckle noise may have also contributed significantly to the SLD noise profile or that this light source is less stable. The intensity−normalized FFTs of LD, SLD, and LD signals in−vitro (Fig. 3) showed that the LD had frequency power two orders of magnitude greater than the LED or SLD across all frequencies, again reflecting contributions from white noise sources such as speckle.
Physiological noise
For the in−vitro recordings, the similarity between the live nerve and dead nerve FFTs suggests that any cellular or molecular level noise contributions fell below the sensitivity of the recording method. In−vivo, two peaks present in the alive rat FFT and absent in the euthanized rat FFT corresponded to physiological noise generators: cardiac at 3.5 Hz and respiration at 1.0 Hz. Both LED and LD FFTs also had power in the low frequencies corresponding to 1/f noise; however, the low frequency density was greater in the alive rats than in euthanized rats, suggesting that other low frequency physiological sources may have contributed to the low frequencies. For example, in−vivo signals may also contain Mayer waves (f = 0.1 – 0.4 Hz, Mayhew et al., 1996), spontaneous oscillations of arterial pressure tightly coupled with the oscillations of efferent sympathetic nervous system activity (for review, see Julien, 2006). However, in optical recordings, 1/f noise dominates at these low frequencies, and we attempted to separate the effects of Mayer waves from the 1/f contribution by subtracting live and dead animal recordings for frequencies between 0 and 0.4 Hz (Table 1).
As LD intensity increased, so did the noise. Since the input range of the photodiode system is limited, we could only increase the laser diode intensity until the variability, perhaps due to the speckle noise, began to saturate the dynamic range of the photodiode system. Ideally, the brighter the light source, the bigger the SNR of the optical signal by overcoming shot noise limitations; however, the added noise of the LD counteracted gains over shot noise achieved with brighter illumination.
In−vitro paradigm
Since physiological noise sources were low in−vitro, higher SNRs were observed due to lower overall RMS noise. The LED SNR profile peaked at 150 averages, but then decreased over the next 850 averages because nerve health and corresponding signal amplitude decayed over time. Laser diode noise failed to increase with the square root of the number of trials like LED and SLD SNRs because below 200 averages, the signal size was significantly below LD noise levels, causing the SNRs in the 1–200 trial range to appear variable. The reduced light source noise of LEDs enabled signal recordings with higher SNRs in fewer averages, an advantage for limited−life, in−vitro preparations.
In−vivo paradigm
The high variability in the optical response amplitude across different rats likely resulted from variables such as the position of the photodiode over the whisker barrels and anesthesia depth. Like the in−vitro experiments, the higher SNRs of hemodynamic signals with the LED over the LD indicate that LEDs are a better light source for non−coherent neural recording applications. In spite of long integration times typically used to reduce speckle noise for the slow hemodynamic signals seen here, LEDs maintain a significant advantage, perhaps due to reduction of noise at low frequencies.
Conclusions
Laser diodes are a commonly used illumination source for in−vivo optical neural imaging and recording in freely moving chronic studies because of their high intensity illumination capabilities; however, we observed that the noise introduced by LDs counteracted benefits of high brightness when compared with low−noise LEDs. LED recordings produced roughly a 10−fold increase in SNRs in−vitro (Fig. 7) and 2− to 3−fold increase in−vivo (Fig. 10) over LD recordings. These gains are significant; however, methods must be pursued to further increase the contrast between intrinsic signals and noise, making single pass measurements more practical. Such efforts may include the development of brighter, more stable non−coherent sources and the application of birefringence recording and imaging in−vivo. Additionally, the LD intensity was limited by laser noise, with peak−to−peak fluctuations that saturated the dynamic range of the amplifiers, both in−vitro and in−vivo. LD SNRs could be improved by reducing the amplifier gain and powering the LD with higher light output. The will efecitvely reduce the proportional contribution of shot noise since it appears from Figure 2 that speckle remains constant as LD intensity increases. However, even when the laser was driven in its optimal range, as shown at the rightmost points in Figure 2, the LD was significantly noisier than the LED for both raw (Fig. 2A) and intensity normalized (Fig. 2B) RMS noise, possibly due to speckle.
We have previously investigated methods to partially decohere the light (also discussed in McKechnie, 1984). However, these efforts usually made speckle worse by breaking the coherent beam into more components, or the method both reduced intensity and increased complexity to the point that made lasers impractical for in−vivo measurements, especially in freely moving animals, further supporting the use of LEDs. Running a coherent source through a long, multimode fiber has been a useful method for reducing speckle noise in optical coherence tomography (Kim et al., 2005). Coupling through a short, multimode fiber propagated coherent light and speckle patterns, and coupling through a single mode fiber cut the intensity to a point which made in−vivo recording impractical. Once the coherent light from the single mode fiber interacted with tissue, the interference patterns began to appear again.
Since light is diffuse in tissue due to scattering, a large single channel detector with a 1 cm or greater diameter might prevent speckle patterns from crossing the edge of the detector and to prevent aperture effects. We used a large area detector for the lobster experiments, but this was impractical for in−vivo, freely moving animal studies. Additionally, speckle interference patterns vary both laterally (xy) and axially (z) in tissue with respect to the detector. Using a large single−channel detector could reduce consequences of detection aperture in x and y, but not in z. Thus, the most effective way to rid signals of speckle noise in scattering tissue is to illuminate with noncoherent light.
Independent of detection aperture effects, constructive interference of coherent light produces bright spots that can saturate points in the middle of the detector, resulting in an output that does not accurately reflect average intensity across the detector. Thus, when these saturating speckles move around the detector, the output will still fluctuate greatly because the photodetector does not accurately measure the total light intensity across the area. If a tightly focused beam of coherent light is not required for an optical measurement (i.e., near infrared diffuse optical tomography and scattered light imaging), non−coherent light is preferred because coherent light speckle may introduce excessive noise. Since low−coherence SLDs offer a bright and narrow beam alternative to highly coherent LDs, we included this light source in our analysis.
While mercury−, xenon−, and mercury−xenon arc lamps are commonly used for fluorescence and voltage sensitive dye applications in microscopy (Zochowski et al., 2000), for this study we selected LEDs over halogen light for a non−coherent source for in−vivo measurements because LEDs are more convenient, just as bright at narrow wavelengths (Foust et al., 2005), and more stable at low frequencies (Rumyantsev et al., 2004) than halogen sources. Some studies have also shown that LEDs have advantages over halogen sources for intrinsic and voltage sensitive dye recordings (Salzberg et al., 2005; Nishimura et al., 2006). LED technology improves each year and has created low power, efficient devices that may eventually exceed intensities possible by halogen and arc lamp sources for narrow wavelengths.
While lasers have been practical for detecting slow hemodynamic changes (i.e., Villringer and Chance, 1997; Boas, 2002), low noise sources such as LEDs are critical in advancing toward single pass measurements of rapid intrinsic optical signals in−vivo. For measurement of slow hemodynamic changes, long integration times (~100 ms) may average out the speckle noise generated in coherent laser beams. However, in measurements of rapid signals with short integration times (10 ms or faster), the speckle noise may swallow the small, transient changes or even the more robust hemodynamic changes recorded in single passes. A close look at the literature over the past year shows many systems use laser diodes for in−vivo chronic measurements of hemodynamic changes. Currently available commercial devices also use laser diodes (e.g., Hamamatsu NIRO−200, Hitachi ETG−4000). Several investigators use halogen sources (e.g., Shtoyerman et al., 2000; Brett−Green et al., 2001; Roe, 2007) for fixed imaging of acute preparations, or restrained preparations with windows. Only recently have some investigators published work with LEDs (e.g., Chen−Bee et al., 2007; Zeff et al., 2007). Recent studies utilizing LEDs in−vivo have achieved some of the most robust signals ever observed, presumably due to the advantages of LEDs highlighted by the present study and by Salzberg et al. (2005).
For freely moving human and animal studies (e.g., Chance et al., 1998; Gratton and Fabiani, 2003), lasers have been popular because LDs with output powers in the FDA approved range (5–30 mW) can be modulated at high frequencies for phase measurements. In the current study, all three light sources could produce about the same output intensity (~4mW, Fig 2). Indeed, there are lasers that are brighter than our LEDs, however, LEDs also share rapid modulation capabilities and are becoming as bright (10−60 mW) as class IIIb lasers in the near−infrared wavelengths, which is encouraging for in−vivo work as light in this frequency range penetrates skin and skull and is scattered by neural tissue (Eggert and Blazek, 1987). For comparison purposes, we used the brightest LED available at the wavelength of our laser diode (~660 nm), as this wavelength was optimal for detecting the hemodynamic changes in−vivo. Brighter near infrared LEDs are currently available, and our preliminary work with these LEDs indicates that they maintain low noise characteristics.
There are several factors that recommend LEDs as practical, inexpensive, and low−noise alternatives to coherent sources for neural recording applications. The sharp increase in RMS noise at lasing threshold suggests that speckle noise contributed significantly to the LD’s lower SNRs. LEDs exhibit greater, low−frequency stability than lasers and halogen sources (Rumyantsev et al., 2004; Salzberg et al., 2005). We tried using both voltage and current sources to drive the LEDs and LDs with no differences in the RMS noise levels. A current regulated power source would minimize very slow variations in intensity due to temperature and drift, but these effects were not significant in our studies. LEDs do not normally require temperature regulation, and can be driven with low power voltage sources, although current sources and temperature regulation may be preferred for applications requiring long−term stability. Many techniques use fiber coupled light from a variety of different sources including halogen, xenon and lasers for delivering photons directly to the animal. However, fiber coupling is bulky and restrictive to animal movement, especially if the animal is as small as a rat or a mouse. Additionally, movement of the fiber results in additional noise in the illumination intensity due to changing photon paths through the fiber and changes in the coupling of the fiber to the animal. In contrast, LEDs are inexpensive, easy to use, and can be easily carried by animal and human subjects.
Acknowledgments
This research was supported by NIH MH60263, the Murdock Foundation, and the WM Keck Foundation. JLS was supported by the Poncin Foundation.
References
- Boas DA, Franceschini MA, Dunn AK, Strangman G. Noninvasive imaging of cerebral activation with diffuse optical tomography. In: Frostig RD, editor. In Vivo Optical Imaging of Brain Function. CRC Press; Boca Raton: 2002. pp. 193–221. [PubMed] [Google Scholar]
- Brett−Green BA, Chen−Bee CH, Frostig RD. Comparing the functional representations of central and border whiskers in rat primary somatosensory cortex. J Neurosci. 2001;21(24):9944–9954. doi: 10.1523/JNEUROSCI.21-24-09944.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carter KM, George JS, Rector DM. Simultaneous birefringence and scattered light measurements reveal anatomical features in isolated crustacean nerve. J Neurosci Meth. 2004;135(1−2):9–16. doi: 10.1016/j.jneumeth.2003.11.010. [DOI] [PubMed] [Google Scholar]
- Chance B, Cope M, Gratton E, Ramanujam N, Tromberg B. Phase measurement of light absorption and scatter in human tissue. Rev Sci Instrum. 1998;69:3457–3481. [Google Scholar]
- Chen−Bee CH, Agoncillo T, Xiong Y, Frostig RD. The triphasic intrinsic signal: implications for functional imaging. J Neurosci. 2007;27(17):4572–4586. doi: 10.1523/JNEUROSCI.0326-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen LB, Keynes RD, Hille B. Light scattering and birefringence changes during nerve activation. Nature. 1968;218(5140):438–441. doi: 10.1038/218438a0. [DOI] [PubMed] [Google Scholar]
- Cohen LB. Changes in neuron structure during action potential propagation and synaptic transmission. Physiol Rev. 1973;53:373–418. doi: 10.1152/physrev.1973.53.2.373. [DOI] [PubMed] [Google Scholar]
- Considine PS. Effects of coherence on imaging systems. J Opt Soc Am. 1966;56:1001–1009. [Google Scholar]
- Dunn AK, Bolay H, Moskowitz MA, Boas DA. Dynamic imaging of cerebral blood flow using laser speckle. J Cereb Blood Flow Metab. 2001;21(3):195–201. doi: 10.1097/00004647-200103000-00002. [DOI] [PubMed] [Google Scholar]
- Eggert HR, Blazek V. Optical properties of human brain tissue, meninges, and brain tumors in the spectral range of 200 to 900 nm. Neurosurgery. 1987;21(4):459–464. doi: 10.1227/00006123-198710000-00003. [DOI] [PubMed] [Google Scholar]
- Foust AJ, Beiu RM, Rector DM. Optimized birefringence changes during isolated nerve activation. Appl Opt. 2005;44(11):2008–2012. doi: 10.1364/ao.44.002008. [DOI] [PubMed] [Google Scholar]
- Foust AJ, Rector DM. Optically teasing apart neural swelling and depolarization. Neuroscience. 2007;145(3):887–899. doi: 10.1016/j.neuroscience.2006.12.068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Franceschini MA, Boas DA. Noninvasive measurement of neuronal activity with near−infrared optical imaging. NeuroImage. 2004;21(1):372–386. doi: 10.1016/j.neuroimage.2003.09.040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Furusawa K. The depolarization of crustacean nerve by stimulation or oxygen want. J Physiol. 1929;67(4):325–342. doi: 10.1113/jphysiol.1929.sp002573. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gratton G, Corballis PM. Removing the heart from the brain: Compensation for the pulse artifact in the photon migration signal. Psychophysiology. 1995;32(3):292–299. doi: 10.1111/j.1469-8986.1995.tb02958.x. [DOI] [PubMed] [Google Scholar]
- Gratton G, Fabiani M. The event−related optical signal (EROS) in visual cortex: replicability, consistency, localization, and resolution. Psychophysiology. 2003;40(4):561–571. doi: 10.1111/1469-8986.00058. [DOI] [PubMed] [Google Scholar]
- Horowitz P, Hill W. The Art of Electronics. 2. Cambridge University Press; Cambridge, MA: 1989. pp. 428–455. [Google Scholar]
- Julien C. The enigma of Mayer waves: facts and models. Cardiovasc Res. 2006;70:12–21. doi: 10.1016/j.cardiores.2005.11.008. [DOI] [PubMed] [Google Scholar]
- Kim E, Oh S, Oh J, Milner TE. Optical coherence tomography speckle reduction by a partially spatially coherent source. J Biomed Opt. 2005;10:064034-1–064034-9. doi: 10.1117/1.2138031. [DOI] [PubMed] [Google Scholar]
- Maclin EL, Low KA, Sable J, Fabiani M, Gratton G. The event−related optical signal to electrical stimulation of the median nerve. NeuroImage. 2004;21(4):1798–1804. doi: 10.1016/j.neuroimage.2003.11.019. [DOI] [PubMed] [Google Scholar]
- Mayhew JE, Askew S, Zheng Y, Porrill J, Westby GWM, Redgrave P, Rector DM, Harper RM. Cerebral vasomotion: a 0.1−Hz oscillation in reflected light imaging of neural activity. NeuroImage. 1996;4(3):183–193. doi: 10.1006/nimg.1996.0069. [DOI] [PubMed] [Google Scholar]
- McKechnie TS. Speckle Reduction. In: Dainty JC, editor. Laser Speckle and Related Phenomena. 4. Springer−Verlag; Heidelberg, Germany: 1984. pp. 123–170. [Google Scholar]
- Nishimura M, Shirasawa H, Song W−J. A light−emitting diode light source for imaging of neural activities with voltage−sensitive dyes. Neurosci Res. 2006;54(3):230–234. doi: 10.1016/j.neures.2005.12.002. [DOI] [PubMed] [Google Scholar]
- Rector DM, Carter KM, Volegov PL, George JS. Spatio−temporal mapping of rat whisker barrels with fast scattered light signals. NeuroImage. 2005;26(2):619–627. doi: 10.1016/j.neuroimage.2005.02.030. [DOI] [PubMed] [Google Scholar]
- Rector DM, Rogers RF, Schwaber JS, Harper RM, George JS. Scattered−light imaging in vivo tracks fast and slow processes of neurophysiological activation. NeuroImage. 2001;14(5):977–994. doi: 10.1006/nimg.2001.0897. [DOI] [PubMed] [Google Scholar]
- Roe AW. Long−term optical imaging of intrinsic signal in anesthetized and awake monkeys. Appl Opt. 2007;46(10):1872–1880. doi: 10.1364/ao.46.001872. [DOI] [PubMed] [Google Scholar]
- Rigden JD, Gordon EI. The granularity of scattered optical maser light. Proc IRE. 1962;50:2367–2368. [Google Scholar]
- Rumyantsev SL, Shur MS, Bilenko Y, Kosterin PV, Salzberg BM. Low frequency noise and long−term stability of noncoherent light sources. J Appl Phys. 2004;96:966–969. [Google Scholar]
- Salzberg BM, Kosterin PV, Muschol M, Obaid AL, Rumyantsev SL, Bilenko Y, Shur MS. An ultra−stable non−coherent light source for optical measurements in neuroscience and cell physiology. J Neurosci Meth. 2005;141(1):165–169. doi: 10.1016/j.jneumeth.2004.06.009. [DOI] [PubMed] [Google Scholar]
- Schmitt JM, Xiang SH, Yung KM. Speckle in optical coherence tomography. J Biomed Opt. 1999;4:95–105. doi: 10.1117/1.429925. [DOI] [PubMed] [Google Scholar]
- Shtoyerman E, Arieli A, Slovin H, Vanzetta I, Grinvald A. Long−term optical imaging and spectroscopy reveal mechanisms underlying the intrinsic signal and stability of cortical mats in V1 of behaving monkeys. J Neurosci. 2000;20(21):8111–8121. doi: 10.1523/JNEUROSCI.20-21-08111.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Steinbrink J, Kohl M, Obrig H, Curio G, Syre F, Thomas F, Wabnitz H, Rinneberg H, Villringer A. Somatosensory evoked fast optical intensity changes detected non−invasively in the adult human head. Neurosci Lett. 2000;291(2):105–108. doi: 10.1016/s0304-3940(00)01395-1. [DOI] [PubMed] [Google Scholar]
- Tasaki I, Byrne PM. Rapid structural changes in nerve fibers evoked by electrical current pulses. Biochem Biophys Res Commun. 1992;188:559–564. doi: 10.1016/0006-291x(92)91092-5. [DOI] [PubMed] [Google Scholar]
- Tasaki I, Watanabe A, Sandlin R, Carnay L. Changes in fluorescence, turbidity, and birefringence associated with nerve excitation. Proc Natl Acad Sci U S A. 1968;61(3):883–888. doi: 10.1073/pnas.61.3.883. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Villringer A, Chance B. Non−invasive optical spectroscopy and imaging of human brain function. Trends Neurosci. 1997;20(10):435–442. doi: 10.1016/s0166-2236(97)01132-6. [DOI] [PubMed] [Google Scholar]
- Yao XC, Foust A, Rector DM, Barrowes B, George JS. Cross−polarized reflected light measurement of fast optical responses associated with neural activation. Biophys J. 2005;88:4170–4177. doi: 10.1529/biophysj.104.052506. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yao XC, Rector DM, George JS. Optical lever recording of displacements from activated lobster nerve bundles and Nitella internodes. Appl Opt. 42:2972–2978. doi: 10.1364/ao.42.002972. [DOI] [PubMed] [Google Scholar]
- Zeff BW, White BR, Dehghani H, Schlaggar BL, Culver JP. Retinotopic mapping of adult human visual cortex with high−density diffuse optical tomography. Proc Natl Acad Sci U S A. 2007;104(29):12169–12174. doi: 10.1073/pnas.0611266104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zochowski M, Wachowiak M, Falk CX, Cohen LB, Lam Y−W, Antic S, Zecevic D. Imaging membrane potential with voltage−sensitive dyes. Biol Bull. 2000;198(1):1–21. doi: 10.2307/1542798. [DOI] [PubMed] [Google Scholar]